Single-Phase Variable Reluctance Motor Design using Particle Swarm Optimization
Latin-American Journal of Computing, vol. 11, núm. 1, pp. 56-65, 2024
Escuela Politécnica Nacional
Recepción: 16 Marzo 2023
Aprobación: 12 Mayo 2023

Abstract: Electrical engines are built under electromagnetism concepts to create mechanical power, those can be seen as simple machines, as it depends on reluctance, even being called as “reluctance motor”, what gives this engine the possibility of being widely used for many purposes. The main objective of this research is to minimize copper losses of a single-phase 6x6 variable reluctance synchronous motor. For that, a Particle Swarm Optimization (PSO) algorithm will be used to obtain the optimum configuration through the Finite Elements Method (FEM). In this context, electric motor design equations were dimensioned based on similar machines. The next procedure was to use FEMM (Finite Element Method Magnetics) software, that allows the magnetic flow density analysis inside the motor air gap. Finally, it is noteworthy that the copper losses results were analyzed before and after the variable reluctance motor optimization with computational tools.
Keywords: single-phase reluctance motor, finite element method, particle swarm optimization.
I. INTRODUCTION
Variable reluctance synchronous motors (VRSMs) are common engines with simple building aspects low computational and financial costs, but with a wide range of applications. These are the main reasons why reference [1] considered these motors competitive. The VRSMs dual capacity of acting like a motor and a generator, which avoids high inrush currents, reduce costs and operates under constant rotation, that are aspects of engines without windings and magnets and with a single source of incitation applied to the stator windings, what intends to minimize all the resistive losses of machinery winding that occur in the stator current flow.
Therefore, it is possible to estimate an optimal motor, based on specifications of power and size of a previous model [2]. In this context, the research objective is to minimize the copper losses, of a variable reluctance motor (VRM), by using the particle swarm method (PSO algorithm). This way, dimension parameters were used to design the original motor and the optimum motor was designed after applying the finite elements method. Finally, after the optimization process, copper losses and magnetic flow densities were evaluated and the results of both original and optimum motors were compared
II. LITERATURE REVIEW
This section will be divided in three parts: Particle Swarm Optimization, Finite Elements Method and Variable Reluctance Motor Design.
A. Swarm Particle Optimization
The PSO algorithm is a computational method that aims to optimize a problem through a proceeding that generates a sequence of approximate solutions that at each interaction, tend to converge to an optimum solution [3]. Comparative studies about the PSO (Particle Swarm Optimization) aspects were inspired on animal behavior, where each individual, of an equally dispersed population inside the problem area, efficiencies were compared. At each executed interaction, the individuals tend to group in smaller spaces around the best solution, therefore, an inertia constant can be estimated, based on the group tendency to find the best solution and considering each individual's best solution.
After a sequence of interactions performed by each individual, the optimum solution for the problem is found [4]. Next the algorithm implementation steps:
Initially, each swarm particle has a
position  inside the search space and the speed
inside the search space and the speed 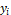 ,
where the positions are automatically generated;
,
where the positions are automatically generated;
For each swarm particle executed
interaction, the particle position 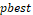 and
the group position
and
the group position 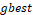 are updated, in case they are better than the
previous.
are updated, in case they are better than the
previous.
During the
interaction, the speeds and positions of each swarm particle are updated by the
Equations 1 and 2, respectively, to obtain the new position: 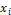 ;
;
 (1)
(1)
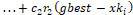
 (2)
(2)
where 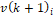 is the updated term for particle speed,
is the updated term for particle speed, 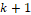 is the actual instant,
is the actual instant, 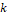 is the previous instant,
is the previous instant,  is the algorithm inertia constant,
is the algorithm inertia constant, 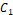 is the individual acceleration coefficient
responsible for controlling the particle movement distance in one interaction,
is the individual acceleration coefficient
responsible for controlling the particle movement distance in one interaction, 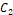 is the group acceleration coefficient,
responsible for controlling a particle movement distance in one interaction,
is the group acceleration coefficient,
responsible for controlling a particle movement distance in one interaction,  is the best particle position, is the most visited position by the particles,
is the best particle position, is the most visited position by the particles, 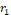 and
and  are aleatory numbers inside the research space
[0,1],
are aleatory numbers inside the research space
[0,1], 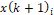 is the new particle position,
is the new particle position, 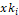 is the previous particle position. So, if the stop criterion is not verified,
the algorithm returns to Step 2, to start the next interaction, otherwise,
is the previous particle position. So, if the stop criterion is not verified,
the algorithm returns to Step 2, to start the next interaction, otherwise, 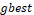 will be used as the intended solution.
will be used as the intended solution.
It is possible to understand that the particle swarm optimization has 3 (three) main steps, knowing the number of interactions is the factor that determines the number of times where the system was evaluated and updated. The main steps, for that, are the following:
Start: set the parameters and the
population (initialize 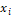 and
and 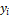 randomly for each particle/individual);
randomly for each particle/individual);
Evaluate: analyze the actual
position of each particle: 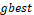 and
and 
Update: update speed and position of
each particle ( 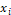 ,
, 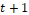 and
and  ,
, 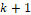 ).
).
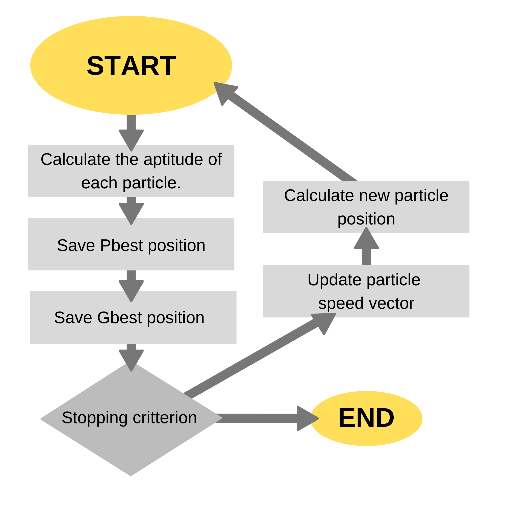
Figure 1 represents the flowchart with the description of the adopted method. This way, it can be considered that the particle swarm optimization comes partially from concepts and mathematical operators for implementation. During the computational process becomes fast and of low cost in terms of speed and memory.
B. Finite Elements Method
The Finite Elements Method (FEM) is a set of different numerical methods that approximate problem solutions with Partial or Ordinary Differential Equations (PDE and ODE, respectively) through a geometry subdivision in smaller elements, known as finite elements. Knowing that the exact solution for this problem is very similar to the result of the approximate solution found through this method [5], [6], [7].
The magnetostatic design equations for magnetic circuits operation are based on Ampère and Gauss generalized laws, and they can be described as:

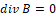 (4)
(4)Where: H is the magnetic field (A/m), J is
the current superficial density 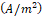 , D is the electrical
induction
, D is the electrical
induction 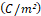 , and B is the
magnetic flow density (T).
, and B is the
magnetic flow density (T).
A magnetic field can be formed by a current in conductive materials, and due to the local form of the building relations, it is known that the flow and the magnetic field H are related, because the final magnetic permeability μ product with the field is, by definition, the magnetic flow density B:

The magnetic permeability describes the degree of opposition of a material to the passage of a flow [6]. In general, the relative permeability of a substance, related to the air permeability, is given by:

C. Single-Phase Variable Reluctance Synchronous Motor Design
Design equations are an essential part of the optimization processes, once the motor size affects the current flow and its distribution along the engine parts. Figure 2 shows the main engine dimensions that must be determined in order to obtain the rotor and stator projects.
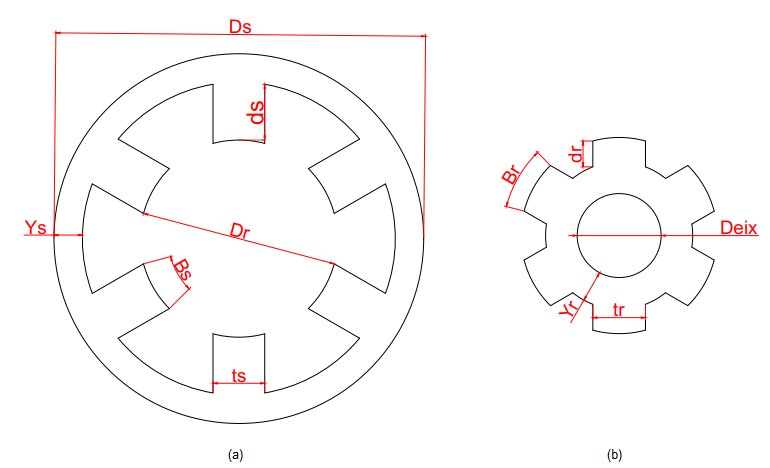
The rotor diameter can be calculated through the input power.
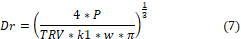
where P is the input power; k1 is a format constant; TRV is the engine volume set; w is a conversion unit from RPM to rad/s [8]. And then, the pile length (L) can be considered a multiple of the rotor diameter (Dr):

Later, the number of poles inside the stator (Nps), will define the poles angles (Bs):

An important consideration is that the smaller the engine air gap, the highest the current flow. With this information, reference [9] considers that the engine air gap size must be close to 0,50% of the rotor diameter. Another possible consideration is to work under the percentage of 0,25%:
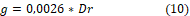
The engine breech can be considered as the difference between the rotor diameter and the poles, and it can stand half the current that goes through the poles. Its size is defined by:

Relations between the rotor diameter (Dr) and the external stator diameter (Ds) must be inside an interval of 0.40 to 0.70. The following relation adopted a standard of 0.55 for the relation previously defined [1]:

The poles width (ts) are another important information, that happens because the flow passes intensely through this material. This measure can be calculated using:
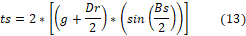
By adding the stator pole width to twice the size of the engine air gap length, the rotor pole width can be found, as can be seen:
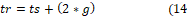
Besides that, the rotor polar arc (Br) is given by:

A crucial information to the motor proportions is the rotor pole height (dr), that can be obtained by:

And another important measure is the engine breech height (Ys), that can be calculated by using the width of the rotor pole (tr) with an addition of 20 to 40%. In this case, the chosen addition was of 20% [9].

After calculating the rotor diameter, its height and breech, the axis diameter (Deix) can be calculated:

And the stator pole height (ds) can be found with:

However, the number of turns, per phase (Ne), is a result of the interaction between the saturated magnetic flow density (Bsat), the peak current (Ip) and the engine air gap width, as can be seen in the equation:
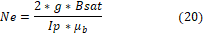
Given that the wire that must be used to form the turns has its transversal section (ac) calculated after the peak current divided by the maximum current flow (Jc) and the square root of the number of phases (q):

This calculus can provide the copper loss results. The first step to understand the losses is to calculate the coil resistance:
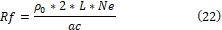
where 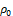 is the copper resistivity and ac the
wire transversal section, what allows finding the losses of copper (Pcopper)
and total (Ptotal). The first one is calculated by multiplying the coil
resistivity (Rf) by any current (
is the copper resistivity and ac the
wire transversal section, what allows finding the losses of copper (Pcopper)
and total (Ptotal). The first one is calculated by multiplying the coil
resistivity (Rf) by any current ( 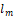 ) that passes through the motor.
The total losses are copper losses in all wire turns.
) that passes through the motor.
The total losses are copper losses in all wire turns.

At the resistive losses (or copper losses), as in the total losses, the results are estimates that can work as a good comparison between analytical and simulated values.
III. METHODOLOGY
A literature review over mathematical models for electrical motors design will be used for modeling the single-phase VRMs. With these models, a PSO algorithm will be executed under the assumptions of the finite element method. The main aim with this procedure is to reduce the copper loss inside this equipment.
Therefore, the simulations will happen through a software that develops numerical models by using electromagnetism concepts. For better understanding about purposes of this text, some items must be highlighted:
In this context, the intention is to write the necessary equations to minimize the single-phase variable reluctance motor copper loss and, later, evaluate through FEMM software the magnetic flow density in order to achieve the research objectives.
IV. DEVELOPMENT AND DISCUSSION
In this section, discussions and results will be presented in three parts: original motor, optimization and optimum motor.
A. Original Motor
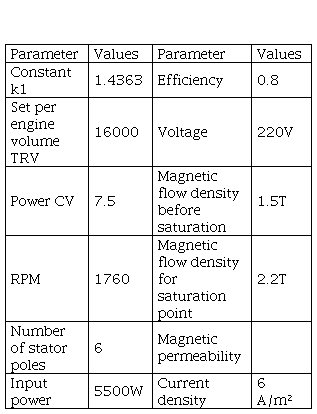
To start comprehending the problem, a single-phase motor with 6 poles was chosen, with the specifications listed on Table I. This is a model by WEG that has characteristics of an induction motor.
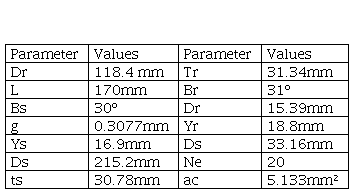
Therefore, a MATLAB algorithm was developed to generate the dimensions of the 6 poles variable reluctance motor stator and rotor, as well as its coils, which took to the construction of the motor via AUTOCAD with a few adjusts, and later exporting this model to FEMM, setting materials and borders. In this way, just enter the file menu and click import .dxf finally open the CAD Drawing file and the drawing will be imported into FEMM. After developing the motor project equations and running the algorithm, the main parameters were found, as shown in Table II.
In order to verify the electromagnetic device, the peak current of 53.34 A is considered, this current was obtained by the sum of the nominal current with the efficient nominal current. This means that the magnetic flow density applied to the peak current (Ip) must not have a module superior to the material magnetic flow saturation density.
The steel saturation is, approximately, of 2.2T. Figures 3 and 4 represent the motor magnetic flow density and the highest value is close to 2.2T, although inferior. In general, single-phase VRMs work close to saturation, if compared to other motors, besides that, the motor performance is still good.
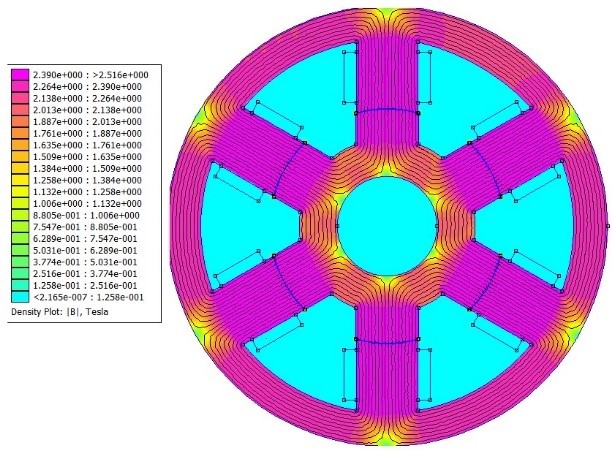
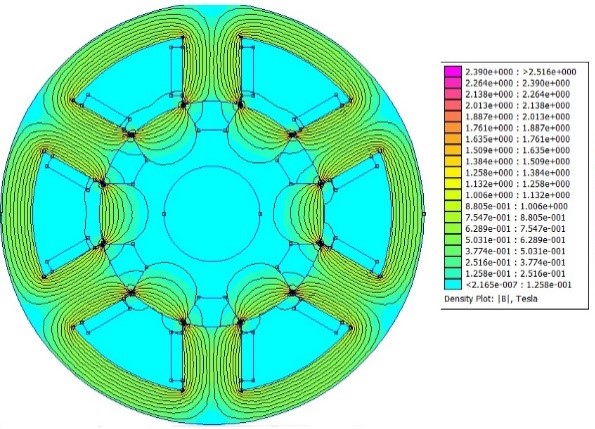
After computational simulation through FEMM software, the total copper loss was found for a peak current of 190.54W, with the analytical solution, the result is 194.52W. Therefore, the error between methods was of 2.04 %. It is concluded that with the increase of input current, the magnetic flow density is increased inside the motor air gap with a proportional relation.
The total losses had a significant scale value, which means specific optimizations will be required to reduce the power loss in the windings.
B. Optimization
Following the PSO steps and considering the Equation 24 as the objective function (OF) of the problem, the objective becomes minimizing the single-phase variable reluctance motor copper losses. Some of the variables, parameters and limits were listed on Table III.
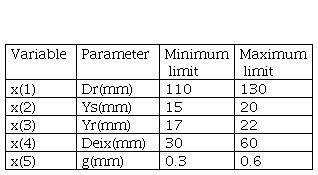
The Objective Function will be Equation 24, in addition, we used lateral constraints that delimit a range of variation for each design variable. It is worth mentioning some settings of the PSO algorithm, such as:
Population size: 50;
Generations number: 50;
Inertia weight: 1;
Inertia weight damping ratio: 0.99;
Personal learning coefficient: 1.5;
Global learning: 2.0.
Thus, the processing time was less than five minutes and the computational cost was also low, followed the settings of the notebook used in the optimization: i5, 10GB and SSD 256GB.
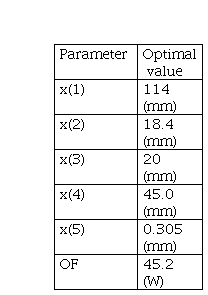
After executing the algorithm, other two parameters were described, as well as the objective function, as seen on Table IV, where a saturation current of 27.65A and the copper losses were considered as 58.59W.
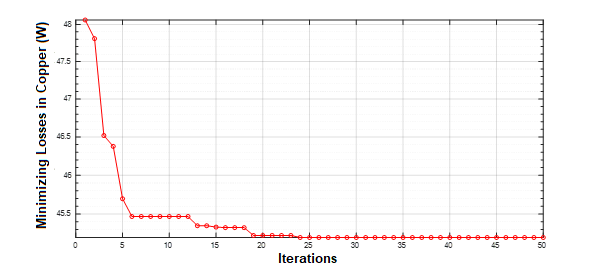
In general lines, the problem is based on a mono-objective function, that with the optimization, reduced the copper loss in 29.62% when using the saturation current, as can be seen in Figure 5.
C. Optimum Motor
After running the algorithm 10 times in the test, it was possible to observe the standard deviation and mean of the design variables and the objective function. Table V shows the details of the executions, showing the optimum motor parameters.
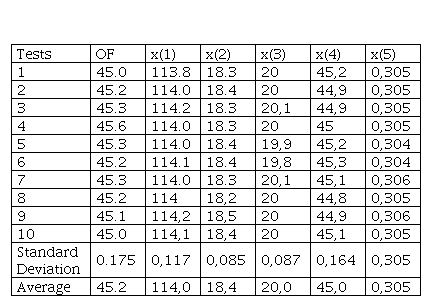
An interesting observation is that the measures were reduced, except for the parameters (Yr) and (Ys), the rotor and stator breeches had a measurement increase.
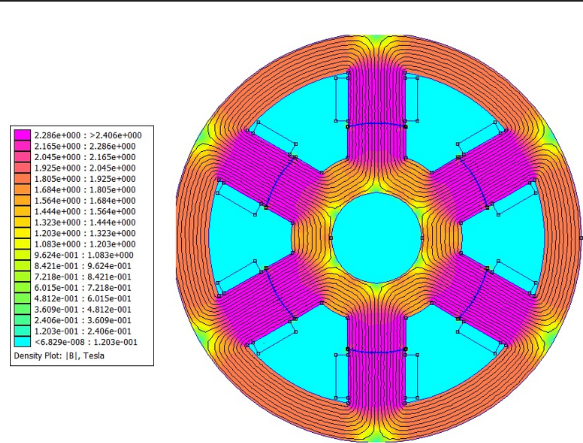
Figures 6 and 7 indicate the magnetic flow density inside the VRM with the peak current after the optimization process.
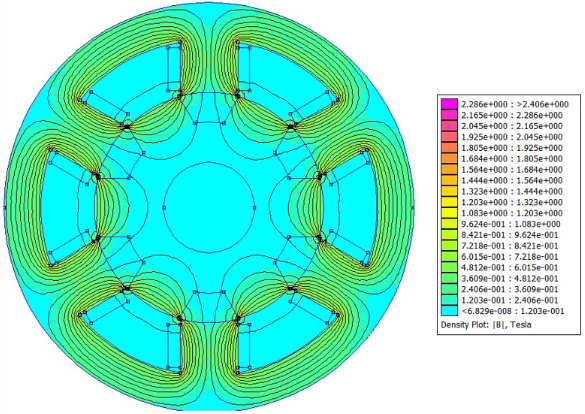
After the optimum motor computational simulation with FEMM software, a total copper loss for a peak current of 183.63W was found. With analytic calculus, the value was 180.78W. This means that the error between analytical and simulated results for the optimum motor is of 1.57%. It can be concluded that the magnetic flow density on the motor after the optimization reduced, what means they are under the material saturation of 2.2T. In this context, it can be observed that the PSO algorithm is effective for the convergence of the mono-objective functions, what means that the total copper loss was successfully reduced.
D. Magnetic Flow Density Analysis
The single-phase variable reluctance motors, in general, work close to the saturation, when compared to other motors, even so, their performance is good. Figures 8 and 9 represent the total airgap length when submitted to the peak current, in the original and the optimized motor.
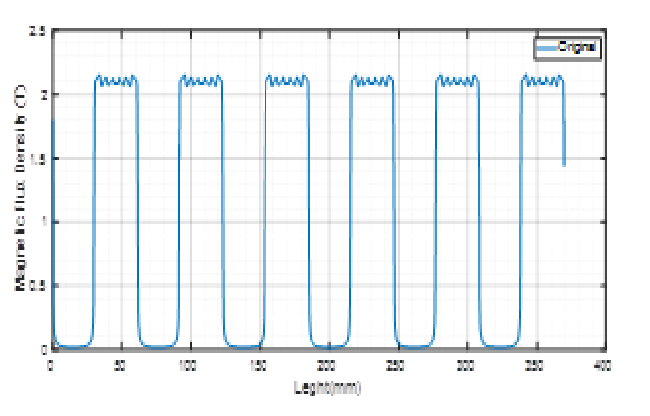
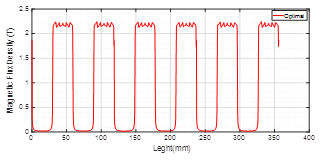
As the magnetic flow density in the airgap to a motor on its original and optimal unalignment, the flow density is low, therefore the data was not proven through graphics, but the flow gets thinner on the gap between stator and rotor. It can be concluded that with the increase of the input current, there is an increase to the magnetic flow inside the airgap of the single phase VRM, therefore, they have a directly proportional relation. The same behavior can be observed with the copper losses. In general, simulations stay under the iron saturation value of 2.2T, when simulated until the peak current. During the optimization procedure, the copper loss was reduced and the magnetic flow density in the airgap was under the saturation point.
V. CONCLUSIONS
Reducing the copper loss and reducing magnetic flow density, guarantees efficiency improvement during the motor operation, in a way that the equipment can convert energy more efficiently. Comparing the properties between both motors: the original and the optimum, it can be considered that the optimization was successful, once the main objective of reducing copper loss was achieved, as well as the ideal measures were presented. It might be necessary to take into consideration the optimization of other parameters, since not all the motor measures were reduced, but some even had some increase. This is an important factor for further research.
Agradecimientos
The authors thank the Institutional Program of Scientific Initiation Scholarships of the Federal University of Paraná and the National Council for Scientific and Technological Development (CNPq) for their support for the development of this research and Coordination for the Improvement of Higher Education Personnel (CAPES).
References
[1] A. E. Fitzgerald, C. Kingsley Jr. y S. Umans, Máquinas elétricas, 7th ed., Porto Alegre, Brazil: Bookman, 2014.
[2] G. Machado, «Projeto de motor a relutância variável e simulação utilizando o método dos elementos finitos (Electrical Engineering Monography),» Federal University of Uberlândia, Uberlândia-MG, Brazil, 2020.
[3] J. Kennedy y R. Eberhart, Swarm Intelligence, San Francisco, US: Morgan Kaufmann Publishers, 2001.
[4] F. Lobato, V. Steffen Jr. y A. Silva Neto, Técnicas de Inteligência Computacional com Aplicações em Problemas Inversos de Engenharia, Curitiba-PR, Brazil: Omnipax, 2014.
[5] P. Dular, «Modélisation du champ magnétique et des courants induits dans des systems tridimensionnels non linéaires (Doctorate thesis),» Université de Liége, Belgium, 1996.
[6] J. Malagoli, «Otimização multiobjetivo aplicada aos motores de indução validada via elementos finitos (Doctorate thesis),» Federal University of Uberlândia, Uberlândia-MG, Brazil, 2016.
[7] M. Luz, «Desenvolvimento de um software para cálculo de campos eletromagnéticos 3D utilizando elementos de aresta, levando em conta o movimento e o circuito de alimentação (Doctorate thesis),» Federal University of Santa Catarina, Florianópolis-SC, Brazil, 2003.
[8] A. Candido, E. Chiarello, J. Malagoli, D. Sanches y T. Terrana, «Projeto de um motor de relutância variável monofásico usando o método dos elementos finitos,» XXIII Encontro Nacional de Modelagem Computacional e XI Encontro de Ciências e Tecnologia de Materiais, XXIII ENMC and XI ECTM anais, vol. 1, pp. 1202-1211, 2020.
[9] R. Dias, «Motores a Relutância Variável 6x4 e 6x6. Estudo Comparativo de Operação e Desempenho,” Dissertation (Masters in Electrical Engineering),» Federal University of Uberlândia, Uberlândia-MG, Brazil, 2011.

