Numerical Modeling For Fracture Mechanics Problems Using The Open-source Fenics Platform
Latin-American Journal of Computing, vol. 11, no. 1, pp. 30-41, 2024
Escuela Politécnica Nacional
Received: 15 March 2023
Accepted: 12 May 2023

Abstract: Fracture mechanics is the mechanical approach to fracture processes, which emerged due to limitations in applying traditional concepts of Mechanics of Materials to predict the behavior of cracked materials. Analytical problem solutions with this approach may be unattainable, so it is necessary to use numerical modeling, such as the finite element method. However, the use of more advanced software that solves engineering problems numerically is limited by its high cost. FEniCS is an open-source computational platform that solves partial differential equations by the finite element method. Thus, from a tutorial for this computational platform, this work proposes to reproduce a classic problem of linear elastic fracture mechanics, based on the validation of a comparison of a linear elastic problem with the commercial software ANSYS ®. With the help of the provided tutorial, a code was built to model a three-point bending test. Implemented with the aid of Gmsh and Paraview, it was possible to obtain satisfactory results and to show that FeniCS is a powerful and accessible tool for solving fracture mechanics problems.
Keywords: Fracture Mechanics, Numerical Modeling, FEniCS, Finite Elements.
I. INTRODUCTION
The Finite Element Method (FEM) is an approach to solving partial differential equations using numerical techniques in which a continuous domain is discretized into finite elements called mesh. With the advancement of technology and, consequently, computational power, more advanced engineering problems have become simpler to solve. This is due to the fact that analytical solutions can be complex and even unreachable, and the error achieved in numerical solutions is considerably acceptable [1].
In general, the use of advanced FEM-based software is restricted to companies and some teaching institutions, as it is the case with ANSYS ® [2]. On the other hand, open-source programs, such as the FEniCS Software [3], which is free, are used more widely due to their availability and ease of access. However, they tend not to have a graphical interface, unlike commercial software, which makes the use of pre- and post-processors essential for visualizing the solution. Even for a simple computational solution approach, the development of the finite element method can be complex, as it requires knowledge about tensor and variational calculus in some cases. The FEniCS [3] software, for example, uses these principles and, based on programming knowledge and the library itself, it is possible to solve partial differential equations using a variational approach. Therefore, this work proposes to present a numerical modeling of a linear elastic problem and two of fracture mechanics, presenting a preliminary comparison with ANSYS® for the linear elastic problem.
A. Fracture Mechanics
Fracture mechanics is the mechanical approach to fracture processes that emerged due to limitations applying traditional concepts of Mechanics of Materials to predict the behavior of materials in the presence of cracks. It was developed and founded after the 2nd World War [4] and is widely used in structural contexts in the areas of civil, mechanical, and metallurgical engineering [5-7]. For materials with brittle behavior, the linear elastic fracture mechanics (LEFM) approach is used, while for materials with ductile behavior, the elastoplastic fracture mechanics (EPFM) is used [4,8].
For example, in industry, a component may have such a high cost that, depending on the conditions and its integrity, it is more viable to have knowledge about fracture mechanics and continue using it with cracks to perform an exchange, which results in a complete pause of an operation. Alan Arnold Griffith studied the behavior of an elliptical hole when external stress is applied and established a thermodynamic model for crack propagation [8]. Griffith concluded that the strength of a material is not only linked to chemical bonding parameters but also to the existing defects. Therefore, it was realized that defects in the material are factors that intensify the applied stress, making it susceptible to exceeding the yield strength of the material and causing a rupture, which is the basis of fracture mechanics [4]. With this, a good characterization of the material must also have experimental parameters of the LEFM, such as the fracture toughness (K IC) and the critical energy release rate (Gc), for example. Fracture toughness is independent of size, geometry, and loading levels for a material with a given microstructure and is the main obtained experimentally properties related to fracture mechanics [8].
II. METODOLOGY
A. Numerical Modeling
The main concept addressed in the FEM is the discretization of a continuous domain into finite geometric elements, in addition to the use of polynomial interpolation to determine the results in the region inside the elements [1]. These elements form a mesh, and each node has a displacement u and a stress σ , which are represented in a linear system and determined through the variational calculus. The stress and strain of the solid are expressed by tensors, which are, by definition, mathematical entities that produce a linear transformation in vectors, transforming them into different vectors [9]. Tensors are represented in Equations (1) and (2), where u , v , and 𝑤 are the horizontal, vertical, and transverse components of infinitesimal displacement. The strain tensor can also be defined as ε=sym𝛻u , that is, the symmetric gradient of u. Both mathematical entities σ and ε have Cartesian x, y, and z components.


Mesh refinement generates more accurate results that are closer to the analytical ones, but there is a computational limit to be respected, which is analyzed through a convergence test, where the best results are sought with the minimum possible elements [9]. In the formulation involving the FEM applied to fracture mechanics, some parameters must be provided to the program, such as Young’s modulus (E), Poisson’s coefficient (𝜈), and the critical energy release rate ( Gc). After providing the input data, using concepts of variational calculus, it is possible to obtain the results, which are observed through a post-processing software.
Simulation allows engineers to use basic principles of modeling, physics, mathematics, and computer science to evaluate design performance in different scenarios. Thus, for the development of Engineering, it is important to analyze solutions via software to ensure that the result obtained is adequate and that it meets the functional needs of a project [10].
1. Numerical modeling for FEniCS software
a. Linear elasticity
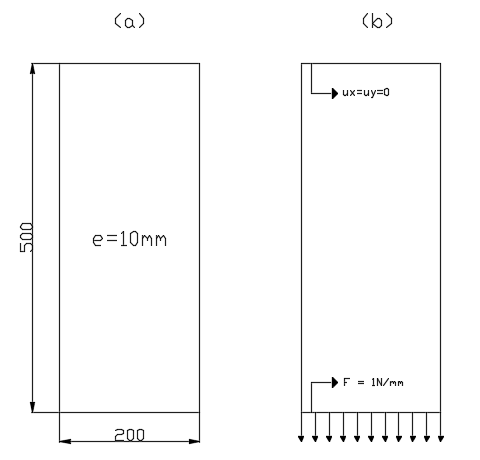
Numerical modeling is used for a linear elasticity problem in a plane strain state [9] shown in Fig. 1, based on the FEniCS library [11]. The problem consists of a three-dimensional plate 200 mm long, 500 mm high and whit thick e = 10 mm subjected to a load. Acting field forces are disregarded and a plane strain state is defined. For the Young’s modulus of the material, 200 GPa was adopted and, for Poisson's coefficient, 0.3. The problem has the following governing equations for a Ω domain.
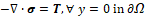
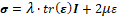

where T is the applied stress, represented by the ratio between the uniformly distributed load at the base of the bar and the thickness, Ⅰ is the three-dimensional identity matrix, and μ and λ are the Lamé constants, which depend on the Young’s modulus and the Poisson’s coefficient of the material. Considering the principle of virtual work, one must find values of u that satisfy the weak formulation [9].
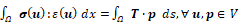
where u and p are the trial and test functions, respectively, and V is the vector field containing them. In this example, second-degree Lagrange polynomials are defined for the interpolation between nodes. The vertical face is fixed, and the load F is uniformly applied in the negative y-direction. The mesh was built using a function from the FEniCS library, containing 48000 tetrahedral elements with 5 mm on each side.
b. Fracture Mechanics
Numerical modeling for the fracture mechanics problem was proposed by [12], using models by [13], with contributions by [14]. It is considered an elasto-static body with a discontinuity, which occupies a domain Ω⊂ R2. The Dirichlet and Neumann boundary conditions [9] are imposed by ΓD and ΓC. In the case of a discrete fracture mechanism, the crack is represented by a discontinuous surface ΓC. The variable that models crack propagation is ϕ∈[0,1]. When it assumes a null value, the material is intact, and when it assumes a unitary value, there is a complete fracture. The crack size is controlled by a variable ℓ, a length scale parameter inherent to the model and which depends on the developed mesh refinement [12-15], called characteristic length. The approximate crack surface energy is defined as:
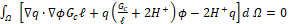 (5
(5Adding the Bulk energy to Eq. (5) the total potential energy of the solid (Ψ) is obtained as:
 (6)
(6)where ψ(ε) is the strain energy density of the solid, in terms of the Lamé parameters and the strain tensor, represented in Eq. (2), whose mathematical expression is:
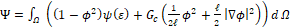 (7)
(7)Applying Gauss's theorem in Eq. (7) the following field equations are obtained, with arbitrary values for the kinematic variables δu and δф.
 (8)
(8)
 (8)
(8)The natural boundary conditions for a traction T are:
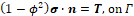 (9)
(9)
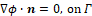 (9)
(9)where n is the normal vector to the surface Γ. With this, the constitutive equations and the boundary conditions are given. The procedure now consists of implementing the finite element method. The main objective is the resolution of the system of equations (8) with the boundary conditions expressed by Eqs. (9.1) and (9.2). However, it is necessary to use the finite element method, discretizing the continuous domain. Equation (8.2) is modified to:
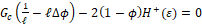 (10)
(10)where H+ is called the variable storage (or history) field, which changes with time, expressed mathematically as:
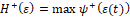 (11)
(11)and ψ+ is the variable strain energy density of the solid, defined as:
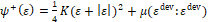 (12)
(12)where K is the Bulk modulus, which can be expressed in terms of the Young’s modulus and the Poisson’s coefficient [9]. Finite element modeling uses a weak, or variational, formulation that uses dimensional trial (𝒰, 𝒫) and test (ℒ, 𝒱) spaces, which contain the trial (u, 𝜙) and test (p, q) functions, respectively. A discrete space (𝒲) is also defined around the mesh that contains the phase field variable (ф) and the displacement field (u). All spaces have a dimension d.
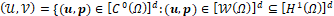 (13)
(13)
 (13)
(13)In the reformulation of the system of constitutive equations, applying the Bubnov-Galerkin procedure, remote tractions and field forces are disregarded, making it:
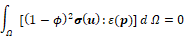 (14)
(14)
 (14)
(14)2. Numerical modeling for ANSYS ® software
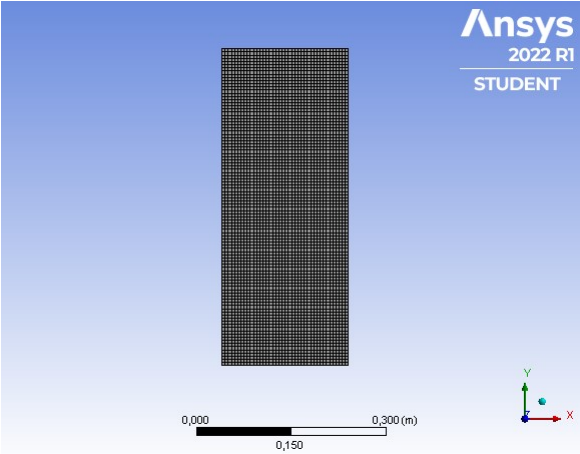
In order to validate the results obtained by FEniCS for the linear elasticity problem (Section II.1.a), a numerical model was implemented in the Ansys ® software, version 2022. The material used in the modeling has the same properties as in Section II.1.a. As it is a three-dimensional model, a load of 0.1N/mm² ( Pressure type ) was applied to the lower face of an xz plane of the structural element in the vertical direction with a downward direction ( -y ). Opposite the load application plane, all nodes were restricted to translation, which represented a crimp. The mesh illustrated in Fig. 2 records the geometry containing 45125 nodes and 8000 cubic elements.
III. RESULTS AND DISCUSSION
A. FEniCS software validation
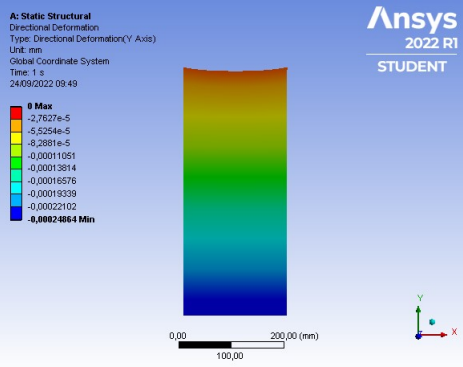
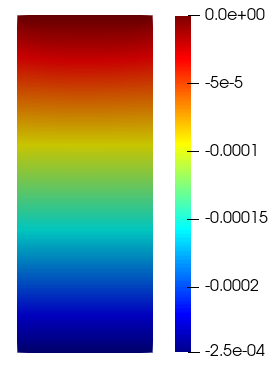
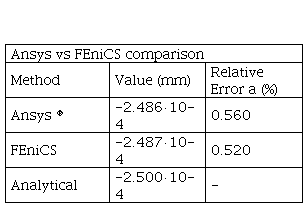
With the help of ANSYS ®, a kind of FEniCS validation was carried out, solving the same linear elasticity problem and comparing the results. Fig. 3 shows the bar displacements obtained by ANSYS ®, and Fig. 4 exposes those obtained by FEniCS, both in the y direction. Note that there is a qualitative similarity regarding the vector field represented by the scale. The maximum supported stresses are found on the crimped face of the bar, opposite to the force application face, and, for both cases, a value of 0.1MPa was obtained. The maximum deformation obtained analytically is -2.500⋅10-4 mm. The comparison between FEniCS and ANSYS ® for the linear elastic problem resulted in errors of less than 0.6%, as shown in Table I. Therefore, free open-source software can be operated safely.
B. Application of the phase field method using FEniCS
1. Tensile test with simple pre-crack
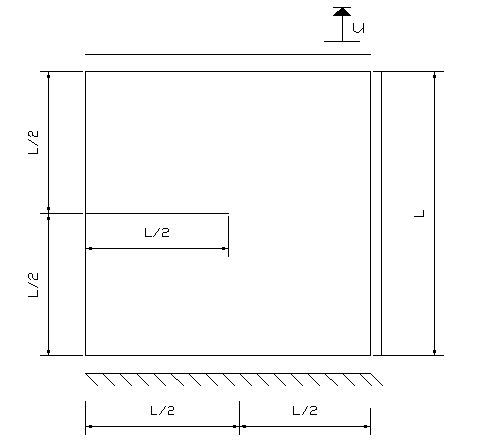
Elaborated by [15], the problem to be solved consists of a representation of a fracture mechanics test of a plate subjected to uniaxial tensile stress that has a pre-crack to simulate a pure fracture in Mode 1, as illustrated in Fig. 5. In order to reduce the computational time, small geometric proportions were considered, being L=0.5 mm. The code structure of this problem, implemented for this work, followed the tutorial developed by [12].
The mesh was built using the Gmsh preprocessor [16] and has 30546 triangular elements. The material has a modulus of elasticity E = 210GPa, a Poisson coefficient 𝑣 = 0.3, and a critical energy release rate Gc = 2.7MPa mm. Thus, the Lamé parameters λ =121153.8MPa and μ = 80769.2MPa were obtained. A value of 0.011mm was also used for the characteristic length ℓ.
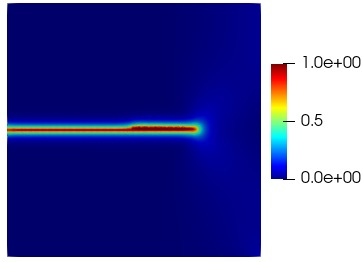
The base of the mesh (y=0) is fixed, and a remote offset of 0.007mm is used as the first iteration. To help with the code, the value of the phase field variable ϕ for every pre-crack was defined as 1. During the execution of the code, the necessary number of iterations for convergence of the solution during a given step is provided. The main results of the analysis are shown in Fig. 6 and Fig. 7. Visualization of crack propagation is easily observed using the post-processor software Paraview [17]. Code execution stops at a value determined as a maximum (t=1.0), at which there has already been catastrophic failure of the material. A change was made regarding the test loading rate, for reasons of computational power. The red region represents the complete failure of the material, and the blue shows the initial state (intact).
The results obtained are satisfactory and close to the literature, as shown in Table II [12,13,15,18], although changes have been made to the code and the mesh used has been less refined.

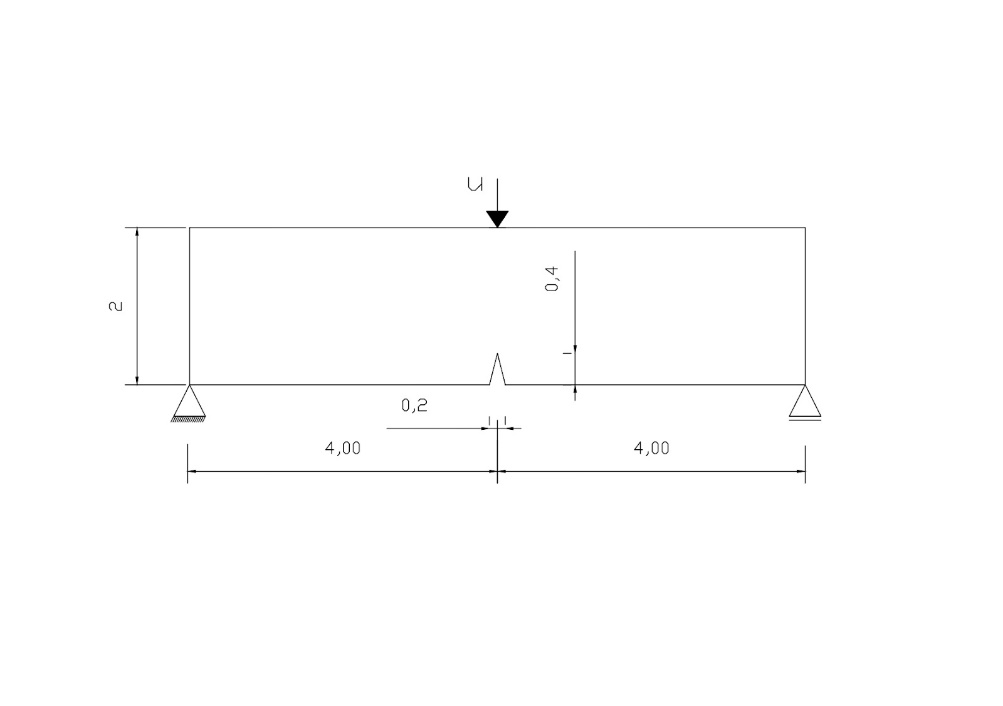
2. Three-point bending test
The following problem consists of a three-point bending test. More details can be seen in [15]. The geometry and boundary conditions are given in Fig. 8. The mesh was built using the Gmsh preprocessor and has 72768 triangular elements, in which a refinement was performed in the center, where the crack is expected to propagate [18]. The material has a modulus of elasticity E = 20.8GPa, a Poisson coefficient 𝑣 = 0.3 and a critical energy release rate Gc = 0.54MPa mm. Thus, the Lamé parameters λ =12000MPa and μ = 8000MPa were obtained. A value of 0.03mm was also used for the characteristic length ℓ, similar to that used in the literature [13,15].
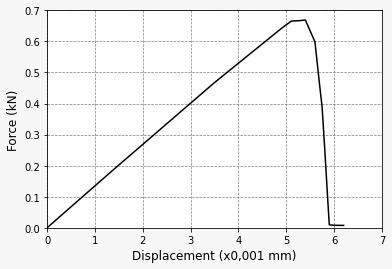
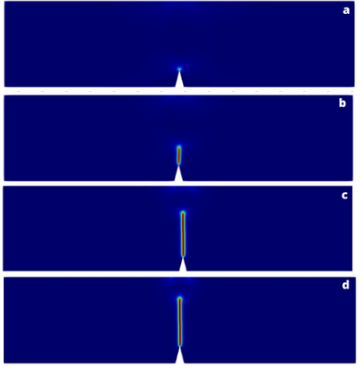
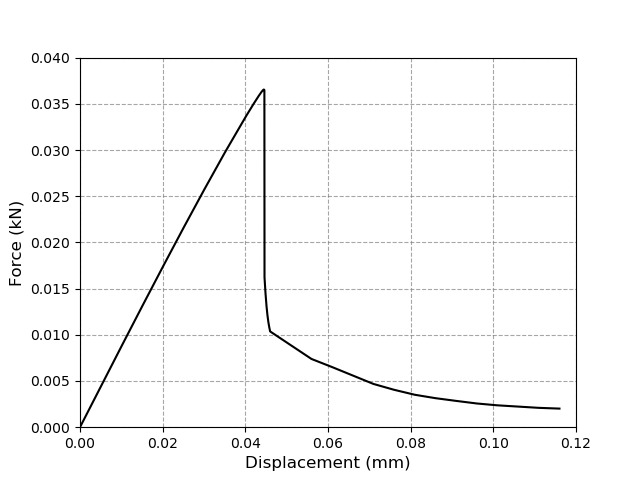
We start with the same numerical modeling for the traction problem but now with a point force. The point (0,0) has zero nodal displacements in x and y. At the point (8,0), the shift is restricted to y only. The force is applied punctually at (4,2). An initial displacement of 0.005mm was defined at the top of the geometry, changing to 0.00001mm when approaching the failure and returning to 0.005mm after the failure to follow the crack in greater detail. Fig. 9 shows the vector field of the phase field variable as a ϕ function of the load level, with representation like the previous problem. The force-displacement curve is shown in Fig. 10. The results obtained are satisfactory and close to the literature, as shown in Table III, even with a variation of displacements different from that used by the authors to reduce computational costs [13,15,18].

IV. CONCLUSIONS
This work proposes the implementation of classic linear elastic fracture mechanics problems based on a tutorial and examples found in the literature, with the help of Gmsh and Paraview. The comparison between the FeniCS and ANSYS software for the elastic linear problem obtained a satisfactory result, with an error, on average, of less than 0.6%. The traction problem presented an error, on average, of approximately 2.9% for the peak value when compared to the literature. The three-point bending problem, on the other hand, presented an error, on average, of approximately 9.7% for the peak value in comparison with the same source. Thus, it is concluded that FEniCS can be used for academic purposes both for solving classic problems of Strength of Materials and MFLE. Furthermore, this tool, together with Gmsh and Paraview, provides users with advanced approaches to learning engineering problem-solving
References
[1] T. R. Chandrupatla and A. D. Belegundu, "Elementos Finitos," 4° ed., Pearson, 2014.
[2] Ansys ® [Ansys Student], Version 2022, Ansys, Inc.
[3] M. S. Alnaes et al., "The FEniCS Project Ver. 1.5," Archive of Numerical Software, vol. 3, 2015.
[4] T. L. Anderson, "Fracture Mechanics - Fundamentals and Applications," 2nd Edition, CRC Press, 1994.
[5] K. Majidzadeh, E. M. Kauffmann, and D. V. Ramsamooj, "Application of Fracture Mechanics in the Analysis of Pavement Fatigue," in Association of Asphalt Paving Technologists Proceedings, pp. 227-246, 1971.
[6] G. Clerc, A. J. Brunner, P. Niemz, and J. Kuilen, "Application of Fracture Mechanics to Engineering Design of Complex Structures," in 1st Virtual European Conference on Fracture, Procedia Structural Integrity, vol. 28, pp. 1761-1767, 2020.
[7] G. J. Neate, G. M. Sparkes, H. D. Williams, and A. T. Stewart, "Application of Fracture Mechanics to Industrial Problems," in Fracture Mechanics, Pergamon, pp. 69-90, 1979.
[8] J. A. L. Rocha, "Termodinâmica da Fratura: Uma Nova Abordagem do Problema da Fratura nos Sólidos," EDUFBA, 2010.
[9] P. T. R. Mendonça and E. A. Fancello, "O Método dos Elementos Finitos Aplicado à Mecânica dos Sólidos," 1st Edition, Orsa Maggiore, 2019.
[10] Ansys ®, "Simulation Is a Superpower," Available: https://www.ansys.com/company-information/simulation-is-a-superpower. [Accessed: May. 14, 2023].
[11] H. P. Langtangen and A. Logg, "Solving PDEs in Python: The FEniCS Tutorial 1," Simula Research Laboratory and Department of Informatics, University of Oslo, 2017.
[12] E. M. Pañeda and H. Hirshikesh, "Phase Field Fracture Implementation in FEniCS," ResearchGate, 2020.
[13] M. Ambati, T. Gerasimov, and L. De Lorenzis, "A Review on Phase-Field Brittle Models of Fracture and a New Fast Hybrid Formulation," Comput Mech, vol. 55, pp. 383-405, 2015.
[14] J. Amor, J. Marigo, and C. Maurini, "Regularized Formulation of the Variational Brittle Fracture with Unilateral Contact: Numerical Experiments," Journal of the Mechanics and Physics of Solids, vol. 57, pp. 1209-1229, 2009.
[15] C. Miehe, M. Hofacker, and F. Welschinger, "A Phase Field Model for Rate-Independent Crack Propagation: Robust Algorithmic Implementation Based on Operator Splits," Comput Methods Appl Mech Eng, vol. 199, pp. 2765-2778, 2010.
[16] C. Geuzaine and J. Remacle, "Gmsh: A 3-D Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities," International Journal for Numerical Methods in Engineering, vol. 79, pp. 1309-1331, 2009
[17] J. Ahrens, B. Geveci, and C. Law, "Paraview: An End-user Tool for Large Data Visualization," in Visualization Handbook, Elsevier, pp. 978-0123875822, 2005
[18] H. Hirshikesh, S. Natarajan and R. K. Annabattula, "A FEniCS Implementation of the Phase Field Method for Quasi-Static Brittle Fracture," Frontiers of Structural and Civil Engineering, vol. 13, 2019.

