Pappus-Guldin theorems applied the study of solid modeling with GeoGebra software
Latin-American Journal of Computing, vol. 11, no. 1, pp. 20-29, 2024
Escuela Politécnica Nacional
Received: 14 March 2023
Accepted: 13 May 2023

Abstract: — In this work, we use Geogebra software to simulate the shape of objects (solids) in three dimensions from their photo and real dimensions using spline interpolation. With the reconstructed object, we analyze its volume and surface area using the Pappus-Guldin Theorems (PGT), the theorems that use mathematical analysis ideas to describe the volume and surface area by the sectional area and by the contour curve of the object. In the simulations, we tested the verification of the modeling for known solids (sphere and torus) and then analyzed some objects used in the industry, such as the packaging of products, pet bottles, yogurt containers, coffee powder packaging, aluminum soda cans, and the packaging of chocolate powder. We also analyzed some objects created by rotating bodies, such as the shape of a jar and an aluminum barrel, and also shapes found in nature, such as the shape of a pear and an egg. Modeling allows us to better understand the packaging used in the industry to minimize manufacturing costs and maximize its utility. Thus, we can modify these packages to obtain the best development of how these products are presented to the public, optimizing its format by analyzing its surface and its volume.
I. INTRODUCTION
Applications involving solid geometric objects that relate to the measurement of dimension or volume of a three-dimensional shape are classic examples that, according to [12], require the study of geometry of these bodies. The simple application of this work would be to calculate the area and volume of any three-dimensional object. This theoretical tool that gives us the volume and surface area of bodies, with the idea centered on axis rotation, are the Pappus-Guldin Theorems (PGT). Automatic fulfillment of the requirements for the use of electronic computers. This tool helps to understand how computational modeling is performed in certain solid models.
Based on the article [3] on rotational shapes and volume calculation, we use the numerical simulation code. The application will be a calculation of area and volume by computational modeling, starting from the analysis of an object from a photograph, which is inserted into the GeoGebra program according to [6] and using the spline command, can be identified the generation of contours of the object, building points on the contours of the image is called a polygonal line. Therefore, we will use the free software GeoGebra to model some objects and find the volume and surface area of these objects, the axis can be formed by rotation around a surface or curve. Throughout the process, we have the minimum surfaces, and surfaces of revolution have a limit that will be discussed so that we can use the Pappus-Guldin theorems (PGT).
We will study these applications from the calculation of surface area and volume. For example, two methods can be compared: organic and industrial composting. In biological and engineering applications, we can use the PGT model to calculate the lateral surface area, and we can know the mass in terms of light and amount of water it produces on the surface in terms of the best fruit, flavor, and size. The industrial application of packaging can help to recycle and is less harmful to environment. We can minimize the product from the packaging in formats: for less heat exchange at room temperature; lower material costs. In the last part of the work, theoretical studies were carried out on the smallest surfaces of the packaging to minimize the design process of the designers of the formats of these packages.
II. METHODOLOGY
Numerical simulations of geometric solids using the mathematical theory of PGT will be applied. This can result in a study of minimizing the manufacturing costs of the products of companies through the packaging format of their products. The software used for the calculations, Geogebra, is free software with mathematical functions developed by mathematician Markus Hohenwarter as part of his Ph.D. thesis [6] at the University of Salzburg. The program aims to develop suitable tools for teaching mathematics and applying mathematics in the fields of geometry and algebra.
In class, we use mathematical and physical concepts to follow theory and practice. However, nowadays they are not always together. There are often people who have the theory and do not know how to put it into practice or vice versa. Therefore, it shows the reality applied in daily practice.
In this article, based on a new technology called Information and Communication Technology (ICT), we use this software to perform numerical simulations. GeoGebra in which we will model command objects with splines according to [4].
For theoretical support, we used the PGT to calculate the surface area and volume of solids. These theorems were proved by the Greek mathematician Pappus of Alexandria and the Swiss mathematician Paul Goulding, who used the concept of the center of rotation of solids to perform analyses and their measurements (see [9], [12], and [13]).
A. Pappus-Guldin theorems
There are two theorems referring to Pappus and Guldin:
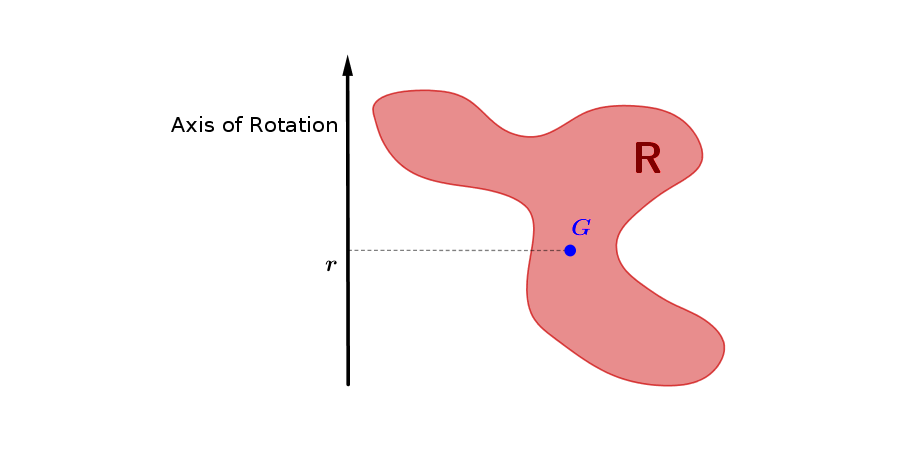
First Pappus-Guldin theorem: Considering R as a plane figure, the solid  formed by rotation of R around an axis r has the volume of the solid is equal to area of R multiplied by the length of circle described by its center of gravity (see Fig.1).
formed by rotation of R around an axis r has the volume of the solid is equal to area of R multiplied by the length of circle described by its center of gravity (see Fig.1).
The volume of the solid is thus given by the equation:
Vol (  ) = dist(r, G) A(R), (3)
) = dist(r, G) A(R), (3)
where G is the center of gravity of R, dist(r, G) is the distance of the line r from the center of gravity, and A(R) is the area of the region R.
Second Pappus-Guldin theorem: Considering C as a plane curve, the surface formed by rotation of C around an axis r has area obtained by multiplying the length of the curve C by length of the circumference passing through its center of gravity G (see Fig.2).
The surface area of is given by the equation:
A(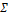 )=
dist(r, G) l(C), (4)
)=
dist(r, G) l(C), (4)
where G is the center of gravity of curve C, dist(r, G) is the distance of the center of gravity of the lines r, and l(C) is the length of curve C.
B. Spline
A spline is defined as a partitioned domain of a polynomial of degree n whose function value and its n-1 continuous first derivatives pass through the connection points. The abscissa of these connecting points are called knots, and these piecewise polynomials are chosen to minimize the least mean square curvature.
According to [1], splines can be divided into two categories:
Interpolation splines, which pass through all control points.
Approximation splines, which run near all control points.
Let a= 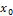 <
< 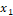 <...<
<...< 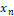 =b, be a subdivision of the interval (a,b). A spline function of degree n with knots at the points
=b, be a subdivision of the interval (a,b). A spline function of degree n with knots at the points 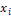 , i=0,1,..., m is a function S with the following properties according to [1]:
, i=0,1,..., m is a function S with the following properties according to [1]:
In each subinterval ( ), i=0,1,..., m-1, S(x) is a polynomial of degree n.
), i=0,1,..., m-1, S(x) is a polynomial of degree n.
S(x) and its first derivatives (n-1) are continuous on the interval (a,b).
According to [8], we can use spline functions to calculate tree volumes. The method used to calculate the volume of a tree would be to calculate the volume from the diameter and height of the trunk, using a cubic spline.

III. NUMERICAL SIMULATION I
In this section, we will perform simulations using Geogebra software and the Pappus-Guldin theorem (PGT) theory in the study of the volume and surface area of sphere and torus to verify the accuracy of the method.
A. Sphere
The 3D modeling of the sphere (see
Fig.3) was performed in GeoGebra software according to [6]. We note that as the
value of n increases, there is a
built-in convergence for the sphere with radius r=4. Given a value and knowing that r is the fixed radius, we conclude that the volume of a sphere
using the PGT ( 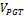 ) in the limit, approximates the
volume value of the sphere using known results, i.e.,
) in the limit, approximates the
volume value of the sphere using known results, i.e.,
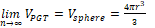
where the locus of r is constant according to [5]. These values of absolute error and relative error decrease when only the value of n increases. We applied the same procedure by calculating a rough estimate of what was done for volume of the sphere with a different algorithm for the area of sphere using GeoGebra software from the creator of the application [6], which confirms the same idea.
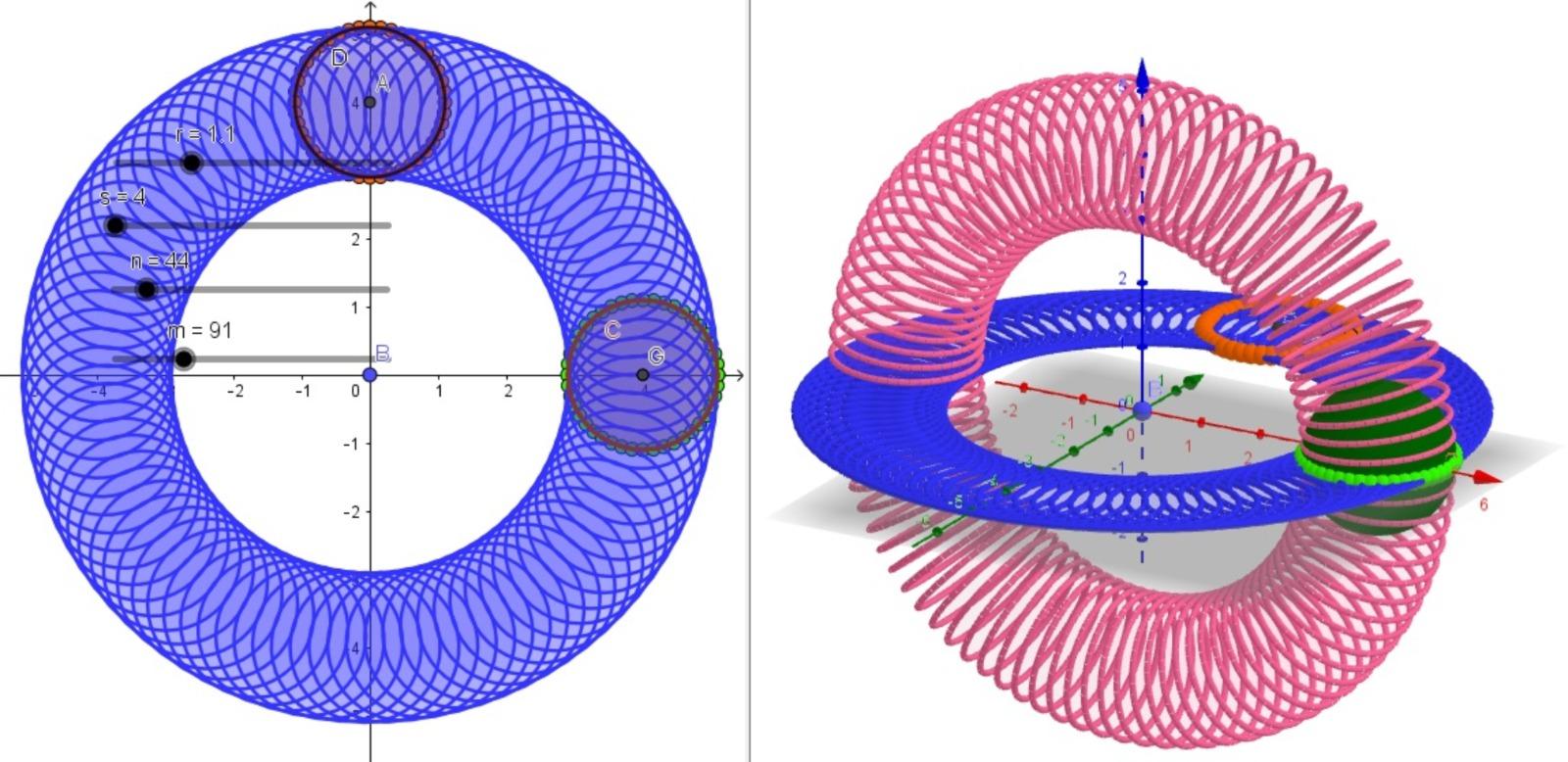
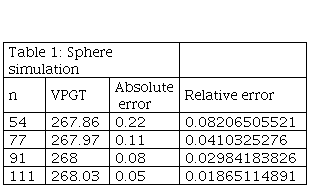
Table I shows the algorithm of the PGT,
which calculated the volume of the sphere in GeoGebra software. In the
numerical simulation, we have a fixed radius of r=4, where we observe that the number of sides of the polygon
inscribed in the circle depends on the value of n. The values of n are chosen randomly. Table I analyzes the value
of the volume of the sphere, which is estimated to be the 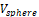 = 268.08 u.v. Then we compare the value
obtained over PGT volume with the modeling, which converges when it is verified
that the value of n increases. We have below Table I:
= 268.08 u.v. Then we compare the value
obtained over PGT volume with the modeling, which converges when it is verified
that the value of n increases. We have below Table I:
B. Torus
The 3D modeling of the torus (see Fig.4) was performed in GeoGebra software. The Cartesian plane coordinates x, y, and z in three dimensions represented by 3D is in the interval [0, ], the torus has its rotational symmetry in the z-axis, R is the distance from the center of the tube to the center of the torus, and r is the radius of the tube.
The volume of the torus is given by:
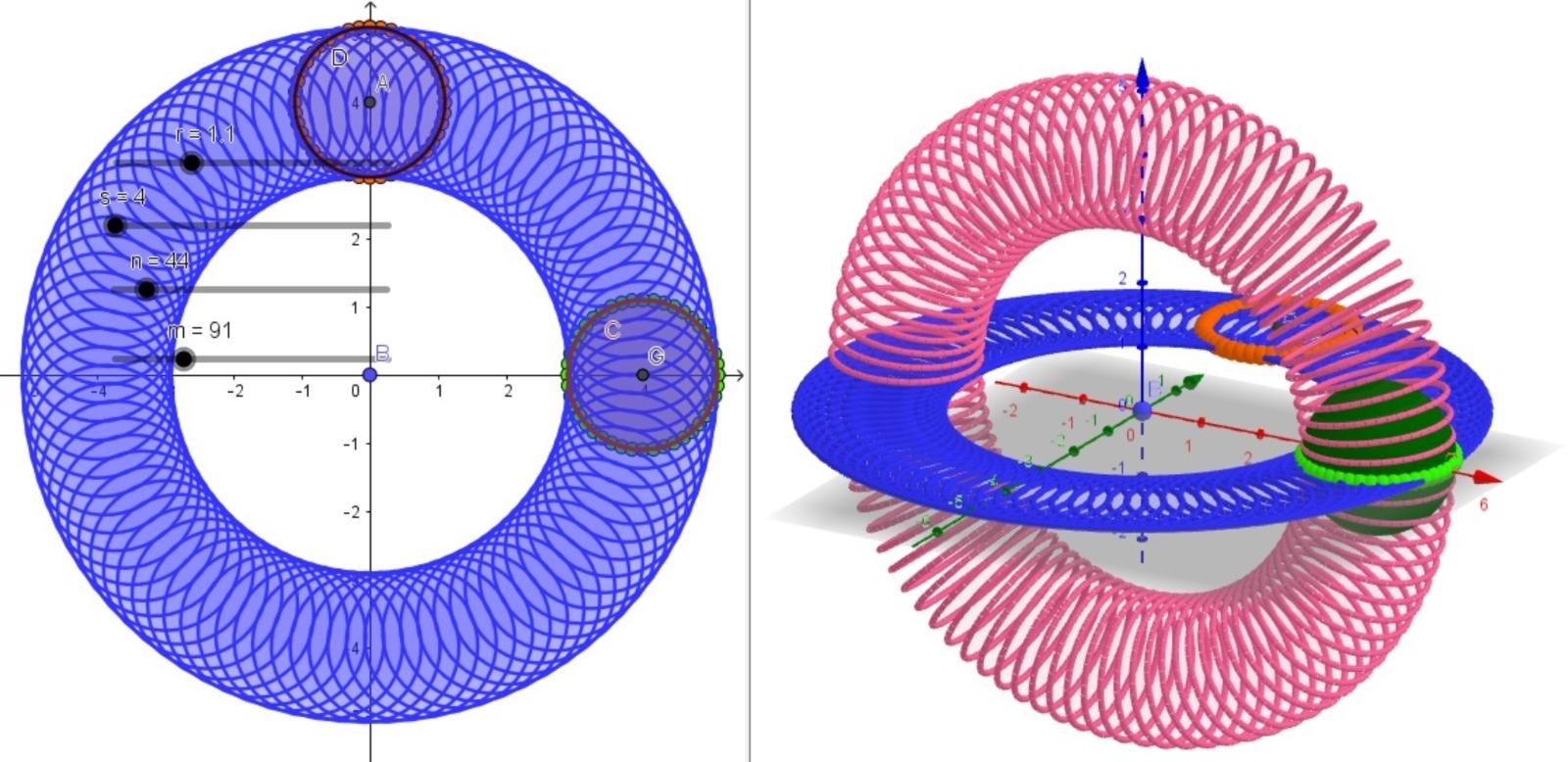
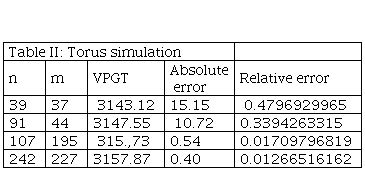
Table II shows the PGT algorithm performed
in GeoGebra software for volume of a
torus. In the numerical simulation, we have fixed radius of r and s, while the
values of n and m can vary, i.e., the number of sides of the inscribed polygon
formed inside the circle. The values of n and m are chosen randomly. Table II
analyzes the value of the volume of a torus estimated at  = 3158.27341. Then we compare the value of the PGT volume with the modeling,
which converges when it finds that the values of n and m increase.
= 3158.27341. Then we compare the value of the PGT volume with the modeling,
which converges when it finds that the values of n and m increase.
Below is Fig. 2 of a torus and table II:
IV. NUMERICAL SIMULATION II
In this section, we will perform simulations using Geogebra software and PGT theory to study the volume and surface area of some solids designed for industrial use, such as packaging and solids found in nature, such as eggs and pears.
A. Simulation in the packaging industry
It can also be shown that there are other objects used in industry, mainly in packaging, so we minimize the cost by optimizing the surface area and occupied volume with GeoGebra software to perform the modeling and analysis. Figures 5 and 6 show two minimal surfaces used as the basis for the production of some packaging, the catenoid, and the helicoid.
Numerical simulations are created by objects of geometric models with mathematical concepts using computer graphics. With its importance in reducing production time and costs, with a potential impact on job creation and income, as seen in [8]. Based on the use of software for manufacture of electronic components, we have used geometric modeling with mathematics according to [10], where the PGT can be applied to determine its volume and surface area in other products used in the industry.
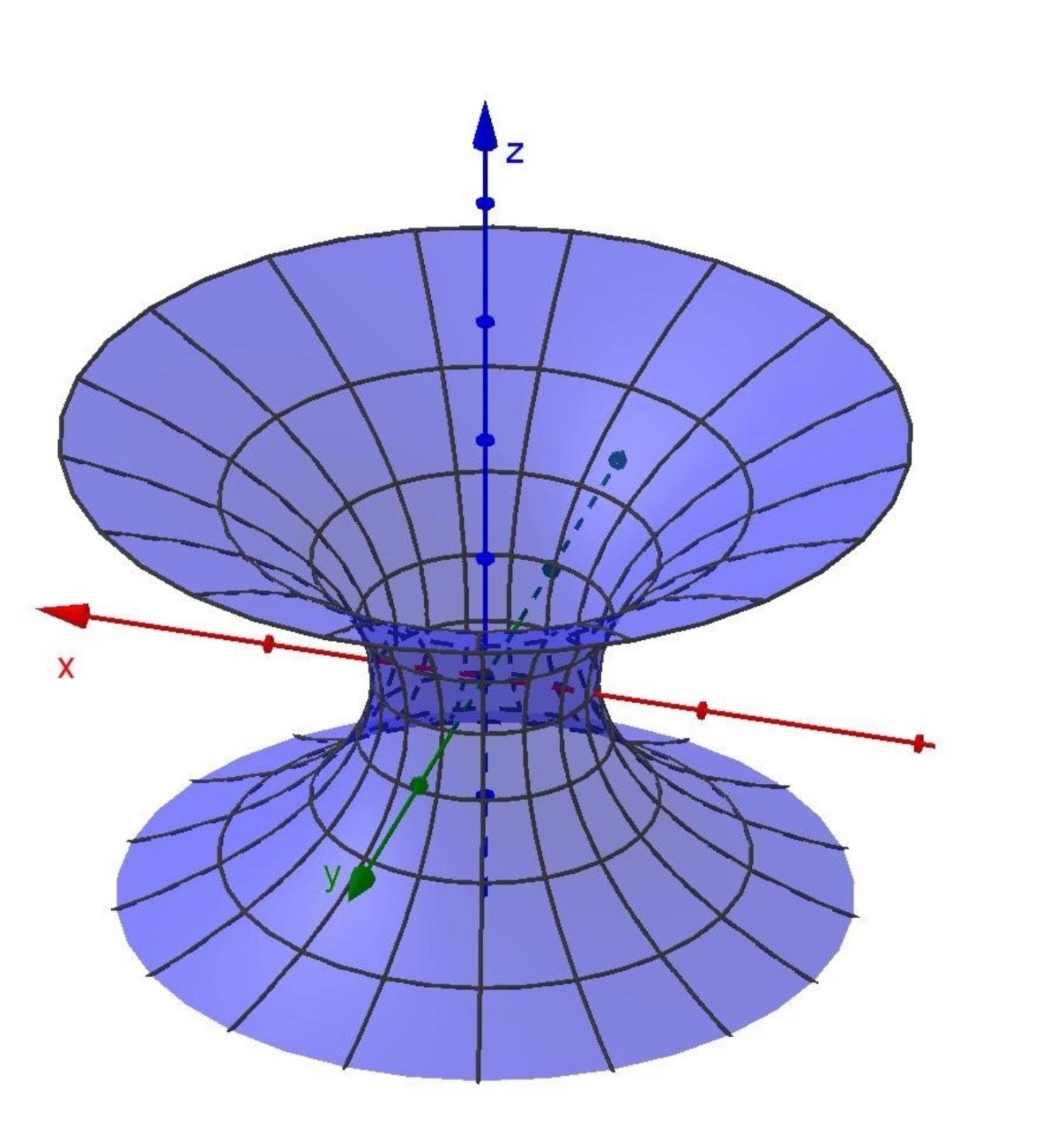
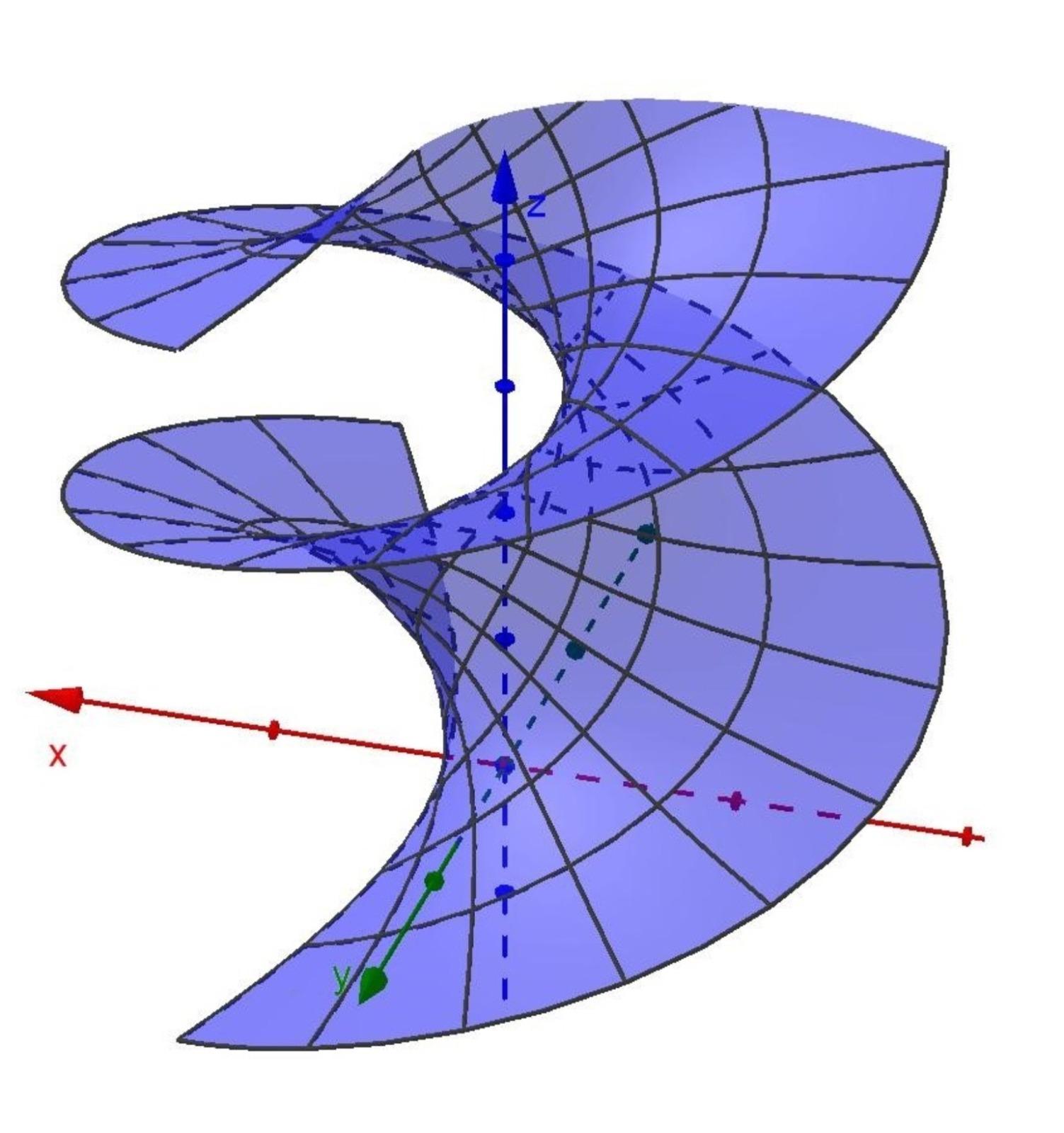
Industry uses packaging to store its products, so it is important to study the format to be used. Reduce packaging costs by paying attention to factors such as format; reduce material costs. Among other things, analyzing these factors can lead to reducing environmental impact and promoting sustainable recycling. We can consider the use of minimal surface areas in industrial packaging. The importance of studying packaging forms, which we refer to in the work of [7], explores the feasibility and importance of new forms of PET bottles. In this case, when designing new packaging, we should primarily consider reducing the environmental impact of packaging damage. The examples of these packages by designers of PET bottle and yogurt figures are surfaces of revolution that have an axis of rotation, but they are not minimal surfaces. To be a minimal surface, it would have to have infinite curves that fix two points on each edge.
B. Numerical models of packaging in the industry
Using real images of objects and using the resources of the Geogebra software, we were able to model some packages used in daily life.
Figures 7 to 13 present simulations considering objects modeled by using splines where the PGT was applied.
Fig. 7 has the modeling of the PET bottle with the number of steps n=150 and the value of the volume over 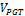 =25.16 and the value over PGT of the area is
=25.16 and the value over PGT of the area is 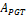 =30.2.
=30.2.
Fig. 8 has the modeling of a yogurt container with number of steps n = 150 and volume value over  =78.75 and value over PGT of the area is
=78.75 and value over PGT of the area is  =62.98.
=62.98.
Fig. 9 has the modeling of coffee powder packaging as a solid of revolution and a catenoid. The packaging is improved by the designer to attract consumer attention and increase sales through a naturally developed format.
From the visual point of view of packaging, the best would be the catenoid, as ours is cheaper to produce and the aluminum can has a strong construction and also for better conservation.
Modeling of coffee powder packaging with the number of steps n = 150 and volume value over 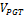 = 48.59 and value over PGT of the area is
= 48.59 and value over PGT of the area is  = 46.91.
= 46.91.
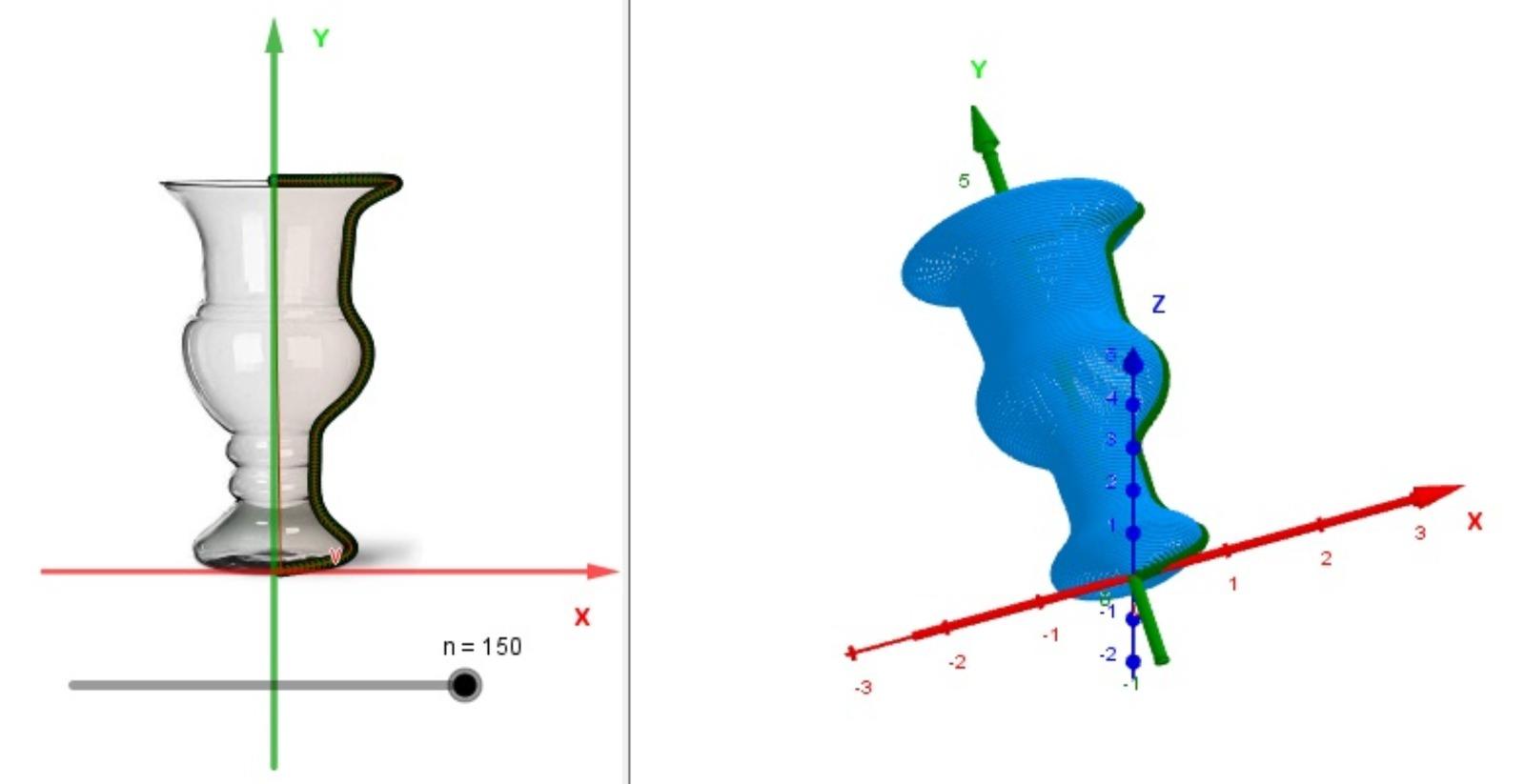
Fig. 10 has the modeling of a jar with the number of steps n = 150 and the volume value over 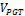 = 2.51 and value over PGT of the area is
= 2.51 and value over PGT of the area is  = 16.19.
= 16.19.
In industry, the packaging of chocolate powder looks like a spiral, but it is not a spiral. This kind of filling cannot be modeled with PGT because we cannot get a generating curve around a fixed axis with the spline, in short, it is not a surface of revolution.
Some packages are modified to achieve the best development of a product to attract the public and sell more products through advertising [2].
In the studied example, the chocolate milk can is not optimized, and the production cost of can must have increased.
Oblique cylindrical shapes are mainly used in the automotive industry, such as drills, screws, rotors, and helical gears, because the material is more evenly distributed and more resistant, which increases the quality of the product.
We can model the packaging of chocolate powder if we assume that it is obtained by a generation curve. To do this, we can use the analysis of the model through PGT, as shown in Fig. 11.
Thus, we obtain a modeling with a number of the steps n = 150 and the volume value over 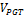 =102.58 and the PGT value of the area is
=102.58 and the PGT value of the area is 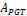 =66.81.
=66.81.
Fig.12 has the modeling of an aluminum soda can with the number of steps n =150 and the volume value over 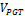 =196.4 and the PGT value for the area is
=196.4 and the PGT value for the area is 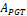 =111.86 .
=111.86 .
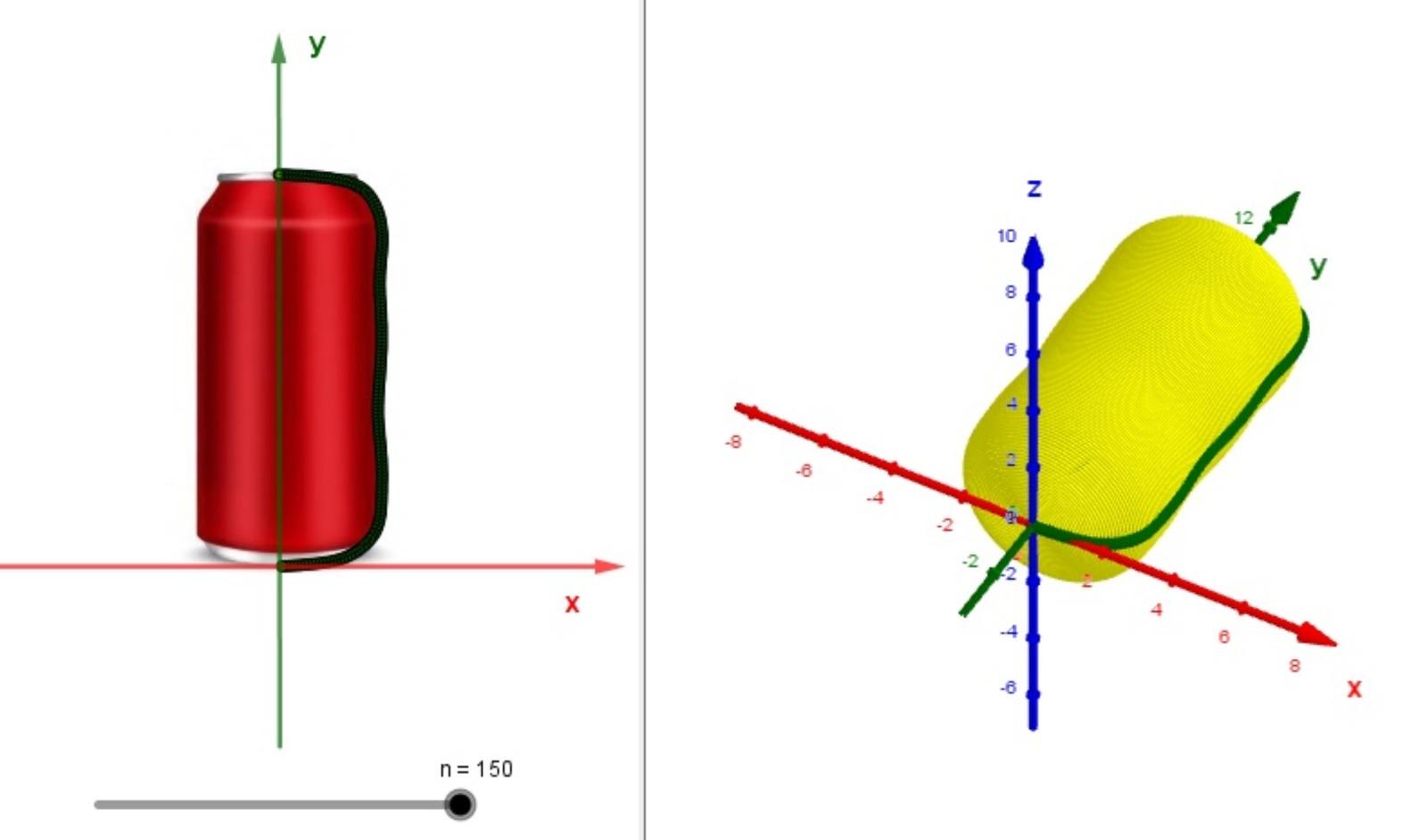
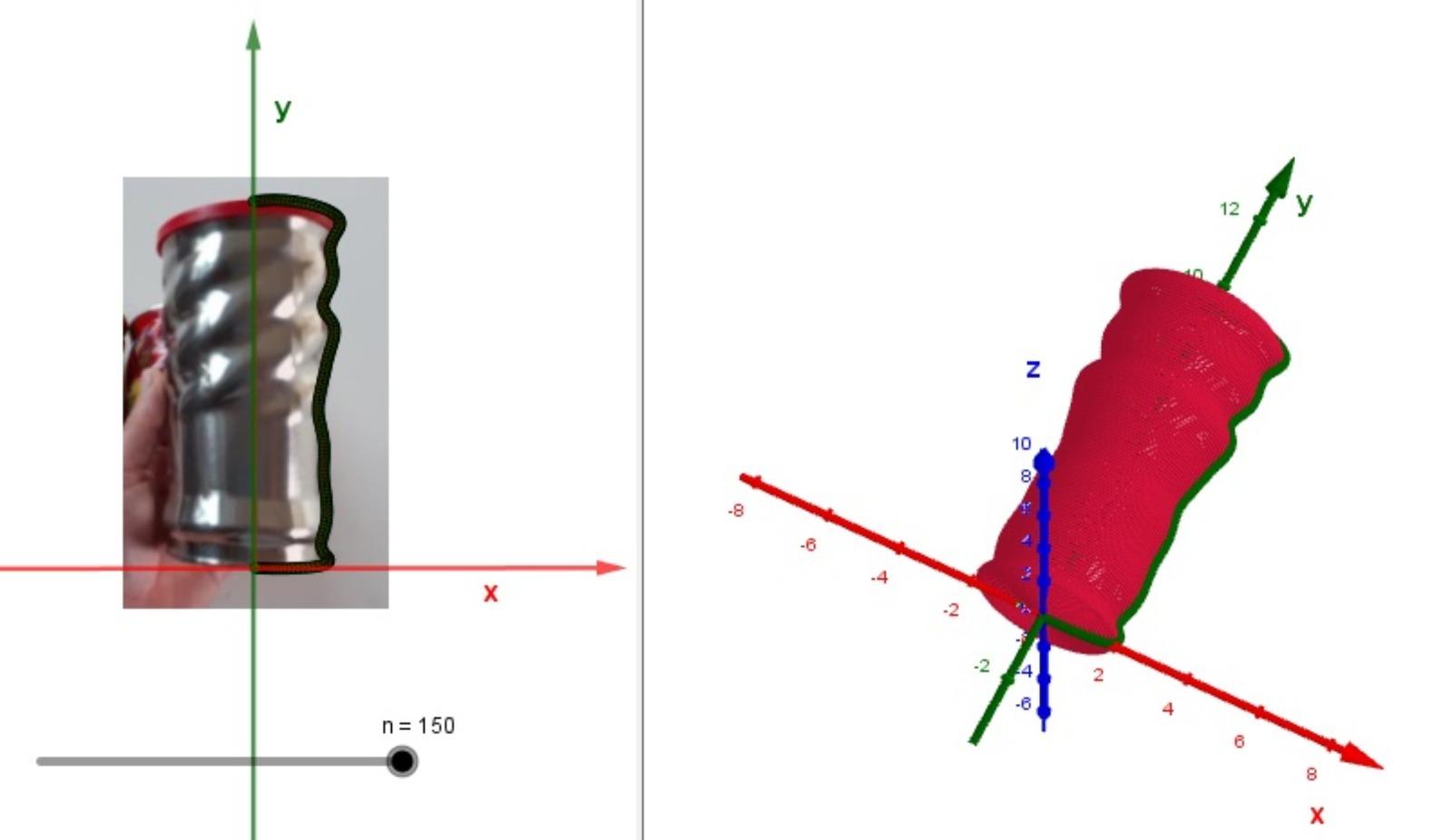
Fig. 13 shows the modeling of an
aluminum barrel with a number of steps n =
150 and the volume value over 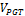 = 95.65 and the PGT value for the area is
= 95.65 and the PGT value for the area is 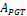 =66.69.
=66.69.
C. Numerical models of packaging in nature
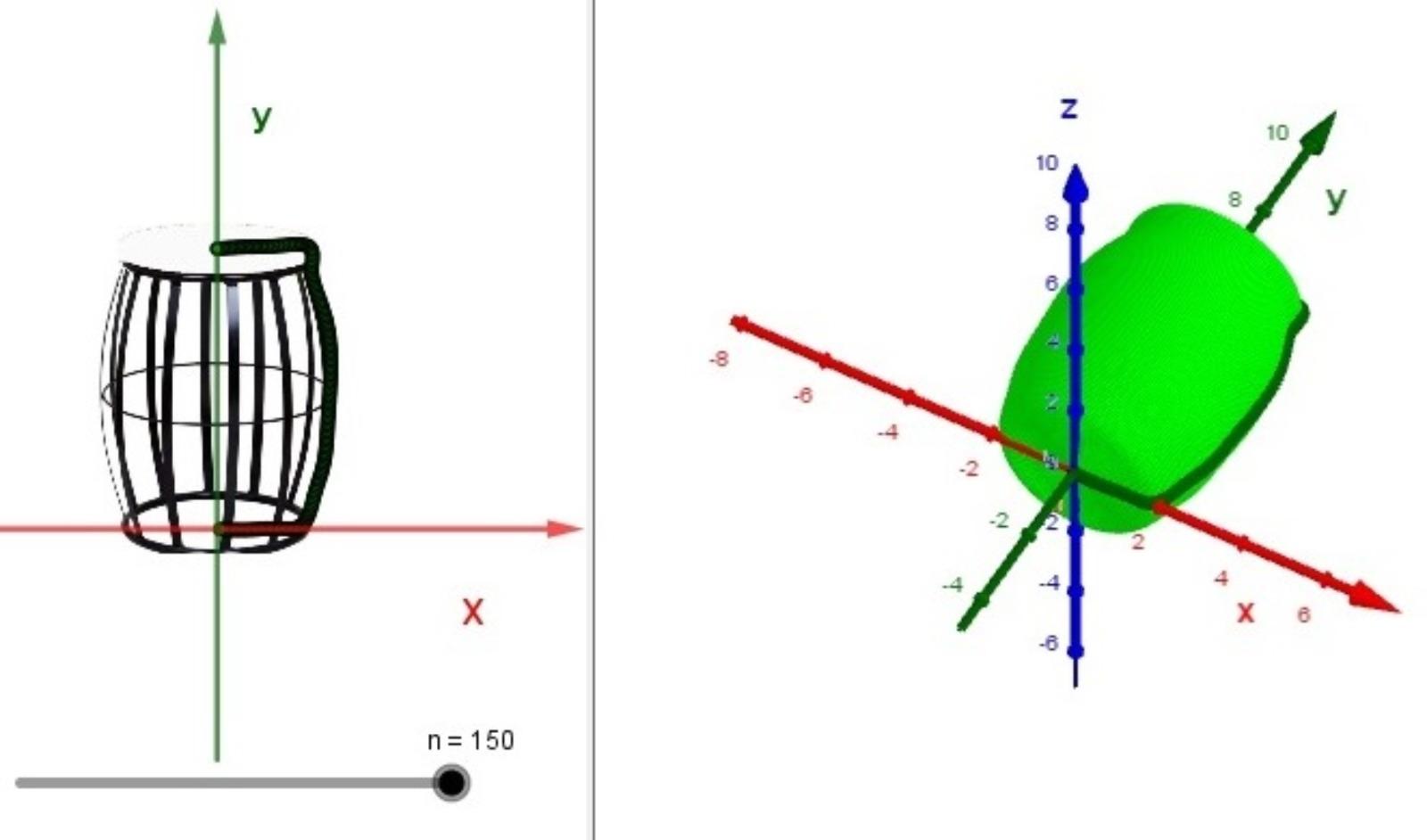
Figures 14 and 15 show the format of some packages found in nature, such as pear and egg.
Fig.14
shows the modeling of the shape of a pear with the number of steps n = 150 and the volume value over  =171.41 and the PGT value of the
area is
=171.41 and the PGT value of the
area is 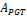 =104.39.
=104.39.
In Fig. 15, we see the modeling of the shape of an egg with the number of steps n = 150 and the volume value over  =106.15 and the PGT value of the area is
=106.15 and the PGT value of the area is  =71.57.
=71.57.
It is important to analyze that the modeling of the pear and the egg by PGT is possible because they are surfaces of revolution which, since they occur in nature, have optimal shapes for their volume and surface.
V. CONCLUSIONS
The modeling was done in free software GeoGebra. The formats of some parcels were constructed by rotation curves on the symmetry axis in both two and three dimensions. These Pappus-Guldin Theorems (PGT) allow us to measure and analyze the numerical value of these models, such as volume and surface area. The advantage of the PGT method is that it allows to analyze of numerical values of objects easily and directly with Geogebra, the disadvantage of the method is that it can be used only for solids obtained by rotation. The applied program provides a simple language as long as the figure has an axis of symmetry according to [14]. Since the work is extensive, we note that we combine theory and practice to provide practical results that can be applied in industries, such as the packaging industry.
In future work, costs can be minimized, especially in the production of packaging, by conducting a study on the use of minimum surface area to determine the shapes of some packaging, as well as a method to improve the use of packaging is to reduce the material used in the construction of this packaging and shaping to be able to reduce overall costs and bring better transportation, storage, distribution, and consumption conditions for the sale and consumption of goods. As a result, logistics would spend less time to reduce costs, a strategy to better serve customers, vehicles that consume less fuel, are less harmful to the environment, and have potential in their use of recycling in packaging.
References
[1] Anton, H., Rorres, C., “Álgebra Linear com aplicações'', Bookman, Porto Alegre, vol 8, p.16, 2001.
[2] Benainous, Edileuza Coelho da Silva.,”Nescau:uma análise da estratégica de Reposicionamento do produto via embalagens”.
[3] Dantas, S.C., Mathias, C.V, "Formas de revolução e cálculo de volume”, Ciência e Natura, vol 39, n. 1, p. 142-155, 2017.
[4] Andrade, M.S., Simulação e modelagem computacional com o software Modellus: aplicações práticas para o ensino de física'', Editora Livraria da Física, 2016.
[5] Carmo, M.P., “Geometria diferencial de curvas e superfícies”, SBM-Sociedade Brasileira de Matemática, 2005.
[6] Hohenwarter, M., (2002). ”GeoGebra'', Available in: http://www. geogebra. org/cms/en. Accessed on June 25, 2022.
[7] Keller, I., Vicente, F., dos Santos, R., “Um Novo Formato de Garrafa Pet'', XI Simpósio de Excelência em Gestão e Tecnologia,AEDB, 2014.
[8] Kirchner, F.F.,Filho, A.F., Scolforo, J.R.S., Machado, S.A., Mitishita, E.A., “O uso de funções spline no cálculo de volumes de árvores'', Floresta, vol 19, n. 1,UFPR,1989.
[9] Kurokawa, C.Y., “`Áreas e volumes de Eudoxo e Arquimedes e Cavalieri e o Cálculo Diferencial e Integral'', UNICAMP, 2015.
[10] Nunes, É,O., “Modelagem Geométrica e Sweeping'', Uff. Available in : http://www.ic.uff.br/~aconci/sweeping.html. Accessed on June 25, 2022.
[11] Pinho, M.S., “ Computação Gráfica Modelagem de Sólidos'', PUCRS.
[12] Rooney, A., “A História da Matemática: Desde a criação das pirâmides até a exploração do infinito'', São Paulo: M. Books do Brasil Editora LTDA, 2012.
[13] Roque, T., “História da matemática'', Editora Schwarcz-Companhia das Letras, 2012.
[14] Trevisan, E.P, Trevisan, A.C.R., “Teorema de Pappus-Guldin com auxílio dos softwares maxima e winplot: atividade a uma turma de cálculo II'', III Simpósio Internacional de Pesquisa em Educação Matemática – III SIPEMAT,UFC, 2012.
[15] Volny, Petr., Volna, Jana., Smetanová, Dana., “Visualization of Numerical Data in Geogebra”, Littera Scripta, n.2, 2012

