Segmentation of Lung Tomographic Images Using U-Net Deep Neural Networks
Latin-American Journal of Computing, vol. 10, no. 2, pp. 106-119, 2023
Escuela Politécnica Nacional
Received: 13 March 2023
Accepted: 17 May 2023
Abstract: Deep Neural Networks (DNNs) are among the best methods of Artificial Intelligence, especially in computer vision, where convolutional neural networks play an important role. There are numerous architectures of DNNs, but for image processing, U-Net offers great performance in digital processing tasks such as segmentation of organs, tumors, and cells for supporting medical diagnoses. In the present work, an assessment of U-Net models is proposed, for the segmentation of computed tomography of the lung, aiming at comparing networks with different parameters. In this study, the models scored 96% Dice Similarity Coefficient on average, corroborating the high accuracy of the U-Net for segmentation of tomographic images.
Keywords: U-Net, Semantic Segmentation, Deep Neural Networks, Biomedical Images.
I. Introduction
In recent years, several works involving Artificial Intelligence (AI) models in biomedical applications have been successful in their proposal. According to [1] and [2], startups such as Ubenwa use acoustic signal processing and machine learning to optimize the diagnosis of asphyxia during birth under low resources.
In other work, Bellemo et al. [3] conducted a study that examines the potential of AI to diagnose diabetic retinopathy in Zambia. Therefore, in view of the great impact and complexity of AI, it is divided into sub-areas of study based on its methods, applications and architectures. One of such areas is Deep Learning (DL) [4].
DL focuses on complex neural networks architectures called DNNs (Deep Neural Networks). According to [5], DL models have architectures with multiple hidden layers, giving depth and complexity to the network. This complexity allows the network to learn different features with various levels of abstraction and generality.
There are several architectures of DNNs, characterized by different method or application, which are used for example for partitioning regions of interest in a set of images. This image processing task is called segmentation and can be applied in various fields such as engineering or medicine.
According to Santos et al. [6], segmentation aids the processing and analysis of medical images by splitting it, and using its parts for correlation with normal anatomy or lesions.
Segmentation of biomedical images has a great importance during a diagnosis, because locating tumors or organs in a medical image is a laborious process, even more so when applied to a large number of images that make up a volume of the examined body [7]. Basically, in a manual segmentation, the professional observes and partitions the objects of analysis.
If the expert uses algorithms or software, then it is a semiautomatic segmentation. For example, local adaptive segmentation algorithms can provide accurate and robust results. However, there is an influence on the quality of segmentation according to the settings applied by each practitioner [8], [9].
Since the manual or semiautomatic methodology is repetitive, it becomes less productive and susceptible to mistakes. Therefore, segmentation has been automated and performed with different mathematical and computational methods such as prototype pairing, geometric modeling, algorithms, statistics, and neural networks [10]–[12].
In this sense, there are several architectures of DNNs for image segmentation, including optimized for medical images such as conventional X-rays, Computed Tomography (CT) and Magnetic Resonance. Some of them are used in the works of Yang et al. [13], Santos et al. [14] and Shusharina et al. [7].
Among the DNNs used for segmentation, U-Net [15] has achieved prominence. The great performance of U-Net in segmentation tasks is a result of its architecture based on successive convolutions and deconvolutions, configuring encoding and decoding sections.
Such a network was first implemented by Ronneberger et al. [15] for biomedical segmentation of 2D images. It was later refined to be applied to 3D images by Çiçek et al. [16]. This peculiarity of U-Net has made it one of the main networks used in the segmentation of medical or biomedical images, even requiring less data (images) to achieve good results [17].
For example, Dong et al. [18] used U-Net for semantic segmentation, highlighting the objects of interest. After segmentation, the objects were classified according to their degree of similarity as lung (left or right), heart, esophagus, or vertebra. Christ et al. [19] applied two U-Net cascade representations, with one of them, they intended exclusively for segmentation and localization of the liver. The other network was in charge of segmenting the tumor within a delimiting region of the CT image.
Therefore, considering the impact that U-Net architecture has on the segmentation of biomedical images, the current work aims to study the performance of U-Net in the segmentation of lung CTs. Analyzing a possible significant influence of the number of levels on the network performance through two architecture configurations. Some training parameters, namely the number of epochs (iterations) and the Batch Size (BS) were also investigated.
Thus, in the present study an evaluation of the effectiveness of some U-Net models is proposed for segmenting healthy lung CT scans. Besides the validation of the networks, it is expected to consolidate one or more models for possible applications in the biomedical area, according to the works of Paiva et al. [20] and Sena et al. [21].
II. Theoretical Background
Some work and descriptions about neural networks, especially U-Net, in image segmentation will be discussed. In this aspect, the work goes through some common literature and reviews on the subject. From this, it was possible to define the types of segmentations seen in the literature, besides describing the U-Net from its particularities.
A. Image Segmentation
Semantic image segmentation is defined as a process that aims to classify the pixels of an image with semantic labels. In the case of instance segmentation, it is possible to partition individual objects. The combination of both processes is known as panoptic segmentation [22]. Thus, in the field of computer vision, segmentation is defined as a step that precedes the classification of objects of interest [23].
Chen et al. [24] reviewed several papers involving the segmentation of cardiac images using DL. Using DNNs, it is possible to highlight anatomical structures of interest, such as ventricles, atria, and vessels. In this aspect, Gosh et al. [23] proposes a study on the different techniques used in image segmentation. The article brings a list of the different neural network architectures used for segmentation as well as their singularities.
In computer vision, the Convolutional Neural Network (CNN) is one of the most widespread techniques for image segmentation [25]. Its learning, in practical terms, occurs by successive segmentations of the input images (forward pass) and the retrofitting of the weights (backward pass) after the calculation of the loss function [26], [27].
Wang et al. [28] investigated segmentation for pathological analysis. Many machine learning algorithms, such as CNNs, have been proposed to automatically segment pathology images. According to the authors, CNNs, such as Fully Convolutional Networks (FCNs), stand out for their accuracy, computational efficiency, and generalizability.
In biomedical applications, the process of segmentation occurs in the partition of an image into multiple segments, simplifying a complex digital image. This procedure allows removing uninteresting information from other objects or artifacts, thus optimizing the image analysis [29].
In this work, the U-Net models propose a semantic segmentation, since it is interested in segmenting the lungs in tomographic images. Therefore, the models are not concerned with partitioning the objects after their detection, not differentiating the left lung from the right lung.
B. U-Net
The U-Net architecture was launched in 2015 [15] and has been improved since 2016 [16]. Its prominence is its effectiveness in segmenting biomedical images without the need for a large number of images to achieve this feature [30]. Since it is a CNN, it is composed of convolution and pooling layers, its particularity lies in the deconvolutions that characterizes the FCN.
Unlike a conventional CNN focused on nominal classification, the goal of the U-Net is to generate new images properly segmented, keeping the dimensions of the input image and the "masks", called Ground Truths (GTs) [26]. The GTs represent the images segmented manually by the professional, they are the ones that together with the input images will feed the network for the beginning of the training.
The insertion of the input images starts the downsampling step, described as the process of successive convolutions that make the image contraction and encodes its information. This process is also called encoder and corresponds to the typical organization process of a CNN [15], [25].
The encoder stage ends at the level where the lower feature map is. From this level on we have the survey layers, also called decoder, which is composed of successive deconvolutions that reduce the number of channels and decode the information, expanding the image by unpooling and highlighting the segmented objects [5]. Sha et al. [31] present an application of U-Net, a semantic segmentation CNN, modified for climate analysis.
The differential of the U-Net architecture is the skip-connections, which are non-sequential neural connections between the symmetric convolution and deconvolution layers. Thus, obtaining an improvement in the updates of the weights and avoiding the saturation gain as the network increases its depth [15].
This particularity causes U-Net architectures to use discrete details learned at the encoder stage to build the segmented image at the decoder layers [30]. Such architecture can be visualized in Fig. 1. Its design diagram represents one of the networks tested in the present work, based on [31], with 5 levels. Fig. 2 represents the second U-Net architecture of the work, with 7 levels.
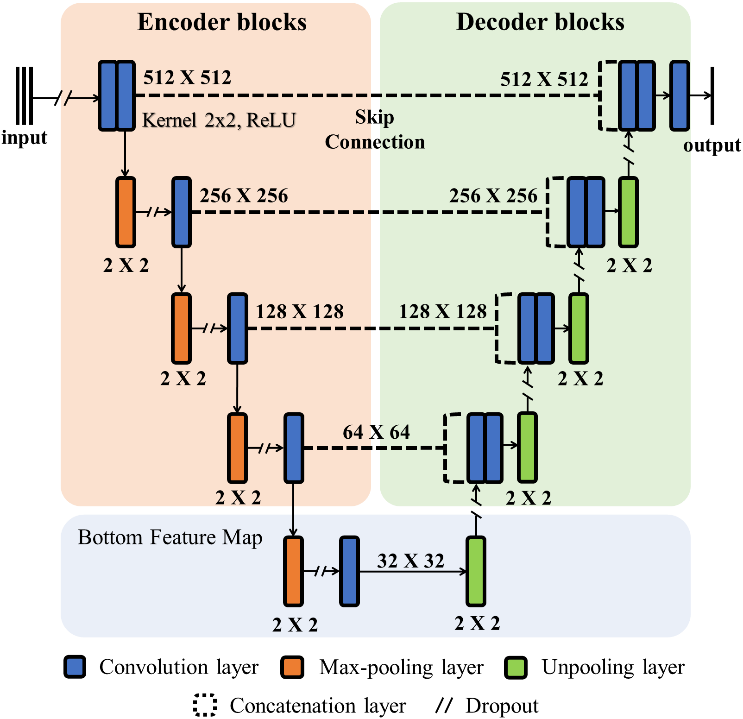

III. Methodology
The methodology used in the work was divided into five parts, aiming at reproducibility. The first and second parts refer to the data used for training the neural network, the third and fourth parts to the architectures of the neural network and its training. The fifth part is about the evaluation method, followed by the metrics used for scoring, and finally the statistical analysis used to verify a possible significant difference between the models.
A. Dataset
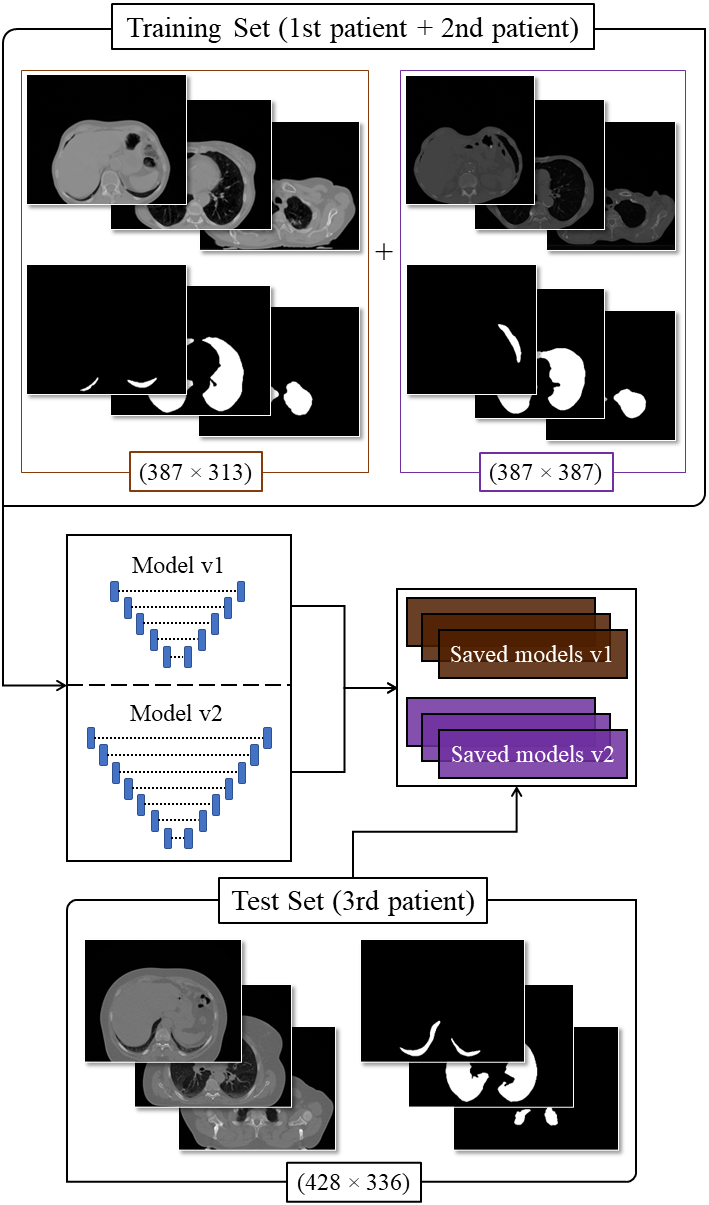
The images used for training and validation of the networks come from the Cancer Image Archive platform (cancerimagingarchive.net). Three of the 60 thoracic CT image sets from the 2017 AAPM Thoracic Auto-segmentation Challenges [32]–[34] were used. Each set is a scan that contains the entire region of a patient's chest, there was concern that the sets chosen were from different patients, aiming for a more generalist training.
Each thoracic volume image battery has manual contours outlined according to the RTOG1106 guidelines. The contours of each tone highlight some organs such as heart, lungs (left and right), esophagus and vertebra. Each raw set of images of the first, second and third patient have 161, 154 and 148 images, respectively.
B. Data Preprocessing
The sets of images obtained have a lot of information that is not relevant to the network, i.e., because they are a full chest scan, they have images without the presence of the lungs. Therefore, in view of the large number of irrelevant images in each set, it was necessary to remove such slices from the total volume.
After this selection, we obtained 193 images of the first plus second patient that were used for training and internal validation. In addition, 71 images of the third patient were separated for testing and network evaluation.
The second step in the grouping was to extract the GTs from each volume, for which it was necessary to use the "3D Slicer" software. This open source program is recommended by the Cancer Image Archive to interpret the images in DICOM (short for "Digital Imaging and Communications in Medicine") format.
Since the objective of the work is to analyze only the segmentation of the lungs. The other contours of the heart, esophagus and vertebra were removed, thus obtaining only the unified and binarized GTs of the lungs.
The images obtained have, by default, 512 × 512 pixels, however, such dimension includes other elements that are not important for the network, such as the table where the person lies down to perform the exam. Therefore, it was necessary to crop the images to remove such elements, resulting in new images with varied dimensions and specified in Fig. 3.
After the cropping, the images were resized to the standard format (512 × 512). It is worth mentioning that the images were extracted in TIF (Tagged Image File) format, aiming for greater compatibility with the Python language and libraries. Besides this change, the resolution of the images was reduced from 32 bits to 8 bits.
Subsequently, the images were imported and interpreted as a list of matrices. Each element of the matrix, which corresponds to the pixels, went through a normalization process from the maximum and minimum pixel values. After normalization, a list of pixel matrices ranging from 0 to 1 was obtained from both the input images and the GTs.
C. Network Architecture
With the images properly formatted, the next step was to build the U-Nets models. Taking into account the impact that the number of levels can have on the final performance, two network configurations were implemented (v1 and v2), respectively with 5 and 7 levels, see Fig. 1 and Fig. 2.
The convolution layers are two-dimensional, followed by max-pooling layers. ReLU [35] is the activation function inherent to the process. The dropout is used to avoid overfitting, while the concatenation layers illustrate the skip-connection action [26], [15].
Training a CNN for segmentation or classification can be summarized as minimizing the loss function. To complement this learning process, the Adam optimizer was used. After the architecture design was finalized, training methods were assigned to the network function.
D. Network Training
One of the techniques used to generalize the input data is "Data Augmentation", which generates new images coming from the input images from different perspectives. Data Augmentation was used to generate input images and their respective GTs horizontally inverted, doubling the amount of images during training.
In view of the investigative study of BSs in the training stage, the callbacks "ReduceLRonPlateaus" and "EarlyStopping" from the Keras library were used. The purpose of this is to establish a common iteration for all models, allowing comparison of BSs.
The callbacks are used by DNN during training, and are a compilation of functions for monitoring the internal states and statistical results of the model [26], [36]. “EarlyStopping” is responsible for terminating the DNN training if the model does not show a decrease in the validation group error after a specific number of epochs, such number is called "patience".
During the training process, if there is no decrease in error for a "patience", "ReduceLRonPlateau" reduces the U-Net learning rate. This method is used to avoid a local optima and find the global optima.
To study the impact of BSs on network progress, the two architectures were trained with three different BSs; 4, 8 and 16. The analysis of the number of epochs was done by studying network performance according to loss.
“EarlyStopping” is a good way to establish the number of epochs a network needs. Through a series of preliminary tests, a number of epochs equal to 80 was empirically estimated for all models. Then, 10 trainings were done for each BS, that is, 30 models of each version of the neural network (v1 and v2), totaling 60 trained models.
E. Evaluation
To evaluate the performance of networks, it is necessary to have a number of models capable of covering various training scenarios. Therefore each net configuration was trained 10 times with random starts. This approach allows the models to be analyzed with a high degree of generalization and reproducibility.
This method consists of training the net with all training samples, for internal validation of the network. One of the sets (the testing set) is separated to test the model after training. The segmented images from the test set are separated and evaluated later.
In this sense, the set of two patients was divided into 80% of the images for training and 20% for internal validation of the network. The images from the third patient was used in the testing stage, where the performance data was collected based on the metrics established in the work.
Such a method is ideal for cases where there is little data, because the model error was calculated for each sample, obtaining a final average of the test volume and reducing the computational cost.
F. Dice Similarity Coefficient
There are several metrics to evaluate and validate DNN models. Generally, each metric can be applied in different situations, but there are certain fields where its use best matches the performance of the neural network, delivering higher reliability.
The Dice Similarity Coefficient (DSC) is a metric that analyzes the similarity between two samples [37]. DSC is commonly used in biomedical image analysis. It can be defined as the ratio of twice the area of overlap between segmentations and GTs by the total number of pixels [22].
The DSC is identical to the F1 Score [38] and has its mathematical representation described in (1). Where |∙| represents the cardinality of sets A and B.
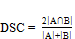 (1)
(1)In other words, the DSC is a measure that quantifies the degree of similarity between the segmented image obtained by the model and the reference image (GT) during the supervised training or testing step. The DSC for each image can vary between 0 (no overlap) and 1 (complete overlap)
G. Statistical Analysis
After the trainings, each model went through the testing step with the third patient data. After segmentation, the DSC of such a set was calculated. The scores were organized according to the network version and BS, so the comparison was made between BSs per model version.
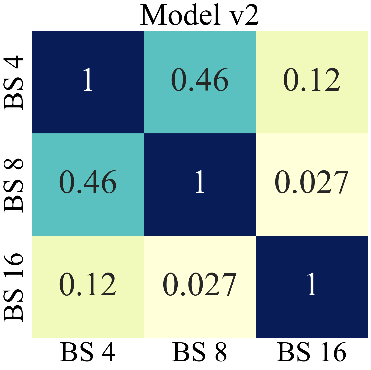
To check for a possible statistically significant difference between BSs, the Kruskall-Wallis test [39] was used on the 6 groups of data, see Table 1. The p-value shows whether or not the null hypothesis shall be rejected for values above or below 5%. In this case, the null hypothesis is that there is no statistically significant difference between the groups if the p-value is less than the 0.05 threshold.
If there is statistically significant differences, Dunn's test [40] shall be used. Dunn's test aims to find which pairs of groups, within each version of the model, have a significant difference

IV. Results and Discussions
As described in the methodology, 60 DNNs were trained and the models were saved to receive the test images. Table 1 shows the scores of the v1 and v2 models with 10 runs for each BS. The bottom of Table 1 displays the mean, standard deviation, and the maximum and minimum value for each column.
From the preview results, it can be seen that all models obtained a performance above 90%, except for one of the v2 models with BS equal to 8. Such results reinforce the positive deliberations about U-Net.
A. Statistical Analysis of The Models
From these data, the Kruskal-Wallis test was applied, and the null hypothesis can be accepted, since the p-value was less than 5% (p-value < 0.05). The boxplots in Fig. 4, 5 and 6 show a trend towards higher DSCs for BSs equal to 16. This observation also occurs in Dunn's test, as described later.
Using larger batches allows the training time to be reduced. Dong et al. [18] used 35 thoracic CT sets to train the network, for these cases, not taking advantage of parallel processing can make training slow and error prone.
In [41]–[43], the authors used different methods to determine the training parameters, either through prior knowledge or experimental testing. The choice of parameters such as BS may be little debated, however, the statistical study of these parameters allows training to be optimized with greater reliability and reproducibility.
Kandel and Castelli [44] show a high correlation between BS and learning rate. According to the authors, large BSs perform better for large learning rates. Such a correlation can be tested in future work by bringing a statistical study on such parameters.
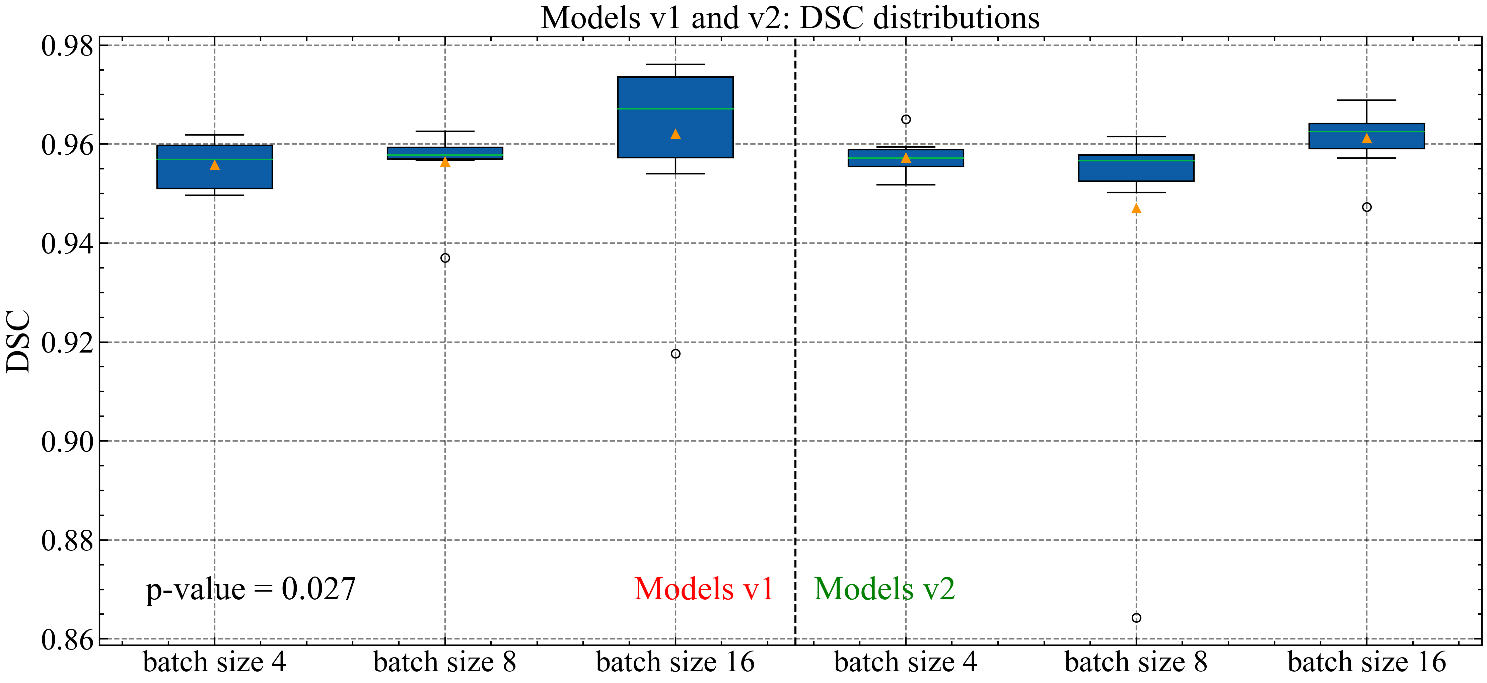


Regarding separately, each model in Fig. 5 and 6, only v2 has a statistically significant difference between the BSs (p-value = 0.026). The isolated results of v1 also tend to be different, but it is not conclusive (p-value = 0.076). Fig. 7 shows Dunn’s test results for each model, highlighting BS 16, the main group responsible for the statistical divergences (p-value = 0.027).
The larger BS was favored with the increase of levels in the v2 model. However, regardless of the model, it is observed that the BS 16 is more likely to obtain better results and be applied in future works.
B. Practical Segmentation Analysis
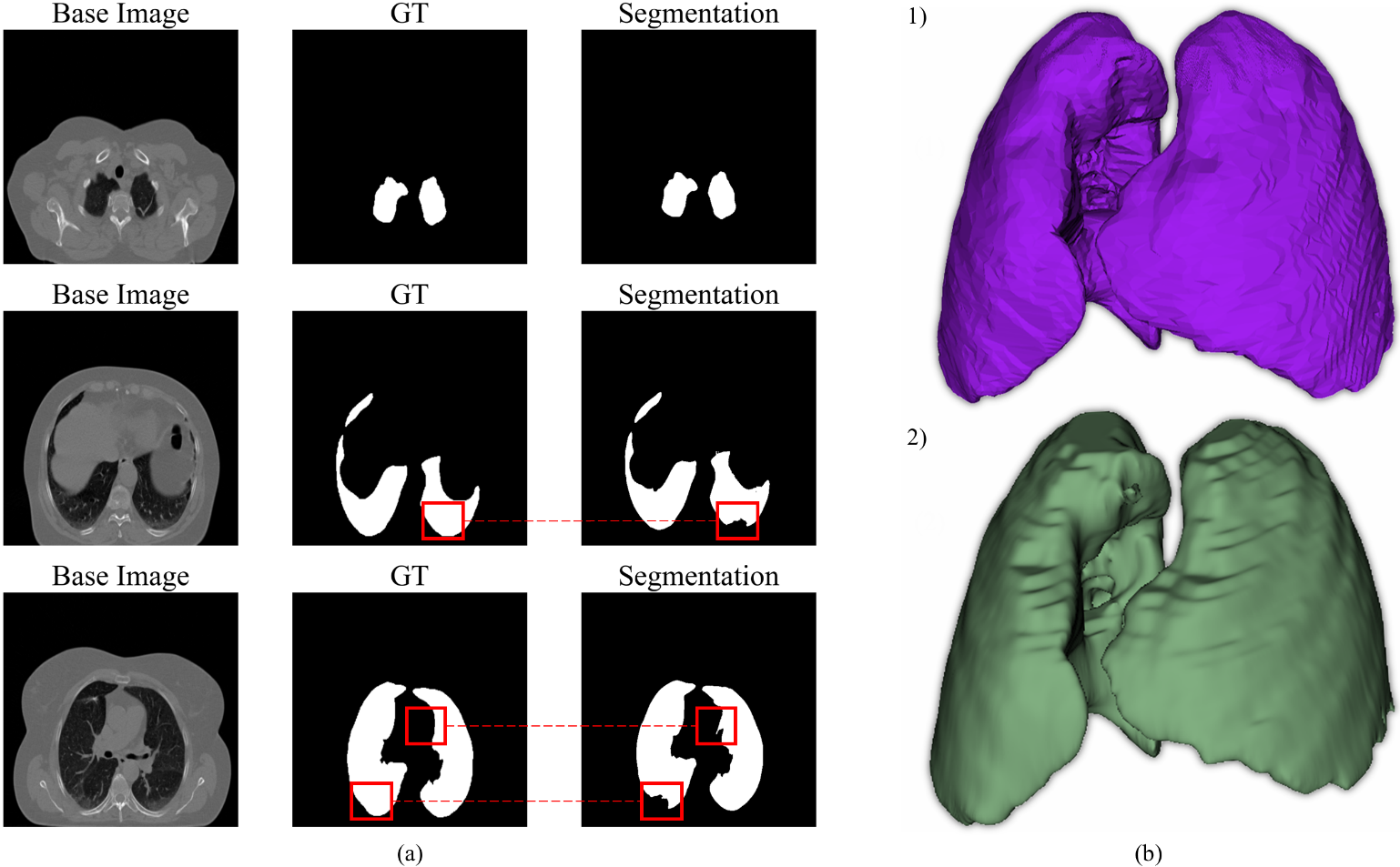
The comparison in Fig. 8a allows exemplifying the origin of most of the losses in the metric, which is mostly located in the lower regions of the tone, such location is highlighted in red. This makes the stereology of the segmented lung volume different from the real one dictated by the GTs, i.e., a loss of white pixels in the segmented images.
The segmented lung volume, Fig. 8b (2), respects the shape of the organ, even with the small differences. Analyzing the volumes, one can see some irregularities on the surface of the segmented lung, a characteristic not found in the real volume, see Fig. 8b (1). In some biomedical applications, the small amount of samples leads to low data volume. The trained models were successful in segmenting the images, even with the use of 2 of the original 60 data sets.

V. Conclusions
From the results, it was possible to establish some aspects regarding the variability of U-Net. BS has a significant impact for model v2. The v1 model, despite not reaching statistical criteria, showed similar behavior to the v2 model. Increasing the levels slightly improved the results, raising hypotheses for future work involving networks with different levels. This perspective can be evaluated with other network parameters.
Although adding levels has achieved a performance gain that is sensitive to statistical tests, there are other ways to achieve considerable gains. New architectures, such as 3D U-Net [16], U-Net++ [45], U-Net 3+ [46] and ELU-Net [47], present a substantial gain through other non-trivial modifications and could be applied in future work.
According to the analyses, BSs equal to 16 provided better results while reducing training time due to parallel processing. Thus, BSs equal to 16 are suitable for future biomedical research, and can be increased as the number of images for training increases.
However, it is hoped to investigate the BS in combination with other parameters and features of the model, such as the learning rate or network levels. In [44] the authors showed the correlation between these parameters, but between different learning optimizers.
References
[1] A. Owoyemi, J. Owoyemi, A. Osiyemi, and A. Boyd, “Artificial Intelligence for Healthcare in Africa,” Front Digit. Health, vol. 2, Jul. 2020, doi: 10.3389/fdgth.2020.00006.
[2] C. C. Onu, J. Lebensold, W. L. Hamilton, and D. Precup, “Neural Transfer Learning for Cry-Based Diagnosis of Perinatal Asphyxia,” in Interspeech 2019, Sep. 2019, pp. 3053–3057. doi: 10.21437/Interspeech.2019-2340.
[3] V. Bellemo et al., “Artificial intelligence using deep learning to screen for referable and vision-threatening diabetic retinopathy in Africa: a clinical validation study,” Lancet Digit. Health, vol. 1, no. 1, pp. e35–e44, May 2019, doi: 10.1016/S2589-7500(19)30004-4.
[4] Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, May 2015, doi: 10.1038/nature14539.
[5] M. A. Wani, F. A. Bhat, S. Afzal, and A. I. Khan, Advances in Deep Learning, vol. 57. Singap.: Springer Singap., 2020. doi: 10.1007/978-981-13-6794-6.
[6] M. K. Santos, J. R. Ferreira Júnior, D. T. Wada, A. P. M. Tenório, M. H. Nogueira-Barbosa, and P. M. de A. Marques, “Artificial intelligence, machine learning, computer-aided diagnosis, and radiomics: advances in imaging towards to precision medicine,” Radiol. Bras., vol. 52, no. 6, pp. 387–396, Dec. 2019, doi: 10.1590/0100-3984.2019.0049.
[7] N. Shusharina et al., “Cross-Modality Brain Structures Image Segmentation for the Radiotherapy Target Definition and Plan Optimization,” in Segmentation, Classification, and Registration of Multi-modality Med. Imag. Data, Cham: Springer, 2021, pp. 3–15. doi: 10.1007/978-3-030-71827-5_1.
[8] P. Iassonov, T. Gebrenegus, and M. Tuller, “Segmentation of X-ray computed tomography images of porous materials: A crucial step for characterization and quantitative analysis of pore structures,” Water Resour. Res., vol. 45, no. 9, Sep. 2009, doi: 10.1029/2009WR008087.
[9] A. Buratti, J. Bredemann, M. Pavan, R. Schmitt, and S. Carmignato, “Applications of CT for Dimensional Metrology,” in Industrial X-Ray Computed Tomography, Cham: Springer Int. Publishing, 2018, pp. 333–369. doi: 10.1007/978-3-319-59573-3_9.
[10] A. Alvarenga de Moura Meneses et al., “Automated segmentation of synchrotron radiation micro-computed tomography biomedical images using Graph Cuts and neural networks,” Nucl. Instrum. Methods Phys. Res. A, vol. 660, no. 1, pp. 121–129, Dec. 2011, doi: 10.1016/j.nima.2011.08.007.
[11] A. El-Baz, X. Jiang, and J. S. Suri, Biomedical Image Segmentation: Advances and Trends. 2016.
[12] A. A. de M. Meneses, D. B. Palheta, C. J. G. Pinheiro, and R. C. R. Barroso, “Graph cuts and neural networks for segmentation and porosity quantification in Synchrotron Radiation X-ray μCT of an igneous rock sample,” Appl. Radiat. and Isot., vol. 133, pp. 121–132, Mar. 2018, doi: 10.1016/j.apradiso.2017.12.019.
[13] J. Yang et al., “Autosegmentation for thoracic radiation treatment planning: A grand challenge at AAPM 2017,” Med. Phys., vol. 45, no. 10, pp. 4568–4581, Oct. 2018, doi: 10.1002/mp.13141.
[14] M. K. Santos, J. R. Ferreira Júnior, D. T. Wada, A. P. M. Tenório, M. H. Nogueira-Barbosa, and P. M. de A. Marques, “Artificial intelligence, machine learning, computer-aided diagnosis, and radiomics: advances in imaging towards to precision medicine,” Radiol. Bras., vol. 52, no. 6, pp. 387–396, Dec. 2019, doi: 10.1590/0100-3984.2019.0049.
[15] O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional Networks for Biomedical Image Segmentation,” in Med. Image Comput. and Computer-Assisted Intervention, Cham: Springer, 2015, pp. 234–241. doi: 10.1007/978-3-319-24574-4_28.
[16] Ö. Çiçek, A. Abdulkadir, S. S. Lienkamp, T. Brox, and O. Ronneberger, “3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation,” in Med. Image Comput. and Computer-Assisted Intervention, Cham: Springer, 2016, pp. 424–432. doi: 10.1007/978-3-319-46723-8_49.
[17] J. C. González Sánchez, M. Magnusson, M. Sandborg, Å. Carlsson Tedgren, and A. Malusek, “Segmentation of bones in medical dual-energy computed tomography volumes using the 3D U-Net,” Physica Medica, vol. 69, pp. 241–247, Jan. 2020, doi: 10.1016/j.ejmp.2019.12.014.
[18] X. Dong et al., “Automatic multiorgan segmentation in thorax CT images using U-net-GAN,” Med. Phys., vol. 46, no. 5, pp. 2157–2168, May 2019, doi: 10.1002/mp.13458.
[19] P. F. Christ et al., “Automatic Liver and Lesion Segmentation in CT Using Cascaded Fully Convolutional Neural Networks and 3D Conditional Random Fields,” in Med. Image Comput. and Computer-Assisted Intervention, Cham: Springer, 2016, pp. 415–423. doi: 10.1007/978-3-319-46723-8_48.
[20] K. Paiva et al., “Performance evaluation of segmentation methods for assessing the lens of the frog Thoropa miliaris from synchrotron-based phase-contrast micro-CT images,” Physica Medica, vol. 94, pp. 43–52, Feb. 2022, doi: 10.1016/j.ejmp.2021.12.013.
[21] G. Sena et al., “Synchrotron X-ray biosample imaging: opportunities and challenges,” Biophys. Rev., vol. 14, no. 3, pp. 625–633, Jun. 2022, doi: 10.1007/s12551-022-00964-4.
[22] S. Minaee, Y. Y. Boykov, F. Porikli, A. J. Plaza, N. Kehtarnavaz, and D. Terzopoulos, “Image Segmentation Using Deep Learning: A Survey,” IEEE Trans. Pattern Anal. Mach. Intell., pp. 1–1, 2021, doi: 10.1109/TPAMI.2021.3059968.
[23] S. Ghosh, N. Das, I. Das, and U. Maulik, “Understanding Deep Learning Techniques for Image Segmentation,” ACM Comput. Surv., vol. 52, no. 4, pp. 1–35, Jul. 2020, doi: 10.1145/3329784.
[24] C. Chen et al., “Deep Learning for Cardiac Image Segmentation: A Review,” Front Cardiovasc. Med., vol. 7, Mar. 2020, doi: 10.3389/fcvm.2020.00025.
[25] Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proc. of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998, doi: 10.1109/5.726791.
[26] Francois Chollet, Deep Learning with Python, 2nd ed. 2021.
[27] D. E. Rumelhart, G. E. Hinton, and R. J. Williams, “Learning representations by back-propagating errors,” Nature, vol. 323, no. 6088, pp. 533–536, Oct. 1986, doi: 10.1038/323533a0.
[28] S. Wang, D. M. Yang, R. Rong, X. Zhan, and G. Xiao, “Pathology Image Analysis Using Segmentation Deep Learning Algorithms,” Am J Pathol, vol. 189, no. 9, pp. 1686–1698, Sep. 2019, doi: 10.1016/j.ajpath.2019.05.007.
[29] A. Voulodimos, N. Doulamis, A. Doulamis, and E. Protopapadakis, “Deep Learning for Computer Vision: A Brief Review,” Comput. Intell. Neurosci., vol. 2018, pp. 1–13, 2018, doi: 10.1155/2018/7068349.
[30] N. Siddique, S. Paheding, C. P. Elkin, and V. Devabhaktuni, “U-Net and Its Variants for Medical Image Segmentation: A Review of Theory and Applications,” IEEE Access, vol. 9, pp. 82031–82057, 2021, doi: 10.1109/ACCESS.2021.3086020.
[31] Y. Sha, D. J. Gagne II, G. West, and R. Stull, “Deep-Learning-Based Gridded Downscaling of Surface Meteorological Variables in Complex Terrain. Part I: Daily Maximum and Minimum 2-m Temperature,” J Appl. Meteorol. Climatol., vol. 59, no. 12, pp. 2057–2073, Dec. 2020, doi: 10.1175/JAMC-D-20-0057.1.
[32] K. Clark et al., “The Cancer Imaging Archive (TCIA): Maintaining and Operating a Public Information Repository,” J Digit. Imaging, vol. 26, no. 6, pp. 1045–1057, Dec. 2013, doi: 10.1007/s10278-013-9622-7.
[33] “Data from Lung CT Segmentation Challenge,” The Cancer Imaging Archive, May 2017.
[34] J. Yang et al., “Autosegmentation for thoracic radiation treatment planning: A grand challenge at AAPM 2017,” Med. Phys., vol. 45, no. 10, pp. 4568–4581, Oct. 2018, doi: 10.1002/mp.13141.
[35] N. Vinod and E. H. Geoffrey, “Rectified Linear Units Improve Restricted Boltzmann Machines,” in ICML, Jan. 2010.
[36] T. Hastie, J. Friedman, and R. Tibshirani, The Elements of Statistical Learning. New York, NY: Springer New York, 2001. doi: 10.1007/978-0-387-21606-5.
[37] T. J. Sorensen, A method of establishing groups of equal amplitude in plant sociology based on similarity of species content and its application to analyses of the vegetation on Danish commons. I kommission hos E. Munksgaard, 1948.
[38] C. Sammut and G. I. Webb, Eds., Encyclopedia of Machine Learning. Springer Science & Business Media, 2011.
[39] W. H. Kruskal and W. A. Wallis, “Use of Ranks in One-Criterion Variance Analysis,” J Am Stat. Assoc., vol. 47, no. 260, pp. 583–621, Dec. 1952, doi: 10.1080/01621459.1952.10483441.
[40] O. J. Dunn, “Multiple Comparisons among Means,” J Am Stat. Assoc., vol. 56, no. 293, pp. 52–64, Mar. 1961, doi: 10.1080/01621459.1961.10482090.
[41] B. Acun, M. Murphy, X. Wang, J. Nie, C.-J. Wu, and K. Hazelwood, “Understanding Training Efficiency of Deep Learning Recommendation Models at Scale,” in 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Feb. 2021, pp. 802–814. doi: 10.1109/HPCA51647.2021.00072.
[42] N. Kumari and B. S. Saini, “Fully Automatic Wheat Disease Detection System by Using Different CNN Models,” in Sentiment Anal. and Deep Learn. Advances in Intell. Syst. and Comput., Singap.: Springer Singap., 2023, pp. 351–365. doi: 10.1007/978-981-19-5443-6_26.
[43] S. R. Nayak, D. R. Nayak, U. Sinha, V. Arora, and R. B. Pachori, “An Efficient Deep Learning Method for Detection of COVID-19 Infection Using Chest X-ray Images,” Diagnostics, vol. 13, no. 1, p. 131, Dec. 2022, doi: 10.3390/diagnostics13010131.
[44] I. Kandel and M. Castelli, “The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset,” ICT Express, vol. 6, no. 4, pp. 312–315, Dec. 2020, doi: 10.1016/j.icte.2020.04.010.
[45] Z. Zhou, M. M. Rahman Siddiquee, N. Tajbakhsh, and J. Liang, “UNet++: A Nested U-Net Architecture for Medical Image Segmentation,” in Deep Learn. in Med. Image Anal. and Multimodal Learn. for Clin. Decis. Support, Cham: Springer, 2018, pp. 3–11. doi: 10.1007/978-3-030-00889-5_1.
[46] H. Huang et al., "UNet 3+: A Full-Scale Connected UNet for Medical Image Segmentation," in ICASSP 2020 - 2020 IEEE Int. Conf. on Acoustics, Speech and Signal Process. (ICASSP), Barcelona, Spain, 2020, pp. 1055-1059, doi: 10.1109/ICASSP40776.2020.9053405.
[47] Y. Deng, Y. Hou, J. Yan, and D. Zeng, “ELU-Net: An Efficient and Lightweight U-Net for Medical Image Segmentation,” IEEE Access, vol. 10, pp. 35932–35941, 2022, doi: 10.1109/ACCESS.2022.3163711.

