1. INTRODUÇÃO
O interesse por esta pesquisa emerge de uma discussão entre as integrantes de um grupo de licenciandas, que realizavam o componente curricular de Produção Acadêmico Científica[1], sobre a abstração do conhecimento matemático e a sua exemplificação através de objetos manipulativos. A partir de nossas vivências em componentes curriculares práticas, realizadas durante o curso de Matemática Licenciatura, foi-se discutido como a matemática pode tornar-se difícil de compreender quando é destituída de um saber concreto e significativo, isto é, quando não permite a interação do aluno com aquilo que ele aprende.
Por outro lado, a equação do 2º grau tornou-se o nosso objeto de estudo por ser um conteúdo sobre o qual podem incidir dificuldades de aprendizagem. Acreditamos que estas podem se dar pelo fato do educando ter problemas ao tentar assimilar a abstração dessas equações. Tais problemas, no que lhes dizem respeito, são ocasionados pela ênfase no uso de fórmulas prontas, o que torna o ensino mecânico e sem significado para o aluno, desmotivando-o a aprender (SILVA, 2010).
Em contrapartida, os Parâmetros Curriculares Nacionais (PCNs) para a área de Matemática e a Base Nacional Comum Curricular (BNCC) afirmam que o ensino de álgebra não deve resumir-se a símbolos matemáticos (BRASIL, 1998; 2018). Desse modo, embasadas nestes documentos, sugerimos que o ensino de equações quadráticas na Educação Básica seja abordado de maneira manipulativa, utilizando material dourado.
O objetivo deste estudo é compreender se o processo manipulativo proporciona aprendizagem sobre o conteúdo de equações do 2º grau, ou seja, se favorece a compreensão das estratégias de resolução de equações quadráticas. Também buscamos investigar a contribuição do uso do material concreto para o processo de abstração e superação das dificuldades relacionadas a esse conteúdo.
À vista disso, a presente pesquisa volta-se para a seguinte problemática: Como uma proposta pedagógica que articule material dourado pode contribuir para a melhoria da aprendizagem da resolução de equações do 2º grau? Dado o seu caráter manipulativo e visual, a hipótese que se lança é que o uso do material dourado para resolver equações quadráticas configura-se em proposta metodológica eficaz para superar as dificuldades de aprendizagem quanto a esse conteúdo.
Este, apesar de acreditarmos ser um método eficaz para proporcionar aprendizagem, ainda é pouco explorado nos livros didáticos, o que traz relevância para este estudo e nos possibilita um espaço favorável para desenvolver propostas e pesquisas que articulem esses dois temas. Assim, a pesquisa poderá trazer contribuições para a área educacional e para a prática docente, uma vez que busca superar dificuldades de aprendizagem presentes no ensino de matemática.
Cabe salientar que a discussão teórica sobre o método não usual que será proposto nesta pesquisa não está intencionada na substituição do método de ensino usual utilizado nas escolas, pelo contrário, o nosso intuito é complementá-lo, apresentando um caminho que pode promover aprendizagens ao aluno, podendo, também, superar dificuldades em resolver equações do 2º grau.
Nas próximas seções dividimos o tema em estudo para melhor compreendê-lo. Na primeira traremos uma revisão de literatura com pesquisas que investigaram a utilização do material dourado como facilitador no processo de ensino e aprendizagem das equações quadráticas. Em seguida, faremos uma análise sobre como esse conteúdo é ensinado na Educação Básica. Logo após, buscaremos compreender como o material concreto pode colaborar para o processo de ensino e aprendizagem das equações do 2° grau. E, por fim, veremos como as equações quadráticas podem ser resolvidas por meio do material dourado.
2. PESQUISAS SOBRE O TEMA EM ESTUDO
Para consubstanciar esta pesquisa, traremos alguns estudos recentes que tratam de material dourado e equações do 2º grau. Ao revisarmos as pesquisas de Costa et al. (2018), Lins et al. (2019), Francisco, Né e Camiotto (2019) buscou-se investigar a utilização do material dourado como um recurso potencialmente significativo no processo de ensino e aprendizagem das equações quadráticas.
Costa et al. (2018) realizou uma pesquisa com o objetivo de propor diferentes recursos didáticos para o ensino de equações do 2º grau, dentre eles o material dourado. A pesquisa teve caráter qualitativo descritivo, com relato de experiência, e foi desenvolvida com estudantes do Ensino Fundamental. No que diz respeito ao material dourado, realizou-se uma proposta com o intuito de trabalhar a representação geométrica para a resolução das equações de segundo grau. A pesquisa chegou à conclusão de que o material dourado é um recurso facilitador do conhecimento, pois propicia a fixação do conteúdo lecionado e estimula a participação dos alunos, que se mostram mais abertos e interessados em aprender.
Lins et al. (2019), em sua investigação, observa que as dificuldades e o desinteresse dos alunos relacionados à matemática se devem ao ensino tradicional que lhes é oferecido. Com o intuito de tornar o ensino de equações quadráticas mais atrativo, a pesquisa propôs a busca de suas soluções por meio do material concreto. O estudo foi desenvolvido com três turmas do 9º ano do ensino fundamental, e o material utilizado consistiu em uma adaptação do material dourado, constituindo-se por placas de produtos notáveis. Os autores concluíram, ao final da pesquisa, que o material utilizado se mostrou um método eficaz para o ensino e resolução das equações do 2º grau, instigando o interesse e a participação dos alunos.
A pesquisa de Francisco, Né e Camiotto (2018) buscou analisar o aprendizado dos estudantes com relação ao conteúdo de equação do 2º grau por meio de um comparativo entre dois métodos de ensino: a fórmula de Bhaskara e o material dourado. O procedimento metodológico foi desenvolvido com duas turmas do 9º ano do Ensino Fundamental que não haviam estudado o conteúdo de equações quadráticas anteriormente. O estudo chegou à conclusão de que o material dourado é um recurso didático que traz novas potencialidades ao processo de ensino e aprendizagem das equações do 2º grau, proporcionando qualidades que apenas a utilização da fórmula de Bhaskara parece não alcançar.
Fica evidente que as pesquisas de Costa et al. (2018), Lins et al. (2019) e Francisco, Né e Camiotto (2019) apontam na mesma direção no tocante ao material dourado e o ensino de equações do 2° grau. Todos os estudos concluíram que o material dourado, à semelhança do que esperamos comprovar, é um recurso metodológico eficaz para proporcionar aprendizagem sobre o conteúdo de equações quadráticas, estimulando a participação e o interesse dos alunos. Na próxima seção buscaremos estabelecer uma conexão teórica entre os referenciais por ora citados e a forma como estes são apresentados nos livros didáticos.
3. O ENSINO DO CONTEÚDO EQUAÇÕES DO 2º GRAU
Para compreender como se dá o ensino das equações quadráticas, apoiar-nos-emos em uma pesquisa realizada por Pereira (2017), que objetivou analisar o conteúdo das equações do 2º grau por meio de um comparativo entre três livros didáticos de Matemática destinados ao 9º ano do Ensino Fundamental de uma escola da rede pública.
Nos livros Matemática e Realidade (LEZZI; DOLCE; MACHADO, 2009), Vontade de Saber (SOUZA; PATARO, 2012) e Praticando Matemática 9 (SILVEIRA; MARQUES, 2013), a resolução das equações quadráticas se apresenta associada à Fórmula de Bhaskara e a metodologia utilizada segue de um referencial teórico, alguns exemplos e baterias de exercícios a serem resolvidos.
A pesquisa de Pereira (2017) evidencia que o ensino do conteúdo das equações do 2º grau está associado a exercícios mecânicos e repetitivos, além de enfatizar a Fórmula de Bhaskara como método resolutivo. Como apresentado no decorrer desta pesquisa, acreditamos que tal metodologia cria uma defasagem matemática sobre esse conteúdo, pois o desassocia do cotidiano do aluno. Além disso, favorece o surgimento de dificuldades relacionadas ao conteúdo algébrico, pois a sua abstração não é exemplificada por meio de um conhecimento concreto.
Em um de seus estudos, House (1995, p.1) nos apresenta a fala de um aluno em relação ao aprendizado da álgebra: “É muito difícil e, apesar de muito instrutiva, noventa por cento das vezes é frustrante”. Observa-se, assim, que os alunos podem não conseguir entender a real função e o objetivo de uma variável em qualquer que sejam as expressões matemáticas, o que nos leva a crer que o conteúdo de equações do 2º grau deve ser abordado com uma metodologia que busque superar essas dificuldades.
Do estudo realizado por Pereira (2017), observamos que nenhum dos livros didáticos analisados sugeriram abordar o conteúdo de equações quadráticas de maneira manipulativa. Todavia, como vimos na seção anterior, o material dourado é um recurso útil para proporcionar aprendizagem sobre tal conteúdo. Desse modo, este estudo ganha relevância ao propor um método eficaz para proporcionar aprendizagem que ainda é pouco explorado nos livros didáticos, e nos possibilita um espaço favorável para desenvolver propostas e pesquisas que articulem esses dois temas. Na seção seguinte, buscaremos explicar como o processo manipulativo pode favorecer o fenômeno da aprendizagem.
4. MATERIAIS CONCRETOS E O PROCESSO DE ENSINO E APRENDIZAGEM DAS EQUAÇÕES DO 2° GRAU
Nesta seção, vamos elucidar a potencialidade do uso do material concreto como um recurso que pode tornar-se eficiente para proporcionar aprendizagens significativas. A princípio, precisamos compreender em que consiste esse material ao qual nos referimos. Reys (1971, apudPASSOS, 2006, p. 2) define material concreto como “objetos ou coisas que o aluno é capaz de sentir, tocar, manipular e movimentar”. Por ter um caráter palpável e visual, ele se caracteriza pelo envolvimento físico dos alunos no processo de aprendizagem.
Lorenzato (2010) acredita que o conhecimento matemático deve começar pelo concreto, partindo de objetos físicos, pois é mais fácil compreender aquilo que é visível e palpável. Assim, utilizar materiais concretos para o ensino de equações do 2º grau, de preferência que estejam presentes na realidade do educando, aproxima-o desse conteúdo, uma vez que cria um elo entre o real visível e aquilo que se aprende, possibilitando um contato prático com o conhecimento. Lorenzato chama esse processo de experimentação, qual seja,
A
experimentação é um processo que permite ao aluno se envolver com o assunto em
estudo, participar das descobertas e socializar-se com os colegas. [...] é o
melhor modo para se conseguir a aprendizagem com significado, uma vez que ela
realça o ‘porquê’, a explicação e, assim, valoriza a compreensão (LORENZATO,
2010, p. 72).
A BNCC também afirma a importância da experimentação na aprendizagem de matemática (BRASIL, 2018). O material concreto cumpre esse papel de experimentação do saber matemático e possibilita que o aluno aprenda com significado, não apenas decorando fórmulas e repetindo padrões de resolução, mas compreendendo o caminho para se chegar ao resultado.
Outra contribuição importante que o material concreto pode fornecer ao ensino de equações quadráticas é possibilitar trabalhar integradamente aritmética, geometria e álgebra. Segundo Lorenzato (2010), essa proposta pode ser útil para atender o currículo espiralado sugerido pela BNCC, que recomenda voltar ao mesmo assunto várias vezes, mas com enfoques diferentes. Além disso, pode ser vantajosa para a aprendizagem das equações quadráticas, uma vez que interliga unidades do conhecimento matemático que conversam entre si, ampliando a percepção do aluno a respeito da matemática como um todo e, consequentemente, de uma parte dela.
Contudo, o material concreto, por si só, não garante aprendizagem, pois não possui um fim em si mesmo. Os conceitos matemáticos que devem ser construídos pelos alunos só serão possíveis com a ajuda do professor, que deverá, ao utilizar o material concreto como um instrumento para aquisição de conhecimento, estimular reflexões e discussões para que o aprendizado ocorra por completo (BALTAZAR, ANJOS, QUADROS, s.d.).
Também é necessário tomar cuidado para que o material concreto não se torne um mero brinquedo sem fundamentação teórica. É de extrema importância a mediação do professor nesse processo, para garantir que o uso de tal recurso não fuja do objetivo de ensino ao qual se propõe, a saber, a aprendizagem (LORENZATO, 2006).
Desse modo, a utilização de materiais concretos para o ensino de equações do 2º grau deve ser precedida de uma competência do professor em saber manuseá-lo e inseri-lo em sala de aula. Apenas manipular objetos não significa que o aluno aprendeu, que compreendeu as estratégias de resolução de uma equação quadrática: é necessário que o professor trace um plano de ensino adequado que permita ao aluno passar do concreto para o abstrato, reconhecendo relações que o levem a pensar, analisar e agir frente a situações-problemas que envolvam tal conteúdo.
5. MATERIAL DOURADO E A RESOLUÇÃO DE EQUAÇÕES DO 2º GRAU: MÉTODO DE COMPLETAR QUADRADOS
Como já mencionado, esta pesquisa propõe que o ensino de equações quadráticas seja abordado de maneira manipulativa, utilizando material dourado. Este recurso, criado no século XX, é um dos muitos materiais idealizados pela médica e educadora italiana Maria Montessori (1870-1952) para o ensino de matemática.
Inicialmente, o material dourado era conhecido como "material das contas douradas", por ser constituído de contas amarelas. Embora especialmente elaborado para o trabalho com aritmética, o seu uso não se restringe apenas às operações básicas, podendo ser utilizado para o estudo de diversos conteúdos matemáticos, dentre eles, as equações do 2º grau (COSTA et al, 2018).
O material dourado é composto por peças que apresentam quatro variações: cubos menores, barras, placas e cubo maior, conforme a Figura 1. Também é possível adaptá-lo, construindo-o com papel quadriculado, EVA ou outros materiais.
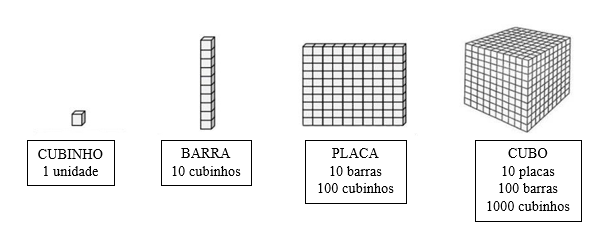 Figura 1
Composição do material dourado
Adaptado de Andressa Biassio et al.
(2018)
Figura 1
Composição do material dourado
Adaptado de Andressa Biassio et al.
(2018)
A resolução de uma equação do 2º grau com o material dourado combina álgebra com geometria para verificar geometricamente a sua solução. Esse método é conhecido atualmente como método de completar quadrados e foi criado pelo matemático árabe Mohammed Ibu-Musa Al-Khwarizmi (780-850). Pouco se sabe sobre sua vida, há indícios de que ele pertence a uma família persa de Khorasan, agora localizada no Uzbequistão.
Segundo Chaquiam (2017), umas das obras mais importantes de Al-Khwarizmi tem
como título “Al-Jabr Wa’l muqabalh”. No livro, o autor aponta métodos algébricos e
geométricos para a resolução de equações quadráticas, no entanto, apenas as raízes positivas
eram consideradas, uma vez que os números negativos só foram conhecidos posteriormente.
Vejamos um exemplo com a equação 𝑥
2 + 10𝑥 = 39, em que ilustramos com a Figura 2, que
descreveremos assim:
traçar um quadrado 𝑎𝑏 para representar 𝑥
2
[quadrado pontilhado], e sobre os quatro
lados desse quadrado colocar retângulos 𝑐, 𝑑, 𝑒 e 𝑓, cada um com largura 2½
[retângulo com listras diagonais]. Para completar o quadrado maior é preciso
acrescentar os quatro pequenos quadrados nos cantos, cada um dos quais tem uma
área de 6¼ unidades [quadrados com listras horizontais]. Portanto, para “completar
o quadrado”, somamos 4 vezes 6¼ unidades ou 25 unidades, obtendo, pois, um
quadrado de área total 39 + 25 = 64 unidades (como fica claro no segundo membro
da equação). O lado do quadrado grande deve, pois, ser de 8 unidades, do qual subtraímos 2 vezes 2 ½ ou 5 unidades, achando 𝑥 = 3 (BOYER, 1974, apud
CHAQUIAM, 2017, p. 56, adaptado em itálico).
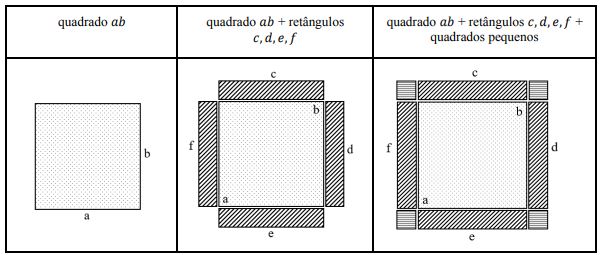 Figura 2
Representação geométrica
Elaborado pelas autoras
Figura 2
Representação geométrica
Elaborado pelas autoras
À semelhança do método de completar quadrados, vejamos como utilizar o material dourado para resolver equações quadráticas. Para desenvolver a resolução da equação do tipo
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0 (1)
bem como as suas variações (equações incompletas), utilizam-se somente três tipos de peças do material dourado: a placa, a barra e o cubo menor.
As peças que compõem o material dourado possuem comprimento, altura e largura,
todavia, não levaremos em consideração esta última dimensão. A placa deve ser considerada
com medidas de largura e altura iguais à 𝑥; a barra, com largura unitária e comprimento 𝑥; e o
cubo menor, com largura e comprimento unitários. Tais dimensões geram como área,
respectivamente, 𝑥
2
, 𝑥 e 1 (Figura 3).
Os coeficientes 𝑎, 𝑏, 𝑐 da equação (1) determinarão a quantidade de placas, barras e
cubos respectivamente. Como serão consideradas apenas duas dimensões do material dourado,
passaremos a utilizar o seu desenho representativo, conforme ilustra a Figura 3.
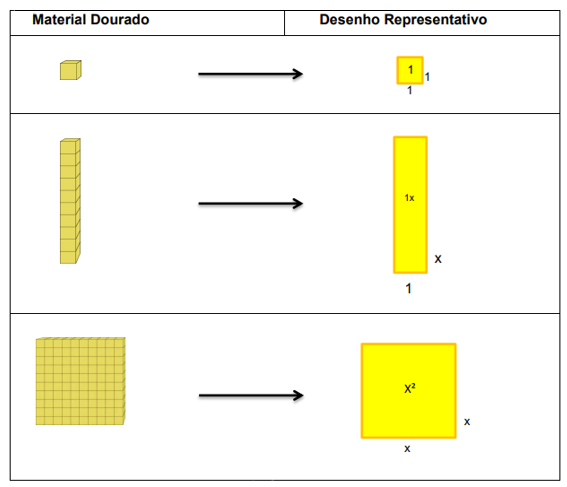 Figura 3
Representação das dimensões das peças do material dourado na equação do 2º grau
Silva e Camargo, 2016
Figura 3
Representação das dimensões das peças do material dourado na equação do 2º grau
Silva e Camargo, 2016
Para entender como representar e solucionar uma equação do 2º grau por meio do
material dourado, apresentaremos um exemplo em particular. Tomemos a equação 𝑥
2 + 3𝑥 +
2 = 0. Os seus coeficientes são 𝑎 = 1, 𝑏 = 3, 𝑐 = 2, assim, teremos uma placa para representar
𝑥
2
, 3 barras para representar 𝑥 e 2 cubinhos para representar o termo independente da equação.
Com estas peças, precisamos construir um quadrado ou um retângulo qualquer.
Para encontrar as raízes da equação, precisamos calcular a área da figura formada. Esse
procedimento fornecer-nos-á um produto envolvendo as expressões algébricas de cada lado da
figura, assim, teremos: (𝑥 + 2)(𝑥 + 1). Como essa expressão é obtida a partir de uma equação
quadrática, o produto de seus fatores se anula, o que nos dá a expressão (𝑥 + 2)(𝑥 + 1) = 0 .
Para encontrar as raízes, basta igualar cada fator a zero, obtendo o conjunto solução {−2, −1}.
Para encontrar as raízes, basta igualar cada fator a zero, obtendo o conjunto solução {−2, −1}.
Vejamos como esse processo resolutivo está ilustrado na Figura 4.
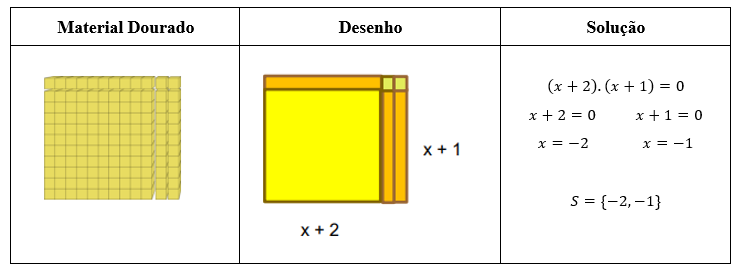 Figura 4
Representação da equação 𝑥
2 + 3𝑥 + 2 = 0 com material dourado e o seu desenho representativo
com a referida resolução
Adaptado de Silva e Camargo, 2016
Figura 4
Representação da equação 𝑥
2 + 3𝑥 + 2 = 0 com material dourado e o seu desenho representativo
com a referida resolução
Adaptado de Silva e Camargo, 2016
Nos casos em que algum dos coeficientes da equação for negativo, é essencial sobrepor as peças do material umas às outras para retirá-lo depois, evidenciando a operação de subtração. Outra possibilidade é utilizar duas cores distintas para diferenciar as peças do material dourado, uma representando os números positivos e outra representando os números negativos.
Para exemplificar, tomemos a equação incompleta 𝑥
2 − 4 = 0. Os seus coeficientes são
𝑎 = 1, 𝑏 = 0, 𝑐 = −4. As peças necessárias para representar esses coeficientes não formam um
quadrado ou retângulo, sendo necessário inserir outras peças para formar uma destas figuras.
Representaremos os coeficientes positivos pela cor branca e os negativos pela cor preta. Com a
inserção de duas barras positivas e outras duas negativas, conservando assim a igualdade, foi
possível completar a figura de maneira a construir um quadrado. A expressão obtida foi (𝑥 −
2)(−𝑥 − 2) = 0, o que nos dá o conjunto solução {−2,2}. Vejamos esse processo na Figura 5.
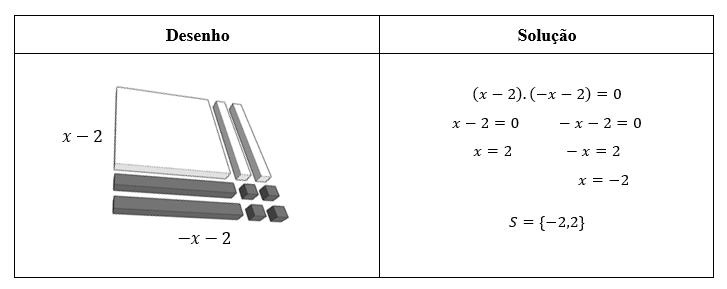 Figura 5
Desenho representativo da equação 𝑥
2 − 4 = 0 com a referida resolução
Adaptado de Francisco, Né e Camiotto (2018)
Figura 5
Desenho representativo da equação 𝑥
2 − 4 = 0 com a referida resolução
Adaptado de Francisco, Né e Camiotto (2018)
Francisco, Né e Camiotto (2018) observaram particularidades a respeito do uso do
material dourado na resolução de equações do 2º grau.
1 - A representação algébrica necessariamente deve considerar a representação de duas dimensões da figura construída [...].
2 - Considerando duas dimensões da figura, poder-se-ia obter uma outra representação
algébrica, por exemplo, (𝑥 + 2). (𝑥 − 2) = 0, mas que daria o mesmo conjunto de
solução. Portanto a representação algébrica em casos como este não é única
(FRANCISCO, NÉ, CAMIOTTO, 2018, p. 9-10).
Nesta seção, observamos de que forma o material dourado, atrelado ao método de
completar quadrados, pode ser utilizado para resolver equações do segundo grau. Mediante o
exposto, reafirmamos a hipótese de que o material dourado é útil para facilitar a compreensão
e a resolução de uma equação de 2° grau.
6. METODOLOGIA
A metodologia utilizada neste estudo se configura, quanto ao seu objetivo, em uma pesquisa exploratória, na qual buscamos investigar a relação existente entre o material dourado e o processo de ensino e aprendizagem do conteúdo equações do 2º grau. Esse tipo de pesquisa, segundo Gil (2002) e Olivares (2017), visa fornecer a compreensão do problema enfrentado pelo pesquisador.
Esta pesquisa também se caracteriza como qualitativa (BOGDAN & BINKLEY, 1994), em que realizamos um levantamento em artigos científicos encontrados na plataforma Google Acadêmico e nos eventos do Encontro Nacional de Educação Matemática – ENEM sobre o tema em estudo.
Na plataforma Google Acadêmico, buscamos documentos científicos que nos permitiram identificar como é ensinado o conteúdo equações do 2º grau em livros didáticos do 9º ano do Ensino Fundamental. Para tanto, utilizamos as seguintes palavras-chave no buscador: “livro didático de matemática”, “equações do 2º grau”. Quando utilizamos essas expressões separadamente, o volume de publicações foi enorme, isto é, milhares de resultados, mas, quando utilizamos as duas expressões juntas, este número reduziu-se expressivamente. Selecionamos as cinco publicações mais citadas que envolvem essas expressões e estabelecem conexão com o uso de material dourado. Assim, optamos por não aplicar filtros temporais, mas sim seletar as referências mais citadas.
Para reconhecer como as equações quadráticas podem ser resolvidas por meio do material dourado e entender como a articulação de ambos proporciona aprendizagem, realizamos um levantamento de artigos encontrados na plataforma Google Acadêmico e nos eventos do Encontro Nacional de Educação Matemática - ENEM. Os termos de pesquisa utilizados foram: “equações do 2º grau”, “material dourado”, “material concreto”. Definimos o período entre 2015 a 2022 para constituição de dados, pois intentávamos encontrar produções atuais sobre o nosso problema investigativo. Obtivemos cerca de 2.690 resultados, dos quais selecionamos as dez produções acadêmicas que mais pareciam convergir para o tema em estudo.
Para a análise das produções científicas encontradas, utilizávamos algumas estratégias de leitura que descreveremos a seguir:
Explorávamos o título a fim de anteciparmos o conteúdo do texto e selecionarmos apenas os documentos vantajosos para a pesquisa. Também realizávamos uma leitura prévia do resumo, para obtermos uma compreensão global do texto e verificarmos se havia convergência para o nosso problema investigativo. Em seguida, realizávamos uma leitura integral do texto, destacando os objetivos de pesquisa, a metodologia de investigação e seus principais resultados. Finalizávamos com uma discussão coletiva sobre cada produção científica encontrada, na tentativa de encontrarmos similaridades em nossas reflexões.
7. CONSIDERAÇÕES FINAIS
Esta pesquisa exploratória, de caráter qualitativo, é fruto do trabalho de conclusão do curso de Matemática Licenciatura, no qual buscamos compreender se o processo manipulativo proporciona aprendizagem sobre o conteúdo de equações do 2º grau, ou seja, se favorece a compreensão das estratégias de resolução de equações quadráticas.
Para tanto, realizamos uma revisão de literatura com pesquisas que investigaram a utilização do material dourado como facilitador no processo de ensino e aprendizagem das equações quadráticas, analisamos como esse conteúdo é ensinado na Educação Básica, compreendemos como o material concreto pode colaborar para o processo de ensino e aprendizagem das equações do 2° grau e, por fim, vimos como as equações quadráticas podem ser resolvidas por meio do material dourado.
Da análise realizada por Pereira (2017), percebe-se que o conteúdo das equações do 2º grau está associado a um ensino mecânico e sem significado. Tal abordagem pedagógica, segundo Silva (2010), ocasiona dificuldades de aprendizagem para o aluno, o que nos leva a crer que o conteúdo das equações do 2º grau deve ser abordado com uma metodologia que busque superar essas dificuldades.
A referida metodologia utiliza o material dourado para resolver equações quadráticas. Concordamos com Lorenzato (2010) que este recurso pode se tornar eficiente para proporcionar aprendizagens significativas, pois, além de permitir a experimentação do conteúdo matemático, possibilita trabalhar integradamente aritmética, geometria e álgebra, atendendo ao currículo espiralado proposto pela BNCC. No entanto, é necessário saber utilizá-lo.
A partir de todos os fatos expostos, concluímos, à semelhança das pesquisas de Costa et al. (2018), Lins et al. (2019) e Francisco, Né e Camiotto (2019) que o material dourado é um recurso metodológico eficaz para proporcionar aprendizagem sobre o conteúdo de equações quadráticas, estimulando a participação e o interesse dos alunos.
A adoção de tal metodologia pode levar o aluno a compreender melhor a abstração do conteúdo de equações quadráticas e a sua solução algébrica, visto que ilustra o processo resolutivo. Além disso, permite, através da experimentação, uma interação ativa no processo de ensino e aprendizagem, possibilitando a construção de um conhecimento real, tangível e com significado.
REFERÊNCIAS
BALTAZAR, Mara Cristina; ANJOS, Sabrini Micheli da Silva; QUADROS, Zilmara Raupp de. O Laboratório de Ensino de Matemática na Formação de Professores. [s.d.]. Disponível em:<http://matinterdisciplinar.pbworks.com/w/file/fetch/87893530/O%20artigo%20materiais%20manipul%C3%A1veis%20como%20recurso%20did%C3%A1tico%20na%20forma%C3%A7%C3%A3o%20de%20professores%20de%20matem%C3%A1t.pdf>;. Acesso em: 22 jun. 2022.
BIASSIO, Andressa; FERNANDES, Isaias; ROLOFF, Fernando; COSTA, Priscila Kabbaz Alves da. Utilizando o material dourado no ensino de álgebra. Simpósio Nacional de Ensino de Ciência e Tecnologia - VI SINECT; Ponta Grossa - PR, 27 a 30 de novembro de 2018. Disponível em:<https://www.researchgate.net/publication/328869446_UTILIZANDO_O_MATERIAL_DOURADO_NO_ENSINO_DE_ALGEBRA>;. Acesso em: 2 jul. 2022.
BOGDAN, R. & BINKLEY, S. (1994). Investigação Qualitativa em Educação: uma introdução à teoria e aos métodos. Porto, Porto Editora.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. 2018.
BRASIL. Ministério da Educação e do Desporto. Parâmetros Curriculares Nacionais. Brasília, DF, 1998.
CHAQUIAM, Miguel. Ensaios temáticos: história e matemática em sala de aula. 1. ed. Belém: SBM, 2017. 241 p. ISBN 978-85-98092-34-8. Disponível em: http:<//www.sbembrasil.org.br/files/historia_matematica.pdf>. Acesso em: 30 jun. 2022
COSTA, Priscila Kabbaz Alves da; PRZYBYVIZ, Fabíola; NASCIMENTO, Jéssica Karolinne Medeiros; STACHESKI, Jaqueline Meni; UCOSKI, Lillyan Fernanda. Uma proposta para o ensino de equações do segundo grau utilizando diferentes recursos didáticos. Encontro Paranaense de Tecnologia na Educação Matemática - EPTEM; Apucarana - PR, 22 a 24 de novembro de 2018. Disponível em:<https://www.researchgate.net/profile/Priscila-Kabbaz-Alves-Da-Costa/publication/329360810_UMA_PROPOSTA_PARA_O_ENSINO_DE_EQUACOES_DO_SEGUNDO_GRAU_UTILIZANDO_DIFERENTES_RECUSOS_DIDATICOS/links/5c04672f45851523d159aae9/UMA-PROPOSTA-PARA-O-ENSINO-DE-EQUACOES-DO-SEGUNDO-GRAU-UTILIZANDO-DIFERENTES-RECUSOS-DIDATICOS.pdf>;. Acesso em: 28 jun. 2022.
FRANCISCO, Gabriela.; NÉ, Adriano Luiz dos Santos; COMIOTTO, Tatiana. Material dourado e equação polinomial do segundo grau: do algébrico ao geométrico, do mecânico ao significativo. EM TEIA – Revista de Educação Matemática e Tecnológica Iberoamericana; Pernambuco, v. 10, n. 3, 2019. Disponível em:<https://docplayer.com.br/188649461-Material-dourado-e-equacao-polinomial-do-segundo-grau-do-algebrico-ao-geometrico-do-mecanico-ao-significativo.html>;. Acesso em: 29 jun. 2022.
GIL, Antônio Carlos. Como Elaborar Projetos de Pesquisa. 4. ed. São Paulo: Atlas, 2002. 176 p. ISBN 85-224-3169-8. Disponível em: <https://files.cercomp.ufg.br/weby/up/150/o/Anexo_C1_como_elaborar_projeto_de_pesquisa_-_antonio_carlos_gil.pdf>;. Acesso em: 27 maio 2022.
HOUSE, P. A. Álgebra: ideias e questões. In: COXFORD, Arthur F. e SHULTE, Albert P. As ideias da álgebra. São Paulo: Atual, 1995.
LINS, G. S.; LÜBECK, M.; MEDEIROS, J.; ANDRETTI, F. L.. O ensino da matemática e a resolução de equações com material concreto. Encontro Nacional de Educação Matemática - XIII ENEM; Cuiabá - MT, 14 a 17 de julho de 2019. Disponível em:<https://www.sbemmatogrosso.com.br/eventos/index.php/enem/2019/paper/download/528/849>;. Acesso em: 28 jun. 2022.
LORENZATO, Sergio. Para aprender matemática. 3. ed. São Paulo: Autores Associados, 2010.
LORENZATO, Sérgio. Laboratório de Ensino de Matemática na Formação de Professores. Campinas: Autores associados, 2006.
OLIVARES, Aurélio Lisboa. 4 Método 4.1. Pesquisa exploratória. Disponível em:<https://docplayer.com.br/25686445-4-metodo-4-1-pesquisa-exploratoria.html>;. Acesso em: 09 jun. 2022.
PASSOS, C. L. B. Recursos didáticos na formação de Professores de Matemática. In: VII Encontro Paulista de Educação Matemática: Matemática na Escola: Conteúdos e Contextos, 2004, São Paulo. Anais do VII Encontro Paulista de Educação Matemática: Matemática na Escola: Conteúdos e Contextos. São Paulo: SBEM/SP, 2004. p. 01-11. Disponível em: <http://docplayer.com.br/66368436-Recursos-didaticos-na-formacao-de-professores-de-matematica-carmen-lucia-brancaglion-passos-ufscar-dme.html>;. Acesso em: 20 maio 2022.
PEREIRA, João Luiz Ribas. Análise de livros didáticos: Comparando Álgebra com enfoque na equação do segundo grau em três livros de matemática do 9º ano do ensino fundamental II. 2017. 35 p. Tese (Mestrado em Especialização para Professores de Matemática,) - Universidade Federal de Minas Gerais, Belo Horizonte, 2017. Disponível em:<https://repositorio.ufmg.br/bitstream/1843/BUOS-AU2J28/1/monografia_joaoribas.pdf>;. Acesso em: 9 jul. 2022.
SILVA, Eva Aparecida Carvalho e; CAMARGO, Joseli Almeida. O Material Dourado aplicado ao ensino e aprendizagem da Equação do 2º Grau. Paraná: Cadernos PDE, 2016. v. 1. ISBN 978-85-8015-093-3. Disponível em:<http://www.diaadiaeducacao.pr.gov.br/portals/cadernospde/pdebusca/producoes_pde/2016/2016_artigo_mat_uepg_evaaparecidacarvalhoesilva.pdf>;. Acesso em: 28 jun. 2022.
SILVA, Sandra Maria da. As dificuldades da aprendizagem dos alunos em equações do 2° grau com uma incógnita. 2017. Trabalho de Conclusão de Curso (Licenciatura em Matemática) - Universidade Federal do Paraíba, Rio Tinto, 2017. Disponível em: <https://repositorio.ufpb.br/jspui/bitstream/123456789/3242/1/SMS13062017.pdf>;. Acesso em: 12 maio 2022.
APÊNDICE 1
AGRADECIMENTOS
Não se aplica.
FINANCIAMENTO
Não se
aplica.
CONTRIBUIÇÕES
DE AUTORIA
Resumo/Abstract/Resumen: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Introdução: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Referencial teórico: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Análise de dados: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Discussão dos resultados: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Conclusão e considerações finais: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Referências: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Revisão do manuscrito: Ariane de Andrade Gomes
Aprovação da versão final publicada: Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
Thamires Silva Soares; Deuseliane Patrícia Oliveira Leal; Yara Letícia Pereira Serra; Mauro Guterres Barbosa.
CONFLITOS DE
INTERESSE
Os autores declararam
não haver nenhum conflito de interesse de ordem pessoal,
comercial, acadêmico, político e financeiro referente a este manuscrito.
DISPONIBILIDADE
DE DADOS DE PESQUISA
Informamos que o conjunto de dados que dá suporte aos resultados da pesquisa foi publicado no próprio artigo.
CONSENTIMENTO DE USO DE
IMAGEM
Não se aplica.
APROVAÇÃO DE COMITÊ DE ÉTICA
EM PESQUISA
Não se aplica.
COMO CITAR - ABNT
SOARES, Thamires Silva, LEAL, Deuseliane
Patrícia Oliveira, SERRA, Yara Letícia Pereira, BARBOSA, Mauro Guterres. Resolução de equações do 2º grau com uso do material dourado. REAMEC – Rede Amazônica de Educação em Ciências e Matemática. Cuiabá, v. 10,
n. 3, e22072, set./dez.,
2022. http://dx.doi.org/10.26571/reamec.v10i3.14243
COMO CITAR - APA
Soares, T. S., Leal, D. P. O., Serra, Y.
L. P., Barbosa, M. G. (2022). Resolução de equações do 2º grau
com uso do material dourado. REAMEC - Rede Amazônica de Educação em Ciências
e Matemática, 3(10), e22072. http://dx.doi.org/10.26571/reamec.v10i3.14243
LICENÇA DE USO
Licenciado sob a Licença
Creative Commons Attribution-NonCommercial
4.0 International (CC BY-NC 4.0). Esta licença permite compartilhar,
copiar, redistribuir o manuscrito em qualquer meio ou formato. Além disso,
permite adaptar, remixar, transformar e construir sobre o material, desde que
seja atribuído o devido crédito de autoria e publicação inicial neste
periódico.
DIREITOS AUTORAIS
Os direitos autorais são
mantidos pelos autores, os quais concedem à Revista REAMEC – Rede
Amazônica de Educação em Ciências e Matemática - os direitos exclusivos de primeira publicação. Os autores não serão
remunerados pela publicação de trabalhos neste periódico. Os autores têm autorização para assumir contratos adicionais separadamente, para distribuição não exclusiva da versão do trabalho publicada neste periódico (ex.: publicar em repositório institucional, em site pessoal, publicar uma tradução, ou como capítulo de livro), com
reconhecimento de autoria e publicação inicial neste periódico. Os editores da
Revista têm o direito de proceder a ajustes textuais e de adequação às normas
da publicação.
PUBLISHER
Universidade Federal de Mato
Grosso. Programa de Pós-graduação em Educação em Ciências e Matemática
(PPGECEM) da Rede Amazônica de Educação em Ciências e Matemática (REAMEC). Publicação
no Portal de
Periódicos UFMT. As ideias expressadas neste artigo são de
responsabilidade de seus autores, não representando, necessariamente, a opinião
dos editores ou da referida universidade.
EDITOR
Rogerio dos Santos Carneiro
Orcid:https://orcid.org/0000-0002-5387-0435
Lattes:http://lattes.cnpq.br/6059313467968676
Notas
[1] A referida componente curricular
orienta a construção de projetos de pesquisa a serem desenvolvidos ao longo do
curso, que podem culminar com a construção não só de um projeto de TCC, mas de
produções outras que insiram os licenciandos em uma perspectiva investigativa
de suas práticas formativas. Nesse caso, esta componente foi ministrada pelo
professor coautor desta pesquisa.
Autor notes
* Graduanda em Licenciatura em Matemática pela Universidade
Estadual do Maranhão (UEMA), São Luís, Maranhão, Brasil.
Discente (UEMA), São Luís, Maranhão, Brasil. Cidade Universitária Paulo
VI, São Luís, Maranhão, Brasil, Caixa Postal 09.
** Graduanda em Licenciatura em Matemática pela Universidade
Estadual do Maranhão (UEMA), São Luís, Maranhão, Brasil.
Discente (UEMA), São Luís, Maranhão, Brasil. Cidade Universitária Paulo
VI, São Luís, Maranhão, Brasil, Caixa Postal 09.
*** Graduanda em Licenciatura em Matemática pela Universidade
Estadual do Maranhão (UEMA), São Luís, Maranhão, Brasil.
Discente (UEMA), São Luís, Maranhão, Brasil. Cidade Universitária Paulo
VI, São Luís, Maranhão, Brasil, Caixa Postal 09.
**** Doutor em Educação em Ciências Matemática pela Universidade
Federal do Mato Grosso (UFMT). Professor Adjunto I da Universidade Estadual do
Maranhão (UEMA), São Luís, Maranhão, Brasil. Cidade Universitária Paulo VI, São
Luís, Maranhão, Brasil, Caixa Postal 09.
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/14243 (pdf)










