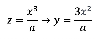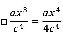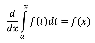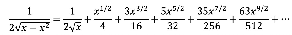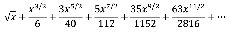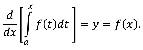I. Introducción
l Teorema Fundamental del Cálculo puede ser abordado desde diferentes puntos de vista. Se decide presentarlo desde los trabajos de Isaac Newton, sin olvidar que este teorema también se le atribuye conjuntamente a Gottfried Leibniz. Emprender el estudio de los trabajos de Newton sobre este asunto particular, resulta emocionante desde el punto de vista matemático e histórico. Así como afirma D.T. Whiteside sobre lo absorbente de seguir un concepto a través de los sucesivos borradores y manuscritos de Newton (Whiteside, 1961), porque, por ejemplo, permite comprender los cambios de notación y filosofía para el fenómeno de movimiento y el problema inverso de las tangentes. Desde el punto de vista didáctico, este trabajo es enriquecedor, toda vez que permite tener una forma alternativa de enseñarlo en el entorno universitario.
Desde el campo de la enseñanza, normalmente los argumentos en los currículos de matemáticas son tomados desde el punto de vista filosófico como inductivos o deductivos. Sin embargo, dicha clasificación limita la gestión y comprensión de los procesos de estudio en matemáticas, además que han caído en desuso en los textos universitarios debido a la introducción de software educativos en las prácticas matemáticas (Lasa et al., 2017). Pero, ¿cómo se evalúa si un estudiante usa un buen argumento? Desde la filosofía y la lógica formal:
Un buen argumento sería
aquel en el que se realizan buenas inferencias, a partir de buenas premisas. La
evaluación de los argumentos de los estudiantes ocupa una parte fundamental de
la práctica operativa y discursiva en el aula de matemáticas, pero el punto de
vista formal de la lógica tiene limitaciones a la hora de evaluar la
argumentación cotidiana, y en particular, la argumentación de un estudiante que
no tiene porqué conocer los entresijos de una axiomática compleja. (Lasa et al., 2017, p. 5)
Luego si la institución donde se
labora acentúa la resolución de problemas en sus currículos, la validez que
aporta el modelo inductivo y deductivo para evaluar los procesos de los
estudiantes no es suficiente. Volcar la mirada a argumentos que fueron
utilizados en ciertos periodos de la historia y que tengan un potencial
heurístico, podría servir a mejorar dicha validación de los procedimientos
realizados por un estudiante, dado que algunos fueron utilizados en momentos
históricos para resolver problemas, además, porque podrían ser representados
mediante un software educativo, permitiendo a los docentes analizar y discutir
de manera curricular los resultados de su implementación.
II. Búsqueda de un teorema análogo
al TFC
Un ejemplo de dichos argumentos históricos sucede en el caso del TFC en Newton, el cual emergió cuando él vio la relación entre el problema de las áreas y el problema inverso de las tangentes. Este argumento es en sí una versión análoga de lo que es reconocido actualmente como TFC, abordándolo más allá de la relación de la integral con la antiderivada. Cabe resaltar eso sí, que Newton estaba más interesado en resolver cierta clase de problemas matemáticos que en crear una teoría formal (Guicciardini, 2008). Pero este argumento tuvo tal desarrollo teórico y sirvió de manera algorítmica a resolver una gran cantidad de problemas, que él mismo lo denominó teorema en 1704, como se verá más adelante.
Este argumento es posible recuperarlo basado en fuentes primarias, gracias al profesor Rob Iliffe y al grupo de trabajo de la Universidad de Oxford The Newton Project. Se utilizarán los manuscritos de Newton de 1665 (Iliffe, 2011a), 1666 (Iliffe, 2011b) y 1669 (Iliffe, 2012). Para el escrito de 1704 se cuenta con la fuente primaria compilada en la página web de la Universidad de Basilea Basilea (Newton, 1704b) y una versión corta (Newton (1704a). Adicionalmente, se cuenta con un soporte bibliográfico de expertos en los trabajos de Newton, tales como Marco Panza (Panza, 2000), D.T. Whiteside (Whiteside, 1961), H.J. Bos (Bos, 1993a) y Niccolò Guicciardini (Guicciardini, 2008, 2009), puesto que como se suele decir: sin documentación no hay historia[2].
El Teorema Fundamental del Cálculo (TFC) es asociado comúnmente con la relación inversa entre derivación e integración, y en el mejor de los casos es recordado por la fórmula que brinda para calcular áreas bajo una curva (Bressoud, 2011; Toumasis, 1993). Pero hay mucho más que analizar. Como se mencionó antes, desde un punto de vista histórico en los trabajos de Newton, una forma de estudiarlo es a partir de la solución que emergió del problema inverso de las tangentes y como esta se conecta con el problema de las áreas.
Ahondando un poco en este tema, como resolución al problema de las áreas se utilizaba desde los griegos la técnica de las cuadraturas. Los problemas de cuadraturas son problemas geométricos que consisten básicamente en que se debía construir un cuadrado cuya área fuera igual a la de una figura inicial dada. Esta construcción debía hacerse con regla y compás, y cumplir con unas normas precisas. Son famosos los problemas de la cuadratura del círculo, la trisección de un ángulo, la duplicación del cubo y aquellos donde se deban inscribir polígonos regulares en una circunferencia (Pérez, 2013).
En la antigua Grecia se sabía cómo hallar la cuadratura de varios polígonos, sin embargo, utilizando esta técnica los griegos no pudieron encontrar el área acotada entre curvas. Este problema tomaría alrededor de dos mil años en resolverse, y no fue sino gracias a la teoría que hoy es conocida como análisis infinitesimal, desde los trabajos de Newton y de Leibniz (entre muchos otros) en el S. XVII, que se encontró una solución.
Esta teoría muestra que el problema de hallar áreas de figuras rectilíneas es en esencia el mismo de hallar longitudes de curvas, siendo así una de las caras de una moneda, cuyo reverso consiste en encontrar tangentes y curvaturas, así como hallar velocidades instantáneas y fuerzas en problemas físicos (Panza, 2000).
Newton y Leibniz utilizaron así los resultados de sus contemporáneos tales como H. van Heuraet (quien resolvió el problema de la rectificación de curvas), J. Hudde y R. Sluse (cálculo de tangentes y normales) en su invención propia del cálculo (Scriba, 2014; Panza 2000). Dos siglos más adelante esta teoría encuentra su punto cumbre con el desarrollo de lo que hoy es reconocido como el Teorema Fundamental del Cálculo.
Por otro lado, el problema de las tangentes consistía en el trazado de ellas a curvas como las cónicas, la cisoide de Diocles y la concoide de Nicomedes. “El concepto de tangencia de los griegos es estático y, naturalmente, geométrico. Inicialmente, la tangente se considera como una recta que toca a la curva sin cortarla” (Pérez, 2013, p.9).
Se puede advertir que con esta definición se descartan una gran cantidad de curvas, por ejemplo, aquellas que se intersectan consigo mismas. Posteriormente, y luego del desarrollo de la geometría analítica, estas tangentes fueron descritas usando varios métodos mediante la relación entre dos variables y para ciertas funciones dadas (Scriba, 2014).
El recíproco a este problema, es el problema inverso de las tangentes, que consistía en hallar la ecuación de una curva sabiendo solamente ciertas propiedades características de sus tangentes (Robson & Stedall, 2009). Descartes fue uno de los que logró resolver un caso especial entre 1638-1639, sin embargo estos problemas eran célebres en el S. XVII, y existían muchos otros estudiosos, como Fermat y Roberval intentando resolverlos (Scriba, 2014; Whiteside, 1961).
Dentro de estos problemas están los propuestos por Florimond Debeaune (de los cuales se conocen y, se tienen registros y correspondencias que lo respaldan) quien sugirió varios ejercicios de este tipo en el otoño de 1638. Descartes logró resolver uno de dichos problemas, y también Leibniz los abordó. Uno de ellos, escrito en notación moderna, podría interpretarse como: hallar una curva tal que .
La explicación de dicha solución puede encontrarse en Scriba (2014) y Whiteside (1961), y podría ser utilizada, por ejemplo, para enseñarse en las primeras clases de un curso de ecuaciones diferenciales, ambientando la presentación geométrica en algún software, y haciendo el paralelo entre los argumentos de la solución de Descartes o Leibniz y los que se usarían para obtener una solución mediante una sustitución diferente.
Hacía falta entonces en esa época un método que generalizara las soluciones puntuales encontradas y que permitiera, en la medida de lo posible, desarrollar la mayor cantidad de problemas de esta clase. Newton no puso demasiado interés en los problemas de trazar tangentes, sin embargo, fue muy receloso al momento de revelar sus métodos de cuadraturas (Guicciardini, 2008).
En sus correspondencias se dilucida una estrategia para proteger su método de resolución del problema inverso de las tangentes, que después se debilita con el paso de los años cuando los métodos de integración publicados por sus contemporáneos, fueron de dominio público. Cabe aclarar que para él la creación de una teoría formal y sus correspondientes leyes tampoco le llamaban la atención, sin embargo, resolver los problemas más destacados de cuadraturas sí eran de su interés, pues en su opinión, sus métodos de series y fluxiones mostraban su poder cuando se enfrentaban contra problemas difíciles de hallarles cuadraturas a ciertas curvas (integrar) o aquellos que usaban el método inverso de las tangentes (integración de ecuaciones diferenciales) (Guicciardini, 2008).
Fue su método uno de los que terminó resolviendo una gran cantidad de problemas de cuadraturas, como se puede ver en sus trabajos de 1666, partiendo de un problema particular, como el mostrado en sus escritos de 1665. Las posteriores versiones son refinamientos de estos trabajos precedentes y, por ejemplo, en la versión de 1704, se verá que para él ya tenían más importancia otras teorías descubiertas que su versión de lo que se conoce como TFC.
Queda una pregunta en el aire: ¿por qué lo que hoy conocemos como TFC se adjudica a Newton y Leibniz y no por ejemplo a Isaac Barrow? (uno de los matemáticos que trabajó previamente con la relación entre el problema de áreas y tangentes). La respuesta es: Barrow, así como otros matemáticos precedentes e incluso contemporáneos (e.g. Bonaventura Cavalieri, Pierre de Fermat, John Wallis, Hendrick van Heuraet, James Gregory, etc.), vieron la relación entre el problema de las áreas y las tangentes, o trabajaron y desarrollaron conceptos u objetos matemáticos que son propios de tal teorema, pero según D.T Whiteside, ellos no ofrecieron un algoritmo para hallar la solución del problema de las áreas, más que mostrar, únicamente, que la derivación e integración son procesos opuestos (Bressoud, 2011; Whiteside, 1961).
Adicionalmente a esto, Guicciardini (2009) afirma, en el caso de Barrow, que:
Barrow no estuvo interesado en desarrollar un algoritmo para enfrentar el problema que involucra estas curvas... porque él estaba convencido de la superioridad de la geometría sobre el álgebra... Lo que en mi parecer quiso realizar él [Barrow] fue demostrar las relaciones generales entre las proposiciones que involucran áreas y las proposiciones que involucran tangentes. (p. 177)
El interés de este escrito es
recordar las diferentes versiones del TFC en los
trabajos de Newton desde 1665 hasta el escrito de 1704, exaltando el argumento
principal de ver geométricamente este teorema como una relación entre el
problema de las áreas y el problema inverso de las tangentes (Panza, 2000), lo
que sería un análogo al actual TFC y que podría
servir de insumo para la enseñanza de dicho teorema a la comunidad
universitaria.
III. TFC actualmente en el contexto
universitario
El TFC se presenta de maneras diversas en los textos universitarios de análisis matemático o de cálculo de una variable, emergiendo así el primer problema al abordar este campo de estudio: ¿a cuál teorema fundamental se refiere? Esta problemática no es única de los textos de cálculo (análisis matemático), los profesores de matemáticas también tienen en su haber versiones diferentes del TFC (Toumasis, 1993).
La presentación más general y más típica de este teorema en los libros universitarios de cálculo es la siguiente:
Teorema Fundamental del Cálculo:
Sea f una función continua en el intervalo [a,b],
1. Si g(x)= ∫ xa f (t)dt, entonces g' (x)= f(x).
2. ∫ ba f(x)dx=F(b)-F(a) donde F es una antiderivada de f, es decir, F' (x)=f(x) (Stewart, 2015).
Este TFC es el que será considerado en este escrito. La primera parte de este teorema se puede denominar como la parte dinámica o acumulativa, la segunda, como la parte evaluativa. Se verá también a lo largo de este ensayo, como emergió este teorema en los trabajos de Newton, evidenciando, además de su cambio de notación, cómo se robustecía con el pasar de los años. Entre todas las versiones de Newton, la que se encuentra en los manuscritos de octubre de 1666, es la versión más completa de su TF
IV. Newton y el TFC en 1665
En el cálculo de Newton, el movimiento de un punto genera una recta, y el movimiento de una recta genera una superficie. Para Newton, las cantidades generadas por un flujo son llamadas fluentes y sus velocidades instantáneas son las fluxiones. Para él, lo que hoy conocemos como el TFC, emergió cuando el algoritmo inverso que resuelve el problema de las tangentes, resolvió el problema de las áreas (Panza, 2000). En 1665 Newton ya tenía el argumento de relacionar los movimientos que describen dos segmentos, es así como usó la notación qp- para dicha relación descrita por los segmentos y , que en notación moderna podría entenderse como y dx d- . Luego el TFC podría verse desde la igualdad q-p = f (x) si f (x) describe una relación entre x y y (Panza, 2000).
Para Niccolò Guicciardini, Newton realizó el descubrimiento del TFC en el año de 1665 aunque de una manera muy general, porque Newton solamente vislumbra la relación entre la curva y y la curva z de la figura de la Figura 1, asegurando que es la pendiente de z (Guicciardini, 2009). Es decir, él realizó el caso puntual donde:
En efecto, Newton define como bg = dh _____ ___βm Ωβ donde dh es la distancia del segmento unitario, βm es el incremento infinitesimal de z y, Ωβ es el incremento infinitesimal en x (la notación en esto punto dista mucho de la más famosa newtoniana: la del punto Ωβ=x ̇). Si se usara nuestra notación moderna (leibniziana por demás) se obtendría que y= dz/dx.
“Se sigue inmediatamente que el área de bpsg (= Ωβ ∙ bg) es igual al área de µκλν(= βm ∙ dh)… [obteniendo] que el área que subtiende la curva y, por ejemplo, dψn es igual al área del rectángulo dhσp" (Guicciardini, 2009, p. 184). Esta última frase muestra que él halló la cuadratura de esa curva polinómica, encontrando un rectángulo cuya área es igual.
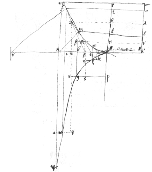 Figura 1
Diagrama del TFC de Newton 1665.
Extraído de:http://www.newtonproject.ox.ac.uk/view/texts/normalized/NATP00128
Figura 1
Diagrama del TFC de Newton 1665.
Extraído de:http://www.newtonproject.ox.ac.uk/view/texts/normalized/NATP00128
Luego Newton supo en 1665, utilizando la notación moderna, que para calcular el área bajo una curva y debía buscar una curva z tal que: . La parte evaluativa del TFC dice que basta un conocimiento de la curva z (la antiderivada de y) para hallar la cuadratura del área bajo la curva y, porque el área es proporcional a la diferencia de las ordenadas de z, es decir, ∫ ba y dx= z (b) - z(a).
Pero hay más, en este año de 1665 Newton desarrolla algunos métodos y algoritmos que los catalogó como teoremas:
Lo que Newton llama teoremas son igualdades generales que proporcionan las subnormales, subtangentes, las coordenadas del centro de curvatura, y el radio de la curvatura de una curva dada, todo en relación a un sistema de coordenadas cartesianas y sin importar cuál sea su ecuación algebraica (Panza, 2000).
Dentro de dichos “teoremas” Newton hace en 1665, lo que hoy se reconoce como la regla de sustitución para hallar ciertas integrales. Estos resultados los tenía en tablas que fueron refinadas y aparecen en su siguiente manuscrito en 1666. En la segunda de estas tablas (que es más completa que la anterior) ya aparece el cálculo de cuadraturas como la inversión del algoritmo de movimientos:
Al redactar estas tablas,
Newton muestra así haber comprendido perfectamente el algoritmo de las
velocidades (movimientos) y el problema de las áreas y, por esta vía, el
vínculo más fundamental, entre este último y el problema de la búsqueda de la
proporción entre velocidades. (Panza, 2000, p. 371)
V. Newton y el TFC en 1666
En este punto se abordará la presentación histórica del TFC desde el manuscrito “The October 1666 Tract on Fluxions”. En este manuscrito Newton desarrolló el problema de las fluxiones en la Proposición 7. Luego, en la Proposición 8 realizó el problema inverso de las velocidades. Según Marco Panza, en este manuscrito esas proposiciones ya podrían ser tomadas como teorema (Panza, 2000).
Posteriormente a estos enunciados, Newton ofrece lo que hoy conoceríamos como una tabla de integrales, mostrando así la fuerza algorítmica de su cálculo al resolver varios problemas de cuadraturas.
Para dicho algoritmo, Newton utiliza la notación de □ para denotar la integral. Hay que leer este símbolo con cuidado, porque también representa para él lo que será en un futuro , e incluso para hablar del área del rectángulo lo denota como □abεd=x. En los ejemplos posteriores a las Proposiciones 7 y 8 Newton escribe, por ejemplo:
Para ver el análisis detallado de la relación que usa Newton para denotar la proporción entre las velocidades de dos objetos pq- puede verse el Capítulo 11 de Panza (2000). En esta búsqueda de argumentos de Newton, emerge uno para calcular la velocidad de la variación del área bajo una curva: en estos manuscritos de 1666 Newton desarrolla en el Problema 5 lo que se reconoce como la parte dinámica del TFC. Dicho problema aparece en la fuente primaria “The October 1666 Tract on Fluxions” (Iliffe, 2011b).
Cabe resaltar que la forma en la
que Newton usó la construcción geométrica para resolver este problema era
bastante común en su época. De hecho, H. J. M. Bos
asegura que los matemáticos de los S. XV al XVII estaban más interesados en resolver problemas que
en probar teoremas o en investigar propiedades de construcciones geométricas (Bos, 1993b).
La explicación del procedimiento utilizado en esta solución realizada por Newton, la construcción geométrica y el análisis del primer ejemplo de ese Problema 5 de 1666, pueden verse en Muñoz Villate (2021). La conclusión más importante relacionado al TFC que realizó Newton de estos manuscritos de 1666 (escrito en notación moderna) es:
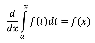
Es decir, se tiene de manera
explícita lo que se reconoce actualmente como la parte dinámica del TFC. A simple vista la notación Xy que aparece en el Problema 5, es similar a la notación que se
utiliza actualmente para escribir las derivadas parciales de manera no leibniziana, es decir, actualmente si se tiene una función f (x, y), se
reconoce fx como la
derivada parcial de f con respecto a x. Newton en este problema utiliza - _Xy Xx =q para la relación de las velocidades puntuales
de las áreas x y y, y que se parece al
recíproco de lo que se reconoce actualmente como la fórmula de la derivada
implícita - _fx fy . Esta fórmula tiene mucho que ver con la subnormal y la subtangente obtenidas por J. Hudde
y R. Sluse (Maronne &
Panza, 2021).
VI. Newton y el TFC en 1669
Años más tarde, Newton retomó su presentación del TFC de 1666, y esta vez, escrita en latín en “de Analysi per aequationes numero terminorum infinitas”, presenta ejemplos diferentes a los suministrados anteriormente, manteniendo la esencia de la mostrada en el Problema 5 de 1666, explicado anteriormente. En efecto, como un ejemplo ahora busca hallar la longitud del arco AD para una circunferencia, que en notación moderna sería y=√x-x², realizando las proporciones con la tangente en el punto D.
Se recuerda que para sus estudios Newton tuvo en cuenta los trabajos de Descartes y de Wallis sobre la manera de escribir curvas por ecuaciones algebraicas, de manera finita y como una serie infinita (preferiblemente de potencias), respectivamente (Guicciardini, 2006). Esto se ve reflejado en el mencionado ejemplo de la circunferencia que desarrolla mediante series infinitas:
Suponga que y=√x-x², y se toma f (x)= x-x², entonces __ y' f'(x) = 1 2√x-x² . A esta respuesta Newton propone expandirla en forma de series:
puesto que la integral de 1 2√x-x² no estaba aún definida en términos de arcoseno. Sin embargo, las antiderivadas
de esa expansión son:
Podría sentirse tentado el/la
lector(a) a pensar que Newton sabía que esta expansión correspondería a sin-1√x, sin embargo, para que esto
hubiera sido posible él debió dejar de concebir arcoseno
desde el punto de vista geométrico como un ángulo o un arco de un círculo. Esta
dificultad persistirá por un largo tiempo, incluso aparecerá en el libro L’analyse de Euler, en pleno siglo XVIII
(Panza, 2000).
VII. Newton y el TFC en 1704
Luego de haber dejado por muchos años las publicaciones de cualquier tratado concerniente a la teoría de fluxiones, Newton decide retomar los resultados obtenidos en sus trabajos juveniles. En efecto, motivado por los trabajos de Leibniz y sus adeptos de llegar mediante el cálculo integral y diferencial a una teoría matemática nueva y potente, y por la posterior disputa (más por aspectos políticos que científicos) sobre la prioridad del descubrimiento del cálculo (Bardi, 2006), Newton publica en 1704 el “Tractatus de Quadratura Curvarum” (tratado de la cuadratura de curvas) con una nueva orientación geométrica de su cálculo matemático inicial. Esta publicación es un apéndice al escrito Óptica.
Marco Panza señala que este escrito de 1704 ya había sido adelantado en “la segunda edición de la Óptica, casi para subrayar el carácter subordinado de esta teoría respecto a las grandes adquisiciones científicas de las cuales él se enorgullecía: la teoría de la gravitación universal y la teoría de la luz” (Newton, 2001, p. 3).
En la Proposición II, Problema II, aparece la frase “Invenire curvas quæ quadrari possint” (encuentre una curva que se le pueda hallar la cuadratura). En el enunciado de dicha proposición aparece la frase “et arearum ABC, ABDE fluxiones erunt ut BC ad BE”, que podría traducirse como y de las áreas ABC y ABDE cuyas fluxiones serán BC y BE, se muestra nuevamente la parte dinámica del TFC presentado en sus manuscritos de 1666. En efecto, esta frase en notación moderna se podría transcribir como:
d dx [Área(ABC)]=BC, esto es, la derivada de esa área es su ordenada. Luego, si BC=y=f(x), es la curva que encierra el Área(ABC), y esta es a su vez es representada como Área(ABC)=∫ xa f (t)dt, entonces:
El caso del paralelogramo, como lo llama Newton, sería más sencillo de transcribir d dx [Área(ABDE)]= BE= d dx [x ∙ BE]. Es decir, la velocidad instantánea del área de ese paralelogramo, es su ordenada.
La notación más popular de Newton para la derivada de un fluente x como x ̇ ya se tiene en este escrito de 1704, como se puede ver en la Figura 2.
 Figura 2:
Notación del punto para las fluxiones
Fuente: (Newton, 1704b, p. 7)
Figura 2:
Notación del punto para las fluxiones
Fuente: (Newton, 1704b, p. 7)
VIII. Conclusiones
- 1.
El
TFC desde el punto de vista histórico de Newton
debe entenderse como una relación inversa entre el problema de las áreas a
aquel de las variaciones de la velocidad instantánea, más que la relación
inversa de las derivadas y las integrales
- 2.
La
versión del TFC de Newton se depuró y se condensó
desde su versión general de 1665 hasta la publicada en 1704, donde quiso
reorientar su cálculo hacia las demostraciones geométricas puras, como lo
hacían los antiguos griegos. Sin embargo, la esencia de la misma, puede estudiarse
a fondo en sus manuscritos de 1666.
- 3.
Es
recomendable realizar en paralelo los estudios y lecturas de fuentes primarias
y de expertos, para no efectuar hipótesis o afirmaciones erróneas, como la
mostrada sobre la función arcoseno.
- 4.
El
desarrollo que ha tenido el análisis matemático a partir del S. XVII ha traído consigo cambios de paradigmas e inserción
de objetos matemáticos que en esta época moderna son estructuras fuertes. Por
ejemplo, el límite formalizado por Augustin Cauchy y a partir del cual se define actualmente la
integración y derivación. Sin embargo, inicialmente estos procesos fueron
abordados desde un punto de vista geométrico por Newton para resolver
problemas. Luego, trabajar desde los puntos de vista histórico permite abrir nuevas
alternativas para la enseñanza de objetos matemáticos.
- 5.
No
se deberían descartar los aportes que pueden brindar los argumentos con
potencial heurísticos al momento de enseñar un objeto matemático o para la
resolución de problemas, porque se ampliaría la posibilidad de la evaluación de
su validez en las practicas matemáticas (brindada hasta el momento por el
modelo inductivo-deductivo de los libros de textos y algunos currículos
universitarios de cálculo o análisis matemático).
IX. Lista
de referencias
Bardi, J. S. (2006). The
Calculus Wars. Newton, Leibniz, and the Greatest Mathematical Clash of All
Time. Book
Bos, H. J. M. (1993a). Lectures in the History of
Mathematics (A. M. Soc. (ed.)). https://books.google.com.co/books/about/Lectures_in_the_History_of_Mathematics.html?id=lSGvPI6LHvwC&redir_esc=y
Bos,
H. J. M. (1993b). On the interpretation of exactness.pdf. Philosophy
of Mathematics, 23.
Bressoud, D. M. (2011). Historical reflections on
teaching the fundamental theorem of integral calculus. American
Mathematical Monthly, 118(2), 99–115.
https://doi.org/10.4169/amer.math.monthly.118.02.099
Guicciardini,
N. (2006). La Época Del Punto :
El Legado Matemático De Newton. 67–109.
Guicciardini, N. (2008). “Gigantic
implements of war”: images of Newton as a mathematician. In The Oxford Handbook Of The History Of Mathematics (pp.
707–737). Oxford University Press.
Guicciardini, N. (2009). Isaac Newton
on mathematical certainty and method. The MIT Press. https://doi.org/10.1007/s10086-013-1369-8
Iliffe, R. (Oxford U. T. R. S. (2011a). Mathematical Notebook. The Newton Project. http://www.newtonproject.ox.ac.uk/view/texts/normalized/NATP00128
Iliffe, R. (Oxford U. T. R. S. (2011b). The October of 1666 Tract on Fluxions. The Newton Project. http://www.newtonproject.ox.ac.uk/view/texts/normalized/NATP00100
Iliffe, R. (Oxford U. T. R. S. (2012). De Analysi per aequationes numero terminorum infinitas.
http://www.newtonproject.ox.ac.uk/view/texts/normalized/NATP00204
Lasa,
A., Wilhelmi, M. R., & Abaurrea,
J. (2017). El problema de la argumentación: una aproximación desde el EOS.
Actas Del Segundo Congreso International Virtual Sobre El Enfoque Ontosemiótico Del Conocimiento y La Instrucción
Matemáticos.
Maronne, S., & Panza, M. (2021). De la méthode des normales de Descartes à l’algorithme
de Newton. Les contributions de Hudde
et Sluse. [Manuscrito Enviado Para
Publicación]
Muñoz Villate,
W. (2021). Aspectos históricos del teorema fundamental del cálculo y posibles
mediaciones tecnológicas. Ciencia y Educación, 5(1),
189–204. https://doi.org/10.22206/cyed.2021.v5i1.pp189-204
Newton, I. (1704a). Incomplete copy
by David Gregory of Tractatus de Quadratura Curvarum. Digital Library, University of Cambridge. https://cudl.lib.cam.ac.uk/view/MS-ADD-09597-00002-00018/226
Newton, Isaac. (1704b). Tractatus De
Quadratura Curvarum. https://www.e-rara.ch/bau_1/content/titleinfo/24001858?lang=de
Newton, Isaac. (2001). Tratado de métodos de series y de fluxiones. UNAM.
Panza, M. (2000). Newton et les origines de l’analyse : 1664-1666.
Sciences de l’Homme et
Société. Ecole des Hautes Etudes
en Sciences Sociales. https://tel.archives-ouvertes.fr/tel-00116744/file/MsPr.pd
Pérez, J. (2013). Orígenes del Cálculo. Universidad de Granada. http://www.ugr.es/~dpto_am/OLD/docencia/Apuntes/Origenes_del_Calculo.pdf
Robson,
E., & Stedall, J. (2009). The
Oxford Handbook of The History of Mathematics.
Scriba,
C. (2014). Method The Inverse of Tangents : A Dialogue between
Leibniz and Newton (1675-1677). In Archive for History of
Exact Sciences (Vol. 2, Issue 2, pp. 113–137).
Stewart,
J. (2015). Calculus. Cengage Learning.
Toumasis, C. (1993). What is the fundamental theorem of
integral calculus? International Journal of Mathematical
Education in Science and Technology, 24(5), 685–687.
https://doi.org/10.1080/0020739930240509
Whiteside,
D. T. (1961). Patterns of mathematical thought in the later seventeenth
century. Archive for History of Exact Sciences, 1(3), 179–388. https://doi.org/10.1007/BF00327940
Notas
[2] https://www.britannica.com/topic/historiography/Methodology-of-historiography
Notas de autor
1] Doctorando de la Universidad Distrital
Francisco José de Caldas, profesor de planta Universidad de La Salle, Colombia.
wmunoz@unisalle.edu.co