Introducción

¿Qué hacer para transformar las aulas universitarias en espacios más hospitalarios e inclusivos y evitar la deserción, especialmente en los primeros años? Esta pregunta ha sido el punto de partida de un proyecto orientado a la inclusión a través de la constitución de grupos colaborativos de reflexión sobre la enseñanza¹ en la Universidad Nacional de Moreno (UNM). La propuesta pretende aportar a la comprensión de los fenómenos de enseñanza en educación superior, con participación de quienes enseñan. Partimos del supuesto de que para incidir efectivamente sobre las posibilidades de aprendizaje de los alumnos no basta con identificar las falencias de la formación anterior, sino que es imprescindible incluir la propia propuesta de enseñanza como objeto de análisis y transformación.

Los aprendizajes de alta intensidad (Davini, 2008), como el matemático, requieren de situaciones que conllevan análisis reflexivo, generación de hipótesis, identificación y elaboración de soluciones, e implican un gran esfuerzo para los estudiantes. Asimismo, su enseñanza debe abordar las interacciones con el grupo que aprende, la organización de un ambiente favorable, claridad en las reglas de organización de la tarea, consideración del contexto y de los artefactos culturales que se integren como andamios o palancas para que los estudiantes pueden aprenderlos (Davini, 2008).

Carlino (2005) afirma que no es posible sostener el compromiso necesario para perseverar y reponerse de los intentos infructuosos si quien lo hace desconfía de sus capacidades para llegar a buen término; y que, dado que los intereses y la autoconfianza se generan en la interacción con el mundo y con los otros, es responsabilidad de la tarea de enseñanza fortalecer la creencia personal de los estudiantes en que conseguirán finalmente aprender los contenidos. Esta condición es excluyente en la UNM, donde entre ocho y nueve de cada diez estudiantes son la primera generación que asiste a la universidad en sus familias.² Como es conocido, las tasas de abandono de las universidades coinciden con quienes tienen padres sin estudios, lo cual perpetúa la desigualdad (Ezcurra, 2007; Gessaghi y Llinás, 2005). En este marco, pretendemos vertebrar la exposición a través de la siguiente pregunta: ¿cómo desarrollar una propuesta que desafíe a las/os estudiantes y les dé las herramientas para afrontar el reto de aprender análisis matemático?

La materia Análisis Matemático (AMI) y la Coordinación del área

Las autoridades de la UNM convocaron a la Coordinación de Matemática para concretar una enseñanza superadora de las prácticas tradicionales y a favor de la inclusión. Esto implicó el desarrollo de un programa, materiales específicos y la conformación de un equipo docente que pudiera involucrarse con las necesidades de los estudiantes.

La propuesta asignó un papel protagónico a los estudiantes, en tanto fueron convocados a resolver problemas. Estos problemas fueron diseñados como situaciones que les ofrecían posibilidades para construir por sí mismos los nuevos conocimientos (Brousseau, 2000). Pensamos en el problema matemático como el medio por el cual los alumnos pueden poner en juego su comprensión y dar cuenta de ella. Entendemos la comprensión como la capacidad de desempeñarse en forma flexible, esto es, reinterpretar, adaptar el sentido de un concepto matemático para innovar frente a un problema y generar recursos que permitan resolverlo (Perkins, 1999). Las intervenciones docentes deben andamiar (Wood, 1976) la distancia entre los saberes de los estudiantes y los requeridos para la resolución del problema. Ahora bien, no se trata solo de considerar el contenido matemático. Durante 2019, el trabajo del equipo estuvo centrado en cómo construir vínculos de confianza entre los estudiantes y entre los estudiantes y profesores. Estos vínculos se vuelven fundamentales para sostener la continuidad de las trayectorias cuando los estudiantes tienen dudas sobre su capacidad para aprender, y no tienen a priori habilitadas ciertas prácticas inherentes a la resolución de problemas, como las de preguntar, conjeturar, equivocarse, rectificarse, etc. En la evaluación del proceso, uno de los profesores decía:

Lo que empezó a transformar lo que pasaba en las clases, fue esa construcción del vínculo con los estudiantes: que llegaran, que hubiera risas en la clase, que hubiera ciertos chistes que eran medio tribales, que tenían que ver con la historia del grupo y las cosas que habían pasado en el aula. Creo que fue lo que hizo que muchos, inclusive los que bastante temprano supieron que no les iba a alcanzar para aprobar la materia, decidieran venir a las clases hasta el final. Eso no pasaba antes, en otros cursos los pibes que iban perdiendo el tren de lo que pasaba en la materia, directamente no venían más. El año pasado muchos siguieron viniendo porque les resultaba formativo y porque querían estar. Ahora estoy sintiendo que enseñar mejor matemática tiene que contemplar cómo llegar a los estudiantes y el vínculo que se construye con ellos, eso me transformó. (Profesor AMI, en entrevista).

Los logros de 2019 sufren un vuelco abrupto con el advenimiento de la pandemia y la repentina transformación de nuestras clases presenciales en cursos a distancia mediados por la plataforma Moodle de la UNM. En el contexto de las condiciones de enseñanza que imponía el Aislamiento Social Preventivo y Obligatorio (ASPO) 2020, ¿era posible reinventar la propuesta sin renunciar al enfoque metodológico ni al tipo de interacciones, para acompañar y sostener a los estudiantes en los aprendizajes?

Enseñar Análisis Matemático en contexto de ASPO

La migración del aula presencial a los formatos virtuales supuso encontrar alternativas para sostener la continuidad de los estudiantes a través de una variedad de propuestas sincrónicas y asincrónicas. Sumamos el uso de la aplicación Telegram al de la plataforma Moodle. Pensamos que nos permitiría construir un espacio de intercambio y contención para acompañar a los estudiantes en una materia que habitualmente no les resulta sencilla.

Ese marco de contención se edificó sobre dos soportes principales. Por un lado, los encuentros sincrónicos en el chat de Telegram, respetando el horario de la cursada presencial. Buscábamos mantener un contacto cercano con los estudiantes. Conocerlos, garantizar el acceso a los materiales y consignas para que todos pudieran cumplir con las tareas asincrónicas y construir con ellos un vínculo que mitigara el efecto del aislamiento. Al mismo tiempo, se buscaba favorecer el diálogo entre los estudiantes y la conformación de grupos de estudio.

Todas las semanas proponíamos tres tareas que podían resolver en forma grupal o individual. Consistían en problemas centrales de la guía de trabajos prácticos de la materia. Las producciones de los estudiantes eran devueltas a través de la plataforma Moodle con comentarios de retroalimentación.

Para nuestra sorpresa, el chat de Telegram nos permitió gestionar clases basadas en la resolución de problemas. Las tareas propuestas y nuestras intervenciones lograron progresivamente habilitar la pregunta, la duda, la consulta, la colaboración entre pares. A continuación, compartimos algunos intercambios posteriores a la etapa de producción individual sobre un problema acerca del concepto de derivada que se aborda a mitad de la cursada. Se los convocó a pasar al debate colectivo en el grupo de chat:³

Docente: Vean el enunciado del Problema 5 (si alguien puede lo copia por acá).

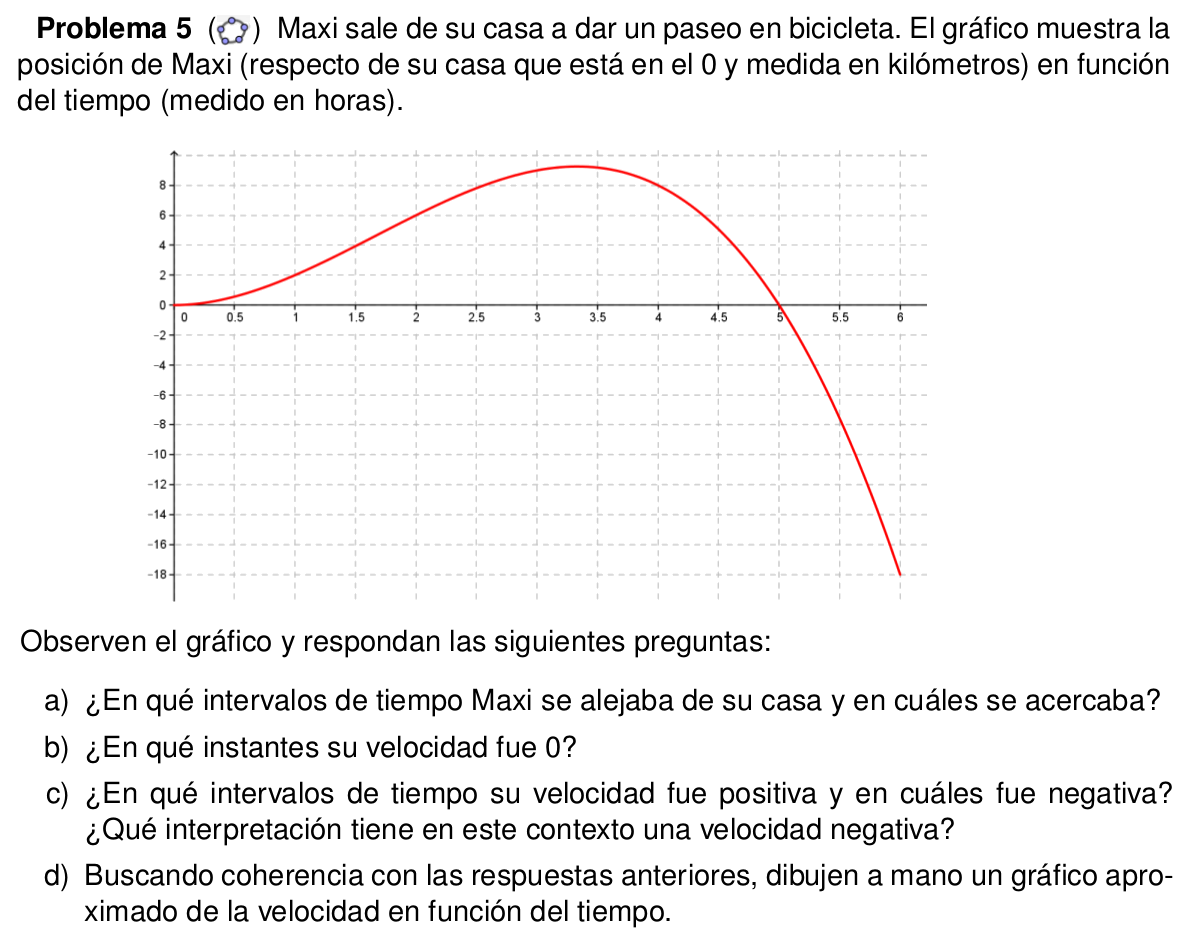Figura 1.
Problema 5

Un estudiante respondió al pedido y compartió como imagen el problema para comodidad del resto de sus compañeros.

Docente: Para comenzar a discutir el problema puede ser divertido hacer unos cañonazos como el otro día y que todos manden sus gráficos al mismo tiempo, a ver con qué nos encontramos. ¿En qué intervalos de tiempo Maxi se alejaba de su casa?

Varios estudiantes envían sus chats a la vez:

Felipe: (0.1,3.5) aprox.; Gerardo: 0 3.5; León: (0, 3.35); Ramón (0;3.33); Carlos: (0,3.5), (5,+inf); Martín: [0,3.5] se aleja. [3.5,5] se acerca. y [5,inf] se vuelve a alejar.

Docente: Dos comentarios: Felipe: fijate que pusiste 0.1 para expresar «un poquito después de 0». Para eso tenés los intervalos abiertos: [0, 3.5) incluiría al 0 y (0, 3.5) no lo incluiría. El otro comentario: ¿acuerdan con los agregados de Carlos y Martín?

Felipe: Ahhh, no lo había entendido. Es que en t=0 y t=5 está en su casa.

Martín: Sí... Yo dudé en considerar que se alejaba entre 5 e inf.

León: Entonces el ciclista, luego de dar la vuelta, vuelve a pasar por su casa pero sigue en la dirección opuesta a la que iba cuando empezó.

Los cañonazos consisten en que los estudiantes envían al mismo tiempo una imagen o un texto con la solución que proponen. Se trata de un recurso que se fue repitiendo y afianzando con la cursada. Este ejemplo los muestra aportando de modo entusiasta al debate general, aun sabiendo que sus producciones pueden ser incorrectas o incompletas. Felipe dio una respuesta con un error conceptual. El docente intervino con una explicación directa para aclarar el detalle. Felipe explicó lo que no había entendido y mostró su sonrisa. El comentario dio pie a Martín para expresar también sus dudas. Por otra parte, el docente puso a consideración las respuestas de Carlos y Martín (correctas) e invitó a los demás a brindar su opinión sobre ellas: «¿Están de acuerdo?». León interpretó la respuesta de sus compañeros dada por la escritura simbólica de los intervalos. Contrastó con el gráfico y tradujo esa respuesta al lenguaje coloquial, mostrando que pudo comprenderla y que lo convenció de reconsiderar la suya. La interpretación física del concepto de derivada (¡que todavía no había sido nombrado!) se fue poniendo en juego. La naturaleza del problema propuesto lo hizo surgir en el debate, tal como se había planeado. Pero experiencias anteriores nos han mostrado que el problema solo no habría bastado. Este surgimiento se ve propiciado porque vale hipotetizar en voz alta, dudar, compartir respuestas incompletas. Se los ve/lee involucrados con el problema. Este ejemplo ilustra el tipo de intercambio que se construyó en la interacción por Telegram. Luego se pasó a debatir si tenía sentido considerar que la bicicleta continuaba viajando durante tiempo infinito solo porque la gráfica de la función lo sugiriera.

Docente: Los intervalos no acotados se escriben abiertos en ese extremo: (5, +∞)

Gerardo: Fue a la esquina, volvió y se fue a Cancún, más o menos.

Felipe: Jaja, claro.

León: Yo digo que se habrá asustado con algo, porque iba tranquilo hasta que dio la vuelta y pedaleó como si su vida dependiera de ello.

Carlos: Porque la pendiente es mayor que en el principio.

Docente: ¡Muy lindo comentario, León! El chiste incluye una noción de velocidad muy acertada, como aclara Carlos. En realidad, aunque la función se puede definir para todos los números reales, en un modelo, en este contexto, no tendría sentido decir que sigue viajando hasta +∞. Ahí falta alguna información que no viene precisada en el problema.

Ahora bien, desde el inicio del proceso se generaron intervenciones para propiciar la participación. A modo de ejemplo, el humor, incluido inicialmente por los docentes, fue un recurso valioso para invitar a los estudiantes a expresarse libremente. No se trataba de planear clases divertidas (aunque a veces lo eran). El humor los descontracturó, les permitió equivocarse y reírse de ellos mismos. Algunos chistes mostraron comprensión del problema abordado o vivencias sobre la pandemia.

El trabajo grupal orientó las interacciones hacia la colaboración, la confianza y el respeto por todos como un contenido más para el equipo docente. Nos interesaba, especialmente en este contexto, que fuera una experiencia positiva. Un alumno comentó al respecto:

El sentido común dice que estamos estudiando, no en un concurso de preguntas y respuestas. Pero hay materias donde si decís que te expliquen algo, y la pregunta es errónea te «mandaban al rincón a pensar», en vez de trabajar sobre eso. Acá la diferencia es esa, no solo los profesores, sino que es un buen grupo de compañeros. Nadie mira por arriba del hombro. (Martín, entrevista final)

La conformación de los grupos de trabajo amplió los apoyos con los que contaban los estudiantes. Los grupos online les permitieron consultar y recibir respuestas de los compañeros y nuestras, incluso sobre cuestiones matemáticas elementales y en el momento en que estaban trabajando. Los estudiantes valoraron el trabajo grupal:

Son muy importantes. Te definen si te quedás o no en una materia, porque tenés en quién apoyarte, quién te saque dudas y podés seguir. Si no preguntás en clase, la podés seguir después, podés ayudar y ser ayudado, se da la reciprocidad, el ida y vuelta, para mí es muy bueno. Sí, es fundamental, para poder dedicarle más tiempo y estar comunicado si no estuviste en clase.

El grupo operó a modo de andamio o palanca para facilitar el aprendizaje de los estudiantes:

Lo primero es formar el grupo y que el profesor lo pida, porque al empezar son cinco o cuatro, pero luego sentís la presión de responder y aportar algo. Porque no es lo mismo hacer un trabajo solo. Si lo hago solo digo «no lo puedo terminar ya fue, no lo entrego». Pero el primer trabajo que hice en grupo lo hicimos entre tres, nos dividimos y debatimos y pudimos hacer un trabajo completo y entregarlo. Yo hice eso porque tenía una cierta responsabilidad, cariño y respeto que hay por el otro y con los otros grupos. (Federico, entrevista final)

Los estudiantes se apropiaron de la modalidad de trabajo. Convocaron, difundieron información y desarrollaron actitudes contenedoras y hospitalarias con sus compañeros. En un chat privado, Felipe comunicó al docente un audio de su compañero Marcelo:

Hay un montón de cosas en que se dan como sabidas y hay muchas de las que yo no tenía ni idea. Pero yo me fijaba en YouTube, copiaba, buscaba, hacía ejemplos y me salían. Si no entendía algo se lo decía al profe porque literalmente me partía la cabeza, y no preguntaba a nadie más. Preguntaba en el grupo que me había tocado y no me contestaba nadie. Y a mí me daba una bronca... Todos los del grupo me clavaban el visto. Entonces me fui, ya está. ¿Para qué? Trabajo yo solo y listo. Y ahora, con vos, gracias al juego ese dinámico que hizo el profesor⁴ se dio que hablamos y ahora te pregunto a vos.

Y agregó Marcelo:

Quería compartir el resultado de estos ejercicios.⁵ Vos [hablándole al docente] te esforzás en hacerlos para que nos comuniquemos y que veas que tienen un fruto. A Marcelo me lo traje a nuestro grupo de estudio. Le pregunté a los chicos [por los demás integrantes] y todos dijeron que sí.

Progresivamente, los estudiantes también se hicieron corresponsables por construir lazos de compañerismo que contribuyeron al aprendizaje de todos. Desde nuestra perspectiva, condición fundamental para la retención.

Reflexiones finales

La experiencia que compartimos en este texto es parte de un trabajo de varios años que tiene la intención de transformar las aulas universitarias en espacios más hospitalarios e inclusivos y prevenir la deserción. El contexto del ASPO nos desafió a reinventar las clases basadas en que los alumnos resuelvan problemas. Nos enfocamos en la construcción de una relación docente–alumno que involucrara la confianza de ambas partes para preguntar y responder, con la certeza de que siempre iban a contar con sus profesores.

El planteo de Laurence Cornu (1999) analiza que la confianza es constitutiva de la relación pedagógica y que su presencia es necesaria para que pueda producirse la transmisión. Por un lado, considera una apuesta sobre el otro que pone en relación el tiempo presente y el futuro, ya que la confianza se produce hoy en torno a lo que se espera que otro pueda realizar luego, en un tiempo posterior al actual. De esta manera se produce una falta de control del otro y del tiempo. Así, resulta parte de la tarea pedagógica no inquietarse y poder tolerar esa ausencia de control, de certezas. La confianza se convierte en parte constitutiva del vínculo entre los actores de una situación de enseñanza: un intercambio con los estudiantes que pone en juego una apuesta sin evidencias sobre aquello que el otro hará pero que progresivamente se va haciendo explícita: confío en ustedes, en sus capacidades para llegar a buen término, creo que son capaces de aprender. Esta apuesta tiene su contrapartida en un paulatino desarrollo de la autonomía sobre los aprendizajes por parte de los estudiantes. Cornu (1999) señala que la responsabilidad es la capacidad de hacerse cargo de decisiones que comprometen el futuro y responder por las consecuencias que estos actos implican en tanto consecuencia generadas por nuestras acciones de modo activo y positivo relacionada con la posibilidad de «tomar responsabilidad» como asunción de ciertos espacios, acciones, decisiones que permitan generar cosas nuevas en vínculo con otros. En el trabajo intentamos comentar brevemente algunas implicancias acerca de hacer lugar a la confianza en las aulas universitarias en tanto responsabilidad para la tarea docente. Entendemos que una enseñanza centrada en reconfigurar los vínculos entre docentes y estudiantes hacia relaciones colaborativas y de corresponsabilidad por el aprendizaje de todos contribuye a sostener el compromiso necesario para perseverar y reponerse de los intentos infructuosos. Como reclama Carlino (2005), es una manera más de fortalecer la creencia personal de los estudiantes de que conseguirán finalmente aprender los contenidos.

Por otra parte, nos queda como interrogante en qué medida la disposición de los estudiantes a participar se ve favorecida por la mediación de las herramientas virtuales. Al consultarlos al respecto y en comparación con las clases presenciales, varios de ellos comentaron:

No había tanta inhibición quizás, al no estar presente, por ahí uno se suelta un poco más. La contención es por Telegram porque fluye la conversación. Por Zoom no podés chatear,⁶ en cambio en Telegram estamos todos en un conjunto y todos nos respondemos a todos.

La experiencia, si bien nació en 2019, encontró este momento de singular desarrollo en el escenario del ASPO. La pandemia y las clases virtuales nos dejan aprendizajes también a los docentes y estará en nosotros llevar lo aprendido a las aulas.

Referencias

Bateson, G. (1998). Pasos hacia una ecología de la mente. Lohlé– Lumen.

Brousseau, G. (2000). Educación y didáctica de las matemáticas. Educación matemática, 12(01), 5–38. http://funes.uniandes.edu.co/10210/1/Educacion2000Brousseau.pdf

Davini, M. C. (2008). Métodos de enseñanza: didáctica general para maestros y profesores. Santillana.

Carlino, P. (2005). Escribir, leer, y aprender en la universidad. Una introducción a la alfabetización académica. Fondo de Cultura Económica.

Chorny, F.; Coll, P.; Mateos, N.; De Lucca, A.; Reynoso, L. (2019). El acompañamiento de la trayectoria de los estudiantes en educación superior. Re︎flexiones en torno a sus implicancias en un aula de matemática. Mimeo. UNM.

Cornu, L. (1999). La confianza en las relaciones pedagógicas. En Frigerio, G. (Comp.). Construyendo un saber sobre el interior de la escuela. Novedades Educativas. Centro de estudios multidisciplinarios.

Ezcurra, A. M. (2007). Los estudiantes de nuevo ingreso. Democratización y responsabilidad de las instituciones universitarias. Cuadernos de Pedagogía Universitaria, (2). Pro–Rectoría de Graduación. Universidad de San Pablo.

Gessaghi, V.; Llinás, P. (2005). Democratizar el acceso a la educación superior (pp. 1–30). CIPPEC.

Perkins D. (1999). ¿Qué es la comprensión? En Stone Wiske, M. Enseñanza para la comprensión. Paidós.

Wood, D.; Bruner, J. S.; Ross, G. (1976). The role of tutoring in problem solving. Journal of Child Psychology and Psychiatry, 17, 89–100. https://acamh.onlinelibrary.wiley.com/doi/10.1111/j.1469-7610.1976.tb00381.x

Notas

Notas de autor