1. Introdução: situando o interesse pelo tema de pesquisa e
definindo a pergunta diretriz
O interesse em pesquisar sobre a Educação de Jovens e Adultos (EJA) surgiu desde a graduação em Licenciatura em Matemática, realizada na Universidade Estadual do Sudoeste da Bahia (UESB), entre os anos de 2012 e 2015. Como trabalho de conclusão de curso, desenvolvi um estudo sobre as dificuldades que alunos da EJA apresentavam ao realizar o cálculo de perímetro e da área de figuras planas. Isso se deu graças ao interesse sobre o público da EJA e à participação no Grupo de Articulação, Investigação e Pesquisa em Educação Matemática (GAIPEM). Contudo, ainda na graduação, também tive contato com as TD, em especial com o uso do GeoGebra, primeiro participando de oficinas e depois ministrando-as para alunos da graduação. Atividades essas realizadas pelo Grupo de Pesquisa e Extensão em Tecnologias Digitais no Ensino (GPETDEN[1]), do qual faço parte. Portanto, a partir dessas experiências, percebi o relevante papel que a tecnologia - em especial o GeoGebra - pode ter na aprendizagem de conceitos matemáticos.
Essas experiências vividas na graduação afloraram ainda mais o desejo de continuar pesquisando sobre o ensino de Matemática na EJA, aliado ao uso das TD. Desse modo, me permiti ampliar os horizontes do trabalho de final de curso realizado na graduação.
Com esse ideal, em 2016, ingressei no Programa de Pós-Graduação em Ensino (PPGEn), da UESB. Já como aluna do mestrado, tive a necessidade de me aprofundar em outras questões relacionadas à pesquisa em si, aos aspectos teóricos e metodológicos da mesma. Também, necessitei consolidar meu interesse de pesquisa, centrando-o em duas dimensões: o público da EJA e o uso das tecnologias digitais. À medida que ia adentrando nessas dimensões, brotaram novos questionamentos, tais como: O uso do software matemático pode contribuir para a aprendizagem matemática? O software GeoGebra pode potencializar a aprendizagem de geometria plana para alunos da EJA? Como se dá a formação de conceitos quando os alunos usam o GeoGebra? Como percebemos essa aprendizagem?
Assim, para atender às dimensões postas - que envolveram reflexões e discussões com a orientadora e no âmbito do grupo de pesquisa -, originou-se a questão de pesquisa da dissertação: “Como ocorre a formação de conceitos geométricos na Educação de Jovens e Adultos mediada pelo software GeoGebra?”.
Com a questão norteadora definida, o passo seguinte foi buscar pesquisas que estivessem relacionadas às temáticas Educação de Jovens e Adultos, ensino de geometria plana e o uso de TD, com o intuito de nos apropriarmos[2] do estado do conhecimento. Além disso, foi necessário ir em busca de um referencial teórico com o qual pudéssemos dialogar para consolidar a pesquisa, respondendo à questão diretriz.
Após buscarmos o estado do conhecimento, nos deparamos com várias pesquisas sobre EJA, contudo identificamos que poucas trataram das dimensões por nós postas. Na maioria das pesquisas sobre a modalidade analisadas, percebemos que o foco foi sobre as relações do ensino com o sujeito social da EJA. Outras, sobre os direitos estabelecidos por lei para esses alunos; algumas, sobre a infantilização de conteúdos matemáticos feita por alguns professores; uma tratou do ensino de geometria e cotidiano na EJA. Nesse sentido, pode-se perceber que poucas são as discussões sobre como se dão os processos de aprendizagem.
Entendemos e reconhecemos a importância dessas discussões citadas, contudo, não podemos nos limitar a elas. Por isso, além dessas questões, também nos preocupamos com os processos mentais e a aprendizagem desses alunos – entendemos processos mentais como o modo segundo o qual o aluno consegue reorganizar as informações prévias e as adquiridas durante a aprendizagem de um conteúdo matemático; seriam conformados pelo algoritmo e pelo pensamento matemático utilizado por esse aluno para compreender e assimilar os conteúdos estudados. Isso porque percebemos que os alunos dessa modalidade de ensino também possuem anseios e desejos de dar continuidade aos estudos, esforçando-se para fazer cursos técnicos e até para cursar o ensino superior. Dessa maneira, em nossa pesquisa, não nos limitamos apenas a reforçar estereótipos sobre o público da EJA, mas propusemos discussões e atividades que tiveram como propósito explorar o pensamento matemático desse aluno.
Como dito anteriormente, buscamos pesquisas que envolvessem a nossa temática, porém identificamos poucas dissertações ou teses que abordassem o ensino de geometria plana na EJA com a tecnologia GeoGebra. Algumas das dissertações que encontramos foram a de Borba (2017), a qual foi realizada na Universidade Federal de Uberlândia (UFU), e a de Fonseca (2017), na Universidade Estadual do Norte Fluminense Darcy Ribeiro (UENF).
A dissertação de Borba (2017) teve como questão de pesquisa “Que contribuições pedagógicas as práticas de ensino com recursos tecnológicos podem oferecer para o ensino e aprendizagem de Matemática para alunos da Educação de Jovens e Adultos?”, cujo objetivo foi analisar possíveis contribuições das tecnologias para o processo de ensino e aprendizagem na EJA. Nessa pesquisa, o autor abordou o ensino de área, perímetro, simetria e ângulos, com três turmas de EJA. Para isso, foram feitos questionários criados no Google Docs e disponibilizados em um blog. Em todos os encontros foram feitas notas de campo e, também, filmagens e os áudios foram gravados pelo professor pesquisador. Durante cada encontro, os alunos registravam as suas produções, salvavam-nas no software utilizado na sala (PowerPoint e GeoGebra) e ao término da aula enviavam esses arquivos para o e-mail do professor. Também foram feitas entrevistas semiestruturadas com dois alunos de cada turma. Ao término dos encontros, os alunos fizeram um relato final sobre a experiência tida, e os textos foram salvos no blog.
Ao término da pesquisa, Borba (2017) chegou às seguintes conclusões: antes da pesquisa, os alunos se sentiam excluídos das atividades que envolviam tecnologias; após a proposta apresentada pelo autor, eles se sentiram motivados e incluídos, apesar das dificuldades encontradas no processo de aprendizagem; as contribuições da proposta foram além das perspectivas tecnológicas e reflexivas, havendo também contribuições sociais, pois através da experiência vivenciada, os alunos tiveram acesso a tecnologias que foram exploradas de acordo com o tempo e conhecimento de cada turma. Borba (2017) também observou mudanças na sua perspectiva sobre tecnologias e prática pedagógica, uma vez que passou a investigar, questionar e averiguar, cada vez mais, os detalhes dos conteúdos matemáticos explorados. Ainda observou a importância da integração de várias tecnologias pois, através dessa experiência, confirmou a hipótese de que uma tecnologia não deve excluir a outra, e, sim, devem ser exploradas de formas distintas. Por fim, o autor afirma a importância e os desafios de inserir propostas de atividades utilizando tecnologias no ensino.
Já a dissertação de Fonseca (2017) teve como questão norteadora da pesquisa “A utilização da linguagem geométrica abstrata, de desenhos estáticos, de fórmulas decoradas e dos recursos pedagógicos utilizados pelo professor dificulta o aprendizado?”. O seu objetivo foi investigar, por meio da utilização de recursos lúdicos e tecnológicos, a aprendizagem de conceitos de geometria em turmas da Nova Educação de Jovens e Adultos (NEJA), utilizando sequências didáticas. Para a produção dos dados, a autora fez entrevista, questionário, teste e uma sequência didática. Os conteúdos abordados foram diferentes em cada uma das quatro turmas que participaram da pesquisa: posições entre ponto, reta e plano; formas geométricas espaciais; fórmula de Euler; Teorema de Tales; distância entre pontos; e sistema cartesiano, dentre outros conteúdos. As atividades eram realizadas no software GeoGebra – explorando as caixinhas do applet que eram previamente salvas no computador -, e os alunos executavam os procedimentos durante os encontros, além de jogo da memória e jogo da velha, uso de folha xerografada, transferidor, régua e outros materiais.
Ao término de sua pesquisa, Fonseca (2017) aponta que a utilização dos recursos lúdicos e tecnológicos foi além da perspectiva motivacional, pois permitiu aos alunos provar, testar, explorar, e, além disso, possibilitou o trabalho em grupo cooperativo. Também afirma que em função da quantidade de participantes da pesquisa não se pode generalizar os resultados; entretanto, o objetivo principal da pesquisa foi contemplado. A autora finaliza afirmando a importância de preparar aulas dinâmicas, sem memorização de conteúdos e que permitam a visualização e o raciocínio.
Assim, analisar essas pesquisas nos ajudou a delimitar o nosso campo de interesse e perceber em que aspectos nossa pesquisa difere dessas duas. Posto isso, enfatizamos que, em nossa pesquisa - do tipo intervenção-, propomos atividades matemáticas para serem realizadas com o software GeoGebra, com duas turmas distintas de alunos da EJA, de uma escola pública de Vitória da Conquista – Bahia, totalizando seis encontros com cada turma, uma com 24 alunos e a outra com 10. Essas atividades foram construídas por nós na forma de roteiros (questões abertas), nas quais, à medida em que iam sendo feitas pelos alunos, sob nossa orientação, os conceitos matemáticos dos conteúdos envolvidos iam aparecendo. Ou seja, analisar como se deu a formação desses conceitos e o papel da tecnologia nesse processo se constituiu em objetivo principal. Para alcançar esse objetivo utilizamos como instrumentos para produção de dados observação sistemática com anotação dessas observações (diário de bordo de cada encontro) e entrevistas individuais com os participantes, no último encontro.
Portanto, nossa proposta de atividades matemáticas não trazia conceitos prontos, os conceitos deveriam ser formados a partir da leitura e entendimento da atividade, construção e manipulação no software para internalização (formação) do conceito. Essa maneira de pensar a aprendizagem matemática com uso da tecnologia nos impulsionou a ir em busca de uma teoria que nos desse suporte, ou seja, que fôssemos além do abordado por Borba, Scucuglia e Gadanidis (2015) sobre o “pensar-com-tecnologia” para algo como: “pensar-com-tecnologia a partir de um roteiro de atividades” e, com isso, formar conceitos matemáticos. Ou seja, os conceitos matemáticos foram explorados no GeoGebra, mas para que isso acontecesse foi necessária a apropriação dos ícones e ferramentas do software – conhecer a ferramenta. Aliado a isso, pensar a atividade matemática. Desse modo, podemos pensar tudo isso como um processo, conforme figura 1, a seguir:
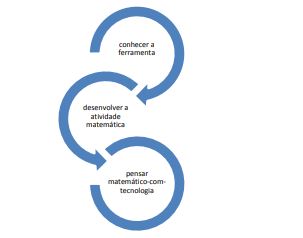 Figura 1
Processo pensar
matemática-com-tecnologia
Fonte: Produção nossa
(2019)
Figura 1
Processo pensar
matemática-com-tecnologia
Fonte: Produção nossa
(2019)
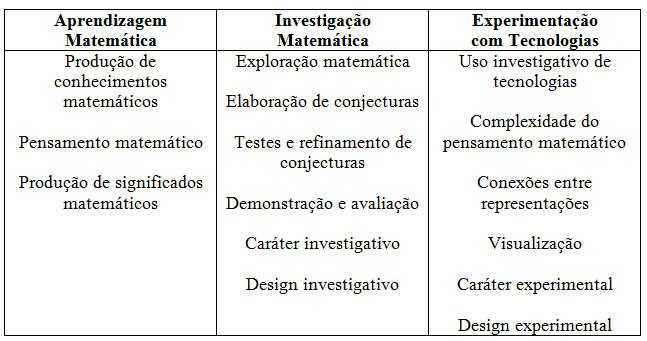
Para explicar pensar-com-tecnologia, Borba,
Scucuglia e Gadanidis elaboraram um quadro, conforme quadro 1. Na nossa
percepção, o pensar-com-GeoGebra quer dizer que uma atividade matemática para
ser realizada em um software, deve
permitir ao aluno encontrar o próprio caminho para a resolução da atividade (o
que pode trazer resultados diferentes); durante as construções no software podem surgir novas estratégias;
as atividades permitem resultados que não são possíveis se realizadas somente
com lápis e papel; e, além disso, possibilitam a exploração dos conceitos
matemáticos.
A
partir da análise do quadro 1, podemos perceber que pensar-com-GeoGebra envolve
a aprendizagem, a investigação e a experimentação com a tecnologia. Ao
realizarmos a atividade denominada “Reta Paralela” (uma das atividades
realizadas em nossa pesquisa, conforme figura 2), identificamos a aprendizagem
matemática, no que tange ao pensamento matemático do que é uma reta paralela;
mas para compreender o que é uma reta paralela é necessário compreender
primeiramente, o que é uma reta. Nesse momento, começamos a perceber a produção
dos significados matemáticos. Na pergunta número 4 da figura 2, está escrito
“Qual é a relação que você observa entre essas retas criadas?”; a partir dessa
pergunta, é necessário que haja uma investigação e reflexão sobre os procedimentos
construídos anteriormente, além de provar se as definições estão corretas ou
não. Por meio do software GeoGebra é
possível visualizar os passos construídos e movimentar os entes geométricos;
dessa maneira, verifica-se se as propriedades dos entes geométricos são válidas
ou não. Na figura 2, abaixo, apresentamos um recorte da atividade “Reta
Paralela” e uma possível construção desses entes geométricos.
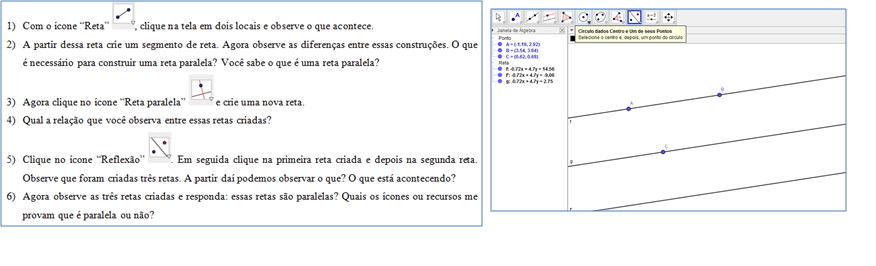 Figura 2
Modelo de atividade
“Reta Paralela”
Fonte: Produção nossa (2019)
Figura 2
Modelo de atividade
“Reta Paralela”
Fonte: Produção nossa (2019)
Assim como Borba (2017) e Fonseca (2017), as autoras Kozelski e Arruda (2017) apontam a importância da utilização de tecnologias nas aulas de Matemática, para o processo de ensino e de aprendizagem. Contudo, afirmam que “O único ponto negativo é que ao professor elas demandam muito tempo de preparo e planejamento. Porém a recompensa é o desafio de buscar e adaptar caminhos de ensino e aprendizagem inovadores” (KOZELSKI; ARRUDA, 2017, p. 2194). Essas considerações feitas pelas autoras também foram percebidas em nossa pesquisa, uma vez que a elaboração dos roteiros demandou muito tempo. Cada atividade foi construída de modo que permitisse a construção, investigação (manipulação do objeto construído) e que isso conduzisse à formação do conceito matemático envolvido (internalização – pensar matemático). Então, cada atividade era primeiro feita no GeoGebra, depois construíamos um roteiro, nós o testávamos para observar possíveis inconsistências para, então, fazermos as correções.
Em vista disso, aliadas a outras ideias sobre atividades matemáticas, pensamos em roteiros de atividades matemáticas, os quais continham instruções e procedimentos, e permitiam que mesmo um leigo pudesse realizar as construções dos entes geométricos no software GeoGebra. Por esse motivo, tivemos a preocupação com o pensar matemático-com-GeoGebra, de maneira que o foco fosse sempre a aprendizagem de conceitos matemáticos. Sendo assim, nas atividades propostas, abordamos as noções de ponto, reta, ponto médio, retas paralelas e perpendiculares, triângulos, quadriláteros e quadriláteros paralelogramos e, por fim, circunferência e círculo. A figura 3 apresenta um recorte da atividade sobre as noções de ponto, reta e ponto médio propostas por nós.
 Figura 3
Recorte de uma das atividades matemáticas
Fonte: Produção nossa (2019)
Figura 3
Recorte de uma das atividades matemáticas
Fonte: Produção nossa (2019)
Além disso, Kozelski e Arruda (2017) também enfatizam a capacitação dos professores em prol do manuseio dessas tecnologias na Educação, pois, para que haja uma aula com esse recurso, é necessário que o professor esteja preparado para planejar a aula e, principalmente, ter conhecimento do recurso tecnológico utilizado por ele. Durante a construção das atividades, cada membro da equipe levava uma proposta de atividade, e, no momento dos testes, novos ícones e modos diferentes eram apresentados e incorporados à resolução da atividade. Além disso, as autoras explicitam que o computador ou notebook pode ser utilizado como material de apoio e, também, como ferramenta de aprendizagem, com a qual o aluno aprende, por meio da tecnologia, a corrigir seus erros e aprende com os colegas, ao comparar os exercícios propostos. O que nos remete à ideia do pensar-com-tecnologias de Borba, Scucuglia e Gadanidis (2014).
Todavia, essas discussões sobre ensino de Matemática com o uso de tecnologias, em nossa pesquisa, não estariam completas se não tratássemos de teorias de aprendizagem, haja vista que nosso foco está na formação de conceitos, o que, a nosso ver, também remete ao pensar-com-tecnologia. Então, na nossa “caminhada” fomos em busca dessa teoria. Em busca de algo que estivesse condizente com a nossa forma de pensar a aprendizagem matemática com tecnologia, que também se alinhasse às atividades que já tínhamos construído. Nessa procura, nos deparamos com os trabalhos de Núñez (2009) que abordavam a Teoria da Assimilação por Etapas das Ações Mentais e dos Conceitos de P. Ya. Galperin (NÚÑEZ, 2009), cujo foco é o desenvolvimento da aprendizagem por meio da formação de conceitos. Assim, o encontro com essa teoria fechou um importante ciclo na consolidação da pesquisa, sendo fundamental para a análise e discussão dos resultados. No tópico a seguir, detalhamos a teoria e mostramos como ela se articulou com nossa pesquisa.
2. Formação de Conceitos e
de Assimilação por Etapas das Ações Mentais e dos Conceitos de P. Ya. Galperin:
origens e desenvolvimento
Para expor a Teoria de Galperin, é necessário fazermos uma breve revisão dos estudos de Lev Semenovitch Vigotski (1896 – 1934) e de Alexis Nikolaevich Leontiev (1903 – 1979), uma vez que os estudos desses dois psicólogos russos serviram de base para o desenvolvimento da teoria de Galperin, outro membro da escola russa de psicologia cognitiva.
Segundo Vigotski (1998), a assimilação de um conceito ocorre quando há a relação entre o conhecimento prévio (conhecimentos espontâneos, construídos com a experiência pessoal e cotidiana) e o conhecimento científico (conhecimento escolar, elaborado em sala de aula, juntamente com a internalização dos conceitos espontâneos); nesse momento, a aprendizagem está ocorrendo. Por exemplo, ao estudar aritmética na escola, possivelmente o sujeito já teve alguma experiência que envolvia os conceitos aritméticos, e, quando ele consegue fazer essa relação e assimila os conceitos, ocorre a aprendizagem. Isso pode ser estendido aos conceitos de geometria, pois os alunos, a partir da realidade, possuem alguma percepção do que é geometria.
Para Vigotski (1998), durante esse processo de aprendizagem, ocorrem dois níveis de desenvolvimento: desenvolvimento real e desenvolvimento potencial. O primeiro se refere ao fato de o sujeito conseguir aprender sozinho algum conteúdo, desenvolvendo suas funções mentais, e, com isso, a capacidade de generalização e abstração do conhecimento. O segundo refere-se a uma situação na qual o sujeito precisa de um mediador para orientá-lo na resolução de um problema. A distância entre esses dois níveis é chamada por Vigotski (1998) de zona de desenvolvimento proximal (ZDP). Desse modo, a ZDP “define as funções que ainda não amadureceram, que estão em processo de maturação, (...) como modos de atividades internalizadas” (NÚÑEZ; FARIA, 2004, p.52). Ou seja, um aluno que consegue se desenvolver sozinho na aprendizagem de um conteúdo pode auxiliar um colega que está com dificuldade de assimilação e, durante esse processo, ocorre a interação entre esses indivíduos, e, dessa forma, aquele que tinha dificuldade pode aproximar-se da zona de desenvolvimento potencial. Esse fato foi um dos objetivos em nossa pesquisa: propusemos nossos roteiros de atividades matemáticas, os quais os alunos tentavam desenvolver sozinhos; a partir do momento em que não conseguiam desenvolvê-los por sua conta, pediam o auxílio do colega e do professor mediador.
Apesar de haver uma distinção entre os conhecimentos espontâneos e escolares, ambos se relacionam em um único processo: o desenvolvimento da formação dos conceitos que serão internalizados pelo aluno. Núñez e Faria (2004, p.53) complementam dizendo: “O processo de formação de um conceito científico é longo, complexo e nunca alcançado por meio de uma aprendizagem receptiva e memorística, mas sim por meio de uma ‘atividade’ produtiva, mediada e social do aluno”. Portanto, não é qualquer ensino ou atividade que vai permitir a formação do conhecimento científico. Por isso, em nossa pesquisa, optamos pelo uso da tecnologia - no caso, o GeoGebra -, acompanhada de um conjunto de atividades mediadoras – denominadas por nós como Base Orientadora da Ação (BOA), baseadas nos estudos sobre Galperin –, acreditando que, com isso, os alunos conseguiriam formar os conceitos matemáticos tratados.
Complementando as ideias de Vigotski, Leontiev estudou as diferenças entre ações individuais e coletivas, e, também, acrescentou a atividade humana em grupo para compreender as ações da teoria proposta inicialmente por Vigotski. Ainda, segundo Núñez (2009), Vigotski tinha o foco na mediação por meio de ferramentas culturais, ao passo que Leontiev pensava a mediação por meios da relação do sujeito (o Homem) e do objeto da atividade (a realidade).
De acordo com Leontiev (2014), um objeto modifica o estado de um sujeito à medida que este interage com aquele, ou seja, uma atividade é caracterizada de acordo com seu objeto. Por exemplo, ao receber uma carta, as reações de uma pessoa alfabetizada e de uma analfabeta são diferentes; alguém que está com muita fome reage ao alimento de forma diferente de quem está satisfeito. Com isso, Leontiev traz as influências dos ambientes para o cérebro humano e o quanto este afeta o ser social e a consciência humana. Além disso, afirma que as relações entre sujeitos e objetos ocorrem pela mediação da atividade humana. Nesse sentido, fazendo um paralelo entre as considerações de Leontiev e nossa pesquisa, consideramos a tecnologia (utilizando o computador, o notebook e o software GeoGebra) como mediadora entre o conteúdo matemático (objeto) e o aluno que aprende (sujeito).
Núñez (2009) afirma que há uma mediação entre o ser humano (sujeito) e o objeto que será transformado pela sua ação. Também diz que um sujeito pode ser transformado por meio das mudanças de valores, atitudes e pensamentos. Pensando nisso, Núñez estruturou a atividade de aprendizagem como um ciclo cognitivo, composto pela orientação (BOA), execução, regulação e ajuste (conforme figura 4). Logo, para que um aluno consiga assimilar os conceitos é necessário que a atividade contemple e envolva essas quatro ações citadas.
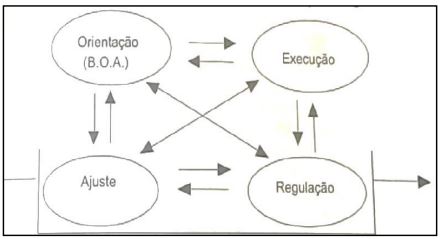 Figura 4
Ciclo cognitivo da
aprendizagem
Fonte: Núñez; Faria
(2004, p. 55)
Figura 4
Ciclo cognitivo da
aprendizagem
Fonte: Núñez; Faria
(2004, p. 55)
Sendo assim, o momento da orientação é o principal passo para a atividade de aprendizagem, pois é constituída por uma Base Orientadora da Ação (BOA), que é uma orientação técnica e será o suporte para a execução da atividade, de modo a guiar o aluno durante a ação. Em nossa pesquisa, a orientação ocorreu por meio dos roteiros de atividades matemáticas que havíamos elaborado antes de conhecermos a Teoria de Galperin; ao percebermos as similaridades entre essa teoria e a nossa proposta, nomeamos nossos roteiros de atividades de “BOA”. O segundo momento da pesquisa é a execução, que é a realização da ação que ocorre após estruturação da BOA, e que, para ser exitosa, depende de como foi feito o seu planejamento, de modo a proporcionar aos alunos reflexão crítica e condições para realizar a atividade. Também alcançamos isso em nossa pesquisa, pois, por meio das BOA, os alunos conseguiam interpretar os procedimentos e realizavam as construções dos entes geométricos no software GeoGebra, sob nossa orientação.
Já o terceiro momento é a regulação e o controle da ação, que permitem o autocontrole e estimulam o aluno a aprender a aprender. Mais uma vez, nossos roteiros de atividade se alinharam às ideias da BOA, haja vista que, para serem realizados, os alunos precisavam refletir sobre os procedimentos e os ícones do software que iriam utilizar nas construções dos entes geométricos. O último momento é a correção ou o ajuste, que é quando se percebem os erros na BOA e, por isso, é necessário o reajuste. Durante o processo de elaboração dos roteiros de atividades, vivenciamos vários momentos de reajuste das mesmas, para que fossem adequadas ao público da pesquisa. Desse modo, identificamos na teoria de Galperin; o que buscávamos para consolidar nossa pesquisa e validar nossos roteiros de atividades.
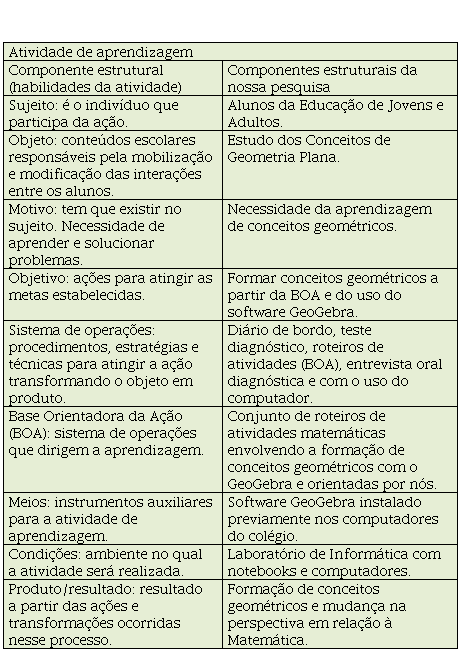
Ainda de acordo com Núñez (2009, p. 75), “a assimilação de uma habilidade na qualidade de tipo específico de atividade humana supõe três momentos bem definidos: 1) o momento inicial ou de planificação, 2) o momento da execução e 3) o momento de controle.” Esses momentos estão presentes em qualquer atividade. Sendo assim, a atividade de aprendizagem possui componentes estruturais invariantes (habilidades da atividade), baseados na Teoria da Atividade de Leontiev, que são responsáveis por sua organização: sujeito, objeto, motivos, objetivo, sistema de operações, base orientadora da ação, meios para realizar a ação, condições de realização e produto. O quadro 2 apresenta a explicação dos componentes estruturais da atividade e a exemplificação desses componentes em nossa pesquisa.
Quadro 2
Componentes estruturais
da aprendizagem
 Fonte: Produção nossa
(2018)
Fonte: Produção nossa
(2018)
|
Atividade
de aprendizagem
|
|
Componente
estrutural (habilidades da atividade)
|
Componentes
estruturais da nossa pesquisa
|
|
Sujeito:
é o indivíduo que participa da ação.
|
Alunos da Educação de Jovens e Adultos.
|
|
Objeto:
conteúdos escolares responsáveis pela mobilização
e modificação das interações entre os alunos.
|
Estudo dos Conceitos de Geometria Plana.
|
|
Motivo:
tem que existir no sujeito. Necessidade de
aprender e solucionar problemas.
|
Necessidade da aprendizagem de conceitos
geométricos.
|
|
Objetivo:
ações para atingir as metas estabelecidas.
|
Formar conceitos geométricos a partir da BOA e do
uso do software GeoGebra.
|
|
Sistema
de operações: procedimentos, estratégias e técnicas para
atingir a ação transformando o objeto em produto.
|
Diário de bordo, teste diagnóstico, roteiros de
atividades (BOA), entrevista oral diagnóstica e com o uso do computador.
|
|
Base
Orientadora da Ação (BOA): sistema de operações que dirigem a aprendizagem.
|
Conjunto de roteiros de atividades matemáticas
envolvendo a formação de conceitos geométricos com o GeoGebra e orientadas
por nós.
|
|
Meios:
instrumentos auxiliares para a atividade de
aprendizagem.
|
Software
GeoGebra instalado previamente nos computadores
do colégio.
|
|
Condições:
ambiente no qual a atividade será realizada.
|
Laboratório de Informática com notebooks e
computadores.
|
|
Produto/resultado:
resultado a partir das ações e transformações
ocorridas nesse processo.
|
Formação de conceitos geométricos e mudança na
perspectiva em relação à Matemática.
|
De acordo com Núñez
(2009), Galperin desenvolveu seis características qualitativas das habilidades
(componentes estruturais), e Talízina (2001), uma das colaboradoras de
Galperin, desenvolveu mais duas. Essas oito características são divididas em
qualidades primárias (forma da ação, grau de generalização, grau de
detalhamento, grau de consciência e grau de independência), que são
fundamentais para que ocorra a ação; e qualidades secundárias (grau de domínio,
grau de solidez e caráter racional), que dependem das primárias. Para
exemplificar melhor as características qualitativas da atividade e como essas
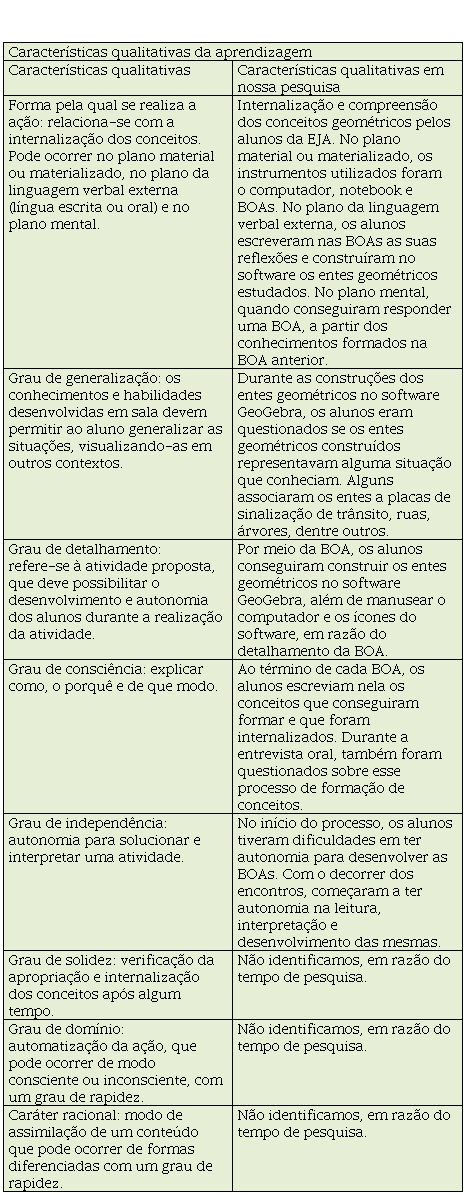
características foram utilizadas em nossa pesquisa, elaboramos o quadro 3.
Quadro 3
Características
qualitativas da aprendizagem
 Fonte: Produção nossa
(2018)
Fonte: Produção nossa
(2018)
|
Características qualitativas da aprendizagem
|
|
Características qualitativas
|
Características qualitativas em nossa pesquisa
|
|
Forma pela qual se realiza a ação:
relaciona-se com a internalização dos conceitos. Pode ocorrer no plano
material ou materializado, no plano da linguagem verbal externa (língua
escrita ou oral) e no plano mental.
|
Internalização
e compreensão dos conceitos geométricos pelos alunos da EJA. No plano
material ou materializado, os instrumentos utilizados foram o computador, notebook e BOAs. No plano da linguagem
verbal externa, os alunos escreveram nas BOAs as suas reflexões e construíram
no software os entes geométricos
estudados. No plano mental, quando conseguiram responder uma BOA, a partir
dos conhecimentos formados na BOA anterior.
|
|
Grau de generalização: os conhecimentos e habilidades desenvolvidas em
sala devem permitir ao aluno generalizar as situações, visualizando-as em
outros contextos.
|
Durante
as construções dos entes geométricos no software
GeoGebra, os alunos eram questionados se os entes geométricos construídos
representavam alguma situação que conheciam. Alguns associaram os entes a
placas de sinalização de trânsito, ruas, árvores, dentre outros.
|
|
Grau de detalhamento: refere-se à atividade proposta, que deve
possibilitar o desenvolvimento e autonomia dos alunos durante a realização da
atividade.
|
Por
meio da BOA, os alunos conseguiram construir os entes geométricos no software GeoGebra, além de manusear o
computador e os ícones do software, em razão do detalhamento da BOA.
|
|
Grau de consciência: explicar como, o porquê e de que modo.
|
Ao
término de cada BOA, os alunos escreviam nela os conceitos que conseguiram
formar e que foram internalizados. Durante a entrevista oral, também foram
questionados sobre esse processo de formação de conceitos.
|
|
Grau de independência: autonomia para solucionar e interpretar uma
atividade.
|
No
início do processo, os alunos tiveram dificuldades em ter autonomia para
desenvolver as BOAs. Com o decorrer dos encontros, começaram a ter autonomia
na leitura, interpretação e desenvolvimento das mesmas.
|
|
Grau de solidez: verificação da apropriação e internalização dos
conceitos após algum tempo.
|
Não
identificamos, em razão do tempo de pesquisa.
|
|
Grau de domínio: automatização da ação, que pode ocorrer de modo
consciente ou inconsciente, com um grau de rapidez.
|
Não
identificamos, em razão do tempo de pesquisa.
|
|
Caráter racional: modo de assimilação de um conteúdo que pode
ocorrer de formas diferenciadas com um grau de rapidez.
|
Não
identificamos, em razão do tempo de pesquisa.
|
Nem todos os alunos conseguem atingir, na íntegra, todas essas qualidades. Isso se dá em função das características individuais de cada sujeito, que possuem níveis e ritmos de aprendizagem próprios. Há de se considerar também o tempo de realização da atividade, haja vista algumas dessas qualidades requererem mais tempo para serem identificadas, e necessitarem de um tempo maior de permanência com os sujeitos. O mesmo pode-se dizer das etapas de aprendizagem – explicaremos a seguir –, isso porque alguns alunos podem pular etapas ou permanecer em uma mesma etapa durante certo tempo.
Assim, a partir dos estudos de Vigotski e Leontiev, Galperin reafirma a importância da interiorização de Vigotski, na qual um sujeito consegue aprender e interagir no meio social a partir das relações externas com outros sujeitos; com isso, desenvolve o pensamento cognitivo, psicológico e intelectual. Dessa maneira, as influências sociais contribuem para o desenvolvimento e formação do pensamento do sujeito, e as informações adquiridas no processo externo (contato com outros indivíduos) começam a ser internalizadas, compreendidas, internamente. Além do conceito de internalização de Vigostki, Galperin se preocupou com o conceito de atividade de Leontiev, que explica as relações do homem com o mundo, por meios das trocas recíprocas do sujeito e objeto que levam à internalização e ao desenvolvimento social e cognitivo.
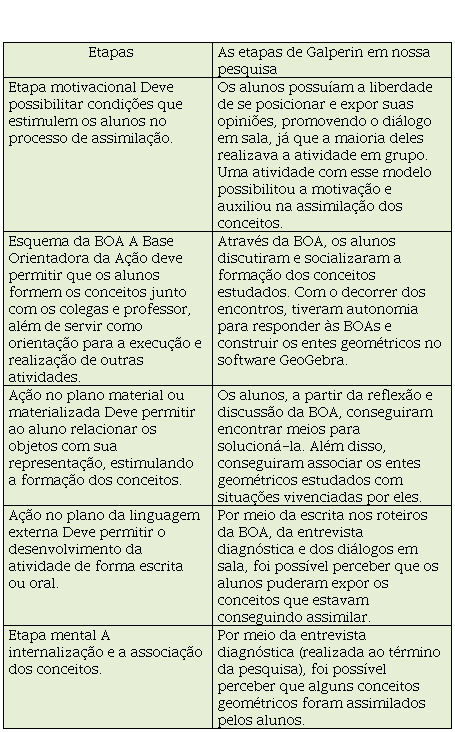
Por meio dessas reflexões, Galperin desenvolveu a Teoria de Assimilação por Etapas das Ações Mentais e dos Conceitos. Nessa teoria, afirma que a assimilação de um conceito acontece por meio de cinco etapas (motivacional; esquema da Base Orientadora da Ação (BOA); plano material ou materializado; linguagem externa; e mental). Segundo Galperin, “para aprender novos conceitos, generalizações e habilidades, o sujeito precisa realizar determinada atividade, que primeiramente, acontece num plano externo e, posteriormente, como consequência da internalização, num plano material interno” (NÚÑEZ; FARIA, 2004, p.63). Ou seja, a assimilação do conhecimento pelo sujeito se desenvolve a partir das etapas da aprendizagem, passando pelas experiências sociais e, posteriormente, para o plano individual, no qual esse sujeito irá assimilar as informações e conhecimentos e, com isso, formar os conceitos e apropriar-se deles. Assim, apresentamos as etapas elaboradas por Galperin no quadro 4.
Quadro 4
Etapas para a
assimilação do conhecimento
 Fonte: Produção nossa
(2018)
Fonte: Produção nossa
(2018)
|
Etapas
|
As
etapas de Galperin em nossa pesquisa
|
|
Etapa
motivacional
Deve possibilitar condições que estimulem os
alunos no processo de assimilação.
|
Os alunos possuíam a liberdade de se posicionar e
expor suas opiniões, promovendo o diálogo em sala, já que a maioria deles
realizava a atividade em grupo. Uma atividade com esse modelo possibilitou a
motivação e auxiliou na assimilação dos conceitos.
|
|
Esquema
da BOA
A Base Orientadora da Ação deve permitir que os
alunos formem os conceitos junto com os colegas e professor, além de servir
como orientação para a execução e realização de outras atividades.
|
Através da BOA, os alunos discutiram e
socializaram a formação dos conceitos estudados. Com o decorrer dos
encontros, tiveram autonomia para responder às BOAs e construir os entes
geométricos no software GeoGebra.
|
|
Ação
no plano material ou materializada
Deve permitir ao aluno relacionar os objetos com
sua representação, estimulando a formação dos conceitos.
|
Os alunos, a partir da reflexão e discussão da
BOA, conseguiram encontrar meios para solucioná-la. Além disso, conseguiram associar
os entes geométricos estudados com situações vivenciadas por eles.
|
|
Ação
no plano da linguagem externa
Deve permitir o desenvolvimento da atividade de
forma escrita ou oral.
|
Por meio da escrita nos roteiros da BOA, da
entrevista diagnóstica e dos diálogos em sala, foi possível perceber que os
alunos puderam expor os conceitos que estavam conseguindo assimilar.
|
|
Etapa
mental
A internalização e a associação dos conceitos.
|
Por meio da entrevista diagnóstica (realizada ao
término da pesquisa), foi possível perceber que alguns conceitos geométricos
foram assimilados pelos alunos.
|
Quanto à formação dos conceitos matemáticos, Talízina (2001) diz que há a implicação do desenvolvimento cognitivo e intelectual do aluno. A autora ressalta, ainda, que a dificuldade dos alunos em assimilarem os conceitos se dá em função do caráter essencialmente formal com que são apresentados. Geralmente, os alunos só são estimulados durante a apresentação de um conceito por meio da reprodução e memorização do que está escrito no livro didático, sem que haja a reflexão e interpretação do conceito.
Desse modo, para que haja a formação dos conceitos matemáticos, é importante propor uma atividade que permita ao aluno investigar, comparar, deduzir e classificar os entes geométricos estudados - no caso, uma BOA -, o que fizemos em nossa pesquisa. Assim, conseguiremos explorar e estimular o pensamento do aluno, potencializando a formação dos conceitos. Entretanto, ao elaborar uma BOA, Volodarskaya (2001) diz que devemos pensar sobre os pré-requisitos necessários para que os alunos consigam formar e assimilar os conceitos estudados. Caso contrário, a BOA deve indicar os caminhos que vão orientar o aluno, para que, dessa forma, ele tenha os subsídios para desenvolver o pensamento cognitivo, e, com isso, formar os conceitos propostos.
Uma vez mais, tomando como exemplo o software GeoGebra, conjecturamos acerca de uma mesma atividade realizada de duas formas: com lápis e papel (tecnologia tradicional e ainda usual por muitos professores) e com o GeoGebra. Essa atividade pode apresentar resultados semelhantes nas duas formas de realização, contudo, feita com o GeoGebra abre para a possibilidade de ampliar os resultados e, além disso, trazer aspectos que não poderiam ser observados se fosse feita apenas com lápis e papel. Tal situação pode ser observada na figura 5, na qual há a construção de um paralelogramo.
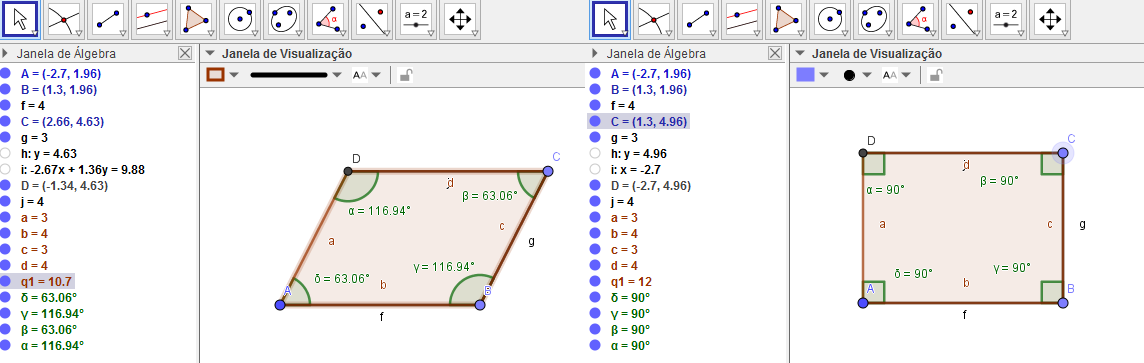 Figura 5
Construção de um
paralelogramo
Fonte: Produção nossa
(2018)
Figura 5
Construção de um
paralelogramo
Fonte: Produção nossa
(2018)
Essa atividade ilustrada na figura 5 também foi realizada em nossa pesquisa. O objetivo ao realizá-la foi provar que o paralelogramo não é somente a figura ilustrada do lado esquerdo, mas que ele é uma figura geométrica que possui seus lados opostos paralelos e seus ângulos opostos congruentes. Somente com lápis e papel é mais difícil provar para um aluno que um retângulo, por exemplo, também é um paralelogramo. Já com a dinâmica do software essa visualização é mais rápida, pois o aluno consegue movimentar o ente geométrico de modo que consiga perceber todas as possibilidades possíveis. Por isso, é importante que todos esses recursos sejam utilizados para o desenvolvimento da aprendizagem dos alunos.
A partir dessas reflexões, percebemos o quanto a Teoria da Assimilação por Etapas das Ações Mentais e dos Conceitos de Galperin é importante para a formação dos conceitos pelos alunos, pois possibilita o raciocínio, a aplicação e a generalização. Saímos do modelo tradicional de “decorar” as definições, fórmulas e regras apresentadas pelo professor, e este deixa de ser o único detentor do conhecimento. Assim, a teoria encaixa-se com o nosso pensamento de que uma atividade realizada com o auxílio do software GeoGebra pode potencializar a formação dos conceitos geométricos, além de permitir a autoconfiança e autonomia nos alunos, durante o desenvolvimento dessas atividades.
3. Considerações finais
Antes de nos apropriarmos da Teoria de Galperin, já estávamos elaborando roteiros de atividades matemáticas para serem realizados no software GeoGebra. O propósito era permitir que as mesmas pudessem ser exploradas tanto por quem tivesse conhecimentos e experiências sobre o manuseio desse software, quanto por quem não os detivesse. Desse modo, ao realizar cada atividade, havia uma troca recíproca: aprenderiam a usar o software e formariam os conceitos matemáticos. Se temos domínio de conceitos matemáticos, conseguimos utilizar o GeoGebra e fazer construções matemáticas com certa facilidade, mesmo sem ter um conhecimento profundo sobre ele. Por outro lado, se conhecemos suas funcionalidades, podemos usá-lo para explorar e entender conceitos matemáticos novos, indo além do pensado inicialmente.
Sendo assim, esses dois pensamentos fundamentaram nossa pesquisa. Passamos a considerar nossos roteiros, como BOA, uma vez que as atividades propostas por nós não remetiam apenas ao uso da tecnologia, mas tinham também como objetivo a formação dos conceitos matemáticos. Logo, buscamos compreender e identificar cada etapa na formação de um conceito quando o aluno realiza a BOA, mediada pelo software GeoGebra. A BOA, nessa perspectiva, não pode ser concebida sem a mediação da tecnologia. Por outro lado, não é possível perceber essa mediação na formação de um conceito sem a BOA. Assim, esse entrelaçamento nos permitiu dispor de argumentos para compreender e analisar como alunos da EJA avançaram na formação de conceitos de Geometria.
Concordamos com as discussões que apontam que a mera introdução das TDs na sala de aula não garante a aprendizagem de conceitos matemáticos, nem mesmo modificam substancialmente as metodologias de ensino. Como também não basta ao professor somente utilizá-las sem algum objetivo pedagógico; ele precisa ter meios para identificar o desenvolvimento dos alunos durante a realização de uma atividade, uma vez que o aluno pode simplesmente utilizar um comando do software e fazer uma determinada construção, mas não refletir sobre o que está fazendo, não formar conceitos. Portanto, a nossa proposta de elaborar BOAs para serem feitas com a manipulação do GeoGebra possibilitou a interação do software com a aprendizagem de conceitos matemáticos, o que permitiu a participação ativa dos alunos durante todo processo.
Entendemos que a compreensão sobre o que se está fazendo é fundamental na formação de conceitos. Isso requer do professor estar atento ao que vai propor aos alunos. Nesse aspecto, propor atividades usando um software matemático como o GeoGebra a partir de um roteiro pensado para a formação de um conceito – para a aprendizagem - é um grande diferencial em relação ao ensino tradicional e ressalta a importância do pensar-com-tecnologia.
Com isso, percebemos que as TDs precisam fazer parte das práticas pedagógicas, em especial no ensino de Matemática. Assim, em nossa pesquisa, optamos pelo uso do software GeoGebra como o artefato midiático que acreditamos ter permitido aos alunos formar conceitos matemáticos sobre geometria plana. Acreditamos, ainda, que o uso da BOA, mediado pelo GeoGebra, pode motivar os alunos na execução das atividades propostas e, também, modificar a visão sobre o ensino de Matemática somente com livro, caderno e quadro.
À vista disso, esses pensamentos embasaram o desenvolvimento da pesquisa, na produção dos dados, bem como na análise e na discussão dos resultados. Ademais, com essa compreensão teórica pudemos perceber que o processo de formação de conceitos com o uso da BOA e mediado pelo software GeoGebra pode ser aplicado para além de turmas da EJA, o que torna possível a realização dessas atividades em qualquer nível de ensino. Essa possibilidade nos instiga a continuar investigando o entrelaçamento entre a BOA e o GeoGebra, nas aulas de Matemática, em projetos futuros.