INTRODUÇÃO
O presente texto apresenta resultados parciais da pesquisa de doutorado em andamento intitulada “Processos e dinâmicas de sistematização de saberes para ensinar problemas aritméticos: Mercante e Thorndike e as transformações do saber profissional do professor dos primeiros anos escolares”, sob orientação do Prof. Dr. Wagner Rodrigues Valente, na Universidade Federal de São Paulo.
Essa pesquisa de doutorado em andamento está inserida no Projeto Temático[2] , projeto este que tem como objetivo geral “investigar os processos e dinâmicas de constituição do saber profissional do professor que ensina matemática no período compreendido entre 1890-1990” (Valente; Bertini; Morais; Pinto; 2017).
Para analisar a constituição do saber
profissional, do mesmo modo que o Projeto Temático objetiva, elegemos como
ferramental teórico-metodológico conceitos advindos da História Cultural, de
estudos Sócio-Históricos, e da História da Educação,
bem como a História da educação matemática. Destes ferramentais destacamos
nesse texto: apropriação
(Chartier, 1990), processos (Burke,2016), saberes profissionais,
(Hofstetter; Schneuwly, 2017) e, mais próximo do nosso objeto teórico, os
conceitos de matemática a ensinar e matemática para ensinar (Bertini;
Morais; Valente,2017).
Segundo
Chartier (1990) a apropriação tem como objetivo uma interpretação e está
vinculada às práticas que produzem essa história. Entretanto, para escrevermos
essa história, existem alguns processos que podem nos
auxiliar. Burke (2016) enuncia quatro estágios que nos dão pistas
metodológicas de como escrever essa história: coletar, analisar, disseminar e
utilizar. Esses passos serão utilizados para a escrita de nossas investigações
acerca do saber profissional.
Nossa
escrita está relacionada à constituição dos saberes profissionais do professor
que ensina matemática entre os anos de 1890 e 1990. Nesses cem anos aconteceram
muitas modificações no saber profissional. Entendemos o saber profissional a
partir das pesquisas de Hofstetter e Schneuwly (2017).
Diferentemente
das várias tipologias que circulam como sendo os saberes
do professor, o saber profissional é sintetizado por esses autores (Hofstetter e
Schneuwly, 2017) em dois tipos: saberes
a ensinar e saberes para ensinar.
Os
saberes a ensinar podem ser identificados como sendo os objetos
do trabalho do professor. As ferramentas utilizadas para os fins de
ensino podemos entendê-las como sendo os saberes para ensinar. Nesse
sentido, podemos exemplificar que os conceitos advindos do campo disciplinar
são os saberes a ensinar, os objetos de ensino. Ter posse de saberes
relacionados ao desenvolvimento do aluno ligam-se aos saberes para ensinar, que são próprios
do exercício docente, as ferramentas de trabalho do professor.
Sendo assim, a matemática a ensinar e
matemática para ensinar (Bertini; Morais; Valente, 2017) é uma apropriação
desses conceitos acima. No caso especifico desse
texto, percebemos a presença de um saber para ensinar problemas que foi
sistematizado por um autor de livro escolar e utilizado/disseminado por
diversos autores em artigos de revistas pedagógicas.
À luz destes referenciais, o objetivo
deste artigo é analisar as apropriações sobre problemas aritméticos realizadas
por Victor Mercante, em seu livro Cultivo y desarrollo
de la aptitud matemática del niño, publicado em 1905
em Buenos Aires. Há indícios da circulação desse livro em São Paulo, pois ele é
referenciado em artigos de revistas pedagógicas e no programa paulista de
ensino publicado em 1949/1950.
VICTOR
MERCANTE E O CULTIVO Y DESARROLLO DE LA APTITUD MATEMÁTICA DEL NIÑO
Victor Mercante nasceu na Argentina em
1870 e iniciou sua carreira como professor em 1890. Foi autor de diversas obras
que tratavam sobre o cotidiano escolar (adolescentes, museus escolares, ensino,
métodos entre outros). Em 1906 começou a trabalhar no Laboratório de Paidologia[3]
na Universidad Nacional de La Plata, ocupou cargos
importantes no Ministerio de la Justicia e Instrucción Pública e
auxiliou na reforma do ensino argentino, tendo como principal ação a defesa do
ensino laico.
Demonstrava interesse pelos estudos psicológicos desenvolvidos por Binet, Decroly, Freud, que estariam mais relacionados à Pedagogia Cientifica e a Psicologia Experimental, entre outros autores (Dussel, 2014).
Seu interesse em matemática aparece em estudo intitulado Enseñanza de la Aritmética dividido em dois livros. O primeiro intitulado Psicologia de la aptitud matemática del niño publicado em 1904 e o segundo Cultivo y desarrollo de la aptitud matemática del niño publicado em 1905.
A importância de Victor Mercante pode ser percebida em artigos
científicos atuais (Ostrovsky, 2011; Dussel, 2014) sobre suas obras e até mesmo nas citações em
artigos das revistas pedagógicas paulistas nas primeiras décadas do século XX.
Neles, Mercante é chamado para justificar o ensino dos
problemas nas aulas de aritmética.
Essa sistematização sobre os problemas aritméticos apareceu em seu livro Cultivo y desarrollo de la aptitud matemática del niño, publicado em 1905. Ao longo de 726 páginas o autor
tratava de diversos assuntos que envolvia o ensino de aritmética e dedicou um
dos treze capítulos, com 144 páginas, para discutir a respeito dos exercícios e
problemas.
Uma das
primeiras argumentações feitas pelo autor referente aos problemas foi
desvinculá-los dos exercícios. Em sua definição os exercícios serviriam com a
finalidade de praticar determinado conceito, ou seja, aplicar uma regra, uma
combinação de operações. Os problemas teriam uma finalidade diferenciada,
estariam mais relacionados a lógica e a linguagem. A dificuldade em resolver um
problema segundo Mercante estaria unicamente pelas palavras, tipo e partes
suprimidas do enunciado, quantidade de dados e as proposições dos teoremas. Em
uma de suas conclusões aponta para o fato de que “resolver exercícios não é
formar a atitude para resolver problemas.” (Mercante, 1905,
p. 509) [4].
Há que se fazer um destaque pois Mercante não defendia que os exercícios fossem retirados das aulas, entretanto fazia um contraponto com respeito aos diferentes objetivos que cada um desenvolvia. Sobre a aplicação deles, ressaltava que a série de exercícios e problemas não deveriam ser do mesmo tipo e complexidade para recapitular algum conteúdo. Ainda sobre os problemas, sob a ótica do autor, estes serviriam para a análise lógica dos enunciados e do entendimento dos adjetivos, verbos, substantivos e complementos.
Em alguns trechos do livro, o autor sugeria que o professor fizesse uso dos problemas de modo oral pois isso facilitaria a compreensão de alunos que não tivessem a fluência leitora, o que era esperado no primeiro ano da escola primária.
Mas afinal como ensinar a resolver os problemas de aritmética segundo Victor Mercante? A depender do tipo de problema, simples ou composto[5], o autor apresentava quatro ou cinco passos que auxiliariam em como ensinar a resolver problemas, são eles: objetivação, indução, decomposição, análise e resposta.
O primeiro passo
para ensinar a resolver um problema seria a objetivação. Era por meio
deste que Mercante propunha a leitura, o entendimento, o desnudar das palavras
que as vezes eram desconhecidas para os alunos com realidades tão diferentes.
Num segundo momento a indução era a oportunidade que o professor poderia fazer perguntas simples que tinham o objetivo de verificar se os alunos sabiam do que estava sendo tratado naquele problema.
O item decomposição seria utilizado somente em problemas ditos compostos, ou seja, que apresentassem mais de uma operação para serem resolvidos. A composição desses problemas era sugerida por Mercante da forma mais variada possível, contemplando as quatro operações fundamentais em diferentes arranjos.
Os arranjos propostos pelo autor para a composição dos problemas seguiam uma gradação, partindo do mais fácil para o mais difícil. Neste caso os problemas iniciariam com adições, passando pelas subtrações, a junção das duas operações em um único problema.
A análise seria o momento em que as relações entre os valores eram feitas. A análise de cada elemento contido no enunciado do problema de modo a finalmente chegar ao resultado.
O último passo sugerido por Victor Mercante era a resposta. Nesse ponto o problema estaria solucionado e os alunos responderiam a uma possível questão presente no enunciado. É o momento em que o aluno chegaria ao todo, podendo assim ter a prática para resolver outros problemas com um mesmo nível de dificuldade.
A partir da leitura dos cinco passos para o ensino de problemas aritméticos sistematizados por Victor Mercante os problemas não deveriam ser utilizados como meio de exercitar o conteúdo aprendido e deveriam ser ensinados nas aulas de aritmética. Tendo em vista essa afirmação questionamos que apropriações foram disseminadas nos artigos de revistas pedagógicas publicadas nas primeiras décadas do século XX que citavam a obra argentina.
UM
TANGO QUE VIROU SAMBA
No tópico anterior, observamos como Victor Mercante sistematizou saberes para ensinar problemas aritméticos em seu livro. Essa forma de ensinar a resolver problemas não circulou apenas por meio de seu livro, mas sim de apropriações feitas por autores de artigos das revistas pedagógicas paulistas.
Os estudos realizados por Catani (1996) e Nery (2009) apontam a importância das pesquisas históricas que tomam os periódicos pedagógicos como fontes privilegiadas. Estes espaços de publicações, de certa forma financiados pelo governo, auxiliam no entendimento da circulação de ideias. Isso pode nos dar indícios de que essas publicações ecoavam vozes afinadas ao discurso posto pelo próprio sistema educacional da época.
Observamos nas revistas pedagógicas paulistas publicadas a partir de 1929, citação sobre o autor Victor Mercante. Destacamos dois impressos. No quadro 1 apresentamos o detalhamento das citações a Victor Mercante e ao seu livro:
Quadro 1
Documentos que citam “Cultivo y desarrollo de la aptitud matemática del niño”
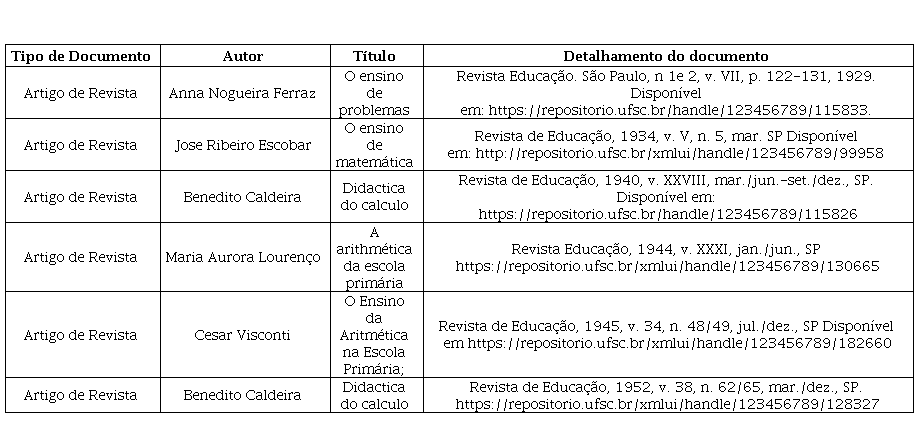 Fonte: A autora com base no RCD/UFSC.
Fonte: A autora com base no RCD/UFSC.
| Tipo de Documento | Autor
| Título
| Detalhamento do documento
|
|
Artigo
de Revista
|
Anna
Nogueira Ferraz
|
O
ensino de problemas
|
Revista
Educação. São Paulo, n 1e 2, v. VII, p. 122-131, 1929. Disponível em: https://repositorio.ufsc.br/handle/123456789/115833.
|
|
Artigo
de Revista
|
Jose
Ribeiro Escobar
|
O
ensino de matemática
|
Revista
de Educação, 1934, v. V, n. 5, mar. SP
Disponível
em: http://repositorio.ufsc.br/xmlui/handle/123456789/99958 |
|
Artigo
de Revista
|
Benedito
Caldeira
|
Didactica
do calculo
| Revista de Educação, 1940, v. XXVIII, mar./jun.-set./dez., SP. Disponível em: https://repositorio.ufsc.br/handle/123456789/115826 |
|
Artigo
de Revista
|
Maria
Aurora Lourenço
|
A
arithmética da escola primária
| Revista Educação, 1944, v. XXXI, jan./jun.,
SP https://repositorio.ufsc.br/xmlui/handle/123456789/130665 |
|
Artigo
de Revista
|
Cesar
Visconti
|
O
Ensino da Aritmética na Escola Primária;
| Revista de Educação, 1945, v. 34, n. 48/49,
jul./dez., SP Disponível em https://repositorio.ufsc.br/xmlui/handle/123456789/182660 |
|
Artigo
de Revista
|
Benedito
Caldeira
|
Didactica
do calculo
| Revista de Educação, 1952, v. 38, n. 62/65,
mar./dez., SP. https://repositorio.ufsc.br/xmlui/handle/123456789/128327 |
Os textos publicados nesse período intentavam cumprir o papel de orientar o trabalho dos professores. Tendo analisado a proposta de Mercante relativamente às suas orientações aos professores sobre o tratamento dos problemas aritméticos e, considerando que os documentos mencionados no Quadro 1 citam esse autor, este artigo busca a análise da apropriação que tais textos fizeram da obra do pedagogo argentino.
O artigo de Ferraz (1929) traz colaborações em alguns aspectos a respeito de pensar os problemas aritméticos como conteúdo de aritmética e não como ferramenta para ensinar um conteúdo. A autora apresenta quatro passos para ensinar a resolver problemas: enunciado, objetivação dos dados, seriação e correção.
No enunciado era o momento no qual
o professor iria explorar a compreensão do aluno. Ferraz (1929) deixa claro que
se o aluno não compreende o que está posto no enunciado, não será capaz de
resolver. Afirma que o problema faz parte de uma análise de períodos
gramaticais.
Na objetivação dos dados seria a
compreensão das quantidades colocadas. Ferraz (1929) ressalta a importância
desse processo, pois seria possível utilizar uma análise intuitiva, concreta e
que desenhos gráficos/figuras poderiam auxiliar nesse passo para resolver um
problema.
Na terceira etapa, a seriação, estaria mais voltada para pensar em como graduar os problemas, partindo do fácil para o difícil, simples para o complexo, problemas com uma operação, depois com duas ou mais operações.
A correção seria o momento, segundo a autora, de compartilhar o raciocínio das crianças. Ela sugeria que o professor chamasse as crianças que tiveram dificuldade e ajudassem a resolver. Entretanto se a criança não conseguisse resolver, o professor deveria chamar outra para ir a lousa. Se a dificuldade em resolver esse problema fosse da maioria da classe, ela sugeria retomar a lição na aula seguinte.
Ao longo do artigo a autora apresenta um exemplo de aula sobre problemas. Apenas no final do texto ela menciona que essas ideias foram extraídas do livro de Victor Mercante.
Outro destaque que podemos dar ao texto de
Ferraz (1929) é o de como os passos sistematizados por Victor Mercante são
apropriados. Apesar deles demonstrarem as ideias do
autor argentino, Ferraz (1929) faz modificações, traduz da melhor forma segundo
seu entendimento, para os professores, oferecendo modelos de como ensinar
problemas.
Escobar
(1934) posicionou-se contrário a todo “[...] exclusivismo
pedagógico. Devemos acolher todas as orientações – alemã, francesa, americana,
italiana ou russa – porque cada uma só percebe uma face do espírito, visando um
só aspecto da educação.” (Escobar, 1934, p.111). Para tal mencionava Kerschnsteiner, Montessori, Dewey, Paytot,
entre outros.
Esse discurso caracteriza
como o Movimento Escola Nova se apresentava com grande variedade de vertentes.
Em meio a essas ideias inovadoras Escobar (1934) no subtítulo “A percepção e o
raciocínio - a análise” defende o método analítico[6] como melhor marcha para
ensinar. Para resolver problemas Escobar (1934) apresentou como questões
auxiliares para o entendimento deles: induções, deduções e conclusão. Em
seguida apresenta que para Victor Mercante um problema composto teria cinco
partes para analisar: Objetivação e análise indutiva, decomposição em
problemas simples, deduções parciais, análise dedutiva e conclusões parciais e
finais. Apresenta um exemplo de problema:
Eis a análise de um problema, feita
por MERCANTE: Um operário ganhou 240$000 em 48 dias;160$000 em 24 dias; e
104$000 em 26 dias; quantos mil réis ele ganhou? As induções são implícitas ou
explicitas as que a mente faz discutindo os dados do enunciado. Indução- I As diversas
quantias foram ganhas pela mesma pessoa? II – Ao perguntar-se quanto deve
entender –se as três vezes que trabalhou? Ganhar significa adquirir, aumentar o
que se tem? Deduções- I – Se as três vezes ganhou, as três vezes adquiriu. II –
À uma quantia deve-se reunir outra III – Reunir significa somar IV- Os três
ganhos se reúnem, somando-os. V -Os três ganhos juntos constituem o ganho.
(Escobar, 1934, p. 131).
Neste artigo é possível perceber que havia muitas ideias circulando a respeito de como ensinar aritmética e que elas precisavam estar subsidiadas pelos seus autores, dando maior veracidade nos discursos. Escobar (1934) apresenta ao longo do texto as ideias de diferentes autores que corroboram para seu discurso de mudança para o ensino. Tendo em vista o ensino de problemas, as propostas de Mercante como um passo-a-passo de como ensinar a resolver problemas pareciam interessantes como sistematização para socializar entre o público leitor da revista.
Caldeira (1940) apresenta em seu artigo algumas sugestões de como trabalhar a aritmética. Afirma que muitos autores já tinham se debruçado sobre isso entre eles Thorndike, Claparede, Aguayo, Comas, Mc Lellan, Alda Lodi entre outros. Apresenta em seu texto o que chama de “centros” nos quais apresenta temáticas para explorar o cálculo, por exemplo: compra de doces, material escolar, economia etc.
Expõe uma definição de problema dada por Victor Mercante: “é chegar a uma decomposição tal, das partes, que se tornem evidentes por si mesmas, isto é, que se expliquem pelos sentidos (intuitivamente); daí recompor e ir de fusão em fusão, de consequência em consequência, de dedução em dedução, a atinar com a pergunta.” (Caldeira, 1940, p. 46).
A respeito de Victor Mercante, Caldeira (1940) posicionou-se contrário a forma como esse autor percebia a criança. O autor parecia avistar os métodos ativos como sendo importantes para nortear o ensino. Utiliza praticamente o mesmo problema citado por Escobar (1934) para mostrar como analisar os problemas de acordo com as quatro etapas propostas pelo pedagogo argentino: objetivação, indução, dedução e conclusão.
Lourenço (1944) apresenta em seu artigo várias expressões exploradas por outros autores: desenvolver raciocínio, problemas reais e práticos, linguagem clara, tipos de problemas, correção.
A autora utilizava uma citação de Victor Mercante para justificar a utilização da linguagem clara nos problemas aritméticos “aprender matemática é analisar enunciados, a-fim-de descobrir operações para fazer. (Mercante)” (Lourenço, 1944, p.190).
Ao longo do artigo Lourenço (1944) apresenta sugestões de como trabalhar diferentes tipologias dos problemas (problemas para vestir). No final do texto a autora elabora um tópico a respeito da correção dos problemas, no qual sugere que poderiam ser individuais ou coletivas e que o professor passasse nas mesas para ver o que cada aluno teria resolvido e ao final chamasse uma criança “fraca” para a lousa a fim de tentar ajudar a raciocinar. Essa correção parece com a proposta feita por Ferraz (1929).
Victor Mercante (1905) aparece como um pequeno complemento ao texto de Lourenço (1944) pois a autora precisava dar ênfase ao entendimento do problema e talvez a menção a esse autor pudesse naquele momento dar o aporte científico para tal afirmação.
Visconti (1945) inicia o artigo afirmando a importância de o ensino ser “racional e prático”, a partir dessa premissa orientou o trabalho com materiais concretos e defendia um ensino das quatro operações a partir da utilização de problemas. Apresenta ao longo do artigo algumas sugestões para o ensino desses, diferentes tipologias de problemas por Aguayo e o cálculo mental proposto por Backheuser.
Visconti (1945) argumentava em favor de que o problema fosse escrito pelo professor na lousa, com letra legível, ortografia correta e palavras mais fáceis para o entendimento das crianças, para tal cita Victor Mercante: “O raciocínio de um problema, nada mais é que a análise de um período gramatical complexo” (Visconti, 1945, p. 106) Parece usar a mesma estratégia de Lourenço (1944), citar trechos da obra de Victor Mercante para dar maior cientificidade ao discurso utilizado para convencer os professores/leitores como ensinar os problemas. O autor do artigo defende a repetição de um problema trocando somente os dados e que isso se repetisse três ou quatro vezes até a classe conseguir resolver.
Anos mais tarde, Benedito Caldeira publica um artigo no qual escreve sobre o ensino de aritmética. Percebemos um movimento do autor na busca por identificar estratégias em diferentes autores as quais julgava serem importantes para as aulas de aritmética.
Nos parece que o artigo de Caldeira (1952) tenta organizar os conteúdos disciplinares de maneira a levar em conta como o aluno aprende, o que parece com a organização proposta pelo Movimento da Escola Nova e as ideias de Mercante a respeito do programa de ensino de Buenos Aires.
Caldeira (1952) praticamente copia o que escreveu sobre Mercante em seu artigo de 1940, deixando apenas a definição do que é resolver um problema e exclui as quatro etapas propostas por Victor e o exemplo de uma resolução. Mas por que ainda o cita mesmo discordando do ponto de vista do autor?
Uma justificativa pode ser a de que Mercante (1905) e os Programas de Ensino Argentinos eram uma das referências bibliográficas no Programa de Ensino de São Paulo publicado em 1949 e como Benedito Caldeira era Inspetor de Ensino, de certa forma representava o Estado e não poderia opor-se.
Nos artigos foi possível perceber diferentes apropriações dos autores a respeito do livro Cultivo y desarrollo de la aptitud matemática del niño escrito por Mercante em 1905. Mesmo quarenta e quatro anos depois de sua publicação ele ainda seria citado no Programa de Ensino.
O Programa de Ensino Paulista publicado em 13 de março de 1949 é extenso e traz explicações de cada conteúdo a ser ensinado. Os problemas ganham um tópico único e:
O fato do capítulo “problemas” aparecer no fim do programa não implica que, só após a técnica dos cálculos, devem ser dados problemas a respeito, mas os cálculos devem ser ensinados, tanto quanto possível, por meio de problemas. O problema não é mais do que uma aplicação do cálculo e não há vantagem alguma em separá-los uma vez que se auxiliam e se completam. (São Paulo, 1949, p. 13)
Apesar do termo problemas serem utilizados desde o
Programa de Ensino Paulista publicado em 1894, é a partir do programa publicado
em 1925, que eles ganham maior visibilidade.
Com
a reforma do ensino paulista na década de 1890 e a vaga intuitiva permeando as
discussões sobre o ensino, os programas de 1894,1905,1918 e 1921, os problemas
estavam mais para um conteúdo ou um meio para avaliar o conteúdo aprendido.
Entretanto nos programas de 1925 e 1934, em meio a ideias disseminadas pelo
Movimento da Escola Nova os problemas ganham maior destaque ficando atrelados
aos conteúdos, como meio de ensiná-los. (Souza, 2019, p.
10).
As afirmações acerca de que os problemas deveriam ser
reais, práticos, com dados verdadeiros aparecem no Programa de 1949. Há a
indicação de cinco sugestões de como os problemas deveriam ser trabalhados:
Chama atenção as
tipologias de problemas que são apresentadas na legislação: problemas com
historieta (história do cotidiano), problemas com completamento
(com todo o enunciado e para completar a resposta), problemas incompletos (no
qual os alunos deveriam elaborar a pergunta), problemas formulados pelos alunos
(aqueles que o professor daria os dados e os alunos elaborariam todo o
problema), problemas formulados livremente pelos alunos (idem), problemas em
torno de assuntos conhecidos pelas crianças (sugestão a partir de Thorndike) e
problemas a partir de listas de objetos (a partir de uma lista com os valores
de determinados objetos o professor elaboraria diversos problemas). (Souza; Giusti,
2019).
Nesse
sentido, nos parece que tanto os artigos das revistas pedagógicas quanto os
programas de ensino tinham como objetivo socializar práticas/modelos que
auxiliariam no trabalho docente.
A partir das análises das fontes anteriores foi possível perceber apropriações da obra de Victor Mercante em textos que mencionavam o ensino de problemas aritméticos. Nos parece que o saber sistematizado pelo autor argentino forneceu pistas para a construção de saberes profissionais específicos para ensinar problemas.
O saber profissional do professor que ensina matemática não é algo dado, imutável e fruto somente do exercício docente. Sua complexa constituição é resultado de longos anos de observações, reflexões, discussões, sistematizações e disseminações.
CONSIDERAÇÕES
PARCIAIS
Victor Mercante, pedagogo argentino, sistematizou um saber para ensinar problemas aritméticos a partir de suas observações como professor e em seu laboratório. Para ele os problemas não eram um meio apenas de ensinar um conteúdo aritmético, mas faziam parte do ensino de aritmética.
Em meio as ideias advindas do Movimento da Escola Nova, o ensino dos problemas modifica-se. Os autores de artigos de revistas pedagógicas respirando os ares inovadores desse Movimento tentam traduzir essas ideias para o ensino de aritmética, mais especificamente o ensino de problemas.
Foi
possível perceber que diferentes apropriações a respeito das sistematizações
postas no livro Cultivo y desarrollo de la aptitud matemática del niño foram demonstradas
nas revistas, entretanto todos os autores reconhecem em Victor Mercante um
personagem que subsidiava os argumentos para ensinar os problemas.
As
pesquisas que relacionavam os estudos do campo educacional e o campo
psicológico ganham destaque em tempos de cientificismo pedagógico. Elas
transformaram a maneira de ensinar as disciplinas alterando os saberes
profissionais do professor que ensina matemática, o que pode ser percebido nas
sistematizações para ensinar problemas.
REFERÊNCIAS
Bertini, L.F.; Morais, R. S.; Valente, W. R. (2017). A matemática a ensinar e a matemática para ensinar: novos estudos para a formação de professores. São Paulo: Editora Livraria da Física.
Burke, P. (2016). O que é história do conhecimento? Trad. Claudia Freire. 1ª ed. São Paulo: Editora Unesp.
Caldeira, B. (1940) Didactica do calculo. Revista de Educação, v. XXVIII, mar./jun.-set./dez., SP. Disponível em: https://repositorio.ufsc.br/handle/123456789/115826
Chartier, Roger. (1990). A história cultural: entre práticas e representações. Rio de Janeiro: Bertrand.
Dussel, I. (2014). Victor Mercante y la produción de um discurso cientifico sobre la educación. Archivos de Ciencias de la Educación, Año 8, nº 8, 4º Época. ISSN 2346-8866 Disponível em http://www.archivosdeciencias.fahce.unlp.edu.ar/
Escobar, J. R. (1934). O ensino de matemática. Revista de Educação, 1934, v. V, n. 5, mar. SP. Disponível em: http://repositorio.ufsc.br/xmlui/handle/123456789/99958
Ferraz, A. N. (1929). O ensino de problemas. Revista Educação. São Paulo, n 1e 2, v. VII, p. 122-131. Disponível em: https://repositorio.ufsc.br/handle/123456789/115833.
Hofstetter, Rita; Schneuwly, Bernard. (2017). Saberes: um tema central para as profissões do ensino e da formação. In: Hofstetter, Rita.; Valente, Wagner Rodrigues. (org.). Saberes em (trans) formação: tema central da formação de professores. 1ª ed. São Paulo: Editora Livraria da Física.
Lourenço, M. A. (1944). A arithmética da escola primária. Revista Educação, 1944, v. XXXI, jan./jun., SP https://repositorio.ufsc.br/xmlui/handle/123456789/130665
Mercante, V. (1905). Cultivo y desarrollo de la aptitud matemática del niño. Buenos Aires: Cabaut e Cin Editores.
São Paulo. (1949) Programa de Ensino da Escola Primária do Estado de São Paulo. São Paulo, SP. Disponível em https://www.imprensaoficial.com.br/DO/BuscaSimplesDO.aspx
Valente, W. R.; Bertini, L. F.; Pinto, N. B.; Morais, R. S.(2017). A Matemática na Formação de Professores e no Ensino: processos e dinâmicas de produção de um saber profissional, 1890-1990. Projeto de Pesquisa. São Paulo: FAPESP. Disponível em:
Visconti, C. (1945). O Ensino da Aritmética na Escola Primária. Revista de Educação, 1945, v. 34, n. 48/49, jul./dez., SP Disponível em https://repositorio.ufsc.br/xmlui/handle/123456789/182660
Notas
[1] Mestre em Ciências pela UNIFESP. Doutoranda em Ciências pela UNIFESP, Guarulhos, SP, Brasil. Endereço para correspondência: Estr. do Caminho Velho, 333, Guarulhos, São Paulo, Brasil, CEP: 07252-312. E-mail: deianandes@hotmail.com
[2] Projeto Temático intitulado “A matemática na formação de professores e no ensino: processos e dinâmicas de produção de um saber profissional, 1890-1990” (
Valente; Bertini; Morais; Pinto; 2017), com financiamento da FAPESP. O projeto conta com financiamento da Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP).
[3] O Laboratório de Paidologia era uma tentativa de junção de duas disciplinas Pedagogia e Psicologia para a melhoria da aprendizagem das crianças. Esse era um movimento internacional e as pesquisas realizadas por Victor Mercante resultaram em um livro publicado em 1927 intitulado “La Paidologia” (
Dussel, 2014). Nesse laboratório, pioneiro na América Latina, eram realizados exames psicológicos e a partir dessas observações Mercante teria conseguido criar ferramentas para ensinar grandes quantidades de alunos fazendo uso do conhecimento científico opondo-se ao ensino enciclopédico.
[5] Para Victor Mercante os problemas simples eram aqueles resolvidos com uma única operação e os problemas compostos solucionados com duas ou mais operações.
[6] O método analítico na alfabetização consiste em ensinar a ler e a escrever a partir de palavras, frases ou textos, ou seja, ensinar do todo para as partes. Pensando em aritmética seria partir dos problemas para as operações chegando aos números.







