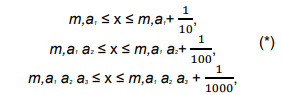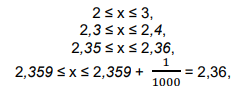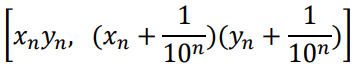Introdução
Os
Parâmetros Curriculares Nacionais (PCN) (BRASIL, 1998), bem como a Base
Nacional Comum Curricular (BNCC) (BRASIL, 2018) recomendam que a Matemática não
seja ensinada aos estudantes apenas por meio de procedimentos. Por
exemplo:
Os
procedimentos não devem ser encarados apenas como aproximação metodológica para
aquisição de um dado conceito, mas como conteúdos que possibilitem o
desenvolvimento de capacidades relacionadas com o saber fazer, aplicáveis a
distintas situações. Esse saber fazer implica construir as estratégias
e os procedimentos, compreendendo os conceitos e processos neles envolvidos.
Nesse sentido, os procedimentos não são esquecidos tão facilmente. Exemplos de
procedimentos: resolução de uma equação, traçar a mediatriz de um segmento com
régua e compasso, cálculo de porcentagens etc. (BRASIL, 1998, p. 50, grifo
nosso).
Essa é uma forma que contribui para o desenvolvimento do
letramento matemático do estudante, definido na BNCC como:
as competências e
habilidades de raciocinar, representar, comunicar e argumentar matematicamente,
de modo a favorecer o estabelecimento de conjecturas, a formulação e a
resolução de problemas em uma variedade de contextos, utilizando conceitos,
procedimentos, fatos e ferramentas matemáticas. (BRASIL, 2018, p. 266).
No que
diz respeito à ampliação das operações elementares em cada novo universo
numérico estudado ao longo da Escola Básica e à permanência ou não das
propriedades das operações, interpretamos tal recomendação como: alguma
discussão deve ser feita com os estudantes, e concordamos com essa afirmação. Ressaltamos que, na BNCC (BRASIL, 2018), as propriedades
da igualdade e das operações estão entre os Objetos de Conhecimento e as
Habilidades para o Ensino Fundamental (Quadro 1).
Quadro 1
Menção a
propriedades das operações na BNCC
 Elaborado pelas Autoras
(adaptado de BRASIL, 2018)
Elaborado pelas Autoras
(adaptado de BRASIL, 2018)
|
Ano
|
Objeto de Conhecimento
|
Habilidade
|
|
4º ano
|
Propriedades das operações para o
desenvolvimento de diferentes estratégias de cálculo com números naturais
|
(EF04MA05) Utilizar as
propriedades das operações para desenvolver estratégias de cálculo.
|
|
7º ano
|
Números racionais na representação fracionária e na decimal: usos,
ordenação e associação com pontos da reta numérica e operações
|
(EF07MA11) Compreender e utilizar a multiplicação e a divisão de
números racionais, a relação entre elas e suas propriedades operatórias.
|
|
8º ano
|
Valor numérico de expressões algébricas
|
(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor
numérico de expressões algébricas, utilizando as propriedades das operações.
|
É natural esperar que o estudante tenha mais
facilidade em aplicar os conceitos e propriedades dos quais se apropriou do que
aqueles sobre os quais só recebeu uma informação sobre os procedimentos a
empregar, sem qualquer argumentação sobre sua validade. Assim, consideramos que
as Habilidades apontadas no Quadro 1 só serão amplamente atingidas se o
estudante compreender por que valem as propriedades operatórias. De fato, uma
discussão sobre as propriedades das operações elementares com os estudantes
contribui não só para o desenvolvimento do pensamento matemático pelo estudante
como também para a compreensão dessas operações. Além disso, são as
propriedades das operações que, junto com a estrutura do sistema de numeração
posicional (no caso, o decimal ou de base 10) amparam todos os seus algoritmos.
A ausência de justificativas matemáticas para algoritmos e procedimentos
certamente atrapalha em muito a aprendizagem das quatro operações elementares,
podendo levar a uma consequência ainda mais grave: a cristalização de uma
concepção errônea sobre a própria matemática. Em lugar de conceber a matemática
como uma ciência dedutiva, cujas verdades devem ser estabelecidas por meio de
argumentos lógicos, a partir de fatos previamente estabelecidos, as crianças
expostas a este tipo de abordagem tendem a formar uma visão da matemática como
um conjunto de regras criadas arbitrariamente e sem conexão. (RIPOLL; RANGEL;
GIRALDO, 2016, p. 117).
No caso específico da multiplicação de números
naturais, Heirdsfield (2001, apud MENDES; BROCARDO; OLIVEIRA, 2013) ressalta que, na
aprendizagem dessa operação, assumem especial relevo a compreensão e o uso das
propriedades comutativa, associativa e distributiva da multiplicação em relação
à adição, que se constituem como importantes suportes para desenvolver a
proficiência multiplicativa dos alunos. Segundo Mendes, Brocardo e Oliveira
(2013), que investigam como evoluem os procedimentos usados pelos alunos quando
resolvem tarefas de multiplicação de números naturais, essas propriedades, junto
com os padrões de valor de posição associados à multiplicação por dez fazem
parte das “grandes ideias” associadas à multiplicação e estão na base da
progressão que os alunos vão fazendo em termos do raciocínio multiplicativo.
A propriedade comutativa da operação de adição, seja de números naturais, inteiros, racionais ou reais, não representa uma dificuldade aos estudantes, porque, em qualquer um desses universos numéricos, adicionar tem o significado de juntar, e juntar é uma ação comutativa. Já o mesmo não acontece com a multiplicação, mesmo no universo dos números naturais. De fato, nem sempre é simples para os alunos nos anos iniciais compreender que adicionar, por exemplo, 5 vezes a parcela 4 leva ao mesmo resultado que adicionar 4 vezes a parcela 5. (RIPOLL; RANGEL; GIRALDO, 2015).
Nos universos numéricos maiores do que o dos naturais, ampliam-se as operações elementares, tornando-se necessário definir, no caso da multiplicação, novos tipos de produtos; por exemplo, não se pode dizer que (-2) x (-3) é a adição de (-2) parcelas iguais a (-3) nem que x é a adição de parcelas iguais a . Assim, só depois de ter-se esclarecido para os estudantes como são ampliadas as operações torna-se viável - e recomendável - discutir-se suas propriedades no novo universo numérico. Por exemplo:
No universo dos números
naturais, é sempre verdade que a soma de dois números é maior que ou igual a
cada um dos números somados. Resultado análogo vale para a multiplicação. Essas
certezas são, muitas vezes, referências importantes para que os alunos avaliem
os resultados em seus cálculos. No entanto, elas deixam de valer no universo
dos números inteiros. Por exemplo, 6+(−10) = −4 e −4 < 6. Da mesma forma,
(−2) · 6 = −12, −12 < −2 e −12 < 6. A ampliação do universo numérico
exige a revisão das propriedades das operações. É importante que o aluno
perceba que algumas propriedades das operações são preservadas, como a
comutatividade; que outras passam a valer, por exemplo, a existência de inverso
aditivo (ou simétrico); e que outras, como a exemplificada, deixam de valer.
(RIPOLL; RANGEL; GIRALDO, 2016, p. 66).
As propriedades das operações são em geral
negligenciadas ou pouco enfatizadas em muitos livros didáticos. Por exemplo, em
Fischer (2020) foi possível constatar, no caso da comutatividade da
multiplicação de frações que as 4 coleções de livros didáticos analisadas não
dão ênfase a discussões como as ressaltadas na citação anterior. Consideramos,
assim, justificado o presente trabalho, que avança nas considerações colocadas
anteriormente, convidando o leitor a refletir sobre a viabilidade de
discutir-se a ampliação da multiplicação e a propriedade comutativa da
multiplicação com os estudantes ao longo da Educação Básica (seções 3, 4, 5, e,
6). Nessa direção, este texto diferencia-se de outros encontrados (BARMBY et al., 2009; MENDES; BROCARDO;
OLIVEIRA, 2013; ZULKARDI, 2013) que, ao tratarem da propriedade comutativa da
multiplicação, elegem algum universo numérico particular, por isso, no lugar de
uma seção de revisão bibliográfica, optamos por mencionar esses textos à medida
que o universo numérico é abordado. São incluídas algumas sugestões de
abordagem de ampliação e de validação da comutatividade. Pretende-se aqui
ressaltar que em nenhum universo numérico pode tal propriedade ser inferida sem
alguma discussão sobre sua validade, tendo em vista que cada universo numérico
tem as suas peculiaridades/características. Se aceitarmos a comutatividade da
multiplicação como uma propriedade naturalmente válida, como não esperar do
estudante o mesmo procedimento, futuramente, ao considerar uma multiplicação de
matrizes?
Este artigo busca contribuir tanto para o
Conhecimento Pedagógico de Conteúdo como para o Conhecimento Matemático para o
Ensino, trazendo o fruto de uma reflexão das autoras sobre o ensino da
ampliação da operação de multiplicação para universos numéricos maiores do que
o dos números naturais e sobre o ensino da propriedade comutativa da
multiplicação ao longo da Educação Básica. Antes de nos concentrarmos na operação
de multiplicação e na propriedade comutativa, procuramos esclarecer, na próxima
seção, do que tratam o Conhecimento Pedagógico de Conteúdo e o Conhecimento
Matemático para o Ensino que fundamentaram este trabalho e que todo professor
deve levar em consideração ao longo de sua formação, seja inicial ou continuada,
bem como em sua prática.
O Conhecimento Pedagógico de Conteúdo, o
Conhecimento de Matemática para o Ensino e a Metodologia utilizada neste
trabalho
Lee S. Shulman, e posteriormente Deborah Ball, foram os
primeiros pesquisadores que se referiram a um conteúdo especializado para o
ensino, sendo que Ball específica para o caso do ensino de Matemática. Com formação em Psicologia Educacional, Shulman (1986; 1987) preocupou-se em compreender de onde
vinham os conhecimentos dos professores, buscando respostas para questões como:
De onde vêm as explicações dos professores? Como os professores decidem
o que ensinar, como representar esse conteúdo, como questionar os alunos sobre
isso e como lidar com problemas de compreensões equivocadas? Quais são as
fontes do saber do professor? O que um professor conhece e quando ele começou a
conhecer? Como os novos saberes são adquiridos, o saber antigo ressignificado e
ambos combinados para formar uma nova base de conhecimento? (SHULMAN, 1986, p.
8, tradução nossa).
Os questionamentos de Shulman
(1986; 1987) foram motivados pela imagem negativa que se tinha sobre o
conhecimento do professor, oriunda de suposições, na década de 1980, de que os
professores da educação básica possuíam uma má formação.
Ninguém perguntou como os tópicos foram transformados em conhecimento do
professor para o conteúdo do ensino. Nem perguntaram como determinadas
formulações desse conteúdo se relacionavam com o que os alunos conheciam ou
interpretavam equivocadamente. (SHULMAN, 1986, p. 6, tradução nossa).
Segundo Ball, Thames e Phelps (2008, p. 390), “[...] tão pouca atenção foi dedicada à análise do conteúdo e seu papel na instrução que Shulman chamou isso de "paradigma perdido" em sua pesquisa sobre ensino e conhecimento do professor”. (tradução nossa).
A pesquisa de Shulman não se concentrou no campo específico da Matemática; contudo, já é possível reconhecer aí diferenças entre o pesquisador de Matemática e o profissional que ensina Matemática na Educação Básica. Shulman (1986) aponta para um conhecimento do professor que não diz respeito ao conhecimento do conteúdo por si só nem ao conhecimento pedagógico geral, mas sim a um conhecimento que está associado a um amálgama entre eles, o que ele denominou Conhecimento Pedagógico de Conteúdo.
Dentro da categoria de saber pedagógico de conteúdo, incluo os tópicos
mais regularmente ensinados na área, as formas mais úteis de representação
dessas ideias, as analogias, ilustrações, exemplos, explicações e demonstrações
mais poderosas – em uma palavra, as formas de representação e formulação do
conteúdo que são compreensíveis para os outros. Uma vez que não há formas
únicas de representação mais poderosas, o professor deve ter em mãos um
verdadeiro arsenal de formas alternativas de representação, algumas das quais derivam
da pesquisa, enquanto outras se originam na sabedoria da prática; também inclui
uma compreensão do que facilita ou dificulta a aprendizagem de tópicos
específicos: as concepções e preconcepções que os alunos de diferentes idades e
origens trazem com eles para aprender os tópicos e lições mais frequentemente
ensinadas. (SHULMAN, 1986, p. 9, tradução nossa).
Ball, Thames e Phelps (2008) desenvolveram suas pesquisas com base nos
pressupostos de Shulman, direcionando-se
especificamente à Matemática, dedicando-se ao que chamaram de Conhecimento Matemático para o Ensino, apontando
que
o ensino pode exigir uma forma especializada de conhecimento de conteúdo
puro – “puro” porque não é misturado com o conhecimento sobre os estudantes nem
com o conhecimento de pedagogia; e “especializada”, porque não é necessária ou
usada em outras configurações senão em ensino da matemática. (BALL; THAMES; PHELPS, 2008. p. 396, tradução nossa,
aspas como no original).
Os mesmos autores destacam diversas habilidades associadas ao conhecimento matemático para o ensino, tais como: identificar erros dos estudantes e suas causas; identificar e validar estratégias de pensamento diversas; escolher exemplos adequados para explicar, justificar ou motivar conceitos que direcionam para uma definição e/ou para uma generalização. Cabe ressaltar que muitas destas habilidades apoiam-se tanto no conhecimento de conteúdo como no conhecimento pedagógico do professor.
A pesquisa que aqui relatamos, é qualitativa,
por ter por foco o processo de como a multiplicação vai sendo ampliada em cada
novo universo numérico e seus efeitos sobre a comutatividade. Assim, ela não
envolve uma coleta de dados, porém inclui propostas de abordagens didáticas.
Como metodologia, na concepção das autoras, a fundamentação no Conhecimento de
Matemática para o Ensino sugere uma primeira etapa que diz respeito ao que é
denominado em Ball, Thames e Phelps (2008) conhecimento de conteúdo puro e que envolveu
uma pesquisa teórica sobre os temas números naturais, inteiros, racionais,
reais e complexos, focando em sua construção e na operação de multiplicação e na
propriedade comutativa, com base em Ferreira (2013), Ripoll,
Ripoll e Silveira (2011), Ripoll,
Rangel e Giraldo (2015; 2016). A seguir, refletiu-se
sobre a transposição desses tópicos para a Escola Básica, construindo-se
propostas de abordagens didáticas que ressaltam uma diversidade imposta pelos
diferentes universos numéricos (por exemplo, ao ampliar-se o universo numérico
dos naturais para os inteiros, arranjos retangulares já não dão mais conta da
abordagem da comutatividade, e uma nova proposta precisa ser apresentada) e
destacam aspectos que devem estar no planejamento do professor.
A propriedade comutativa da multiplicação no
universo dos números naturais
Como já ressaltado, a propriedade comutativa da
adição não representa uma dificuldade aos estudantes, porque adicionar tem o
significado de juntar em qualquer um desses universos numéricos, e juntar é uma
ação comutativa. Isso atribui às quantidades que estão sendo adicionadas
(chamadas parcelas) igual papel na ação de adicionar. O mesmo não acontece com
a multiplicação de números naturais, como bem aponta Vergnaud
(2009, p. 183), criador da Teoria dos Campos Conceituais:
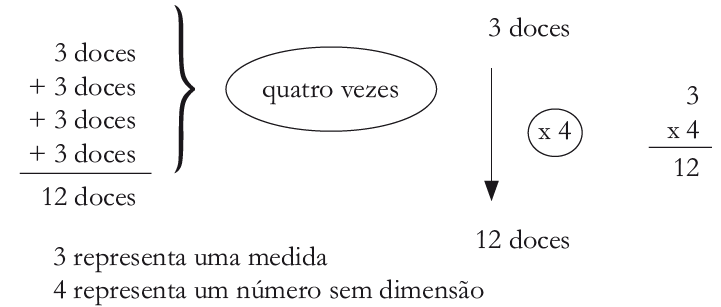
Partir de um material concreto para ensinar a multiplicação leva
obrigatoriamente a introduzir a multiplicação como adição reiterada de uma
mesma quantidade e, em consequência, a fazer do multiplicando uma medida, e do
multiplicador um simples operador sem dimensão física. (Figura 1).
O autor alerta que é possível inverter o papel
do multiplicador e o do multiplicando.
No entanto
“são necessárias certas precauções pedagógicas para que as crianças aceitem
essa comutatividade, porque lhes é preciso, na verdade, fazer a abstração do
que esses números representam” (VERGNAUD, 2009, p.184). Além disso, cabe
ressaltar que a nomenclatura “fatores” para ambos os termos, sugerindo que os
termos têm um mesmo papel também na multiplicação, só procede depois de provada
a propriedade comutativa.
Na pesquisa bibliográfica realizada pelas autoras, com exceção de Mendes, Brocardo e Oliveira (2013), foi possível perceber a convicção dos autores em introduzir-se a multiplicação de números naturais como uma adição de parcelas iguais (BARMBY et al. (2009), RIPOLL; RANGEL; GIRALDO (2015), VERGNAUD (2009), ZULKARDI (2013)). É consenso entre todos esses autores, no entanto, que se faz necessário discutir a propriedade comutativa com a criança, pois para ela esta propriedade não é natural: por exemplo, por que a soma de 5 parcelas todas iguais a 4 determina o mesmo resultado que a soma de 4 parcelas todas iguais a 5, ou seja, que 5 × 4 = 4 × 5?
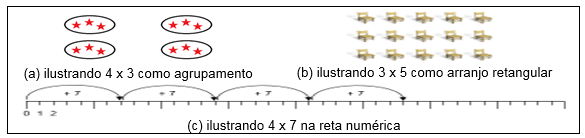
Zulkardi (2013), que apresenta uma sequência de atividades procurando estimular alunos do 2º ano da Indonésia a compreender a propriedade comutativa e a usá-la para resolver problemas de multiplicação, menciona três modelos para representar uma multiplicação de números naturais: i) como agrupamento; ii) como um arranjo retangular; iii) na reta numérica (Figura 2).
Barmby et al. (2009), ao investigarem se arranjo retangular pode apoiar a
compreensão e raciocínio na multiplicação, apontam que, ainda que as
representações por agrupamento e na reta numérica ilustrem a adição de parcelas
iguais, nenhuma delas ilustra dois importantes aspectos da multiplicação aqui
já salientados, a saber, a comutatividade da multiplicação e a distributividade
da multiplicação em relação à adição. Ressaltam que o arranjo retangular
enfatiza a natureza binária da multiplicação e tem a vantagem de, com ele, ser
possível mostrar-se claramente a propriedade comutativa. Zulkardi
(2013) concorda com esses autores, e complementa que o arranjo retangular ainda
permite ao estudante contar por agrupamento e usar adição repetida (Figura 3). Cabe ressaltar que as
reinterpretações apontadas na Figura 3 oportunizam a generalização da ideia
embutida no exemplo aí mencionado, momento em que a propriedade comutativa da
multiplicação (de números naturais) pode ser então explicada em palavras com
estudantes dos anos iniciais, ainda apoiada no arranjo retangular: não importa quanto valem multiplicando e
multiplicador, seus papéis podem ser trocados porque o resultado produzido é o
mesmo.
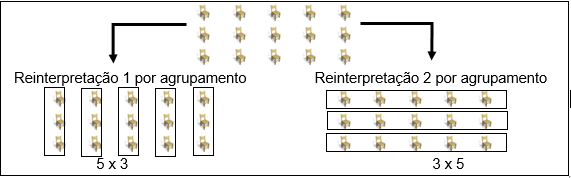 Figura 3
Reinterpretação do arranjo
retangular: diferentes agrupamentos levam a 5 × 3 = 3 × 5
Elaborado pelas Autoras
Figura 3
Reinterpretação do arranjo
retangular: diferentes agrupamentos levam a 5 × 3 = 3 × 5
Elaborado pelas Autoras
Todos os trabalhos encontrados que falam da
comutatividade da multiplicação de números naturais apontam o arranjo
retangular como uma das representações mais potentes para abordar tal
propriedade e amparar a evolução do raciocínio multiplicativo de estudantes dos
anos iniciais ou mesmo do 6º ano de escolaridade, apesar de Battista et al. (1998), em sua pesquisa sobre
como estudantes constroem e organizam mentalmente um arranjo retangular, terem
constatado que muitos estudantes não “enxergam” um arranjo retangular como uma
disposição de linhas por colunas. De fato, Zulkardi
(2013) concluiu que os estudantes de segundo ano que participaram de sua
pesquisa não visualizaram a multiplicação no arranjo retangular, insistindo na
contagem “um a um”. Assim, o professor deve estar bastante atento à compreensão
dos estudantes quanto ao arranjo retangular como interpretação da multiplicação
e ao nível cognitivo dos mesmos antes de convidá-los a uma generalização que
leva ao enunciado da propriedade comutativa.
A multiplicação e a comutatividade no universo
dos números inteiros
Na escola básica, a introdução dos números
negativos precisa garantir alguns aspectos fundamentais, entre eles: a
ressignificação do zero, que agora, além de manter o significado de ausência de
quantidade, passa a ser compreendido também como um referencial; a compreensão
de número como uma quantidade munida de uma orientação. Assim, as quantidades
passam a ser registradas em relação ao referencial zero, o que oportuniza a
ideia de oposto (RIPOLL; RANGEL; GIRALDO, 2016). A partir das ideias de referencial e de
oposto, o estudante deve reconhecer que “tomar o oposto de” é uma ação que
anula a si própria, ou seja, que o oposto do oposto de um número é o próprio
número.
Como consequência da incorporação da noção de orientação ao conceito de número, originando os inteiros positivos e negativos, os conceitos
existentes no universo dos números naturais não mais amparam, pelo menos
diretamente, as operações elementares com números inteiros. De fato, já não faz
sentido, por exemplo, encarar (-2) x 3 como uma adição de parcelas iguais a 3. O produto (-2) x 3
deve, então, ser definido.
Neste momento, cabe mencionar uma possibilidade de encaminhamento
utilizada em muitos livros didáticos e que consiste em definir (-2) x 3 como
sendo igual a 3 x (-2) porque queremos que a multiplicação “continue”
comutativa. Essa posição de definir (-2) x 3 como sendo igual a 3 x (-2) parece
seguir o Princípio de Permanência de H. Hankel,
que estabelece que as operações em ℤ e em ℚ são
ampliadas de modo a serem preservadas ao máximo as propriedades que valem no
universo numérico menor. Em sua obra Theorie der complexen Zahlensysteme publicada em 1867, o matemático alemão
Hermann Hankel apresenta um tratamento bastante
axiomático dos fundamentos da aritmética, na qual aparece explicitamente o
princípio de permanência como a base conceitual para estender o significado de
operações a novos domínios de números. Seguindo este princípio, no caso dos
números, a escolha para as definições dos novos produtos (positivo x negativo,
negativo x positivo, negativo x negativo) não é arbitrária, mas sim única. Ou
seja, seguindo este princípio, é possível provar que a regra dos sinais
da multiplicação é a única forma de estender-se a multiplicação dos naturais
para os inteiros de tal forma que suas propriedades fundamentais sejam
preservadas (precisamente, aquelas que garantem a ℤ a estrutura de anel). (RIPOLL; RANGEL; GIRALDO,
2016).
Não recomendamos que este princípio seja utilizado com estudantes do 7º
ano, por dois motivos: apenas sugerir que seja preservada a propriedade que já
vale para números naturais, sem justificativas para o estudante, não o ajudará
na compreensão da multiplicação de inteiros; além disso, ressaltamos que a
proposta de definição para (-2) x 3 apoiada na comutatividade não serve para
definir o produto de números negativos, como (-2) x (-3) e, neste caso, o argumento apoiado no Princípio de
Permanência de Hankel é mais complexo ainda do que
aquele que justifica que (-2) x 3 deve ser igual a 3 x (-2). Por isso,
consideramos que a definição de produto de inteiros na escola carece de
significado, sendo recomendável encontrar-se alguma motivação para ela que lhe
dê mais significado.
No que segue, trazemos uma proposta de encaminhamento da definição de produto de inteiros para estudantes de 7º ano. Começamos apontando que é possível buscar inspiração nas operações com números naturais para estabelecer/definir a multiplicação nos novos casos de produtos de números inteiros: positivo x negativo, negativo x positivo e negativo x negativo, atribuindo-lhes algum significado, ainda que nem sempre de forma imediata. Por exemplo, é natural para os estudantes aceitar (definir, na verdade) a multiplicação de número inteiro positivo por número inteiro negativo ainda como adição de parcelas iguais. Assim, da mesma forma que 3 x 5 = 5 + 5 + 5, define-se que 3 x (-5) é igual a (-5) + (-5) + (-5), e, em geral, define-se, de forma análoga, o produto de qualquer inteiro positivo por um inteiro negativo. A seguir, com o apoio da reta numérica (Figura 4) e da operação de adição de inteiros aí já visualizada, o estudante pode ainda perceber que 3 x (-5) é o oposto de 3 x 5, propriedade que, simbolicamente, é expressa pela igualdade 3 x (-5) = - (3 x 5) (oposto de 3 x 5).
 Figura 4
Apoio na reta
numérica para perceber que 3 x (-5) é o oposto de 3 x 5
Elaborado pelas Autoras
Figura 4
Apoio na reta
numérica para perceber que 3 x (-5) é o oposto de 3 x 5
Elaborado pelas Autoras
Ainda com a reta numérica ajudando na
visualização e na imaginação, a propriedade pode ser generalizada para outros
valores e, posteriormente, para valores quaisquer, chegando-se à conclusão de
que, para quaisquer que sejam os números naturais a, b,
a x (-b)
= - (a x b) (oposto de a x b), (*)
propriedade
que, em um primeiro momento, pode ser registrada em palavras, sem o uso de
simbologia matemática.
Já não é tão imediato buscar inspiração nas
operações com números naturais para definir o produto (-3) x 5, mas ainda é
possível. De fato, a definição para esse caso pode vir da observação de uma
regularidade na multiplicação de naturais: por exemplo, na sequência de
produtos na coluna da esquerda da Figura 5 observa-se que o resultado de uma
linha é sempre 5 unidades a menos da linha anterior. Portanto, a definição de
(-1) x 5, (-2) x 5 etc. pode continuar apoiando-se em tal regularidade e assim
definir-se que (-3) x 5 = -15 (coluna da direita da Figura 5).
 Figura 5
Regularidade
motivadora da definição de (-3) x 5
Elaborado pelas Autoras
Figura 5
Regularidade
motivadora da definição de (-3) x 5
Elaborado pelas Autoras
Novamente a Figura 5 e a reta numérica podem auxiliar o estudante a reconhecer e, posteriormente, a generalizar para outros valores, que, a partir dessa regularidade, (-3) x 5 é também o oposto de 3 x 5, pois percebe-se que, afinal, retira-se, a partir do zero, 3 vezes 5 unidades, agora interpretando as flechas que apontam para o sentido decrescente da reta na Figura 4 como “retirando 5 unidades”. Assim, levando em conta que retirar é o oposto de acrescentar, como já trabalhado no universo dos números naturais, o estudante deve perceber que
(-3) x 5 = - (3 x 5)
Aceitando-se a regularidade mencionada como motivadora para a definição de (-3) x 5, reconhece-se (-3) x 5 como o oposto de 3 x 5, ou, de forma genérica, para quaisquer que sejam os números naturais a, b,
(-a) x b = - (a x b) (oposto de a x b), (**)
propriedade que, em um primeiro momento, pode ser estabelecida só em palavras.
De forma análoga, agora aproveitando a definição já estabelecida de multiplicação de número inteiro positivo por número inteiro negativo, exploramos o mesmo tipo de regularidade utilizada para inspirar a definição do produto de dois números inteiros negativos, registrada na Figura 6 e que nos leva a definir
(-3) x (-5) = 3 x 5.
 Figura 6
Regularidade motivadora da definição
de (-3) x (-5)
Elaborado pelas Autoras
Figura 6
Regularidade motivadora da definição
de (-3) x (-5)
Elaborado pelas Autoras
A regularidade apresentada na Figura 6, se tomada como motivação para a definição do produto (-3) x (-5), permite-nos interpretar (-3) x (-5) como acrescentar, a partir do zero, 3 vezes 5 unidades. Permite também interpretar (-3) x (-5) como o oposto de 3 x (-5), ampliando a propriedade (**) para o caso em que o segundo fator é um número negativo, uma vez que, pela propriedade (*),
- (3 x (-5)) = oposto de 3 x (-5) oposto de (oposto de 3 x 5)
= oposto de (oposto de 15) = 15 = 3 x 5
A mesma ideia pode ser repetida para outros valores negativos e, posteriormente, generalizada (em palavras) para inteiros negativos arbitrários, concluindo-se que, para quaisquer que sejam os números naturais a, b,
(-a) x (-b) = oposto de a x (-b) oposto de (oposto de (a x b) = a x b,
portanto,
(-a) x (-b) = a x b. (***)
A discussão da propriedade comutativa também precisa ser feita em casos. O professor pode estimular o mesmo pensamento genérico que ajudou os estudantes a estabelecerem as propriedades (*) e (**) para que os estudantes concluam que a propriedade comutativa vale quando os fatores têm sinais opostos. Para o caso de ambos os fatores serem negativos, encaminhamento semelhante pode ser feito, agora utilizando a propriedade (***): partindo de exemplos, tais como
(-3) x (-5) 3 x 5 = 5 x 3 (-5) x (-3),
os estudantes devem perceber que a comutatividade da multiplicação de números naturais, utilizada na segunda igualdade acima, ampara a comutatividade da multiplicação desses inteiros e, a seguir, perceber que o argumento é o mesmo para quaisquer fatores negativos, concluindo que também nesse caso a multiplicação é comutativa.
A multiplicação de inteiros e a comutatividade
por meio do ábaco dos inteiros
Em Meinerz (2020) encontramos a descrição do Objeto Digital de
Aprendizagem Ábaco Virtual dos Números
Inteiros(Figura 7) como ferramenta para apoiar as
operações com números inteiros:
o Objeto Digital de
Aprendizagem é constituído de duas hastes: a haste da esquerda para colocar as
argolas [vermelhas] que representam as unidades negativas e a haste da direita
para colocar as argolas [azuis] que representam as unidades positivas. Para
utilizar o Ábaco dos Números Inteiros é necessário observar três regras: uma
argola na haste das unidades positivas, representa uma unidade positiva; uma
argola na haste das unidades negativas, representa uma unidade negativa; uma
argola na haste das unidades positivas “anula” uma argola na haste das unidades
negativas. (MEINERZ, 2020, p. 44-45).
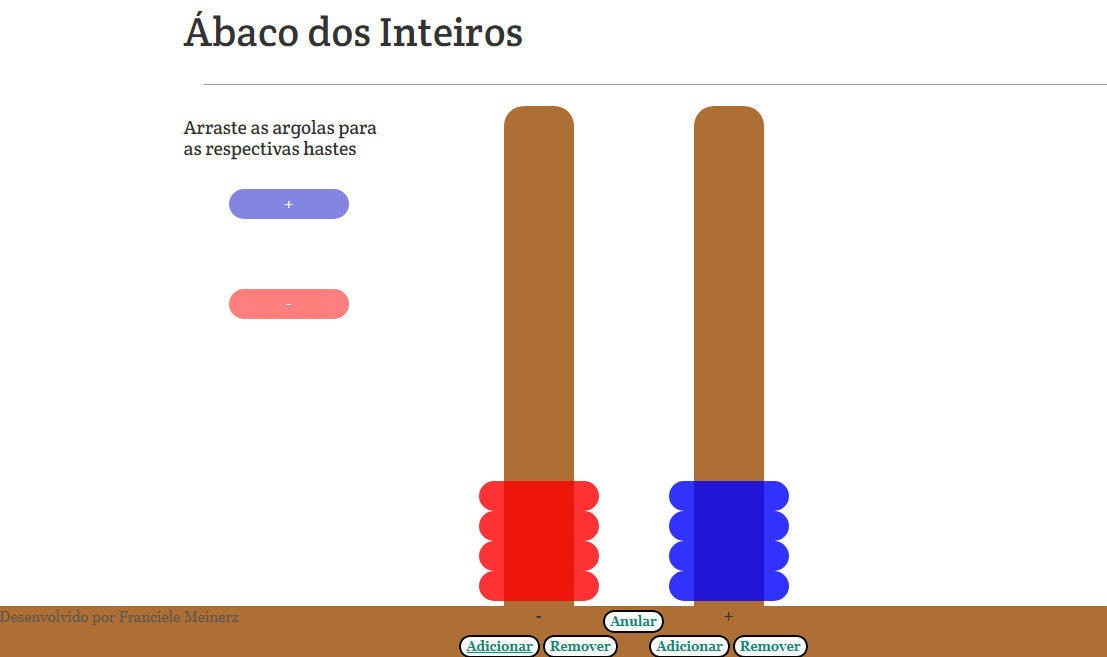 Figura 7
Foto da tela do Objeto Digital de
Aprendizagem Ábaco Virtual dos Números
Inteiros
Meinerz
(2020, p. 45)
Figura 7
Foto da tela do Objeto Digital de
Aprendizagem Ábaco Virtual dos Números
Inteiros
Meinerz
(2020, p. 45)
A regra “uma argola na haste das unidades positivas ‘anula’ uma argola na haste das unidades negativas” apoia-se em discussão anterior à apresentação do ábaco e reporta-se ao conceito de número negativo, de oposto e à propriedade de que, ao se adicionar dois números opostos, obtém-se zero como resposta. Assim, no ábaco, o zero pode ser representado de várias formas, por meio das colunas de unidades negativas e positivas preenchidas com a mesma quantidade de argolas, fato que será utilizado adiante.
Além do uso do ábaco para explorar a adição e a subtração de números inteiros, é possível fazer também uso desse material para explorar a multiplicação de inteiros e deduzir as regras de sinais.
Em sua prática, Meinerz faz uso do ábaco para trabalhar as operações com números inteiros e afirma que os estudantes aceitam com naturalidade a definição, por exemplo, do produto 3 x (-5) como a adição de 3 parcelas iguais a (-5), posteriormente generalizada para o caso positivo x negativo; ainda, levando em conta que adicionar tem o significado de juntar, mas também de acrescentar, a partir da ideia de que para obter-se 3 x (-5) acrescentam-se 3 parcelas iguais a (-5), os estudantes também aceitam com naturalidade a definição do produto (-3) x alguma coisa como o oposto de adicionar (ou acrescentar) 3 parcelas iguais a esta alguma coisa, o que corresponde a retirar 3 parcelas iguais a esta alguma coisa. Assim, (-3) x 5 seria definido como retirar 3 parcelas iguais a 5, enquanto (-3) x (-5) seria definido pelo “oposto de acrescentar 3 parcelas iguais a (-5)”, ou seja, retirar 3 parcelas iguais a (-5). Com a utilização do ábaco, os estudantes têm a oportunidade de perceber que “retirar 3 parcelas iguais a (-5)” é equivalente a “acrescentar 3 parcelas iguais a 5”. A Figura 8 ilustra o processo da multiplicação (-3) x (-5) no ábaco. Para retirar, a partir do zero, 3 parcelas iguais a -5, antes temos que fazê-las aparecer no ábaco; para isto, representamos convenientemente o zero no ábaco. Por exemplo, representamos o zero por meio do uso de (no mínimo) 15 argolas positivas e 15 argolas negativas (Figura 8 (a)); agora torna-se possível retirar do ábaco 3 parcelas de 5 unidades negativas (Figura 8 (b)), resultando em +15 (Figura 8 (c)), o que é equivalente a adicionar 3 parcelas iguais a 5.
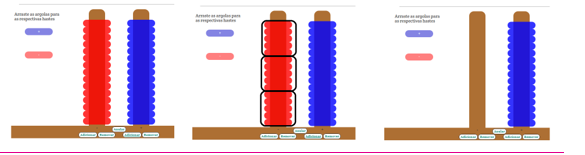 Figura 8
Foto da tela do Objeto Digital de
Aprendizagem Ábaco dos inteiros
Elaborado pelas Autoras
Figura 8
Foto da tela do Objeto Digital de
Aprendizagem Ábaco dos inteiros
Elaborado pelas Autoras
A condução com a utilização do ábaco que acabamos de descrever oportuniza aos estudantes a descoberta das “regras dos sinais” apresentadas em (*), (**) e (***) que, por sua vez, foram motivadas pela ideia de manter a determinada regularidade descrita nas Figuras 5 e 6. Assim, o professor que fez uso do ábaco para deduzi-las também pode utilizá-las para abordar a comutatividade da multiplicação, da mesma forma que a apresentada anteriormente, ou seja, a partir das propriedades (*), (**) e (***).
A multiplicação e a comutatividade no universo dos números racionais
positivos
Druck (2006), ao tratar de dificuldades conceituais relacionadas às ideias de fração, de relação de equivalência, bem como das operações fundamentais no universo das frações, ressalta que, na ampliação da operação de multiplicação, dificuldades conceituais importantes se apresentam, e alguns significados que os alunos trazem do universo dos naturais, já não farão mais sentido no novo universo numérico. “Seria absurdo perguntar, por exemplo, qual é o valor da soma de consigo próprio de vezes. [...] Ou seja, o produto como soma de parcelas iguais ou como número de combinações entre elementos de dois conjuntos perde tipicamente o sentido no campo das frações” (DRUCK, 2006, p. 9) nos casos em que ambos os termos são frações e quando o fator é um número fracionário ou. Assim, antes de focar-se no algoritmo, deve-se dar sentido às operações de multiplicação de frações.
Com relação à operação de multiplicação de frações, nos PCN (BRASIL, 1998) é recomendado que ela seja pensada como parte de partes de um total, e é destacada a necessidade da ruptura da ideia de que a multiplicação é a adição de parcelas iguais. Não apenas defendemos esta ideia como a reiteramos: a ampliação da operação de multiplicação para o conjunto das frações deve ser definida, para e frações quaisquer, como
de ,
de modo que é essencial que o estudante construa, anteriormente a esta definição, uma estratégia que lhe permita calcular, por exemplo, “ de”.
Sobre a propriedade comutativa da multiplicação de frações, Fischer ressalta que,
em situações concretas, não é natural aplicar a propriedade comutativa,
por exemplo, tomar o dobro de meia maçã, não é a mesma ação que tomar metade de
duas maçãs, apenas o resultado é o mesmo. A discussão sobre a validade das
propriedades (ou da ampliação das propriedades) das operações deve, sim, na
nossa opinião, ser oportunizada nos livros didáticos e nas salas de aula.
(FISCHER, 2020, p. 86).
A pesquisa desenvolvida por Fischer (2020) abordou a ampliação da multiplicação de naturais para o caso natural x fração ancorando-se no significado de “o dobro de”: assim como 2 5 significa o dobro de 5, ou seja, 5 + 5, o produto significa o dobro de , ou seja . Relata que este caso foi aceito com naturalidade pelos estudantes de 6º ano pesquisados.
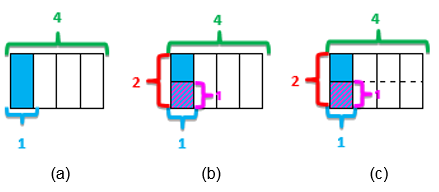
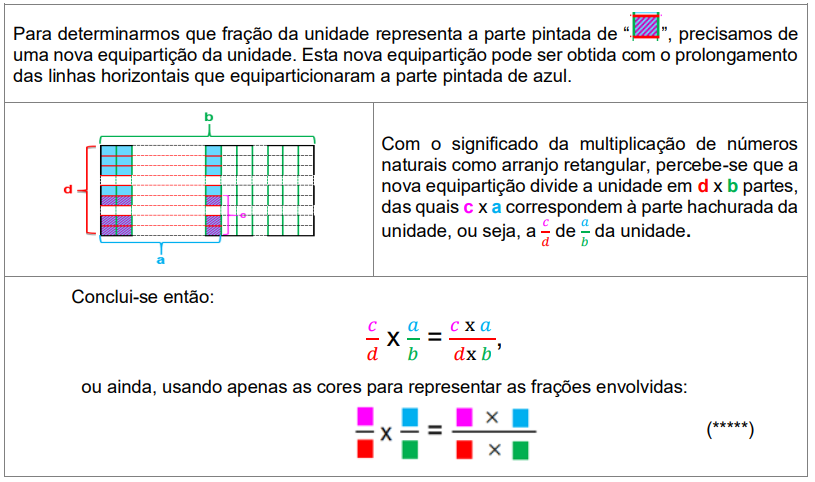
Já o caso “fração x” foi precedido por diversas atividades que, com o auxílio de material concreto, exploraram “fração de” e que tiveram como objetivo que os estudantes construíssem uma estratégia para determinar fração de uma grandeza discreta e fração de uma grandeza contínua. Esta etapa de exploração do significado de “fração de” oportunizou que os estudantes percebessem que a unidade também pode ser uma fração. A Figura 9 ilustra a estratégia utilizada para determinar de de uma grandeza contínua: em (a) marca-se da unidade, pintando-a de azul; em (b) o estudante deve concentrar-se na parte pintada de azul, sendo levado a considerar como uma nova unidade e da qual precisa determinar a metade, pintando-a de rosa; em (c) o estudante deve determinar que fração da unidade original, afinal, é a parte pintada de rosa, sendo então levado a construir uma nova equipartição da unidade original.
Nesse processo, a autora ressalta que o uso de uma unidade retangular com linhas paralelas aos lados do retângulo (de agora em diante referidas por horizontais e verticais), bem como o uso de diferentes cores ajudam não só na percepção de que a nova equipartição da unidade contará com 4 x 2 partes como também na generalização do processo para frações quaisquer, quando o estudante poderá perceber que o numerador do produto é proveniente do produto dos numeradores dos fatores e o denominador do produto é proveniente do produto dos denominadores dos fatores.
O próximo passo consiste da definição da multiplicação “fração x“ como “fração de”; Fischer (2020) apoiou-se novamente na multiplicação de números naturais: assim como “2
x“ é sinônimo de “o dobro de”, define-se “ “como “ de“, por exemplo:
(****)
(****) Importar tabla
Assim, a definição (****) “não só pode ser motivada no conhecimento que o estudante traz do universo dos números naturais como pode apoiar-se na representação pictórica, ambas ajudando a deduzir o algoritmo usual para a multiplicação de frações” (FISCHER, 2020, p. 253). Fischer relata que
os alunos aceitaram bem
a motivação da ampliação da multiplicação de naturais para todos os outros
casos envolvidos na multiplicação de frações (natural x fração, fração x natural, fração x fração); foram
capazes de aplicar a definição da multiplicação em vários momentos,
reconhecendo que a expressão “de” está diretamente ligada (por meio da
definição) à operação de multiplicação. (FISCHER, 2020, p.
254).
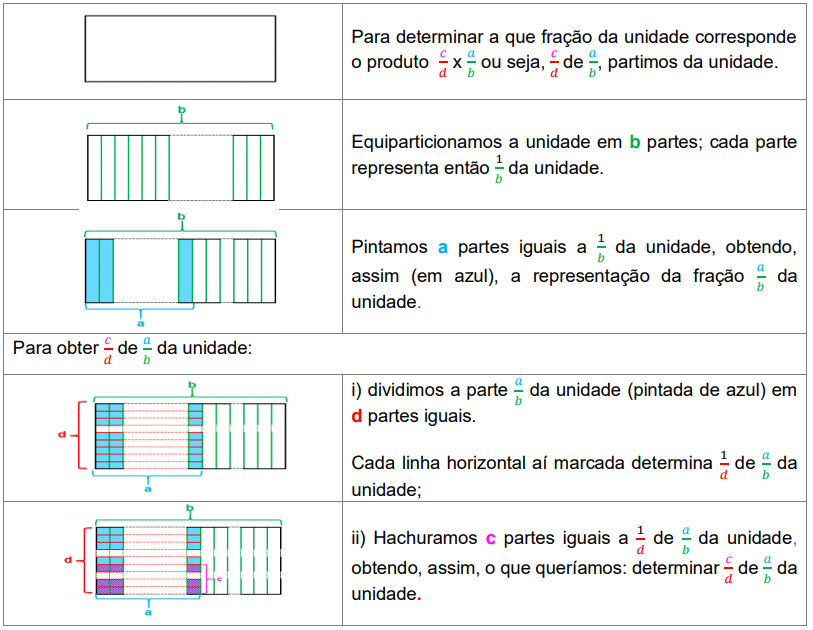
Os Quadros 2 e 3 trazem uma sugestão ao
professor de como encaminhar a obtenção do algoritmo usual da multiplicação de
frações para o caso de fração própria x fração própria, apontando que, para os
estudantes, o uso de cores pode substituir o uso de letras e que é recomendável
começar a discussão com casos particulares.
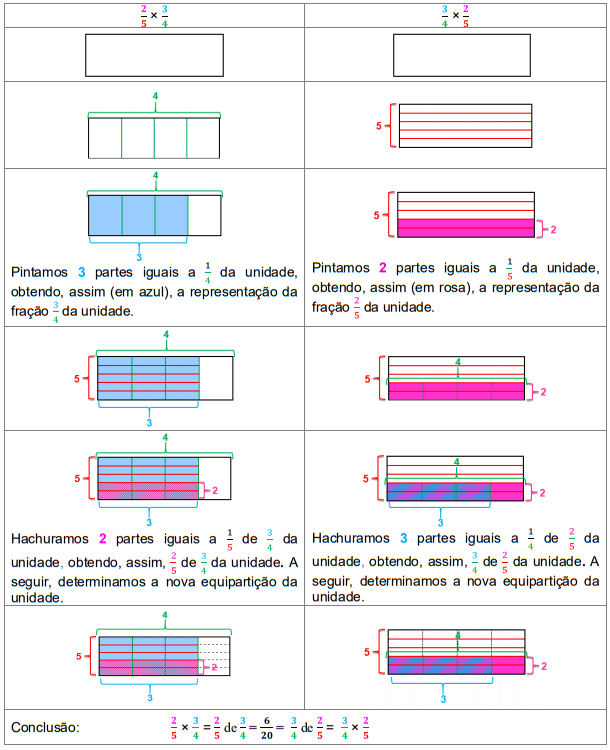
No Quadro 4 é sugerida uma abordagem para explorar a propriedade comutativa da multiplicação de frações, baseada no encaminhamento sugerido nos Quadros 2 e 3: na primeira coluna determina-se de , enquanto na segunda coluna calcula-se de .
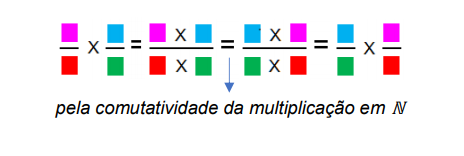
A generalização do argumento apresentado para frações quaisquer (começando por frações próprias) pode ser amparada pelas cores, não sem antes o estudante perceber a necessidade de fazer uso da comutatividade da multiplicação de números naturais:
Outra alternativa que pode ocorrer aos
estudantes é fazer uso do algoritmo já deduzido em (*****) e que também utiliza
a comutatividade da multiplicação de números naturais:
Quadro 4
Explorando a propriedade comutativa da multiplicação em um caso particular
 Elaborado pelas Autoras
Elaborado pelas Autoras
Encerramos esta seção ressaltando que a
relevância da discussão em questão recai sobre a multiplicação de números
positivos, sejam eles racionais ou reais (abordados na próxima seção), uma vez
que multiplicação envolvendo números negativos é uma ampliação das regras de
sinais (*), (**) e (***) estabelecidas para números inteiros.
A multiplicação e a comutatividade no universo
dos números reais positivos
Como no universo dos números inteiros, antes de discutir-se a ampliação da multiplicação de números reais e a propriedade comutativa, é preciso deixar claro o conceito de número real. Em Ripoll, Ripoll e Silveira (2011), introduz-se o conceito de número real absoluto (que, posteriormente, corresponde ao de número real positivo) como sendo o número que expressa a medida de algum segmento de reta. Para representá-lo, faz-se uso do sistema decimal; assim, escrevemos
x= m,a1 a2 a3....
sendo m um número natural (também representado no sistema decimal) e a1, a2, a3 e, mais geralmente, ai para cada i Є ℕ, um número natural do conjunto {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} e que passamos a denominar algarismo. Com tal representação e apoiando-se nos números racionais (positivos, agora representados também no sistema decimal), consegue-se esclarecer a quantidade representada pelo número x, a saber, se x= m,a1 a2 a3...., então
m ≤ x ≤ m+1,
mas também
e assim sucessivamente, obtendo, a cada etapa, uma maior precisão. Assim, por exemplo, dizer que x é um número da forma x= 2,3597... implica
e nada mais podemos afirmar.
Cabe ressaltar que, no sistema decimal, a
representação para um número real (e também de infinitos números racionais)
pode envolver infinitos algarismos não nulos, de modo que, na grande parte das
vezes, trabalha-se com aproximações racionais para esse número; neste
caso, a precisão é estabelecida a partir do número de casas decimais que
se quer considerar, daí a importância das desigualdades em (*). As operações elementares com números reais
positivos são definidas também se fazendo uso dessas desigualdades, que ajudam
ainda a obter a representação decimal do produto:
pela
comutatividade da multiplicação em ℕ
Definição (multiplicação de reais positivos): Dados x e y números reais posi- tivos, com expansões decimais x = m,a1a2... e y = M,b1b2..., definimos, para cada n ≥ 1, os números racionais
xn= m,a1a2...an e yn= M,b1b2...bn .
A multiplicação dos números reais positivos x e y produz um resultado chamado produto, o qual é denotado por x ● y ou simplesmente xy, e é definido como sendo o único número real comum a todos os elementos da sequência de intervalos
(RIPOLL; RIPOLL; SILVEIRA, 2011, p. 278).
Por
exemplo, se multiplicarmos os números reais positivos a e b, sabendo que a e b são da forma a = 1,414414414... e b =
3,010010001..., aplicando a definição, podemos afirmar que
1 ≤ a ≤ 2 e 3 ≤ b ≤ 4 → 1 x 3 ≤ ab ≤ 2 x 4 , ou seja, ab Є [3 ; 8],
mas também
1,4 ≤ a ≤ 1,5 e 3,0 ≤ b ≤ 3,1 → 1,4 x 3 ≤ ab ≤ 1,5 x 3,1, ou seja, ab Є [4,2 ; 4,65],
[4,2 ;
4,65],
o que já
nos permite afirmar que ab é da forma
ab = 4,... .
Podemos observar que uma maior precisão depende do número de casas de precisão consideradas para cada um dos fatores:
1,41 ≤ a ≤ 1,42 e 3,01 ≤ b ≤ 3,02 → 1,41 x 3,01 ≤ ab ≤ 1,42 x 3,02, ou seja,
ab Є [4,2441; 4,2884], o que já nos permite afirmar que ab é da forma
ab = 4,2...;
ainda, 1,414 ≤ a ≤ 1,415 e 3,010 ≤ b ≤ 3,011→ 1,414 x 3,010 ≤ ab ≤ 1,415 x 3,011,
ou seja, ab Є [4,24614; 4,26057]; e também
1,4141 ≤ a ≤ 1,4142 e 3,0100 ≤ b ≤ 3,0101→ 1,4141 x 3,0100 ≤ ab ≤ 1,4142 x 3,0101,
ou seja, ab Є [4,25644 ; 4,25688], o que já nos permite afirmar que ab é da forma
ab = 4,25....
Observando a Definição de multiplicação de reais
positivos, vemos que o produto xy (ou ab do Exemplo anterior) é sempre cercado por um
produto de números racionais; também é possível constatar que os racionais
envolvidos nesta cercania serão os mesmos, tanto para calcular o produto xy como o produto yx (ou o produto ab como o produto ba no exemplo
mencionado). Sugerindo-se aos estudantes dos anos finais do Ensino Fundamental
calcularem os produtos ab
e ba,
acredita-se que perceberão que, como a multiplicação de números racionais é
comutativa, os números racionais que limitam, a cada etapa, os produtos ab e ba são os
mesmos números racionais, portanto ab = ba. Com mais alguns exemplos, se necessário,
acredita-se que estudantes dos anos finais do Ensino Fundamental e estudantes
do Ensino Médio não terão dificuldade em generalizar sua conclusão para a
multiplicação de dois quaisquer números reais positivos.
A multiplicação e a comutatividade no universo dos números complexos
A definição “um número complexo é uma expressão
da forma a+bi, sendo a, b Є IR e i chamada unidade imaginária” é abstrata, sendo por isso tratada
só no Ensino Médio. A multiplicação de dois números complexos a+bi e c+di, (sendo a, b, c, d Є IR) é
definida por
(a+bi) x (c+di) = (ac – bd) + (ad+bc)i,
e, a partir dela, percebe-se que i2 = (0+1i)2 = -1 (esta na verdade é a motivação para a definição de número complexo); percebe-se também que
(c+di) x (a+bi) = (ca – db) + (cb + da)i.
Como a adição e a multiplicação de números reais são comutativas, tem-se
ca – db = ac – bd, bem como cb + da = ad+bc
e
daí percebe-se a comutatividade da multiplicação também de números complexos:
(a+bi) x (c+di) = (ac – bd) + (ad+bc)I = (ca – db) + (cb + da)i = (c+di) x (a+bi).
(a+bi).
Após ser convidado a calcular alguns produtos, acredita-se que um estudante do Ensino Médio, que já deve estar mais familiarizado com a linguagem simbólica, não deverá ter dificuldades em ele mesmo construir este argumento para demonstrar a comutatividade da multiplicação de números complexos.
Considerações Finais
Neste artigo, procurou-se trazer uma reflexão das autoras sobre a ampliação da operação de multiplicação e a propriedade comutativa da multiplicação ao longo da Educação Básica, à luz do Conhecimento Pedagógico de Conteúdo e do Conhecimento Matemático para o Ensino. Diferentemente da adição, a discussão da comutatividade da multiplicação de números naturais é essencial para que seja viável, por exemplo, chamar-se ambos os termos da multiplicação (multiplicando e multiplicador) de fatores. E, a partir da ampliação com significado para a escola básica da multiplicação em cada universo numérico, ficou evidenciada a necessidade de discutir-se a validade da propriedade comutativa. Assim, refletindo sobre os novos números do universo numérico, fica claro que, na escola básica, em nenhum universo numérico pode a propriedade comutativa da multiplicação ser inferida sem uma discussão sobre sua validade.
É imprescindível, na opinião das autoras, que uma atenção especial seja dada às propriedades das operações, para que os estudantes possam, por exemplo, já desde os anos iniciais, melhor compreender por que valem os algoritmos operatórios e até criar estratégias pessoais de cálculo.
Após discutir-se a ampliação da multiplicação em cada universo numérico maior do que o dos números naturais, foram sugeridas algumas abordagens para a sala de aula, bem como abordagens que buscam fazer com que os estudantes reflitam a respeito da propriedade comutativa em cada novo universo numérico, ficando evidenciada uma diversidade imposta pelos diferentes universos numéricos. Reconhecemos que, no entanto, a validação de uma proposta didática só ganha força se, em algum momento for implementada. Assim, espera-se, com este trabalho, contribuir com a reflexão sobre o ensino que todo professor deve manter presente, reiterando assim a importância do Conhecimento Matemático para o Ensino (BALL, 2008; SHULMAN, 1986; 1987).