Introdução

Este escrito faz parte de um recorte parcial de uma dissertação de mestrado, realizada no Instituto Federal de Educação, Ciência e Tecnologia do Estado do Ceará (IFCE). Neste trabalho, tratamos sobre as Olimpíadas de Matemática, em específico a Olimpíada Brasileira de Matemática de Escolas Públicas e privadas (OBMEP), que vem se destacando no cenário nacional desde 2005, ano de sua criação, estimulando o ensino e a aprendizagem da matemática e a descoberta de talentos na área (OBMEP, 2020).

Realizamos um estudo sobre o tema da pesquisa, ao que diz respeito ao uso dos problemas de olímpiadas em sala aula e quanto às dificuldades que impedem a inserção de um número mais elevado de alunos e professores a vivenciar os aspectos culturais das competições. Este estudo foi apoiado pela etapa de Análises preliminares da Engenharia Didática (ED) e, relacionado a esse estudo, observamos, em alguns artigos, a ênfase em relação à qualidade dos problemas que são abordados em provas de competições, apresentados de forma desafiadora e atrativa. Conforme Theodorovski e Oliveira (2020, p. 227), sobre a OBMEP:

É uma avaliação externa que abrange as escolas do país e ofertada a todos os alunos de uma rede de ensino que tem como seu foco a aprendizagem em matemática. E tem conseguido isso por apresentarem situações contextualizadas que requerem raciocínio lógico, estratégias de resolução, autonomia e criatividade. Contrapondo o modelo tradicional de ensino que a tempo domina as salas de aula que é o de retransmitir problemas e soluções padronizadas apresentados em livros didáticos.

Essas características, presentes nas questões, estimulam o aluno a interagir com o propósito de resolvê-las devido à maneira desafiadora como se apresentam e pela diversidade de formas de resolução.

Porém, diante de todas essas qualidades, esses problemas não são acessíveis a toda a comunidade escolar (estudantes), até pelo grau de formalidade e raciocínio que é utilizado em sua resolução, o que exclui e afasta uma maioria de estudantes que apresentam dificuldade na disciplina de matemática. De acordo com Araújo e Monsores (2017, p. 3) sobre essa exclusão, destaca que

pode-se argumentar, por exemplo, que a competição é excludente para boa parte dos alunos, e não motivadora. Ou que as habilidades avaliadas nas competições não são relevantes para o aluno médio, que não pretenda seguir carreira na área de ciências exatas.

Essa exclusão, citada anteriormente, não se restringe apenas a estudantes, mas também se amplia às dificuldades que os professores de matemática têm em relação à resolução e à aplicação desses problemas em sala de aula. Segundo Azevedo (2020, p. 16) sobre essas dificuldades diz que

são notórias as dificuldades enfrentadas por alguns professores de matemática quando a situação é resolver problemas de Olimpíadas, pois exige maior investimento profissional, ou seja, mais estudo e formação aprofundada nos conteúdos matemáticos. O professor precisa conhecer e trabalhar com materiais além do livro didático, passar por momentos/formações onde aconteçam discussão e análise de estratégias de ensino.

Quanto a isso, existe uma necessidade, para os professores, de metodologias de ensino que possibilitem essa adaptação dos problemas contidos em avaliações da OBMEP (por meio de jogos, softwares dinâmicos, resoluções de problemas) para que seja possível submeter os estudantes a esses modelos de questões em sala de aula. E, com essa possibilidade de adaptação, não distanciar de seu planejamento esse material de qualidade que apresenta uma diversidade de possibilidades que os levam à solução. Em relação a essa diversidade, a BNCC (2019, p. 519) destaca que:

Os estudantes devem desenvolver habilidades relativas aos processos de investigação, de construção de modelos e de resolução de problemas. Para tanto, eles devem mobilizar seu modo próprio de raciocinar, representar, argumentar, comunicar e, com base em discussões e validações conjuntas, aprender conceitos e desenvolver representações e procedimentos cada vez mais sofisticados.

Frente a isso, abordamos nesta investigação a Teoria das Situações Didáticas — TSD, desenvolvida por Guy Brousseau (1986), a qual, de acordo com Ferreira (2016, p. 57), tem “o objetivo de modelar o conhecimento matemático de modo que este seja acessível ao aluno e que lhe permita alcançar uma aprendizagem significativa”. Essa teoria de ensino possibilita que o discente percorra o caminho de um matemático, agindo, formulando e validando conjecturas, durante a resolução de um problema (ALMOULOUD, 2007).

Com base na Teoria das Situações Didáticas (TSD), buscamos modelar os Problemas Olímpicos (PO) (como chamaremos os problemas de olimpíadas de matemática), com o objetivo de dar oportunidades aos discentes para a construção do conhecimento/saber matemático. Essa modelagem será representada pela expressão: SDO = PO + TSD, em que os Problemas Olímpicos (PO) (problemas retirados de provas de competições, que se direcionam de maneira restrititiva a alunos e cujo objetivo é a obtenção de medalhas), modelados pela Teoria das Situações Didáticas (TSD), façam emergir as etapas de ação, formulação, validação e institucionalização. Essa modelização é denominada de Situações Didáticas Olímpicas (ALVES, 2019; 2020). No referido artigo, trouxemos uma SDO que tem como conteúdo a geometria plana, o qual possibilita o uso do software GeoGebra, ferramenta utilizada na trasposição didática ou adaptação para a sala de aula.

Diante desse contexto, nosso objetivo foi apresentar dados parciais de uma investigação que trata do uso de Situações Didáticas Olímpicas (SDO) para o ensino de geometria plana. Na trasposição didática dos Problemas Olímpicos (PO), utilizamos o software GeoGebra na disponibilização de subsídios (controles deslizantes, caixa de exibir/ esconder objetos), na visualização e movimentação das figuras para o discente durante a resolução da SDO (SILVA; ALVES; MENEZES, 2020).

Estruturamos o referido estudo com aporte à Engenharia Didática de Formação (EDF), que tem como base as etapas da metodologia de pesquisa Engenharia Didática (ED) (Análises Preliminares, Análise a priori e Concepção das situações didáticas, Experimentação e Análise a posteriori e validação), mas com o objetivo na formação de professores e desenvolvimento de recursos para o ensino de matemática (PERRIN-GLORIAN; BELLEMAIN, 2019).

Utilizamos a metodologia EDF em consonância com a Teoria das Situações Didáticas (TSD), que serviu para a organização da sequência didática e para o critério de análise dos dados obtidos no experimento (VIEIRA; MANGUEIRA; ALVES; CATARINO, 2021), o qual ocorreu com 6 (seis) estudantes do curso de Licenciatura em Matemática na Universidade Estadual Vale do Acaraú (UVA), pela plataforma Google Meet, por intermédio do Ensino Remoto.

Teoria das Situações Didáticas e as Situações Didáticas Olímpicas

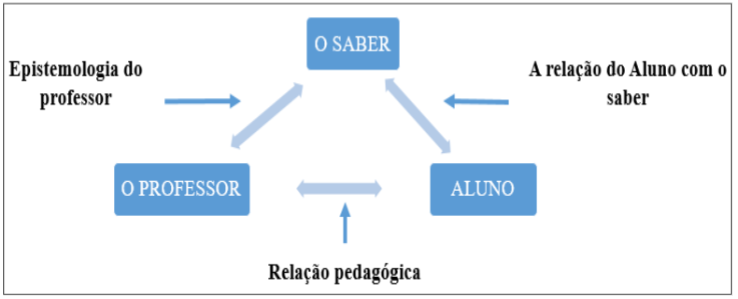
Com o propósito de utilizar esses problemas da OBMEP para a criação de um modelo de ensino, baseamo-nos na TSD desenvolvida na França por Guy Brousseau (1986), que possibilita a construção de um modelo que busca “verificar situações que visam o conhecimento e as relações existentes entre a tríade de ensino (professor-aluno-saber)” (VIEIRA et al., 2021, p. 7). O objetivo dessa teoria se consubstancia na situação didática, na qual necessariamente deve ocorrer a interação que se baseia no triângulo didático composto por professor, aluno e saber (Figura 1), a partir de um meio criado e planejado pelo professor.

Figura 1
Triângulo Didático
Almouloud (2007, p.35)

Sobre a perspectiva de Almouloud (2007, p. 32), a TSD se baseia em três hipóteses:

i. O aluno aprende adaptando-se a um milieu que é fator de dificuldades, de contradições, de desequilíbrio[...]. Esse saber, fruto da adaptação dos alunos, manifesta-se pelas respostas novas, que são a prova da aprendizagem. ii. [...]. O professor deve criar e organizar um milieu que seja suficiente para desenvolver situações suscetíveis de provocar essas aprendizagens. iii. A terceira hipótese postula que esse milieu e essas situações devem engajar os conhecimentos matemáticos envolvidos durante o processo de ensino e aprendizagem.

Sendo assim, o professor deve basear-se nessas hipóteses para a construção de uma situação didática, o que Brousseau, Brousseau e Warfield (2014) chama de categorias, e para que, dentro desta, o estudante consiga vivenciar três subcategorias necessárias para a genêse do conhecimento sobre o conceito matemático, são elas: Situação de Ação, Formulação e Validação. Em relação a essas três subcategorias, Vieira et al., (2021, p. 7-8) destaca que elas devem ocorrerem da seguinte maneira:

Na fase de ação, o aluno pode refletir e explorar seus conhecimentos prévios, com o intuito de escolher um procedimento para realizar a resolução do problema. Na fase de formulação, o aluno já apresenta uma estratégia de solução, seja ela escrita ou oral, na qual o aluno utiliza um raciocínio de natureza mais teórico e vai transformar essa estratégia em uma linguagem mais adequada, com o intuito de realizar conjecturas do objeto estudado. Na etapa de validação os estudantes irão utilizar as demonstrações e provas matemáticas com o intuito de convencer a veracidade das afirmações encontradas.

Em relação às três subcategorias, Almouloud (2007, p. 34) denomina como situações adidáticas uma “situação na qual a intenção de ensinar não é revelada ao aprendiz, mas foi imaginada, planejada e construída pelo professor para proporcionar a estes condições favoráveis para a apropriação do novo saber” ou seja, o professor acompanha, com a mímina interferência, deixando os sujeitos (no caso os discentes) criarem suas conjeturas de forma autônoma ou em grupo, sem participação efetiva, e agindo apenas como mediador do conhecimento matemático.

Na quarta etapa da TSD, a institucionalização, é o momento da participação efetiva do professor, para consolidar o aprendizado ou corrigir determinados entraves que os sujeitos obtiveram nas etapas anteriores, segundo Vieira et al., (2021, p. 8) “o docente retoma a situação-problema com a intenção de identificar, sistematizar e reconhecer o saber construído e, é nessa fase que a intenção do professor é revelada e todo procedimento matemático é verificado”.

Portanto, podemos observar, com base nos parágrafos anteriores, o constructo do conhecimento/saber em que um sujeito perpassa seguindo as etapas de ação, formulação, validação e institucionalização da TSD. Por isso, pretendemos direcionar esta proposta aos professores de matemática, quanto ao uso de Problemas Olímpicos (PO) modelados pela Teoria das Situações Didáticas (TSD) para o ensino de conceitos de geometria plana em sala de aula, proporcionando a responsabilidade da construção do conhecimento/saber para o estudante.

Essa modelização que trata do uso dos Problemas Olímpicos (PO) e a Teoria das Situações Didáticas (TSD) é denominada por Santos e Alves (2017, p. 285) como

Um conjunto de relações estabelecidas implicitamente ou explicitamente, entre um aluno ou grupo de alunos, um certo meio (compreendendo ainda o conhecimento matemático abordado por intermédio de problemas de competição e de olimpíadas) e um sistema educativo, com o objetivo de permitir a apropriação, por parte destes alunos de um conhecimento constituído ou em vias de constituição, oriundo de um ambiente de competição.

Essa proposta parte do interesse da utilização das Situações Didáticas Olímpicas (SDO) para o ensino de conceitos matemáticos de um determinado conteúdo (nesse caso a geometria plana), como também uma metodologia de ensino que venha a se diferir dos modelos tradicionais — a qual coloca o aluno como construtor do conhecimento/saber, fazendo com que ele possa agir, formular conjecturas e validá-las com autonomia, com a mínima participação do professor, que age apenas como mediador do conhecimento (SILVA; ALVES; MENEZES, 2020).

Metodologia

Utilizamos a EDF como percurso metodológico da referida pesquisa que tem como foco a formação de professores, inicial ou continuada (PERRIN-GLORIAN; BELLEMAIN, 2019). Essa tendência surge na Didática da Matemática por volta da década de 90 e é baseada na Engenharia Didática clássica (ARTIGUE, 1995), mas com direcionamento à formação de professores e à produção de recursos para o ensino de matemática.

A noção de Engenharia Didática emergiu na Didática da Matemática (enfoque da didática francesa) no início dos anos 80. Segundo Artigue (1988), é uma forma de trabalho didático comparável ao trabalho do engenheiro que, para realizar um projeto, se apoia em conhecimentos científicos de seu domínio, aceita se submeter a um controle de tipo científico, mas ao mesmo tempo, é obrigado a trabalhar objetos mais complexos que os objetos depurados da ciência. (ALMOULOUD; COUTINHO, 2008, p. 65).

Essa metodologia também se caracteriza por ser realizada por meio de experimento baseado em sessões didáticas em sala de aula, assim, ela nos permite a concepção, a realização, a observação e a análise. Além disso, tem como um diferencial a forma interna de validação que se apoia no confronto entre análise a priori e análise a posteriori, abordada neste trabalho.

A Engenharia Didática clássica limita-se ao estudo da situação didática sem levar em conta o papel do professor de matemática, tendo como propósito “a elaboração e o estudo de uma proposta de uma transposição didática para o ensino, sendo essa transposição didática o objetivo principal da pesquisa” (ALMOULOUD; SILVA, 2012, p. 27).

Ao que diz respeito à Engenharia Didática de Formação (EDF), esta “tem por primeiro objetivo o desenvolvimento de recursos (ou objeto de aprendizagem) para o ensino regular, ou a formação de professores” (ALMOULOUD; SILVA, 2012, p. 28). O desenvolvimento desses recursos para o ensino necessita da participação dos professores em um ambiente de análise e adaptações para a realidade da sua sala de aula “o que consequentemente, necessita de vários níveis de construção” (ALMOULOUD; SILVA, 2012, p. 28).

Nesse caso, aplicamos com licenciandos em formação, por intermédio da Situações Didáticas Olímpicas (SDO), para que os sujeitos possam replicá-los em seu ambiente escolar em atuação como docente. Assim, a escolha do público-alvo (licenciandos e orientadores do PIC) perpassou pela escolha da EDF, que segundo Lima e Neves (2019, p. 704), “possui um status de “objeto” a ser estudado e reconstruído a partir de sua realidade”.

Apresentamos o percurso baseado em uma Engenharia Didática de Formação (EDF) de acordo com Tempier e Chambris (2017), a qual estrutura a referida investigação (Figura 2).

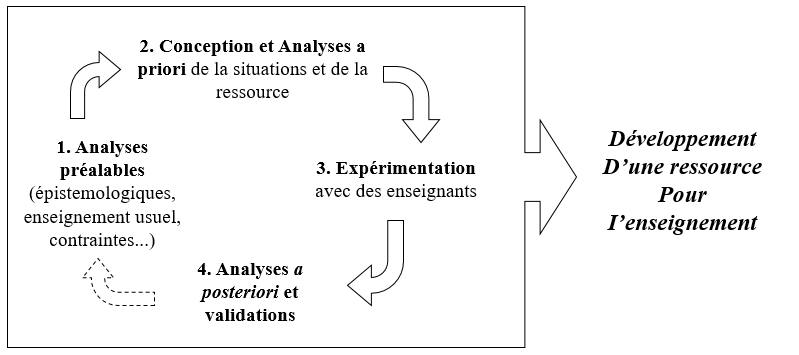Figura 2
Estrutura do percurso realizado pela Metodologia EDF
Engenharia Didática de Formação proposto por Tempier e Chambris (2017).

Esse percurso realizado pela metodologia EDF nos permite vivenciar três fases necessárias quando se trata do ofício do professor de matemática, são elas: “a preparação/concepção, a realização de uma mediação em sala de aula, e a correspondente avaliação das etapas predecessoras, tanto em seu conjunto, de modo individual (e local) ” (ALVES; CATARINO, 2017, p. 122). Essas fases são características necessárias para a capacitação do docente e para o seu desenvolvimento em qualquer ambiente escolar.

Sendo assim, a Investigação seguiu o respectivo percurso: na etapa de Análises preliminares, realizamos um estudo baseado no objeto de estudo (OBMEP) no que diz respeito aos problemas recorrentes no uso dos problemas de olimpíadas em sala de aula, observando as dificuldades que professores e alunos enfrentam quando se deparam com esse tipo de questão. Observamos também a pouca adesão em relação a programas de formação direcionados à preparação de professores que ensinam matemática por meio dos problemas de olímpíadas. O estudo foi realizado por meio de uma busca em artigos e dissertações que tratam sobre o tema olimpíadas de matemática, como: Araújo e Monsores (2017), Santos e Alves (2017), Santos (2018), Alves (2019; 2020), Theodorosvski e Oliveira (2020), Azevedo (2020), entre outros.

Na Análise a priori e concepção da situação didática, foi elaborado e planejado um conjunto de situações didáticas, a partir de PO retirados das provas da OBMEP que abordam conceitos de geometria plana. As situações didáticas seguem os pressupostos da TSD, além disso, todas as questões foram adaptadas com o auxílio do software GeoGebra, que também foi utilizado como objeto para a construção e modificação do comportamento dos professores em formação inicial durante a resolução dos problemas. No entanto, neste artigo apresentamos apenas uma Situação Didática Olímpica (SDO).

A etapa de Experimentação foi aplicada em um grupo de estudos composto por licenciandos do curso de Matemática da Universidade Estadual Vale do Acaraú (UVA), localizada na Cidade de Sobral – CE, e que participavam do Programa de Iniciação Científica - PIC^[1] como professores orientadores. Cada aula teve duração de 90 minutos, as coletas de dados foram registradas por áudios, registros fotográficos, cálculos realizados pelos discentes, além das observações obtidas, sendo que, as aulas foram realizadas pela plataforma Google Meet e os dados analisados com base nas categorias que representam as etapas da TSD.

Na Análise a posteriori e Validação (interna), foram realizadas as análises dos dados, confrontando-os com a Análise a priori com o propósito de atingir os objetivos e hipóteses elencados neste trabalho, além disso verificar a adequabilidade dos Problemas Olímpicos (PO) resolvidos pelos professores e sua análise quanto à utilização em sala de aula.

Nessa perspectiva, a nossa investigação perpassou por essas etapas, afinal, preparamos um ambiente que envolve problemas de olimpíadas, integrando ao uso do software GeoGebra com o propósito de apresentar ao docente uma metodologia que agregue na sua sala de aula. Essa metodologia vivenciada por esses docentes ou futuros docentes contribui em sua formação, conforme Perrin-Glorian e Bellemain (2016, p. 38) “para que os trabalhos possam contribuir para o melhoramento do ensino e para a formação de professores, se mostra imprescindível a consideração do real funcionamento da sala de aula e das necessidades dos professores”.

Essa experiência obtida parte da ideia de Cardim e Grando (2011) quanto à evolução das discussões sobre o

“saber como fazer” (paradigma processo-produto), considerando a dimensão “do onde”, “para quem”, “em que circunstância” e principalmente “para que” (paradigma do pensamento do professor), focando não apenas o resultado que advém do processo educativo, o seu produto, mas de como este tem potencialidade para estruturar ideias e conceitos, levando a se pensar tanto nos objetos de ensino, quanto em sua utilidade na vida cotidiana e intelectual dos alunos, ajudando-os a compreender, explicar e organizar a sua realidade (CARDIM; GRANDO, 2011, p. 6).

Esse conhecimento de todo o contexto da realidade escolar perpassa pelo o modo de investigação que se utiliza em relação à formação do sujeito, metodologia que oferece ao docente esse suporte. Sendo assim, a EDF dispõe dessas características e qualifica o professor quanto à preparação, mediação e a análise das sessões de ensino.

Resultados

O experimento ocorreu com 6 (seis) estudantes, identificados por L2 a L7, de licenciatura do curso de Matemática da Universidade Estadual Vale do Acaraú (UVA), pela plataforma Google Meet devido à paralização das instituições de ensino superior em razão da pandemia de Covid-19. Vale lembrar que a experimentação “é o momento no qual as atividades elaboradas são desenvolvidas em sala de aula com os alunos” (LIMA; NEVES, 2019, p. 699).

O critério de escolha dos sujeitos partiu de um contato com uma professora da Universidade Estadual Vale do Acaraú (UVA), coordenadora do Programa de Iniciação Científica - PIC Jr, que realizava um curso de formação direcionada a discentes de licenciatura do curso de Matemática da Universidade com foco em medalhistas da OBMEP. Esses estudantes, além de alunos do curso de Matemática, também faziam parte do grupo de professores orientadores do PIC Jr. Em um total de 9 alunos, apenas 6 participaram da pesquisa por livre e espontânea vontade. A seguir, apresentamos o Problema Olímpico proposto.

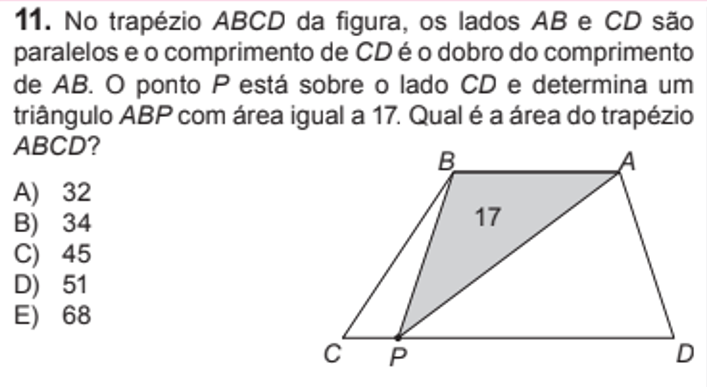Figura 3
Problema Olímpico (PO) retirado da prova da OBMEP 2016, nível 2.
OBMEP (2020)

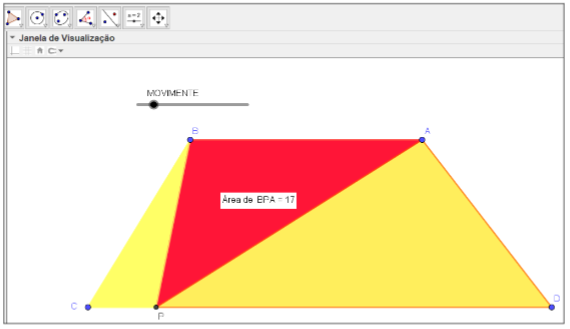
O problema Olímpico (PO) apresentado (Figura 3) foi abordado na prova do ano de 2016, nível 2, direcionado aos alunos do ensino fundamental para as turmas de 8° e 9° ano. Essa questão traz conceitos referentes ao conteúdo de geometria, por exemplo, a área do trapézio, área do triângulo, mas com ênfase na propriedade fundamental da equivalência. Como complemento aos alunos e na transposição didática do PO, usamos o software GeoGebra para dar um maior dinamismo a figura (Figura 4).

Figura 4
Transposição didática do Problema Olímpico para o software GeoGebra.
Elaborada pelos Autores

Ao disponibilizar a construção do problema no software GeoGebra, por intermédio do aplicativo de mensagens WhatsApp em arquivo ggb, os licenciandos tiveram o primeiro contato ao observarem alguns incrementos na figura.

Figura 5
Contato inicial com o problema por intermédio do software GeoGebra.
Acervo da Pesquisa

Ao realizar o primeiro contato, os alunos deram o início à situação de ação, realizando tentativas e apresentando algumas sugestões aos colegas. Essas sugestões iniciais também envolvem um momento de discussão entre os licenciandos — o que caracteriza simultaneamente com a etapa de formulação.

L5: Por analogia, utilizando o controle deslizante, relacionado ao ponto P, e levando-o ao meio da base inferior $\left(\overline{\text{CD}}\right)$ podemos considerar que será formado três triângulos iguais. Desse modo, utilizando a lógica podemos afirmar que a área do trapézio será três vezes a área do triângulo $\Delta \text{ABP}$ (Figura 6). Agora vou procurar um argumento que comprove essa minha analogia.

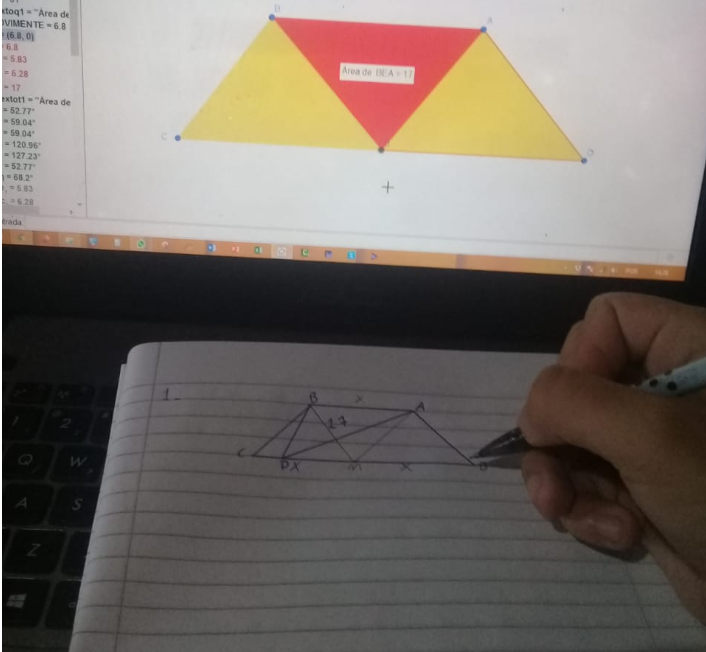Figura 6
Movimentando o controle deslizante levando o ponto P ao meio do segmento
Acervo da Pesquisa

L6: Mas, mesmo se não forem iguais, o valor da área desse trapézio vai ser a soma da área dos três triângulos! Então, tentamos calcular a área desses triângulos e encontraremos a área do trapézio.

L2: L5 você falou que a área do trapézio será três vezes a área do triângulo? No caso, seria 51, é isso? Porque eu fiz aqui deslocando o ponto P perpendicular ao ponto B, considerando esse segmento como a altura do trapézio. Então, fazendo pela área do triângulo, dá para encontrar a altura em função de $\overline{\text{AB}}$ e depois joga na área do trapézio, encontrando o mesmo resultado 51 (Figura 7), mas não sei se o desenvolvimento está correto.

L6: Deslizando o ponto P, verificamos três triângulos aparentemente iguais.

Figura 7
Estratégia utilizada pelo licenciando L2
Acervo da Pesquisa

O professor continuou a indagar, por exemplo, “Por que, ao movimentar o ponto P, a altura não muda?”, “Por que a área permanece a mesma?”. Esses questionamentos estimulavam os participantes a comprovarem a estratégia por meio de uma propriedade matemática ou teorema que o leve à veracidade da proposta.

L5: Vamos lá, levando em consideração que o segmento $\overline{\text{CD}}$ é o dobro do segmento $\overline{\text{AB}}$, se eu trago o ponto P para o meio do segmento $\overline{\text{CD}}$, encontrarei três triângulos de mesma base e, consequentemente, a altura será a mesma. Utilizando a fórmula do triângulo que é $\frac{b·h}{2}$, se a base $b$ e altura $h$ são a mesma, eu acho que área dos três triângulos será a mesma.

Professor: Por que, ao movimentar o ponto P, a altura não muda?

L2: No caso, a altura desse triângulo seria a altura do trapézio, seria não?

L6: Eu não estou lembrando bem do nome, mas não sei se é porque é regular ou coisa assim. Eu sei que, quando a figura está assim, você pode modificar ela (falando em relação à movimentação do ponto P sobre o segmento $\overline{\text{CD}}$ que a área continua a mesma). Acho que já vi em uma disciplina que fiz anteriormente utilizando o GeoGebra.

L4: A altura vai ser um segmento perpendicular, então a distância permanece a mesma. Eu traço um segmento perpendicular em relação ao segmento $\overline{\text{AB}}$ formando um triângulo de 90°, então essa altura não se modifica (Figura 8).

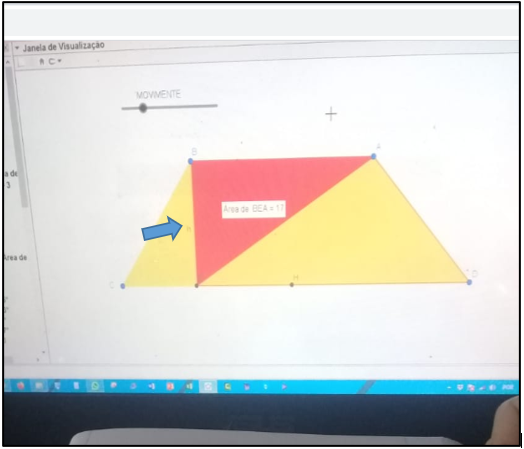Figura 8
Segmento perpendicular ao segmento
Acervo da Pesquisa

As discussões anteriores envolveram a utilização de propriedades e o uso de uma matemática formalizada, aproximando a propriedade que possibilita a movimentação do ponto P sobre o segmento CD. De acordo com Galvez (1996, p. 29), “não basta a comprovação empírica que o dizem que é certo; é preciso explicar, necessariamente, deve ser assim”.

O momento em que esse convencimento acontece caracteriza-se pelo modo de validação da Teoria das Situações Didáticas (TSD), em que “os alunos devem elaborar provas para demonstrá-las” (GALVEZ, 1996, p. 29). Seguindo essa perspectiva, o licenciando L4 valida sua estratégia apresentando-a da seguinte maneira:

L4: Como o segmento $\overline{\text{AB}}$ é paralelo ao segmento $\overline{\text{CD}}$ e a altura é a distância entre os dois segmentos, então independentemente de onde estiver o ponto P a altura vai permanecer a mesma. Podemos afirmar baseando-se no enunciado e por intermédio da movimentação na própria figura (Figura 9)

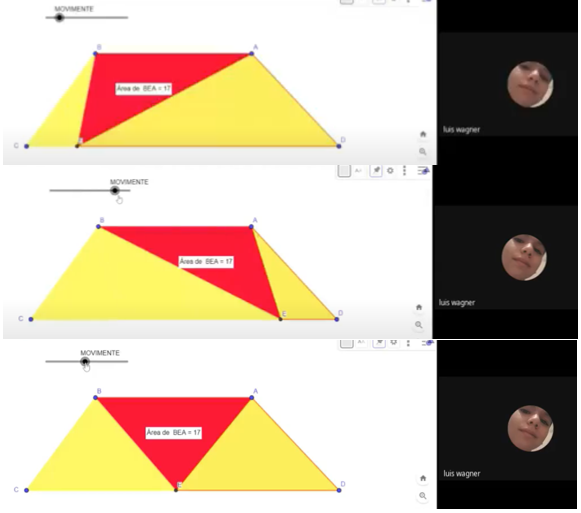Figura 9
Demonstração e validação da propriedade que possibilita a movimentação do ponto P sobre o segmento
Arquivo pessoal.

A figura 9 apresenta a movimentação do controle deslizante que representa o ponto P, demonstrando e validando o que foi dito pelo L4. Então, a partir da movimentação do ponto P, a área do triângulo $\Delta \text{BAE}$ permanece a mesma — o que possibilitou que o licenciando o levasse até o ponto médio do segmento $\overline{\text{CD}}$, construindo três ângulos de mesma área e chegando à solução final, equivalente a 51 unidades de área. Além dessa solução, outra foi apresentada pelo licenciando L2, que chegou ao mesmo resultado (Figura 7).

Na etapa de institucionalização, o professor retoma o seu posto, explicando o objetivo da SDO e consolidando o aprendizado dos licenciandos. Ademais, a SDO perpassou pela apresentação do principal conceito objetivado pelo professor, relacionando à “propriedade fundamental da equivalência”, abordando que a movimentação realizada pelo ponto P foi permitida devido a essa propriedade e, por isso, a área permaneceu a mesma, independentemente da sua localização.

A utilização do software GeoGebra, nesse caso, permitiu que o licenciando explorasse propriedades que não são perceptíveis sem o seu auxílio. Desse modo, o pesquisador previu o alcance da seguinte propriedade matemática:

A propriedade apresentada se refere ao cálculo da área de um triângulo, que pode ser definida da seguinte maneira, conforme Costa et al. (2012, p.121):

Definição: duas figuras são equivalentes quando possuem áreas iguais.

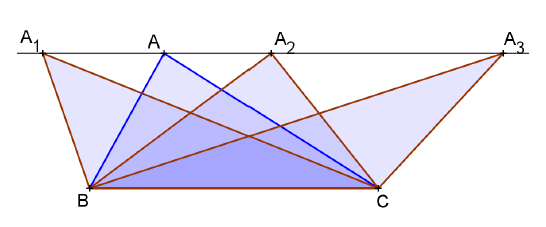
Propriedade fundamental da equivalência:considerar um triângulo ABC. Conduzir pelo vértice A uma reta r paralela ao lado BC. Considerar os pontos A1, A2, A3, ... pertencentes à reta r. Os triângulos de base BC comum e vértices A1, A2, A3, ... são todos equivalentes (Figura 10).

De fato, área ∆ABC = área ∆A₁BC = área ∆A₂BC = ... = $\frac{\text{BC}·h}{2}=\frac{b·h}{2}$, pois não foi alterada a medida da base e nem da altura.

Figura 10
Demonstração geométrica da propriedade fundamental da equivalência
Costa et al., (2012, p. 121)

Portanto, na situação de institucionalização, Almouloud (2007, p. 40) esclarece que “uma vez construído e validado, o novo conhecimento vai fazer parte do patrimônio da classe embora não tenha ainda o estatuto de saber social”.

Conforme observamos nos resultados obtidos conforme as etapas da Teoria das Situações Didáticas (TSD), é possível utilizar os Problemas Olímpicos (PO) para o ensino de conceitos matemáticos, nesse caso da geometria plana, mas perpassam por um trabalho extra do professor de matemática que pretende aplicá-los em sala de aula.

Esse trabalho extra pode ser representado pela escolha do Problema Olímpico (PO), pela preparação para a transposição didática com o objetivo de adequá-los à superação dos obstáculos que o estudante venha a se deparar durante a resolução da SDO. Tudo isso qualifica ainda mais o trabalho do docente.

Isso porque nem todos os Problemas Olímpicos (PO) podem ser considerados Situações Didáticas Olímpicas (PO), ou seja, eles devem seguir alguns critérios como:

i. A partir de uma transposição didática adequada dos problemas olímpicos, permitir o acesso ou inclusão de um conjunto maior de estudantes ao ambiente de discussão ou « clima » de competição matemática, visando a elaboração de conhecimentos; ii. A partir de uma transposição didática adequada permitir ao professor de Matemática perspectivar novas formas de abordagem (com o uso da tecnologia e exploração de softwares de Matemática) e descrição de problemas olímpicos, que não sejam intimamente restritos a uma tarefa de resolução de problemas, com o tempo previamente demarcado e atividades hegemonicamente individuais; iii. Divulgar e promover a sociabilização das ideias matemáticas intuitivas e estratégias características de situações problemas de olimpíadas não apenas para alunos reconhecidos como mais habilidosos diante do conhecimento matemático (SANTOS, 2018, p. 43).

Por isso, entendemos que as participações diretas dos licenciandos em formação inicial na Experimentação da Engenharia Didática de Formação (EDF), vivenciando a proposta (SDO), podem ajudar a identificar qual a real necessidade da sua comunidade escolar (estudantes) e se essa proposta pode ser utilizada como modelo de ensino na sua sala de aula quando professor.

Considerações Finais

Este escrito objetivou apresentar uma proposta de ensino por intermédio de situações didáticas, utilizando um problema da OBMEP (Situações Didáticas Olímpicas), junto ao software GeoGebra para o ensino de conceitos de geometria plana, nesse caso a Propriedade fundamental da equivalência.

Destacamos que apenas apresentamos alguns resultados obtidos na investigação, mas que, como mostramos e observamos, trouxeram resultados promissores. A proposta (SDO) foi satisfatória, trazendo uma dinamização proporcionado pelo GeoGebra, pela liberdade, autonomia dos sujeitos em relação à resolução do problema e na construção dos conhecimentos matemáticos, por meio das discussões, da propriedade fundamental da equivalência. A SDO também propiciou aos sujeitos as ações de agir, formular e validar conjecturas apoiada pelas etapas da Teoria das Situações Didáticas, percorrendo o caminho análogo ao caminho de um matemático.

Seguimos o percurso metodológico baseado na Engenharia Didática de Formação (EDF), que nos permitiu a fundamentação por intermédio do estudo sobre a temática na etapa de Análises preliminares, a construção na Análise a priori, a experimentação e análise da situação didática proposta no trabalho, identificando cada momento do aprendizado dos sujeitos, categorizadas pelas etapas da TSD.

Os dados coletados foram categorizados conforme as etapas da Teoria das Situações Didáticas (TSD) — o que nos possibilitou identificar as ações dos sujeitos durante a Situação Didática Olímpica (SDO) mediante imagens, áudios e escritos. Isto também tornou possível que o pesquisador/professor agisse em momentos adequados como mediador do conhecimento matemático, para que não impossibilitasse a autonomia e liberdade do educando. Esse aspecto nos proporcionou um maior controle sobre as ações, dando oportunidade aos estudantes de, por meio de indagações, ir ao encontro do conceito proposto (Propriedade fundamental da equivalência).

Durante a realização da pesquisa, tivemos alguns obstáculos que nos fizeram mudar o formato da aplicação do experimento, antes presencial. Realizamos a pesquisa pela plataforma Google Meet, nunca utilizada antes pelo pesquisador, o que nos tirou a análise presencial e o contato da sala de aula. Por outro lado, propiciou a vivência de uma nova experiência com o uso de plataformas, softwares e aplicativos de mensagens, acrescentando novas opções aos docentes frente ao ensino de matemática.

Portanto, este artigo apresentou uma proposta didática (SDO), utilizando problemas de olimpíadas de matemática, em específico da OBMEP, com o objetivo de proporcionar metodologias alternativas para o ensino em ambientes preparatórios, para o ensino em sala de aula, propiciando aos docentes a inclusão de problemas desafiadores, instigantes, junto ao uso da tecnologia. Isso porque, baseado em Trainotti, Gayeski e Nunes (2018, p. 199) “as questões que compõem a prova são situações problema que procuram desafiar os alunos na busca de soluções”, e o uso dessas questões, em sala de aula (Problemas Olímpicos), pode atrair uma maior quantidade de alunos.

Referências

ALMOULOUD, S. Fundamentos da didática da matemática: 121. ed. Curitiba: UFPR, 2007.

ALMOULOUD, S.; COUTINHO, C. Q. S. Engenharia Didática: características e seus usos em trabalhos apresentados no GT-19 / ANPEd. Revemat. v. 3. n. 6, p. 62-77, 2008.

ALMOULOUD, S.; SILVA, M. J. F. Engenharia Didática: evolução e diversidade. Revemat, Florianópolis, v. 07, n. 2, p. 22-52, 2012.

ALVES, F. R. V. Situações Didáticas Olímpicas (SDOs): ensino de Olimpíadas de Matemática com arrimo no software Geogebra como recurso na visualização. ALEXANDRIA: R. Educ. Ci. Tec., v. 13, n. 1, p. 1-30, 2020.

ALVES, F. R. V. Visualizing the olympic didactic situation (ods): teaching mathematics with support of the geogebra software. Acta Didactica Napocensia, România, v. 12, n. 2, p. 97-116, 2019.

ALVES, F. R. V.; CATARINO, P. M. M. C. Engenharia Didática de Formação (EDF): repercussões para a formação do professor de matemática no Brasil. Educação Matemática em Revista-RS, v.2, n. 18, p. 121-137, 2017.

ARAÚJO, O.; MONSORES, J. F. Educação e competição: a OBMEP como fator de aprimoramento do ensino da Matemática. Revista caleidoscópio. v. 9, n. 1, p. 1-11, 2017.

ARTIGUE, M. Ingenieria Didática. In: ARTIGUE, M.; DOUADY, R.; MORENO, L.; GOMEZ, P. (eds.), Ingeniéria didatica en Educacion Matemática: Un esquema para la investigación y la innovación en la enseñanza y el aprendizaje de las matemáticas. Bogotá: Grupo Editorial Ibero-americano. 1995, p. 33-61.

AZEVEDO, I. F. Situações Didáticas Profissionais (SDP): uma perspectiva de complementaridade entre a teoria das situações e a didática profissional no contexto das olimpíadas de matemática. (Dissertação de Mestrado acadêmico em ensino de Ciências e Matemática, Instituto Federal de Educação Ciência e Tecnologia do Ceará – IFCE), 2020.

BROUSSEAU, G. Théorisation des phénomènes d'enseignement des mathématiques. Mathematics. Université Sciences et Technologies. (Tese de Doutoramento). L'université de Bordeaux I – França, 1986.

BROUSSEAU, G.; BROUSSEAU, N.; WARFIELD, V. teaching fractions through Situations: A fundamental Experiment. New York, London. Springer, 2014.

CARDIM, V. R. C.; GRANDO, R. S. Saberes sobre a docência na formação inicial de professores de matemática. Educação Matemática em Pesquisa, São Paulo, v.13, n.1, p.1-34, 2011.

COSTA, D. M. B.; TEIXEIRA, J. L.; SIQUEIRA, P. H.; SOUZA, L. V. Elementos da geometria plana. Curitiba: UFPR, 2012.

FERREIRA, M. B. C. Uma organização didática em quadriláteros que aproxime o aluno da licenciatura das demonstrações geométricas. (Tese de doutoramento em Educação Matemática). Pontifica Universidade Católica de São Paulo – PUC, São Paulo – Brasil, 2016.

GALVEZ, G. Didática da Matemática. In: PARRA C.; SAIZ, I. (Org.). Didática da matemática: reflexões psicológicas. Porto Alegre, Brasil: Artes Médicas. 1996. p. 26-35.

LIMA, R. G. A.; NEVES, T. G. Possibilidades de uso da engenharia didática na educação matemática e no ensino regular. Educação matemática em pesquisa, são Paulo, v. 21, n. 5, p. 694-708, 2019.

Ministério da Educação. Ministério da Educação. Secretaria de Educação Básica. Base Nacional Comum Curricular. Brasilia: MEC/SEB, 2018.

OBMEP. Apresentação. 2020. Disponível em: http://www.obmep.org.br/apresentacao.htm. Acesso em: 07 de jul. 2020.

PERRIN-GLORIAN, M. J.; BELLEMAIN, P. M. B. L’ingenierie didactique entre recherche et ressource pour l’enseignement et la formation des maitres. Anais... I Simpósio Latino-Americano de Didática da Matemática, Bonito - Mato Grosso do Sul – Brasil, 2016.

PERRIN-GLORIAN, M. J.; BELLEMAIN, P. M. B. L’ingenierie didactique entre recherche et ressource pour l’enseignement et la formation des maitres. Caminhos da Educação Matemática em Revista/Online. v. 9, n. 1, p. 45-82, 2019.

SANTOS, A. P. R. A. Situações Didáticas Olímpicas: Um contributo da Engenharia Didática Clássica no Ensino de Olimpíadas. 141f. 2018. Dissertação (Mestrado Acadêmico em Ensino de Ciências e Matemática). Instituto Federal de Educação, Ciência e Tecnologia do Ceará – IFCE. Fortaleza, 2018.

SANTOS, A. P. R. A; ALVES, F. R. V. A Teoria das Situações Didáticas no ensino das Olimpíadas de Matemática: Uma Aplicação do Teorema de Pitot. Revista IndagatioDidactica, Portugal, v. 9, n. 4, p. 279-296, 2017.

SILVA, J. G. A.; ALVES, F. R. V.; MENEZES, D. B. Situações Didáticas Olímpicas para o ensino de geometria plana no contexto da obmep: uma experiência no curso de Matemática do IFCE. Educação Matemática em Revista – RS. v.21, n.2, p. 66-78, 2020.

THEODOROVSKI, R.; OLIVEIRA, F. Padrões e o trabalho com sequências recursivas: uma abordagem no desenvolvimento do pensamento algébrico. Revista de Ensino de Ciências e Matemática, v. 11, n. 1, p. 219-236, 1 jan. 2020.

TEMPIER, F.; CHAMBRIS, C. Concevoie une ressource pour l´enseignment de la numération décimale de position. Recherche En Didactique des Mathématiques. v. 37, n. 2 – 3, p. 289 – 332, 2017.

TRAINOTTI, A.; GAYESKI, R. G.; NUNES, L. N. O conteúdo de estatística nas provas da olimpíada brasileira de Matemática das escolas públicas (OBMEP). Revista de Ensino de Ciências e Matemática, v. 9, n. 2, p. 193-209, 28 maio 2018.

VIEIRA, R.; MANGUEIRA, M. C.; ALVES, F. R.; CATARINO, P. M. Engenharia Didática e uma investigação do processo de hibridização da Sequência de Fibonacci. Revista de Ensino de Ciências e Matemática, v. 12, n. 1, p. 1-22, 1 jan. 2021.

Notas

Ligação alternative

https://revistapos.cruzeirodosul.edu.br/index.php/rencima/article/view/2850/1522 (pdf)