Recepção: 20 Julho 2020
Aprovação: 25 Outubro 2020
Resumo: A Resolução de Problemas tem se mostrado presente nas recomendações de documentos oficiais nacionais e internacionais e se consolidado como fulcral para o campo da Educação Matemática. Nesta perspectiva, objetivamos, por meio desta pesquisa, analisar quais concepções são atribuídas por professores de matemática à Resolução de Problemas. Em relação à temática, vários são seus enfoques e abordagens, dos quais destacamos autores como Polya, Vila e Callejo, Onuchic e Allevato, Schoenfeld, dentre outros que recorremos como suporte teórico. A investigação foi realizada com sete professores de Matemática do município de Breves - PA, que participaram de uma entrevista semiestruturada. Observamos as concepções que os professores mobilizam em relação à Resolução de Problemas estabelecem relação aos seus conhecimentos sobre suas próprias práticas pedagógicas, que incluem crenças, conceitos e ideias, e que refletem e acarretam mudanças em suas práticas profissionais.
Palavras-chave: Resolução de Problemas, Concepções, Ensino de Matemática.
Abstract: The Problem Solving from the official documents and international , comes consolidating as important for the field of Mathematics Education. In this perspective, we aim analyze what are the senses attributed by mathematics teachers to Problem Solving. Regarding the theme, there are several focuses and approaches, of which we highlight authors like Polya, Vila and Callejo, Onuchic and Allevato, Schoenfeld, among others, who we resort as theoretical support. An investigation was carried out with seven mathematics teachers from the city of Breves - PA, who responded a semi-structured interview. We observe what conceptions that teachers mobilize in relation to Problem Solving, and as they establish a relationship with knowledge about their pedagogical practices, concepts and ideas, change their professional practices.
Keywords: Problem Solving, Conceptions, Mathematics teaching.
1. INTRODUÇÃO
Por meio de pesquisas na área de Educação de Matemática (POLYA, 2006, 1997; DANTE, 2010, 2002; ONUCHIC, 1999; ONUCHIC; ALLEVATO, 2011, 2005; ALLEVATO, 2005; VILA; CALLEJO, 2006; SCHOENFELD, 1998, 1992) temos notado que a Resolução de Problemas tem sido explorada no campo educacional e científico em diferentes perspectivas, uma vez que ela pode ser caracterizada como metodologia de ensino, pode estar presente como atividade avaliativa e, ainda, porque é citada como elemento importante nas orientações curriculares nacionais (BRASIL, 2007, 1998) e internacionais (NCTM, 2000), bem como permeia os processos de heurística.
Ocorre que essas características da Resolução de Problema demandam planejamento na elaboração das atividades de matemática para serem desenvolvidas em sala de aula, uma vez que é importante definir quais concepções serão atribuídas por professores nesse processo.
Nesse sentido, a proposta deste artigo é discutir as concepções de professores de Matemática sobre esse tema a partir das orientações de Thompson (1992, p.130, tradução livre), enquanto “estrutura mental mais geral, que incluem crenças, significados, concepções, proposições, regras, imagens mentais, preferências e gostos”. Entendemos que a identificação e reconhecimento dessas concepções podem propiciar importantes reflexões para a Educação Matemática, tendo em vista que os professores podem ser influenciados por crenças em suas práticas de ensino acerca da Resolução de Problemas.
O estudo sobre este assunto teve início na década de 1940, tendo como seu principal representante George Polya, com a clássica obra intitulada A arte de resolver problemas: um novo aspecto do método matemático, fase que inaugurou o desenvolvimento da Matemática moderna. De acordo com Polya (2006, p. 131): “Ensinar a resolver problemas é educar à vontade”. Com esse posicionamento, o professor assume um papel importante para que a Resolução de Problemas possa ser explorada nas aulas de matemática.
Nesta direção, objetivamos analisar quais concepções são atribuídas por professores de Matemática à Resolução de Problemas por considerarmos importante que esses profissionais tenham conhecimentos dos princípios que fundamentam essa metodologia de ensino para que possam utilizá-la.
Sendo assim, as seções subsequentes abordam sobre as concepções apresentadas por professores de Matemática em relação à Resolução de Problemas.
2. REFERÊNCIAL TEÓRICO
2.1. Os problemas e o professor: atribuição de sentidos
Em relação a problemas matemáticos, ressaltamos que existem várias ideias e concepções sobre o tema proposto. Para os Parâmetros Curriculares Nacionais (BRASIL, 1998, p. 41), um problema matemático “é uma situação que demanda a realização de uma sequência de ações ou operações para obter um resultado”. Nesse sentido, o resultado não é o mais importante, mas sim as estratégias, os procedimentos e os conceitos envolvidos. Para Dante (2002, p. 9), “problema é qualquer situação que exija o pensar do indivíduo para solucioná-la”. Onuchic e Allevato, por sua vez, situam que problema “é tudo aquilo que não se sabe fazer, mas que se está interessado em fazer” (ONUCHIC; ALLEVATO, 2011, p. 81).
Segundo Polya (2006, p. 5), “[o] problema deve ser bem escolhido, nem muito difícil nem muito fácil, natural e interessante [...]”. Isso porque os problemas, se forem muito difíceis, irão desestimular e fazer com que o aluno não tenha interesse em resolvê-los. Por outro lado, se forem muito fáceis, o aluno não vai se sentir desafiado. Nesse âmbito, os estudos de Onuchic e Allevato (2011, p. 82) enfatizam que “[o] professor precisa preparar, ou escolher, problemas apropriados ao conteúdo ou ao conceito que pretende construir”. Sobre essa decisão, Dante (2010) corrobora afirmando que um bom problema deve possuir algumas características tais como: ser desafiador, ser interessante e possuir o elemento desconhecido a ser buscado. Com isso, as situações problemas em matemática não podem consistir na aplicação evidente e direta de estratégias algorítmicas.
A Resolução de Problemas como metodologia de ensino advoga como proposta de aquisição conceitual, regras e métodos matemáticos que podem ser evidenciados através de situações problemas. Em resumo, uma situação problema pode ser constituir como o ponto de partida para a atividade matemática, conforme pontuado na Base Nacional Comum Curricular (BNCC) (BRASIL, 2017).
Para tal, destacamos a importância de que o professor conheça e saiba utilizar essa metodologia, bem como o que preconizam os documentos oficiais BNCC e PCN’s, tomando-os como necessários no reconhecimento dos princípios que os fundamentam. Entendemos que a matemática necessita de práticas que possibilitem a compreensão da Resolução de Problemas à formação de professores.
Esse cenário ainda tem um longo caminho para ser alcançado, e, como aponta Dante, essa não é uma tarefa fácil:
Ensinar a resolver problemas é uma tarefa mais difícil do que ensinar conceitos, habilidades e algoritmos matemáticos, não é um mecanismo direto de ensino, mas uma variedade de processos de pensamentos que precisam ser cuidadosamente desenvolvidos pelo aluno com o apoio e incentivo do professor (DANTE, 2002, p. 30).
Na ideia defendida pelo autor, percebemos que a Resolução de Problemas propicia a uma variedade de processos de pensamentos matemáticos, que devem ser encorajadas pelos professores aos seus alunos. Dessa forma,
O professor que deseja desenvolver nos estudantes a capacidade de resolver problemas deve incutir em suas mentes algum interesse por problemas e proporcionar-lhes muitas oportunidades de imitar e de praticar. Além disso, quando o professor resolve um problema em aula, deve dramatizar um pouco as suas ideias e fazer a si próprio as mesmas indagações que utiliza para ajudar os alunos. Graças a esta orientação, o estudante acabará por descobrir o uso correto das indagações e sugestões e, ao fazê-lo, adquirirá algo mais importante do que o simples conhecimento de um fato matemático qualquer (POLYA, 2006, p. 4).
Na perspectiva de Polya (2006, 1997), ter um problema é buscar por uma ação apropriada, claramente definida por um objetivo, o que não significa que a proposta de resolver problemas perpasse por aquilo que seja imediatamente atingível. Assim, consideramos importante pensar que a busca pela resposta dos problemas propostos pelos alunos e o caminho que os mesmos terão que percorrer para solucioná-lo são fundamentais para que eles descubram quais são as melhores estratégias.
Notamos, também, que a BNCC (BRASIL, 2017), ao propor o ensino de Matemática sob a orientação de desenvolvimento de competências e habilidades, reforça a necessidade de se trabalhar com a Resolução de Problemas em sala de aula. Respondendo às preocupações mundiais, o National Council of Teacher of Mathematics (NCTM, 2000) recomendou a Resolução de Problemas, visando ao currículo de matemática.
Monteiro et al. (2020) destacam, nesse contexto, que a Resolução de Problemas pode se constituir em um bom método de ensino, uma vez que proporciona avanços no processo de ensino da matemática, possibilitando que o professor acompanhe todo o processo de investigação desenvolvido pelos alunos.
Outrossim, o cenário merece destaque, ainda, a importância do papel do professor no desenvolvimento curricular para propiciar um ambiente apropriado para que os alunos se desvencilhem de comportamentos inadequados nas atividades com Resolução de Problemas nas aulas de matemática.
3. METODOLOGIA
O modelo metodológico adotado nesta pesquisa foi de natureza qualitativa, do tipo pesquisa de campo, realizada por meio de entrevistas considerando que, segundo Gaskell (2002), as entrevistas permitem a compreensão minuciosa das motivações, atitudes, valores, e crenças dos sujeitos pesquisados. Na perspectiva de Minayo:
Pesquisa qualitativa responde a questões muito particulares. Ela se preocupa, nas ciências sociais, com um nível de realidade que não pode ser quantificado, ou seja, ela trabalha com o universo de significados, motivos, aspirações, crenças, valores e atitudes, o que corresponde a um espaço mais profundo das relações dos processos e dos fenômenos que não podem ser reduzidos à operacionalização de variáveis (MINAYO, 1995, p. 21-22).
Neste sentido, em nosso estudo, por meio de uma entrevista com foco na narrativa da experiência profissional de professores de Matemática, exploramos quais concepções podem ser observadas em relação à Resolução de Problemas. Segundo Lakatos e Marconi (1993), a entrevista é uma aliada na pesquisa por estabelecer um feedback ao jogo de perguntas e respostas entre o entrevistador e o entrevistado.
Minayo (1995), por seu turno, destaca que, ao usar entrevistas, é importante que o entrevistador não fique preso a formulações pré-fixadas, e sim que tenha um roteiro para facilitar a comunicação entre ambos. Em nosso estudo estabelecemos, inicialmente, o contato com os professores para explicar o objetivo da pesquisa, os quais, já neste primeiro encontro, se mostraram cordiais e participativos. Foram entrevistados sete professores de Matemática que atuam nas séries finais do ensino fundamental da rede municipal de Breves-PA. Cada entrevista teve duração de, aproximadamente, 30 minutos. Por fim, procedemos à transcrição e à análise das entrevistas.
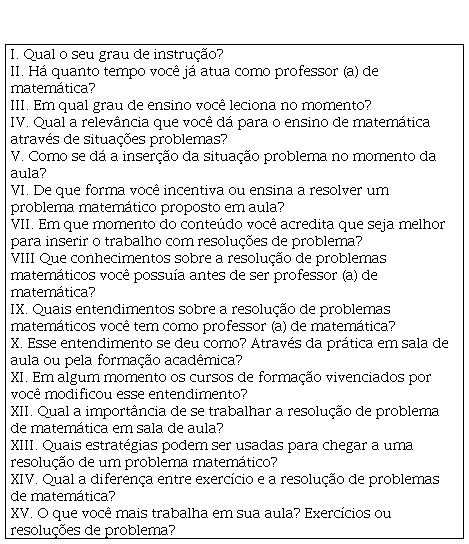
Com intuito de organizar a entrevista, foi idealizado um roteiro de perguntas semiestruturadas, a fim de melhor evidenciarmos as concepções desses professores, conforme mostra o Quadro 1:
Nas perguntas de I a III, objetivamos conhecer um pouco os professores, para que pudéssemos traçar um perfil. Já nas perguntas de IV a XI, buscamos compreender o grau de familiaridade que eles possuíam com as resoluções de problemas, e de que forma as utilizam em suas aulas, iniciando, assim, a busca por evidências sobre suas concepções. Quanto às perguntas de X a XV, foram elaboradas com o intuito de evidenciar, com maior profundidade, as concepções dos professores sobre a Resolução de Problemas, buscando compreender se essas são construídas e consolidadas durante sua trajetória, tanto acadêmica, como profissional, ou se foram alteradas durante a prática em sala de aula, ou por meio de cursos de formação. Para a análise das respostas, estas foram categorizadas conforme apresentado a seguir.
3.1. Perfis dos Professores
Todos os professores possuem licenciatura em Matemática e pós-graduação na área específica de atuação. Os entrevistados atuam do 6º ao 9º ano do ensino fundamental, somente com Matemática. Dos sete professores, um atua na zona rural e os outros seis na zona urbana do município de Breves-PA.
3.2. As Categorias
As concepções são constituídas a partir de um movimento que perpassa pela motivação de um indivíduo e por suas experiências prévias que influenciam nas ações desse indivíduo, formando conhecimentos, nos quais se manifestam. Nesse sentido, construímos três categorias (Quadro 2), que nos possibilitaram organizar as respostas dos professores de modo que pudéssemos captar e compreender as concepções dos professores envolvidos.
Portanto, o Quadro 2 foi elaborado a partir da entrevista concedida pelos professores, na qual puderam falar sobre o enfoque dado à Resolução de Problemas.
4. RESULTADOS E DISCUSSÃO
A seguir, descrevemos cada uma das categorias que emergiram a partir das análises das entrevistas concedidas pelos participantes.
4.1. Conhecimentos Sobre a Resolução de Problemas
Para a análise da primeira categoria, organizamos no Quadro 3 as respostas nas quais identificamos características diferentes em relação aos conhecimentos sobre Resolução de Problemas.
A partir do questinamento VIII é possivel inferir que os professores já possuíam algum conhecimento acerca da Resolução de Problemas e que a utilizavam em suas aulas, reconhecendo-a como uma importante metodologia de ensino da Matemática. Nesse sentido, Allevato corrobora tais perspectivas ao afirmar que “[...] quando o professor adota essa metodologia, os alunos podem aprender tanto sobre resolução de problemas, quanto aprendem Matemática para resolver novos problemas” (ALLEVATO, 2005, p. 61).
Nesta categoria, observamos que os professores se remetem a dois tipos de conhecimento, o teórico e o prático. Na resposta de P2 ao questionamento XIII, por exemplo, “Eu tinha o conhecimento sobre as resoluções de Polya” é possível notarmos que se remete a uma das principais referências em Resolução de Problemas. Já na resposta de P4, no questinamento X, temos: “Olha... nos dois, por incrível que pareça, claro, que a prática você vai aperfeiçoando seu conhecimento acadêmico. A partir dela podemos observar o reconhecimento da articulação entre teoria e prática para o desenvolvimento de um bom trabalho com a Resolução de Problemas.
Em relação ao conhecimento a partir da prática, P5 relata que: “Assim, eu trabalhei sempre muito com arte gráfica, desenho, com pinturas, e então, assim, pra mim que sempre trabalhei...”. Notamos essa característica também no questionamento X, quando P3 Pontua: “[...] eu acredito que aprendi muita coisa, mas na prática na sala de aula”. Essa consideração demonstra que os professores reconhecem a importância do trabalho com essa metodologia a partir das necessidades apresentadas em sala de aula. Aqui se coloca a experiência como construções e reconstruções da prática.
Nessa érspectiva, salientamos que os conhecimentos teóricos e práticos são fundamentais para o desenvolvimento do trabalho por meio da Resolução de Problemas, pois permitem ao professor uma melhor preparação ou escolha dos problemas que pretende desenvolver (ONUCHIC; ALLEVATO, 2011).
Ao observamos as respostas referentes ao questionamento IX, notamos outros desdobramentos relacionados quanto ao conhecimento sobre da Resolução de Problemas: a) relativo à sensação; e b) como significado da prática profissional.
Da sensação desencadeiam-se outras reações que indicam a impressão, a intuição, a noção, isto é, conhecimentos imediatos e espontâneos. Dessa forma, notamos uma preocupação dos professores em fazer com que a Matemática se aproxime da realidade dos alunos, propiciando uma sensação imediatista da Matemática como se ela os pertencence. Contudo, advertimos, também, que uma crença possa ser gerada a partir de conhecimento imediato e espontâneo, como a aplicação/contexto, uma vez que nem todo conteúdo matemático é passível de uma contextualização, por exemplo. Logo, podemos atribuir uma concepção prático-utilitária ao conhecimento matemático.
Sendo assim, caracterizamos a próxima categoria: Motivação para o ensino com Resolução de problemas. Sobre ela, desvelamos como as percepções sobre a motivação implicam nos processos subjacentes à aprendizagem matemática.
4.2. Motivação Para o Ensino Com Resolução de Problemas
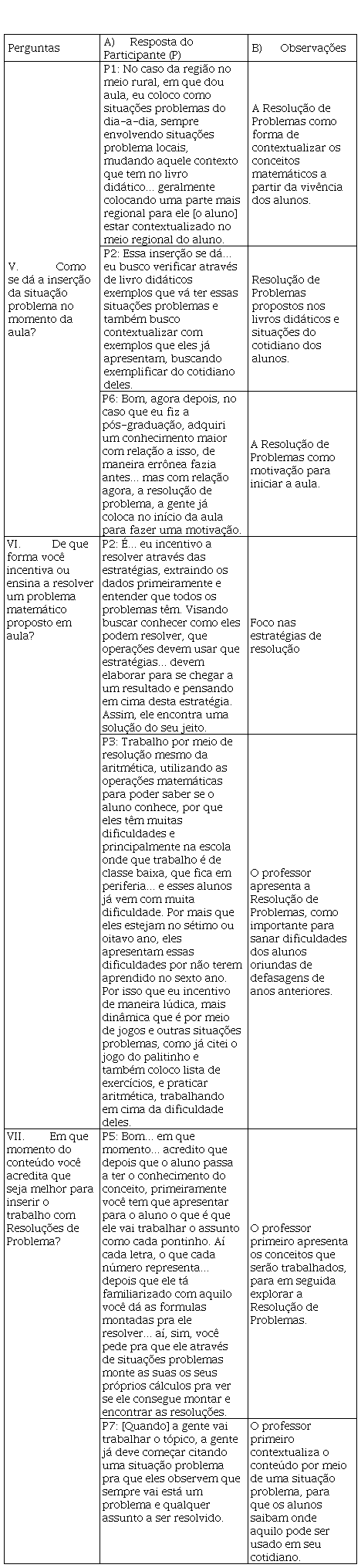
Aqui apresentamos algumas características sobre a motivação no trabalho com a Resolução de Problemas, conforme o Quadro 4, que segue:
Quando questionados como inserem a Resolução de Roblemas em suas aulas, observamos que, entre os entrevistados, prevalece a concepção de que a Resolução de Poblemas propicia trabalhar a Matemática de forma contextualizada, a aproximando da realidade dos alunos. Isso ficou evidenciado na resposta de P1, quando relata: “No caso da região no meio rural, em que dou aula, eu coloco como situações problemas do dia-a-dia, sempre envolvendo situações problema locais[...]”. Nesse caso, pelo fato de P1 lecionar no meio rural, ele procura contextualizar situações da realidade daquele local em que está ambientado.
Já quando questionados sobre como incentivam seus alunos a trabalharem com a Resolução de Problemas, P2 e P3, respectivamente, deixam entrever dois outros argumentos interessantes; um se remete à valorização da autonomia dos alunos para traçarem suas estratégias de resolução, como observado na resposta: “É... eu incentivo a resolver através das estratégias, extraindo os dados primeiramente e entender, que todos os problemas têm. Visando buscar conhecer como eles podem resolver que operações”. Outra característica apontada foi a preocupação em sanar defasagens de anos anteriores, como o expresso em: “Trabalho por meio de resolução mesmo da aritmética, utilizando as operações matemáticas para poder saber se o aluno conhece, porque eles têm muitas dificuldades...”. Estas falas pontuam um caráter putativo ao ensino de Matemática, vinculado à crença na Resolução de Problemas, que supõe sua realização condicionada a fatos correlatos de não aprendizagens anteriores e não como um momento privilegiado de avaliação de aprendizagem.
Nesse âmbito, Schoenfeld (1998) destaca, em seus estudos, um modelo denominado por ‘ensino no contexto’, o qual forneceu evidências da existência de crenças nas ações de professores, quando estes explanavam, bem como no porquê de decisões específicas e em comportamentos tomados.
Quando questionamos sobre qual seria o momento oportuno para introduzir a Resolução de Problemas, observamos duas concepções diferentes: em uma delas, essa prática é explorada após os conceitos serem desenvolvidos em aula. Isto pauta a Resolução de Problemas não como uma metodologia de ensino, mas sim como um mecanismo de consolidar conhecimentos prévios, como o observado na fala de P5: “Bom... em que momento, acredito que depois que o aluno passa a ter o conhecimento do conceito... primeiramente você tem que apresentar para o aluno o que é que ele vai trabalhar o assunto como cada pontinho” .
Já na fala de P7, “Quando a gente vai trabalhar o tópico, a gente já deve começar citando uma situação problema pra que eles observem que sempre vai está um problema e qualquer assunto a ser resolvido”, notamos a preocupação em iniciar com a Resolução de Problemas, o que nos remete às orientações da BNCC (BRASIL, 2007), quando estas destacam que o problema deve ser utilizado como ponto de partida, no qual o aluno deve ser levado a interpretar o enunciado utilizando-se de conhecimentos previamente adquiridos. Contudo, as crenças quanto à motivação podem estar relacionadas aos ‘bons resolvedores de problemas’. Essa concepção de fortalecimento e constituição de “exímios resolvedores de problemas” tem sido muito limitada e problemática, reforçando, assim, a averssão para aprendizagem Matemática.
Por fim, apresentaremos a última categoria em que diz respeito à prática profissional do professor, em que assinalamos sobre suas preferências, pontos de vistas e perspectivas.
4.3. Experiências com Resolução de Problemas
Nesta categoria nos concentramos em analisar as concepções a partir da experiência com a Resolução de Problemas (Quadro 5).
A partir do questionamento XI notamos que os professores se preocupam em buscar conhecimentos para melhorarem suas práticas em sala de aula e que este movimento influencia de forma positiva na mudança de suas concepções. Percebe-se nesses relatos, ainda, o anseio dos professores em se aperfeiçoarem na temática sobre Resoluções de Problemas.
Nesses relatos observamos que eles reconhecem que o conhecimento que possuíam não era suficiente para o trabalho com os alunos e, por isso, buscaram o aperfeiçoamento, como evidenciado no trecho do relato do professor P2: “[...]quando estuda esse conhecimento, vai melhorando e se modificando. Com isso, modifica também sua prática [...]”. Nesse sentido, compreendem Allevato e Onuchic (2011) que a Resolução de Problemas tem sido a força propulsora para a construção de conhecimento, bem como a direção de novas estratégias que decorrem de sua aplicação.
Os professores entrevistados, como situado no trecho da fala de P4: “A estratégia, como eu falo para os alunos, é você ter uma boa interpretação do comando da questão [...]” destacaram a importância da interpretação, sendo orientadas segundo o entendimento de Polya (2006) e Dante (2002), a partir do qual, para se resolver um problema, alguns aspectos importantes como interpretar, compreender estabelecer um plano de execução e, após, realizar um retrospecto da solução devem ser ser observados. Para Lacerda (2019a), as necessidades de comunicar a linguagem matemática demandam ao ensino a capacidade de ler com atenção, com o intuito de melhorar as técnicas de ensino.
Quando solicitados a diferenciarem um exercício de um problema, identificamos três concepções diferentes, conforme descritas nos relatos dos participantes P2, P6 e P7. O participante P2 se refere aos exercícios como atividades cuja resolução se dá por meio de técnicas; já os problemas demandam estratégias de resolução próprias dos alunos. O professor P6 relata que o exercício se constitui como uma atividade fechada, ou seja, a solução final é previsível, enquanto a Resolução de Problemas é classificada como uma atividade aberta, isto é, de resposta não previsível. P7, por sua vez, classifica um problema como uma atividade contextualizada, enquanto os exercícios, para ele, não têm contexto.
Observamos, ainda, duas concepções acerca de problemas na transcrição da fala de P7: “Pra mim entender exercício, como digamos, você coloca aquelas continhas arma e efetue e já na resolução matemática o aluno ele vai e resolve”. Podemos inferir, a partir desse relato, dois tipos de enunciados que dizem respeito à linguagem adotada com problemas verbais e não verbais O primeiro está atrelado ao entendimento da relação entre a língua materna e a Matemática, que requer a intepretação para a solução de problemas. Já o segundo se reporta a concepções do tipo arme e/ou efetue, que requerem mais o domínio de operações. Ocorre que proceder à realização de cálculos está associado a enunciados imperativos, que expressam uma ordem, uma indicação, uma proibição, etc., e o uso dessas palavras pode conduzir a um determinado comportamento. Para Lacerda (2009b), a linguagem é entendida como instrumento de ação comunicativa e, por isso, seu emprego associa-se com os estados de coisas, dependendo de circunstâncias e contextos em que as palavras são proferidas.
Observamos nas concepções sobre problemas apresentados por professores algumas aproximações com a perspectiva de Dante (2007, p. 9), ao afirmar que "problema é qualquer situação que exija o pensar do indivíduo para solucioná-la”. Se pensarmos na perspectiva de Onuchic e Allevato (2011, p. 81), “é tudo aquilo que não se sabe fazer, mas que se está interessado em fazer”. Esse ponto de vista é frisado por P2. Entretanto, nenhum dos entrevistados assinalou com a perspectiva de que: “O problema deve ser bem escolhido, nem muito difícil nem muito fácil, natural e interessante [...]” (POLYA, 2006, p. 5).
Conforme assinala Schoenfeld (1992), há um amplo leque de conceitualização para a Matemática, e suas transformações nos sugerem que deve ser envolvido o esforço de considerar a linguagem matemática. Logo, é preciso:
a) procurar soluções, não apenas memorização de procedimentos;
b) explorar padrões, não apenas memorização de fórmulas;
c) formular conjecturas, não apenas fazer exercícios.
Para este Schoenfeld (1992), no processo de aprendizagem de Matemática, os alunos devem ser encorajados a conhecer a discilina como ciência, e não meramente como um conjunto de regras e procedimentos numéricos.
Vila e Callejo (2006, p. 29) ressaltam que, “[...] o ensino/aprendizagem por meio da resolução de problemas é uma tentativa de modificar o desenvolvimento habitual das aulas de matemática”. Nessa perspectiva, P6 corrobora: “Sim, o conhecimento que tinha antes da pós-graduação, até mesmo terminada a graduação, ainda não era o mesmo. Eu tinha uma ideia errônea de resolução de problemas, achava que devíamos primeiro passar o conteúdo para depois resolver, ter um saber algorítmico pra depois resolver problema”.
Podemos observar nesse relato um sentimento de que as verdades até então inquestionáveis aprofundam convicções, e de que a modificação de posturas leva a uma importante transformação pessoal, que pode ressignificar uma mudança de atitude na prática em sala de aula.
CONSIDERAÇÕES
Este estudo procurou, fundamentalmente, o entendimento de como os professores concebem a Resolução de Problemas e e como a propõem em sala de aula. Com ele, buscamos avaliar e colocar em debate a ideia de sentidos atribuídos à Matemática como disciplina exata e que requer apenas estratégias algorítmicas em suas soluções.
Nesse âmbito, destacamos a leitura e interpretação de texto como estratégias de uma boa prática atrelada à Resolução de Problemas, o que nos evidencia a importância da linguagem matemática, que diz respeito às habilidades de leitura e escrita nessa área de estudos. Essa ênfase vem ganhado força na atualidade com os apontamentos do letramento matemático, preconizado, sobretudo, nos manuais e recomendações oficiais, como as da BNCC. Portanto, entendemos necessário pautar novas preocupações que compreendam o ensino e a aprendizagem de Matemática no Brasil.
A avaliação nas aulas de Matemática por meio da Resolução de Problemas ainda é pouco refletida, privilegiada em sala e debatida. Nesse sentido, uma prática melhor orientada e, assim, mais fecunda, que pode resultar no processo de criação de como algo é realizado e percebido pelo sujeito. Portanto, a Resolução de Problemas, embora nos remeta a uma metodologia de ensino, com o advento de novas regiões de inquéritos para Educação Matemática, passou a incorporar novas searas do conhecimento, tais como Psicologia, a Antropologia, a Linguística, a Sociologia, dentre outras.
REFERÊNCIAS
ALLEVATO, N. S. G. Associando o computador à resolução de problemas fechados: análise de uma experiência. 2005. 370. (Tese de Doutorado em Educação Matemática). Universidade Estadual Paulista Júlio de Mesquita Filho, Rio Claro, SP, 2005.
BRASIL, Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: (5ª a 8ª série) Matemática. Brasília, DF: MEC/SEF, 1998.
BRASIL. Base Nacional Comum Curricular: Educação Infantil e Ensino Fundamental. Brasília: MEC/Secretaria de Educação Básica, 2017.
DANTE, Luiz Roberto. Didática da Resolução de Problemas de Matemática. 12ª ed., São Paulo: Ática, 2002.
DANTE, Luiz Roberto. Formulação e resolução de problemas de matemática. 1. ed. São Paulo: Editora Ática. 2010.
GASKELL, G. Entrevistas individuais e grupais. In: BAUER, M. W.; GASKELL, G. (Orgs.), Pesquisa qualitativa com texto, imagem e som: um manual prático. Petrópoles/Brasil: Editora Vozes, 2002. p. 64-89.
LACERDA, A. G. Para Ler e Interpretar o Texto: reflexões a partir da linguagem e suas implicações para o ensino e aprendizagem de Matemática. REMATEC, n. 31, p. 09-27, 2019a.
LACERDA, A. G. A linguagem como ação numa perspectiva wittgensteiniana: a comunicação e o desenvolvimento de significados à leitura. Revista BOEM, v. 7, n. 14, p. 1-21, 2019b.
LAKATOS, E. M.; MARCONI, A M. Fundamentos de metodologia científica. São Paulo: Atlas, 1993.
MINAYO, M. C. S. Pesquisa Social: Teoria, Método e Criatividade. Petrópolis: Vozes, 1995.
MONTEIRO, R, B; LARANJEIRA, S, R, A; ANDRADE, L, D, M; NETO, J, G, R. Contribuição da Resolução de Problemas como Metodologia de Ensino de Matemática. REAMEC, n. 02, p. 57-68, 2020.
NCTM. Principles and Standards for School Mathematics. Reston, VA: National Council of Teachers of Mathematics, 2000.
ONUCHIC, L. R. Ensino-aprendizagem de matemática através da resolução de problemas. In: BICUDO, M. A. V. (Org.). Pesquisa em educação matemática: concepções e perspectivas. São Paulo: Editora da UNESP, 1999. p. 199-200.
ONUCHIC, L. R.; ALLEVATO, N. S. G. Novas Reflexões sobre o ensino aprendizagem de matemática através da resolução de problemas. In: BICUDO, M. A.V.; BORBA, M. de C. (Org.). Educação Matemática: pesquisa em movimento. São Paulo: Cortez, 2005.
ONUCHIC, L. R.; ALLEVATO, N. S. G. Pesquisa em resolução de problemas: caminhos, avanços e novas perspectivas. Bolema, Rio Claro, ano 25, n. 41, p. 73-98, dez. 2011.
POLYA, George. A Arte de Resolver Problemas. Rio de Janeiro: Interciência, 2006.
POLYA, George. Sobre a resolução de Problemas de Matemática na high school. In: KRULIK, Stephen; REYS, Robert E. A Resolução de Problemas na Matemática Escolar. São Paulo: Atual, 1997.
SCHOENFELD, A. H. Toward a theory of teaching-in-context. Issues in Education, v.4(1), 1998, p. 1- 94.
SCHOENFELD, A. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In: GROUWS, D. A (Ed.). Handbook of research on mathematics teaching and learning. New York: Macmillan, 1992. p. 334 – 370.
THOMPSON, A. G. Teachers’ Beliefs and Conceptions: a synthesis of the research. In: GROUWS, D. A (Ed.), Handbook of research on mathematics teaching and learning. New York: Macmillan Publishing Company, 1992. p. 127 – 146.
VILA, A.; CALLEJO, M. L. Matemática para aprender a pensar: o papel das crenças na resolução de problemas. Porto Alegre: Artmed, 2006.
Notas
Autor notes
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/10850 (pdf)
