

GEOGEBRA, HISTÓRIA DA MATEMÁTICA E GEOMETRIA ANALÍTICA
GEOGEBRA, HISTORY OF MATHEMATICS AND ANALYTICAL GEOMETRY
REAMEC – Rede Amazônica de Educação em Ciências e Matemática, vol.. 8, núm. 3, 2020
Universidade Federal de Mato Grosso


Recepção: 15 Junho 2020
Aprovação: 10 Julho 2020
Resumo: O presente artigo discute uma proposta pedagógica que integra a História da Matemática e as Tecnologias da Informação e Comunicação (TIC) para a resolução de equações algébricas do segundo grau. Este estudo é fruto de uma tese defendida em 2018, no programa REAMEC - Rede Amazônica de Educação em Ciências e Matemática. Para tanto, adotou-se o livro A Geometria, de Descartes, como fonte original, aliada à utilização da tecnologia com o software GeoGebra. Por meio de uma pesquisa bibliográfica em fontes históricas, constatou-se que o método de Descartes para a resolução de equações pode ser utilizado em sala de aula. A pesquisa apresenta uma abordagem qualitativa e para a produção dos dados foram utilizados questionários, entrevistas, registros no caderno de campo, além da resolução de problemas. Os colaboradores da pesquisa são cinco acadêmicos de Licenciatura em Matemática integrantes do PIBID, da Universidade do estado de Mato Grosso, que voluntariamente participaram do estudo. A escolha desse universo deve-se ao fato de poder se observar e analisar o impacto dessa proposta para o ensino de tópicos de Geometria Analítica no Ensino Médio. Constatou-se que a História da Matemática, inserida no ensino de Geometria Analítica, e o uso do software GeoGebra possibilitaram aos alunos desenvolver estratégias de resolução que, sem dúvida, contribuíram para eles ressignificarem os conceitos básicos, tanto da Geometria quanto da Álgebra. Daí a relevância desta pesquisa, pois ela pôde oportunizar uma discussão mais ampla em relação a questões pertinentes à proposta de ensino da Matemática, tais como a relação entre a teoria e a prática e suas implicações na formação inicial dos licenciandos em Matemática. Em assim sendo, enfatiza-se a viabilidade de uso de uma proposta pedagógica que integre o uso da História da Matemática e as Tecnologias para a resolução de equações algébricas do segundo grau.
Palavras-chave: História, Geometria Analítica, Tecnologia.
Abstract: In this article we propose to discuss a pedagogical proposal that integrates the History of Mathematics and ICTs for solving algebraic equations of the second degree. This study is the result of a thesis defended in 2018, in the program REAMEC - Amazonian Network of Education in Science and Mathematics. For this purpose, we adopted Descartes' book "Geometry", as an original source combined with the use of technology with the GeoGebra software. Through a bibliographic search in historical sources we found that Descartes' method for solving equations can be used in the classroom. The research presents a qualitative approach, for the production of data we use questionnaires, interviews, records in the field notebook, in addition to problem solving. The research collaborators are five undergraduate Mathematics students from PIBID, from the State University of Mato Grosso, who voluntarily participated in the research. The choice of this universe is due to the fact of being able to observe and analyze the impact of this proposal for the teaching of Analytical Geometry topics in High School. We believe that the development of this research will enable a broader discussion in relation to issues pertinent to the mathematics teaching proposal, such as: the relationship between theory and practice, as well as the implications of these practices in the initial training of undergraduate mathematics students. We emphasize the feasibility of using this pedagogical proposal that integrates the use of the History of Mathematics and Technologies for solving algebraic equations of the second degree.
Keywords: History, Analytical Geometry, Technology.
1 INTRODUÇÃO
Na atualidade, o professor passa a assumir o papel de mediador e o aluno de protagonista do seu processo formativo. O que vem ao encontro da Base Nacional Comum Curricular – BNCC (BRASIL,2016), que influencia diretamente a forma como o professor desenvolve as práticas pedagógicas em sala de aula. Nesse contexto, apresentamos uma pesquisa que buscou aliar a autonomia do aluno a uma proposta pedagógica que une a História da Matemática com as Tecnologias.
O objetivo deste artigo é expor uma proposta pedagógica para a resolução de equações algébricas, integrando a História da Matemática e os recursos tecnológicos como o software GeoGebra, para possibilitar ao aluno analisar e entender estratégias para resolver determinados problemas de geometria analítica, viabilizando, assim, uma melhor compreensão ou ressignificação dos conceitos de ponto, coordenadas e equação da reta. Para isso consideramos no processo de análise dos dados da pesquisa a seguinte questão norteadora: que estratégias os alunos utilizam, a partir da experiência com a História da Matemática e com o GeoGebra, para resolver determinados problemas que envolvam coordenadas, ponto e equação da reta?
Neste artigo, mostramos os dados produzidos por meio de questionários, entrevistas, registros em caderno de campo e de problemas resolvidos pelos alunos do curso de Licenciatura em Matemática da Universidade do estado de Mato Grosso, participantes do PIBID[3] e colaboradores da pesquisa.
Oferecemos uma oficina com carga horária de 15 horas, em que abordamos as Tendências da Educação Matemática, elaboradas por Miguel (1993); discutimos questões históricas que tratam dos conteúdos de coordenadas, ponto e equação da reta; apresentamos as principais funcionalidades do software GeoGebra; assim como resolvemos problemas do Exame Nacional do Ensino Médio – Enem. Optamos pelas questões do Enem por serem problemas com os quais os acadêmicos já estariam familiarizados por terem ingressado na universidade por este sistema. Também escolhemos problemas que girassem em torno do tema de ponto, coordenadas e equação da reta e que trouxessem em seu enunciado diferentes representações semióticas, de forma a nos permitir compreender como o aluno lida com essas representações. Procuramos identificar tanto a compreensão do aluno perante a coordenação dos registros semióticos, quanto a utilização da História da Matemática, por meio da perspectiva sociocultural do uso do Jogo de Vozes e Ecos, na forma de “ecos ressonantes”.
Cabe ressaltar a importância de introduzir novas práticas pedagógicas que, articulando metodologias e práticas pedagógicas, auxiliem no processo de ensino e aprendizagem e possibilitem ao aluno tornar-se sujeito ativo no seu processo formativo.
Iniciaremos nossa discussão, explanando brevemente sobre a semiótica e as suas implicações para o ensino e aprendizagem de Matemática, para, então, a partir destas perspectivas, apresentar uma proposta pedagógica que integrou a História da Matemática com as TIC, e foi desenvolvida com os alunos do Curso de Licenciatura em Matemática (CLM), participantes do PIBID da Universidade do estado de Mato Grosso, Câmpus de Sinop
2 SEMIÓTICA: IMPLICAÇÕES PARA O ENSINO E APRENDIZAGEM DE MATEMÁTICA
Ao trabalharmos com objetos matemáticos, estes podem ser reconhecidos somente por meio de suas representações semióticas. Todavia é importante não confundir os objetos matemáticos com suas representações.
Os pesquisadores Henriques e Almouloud (2016) salientam que, dentre os registros de representação semiótica que se podem pensar na Educação Matemática, quatro são predominantes, embora não se descarte a existência de muitos outros. Estes podem ser observados na Figura 1.

Assim sendo, cumpre trabalhar com representações variadas, pois os objetos matemáticos não existem no ambiente físico. A Semiótica e a Matemática são áreas de conhecimento independentes, mas que se complementam, ou seja, a Semiótica pode auxiliar a compreensão do ensino da Matemática devido à sua complexidade de representações e à sua subjetividade.
Conforme Duval (2011), para acessar os objetos matemáticos, como números, funções e relações geométricas, é necessária uma atividade de produção semiótica. Nesse sentido, acreditamos que a representação é que proporciona o desenvolvimento do conceito matemático.
Do ponto de vista epistemológico, Duval (2009) afirma que a noção de representação é essencial, pois, desde Descartes e Kant, ela já vem estando no centro de toda a reflexão com relação à construção do conhecimento. Não há conhecimento que não possa ser mobilizado sem uma atividade de representação.
Portanto, para que, de fato, a aprendizatem tenha um significado, os alunos precisam desenvolver a capacidade de colocar em correspondência as diferentes representações semióticas de um determinado objeto matemático.
Duval (2009, p.17) salienta que “Não há noésis[4] sem semiósis[5], é a semiósis que determina as condições de possibilidade e exercício da noésis”. Ou seja, não há a apreensão do conhecimento de um objeto matemático sem se recorrer ao sistema de representação semiótico. Um registro de representação possibilita algumas atividades cognitivas, ligadas à semiose como: o tratamento e a conversão de representações.
Para D’Amore, Pinilla e Iori (2015, p.155),
[...] a construção cognitiva dos objetos matemáticos é profundamente dependente da capacidade de utilizar vários registros de representação semiótica de tais objetos, a fim de:
• representar os objetos em um dado registro;
• tratar as representações dos objetos no interior de um mesmo registro;
• converter tais representações de um dado registro para outro.
Percebemos, então, que há uma distinção entre os sistemas semióticos, de acordo com as atividades cognitivas que eles são capazes de desenvolver o dinamismo das representações semióticas em matemática e com a mobilização desses conceitos pelos alunos. Ademais, durante o processo de coordenação, o aluno deverá conseguir identificar as diferentes representações semióticas de um mesmo objeto matemático, além de dominar o processo de transformação de uma representação em outra.
Em vista disso, acreditamos que o computador e os softwares podem auxiliar na construção de representações semióticas. Assim, cabe observar:
Os computadores não constituem um novo registro de representação. E isso por uma razão simples: as representações que eles exibem são as mesmas aquelas produzidas graficamente no papel para uma apreensão visual. Ver uma figura geométrica no monitor ou vê-la no papel exige que nosso olhar faça a mesma desconstrução dimensional ou antecipe as mesmas operações merológicas. Analogamente, ver gráficos em monitor exige que sejamos capazes de reconhecer os valores visuais matematicamente pertinentes e coordená-los com os termos da equação ou do sistema de inequações correspondentes. No entanto, eles constituem um modo fenomenológico de produção radicalmente novo, fundamentado na aceleração dos tratamentos. Eles exibem no monitor tão rapidamente quando à produção mental, mas com uma potência de tratamento ilimitada em comparação com as possibilidades da modalidade gráfico-visual. Obtemos, imediatamente, muito mais que tudo o que poderíamos obter à mão livre após, talvez, vários dias de escritas e cálculos ou construção de figuras. A novidade fenomenológica mais espetacular se deve ao fato de que as representações semióticas não discursivas tornam-se manipuláveis como objetos reais. Podemos desloca-las, fazê-las rodar ou estendê-las a partir de um novo ponto. Esse aspecto “dinâmico” é apenas uma consequência da potência limitada do tratamento. Mas ele permite desenhar uma função que nenhum dos outros modos fenomenológicos permite: a função de simulação. Extremamente importante ora da matemática, essa função de simulação permite a exploração heurística de problemas matemáticos. (DUVAL, 2011, p.137, grifo no original)
Concordamos com Duval (2011), sobre o uso do computador, em especial, na formação inicial do futuro licenciando em Matemática, uma vez que, ao auxiliar na elaboração de atividades cognitivas que vão além da sua utilização, ele colabora para a construção do conhecimento e das habilidades que permitem ao aluno elaborar o conhecimento matemático, ou seja, o computador viabiliza realizar ações que levem à resolução de questões matemáticas. Já tendo discutido nesta seção acerca da semiótica e suas implicações para o ensino e a aprendizagem de matemática, a seguir indicaremos a metodologia da pesquisa.
3 METODOLOGIA
A opção metodológica que orientou a pesquisa foi a abordagem qualitativa, uma vez qua a natureza dos dados e a sua análise se constituem em uma forma mais textual, conforme descrito por Gonsalves (2007, p.69), ao salientar que a pesquisa qualitativa se preocupa mais "[...] com a compreensão, com a interpretação do fenômeno, considerando o significado que os outros dão às próprias práticas". Portanto, a pesquisa qualitativa é aquela que busca compreender concepções, atitudes e comportamentos dos sujeitos, participantes da pesquisa.
Em assim sendo, situamos esta pesquisa como um estudo de caso, isso porque, conforme pontua Yin (1989, p. 23), “O estudo de caso é uma inquirição empírica que investiga um fenômeno contemporâneo dentro de um contexto de vida real, quando a fronteira entre o fenômeno e o contexto não é claramente evidente e onde múltiplas fonte de evidencia são utilizadas”.
Esta pesquisa caracteriza-se, então, por ser um estudo de caso, visto que adota uma realidade específica de uma proposta pedagógica para a resolução de equações algébricas, integrando a História da Matemática e os recursos tecnológicos, no caso o software GeoGebra.
Para análise dos dados, adotamos duas perspectivas: a primeira para compreender como os alunos apreendem a História da Matemática e se valem dela; e a segunda, para examinar os problemas resolvidos. Para pôr em prática a primeira perspectiva, elegemos o Jogo de Vozes e Ecos, de Isoda (2000) e Boero, Pedemontti, Robotti(1997) e, para a segunda, os registros de representação semiótica de Duval (2009, 2011).
Por meio do uso da teoria de Jogos de Vozes e Ecos, assumida por Isoda (2000) e Boero, Pedemontti, Robotti(1997), procuramos compreender não apenas as ações, mas como elas são percebidas, o que elas refletem e como produzem o aprendizado da Geometria Analítica, a utilização da História da Matemática na construção de conceitos de Geometria Analítica e do software de geometria dinâmica GeoGebra como ferramenta para o ensino e aprendizagem dos conceitos de ponto, coordenadas cartesianas e equação da reta.
Esta perspectiva adota o construto teórico Vozes, de Bakhtin, que valida as concepçõesde Boero e a significação de aprendizagem (BOERO; PEDEMONTE; ROBOTTI, 1997).
Esta ótica busca compreender os conhecimentos culturais, aliados aos conhecimentos matemáticos, para proporcionar ao aluno a ampliação crítica do conhecimento. Assim sendo, o conhecimento é fruto de uma prática cultural mediada, resultante de atividades baseadas na cultura local, fruto da ação de pessoas comprometidas.
De acordo com este pensamento, adotamos em nosso trabalho a seguinte visão de cultura: “Consideramos cultura como o conjunto de mitos, valores, normas de comportamento e estilos de conhecimento, compartilhados por indivíduos vivendo num determinado tempo e espaço” (D’AMBROSIO, 2005, p.104).
A História da Matemática não é linear, seguindo uma linha vertical em relação ao tempo, pelo contrário, ela constrói conceitos de maneira localizada em um determinado tempo no espaço, como no caso de Oresme, Descartes, Fermat, Lacroix e tantos outros, pertencentes a uma realidade histórico-cultural de sua época.
O enfoque sociocultural de Jogos de Vozes e Ecos busca estabelecer uma conexão entre o passado e o presente, considerando suas representações, seus contextos históricos e sociais e seus significados próprios, sem que haja algum tipo de superioridade de um sobre o outro, mas sim, um diálogo. Como para nós é intangível alcançar o significado real de um conceito no passado, podemos (re)significá-lo no presente, utilizando como base nosso comportamento, nossas ferramentas tecnológicas e nossas concepções socioculturais históricas.
Desta forma, o conhecimento matemático passa por transformações, ou seja, é recriado ou podemos dizer que há uma coautoria-criação do aluno por meio da utilização de signos. Assim, os Jogos de Vozes e Ecos seriam as atividades que mediariam e permitiriam que essa apropriação se concretizassem, por criarum ambiente dialógico de aprendizagem.
O Eco é uma forma de ligação estabelecida entre pessoas e diferentes épocas e culturas com base em seus diferentes propósitos, experiências, concepções e sentidos, ou melhor, a interpretação que é dada a essa Voz do passado.
Vozes seriam as grandes descobertas da humanidade, como a teoria da queda dos corpos de Galileu e de Newton por exemplo, e as demonstrações matemáticas. Essas evoluções históricas exigiram a superação de vários obstáculos epistemológicos e a incorporação de conhecimentos anteriores.
A nossa escolha por utilizar fontes originais não é apenas para a compreensão, mas para:
[...] a produção de significações novas em suas próprias experiências e relacionamentos e aplicar em outras situações de ensino, quer seja uma aplicação direta envolvendo o mesmo assunto e a natureza dos registros usados quer seja uma aplicação indireta que promova uma aplicação de sua maneira integrada da História da Matemática com a situação educacional. (DYNNIKOV; SAD, 2007, p.07)
Boero, Garuti, Pedemonte e Robotti (2001, p.1) destacam que o "Jogo de Vozes e Ecos consiste na apropriação das vozes" da história pelos alunos (sob a orientação do professor) e da produção de “ecos”, que se materializam em novos conhecimentos, submetidos a um contexto. Conforme Boero, Pedemonte e Robotti (1997), durante a execução de atividades adequadas propostas pelo professor, o aluno tem a possibilidade de fazer as conexões com a voz e, com base nas suas próprias concepções e experiências, produzir um “eco”. Salientamos que este “eco” produzido é uma ação individual de cada aluno, portanto cada aluno pode produzir ecos de diferentes tipos.
Os ecos se apresentam de três tipos:
a) Eco mecânico: consiste em repetição precisa da voz;
b) Eco de assimilação: refere-se a uma transferência de conteúdo ou método
expressa pela voz em outra situação problema.
c) Eco ressonante: é uma apropriação de uma voz como um modo de reconsiderar e apresentar sua própria experiência. (DYNNIKOV; SAD, 2007,p.08)
Nós podemos adicionar às vozes explicitadas pelas autores a voz do professor. O que se espera é que o conjunto dessas vozes, aliado às atividades realizadas, produzam ecos ressonantes nos alunos, integrando-se às suas vozes.
No contexto da formação inicial, partindo dos dados produzidos, buscamos também compreender como a atividade geométrica, aliada ao GeoGebra e à História da Matemática, atuam para o desenvolvimento do pensamento geométrico, relacionado aos conceitos de ponto, sistema de coordenadas e equação da reta, para conjecturarmos acerca desses saberes, no que diz respeito à Geometria.
Após a realização do mapeamento de pesquisas brasileiras que envolvessem a temática estudada, escolhemos o software GeoGebra por ser ele um software que combina a Álgebra com a Geometria em uma única interface gráfica. Para mais, o software pode proporcionar ao aluno ter um contato mais direto com os objetos abstratos da matemática e trabalhar com representações geométricas e algébricas, simultaneamente. Com a possibilidade de movimentar, alterar, criar, comparar e deletar objetos matemáticos, o GeoGebra configura-se como um excelente recurso para o ensino e a aprendizagem de Matemática.
Para a produção dos dados, valemos-nos dos seguintes instrumentos:
• Questionário 1 - Caracterização dos colaboradores. Esse questionário, aplicado no início da oficina com os colaboradores, visava conhecer o perfil de nossos colaboradores, assim como identificar, em suas manifestações escritas, quanto à Geometria, aspectos positivos (por exemplo, gosto pela disciplina) ou negativos (por exemplo, experiências não tão boas vivenciadas na aprendizagem da Geometria)
• Aplicação dos Problemas Matemáticos. Foram aplicados seis problemas do Enem, selecionados após a aplicação do projeto piloto. A partir dos problemas, foram identificados, por meio das manifestações orais e escritas dos alunos, aspectos acerca da utilização da História da Matemática e das tecnologias para a resolução dos problemas. Os problemas foram resolvidos por eles sem qualquer intervenção da pesquisadora e, aofinal de cada problema, o colaborador recebia outro instrumento, o questionário de fechamento do problema.
• Questionário 2 – Fechamento do Problema. Este instumento tinha o propósito deconhecer não apenas quais conteúdos os alunos mobilizaram para resolver os problemas, como também identificar o nível de dificuldade atribuído a cada problema pelos colaboradores.
• Questionário 3 – Fechamento da Oficina. Por meio deste instrumento,aplicado no final do piloto e da oficina, buscamos conhecer quais os conteúdos que influenciaram os alunos, de maneira geral, para resolver os problemas, segundo as suas próprias declarações.
Além dos instrumentos já citados, utilizamos mais dois, que foram aplicados durante a produção dos dados, quais sejam:
• Entrevistas. Feitas no decorrer da produção dos dados, de forma dialogada, buscando informações adicionais às respostas dos problemas, pois somente os registros escritos não seriam suficientes para realizar as análises.
• Registro da produção de dados por meio de caderno de campo, questionário e gravação de áudio e audiovisual. Estes registros foram valiosos para a análise dos dados produzidos, pois nos permitiu cotejá-los.
A partir da resolução dos alunos, queríamos identificar os ecos produzidos por eles, oriundos das vozes do passado, o que possibilitaria a utilização de técnicas geométricas na resolução dos problemas, o processo de construção das resoluções pelos alunos, fazendo uso da tecnologia. Eles resolveram os problemas sem qualquer intervenção da pesquisadora.
A oficina foi realizada no laboratório de informática, pois se configura num ambiente tranquilo, onde temos à disposição o GeoGebra como ferramenta computacional para a resolução das atividades e é de fácil acesso aos colaboradores. A oficina foi organizada conforme o Quadro 1.
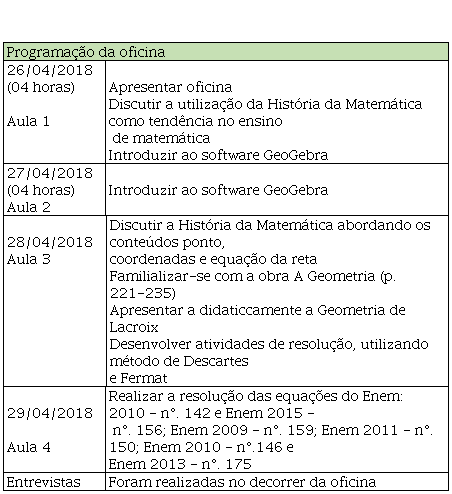
Didáticamente, dividimos a oficina em quatro etapas:
Etapa 1 – Expusemos alguns tópicos da história da Geometria Analítica, como o surgimento do sistema de coordenadas com Oresme, Lacroix e a geometria utilizada por Descartes e Fermat. Realizamos ainda a leitura de fragmentos da obra original traduzida A Geometria, de Descartes (p.221-234), para que os colaboradores conhecessem o método geométrico por ele apresentado. Nesta etapa, os alunos utilizaram, , no ambiente Lápis e Papel, régua e compasso para resolver os problemas, conforme proposto por Descates.
Etapa 2 - Desenvolvemos uma oficina, apresentando uma breve introdução das funcionalidades do software GeoGebra.
Etapa 3- Abordamos a geometria de Descartes a partir da resolução de problemas que envolvessem produto de segmentos, resolução da raiz quadrada, resolução de equação do primeiro grau e quadrática, utilizando o ambiente Lápis e Papel e o ambiente do software GeoGebra.
Etapa 4 - Apresentamos alguns problemas, previamente selecionados de provas do Enem, que trouxessem em seu enunciado tipos de representação semiótica distintos, de forma a nos permitir compreender como o aluno lida com essas representações. Também procuramos identificar as representações que os alunos utilizavam para resolver os problemas e as questões, e se eles demonstraram domínio na coordenação dos registros. Além disso, esperávamos identificar se haveria uso ou não da História da Matemática, por meio das vozes do passado, ou seja se haveria a produção de “ecos ressonantes” que influenciaram os alunos quando na resolução dos problemas.
4 ANÁLISES E RESULTADOS
Tecendo uma breve análise das observações realizadas durante a oficina. Os alunos manifestaram, em suas falas, a incredulidade no método geométrico, tanto que chegaram a testar este método com números de vários dígitos, a ponto de travar o computador. Inclusive, mostraram-se resistentes quanto ao método, por considerarem-no chato e demorado por terem que utilizar a régua e o compasso. Acreditamos que isso tenha ocorrido, por eles não estarem acostumados com a utilização destes instrumentos.
Um ponto positivo observado foi eles terem tido uma postura questionadora, de dúvida, não aceitando uma verdade por imposição da professora. Os dados foram coletados durante a oficina, buscando "ecos ressonantes" e transformações semióticas.
Optamos por desenvolver na oficina atividades que abordassem o uso de conteúdos da História da Matemática integrados à matemática contemporânea. Tínhamos uma expectativa de que os alunos utilizariam, como inspiração, os conteúdos da História da Matemática para resolver os problemas, gerando, assim, "ecos ressonantes".
Ancorados em Duval (2011, p.99), que afirma: "pensar em matemática mobiliza pelo menos dois registros" e "em geometria mobiliza a visualização e a linguagem", solicitamos que os alunos, para as respostas de cada problema do Enem, justificassem as suas respostas e utilizassem os ambientes Lápis e Papel e o software GeoGebra em suas resoluções. Tínhamos a intenção de integrar a teoria de Jogos de Vozes e Ecos, de Isoda (2000); Boero, Pedemonti, Robotti (1997) e a de Duval (2009, 2011), que nos permite analisar as respostas dos colaboradores e nos enseja responder ao problema central da presente pesquisa, qual seja: que estratégias os alunos utilizaram a partir da experiência com a História da Matemática e com o GeoGebra para resolver determinados problemas que envolvem coordenadas, pontos e equação da reta?
As resoluções individuais dos alunos colaboradores foram analisadas com base nos seus raciocínios matemáticos, expostos na forma de registos discursivos e não discursivos, e também com relação às suas falas e escritas, durante a resolução dos problemas na oficina. Consideramos sucessos, fracassos, hesitações, dúvidas com atenção especial para identificar os "ecos ressonantes” e as representações semióticas que poderiam surgir nesse processo. Optamos por realizar os registros, tanto na forma oral quanto escrita, pois vamos ao encontro da colocação de Duval (2011, p.105) que destaca que "[...] a produção oral e escrita não tem os mesmos papeis na tomada de consciência, pelos alunos, das operações específicas de cada registro e das unidades de sentido matematicamente pertinentes em uma representação". Neste contexto, muitas vezes, pode ser fácil para o aluno falar sobre uma determinada resolução oralmente, mas, diante da necessidade de se expressar por escrito, surgem questões relacionadas à tomada de consciência para a organização da escrita.
Levando em conta os pressupostos de Duval (2011), realizamos as análises, procurando identificar o raciocínio matemático que o aluno utilizou para responder corretamente o problema.
Sendo assim, observamos:
- se o problema foi resolvido corretamente;
- o tipo de registro que o aluno mobilizou durante a resolução do problema;
- o tipo de registro presente na resolução;
- a congruência entre os registros de representação semióticos;
- o aparecimento de “ecos ressonantes”.
Apresentaremos um recorte das atividades desenvolvidas, a fim de ilustrar a proposta pedagógica de integrar a História da Matemática e as TIC, evidenciando as resoluções do problema do Enem n.° 159, Caderno 7 – Azul, p. 25, desenvolvida pelos licenciandos, denominados aqui, ficticiamente, de Thiago e Sandra

Esperávamos que os alunos explorassem conhecimentos matemáticos que envolvessem ponto cartesiano, coordenadas cartesianas e encontrassem a equação da reta dados dois pontos. Assim como não tivessem dificuldades em resolver o problema, compreendendo as representações semióticas contidas no enunciado e, portanto, solucionassem corretamente o problema.
No questionário de caracterização do sujeito, observamos que tanto Thiago quanto Sandra não tinham manifestado uma atitude muito positiva quanto à Geometria, e para melhor entender o posicionamento deles, foi-lhes perguntado: “Se a geometria fosse descrita como um animal, qual você escolheria e por quê?”. Thiago respondeu:

A resposta de Thiago revela sua posição, quando ele faz uma analogia entre a Geometria e o elefante, dizendo: “se você não se cuidar pode passar em cima de você”.
Thiago resolveu o problema sem apresentar dificuldades com a leitura e a interpretação das informações contidas no enunciado. No GeoGebra, ele realizou duas estratégias de resolução distintas, as quais consideramos interessante apresentar. O aluno, ao utilizar o software GeoGebra, realizou duas conversões, a primeira é demonstrada, quando ele converteu da Representação Auxiliar de Transposição (tabela), apresentada no enunciado do problema, para o Registro Monofuncional Não Discursivo (RG), em que inseriu as coordenadas e traçou a reta que passa pelos pontos.
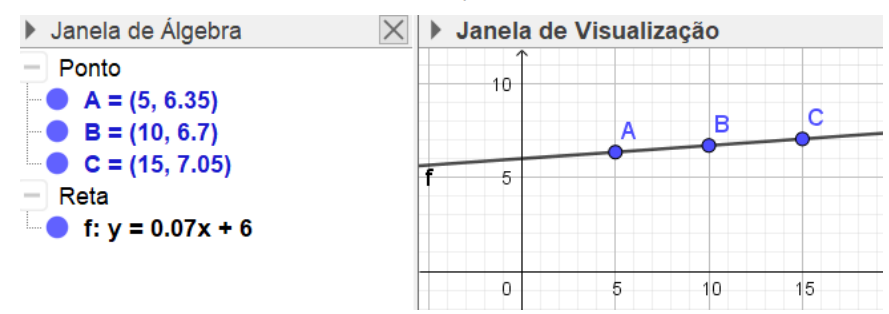
Em um segundo momento, fez uma segunda conversão, utilizando Registro Monofuncional Não Discursivo (RF – Registro figural), revelando um “eco ressonante”, pois realizou o cálculo, utilizando segmentos, conforme o método geométrico, utilizado por Descartes.
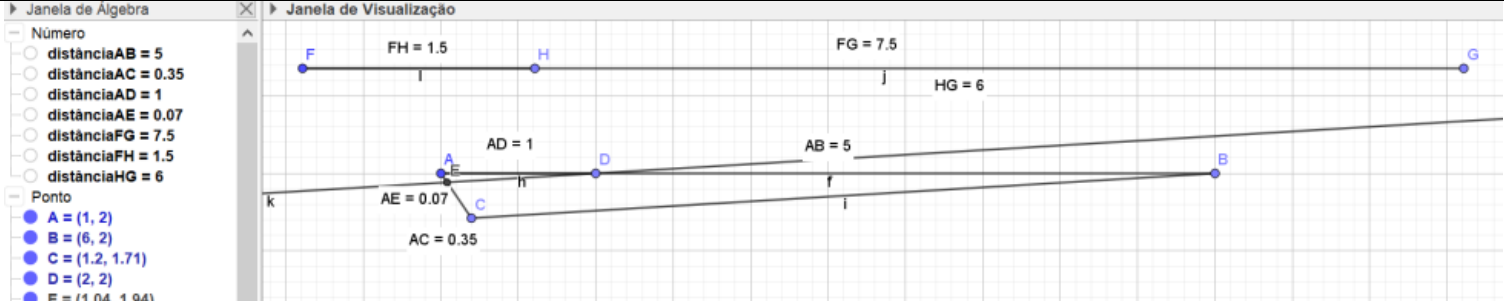
Ao ser solicitado utilizar uma resolução analítica, o aluno apresentou a resolução de um determinante para encontrar a equação da reta.
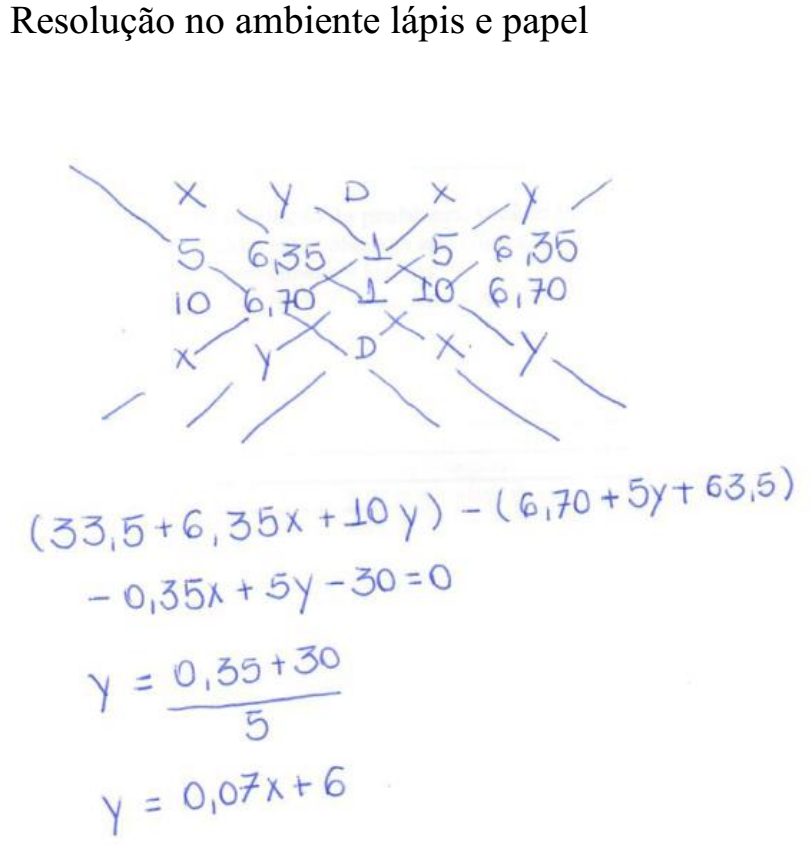
No ambiente Lápis e Papel, o aluno realizou uma conversão da Representação Auxiliar de Transposição (tabela) apresentada no enunciado do problema para o Registro de Representação Discursivo (RA).
Quanto à integração entre Tecnologia e História da Matemática, Thiago assim relatou:
Thiago: Alguns problemas usei conceitos históricos, outros usei conceitos matemáticos e o software também me ajudou a resolver os problemas. As atividades mudaram a minha forma de ver e fazer a Matemática.
(Relato de Thiago, 2018).
Ao analisarmos as respostas do questionário de caracterização do sujeito, as resoluções em ambos os ambientes, as entrevistas, os registros em caderno de campo e o questionário de fechamento do problema, foi possível constatar que, mesmo Thiago, demonstrando algum receio do conteúdo de Geometria, ele conseguiu superá-lo e integrar a História da Matemática com a Tecnologia.

O aluno expressou, no questionário de fechamento do problema, que, para resolver a questão, se valeu tanto dos conhecimentos já aprendidos, quanto daqueles adquiridos durante a oficina, gerando, assim, “ecos ressonantes”.
No caso de Sandra, ao analisarmos o questionário de caracterização do sujeito, percebemos que ela, do mesmo modo, não demonstrou um sentimento positivo com relação à Geometria, pois a comparou a um Leão, ressaltando temor em sua resposta, ao escrever “se você não se cuidar ele te mata”.
Tanto Thiago como Sandra revelaram em suas respostas no questionário de caracterização do sujeito algum temor quanto à Geometria, pois ambos a compararam a um animal poderoso que pode matar.

Sandra relatou sentir dificuldades no processo de resolução do problema e na interpretação das informações contidas no enunciado. Mas chegou à resposta correta para o problema em ambos os ambientes. Em registro oral, a aluna revelou ter tido dúvidas na interpretação, ou seja, na compreensão das representações semióticas contidas no enunciado do problema, mas conseguiu vencer essa dificuldade.
No ambiente do software GeoGebra, apresentou uma resolução semelhante à segunda realizada por Thiago, neste ambiente.
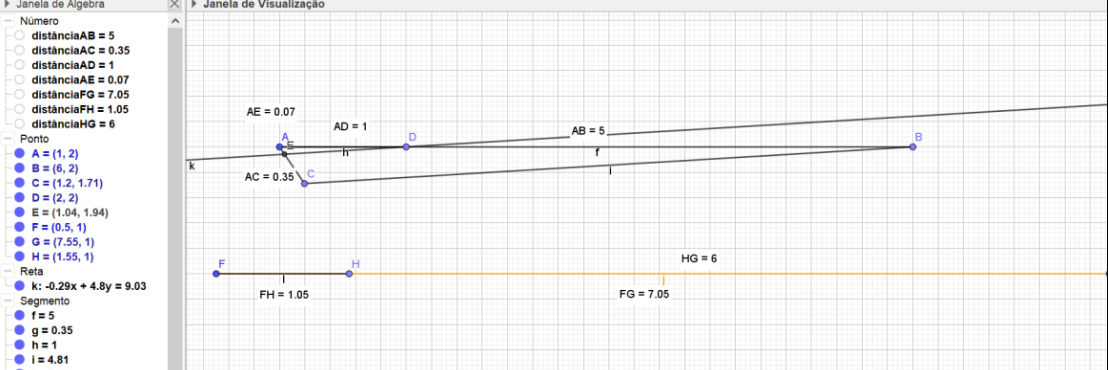
No ambiente Lápis e Papel, a aluna revelou pensamento algébrico, pois partiu da equação reduzida da reta, usando os pontos conhecidos no enunciado do problema para encontrar os coeficientes a e b., realizando a segunda conversão, apresentando em sua resolução o Registro Monofuncional Discursivo (RA).

A resposta dada por Sandra nos levou a perceber a presença do “eco ressonante”, pois, ao ter contato com a obra original traduzida A Geometria, de Descartes, ela conseguiu transpor o pensamento ali presente para a resolução de um problema atual. A fala dela indica ter havido um “eco ressonante”:
No GeoGebra resolvi a questão utilizando o pensamento de Descartes sobre cálculos
com retas (Relato Sandra, 2018)
Ao analisarmos as respostas do questionário de caracterização do sujeito, as resoluções em ambos os ambientes, as entrevistas e os registros em caderno de campo, foi possível constatar que mesmo Sandra, apresentando alguma dificuldade e receio do conteúdo de Geometria, conseguiu superá-los.

E, ao observarmos as resoluções em ambos os ambientes, integrando a História da Matemática e a Tecnologia, e a resposta dada pela aluna no questionário de fechamento do problema, vemos que ela ressignificou o que já tinha aprendido, gerando, portanto, “ecos ressonantes”.
5 CONCLUSÕES
Em nossa investigação, escolhemos trabalhar com uma proposta pedagógica que integrasse a História da Matemática e os recursos tecnológico, como o software GeoGebra, em atividade de resolução de problemas matemáticos. Para alcançarmos nosso objetivo, ofertamos uma oficina, onde trabalhamos, de maneira integrada, a História da Matemática e as Tecnologias, permitindo que os alunos desenvolvesem estratégias cognitivas, construissem significações, favorecendo a compreensão de conceitos como ponto, coordenadas e equação da reta. Por meio dessa oficina, foi possível responder à nossa questão norteadora da pesquisa que era: “Que estratégias os alunos utilizam a partir da experiência com a História da Matemática e com o GeoGebra para resolver determinados problemas que envolvam coordenadas, ponto e equação da reta? Verificamos, com base nos relatos expressos nas entrevistas e nos registros dos questionários de fechamento dos problemas, que os alunos mobilizaram conhecimentos algébricos, conceitos matemáticos, lógicos e históricos para a resolução das atividades, pois eles fizeram representações semióticas, realizadas nos ambientes Lápis e Papel e no do software GeoGebra, como também executaram a convergência entre esses registros de representação semiótico, presentes nos exercícios.
Apontamos a viabilidade da prática pedagógica proposta, já que, por meio da História da Geometria Analítica e do uso do software GeoGebra, os alunos puderam construir significações, favorecendo a compreensão de conceitos como ponto, coordenadas e equação da reta. A construção do conhecimento geométrico por parte dos alunos se deu de forma ativa, permitindo-lhes se apropriarem das "vozes do passado" e, por meio dos "ecos" produzidos, resolverem os problemas propostos.
A proposta pedagógica desenvolvida favoreceu que os alunos tanto construíssem o conhecimento matemático, por meio da exploração e da argumentação, quanto refletissem acerca dos conceitos matemáticos, como pudemos constatar na fala de um participante que revelou ter havido uma mudança na forma de perceber a Matemática e na sua concepção do que é "ver e fazer" matemática. Ao criarmos oportunidades para os alunos discutirem e pensarem sobre o "fazer" e “ver” matemática, promovemos um amadurecimento quanto às convicções teóricas e práticas deles.
Percebemos que os alunos tiveram que ressignificar o que foi aprendido para encontrar estratégias de resolução para os problemas propostos, o que vem ao encontro da teoria de Duval (2011) que afirma que o aluno pode dar um significado novo àquilo que já foi aprendido.
Em algumas resoluções dos alunos participantes, “ouvimos” “ecos ressonantes” da História da Matemática, pois, inicialmente, conseguiram compreender o conhecimento transmitido pela voz e, posteriormente, adaptaram e transferiram o método para outras situações, se apropriando, então, do conteúdo da voz e expressando o conceito com suas próprias palavras.
Observamos que, ao serem apresentados diferentes olhares sobre um mesmo objeto matemático, isso ajuda na construção de um cenário que permite construir o nosso próprio conhecimento, com base em nossas experiências e conclusões acerca das representações apresentadas.
Salientamos também o caráter dinâmico do software como uma possibilidade de formatação e registro semiótico, que, aliado aos demais, oportuniza a a construção do conhecimento.
Diante dos dados obtidos na pesquisa, concluímos a significância da utilização de diversas representações semióticas e de suas conversões para o aprendizado da Matemática, pois, desse modo, contribuiremos para que os nossos alunos desenvolvam os seus processos cognitivos, melhorando a capacidade de raciocínio, interpretação, visualização e análise.
E ainda julgamos ter não apenas respondido à nossa questão investigativa como fomos muito além do que esperávamos, considerando a presença de distintas representações semióticas e resoluções produzidas pelos alunos na resolução dos problemas e atividades propostas, assim como a postura de independência, apresentada pelos eles durante esse processo, e a produção de "ecos ressonantes". Cumpre afirmar que a História da Matemática, inserida no ensino de Geometria Analítica, e o uso do software GeoGebra possibilitaram ao aluno desenvolver estratégias de resolução que, sem dúvida, contribuíram para ele ressignificar os conceitos básicos tanto da Geometria quanto da Álgebra.
REFERÊNCIAS
BOERO, P.; PEDEMONTE, B.; ROBOTTI, E. Approaching Theoretical Knowledge Through Voices and Echoes: a Vygotskian perspective. In: PME CONFERENCE, 21nd, 1997, Finlândia. Anais eletrônicos[...]. Disponível em https://www.researchgate.net/profile/Paolo_Boero2/publication/239864337_APPROACHING_THEORETICAL_KNOWLEDGE_THROUGH_VOICES_AND_ECHOES_A_VYGOTSKIAN_PERSPECTIVE/links/0a85e52f2cdc1ae280000000.pdf Acesso em: 01 fev.2016
BOERO, P.;GARUTI, R.;PEDEMONTE, B.; ROBOTTI, E. Il "gioco voci-echi" come metodologia per la mediazione degli aspetti salienti delle teorie. In: INTERNUCLEI SCUOLA DELL'OBBLIGO, IV, 2001, Itália. Anais eletrônicos [...]. Disponível em: http://www.math.unipr.it/~rivista/guzzoni/AVVENIMENTI/PDFMONTICELLI/BOERO.PDF. Acesso em: 15 jan. 2017.
BRASIL, Ministério da Educação. Base Nacional Comum Curricular (2.ver.). Brasília, DF: MEC, 2016. Disponível em: http://basenacionalcomum.mec.gov.br/wp-content/uploads/2018/02/bncc-20dez-site.pdf Acesso em: 08 out. 2017.
D’AMBRÓSIO, U. Sociedade, cultura, matemática e seu ensino. In: Educação e Pesquisa – Revista da Faculdade de Educação da Universidade de São Paulo, v. 31, n. 1, p. 99-120, jan./abr. 2005
D’AMORE, B.; PINILLA, M.; IORI , M. Primeiros elementos da semiótica: sua presença e sua importância no ensino e aprendizagem da matemática. São Paulo: Editora Livraria da Física, 2015.
DESCARTES, R. A Geometria. Tradução Emídio César de Queiróz Lopes. Lisboa: Editorial Prometeu, 2001.
DUVAL, R. Semiósis e pensamento humano: registro semiótico e aprendizagens intelectuais. São Paulo: Editora Livraria da Física, 2009.
______. Ver e ensinar a matemática de outra forma: entrar no modo matemático de pensar: os registros de representações semióticas. São Paulo: PROEM, 2011.
DYNNIKOV, C. M.S. da S.; SAD, L. A. Uma abordagem pedagógica para o uso de fontes originais em História da Matemática. Guarapuava: SBHMat, 2007
ENEM 2009 – Exame Nacional do Ensino Médio. INEP -Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Ministério da Educação.
GONSALVES, E. P. Iniciação à Pesquisa Científica.4. ed. Campinas -SP: Alínea, 2007.
HENRIQUES, A.; ALMOULOUD, S. A. Teoria dos registros de representação semiótica em pesquisas na Educação Matemática no Ensino Superior: uma análise de superfícies e funções de duas variáveis com intervenção do software Maple. Ciência e Educação, Bauru, v.22 n.2, p. 465 - 487, abr./jun 2016. Disponível em:http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1516-73132016000200465. Acesso em: 12 fev 2017.
ISODA, M. Inquiring mathematics with history and software. History in mathematics educacion. The ICMI study. Dodrecht, Boston, London: Kluwer Academic Publishers, 2000, p.351 - 358.
MIGUEL, A. Três estudos sobre História e Educação Matemática. 1999.361 f.Tese (Doutorado), - Faculdade de Educação, Departamento de Metodologia de Ensino, Universidade Estadual de Campinas, 1993. Disponível em: http://repositorio.unicamp.br/jspui/handle/REPOSIP/253114. Acesso em: 03 mar. 2017.
YIN, Robert K. Case study research - design and methods. Sage Publications Inc., USA, 1989.
Notas
Autor notes
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/10622 (pdf)

