INTRODUCCIÓN:
El origen del análisis multivariado se remonta a los
comienzos del siglo XX, con Pearson y Sperman. En términos generales, el
análisis multivariado se refiere a todos aquellos métodos estadísticos que
analizan simultáneamente medidas múltiples (más de dos variables) de un
fenómeno (IPGRI, 2003). En muchas ocasiones el investigador tiene una matriz de
información en la que se puede prescindir de algunas variables sin que la
información total disminuya. El método de los componentes principales y el
análisis factorial son métodos que permiten explicar con un número reducido de
nuevas variables (factores), la información de determinado experimento
(Álvarez, 1995).
Cádiz: Servicio de publicaciones de la Universidad de Cádiz. ducir la dimensionalidad de un conjunto de datos dentro de una nueva combinación lineal de nuevas variables (o componentes principales) con la capacidad de retener toda la variabilidad de las variables originales. En la práctica de la caracterización, re- ordena a las poblaciones en términos de una combinación de nuevas variables o componentes principales no correlacionados (Jolliffe, 1972). Este análisis extrae las componentes principales ortogonales de forma que la primera de ellas tiene una mayor varianza asignada que aquella existente en el espacio definido por la variables originales, procediendo con el mismo criterio de extracción para el resto de las siguientes componentes principales, pero sobre la varianza que ha sido asignada a las anteriores componentes que ya han sido extraídas (Salafranca, Sierra, Núñez, Solanas y Leiva 2005).
Las nuevas variables son combinaciones lineales de las anteriores y se van construyendo según el orden de importancia en cuanto a la variabilidad total que recogen de la muestra. De modo ideal, se buscan menor cantidad de variables que sean combinaciones lineales de las originales y que no estén incorreladas, recogiendo la mayor parte de la información o variabilidad de los datos. Si las variables originales están incorreladas de partida, entonces no tiene sentido realizar un análisis de componentes principales. El análisis de componentes principales es una técnica matemática que no requiere la suposición de normalidad multivariante de los datos, aunque si esto último se cumple se puede dar una interpretación más profunda de dichos componentes (Marín, 2006).
El análisis factorial por su parte, es una técnica de
interdependencia, cuyo objetivo principal es disminuir la estructura subyacente
entre las variables en análisis. (Hair,
Black, Babin, y Anderson, 2010). Su
finalidad es la de describir o explicar en una
forma parsimoniosa la estructura de dichas relaciones, de acuerdo con un modelo
previo basado en una serie de supuestos generales. Dependiendo del tipo
de rotación que se utilice, los factores
latentes pueden estar correlacionados o, por el contrario, ser independientes.
Las variables observadas pueden estar afectadas por más de un factor, incluso
por todos los factores. Todas las variables observadas están afectadas por un
único término de error (Barbero, Vila y Holgado, 2013).
En el análisis factorial, las variables que interesan reciben el nombre de variables latentes y estas se relacionan con las variables observadas, siendo este un modelo de regresión múltiple. Tiene muchas similitudes con el análisis de componentes principales, y busca esencialmente nuevas variables o factores que expliquen los datos. En el análisis de componentes principales, sólo se hacen transformaciones ortogonales de las variables originales. En el análisis factorial, interesa más explicar la estructura de las covarianzas entre las variables. En ambos es necesario que las variables originales no estén incorreladas (Marín, 2006).
El hecho de tomar un número adecuado de factores k para representar las covarianzas observadas es muy importante: entre una solución con k ó con k + 1 factores se pueden encontrar pesos factoriales muy diferentes, al contrario que en el método de componentes principales, donde los primeros k componentes son siempre iguales. Cuando se consigue una estructura simple, las variables observadas se encuentran en grupos mutuamente excluyentes de modo que los pesos son altos en unos pocos factores y bajos en el resto (Marín, 2006).
Para el presente análisis se utilizaron datos correspondientes a los indicadores utilizados por el Banco Mundial (2015) para hacer estudios sobre el cambio climático global, tanto sus causas, como sus consecuencias sobre la población. Se prevé que el cambio climático afectará más gravemente a los países en desarrollo. Sus efectos (altas temperaturas, cambios en el régimen de precipitaciones, aumento del nivel del mar y desastres más frecuentes relacionados con el clima) representan riesgos para la agricultura, los alimentos y el suministro de agua. El Grupo del Banco Mundial y sus países asociados, otorgan datos para su estudio que cubren los sistemas climáticos, la exposición a los impactos del clima, la adaptación, las emisiones de gases de efecto invernadero y el consumo de energía.
Para el análisis estadístico se utilizó el programa de acceso libre “R”. R es un lenguaje de programación y un entorno para el análisis estadístico y la realización de gráficos. Fue inicialmente escrito por Robert Gentleman y Ross Ihaka, del Departamento de Estadística de la Universidad de Auckland en Nueva Zelanda. R actualmente es el resultado de un esfuerzo de colaboración de personas de todo el mundo. La calidad de los gráficos producidos y la posibilidad de incluir en ellos símbolos y fórmulas matemáticas, posibilitan su inclusión en publicaciones. Usa el “objeto” como entidad básica. Cada objeto pertenece a una clase, de forma que las funciones pueden tener comportamientos diferentes en función de la clase a la que pertenece su objeto argumento (Arriaza, Fernández, López, Muñoz, Pérez y Sánchez, 2008).
DESCRIPCIÓN DE
DATOS:
Dado que los datos son muy variados y para muchos países,
se seleccionaron algunos no correlacionados para ver si tienen alguna
correlación hacia conceptos más
generales, por medio de las componentes principales y el
análisis factorial. Para este caso se seleccionaron datos correspondientes
al año 2012, puesto que son los más completos encontrados.
Se eligieron los países de América
Latina, 21 en total, pues en su mayoría sus condiciones son similares. Se seleccionaron datos que intentan correlacionar la pérdida de área selvática y áreas protegidas (como pulmones naturales), contra la presión de la agricultura y la población. Se tomaron para cada país las siguientes variables: Tierras agrícolas (% del área de tierra), Área selvática (% del área de tierra), Áreas terrestres protegidas (% del total del área de la tierra), Crecimiento de la población (% anual),Población total (habitantes), Crecimiento de la población urbana (% anual), Población urbana (habitantes).Como se puede ver, las variables seleccionadas tienen cierta correlación, un requisito indispensable para hacer el análisis de sus componentes principales y un análisis factorial. Para este último análisis, estos datos se verán reducidos para encontrar grupos homogéneos de variables puesto que unos grupos son independientes de otros. A diferencia de lo que ocurriría si se usaran otras técnicas como el análisis de varianza o el de regresión, en el análisis factorial todas las variables del análisis cumplen el mismo papel:todas ellas son independientes en el sentido de que no existe a priori una dependencia conceptual de unas variables sobre otras. Los datos son presentados a continuación en la Tabla I.
Tabla I
Datos seleccionados de indicadores del desarrollo humano para 2012.
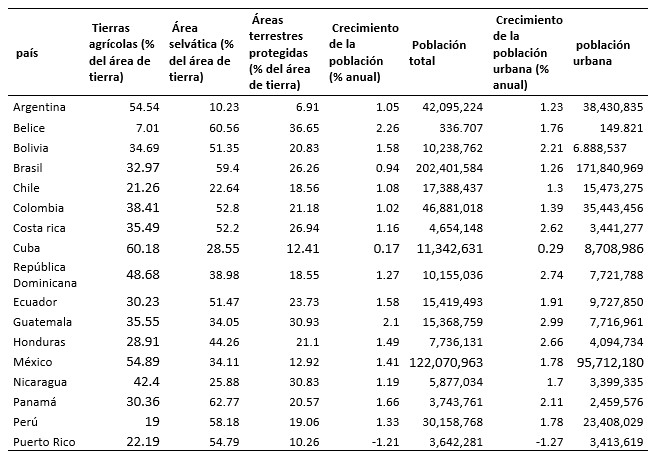 Elaboración propia con datos de licencia abierta del Banco Mundial (2015)
Elaboración propia con datos de licencia abierta del Banco Mundial (2015)
Los datos son cargados a R, a partir de un archivo de texto
(datos.txt, por ejemplo), separado por tabulaciones. Para la carga se utilizan el comando read.table y se asigna a un objeto al se
le da un nombre, por ejemplo “data”, así: data <- read.table("datos.txt", header=TRUE). Esta será la base de datos a utilizar en el análisis.
RESULTADOS
OBTENIDOS DEL ANÁLISIS COMPONENTES PRINCIPALES:
Se ingresaron los datos siendo estos las
21 filas de países y las 7 variables a analizar. En este caso no se descartó
ninguna del análisis inicial, pues no se considerar directamente dependiente
una de todas las demás. Para facilitar la interpretación de datos se hizo la
asignación de los nombres reales a la columna 1. Se hizo el cálculo de las
componentes principales, utilizando la
función princomp, asignada al objeto
nombrado “cp”, así: cp
<- princomp(data[,-1], cor=TRUE) y a continuación se
obtuvo la tabla de la importancia de las componentes, con la instrucción summary, aplicada al objeto “cp”, así: summary(cp),
cuyos resultados se muestran en la Tabla II, de mayor a
menor de acuerdo a su varianza. Tabla II
Tabla II
Importancia de las componentes principales de los datos de la Tabla I.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
Se puede observar que para las componentes de 1 hasta 3 se
tienen valores de la desviación estándar mayores a 1, por lo que son las componentes
principales a analizar, las que pueden dar una agrupación de datos que
delimiten un concepto. En las demás componentes (de 4 a 7), el valor de la desviación disminuye, pero
la proporción acumulada de la varianza aumenta, por lo que no les hace útiles
en el análisis en general. De esta forma se reduce de 7 variables
correlacionadas de alguna manera a 3
componentes no correlacionadas, pero que pueden describir
conceptos diferentes que no tienen que ver con las correlaciones posibles
iniciales. Se genera el gráfico de auto-valores para las componentes
principales (Gráfico 1), con la instrucción plot,
así: plot(cp,type="lines"). Gráfico 1
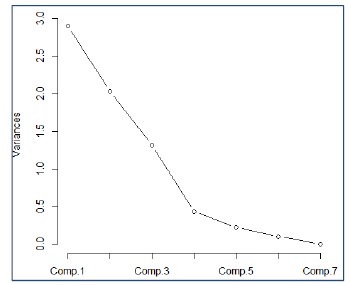 Gráfico 1
Auto-valores de componentes principales. Fuente: Generada por R de datos asignados.
Gráfico 1
Auto-valores de componentes principales. Fuente: Generada por R de datos asignados.
Se puede observar en el gráfico que todos los valores de varianza son mayores a 1 en las componentes principales de 1 a 3. Esto es un requisito indispensable para que sean útiles en el análisis del concepto que las variables asociadas pueda agrupar. A continuación se genera la tabla de datos (Tabla III) que reporta los coeficientes significativos de las componentes principales, aquí se pueden identificar las variables que están asociadas a cada componente. Esto se hace con la función loadings, siempre asignada al objeto “cp”, así:loadings(cp). Este comando da los datos tanto para las variables de estudio, como para los países estudiados. Tabla III
Tabla III
Coeficientes significativos de las componentes principales.
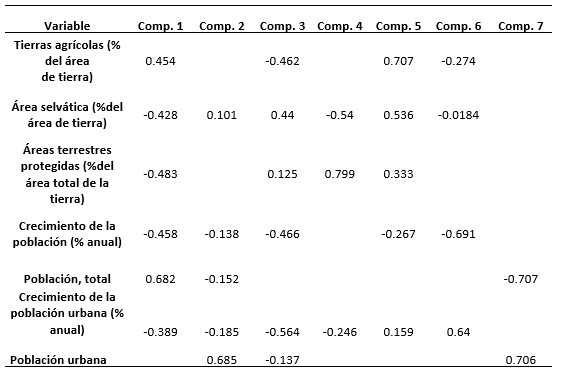 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
En estos datos ya se
pueden ver algunas relaciones interesantes. Para la componente 1 se puede ver
que la población total y las tierras agrícolas van en el mismo sentido, lo
empieza a dilucidar un concepto de necesidad de alimentación. En el caso de
la componente 2 se puede ver que el área selvática es contraria a los
crecimientos de población en la misma proporción, que empieza a verse como el
concepto de necesidad de tierra para vivienda. En el caso de la tercera
componente se puede ver que el crecimiento de la población urbana va junto con el crecimiento total y las tierras agrícolas, pero
en contra de la tierra selvática,
que propone el concepto de pérdida de
ecosistemas. Ahora se pueden ver los
coeficientes significativos de las tres componentes principales (de 1 a 3) pero desde el punto de vista de
los países y su relación con estas componentes (Tabla IV). En este caso se puede observar cuanto se
acercan o alejando de los conceptos que ya se ha esbozado cada uno de
los países. Se pueden observar
países como Cuba, México y Puerto Rico que van teniendo ciertos valores particulares y que se alejan de la tendencia marcada por las componentes principales, esto demuestra que se pueden alejar de los conceptos creados. Por el otro lado se puede ver laque mayoría tienden a tener valores menos variantes y más cercanos a los conceptos que se empiezan a marcar. Esto es más notorio en la representación gráfica comparativa de las componentes principales. Tabla IV
Tabla IV
Coeficientes significativos respecto a los países en estudio.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
Luego se general los gráficos 2 y 3, con que comparan las
componentes principales obtenidas, esto con el comendo biplot, para ambos casos, respectivamente: biplot(cp, choices=1:2) y biplot(cp, choices=2:3). En el
caso del Gráfico 2, se puede observar que se marca una tendencia hacia la
agrupación de los crecimientos poblacionales en general junto con la tendencia
en el eje opuesto de las áreas selváticas y protegidas (este en menor cantidad
puesto que presenta cambios o representatividades mínimas contra el total de la
tierra), y balaceado por la marca positiva de la tendencia a mayor cantidad de
tierras agrícolas. Esto refuerza la creación del concepto de “Necesidad de alimento”, que ya se relaciona con la componente 1. Por el lado de la componente 2, se puede observar que estando las tierras agrícolas cercana al origen de este eje, y las fuertes diferencias en las demás variables, se puede también cimentar el concepto de “Necesidad de tierra para vivienda”, pues las relaciones de habitantes y crecimientos se manejan en este eje en oposición contralas áreas protegidas o selváticas. Aquí se puede observar los países que empiezan a ver mayormente afectados por estos fenómenos, en especial hacia el lado de la componente 2 y el concepto de “Necesidad de tierra para vivienda”, pues por razones de áreas protegidas y tamaño puede no tener mayores incrementos entierras agrícolas. Caso contrario en los países como Brasil y México, donde el aumento de tierras agrícolas contra la población es grande y remarca el concepto de “Necesidad de alimento”. También está el caso de países como Cuba, Argentina y Uruguay, donde no esta tan marcada ninguna de estas dos relaciones,tendiendo un poco más hacia la componente 2.
Para el gráfico 3, el concepto asociado a la componente 2
se remarca mucho más, pues el crecimiento poblacional sigue estando
marcadamente relacionado con el aumento en las tierras agrícolas. Aquí se puede ver muy bien la componente 3, donde en sentidos opuestos muy marcados se
puede ver que las áreas selváticas y protegidas van en total contraposición de los demás
indicadores, reforzando el concepto de “Pérdida de ecosistemas”, asociado al
desarrollo humano por crecimiento poblacional.
 Gráfico 2
Componente 1 versus Componente 2.
Generada por programa R de datos asignados.
Gráfico 2
Componente 1 versus Componente 2.
Generada por programa R de datos asignados.
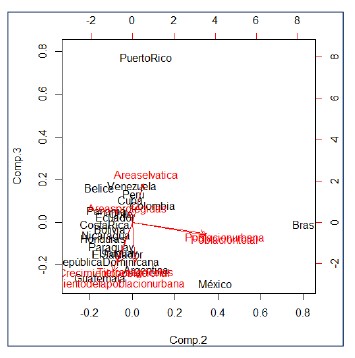 Gráfico 3
Componente 2 versus Componente 3.
Generada por programa R de datos asignados.
Gráfico 3
Componente 2 versus Componente 3.
Generada por programa R de datos asignados.
RESULTADOS
OBTENIDOS DEL ANÁLISIS FACTORIAL:
En el caso del análisis factorial, con los mismos datos anteriores, se prueba una solución factorial con un factor. Esto se hace con la función factanal, asignada al objeto que se llamó “factor1”, así:
factor1 <- factanal(datos[,-1], factors=1, rotation="none", scores="regression")
Al reportar los datos se pueden obtener las siguientes tablas. En la Tabla V, se pueden observar las singularidades de las variables, esta es una parte de variabilidad única, individual o específica de la variable, no asociada con ninguno de los factores asociados a esta. Tabla V
Tabla V
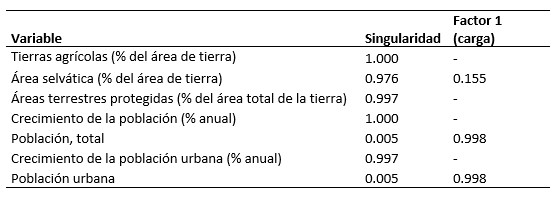
Singularidad y Carga de las variables, solución factorial de 1 factor.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
Se puede observar que para las variables de suma total de población (total y urbana) las cargas son las más grandes, y una mínima en área selvática. Las demás variables tienen una carga tan pequeña que el programa R no las muestra para denotar las de mayor valor. Estos valores para estas variables observadas, son los que más aportan a la varianza de total de las variables latentes, pues muestran que son los que más se alejan de la correlación buscada. Esto también se puede observar y de mejor manera al analizar los valores obtenidos para las singularidades de cada variable. En estas se puede ver que los valores más bajos son para estas variables, estando muy cercanas a cero. Por el contrario se puede ver que existe una relación directa entre el crecimiento de la población y el de las áreas de tierras agrícolas, con un valor máximo de 1. Después también se observa que las áreas protegidas y el crecimiento de población urbana están también relacionados y con valores muy cercanos a las primeras dos. En el punto intermedio, pero con una carga más baja y una singularidad relativamente alta está el área selvática, pues esta debe tener más relación con las áreas protegidas y su disminución debido al crecimiento de la población en total y la población urbana.
La suma de cargas factoriales para este primer factor da un valor de 2.023, que es el “valor propio” de este factor y cuya cifra es elevada. Esto se corrobora con la varianza proporcional con un valor de 0.289 que es muy bajo, lo que dice que este primer factor no puede explicar las variables latentes de esta serie de datos.
De tal cuenta se realiza el mismo ejercicio pero para dos factores más. Los valores de singularidad para los factores 2 y 3 se muestran en la Tabla VI.
Tabla VI
Singularidad para las soluciones factoriales de 2 y 3 factores.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
En la singularidad de 2
factores se puede ver que se relacionan otras variables, distintas a la de un
factor. En este caso las tierras agrícolas, áreas selváticas y protegidas se
relacionan íntimamente en este análisis. Es bastante apegado al marco teórico
que precede a las variables, pues en los tres casos se valoriza el uso de la
tierra. Los demás factores asociados a la población se ven excluidos. Se colocó
el mismo cuadro la singularidad para 3 factores para hacer un
comparativo y en este caso las singularidades disminuyen su valor, llegando simplemente a relacionar áreas selvática y protegida, aportando datos más dispersos que el anterior. Tabla VII
Tabla VII
Carga de las variables para la solución factorial de 2 factores.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
En la Tabla VII, se presentan los datos que corresponden a
las cargas para dos factores se puede observar que también los valores más
bajos se expresan para las variables relacionadas con el uso de la tierra. Para la carga del factor 2 se puede observar que como en análisis de un factor,
la población total y urbana se relacionan y discrepan de los demás
resultados que no se presentan por tener valores muy bajos. Posteriormente se calculan los auto-valores y
las varianzas para conocer si es válido el análisis de 2 factores analizando de
acuerdo al test de la hipótesis nula. Los datos se presentan en la Tabla VIII.
Tabla VIII
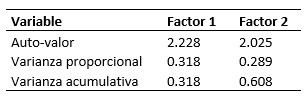
Auto-valores y varianzas para la solución factorial de 2 factores.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
Se puede observar que para el factor 2 la varianza acumulativa llega a 0.608 lo que es mejor al análisis de un factor donde solo era 0.289. Sin embargo se puede ver la prueba de hipótesis que se tiene 8 grados de libertad, en menor que los 14 grados del anterior análisis, pero aún es alto, por lo que se realiza continua con el análisis para 3 factores. Tabla IX
Tabla IX
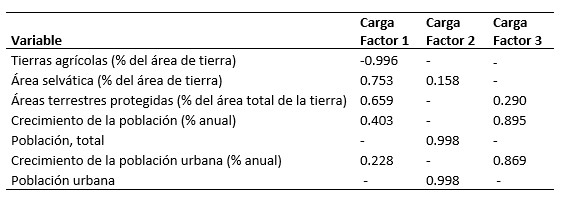
Carga de las variables para la solución factorial de 3 factores.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
En
este análisis ya se puede ver las cargas mejor adaptadas para cada variable. El
Factor 1 se ve asociado nuevamente a las áreas protegidas y selváticas, contra
las tierras agrícolas, esto quiere decir que expresa el uso de la tierra como
concepto principal. El Factor 2 relaciona las poblaciones y en menor medida el
área selvática, por lo que se puede asociar este al concepto de relación de
población urbana versus la total. El Factor 3, toma los últimos conceptos y en
este caso relaciona los crecimientos poblacionales (tanto urbana como total)
contra las áreas protegidas, se puede discernir el concepto de pérdidas de
áreas protegidas por crecimientos poblacionales.
Tabla X
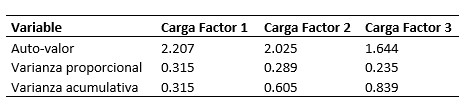
Auto-valores y varianzas para la solución factorial de 3 factores.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
En la Tabla X se puede ver que los auto-valores
van disminuyendo hasta el factor 3. También la varianza proporcional. La
varianza acumulativa disminuye hasta un valor de 0.839, lo que ya es aceptable
para considerar que este análisis es el más adecuado. Se corrobora con la prueba de hipótesis nula que baja los grados de libertad hasta 3, un margen de error mínimo y aceptable.
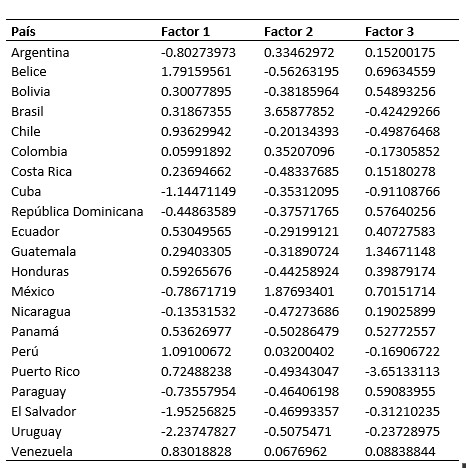
Tabla XI
Calificaciones para la solución factorial de 3 factores.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
En la Tabla XI, se muestran las calificaciones para los
tres factores en el análisis factorial. Esta calificación denota la importancia
relativa a los conceptos asociados para cada factor. Sin embargo de esta forma
no es muy fácil visualizarlo, por lo que se hace una ponderación, por
ejemplo sobre 10 de estos valores. Para el factor 1, se observa en la Tabla XII, utilizando una media de 6.5 y una
desviación estándar de 2. Tabla XII
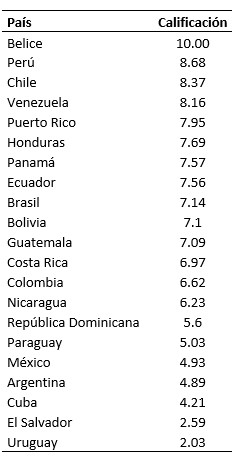
Tabla XII
Calificaciones para la solución factorial de 3 factores, del Factor 1.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
Para el factor 1, se asoció el concepto de uso de la tierra. En la ponderación
asignada y ordenada se puede ver que países como Belice y Perú aparecen
como primeros. Esto tiene en cuenta que sus áreas protegidas y selváticas son
mayores en relación a la tierra total. Por el contrario los últimos países como
El Salvador y Uruguay con extensión territorial menor tienen más baja esta
relación. Para el factor 2 se hizo el mismo ejercicio y los datos de las ponderaciones se presentan en la
Tabla XIII, con los mismo parámetros
de media y desviación estándar. Tabla XIII
Tabla XIII
Calificaciones para la solución factorial de 3 factores, del Factor 2.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
Este caso es totalmente diferente pues el concepto asociado es básicamente la cantidad de habitantes, población total contra área selvática. Los países con mayor densidad poblacional lideran esta lista, como lo son Brasil y México y en especial estos dos por su población en áreas urbanas. Poco tendría que ver aquí la tercera variable que es área selvática, pues las cantidades de población son muy grandes para encontrar una relación directa de los conceptos.
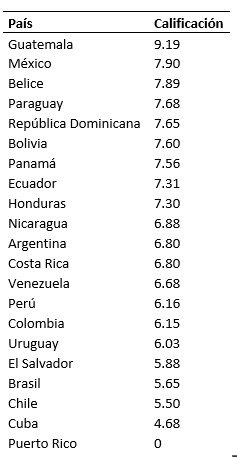
Para el factor 3, el mismo análisis se presenta en la Tabla XIV. En este se presentan datos muy interesantes, pues se ve a nuestro país en primer lugar, y es porque este factor se asocia con el concepto de crecimientos poblacionales y el detrimento de las áreas protegidas, algo que es evidente en Guatemala. También le sigue México con importantes crecimientos en la población. Se puede observar hasta el final de la tabla las islas de Cuba y Puerto Rico, donde la misma extensión territorial y la cultura hacen que sus crecimientos no sean tan pronunciados.
Tabla XIV
Calificaciones para la solución factorial de 3 factores, del Factor 3.
 Elaboración propia de los datos obtenidos del programa R.
Elaboración propia de los datos obtenidos del programa R.
CONCLUSIONES:
· Los datos aportados de las bases de datos del Banco Mundial para el cambio climático, pueden ser usadas para la correlación de muchos datos de desarrollo humano, por la cantidad importante que representa. Para el caso particular de estudio, se pudieron elaborar conceptos asociados a datos poblacionales y del uso de la tierra. (IPGRI, 2003)
· El primer concepto asociado a las componentes principales es la “Necesidad de alimento”, pues se puede ver como los crecimientos poblacionales marcan el uso de la tierra.
· El segundo concepto asociado es la “Necesidad de tierra para vivienda”, este como resultado de que no todo los datos marcan que sea total el cambio de uso de la tierra solo para agricultura, pues queda un remanente que por el crecimiento poblacional puede dar la idea de la pérdida de selvas y áreas protegidas para otros usos.
· El tercer concepto asociado es la “Pérdida de ecosistemas”, pues al final como remanente de los otros dos conceptos, se puede ver que sea por alimento o para vivienda, la cantidad de habitantes se relaciona directamente con la menor cantidad de áreas protegidas y áreas selváticas.
· El primer concepto obtenido del análisis factorial, asociado al factor 1 es el “Uso de la tierra”, pues se presentan las variables que expresan estos datos juntas y como su relación coincide con lo visto en la práctica y lo citado en la teoría. Existen países que priorizan las áreas protegidas y selváticas frente a las cultivables.
· El segundo concepto asociado al factor 2 son las “Poblaciones totales”, se puede ver como ciertos países concentran su población en áreas urbanas y que de cierta forma refleja pérdidas en áreas selváticas.
· El tercer concepto asociado al factor 3 son los “Crecimientos poblacionales”, donde nuestro país está en el primer puesto y las islas en últimos puestos, esto por factores principalmente culturales y también de espacio. Al final esto también incide en la disminución de áreas protegidas.
· El análisis factorial para esta serie de datos aporta conceptos más apegados al marco teórico relacionado con las variables observadas, dando mejores cimientos a los nuevos conceptos como variables latentes.
· Comparando el análisis factorial con el de componentes principales, para esta serie particular de datos, resulta más útil el primero, pues se pudo observar 3 grupos bien definidos de factores que relacionan conceptos muy cercanos.
· Se pudo observar la utilidad de los métodos multivariados para el análisis de datos que no tienen una correlación directa tan clara, pero que pueden tener relaciones teóricas que se evidencian en este análisis estadístico, que aporta una simplificación de un número grande de datos y variables con sus implicancias.





















