1 Introdução

No Ensino Básico, um dos tópicos mais importantes é o conhecimento dos números fracionários, considerado conhecimento-chave para obtenção de sucesso dos estudantes em Álgebra e em disciplinas matemáticas posteriores (BAILEY et. al. 2012; BOOTH e NEWTON, 2012;SIEGLER et al. 2012; TORBEYNS et al. 2015). No caso de Álgebra, esta, encontra-se repleta de exemplos, direta e indiretamente, relacionados com as frações, tanto nas equações lineares e naquelas em que é preciso completar quadrados quanto na resolução de sistemas de equações lineares e na resolução de equações racionais, como também nas razões que aparecem associadas a probabilidades simples e continuam presentes até o teorema binomial. Uma grande parte da base do pensamento algébrico repousa sobre um claro entendimento do conceito de números racionais (DRISCOLL, 1982; KIEREN, 1980;LAMON, 2005;WU, 2001), bem como sobre a capacidade de operar e manipular frações. Tal como nas demais facetas da Álgebra, o conhecimento dos números fracionários é fundamental à compreensão futura de Teoria dos Limites, Cálculo, Análise Numérica, Análise Real, entre outros.

A aprendizagem e o estudo das frações, a construção de sentido e o domínio de suas operações e propriedades, determinantes no currículo escolar, constitui o aspecto fundante da discussão apresentada neste artigo. O estudo se volta à uma discussão a respeito da representação dos números racionais, da construção desse conceito e de sua apresentação e representação no livro didático, ou seja, o estudo põe em evidência o tratamento e o desenvolvimento das frações nos livros brasileiros aprovados pelo Programa Nacional do Livro Didático (PNLD). Nessa perspectiva, nosso estudo procura investigar a seguinte questão: Como os livros didáticos brasileiros de Matemática introduzem a noção de fração e trabalham a sua relação com representações visuais?

Em busca de respostas e visando aos processos de ensino e de aprendizagem matemática, analisamos políticas públicas e o referido Programa, desde teoria subjacente à construção da noção de fração. Igualmente, consideramos o aporte teórico que fundamenta estudos a respeito de representação visual no estudo de frações, apresentados em nível nacional nos Parâmetros Curriculares Nacionais (PCN) e na Base Nacional Comum Curricular (BNCC). Logo, compreender a ontologia e o desenvolvimento das diferentes formas de representação para frações é de interesse da Educação, principalmente nos campos que envolvem a Psicologia, incluindo a Psicologia do Desenvolvimento.

O estudo contempla uma amostra de 14 livros didáticos de Matemática^[1] do 4º ano do Ensino Fundamental, aprovados pelo PNLD-2019, com o olhar focado no tema frações, sua representação numérica, gráfica, figural e resolução de situações-problema, tendo em vista possibilidades exploratórias e interpretativas. Ao apresentarmos alguns exemplos presentes nos livros didáticos, considerando o questionamento do estudo, o objetivo é promover uma reflexão que atenda a noção, a representação e interpretações do conceito de fração.

Na sequência deste artigo, apresentamos as seções que promovem uma breve reflexão a respeito de políticas públicas, em especial, ao que se refere ao PNLD, bem como sobre os números fracionários, visualização e representação, e por fim, dados e discussão dos resultados.

2 Políticas públicas para a educação e o Programa Nacional do Livro Didático

Para Dourado (2007), estudos a respeito de políticas educacionais abordam temáticas com variadas perspectivas, concepções e cenários, além de envolver um conjunto determinado de atores do processo escolar. As políticas públicas, neste artigo, são vistas no campo da Educação como direito previsto em lei e assegurado pelo Estado pelo fato de abranger ações realizadas no ambiente escolar em conjunto com a comunidade escolar.

Em relação à Educação, segundo Oliveira e Tonini (2014), esta é vista como um direito fundamental e de natureza social, previsto na Constituição Federal de 1988. Em conformidade com os autores, a educação está relacionada às políticas públicas e a programas direcionados à gestão educacional, contemplando aspectos das políticas educacionais e dos projetos pedagógicos das escolas. Sendo assim, a implantação dessas políticas no campo educacional deve considerar a educação como direito social, que contempla a participação de todos do ambiente escolar, em acordo com propostas públicas de municípios e estados, alinhadas às propostas federais.

A partir dessa breve contextualização, entendemos que o termo política pública, por sua origem etimológica, aproxima-se da definição apresentada por Santos (2015, p. 5): “ações geradas na esfera do Estado e que têm como objetivo atingir a sociedade como um todo, ou partes dela”. Ademais, em virtude de o Estado constituir um conjunto de instituições permanentes, vale observarmos que as políticas públicas são criadas por diferentes governos que assumem o poder em tempos cronológicos diferentes, o que implica atuações distintas em decorrência de características e tensões sociais, econômicas, culturais e tecnológicas postas nos diversos períodos. Desse modo, cada governo aplica diferentes deliberações com marcas particulares, o que configura as políticas de governo ou políticas de Estado. Com o intuito de caracterizarmos as políticas públicas de Estado e de governo, baseamo-nos nas definições de Santos (2015, p. 8):

[....] enquanto uma política de governo refere-se a um plano, um programa ou uma ação desenvolvida para vigorar durante o período de um mandato governamental, uma política de Estado alude a um plano, uma ação ou um programa educacional com objetivos de longo prazo elaborado de modo a durar por um período de tempo que vai para além do exercício político de determinado partido (ou do representante deste) à frente de uma entidade do Estado (em nível municipal, estadual ou federal).

Nesse contexto, vale ressaltarmos que as políticas públicas para educação, geralmente, são criadas para atender a um direito que, segundo Cury (2002), só existem políticas educacionais porque existe o direito à educação. O PNLD, com início em 1937, é o mais antigo dos programas voltados à distribuição de obras didáticas aos estudantes da rede pública de ensino brasileira. O programa já passou por diferentes aperfeiçoamentos, bem como já apresentou denominações distintas, com variadas formas de realização. Atualmente, volta-se à Educação Básica e é direcionado à aquisição e distribuição integral de livros aos alunos do Ensino Fundamental e Médio e a reposição e complementação do ano anterior, para as diferentes modalidades de ensino.

Essa distribuição é regulamentada por edital que contempla fases específicas, a saber: a) Adesão: podem participar do programa as escolas federais e os sistemas de ensino estaduais, municipais e do Distrito Federal que manifestam interesse por meio de adesão formal; b) Editais: estabelecem as regras para a inscrição da coleção de livros didáticos, são publicados no Diário Oficial da União e disponibilizados no portal do Fundo Nacional para o Desenvolvimento da Educação (FNDE) na internet; c) Inscrição das editoras: determinam o prazo e os regulamentos para habilitação e inscrição das coleções pelas empresas detentoras de direitos autorais; d) Triagem/Avaliação: verificam se as obras inscritas se enquadram nas exigências técnicas e físicas do edital; após a triagem, os livros selecionados são encaminhados à Secretaria de Educação Básica do Ministério da Educação (SEB/MEC), responsável pela avaliação e pela elaboração do guia de livros didáticos.

3 Os números fracionários

A noção de fração abordada na escola assume seu papel na medida em que desperta conceitos que ganham significado para o estudante a partir da vivência de situações concretas de construção e significação da noção, bem como de condições para resolução de problemas de sua vida diária. As principais abordagens do conceito de fração trabalhadas na escola, especialmente em relação à abrangência que o mesmo adquire no momento de sua construção, são destacadas por pesquisas (VAZ, 2013;LIMA, 2014;SEGETI, 2015;AVEIRO, 2015;CUNHA, 2016) que têm apontado que o ensino de frações, na escola, é fortemente influenciado, de modo especial, pela ideia de divisão de um inteiro em partes iguais. Essa abordagem em que uma área ou conjunto discreto se divide em partes iguais denomina-se parte-todo.

Segundo Powell (2018), a noção de parte-todo e as práticas correspondentes têm como fundamento a visão ontológica de frações, ou seja, a perspectiva de partição. Para o autor, ater-se apenas nesta interpretação de frações limita a compreensão dos estudantes, uma vez que não é suficiente como fundação para o sistema de números racionais. Behr et. al. (1997), baseando-se nas considerações de Kieren (1976), apresentam quatro interpretações para uma fração: quociente, razão, operador e medida.

Consoante Fazio e Siegler (2011) e Siegler e Forgues (2017), as retas numéricas constituem ferramenta de representação para ensinar o conceito de fração e outros relacionados à mesma. Os autores defendem a utilização da reta numérica como uma maneira eficaz que garante aos alunos a compreensão das frações como números com magnitudes. Sob essa ótica, “todas as frações podem ser representadas nas retas numéricas e estas ilustram a correspondência de cada fração a uma determinada magnitude” (FAZIO e SIEGLER, 2011, p. 10). Nesse sentido, além de ajudar a compreender a fração como um número, a utilização da reta numérica pode auxiliar na compreensão de conteúdos como equivalência e comparação de frações.

O sentido de número fracionário como um todo, para Powell e Ali (2018), inclui a habilidade de aproximar e tomar decisões relacionadas ao tamanho dos números. Ou seja, ao considerar a propriedade e a grandeza que todo número tem, incluindo inteiros e frações, o conhecimento e facilidade para lidar com eles e com as operações, vai muito além de aplicar estas operações com números e definições no computador, justificando assim, a utilização de materiais manipulativos em complementação à prática de sala de aula. Outro sentido discutido pelos autores, apoiados em Kieren (1980), relaciona-se à grandeza, isto é, as frações são reconhecidas como números e pensadas como relação de parte-todo, razão, quociente, medida ou operadores.

Powell e Ali (2018) em uma desgin research^[2] com estudantes da faixa etária entre 7 a 8 anos, o segundo autor desenvolve atividades com materiais manipulativos, especificamente as barras de Cuisenaire (Figura 1), na discussão e construção do conceito de fração. A pesquisa envolve questões da aprendizagem e dos significados a partir de análise reflexiva e da interação com os materiais manipulativos (POWELL, 2019).

Figura 1
Imagens do trabalho com as barras de Cuisenaire em processo evolutivo de sessões
Acervo dos Autores

Powell e Ali (2018) também se referem ao sentido de fração voltado à compreensão de magnitude, o qual implica a determinação da razoabilidade das respostas, envolvendo comparação, e a flexibilidade no uso de representações fracionárias para as magnitudes específicas nas resoluções de problemas. Esse sentido de fração é descrito em termos de três categorias — flexibilidade, razoabilidade e magnitude —, incluindo todas as representações não-simbólicas e simbólicas. A linha de pensamento necessária para envolvimento nessas atividades mentais se sobrepõe ao conhecimento de magnitude. Nesse sentido, em síntese vale considerar David e Fonseca (1997), quando apontam um aspecto prático para os números racionais em suas diferentes representações, e sinalizam que esses conceitos surgem com frequência nas diversas situações relacionadas à expressão de medidas e de índices comparativos.

4 As orientações dos PCN e BNCC para o tema frações

Os Parâmetros Curriculares Nacionais de Matemática para os anos iniciais do Ensino Fundamental – PCN (BRASIL, 1997) consideram as diversidades regionais, culturais e políticas do país; voltam-se à construção de referenciais nacionais comuns. Em seus objetivos gerais, consideram aspectos que se tornam fundamentais para as crianças em processo de alfabetização, tais como: utilizar as diferentes linguagens verbal, musical, matemática, gráfica, plástica e corporal como meio para produzir, expressar e comunicar ideias; atender a intenções e situações de comunicação; utilizar diferentes fontes de informação e recursos tecnológicos na aquisição e construção de conhecimentos; questionar a realidade na formulação e resolução de problemas, utilizando o pensamento lógico, a criatividade, a intuição e a capacidade de análise crítica. Tais objetivos evidenciam a importância do conceito de frações, desenvolvido nos anos iniciais de forma implícita, considerando diferentes formas de manifestação e a valorização das tecnologias digitais neste processo. Por outro lado, de modo complementar, a Base Nacional Comum Curricular (BNCC) estabelece que

[...] o Ensino Fundamental tenha compromisso com o desenvolvimento do letramento matemático, apresentando as competências e habilidades de raciocinar, representar, comunicar e argumentar matematicamente, de modo a favorecer o estabelecimento de conjecturas, a formulação e a resolução de problemas em diferentes contextos, utilizando conceitos, procedimentos, fatos e ferramentas matemáticas como forma de assegurar e reconhecer que os conhecimentos matemáticos são fundamentais para a compreensão e atuação no mundo. (BRASIL, 2017, p. 262)

Relevante destacarmos a valorização atribuída ao caráter de jogo intelectual da Matemática como algo que favorece o desenvolvimento do raciocínio lógico e crítico, estimula a investigação e pode ser prazeroso. Quanto aos aspectos previstos e contemplados nos PCN, referentes à educação para cidadania, a BNCC provoca uma sedimentação ao contemplar o letramento matemático. Nesse documento, os processos matemáticos de resolução de problemas, de investigação, de desenvolvimento de projetos e de modelagem matemática são citados como formas privilegiadas da atividade matemática, motivo pelo qual são vistos ao mesmo tempo enquanto objeto e estratégia à aprendizagem ao longo de todo o Ensino Fundamental.

Os PCN destacam aspectos dos números fracionários como conceituação, diferentes abordagens de significados e formas de representação. Relativamente às frações, destacam-se: a noção de equivalência; a ação de comparação de frações; a classificação e as operações com números fracionários; o conhecimento matemático, apresentado como historicamente construído e em permanente evolução. De acordo com esse documento, a Matemática pode ser vista, em sua prática filosófica, científica e social, com problemas e soluções que não se encontram no campo dos números naturais. Isso torna possível uma aproximação da noção de número racional pela compreensão das interpretações quociente, parte-todo e razão, nas representações fracionária e decimal. Ciclo que, em conformidade com os PCN, não constitui “um marco de terminalidade” (BRASIL, 1997, p. 58), o que significa um trabalho com números naturais e racionais, operações, medidas, espaço e forma e o tratamento da informação.

Na construção do conceito de frações, os PCN indicam dois aspectos fundamentais: as interpretações que as frações assumem em diferentes situações, baseadas na resolução de problemas, relacionando as partes do inteiro, os conjuntos discretos, ou até mesmo, a ideia de divisão e as diferentes formas para a sua representação, que podem ser por uma grandeza de natureza discreta ou contínua. Também orientam para a necessidade de serem trabalhadas três interpretações para as frações no segundo ciclo do Ensino Fundamental, isto é, parte-todo, razão e quociente, destinando a interpretação de operador para o terceiro ciclo, ou seja, do 6º e 7º anos. Os ciclos posteriores, previstos pelos PCN tratam da interpretação da fração como operador quando este desempenha papel de transformação, ou melhor, de algo que atua sobre uma situação e a modifica, por exemplo: Que número devo multiplicar por 7 para obter 3?

Ao analisarmos comparativamente os PCN com a BNCC, verificamos que esta apresenta a discussão do tema frações, pela primeira vez, na unidade correspondente ao 4º ano do Ensino Fundamental, com significados de metade, terça parte, quarta parte, quinta parte e décima parte. No 2º ano, há apenas problemas envolvendo os significados de dobro, metade, triplo e terça parte, mais relacionados à divisão e não à fração. No 4º ano, são apresentados os números racionais: frações unitárias mais usuais$(\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{10}e\frac{1}{100})$e representação decimal para escrever valores do sistema monetário brasileiro. No 5º ano, os números racionais, cuja representação decimal é finita, são apresentados em problemas de multiplicação e divisão de números racionais em que a representação decimal é finita por números naturais.

A partir dessas noções de Matemática, a BNCC destaca como habilidades para os alunos do 1º ao 5º anos: a associação do quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima partes; reconhecimento das frações unitárias mais usuais como unidades de medida menores do que uma unidade, utilizando a reta numérica como recurso.

Outro aspecto a ser considerado na BNCC é o reconhecimento de que as regras do sistema de numeração decimal podem ser estendidas para a representação decimal de um número racional, além de relacionar décimos e centésimos com a representação do sistema monetário brasileiro. Nesse sentido, o documento propõe a leitura, escrita e ordenação dos números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal a partir de recursos como a composição e decomposição e a reta numérica.

A BNCC valoriza a identificação e a representação de frações — menores e maiores que a unidade —, associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando também a reta numérica como recurso e a conferência de frações equivalentes. De maneira igual, valoriza a comparação e ordenação de números racionais positivos — representações fracionária e decimal —, relacionando-os a pontos na reta numérica, e a associação das representações 10%, 25%, 50%, 75% e 100% respectivamente à décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens, em contextos de Educação Financeira e outros. Além disso, a BNCC considera a elaboração e resolução de problemas de adição e subtração com números naturais e racionais, de representação decimal finita, utilizando estratégias diversas, problemas de multiplicação e divisão com números naturais e com números racionais cuja representação decimal é finita — com multiplicador e divisor natural e diferente de zero —, como cálculo por estimativa, cálculo mental e algoritmos.

A análise comparativa dos dois documentos curriculares no que tange ao tema frações possibilitou-nos identificar um caráter contínuo, evolutivo, experimental e cíclico em ambos, o que deixa transparecer que a exploração vai se constituindo, adaptando-se e se reajustando num processo de aprendizagem que contribui para a construção de conjecturas que estabelecem relações a partir de argumentação oral e de representação escrita.

5 Visualização e representação

Em nosso percurso analítico e reflexivo, também dirigimos um olhar atento aos livros didáticos e às suas representações, tendo em vista a passagem e a associação entre as representações que ocorrem no percurso de construção da ideia de fração e abstrações dos conceitos de números naturais, inteiros e racionais. Desse modo, procuramos nos ater à abordagem concernente à visualização e à representação porque, no material empírico, haverá um foco analítico nesses aspectos. Consequentemente, enquanto o objeto matemático que é de natureza mental e só pode ser pensado, a representação matemática ou os símbolos matemáticos assumem natureza material, existem no mundo à nossa volta e são percebidos pelos sentidos. (BRANDT e MORETTI, 2005)

As representações matemáticas envolvem também a fala e a escrita. A palavra é considerada um símbolo que significa algo sensível, capaz de substituir o que está ausente aos sentidos ou que é imperceptível diretamente (SCHEFFER, 2017). Neste trabalho, a palavra representação pode significar a apresentação de um símbolo, uma lembrança e a representação no plano da memorização. Em se tratando da representação matemática e dos registros escritos dos estudantes, os documentos oficiais como PCN (BRASIL, 1997) e BNCC (BRASIL, 2017) enfatizam a necessidade de valorização da palavra do estudante; e um dos princípios propostos nesses documentos considera a ação de relacionar observações do mundo real com representações e conceitos matemáticos.

À vista disso, a utilização de diferentes representações no ensino de Matemática torna possível a manifestação de sentido aos estudantes, oportunizando-lhes possibilidades de ensino e aprendizagem, tais como representação escrita e numérica de frações; representações gráfica e geométrica, presentes no livro didático e software; e representação obtida a partir de materiais manipulativos. Um exemplo desse tipo de material é o jogo das barras de Cuisenaire, ilustrado na Figura 2, com as suas diferentes cores e comprimentos. Essas barras constituem material que estimula a evidência e as manifestações de entendimentos de forma falada e escrita, o que contribui para a formalização de significados e conceitos matemáticos.

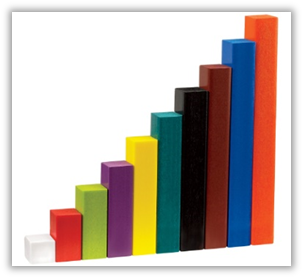Figura 2
As dez diferentes barras de Cuisenaire em forma de uma escala
Acervo dos Autores

No que diz respeito à visualização, esta é vista por Leivas (2009) como reconhecimento por meio de um processo de formação de imagens mentais; sua finalidade é a de construir e comunicar determinado conceito matemático, para auxiliar na resolução de problemas analíticos ou geométricos. Este autor amplia o sentido da visualização ao colocá-la não como uma forma de representação em termos de uma figura ou representação de um objeto, mas sim, como um processo capaz de auxiliar na construção do fazer matemático, bem como na comunicação dos conceitos presentes nas diversas áreas do conhecimento matemático.

Por outro lado, a representação supõe a construção de uma imagem distinta. Sendo assim, a visualização e a representação passam a ser elementos indissociáveis na compreensão matemática e geométrica. Flores, Wagner e Buratto (2012), apoiados em Zimmermann e Cunningham (1991), definem visualização matemática como um processo de formação de imagens — mentais, com lápis e papel ou com o auxílio de tecnologias digitais —, no qual essas imagens são usadas, de forma eficaz, para a descoberta e compreensão da Matemática. Desse modo, a visualização não é vista como um fim, mas como um meio para entendimento de conceitos matemáticos, e o programa de construção e transformação de imagens visuais e mentais passa a ser uma atividade cognitiva semiótica, processo de formação de imagens para compreender Matemática e a forma de pensamento que torna visível aquilo que se vê (FLORES, WAGNER e BURATTO, 2012).

Outra relação estabelecida trata do binômio objeto e representação: “não se pode ter compreensão em Matemática, se nós não distinguimos um objeto de sua representação” (DUVAL, 2009 apud LOURENÇO e OLIVEIRA, 2014, p. 14). Isso confirma a necessidade de diferenciar os objetos matemáticos com suas representações, pois diversas representações podem estar associadas ao mesmo objeto matemático. Para Duval (2009), a visualização é uma atividade cognitiva intrinsecamente semiótica, já a atividade que vai além da percepção visual é a representação.

Nessa ótica, ao nos referirmos à representação escrita, consideramos os pressupostos defendidos por Powell e Bairral (2006) ao afirmarem que ela ajuda os estudantes não só a adquirirem um vocabulário rico, como também a usarem este vocabulário no horizonte da própria compreensão matemática. Esses autores destacam que diferentes objetivos podem ser alcançados no momento quando os estudantes escrevem sobre a Matemática que estão produzindo. Assim, a escrita se torna um meio que permite tanto aos estudantes quanto aos professores examinarem o desenvolvimento do pensamento matemático, consequentemente, a visualização e a representação passam a contribuir na construção de significados e sentidos. Tendo em vista esses sentidos, apresentamos, na sequência, a análise dos dados obtidos nos livros didáticos do PNLD 2019.

6 O estudo

Este estudo assume características de pesquisa qualitativa. A seleção da amostra dos livros didáticos para a coleta de dados foi feita diretamente na relação que consta no Guia do PNLD 2019. Coletamos dados nos livros que estavam disponíveis para consulta no período, o que definiu uma amostra total de 14 obras. Foram analisados livros do 4º ano do Ensino Fundamental, por ser nesse ano que todas as coleções apresentaram o início da discussão do tema. Na análise dos livros didáticos, descrevemos, em termos gerais, a estrutura e o percurso assumido no desenvolvimento e na apresentação do tema, os conceitos, as ilustrações, a sequência de atividades e os problemas relacionados às frações.

Os dados são apresentados em quadros explicativos que contemplam as características físicas dos livros didáticos, a estrutura apresentada no desenvolvimento do tema em relação à cada conceito, e à presença implícita dos significados importantes à construção do conceito de fração e a resolução de problemas. Convém destacarmos que a análise documental das diferentes coleções nos forneceu características que possibilitam identificar o número de unidades de estudo que cada livro destina para a exploração do tema números racionais — frações e o desenvolvimento de seus conceitos.

Para a estrutura apresentada, consideramos além do número de páginas destinado para exploração do tema, o número de atividades desenvolvidas, as ilustrações, os exercícios propostos e a resolução de problemas. Quanto às situações-problema, atemo-nos na análise empírica à quantidade apresentada, ao tipo de problema e ao grau de reflexão promovido pela resolução.

Como organizamos os dados em quadros, a análise conta com categorias de conteúdo de acordo com Bardin (2011), tais como: a) Contexto de desenvolvimento do tema — examina se há problematização, ou tematização no livro didático quanto à uma realidade de aplicação ou contextualização do tema; b) Práticas sugeridas para discussão dos conceitos — destaca o tipo de atividades e ações sugeridas, utilização de materiais manipulativos, ilustrações e incentivo à utilização de tecnologias informáticas; c) Interpretações mais evidentes — destaca as coleções analisadas como um todo, tendo em vista a ideia de frações e a noção que predomina na apresentação do tema no decorrer do desenvolvimento da unidade; d) Resolução de problemas — apresenta dados relacionados aos tipos de problemas, suas aplicações e raciocínios de resolução envolvidos.

7 Dados e resultados

Os dados apresentados resultam da observação e análise de um total de 14 coleções publicadas por nove editoras brasileiras: Moderna, FTD, Saraiva, SEI, AJS, Ática, Zapt Editora, Editora do Brasil e Scipione. Um guia prático, destinado ao professor, acompanha todas as coleções e aborda os temas e a série a que se destina cada livro didático. O desenvolvimento dos temas engloba desde o letramento matemático até a avaliação da aprendizagem, considerando a necessidade de se trabalhar com materiais manipulativos e com a resolução de problemas. O guia prático também faz referência aos objetivos da BNCC, uma vez que são contemplados no desenvolvimento dos diferentes conteúdos do volume correspondente ao 4º ano do Ensino Fundamental.

A discussão do tema números racionais, nos livros didáticos brasileiros e demais documentos oficiais que promovem a reflexão curricular, tem início com a apresentação do conjunto dos números naturais, que representa partes inteiras. Para expressar os números que não representam o todo, mas sim parte dele, utilizam os números racionais que, em sua maioria, significam o quociente ou divisão de dois números inteiros naturais. Os livros didáticos analisados priorizam, de modo geral, alguns significados em detrimento de outros. Um exemplo claro disso se relaciona às interpretações de número inteiro e de quociente entre dois números inteiros, que são pouco abordadas nos livros didáticos. A falta dessa discussão no livro didático promove lacunas no planejamento dos professores que desconhecem essa relação como um número racional ou fracionário e utilizam o livro didático como único guia do planejamento, ou não possuem material didático que possa auxiliá-los na interpretação e representação matemática das frações.

Uma das representações de frações é obtida por meio da divisão, ou seja, os números inteiros utilizados são chamados de numerador e denominador, separados por um traço que significa divisão dos dois números inteiros. Assim, na sequência, as frações são classificadas em próprias, impróprias, aparentes e equivalentes. Em alguns livros da amostra investigada, há introdução às operações com frações, principalmente adição e subtração, cuja solução é obtida a partir da equivalência de frações.

Por outro lado, os livros, em sua maioria, enfatizam o significado de parte-todo para o ensino de frações, com o propósito de tornar essa interpretação predominante na exploração do conceito de números racionais. Nessa linha de pensamento, Teixeira (2008) destaca que o livro didático é visto como principal instrumento de apoio didático ao professor, todavia, deixa lacunas quanto aos significados de fração, haja vista que nem todos os significados são explorados.

Para Spinillo, Bezerra e Magina (2009), são inúmeras as críticas a respeito do ensino de frações na escola. Os autores destacam que o ensino de frações tem se caracterizado por uma ênfase maior no simbolismo e na linguagem matemática, na aplicação mecânica de algoritmos — sobretudo, na aritmética de frações — e no uso de representações diagramáticas. Diante disso, as mudanças e inovações no contexto escolar podem auxiliar os professores na busca de novos instrumentos pedagógicos para o ensino de frações, a exemplo das tecnologias digitais.

Tendo em vista a progressão deste estudo, apresentamos e descrevemos, a seguir, os dados em termos gerais, a estrutura e caminhos assumidos pelos autores no desenvolvimento e apresentação do tema frações, os conceitos, as ilustrações, a sequência, atividades e problemas relacionados ao tema nos diferentes livros didáticos. Em síntese, os dados estão organizados em quatro quadros que contemplam as categorias de análise.

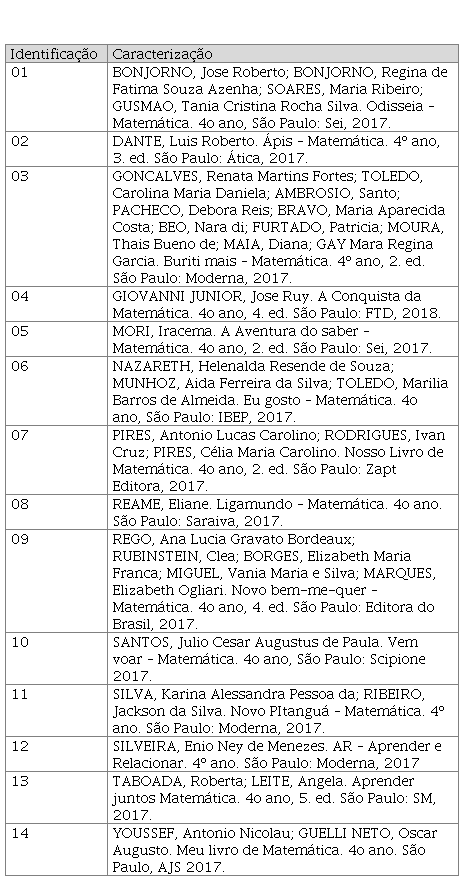
Antes, apresentamos no Quadro 1 a identificação dos 14 livros analisados, sendo todos eles a versão manual do professor.

Quadro 1
Livros analisados, aprovados pelo PNLD 2019

Elaboração dos Autores

Identificação	Caracterização
01	BONJORNO, Jose Roberto; BONJORNO, Regina de Fatima Souza Azenha; SOARES, Maria Ribeiro; GUSMAO, Tania Cristina Rocha Silva. Odisseia – Matemática. 4o ano, São Paulo: Sei, 2017.
02	DANTE, Luis Roberto. Ápis – Matemática. 4º ano, 3. ed. São Paulo: Ática, 2017.
03	GONCALVES, Renata Martins Fortes; TOLEDO, Carolina Maria Daniela; AMBROSIO, Santo; PACHECO, Debora Reis; BRAVO, Maria Aparecida Costa; BEO, Nara di; FURTADO, Patricia; MOURA, Thais Bueno de; MAIA, Diana; GAY Mara Regina Garcia. Buriti mais – Matemática. 4º ano, 2. ed. São Paulo: Moderna, 2017.
04	GIOVANNI JUNIOR, Jose Ruy. A Conquista da Matemática. 4o ano, 4. ed. São Paulo: FTD, 2018.
05	MORI, Iracema. A Aventura do saber – Matemática. 4o ano, 2. ed. São Paulo: Sei, 2017.
06	NAZARETH, Helenalda Resende de Souza; MUNHOZ, Aida Ferreira da Silva; TOLEDO, Marilia Barros de Almeida. Eu gosto – Matemática. 4o ano, São Paulo: IBEP, 2017.
07	PIRES, Antonio Lucas Carolino; RODRIGUES, Ivan Cruz; PIRES, Célia Maria Carolino. Nosso Livro de Matemática. 4o ano, 2. ed. São Paulo: Zapt Editora, 2017.
08	REAME, Eliane. Ligamundo – Matemática. 4o ano. São Paulo: Saraiva, 2017.
09	REGO, Ana Lucia Gravato Bordeaux; RUBINSTEIN, Clea; BORGES, Elizabeth Maria Franca; MIGUEL, Vania Maria e Silva; MARQUES, Elizabeth Ogliari. Novo bem-me-quer – Matemática. 4o ano, 4. ed. São Paulo: Editora do Brasil, 2017.
10	SANTOS, Julio Cesar Augustus de Paula. Vem voar – Matemática. 4o ano, São Paulo: Scipione 2017.
11	SILVA, Karina Alessandra Pessoa da; RIBEIRO, Jackson da Silva. Novo PItanguá – Matemática. 4º ano. São Paulo: Moderna, 2017.
12	SILVEIRA, Enio Ney de Menezes. AR – Aprender e Relacionar. 4º ano. São Paulo: Moderna, 2017
13	TABOADA, Roberta; LEITE, Angela. Aprender juntos Matemática. 4o ano, 5. ed. São Paulo: SM, 2017.
14	YOUSSEF, Antonio Nicolau; GUELLI NETO, Oscar Augusto. Meu livro de Matemática. 4o ano. São Paulo, AJS 2017.

a) Categoria 1: Contexto e desenvolvimento do tema

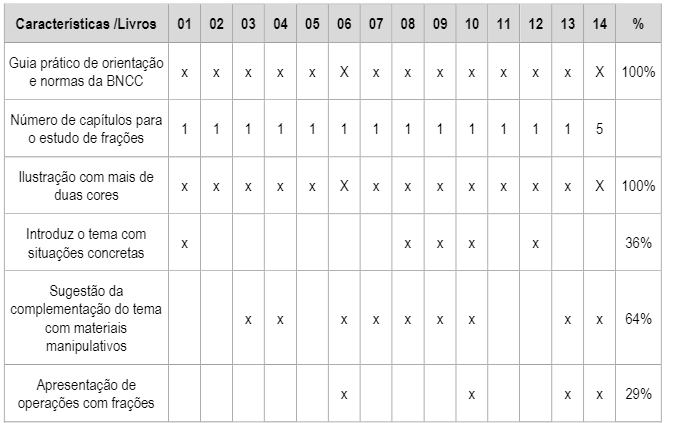
Quadro 2
Características físicas – contexto e desenvolvimento do tema

Dados da Pesquisa

Todas as coleções analisadas, conforme consta no Quadro 2, apresentam as seguintes características: capa colorida, com ilustrações que passam uma ideia de alegria e satisfação ao estudar Matemática; editados em papel de boa qualidade; contam com mais de três cores; atualizados, com informações relativas à BNCC; apresentam, pelo menos, um capítulo dirigido ao estudo de frações. Além do mais, 36% dos livros dão amplo destaque à ilustração de situações concretas de utilização das frações e 64% deles sugerem a utilização de material concreto em paralelo para trabalhar com frações, trazendo, inclusive em anexo, fichas de trabalho que podem ser recortadas para produção de alguns kits de materiais de equivalência, discos de frações e jogos. Outro aspecto se relaciona à introdução do estudo das operações com frações, com 29% dos livros com um capítulo voltado às operações.

Nos livros didáticos analisados, o conceito de fração é explorado, de forma intuitiva, a partir da relação parte-todo, envolvendo discussão a respeito de situações cotidianas como a divisão em partes iguais de uma pizza, de um queijo, de um bolo, entre outros alimentos. Contudo, a relação parte-todo aparece quando um todo é dividido em partes iguais e a fração indica a relação que existe entre um número de partes e o total de partes como ilustra a Figura 3.

Figura 3
Divisão de um queijo e de uma pizza em partes iguais
(Livro 12, p. 177 e Livro 3, p.154)

Sob nosso ponto de vista, os alimentos não são bons exemplos para a divisão em partes iguais, pois envolvem uma medida de massa em que os pedaços, após o corte, jamais correspondem em igualdade de tamanho e massa. Outro aspecto que nos chama a atenção, nesse exemplo, é o significado de numerador e denominador de uma fração, com estabelecimento de relações de linguagem para as partes tomadas em relação às partes do todo. Aqui, já se apresentam situações que exigem relações e transferências entre representações. De acordo com Escolano e Gairin (2005), essa exigência corresponde à interpretação da representação gráfica na relação parte–todo e à representação de forma simbólica estabelecida entre os números naturais.

Pesquisas desenvolvidas por O´Halloran (2017), Berger (2017), Ripoll e Carvalho e Rezat e Sträber (2017) destacam como aspectos de seleção para análise de livros didáticos de Matemática de diferentes partes do mundo, o uso excessivo de símbolos representativos para os números nas relações matemáticas e a importância entre leitura e argumentação, promovida pela relação entre leitura e habilidades de resolução de problemas. Isso tem estabelecido mediação entre os objetivos, o conhecimento e as crenças dos professores e estudantes, a partir da influência de imagens matemáticas, também consideradas em nossa análise. A seleção e a apresentação dos conteúdos são vistas, portanto, como aspetos importantes nos livros didáticos por estabelecerem relações entre discurso e representação escrita.

b) Categoria 2: Práticas sugeridas para discussão dos conceitos

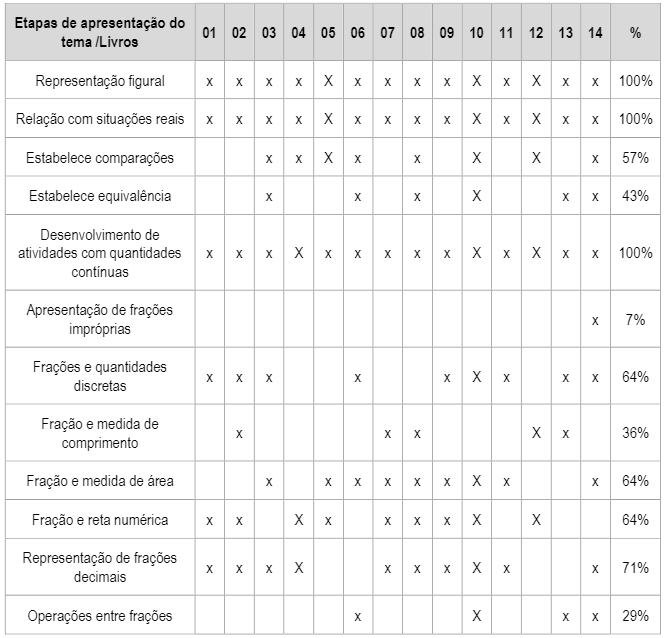
Nessa categoria, analisamos as práticas sugeridas nos livros didáticos para a discussão dos conceitos relacionados ao tema frações, conforme Quadro 3, como as representações figurais, que são inúmeras, em 100% dos livros didáticos analisados; igualmente, com o mesmo percentual, a relação com situações reais, principalmente as que envolvem alimentos na discussão. Em algumas situações, identificamos o trabalho com medidas de comprimento e áreas como de jardim e horta, com uma certa quantidade de pés de alface plantada, conforme ilustra a Figura 4. Do total de livros analisados, 43% estabelecem equivalência entre frações; 64% estabelecem comparações; 100% desenvolvem atividades com quantidades contínuas e discretas. Apenas 7% dos livros se referem às frações impróprias, enquanto 71% contemplam a representação de frações decimais e 29% se voltam às operações entre frações na série analisada.

Quadro 3
Estrutura apresentada no desenvolvimento do tema – práticas sugeridas

Dados da Pesquisa

Outra interpretação de frações muito evidente nos livros didáticos é a de quociente, tendo como base a divisão de dois números naturais, a e b. Comum também nos livros didáticos é a consideração da noção intuitiva a partir da divisão de uma barra de cereal em duas partes, comendo uma dessas partes. Alimentos como bolos e pizzas são considerados distintamente às situações em que a área da horta é dividida em duas ou em três partes iguais, porém a imagem da horta incita o estudante a contar o número de plantas que aparecem em cada parte (Figura 4), relacionando o conceito de fração com quantidades discretas, além da interpretação de noção parte-todo.

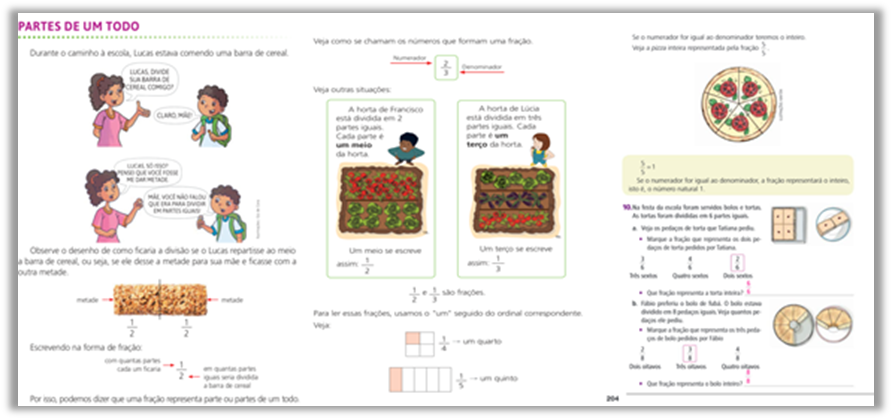Figura 4
Apresentação de significados de fração e representação figural
(Livro 14, p. 162-163 e Livro 1, p. 204)

As atividades apresentadas na Figura 4 nos levam a refletir sobre as contribuições da visualização para a representação matemática. A tentativa de contextualização do significado presente nestas atividades tem função de desencadear processos de análise para a abstração, bem como de síntese para a generalização, considerando o significado do conceito de fração, pois consoante Flores, Wagner e Buratto (2012), o reconhecimento da visualização passa a problematizar a aprendizagem matemática levando em consideração a imagem e a representação. Desse modo, a visualização pode proporcionar aos estudantes (ou professores) condições para que eles relacionem um problema (ou conceito) à sua representação.

As atividades expostas na Figura 4 evidenciam a necessidade de se trabalhar a visualização a fim de desenvolver a imaginação do estudante para o conceito de fração, neste caso, como parte-todo. Na contextualização e representação de situações presentes no dia a dia, apesar da noção de divisão em partes iguais, quando se relaciona à massa, além da área visual, não corresponde a uma representação de partes iguais, pois como assevera Leivas (2009), a visualização é vista não como uma forma de representação em termos de uma figura ou representação de um objeto, mas como um processo capaz de auxiliar na construção do fazer matemático.

c) Categoria 3: Interpretações mais evidentes

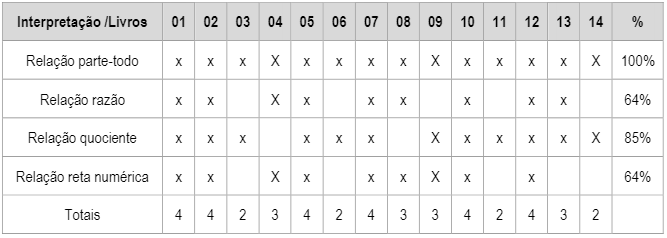
Quadro 4
Interpretação mais evidente

Dados da Pesquisa

De acordo com os dados explicitados no Quadro 4, verificamos que a interpretação parte-todo é a mais usual, ou seja, aparece em 100% dos livros didáticos analisados. Esse resultado se justifica pelo fato de a fração poder ser pensada como parte de um todo, expresso por uma grandeza contínua. O contexto intuitivo, muito utilizado na escola, também se sobressai nos livros didáticos, pois envolve atividades com partição de chocolate, pizza, bolos e demais alimentos que têm características geométricas retangulares ou circulares conforme Figuras 3 e 4.

A interpretação como razão é usual em, aproximadamente, 64% dos livros que apresentam frações utilizadas para representar uma comparação entre grandezas que podem ser contínuas ou descontínuas (Figuras 4 e 5). Os livros didáticos contemplam, do mesmo modo, a comparação entre duas quantidades discretas de uma grandeza, ou seja, quando é interpretada como relação razão, a exemplo da seguinte situação: 2 de cada 4 habitantes de determinada cidade são imigrantes. Outros exemplos que envolvem a possibilidade de sorte como 3 em 12, ou $\frac{3}{12}=\frac{1}{4}$; de escalas em mapas, a escala é de 1 cm para 100 m; de porcentagem, 25 em cada 100 alunos da escola gostam de voleibol. Essas ideias têm papel fundamental na forma como as questões são expostas nos livros didáticos.

Quanto à interpretação como quociente, percebemos que esta se faz presente em 85% dos livros analisados, pois a fração é tida como quociente, isto é, como resultado da divisão entre dois números naturais como ilustra a Figura 5. Já a interpretação como ponto na reta numérica é possível de ser identificada em 64% dos livros analisados. Ou seja, os números racionais, inclusive as frações, são interpretados como pontos sobre uma reta numérica, o que pode expressar uma medida, como podemos observar nas atividades expostas na Figura 5.

Figura 5
Exploração de fração como medida, na reta numérica e quociente de quantidades discretas e contínuas
(Livro 1, p. 206 e Livro 13, p. 227)

Inferimos, pelos dados apresentados e exemplos ilustrados, que os livros didáticos analisados consideram as quatro interpretações de frações, no entanto, com maior intensidade na relação parte-todo como podemos conferir na Figura 5 e no Quadro 4.

Para Kieren (1988), os números racionais só podem ser compreendidos se forem levadas em conta as diferentes características que os mesmos assumem, ideia que o autor denominou subconstruto. Para ele, o conceito de número racional pode ser construído a partir da consideração das seguintes interpretações: quociente, operador, medida e razão. Em conformidade com os dados obtidos nos livros didáticos que constam na Figura 5, observa-se a predominância da abordagem relativa à interpretação parte-todo, aspecto que, segundo Escolano e Gairin (2005), é um limitante para o ensino do número racional, porque as demais interpretações também têm sua importância na construção da ideia de fração.

Ao levarmos em consideração esse aspecto, estabelecemos uma comparação com outro estudo, realizado por Alajmi (2012), o qual analisa livros didáticos do Ensino Fundamental de três países. O autor destaca que o texto dos livros dos Estados Unidos da América (EUA) utiliza, principalmente, três modelos para representar frações: modelos que envolvem a representação de áreas para discutir frações como parte-todo; modelo discreto para representar frações como parte de um conjunto de objetos; e modelo linear (linha numérica), características também presentes nos livros didáticos brasileiros. Aspectos, enfim, que se alinham à análise dos livros brasileiros e transitam, em sua maioria, no modelo parte-todo, enfatizando, com menor intensidade, as formas de representação como razão, quociente e reta numérica.

d) Categoria 4: Resolução de problemas

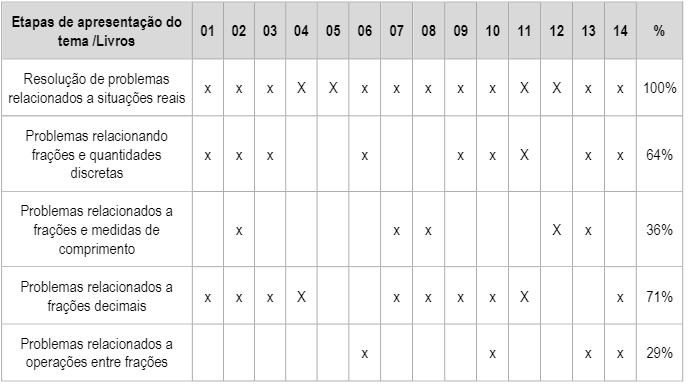
Quadro 5
Resolução de problemas

Dados da Pesquisa

Nessa categoria, apontamos e discutimos a presença da resolução de problemas na exploração do tema frações nos livros didáticos. O aspecto com maior incidência é o relacionado com as situações reais, identificado em 100% dos livros; em segundo lugar, os problemas relacionados a frações decimais, apontados em 71%; na sequência, os relacionados a quantidades discretas, numa ocorrência de 64%. Com um índice de 36%, os problemas relacionados à fração e medidas de comprimento e, por último, em 29% dos livros analisados, os problemas abrangendo as operações, haja vista que, na maioria dos livros didáticos, essa introdução não é feita na série analisada.

A resolução de problemas nessa categoria se apresenta como uma possibilidade de praticar as atividades sobre a noção de frações e números racionais de forma ilustrada e contextualizada. Na Figura 6, destacamos exemplos de problemas apresentados nos livros didáticos analisados. De modo geral, os problemas tratam de quantidades contínuas e descontínuas, envolvendo classes de equivalência, representação gráfica de áreas, comparação e, principalmente, a relação parte-todo.

Figura 6
Resolução de problemas de frações
(Livro 5, p. 202)

A resolução de problemas presente nos livros didáticos envolve, de modo especial, situações do cotidiano que implicam a necessidade da aplicação de frações para a resolução. Essas situações-problema, dependendo de como são exploradas, podem dar sentido e significado à noção de fração, pois possuem características que promovem uma reflexão que vai desde a representação gráfica até a simbólica matemática.

Na BNCC (BRASIL, 2017), os significados de metade, terça parte, quarta parte, quinta parte e décima parte constam no 4º e 5º anos, as frações unitárias mais usuais são $(\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{10}e\frac{1}{100})$, e a representação decimal é utilizada para escrever valores do sistema monetário brasileiro. As habilidades destacadas para alunos do 1º ao 5º anos voltam-se, fundamentalmente, à ação de associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10, o que representa as ideias de metade, terça, quarta, quinta e décima partes, reconhecendo as frações unitárias mais usuais como unidades de medida menores do que uma unidade, utilizando, principalmente, a reta numérica como recurso.

Por outro lado, o estudo de Alajmi (2012), sinaliza que os procedimentos predominantes nos três primeiros anos abrangem basicamente a utilização de lápis, papel e livro didático. Em seu estudo comparativo, aponta que, enquanto nos EUA os estudantes são encorajados a usar diferentes estratégias para resolver problemas, os livros didáticos de Matemática do Kuwait apresentam problemas de contextos do mundo real a partir do 4º ano, aspecto evidenciado também nos livros didáticos brasileiros.

8 Palavras Finais

A partir da questão norteadora deste estudo relacionada à introdução da noção de fração no livro didático de Matemática, e como são trabalhados em coleções analisadas, aspectos fundamentais como a sua relação com a representação visual matemática, os diferentes tipos de representações visuais e a relação entre estas representações e a noção de fração, apresentamos, aqui, uma discussão dos resultados obtidos.

Os livros didáticos analisados desenvolvem, de modo geral, o tema frações no 4º ano do Ensino Fundamental, conforme prescreve a política da Base Nacional Comum Curricular (BNCC), uma vez que ideias iniciais da noção são desenvolvidas em anos anteriores a esta série. O índice percentual de frequência das interpretações do estudo de frações predominante nos livros didáticos, de 100%, corresponde à noção parte-todo. Em sua maioria, os exemplos envolvem a noção de divisão do inteiro em partes iguais e fazem uso de alimentos para exemplificação, ou seja, relacionam com situações concretas e com quantidades contínuas e discretas do dia a dia. Já as interpretações da razão e do ponto na reta numérica, com um índice de aproximadamente 64%, envolvem a resolução de problemas em diferentes tipos de quantidades, enquanto na interpretação de quociente a frequência é de 85%, conforme ilustram o Quadro 4 e as Figuras 3, 4 e 5. Logo, a reflexão no tocante à noção de fração e a passagem da representação gráfica para a representação simbólica matemática recebem influência da noção parte-todo de forma mais intensa que as demais interpretações.

Por outro lado, pelo que observamos nos livros didáticos, as operações entre frações são introduzidas apenas em algumas coleções, pois este não é o objetivo do 4º ano do Ensino Fundamental no Brasil, tanto que não estão previstas nas políticas dos PCN e da BNCC, assim como as diferentes representações para as interpretações de fração. Podemos concluir, então, que nos livros didáticos de Matemática brasileiros, para os anos iniciais, a concentração maior está na construção da noção de números racionais e de frações, o que vai ao encontro das especificações dos documentos oficiais, deixando para anos finais do Ensino Fundamental o avanço nas operações com frações.

No estudo realizado por Alajmi (2012), relativo ao tema frações, considerando seu desenvolvimento e apresentação nos livros didáticos de três países como Japão, Kuwaiti e Estados Unidos, o autor destaca que a adição e subtração de frações semelhantes são as primeiras operações com frações apresentadas nos livros desses países, e as operações de adicionar e subtrair frações com denominador comum inicia principalmente no 3º ano. No caso dos livros didáticos brasileiros, o percentual que se apresenta para a resolução de problemas, envolvendo operações com frações na amostra analisada, é de 29%, um índice que pode ser considerado baixo em relação aos demais países.

Sendo assim, depreendemos que os livros analisados abordam, em diferentes percentuais, o tema a partir das diferentes interpretações para o estudo das frações, ou seja, na reta numérica se relaciona com medidas, com a reserva de um espaço para a resolução de problemas relacionados a medidas de comprimento. No entanto, as atividades, em sua maioria dirigem-se, basicamente, à discriminação visual de quantidades e de partes, relacionada à interpretação parte-todo, discreto ou não, que passa pela discussão da noção de fração enquanto objeto matemático. A resolução de problemas, também presente nos livros, trata o tema em diferentes contextos de representação e relações de equivalência, de medidas de comprimento, de tempo e de comparação entre medidas.

Inúmeras atividades que estruturam as coleções evidenciam ideias de frações, relacionando o conceito a aspectos intuitivos que se voltam à divisão e à visualização de alimentos como bolos, pizzas, maçãs, laranjas, xícaras de suco, dentre outros, aspecto que, segundo Escolano e Gairin (2005), pode ser um limitante para o ensino do número racional.

Complementarmente, consideramos a definição de representação que indica, em conformidade com os estudos de Flores, Wagner e Buratto (2012), a construção de uma imagem distinta, sendo que a visualização e a representação passam a ser elementos indissociáveis na compreensão matemática. Nesse sentido, a visualização (DUVAL, 2009;LEIVAS, 2009;SIMONI e SCHEFFER, 2019) assume características de processo de formação de imagens, sejam mentais, com lápis e papel ou com o auxílio de tecnologias digitais. Apesar disso, não é vista como um fim, mas como um meio para entendimento de conceitos matemáticos, configurando uma atividade cognitiva semiótica, considerada representação, que vai além da percepção visual.

Neste estudo valorizamos, igualmente, a representação escrita que, para Powell e Bairral (2006), ao fazer parte da vivência escolar, ajuda os estudantes não só a adquirirem um vocabulário rico, mas a usarem este vocabulário no horizonte da própria compreensão matemática, aspecto ilustrativo que complementa as atividades destacadas no presente artigo. Isso revela, portanto, a importância da metodologia usada na discussão e na apresentação da noção e dos conceitos de fração na ação escolar, englobando estratégias que vão desde a utilização de materiais didáticos, visualização e representação escrita até a interpretação das representações presentes nos livros didáticos.

Para finalizar podemos dizer que, nos livros didáticos analisados neste estudo, há uma tendência, embora não explícita, que contempla, de forma diferenciada, as abordagens da noção de fração no desenvolvimento das atividades. Ou seja, os autores dos livros tentam estabelecer conexão entre a representação figural e a representação matemática por intermédio da reprodução de desenhos que representam situações do dia a dia vivenciadas pelos estudantes.

Destarte, conforme exploração em sala de aula, esse aspecto pode ou não contribuir para que os estudantes atribuam significação ao tema. Os autores dos livros didáticos utilizam as ideias de dividir e repartir em partes iguais alimentos que representam quantidades contínuas, quantidades discretas e, também, em percentuais diferenciados, bem como aplicam essas noções na resolução de problemas, conforme destacado no Quadro 4. Ademais, as diferentes interpretações de fração são trabalhadas, como também situações que podem se constituir em obstáculo ao entendimento do conceito de fração, como é o caso da divisão de alimentos em partes iguais.

Referências

ALAJMI, Amal Hussain. How do elementary textbooks address fractions? A review of Mathematics textbooks in the USA, Japan and Kuwait. Educational Studies in Mathematics, v. 79, n. 2, p. 239-261, feb. 2012.

AVEIRO, José Carlos. Formalização do conjunto dos números racionais e alguns jogos com frações. 2015. 54f. Dissertação (Mestrado em Matemática em Rede Nacional) – Instituto de Biociências, Letras e Ciências Exatas. Universidade Estadual Paulista. São José do Rio Preto.

BAILEY, Drew H.; HOARD, Mary K.; NUGENT, Lara; GEARY, C. David. Competence with fractions predicts gains in mathematics achievement. Journal of Experimental Child Psychology, v. 113, n. 3, p. 447-455, nov. 2012.

BARBOSA, Jonei; OLIVEIRA, Andreia. Por que a pesquisa de desenvolvimento na Educação Matemática? Perspectivas da Educação Matemática, Campo Grande, v. 8, n. 18, p. 526-546, 2015.

BARDIN, Laurence. Análise de conteúdo. Tradução de Luís Antero Reto e Augusto Pinheiro. São Paulo: Edições 70, 2011.

BEHR, Merlyn J.; KHOURY, Helen A.; HAREL, Guershon; POST, Thomas; LESH, Richard. Conceptual units analysis of preservice elementary school teachers' strategies on a rational-number-as-operator task. Journal for Research in Mathematics Education, v. 28, n.1, p. 48-69, jan. 1997.

BERGER, Margot. Reading Mathematics textbooks: diferent Reading Styles. In: INTERNATIONAL CONFERENCE ON MATHEMATICS TEXTBOOKS RESEARCH AND DEVELOPMENT, 2, 2017, Rio de Janeiro. Anais do ICTM-2017. Rio de Janeiro: SBM, 2017, p. 70-71.

BOOTH, Julie L.; NEWTON, Kristie J. Fractions: could they really be the gatekeeper’s doorman? Contemporary Educational Psychology, v. 37, n. 4, p. 247-253, 2012.

BRANDT, Célia Fink; MORETTI, Méricles Thadeu. O papel dos registros de representação na compreensão do sistema de numeração decimal. Educação Matemática Pesquisa, São Paulo, v. 7, n. 2, p. 201-227, jul./dez. 2005.

BRASIL. Ministério da Educação. Secretaria de Educação Básica. Base Nacional Comum Curricular. Brasília: MEC/SEB, 2017.

BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF,1997.

CUNHA, Edson Carlos. Reforço escolar: o uso de jogos e materiais manipuláveis no ensino de frações. 2016. 122f. Dissertação (Mestrado em Educação Escolar) – Núcleo de Ciências Humanas. Universidade Federal de Rondônia. Porto Velho.

CURY, Carlos Roberto Jamil. Direito à educação: direito à igualdade, direito à diferença. Cadernos de Pesquisa, São Paulo, n. 116, p. 245-262, jul. 2002.

DAVID, Maria Manuela Martins Soares; FONSECA, Maria da Conceição Ferreira Reis. Sobre o conceito de número racional e a representação fracionária. Presença Pedagógica, Belo Horizonte, n. 14, p. 59-71, mar./abr. 1997.

DOURADO, Luiz Fernando. Políticas e gestão da Educação Básica no Brasil: limites e perspectivas. Educação & Sociedade, Campinas: v. 28, n. 100, p. 921-946, out. 2007.

DRISCOLL, Mark. Research within reach: secondary school Mathematics. Reston: National Council of Teachers of Mathematics, 1982.

DUVAL, Raymond. Semiósis e pensamento humano: registro semiótico e aprendizagens intelectuais. Tradução de Lênio Fernandes Levy e Marisa Rosâni Abreu da Silveira. São Paulo: Editora Livraria da Física, 2009.

ESCOLANO, Rafael Vizcarra; GAIRIN, Joaquim Sallán. Modelos de medida para la enseñanza del número racional em Educación Primaria. UNIÓN – Revista Iberoamericana de Educação Matemática, n. 1, p. 17-35, mar. 2005.

FAZIO, Lisa; SIEGLER, Robert. S. Teaching fractions. Geneva: International Academy of Education; International Bureau of Education: 2011.

FLORES, Cláudia Regina; WAGNER, Débora Regina; BURATTO, Ivone Catarina. Pesquisa em visualização na Educação Matemática: conceitos, tendências e perspectivas. Educação Matemática e Pesquisa, São Paulo, v. 14, n. 1, p. 31-45, jan./abr. 2012.

KIEREN, Thomas E. Personal knowledge of rational numbers: its intutive and formal development. In: HIEBERT, James; BEHR, Merlyn. (Ed.) Number concepts and operations in the Middle Grades. Hillsdale, New Jersey: Erlbaum, 1988, p. 162-180.

KIEREN, Thomas E. On the mathematical, cognitive and instructional foundations of rational number. In: LESH, Richard A. (Ed.). Number and measurement. Columbus, Ohio: ERIC Clearinghouse for Science, Mathematics, and Environmental Education, 1976, p. 101-144.

KIEREN, Thomas E. The rational number construct-Its elements and mechanisms. In: KIEREN, Thomas E. (Ed.). Recent research on number learning. Columbus, Ohio: ERIC Clearinghouse for Science, Mathematics, and Environmental Education, 1980, p. 125-150.

LAMON, Susan J.. Teaching fractions and ratios for understanding: essential content knowledge and instructional strategies for teachers. 2. ed. New York: Lawrence Erlbaum Associates, 2005.

LEIVAS, José Carlos Pinto. Imaginação, intuição e visualização: a riqueza de possibilidades da abordagem geométrica no currículo de cursos de Licenciatura em Matemática. 2009, 294f. Tese (Doutorado em Educação) – Setor de Educação. Universidade Federal do Paraná. Curitiba.

LIMA, Rafael Pontes. O ensino e a aprendizagem significativa das operações com frações: sequência didática e o uso de tecnologias digitais para alunos do Ensino Fundamental II. 2014. 240f. Tese (Doutorado em Educação em Ciências e Matemática) – Rede Amazônica de Educação em Ciências e Matemática. Universidade Federal do Pará. Macapá.

LOURENÇO, Edrei Henrique; OLIVEIRA, Paulo César. O conceito de função na produção acadêmica da PUC/SP via registros de representação semiótica. Educação Matemática Pesquisa, São Paulo, v. 16, n. 2, p. 369-383, maio/ago. 2014.

O´HALLORAN, Kay. A multimodal approach for theorising and analysing Mathematics textbooks. In: INTERNATIONAL CONFERENCE ON MATHEMATICS TEXTBOOKS RESEARCH AND DEVELOPMENT, 2, 2017, Rio de Janeiro. Anais do ICTM-2017. Rio de Janeiro: SBM, 2017, p. 25-48.

OLIVEIRA, Breynner R.; TONINI, Adriana M. (Org.). Gestão escolar e formação continuada de professores: o Programa Nacional de Gestores na Universidade Federal de Ouro Preto. Juiz de Fora: Editar, 2014.

POWELL Arthur Belford; ALI, Kendell. Design research in Mathematics Education: investigating a measuring approach to fraction sense. In: CUSTÓDIO, José Francisco; COSTA, David Antônio; FLORES, Cláudia Regina; GRANDO, Célia Regina. (Org.). Programa de Pós-Graduação em Educação Científica e Tecnológica (PPGECT): contribuições para a pesquisa e ensino. São Paulo: Editora Livraria da Física, 2018, p. 221- 242.

POWELL, Arthur Belford. Measuring perspective of fraction knowledge: Integrating historical and neurocognitive findings. Revista Sergipana de Matemática e Educação Matemática, Alagoas, v. 4, n. 1, p. 1-19, 2019.

POWELL, Arthur Belford. Recuando para avançar: rumo a uma abordagem do século XXI para conhecimento de fração com o Modelo-4A de Instrução. Perspectiva, Florianópolis, v. 36, n. 2, p. 399-420, abr./jun. 2018.

POWELL, Arthur Belford; BAIRRAL, Marcelo Almeida. A escrita e o pensamento matemático: interações e potencialidades. Campinas: Papirus, 2006.

REZAT, Sebastian, STRÄBER, Rudolf. Textbook use by teachers and students: results and methods. In: INTERNATIONAL CONFERENCE ON MATHEMATICS TEXTBOOKS RESEARCH AND DEVELOPMENT, 2, 2017, Rio de Janeiro. Anais do ICTM-2017. Rio de Janeiro: SBM, 2017, p. 66.

RIPOLL, Cydara Cavedon; CARVALHO, Sandro Azevedo. The introduction to Algebra in textbooks. In: INTERNATIONAL CONFERENCE ON MATHEMATICS TEXTBOOKS RESEARCH AND DEVELOPMENT, 2, 2017, Rio de Janeiro. Anais do ICTM-2017. Rio de Janeiro: SBM, 2017, p. 116-127.

SANTOS, Pablo Silva Machado Bispo. Guia prático da política educacional no Brasil: ações, planos, programas, impactos. São Paulo: Cengage Learning, 2015.

SCHEFFER, Nilce Fátima. Tecnologias digitais e representação matemática de movimentos corporais. Curitiba: Appris, 2017.

SEGETI, Liliane Giglio Canelhas de Abreu. O ensino de frações por uma abordagem inspirada nos pressupostos educacionais da Teoria das Inteligências Múltiplas. 2015.164f. Dissertação (Mestrado em Ensino, História e Filosofia das Ciências e Matemática) – Centro de Ciências Naturais e Humanas. Universidade Federal do ABC. Santo André.

SIEGLER, Robert S.; DUNCAN, Greg; DAVIS-KEAN, Pamela; DUCKWORTH, Kathryn; CLAESSENS, Amy; ENGEL, Mimi; SUSPERREGUY, Maria Ines; CHEN, Meichu. Early predictors of High School Mathematics achievement. Psychological Science, v. 23, n. 7, p. 691-697, jun. 2012.

SIEGLER, Robert S.; FORGUES, Hugues Lortie. Hard lessons: why rational number arithmetic is so difficult for so many people. Current Directions in Psychological Science, v. 26, n. 4, p. 346-351, aug. 2017.

SIMONI, Tatiéle Carla Costella; SCHEFFER, Nilce Fátima. A superação do erro no estudo de frações: uma discussão quanto a contribuições das TIC e de materiais manipulativos. Revista Sergipana de Matemática e Educação Matemática, v. 4, n. 1, p. 20-36, 2019.

SPINILLO, Alina; BEZERRA, Francisco Brado; MAGINA, Sandra. Como desenvolver a compreensão da criança sobre fração? Uma experiência de ensino. Revista Brasileira de Estudos Pedagógicos, Brasília, v. 90, n. 225, p. 411-432, maio/ago. 2009.

TEIXEIRA, Alexis Martins. O professor, o ensino de fração e o livro didático: um estudo investigativo. 2008. 195f. Dissertação (Mestrado em Ensino de Matemática) – Faculdade de Ciências Exatas e Tecnologias. Pontifícia Universidade Católica de São Paulo. São Paulo.

TORBEYNS, Joke; SCHNEIDER, Michael; XIN, Ziqiang; SIEGLER, Robert. Bridging the gap: fraction understanding is central to mathematics achievement in students from three different continents. Learning and Instruction, v. 37, p. 5-13, jun. 2015.

VAZ, Rafael Filipe Novoa. Metodologia didática de análise de soluções aplicada ao ensino de frações. 2013. 81f. Dissertação (Mestrado em Ensino de Matemática) – Instituto de Matemática. Universidade Federal do Rio de Janeiro. Rio de Janeiro.

WU, Hung-Hsi. How to prepare students for Algebra. American Educator, v. 25, n. 2. p. 1-7, 2001.

ZIMMERMANN, Walter; CUNNINGHAM, Steve. Editors´ Introduction: What is Mathematical Visualization? In: ZIMMERMANN, Walter; CUNNINGHAM, Steve. (Ed.). Visualization in teaching and learning Mathematics. Washington: MAA, 1991, p. 1-7.

Notas

Ligação alternative

https://periodicos.ufop.br/revemop/article/view/1977/1674 (pdf)