1 Understanding Conceptual Metaphor
Everyone does use metaphors in their day-to-day interactions with others. People may use metaphors even without noticing it. People understand some abstract and difficult concepts through the connection with familiar objects. The familiar concepts are based on their own experiences and cultural activities. Metaphor can facilitate to understand the abstract phenomena. Metaphor is a mapping between two conceptual domains which provides a powerful tool to understand one domain of knowledge in terms of another. The conceptual metaphors help to deal with relatively unfamiliar and abstract domains of experience in a familiar and tangible way. The set of known and familiar ideas helps to understand difficult and abstract concepts.
There are two parts of a conceptual metaphor: target domain and source domain. Basically, metaphor is a mapping between the source domain and the target domain. The source domain is familiar, concrete and based on everyday activities and experiences of learners whereas the target domain is an unknown, abstract and difficult set of ideas. Some common everyday conceptual metaphor includes “LIFE is a JOURNEY”. Here, LIFE is the target domain as it holds unknown and abstract ideas whereas JOURNEY is the source domain because it is the class of concrete vehicles that help to understand the target. Some people may have a journey but may not have a destination. There may arise obstacles during the journey, sometimes may come joyful moments as well.
People may face ups and downs during their journey. JOURNEY helps to understand the term LIFE in terms of various familiar activities and experiences. In fact, metaphor is a mapping between two conceptual domains, which provides a powerful tool to understand the target domain of knowledge in terms of simple and familiar ideas. Metaphor simply means the representation of abstract entities through very simple, familiar and meaningful objects. It can be taken as a mapping that the abstract ideas map into concrete, strong and meaningful images that are developed in different social and cultural context for a different purpose.
English (1997) sees metaphors as a tool for creating formal concepts out of image schemas, and of restructuring these concepts in complex ways. Lakoff and Nunez (2000) also argue that “the conceptual metaphor’s primary function is to allow us to reason about relatively abstract domains using the inferential structure of relatively concrete domains,” (p. 42) with structures of image schemas preserved by this mapping. Thus, metaphor can be considered as a mechanism for connecting two types of knowledge of which the new knowledge is comprehended through already existed familiar concepts.
Lakoff and Nunez (2000) created three types of conceptual metaphors and they are known as grounding metaphors, linking metaphors and extraneous metaphors. The grounding metaphors allow us to ground our understanding of mathematical ideas based on everyday experience. For instance, the abstract mathematical idea of addition as putting things into piles/bags or adding things to a collection, subtraction as taking things away from a collection, sets as containers, members of a set as objects in a container. In this regard, Danesi (2007) argued that thermometer, as students are familiar with this device, helps to conceptualize positive integer, negative integer and number zero. The negative integers are placed below the zero and positive integer is above zero in thermometers. Thus, the thermometer is a grounding metaphor to understand an abstract concept of integers.
The linking metaphors allow us to link one branch of mathematics to its other branches. For example, the metaphor “NUMBERS is a POINT ON A LINE” links arithmetic to geometry. Thus, the linking metaphors allow conceptualizing the ideas of arithmetic in terms of geometry. And the next is extraneous metaphors. Lakoff and Nunez (2000) affirm that “extraneous metaphor or metaphors that have nothing whatever to do with either the grounding of mathematics or the structure of mathematics itself. Unfortunately, the term metaphor when applied to mathematics has mostly referred to such extraneous metaphors” (p. 53). The staircase is an example of extraneous metaphor of the “step function” because when graphed the step function can look similar to a staircase. The image of staircase has nothing whatever to do with either the inherent content of the grounding of the mathematics, although the visual is a helpful reminder of how this function would look when graphed (LAKOFF & NUNEZ, 2000; BEARDEN, 2012).
Likewise, “FUNCTION is a MACHINE” is a metaphor. The source domain of this metaphor is MACHINE and the target domain is the mathematical concept of FUNCTIONS. Extraneous metaphors can be eliminated without any substantive change in the conceptual structure of mathematics, whereas eliminating grounding or linking metaphors would make much of the conceptual content of mathematics disappear. Fyhn (2007) maintained that “Some Sami mittens have the pattern grouse footprints on their edges. These repeating patterns show a connection between embodied experiences and ornamentation. Ski trails, as well as animal footprints, perform patterns in the snow, patterns with different symmetry properties” (p. 246). The patterns in snow are concrete and familiar example of some geometrical ideas, which facilitates to understand abstract geometrical concepts.
And footprints in the snow are the source domain to understand the target domain, some properties of symmetry. In this paper, the metaphors are the tools whose source domains are the out-of-school mathematical ideas embedded in cultural artefacts, monuments, arts, language and literature, games, and their everyday activities and the school mathematics, the target domain. The use of cultural artifacts in mathematics classroom activities can be articulated in various stages of teaching and learning of content objectives. The use of some artifacts like bottle and labels, restaurant bill, electricity bill, the weather forecast presented in a newspaper, etc., enables the teacher to pose a great deal of possible questions, remarks, culturally and scientifically interesting inquiries in the process of instruction.
In this study, I take the term (cultural) metaphor as the material culture that can be mediated to the teaching and learning of school mathematics. It has educative significance and source of inspiration for the mathematical knowledge generation, transformation, distribution and diffusion to the students and teachers of mathematics. The ethnomathematical ideas embedded in cultural artefacts can serve as the most powerful metaphor in the process of teaching and learning of formal mathematics. In my study, cultural metaphors are tools, which connect students’ out-of-school environmental activities to understand school mathematics.
2 Cultural Artefacts and
Ethnomathematics
Cultural artefacts are anything or object that is created by the culture of a particular group of people that helps to define their culture. Gueudet and Trouche (2009) extend the definition of artefact by introducing the term resources to encompass any artefact with the potential to promote the process of learning. There are different types of cultural artefacts, which reflect the cultural identity of different groups of people. Some of them are dress, house, utensil, basket, ornament, painting, design and so on. All these artefacts give the information about the culture of its creators and the ideas associated with these objects. Bonotto (2007) viewed that the extensive use of cultural artefacts makes school mathematics more meaningful. For him, the cultural artefacts introduced into mathematics classroom are concrete materials, which children typically meet in real-life situations. These concrete materials can be a suitable tool to transfer one domain of knowledge to another. In this paper, I explored mathematical ideas embedded in cultural artefacts of different physical objects and its use as an instructional material that mediated the teaching and learning of school mathematics.
Bishop (1991) believes that mathematics is a cultural product, which has developed as a result of various activities, and that counting, locating, measuring, designing, playing, and explaining are all part of that cultural product. Everyday life is impregnated in the knowledge and practices of a culture. At all times, individuals are comparing, classifying, quantifying, measuring, explaining, inferring, generalizing, and evaluating, using the material and intellectual instruments that belong to their culture (D’AMBROSIO, 2006). The cultural activities of human beings invented some kind of mathematical knowledge and concepts. Every culture has developed mathematics practices consistent with their needs and interest in everyday activities. Naturally, it is not surprising that extremely practical concepts such as numbers and counting have arisen in all cultures.
There is a lack of evidence and the exact date that the people of the world started to weave the items. For thousands of years, people have been weaving baskets, hats, mats and other items. Different cultures have carried out weaving using different materials like grass, leaves, clothes, feathers, paper and other local materials. An artefact may be considered as any human creation and it has different purposes for different peoples. The cultural artefacts are potentially a very powerful metaphor to communicate abstract mathematical ideas. For example, CIRCLE is a BANGLE is an extraneous metaphor in which abstract concept of CIRCLE can be understood with the help of known and familiar artefacts, the BANGLE. On the same note, the money of different denominations has some sort of purpose for some community members but in an educational context to be used as a metaphor for teaching and learning of different concepts of mathematics. In this study, I have collected some cultural artefacts that have potentially very powerful teaching and learning tool to communicate abstract mathematical ideas.
Ethnomathematics
may be described as the study of mathematical ideas and activities as embedded
in their cultural context. Further D’ Ambrosio (2006) defined ethnomathematics
as “the mathematics which is practiced among identifiable cultural groups such
as national-tribe societies, labor groups, children of certain age brackets and
professional classes and so on" (p. 44). Ethnomathematics can be described
as the way people from a particular culture have common systems for dealing
with quantitative, relational, and spatial aspects of their lives (BARTON,
1996). It follows what Knijnik (1997) cited by Alangui (2017) describes
as an ethnomathematical approach, one that is characterized by the
investigation of the traditions, practices, and mathematical concepts of a
subordinated social group and the pedagogical work, which was developed in
order for the group to be able to interpret and decode its knowledge.
The ethnomathematical ideas of the group of people have generally been excluded from discussions of formal and academic mathematics. Rosa and Gavarrete (2017) also viewed that their mathematical knowledge and learning approaches are not taken into consideration in the formal school mathematics curricula. The mathematical ideas from the group of working-class people culture, the acknowledgment of their ways of knowledge generation and transmission, and students’ experiences should be blended with formal mathematics in the classrooms (PRADHAN, 2017). In attempting to create and integrate mathematical materials related to different cultures and that draw on students’ own experiences in an instructional mathematics curriculum, it is possible to apply ethnomathematical strategies in teaching and learning mathematics (ROSA & GAVARRETE, 2017).
Pradhan (2012) did a study to explore the knowledge generation of Chundara and to compare and contrast the ways that they learn and teach in their everyday activities from the school pedagogy. The main finding of the study was that Chundaras teaching and learning activity involved participatory and cooperative approaches in which they learn with the help of their parents as Vygotsky (1978) seeing learning as an activity in which shared mathematical meanings are constructed socially. However, they are using implicit mathematical knowledge in their everyday activities and the construction of these wooden stuffs. Millroy (1992) found that the group of carpenters used the concept of tacit knowledge of mathematical ideas. This concept of tacit knowledge implies that most people know more than they can tell. Tacit knowledge manifests itself through human activities and is not necessarily expressed or expressible in written or spoken form. Such knowledge helps them to develop mathematical ideas and thinking in those groups of people. The group of people in the out-of-school context have been developing their own mathematical ideas and knowledge and practicing for long to sustain their lives.
The studies reveal that all cultures have basic counting, sorting and deciphering methods and that these have arisen independently in different places around the world. It is important to connect the out-of-school mathematical ideas for the understanding of the abstract concept of mathematics. The familiar concepts of students based on their culture, everyday activities and experiences would be the source to understand the target that is relatively abstract, difficult and unfamiliar to them. As metaphor is a mapping between two conceptual domain, the ethnomathematical ideas, concepts embedded in different cultural artefacts, and associated practices are the source domain which mediates to understand difficult and abstract concepts of school mathematics. Thus, ethnomathematical ideas embedded in cultural artefacts help to conceptualize abstract mathematical ideas by connecting children's everyday activities. In this paper, I argued that the cultural artefacts and embedded ethnomathematical ideas and concepts facilitate the understanding of school mathematics.
3 Research Questions
The main
objective of this study was to explore the ethnomathematical ideas embedded in
different cultural artefacts and analyze its contribution to the teaching and
learning of mathematics. In order to achieve this objective, I formulated the
following research questions:
-
· What mathematical ideas embed in cultural artifacts?
· How do cultural artifacts facilitate teaching and learning of school mathematics?
4 Conceptual Framework
The framework
developed in this study shows how the cultural artefacts and ethnomathematical
ideas of different groups of people can be a mediated tool for the teaching and
learning of school mathematics. It is assumed that students’ familiar contexts
become a powerful source in mathematics teaching and learning. Connecting students’
out-of-school mathematical ideas to teaching school mathematics is really a
great problem for the teachers. Regarding the incorporation of cultural
knowledge in classroom teaching, Paulo Freire (1970) suggested that “children’s
cultural capital — the knowledge children bring to
school from their home and cultural environment — should be welcomed and
utilized in school for teaching and knowledge building purposes” (as cited in
STRINGER, CHRISTENSEN & BALDWIN, 2010, p. 24). In this way, students’ out-of-school knowledge that is
embedded in their culture of the community is celebrated and utilized as a
source domain of the conceptual metaphor in an appropriate way in the classroom
teaching and learning process. The mathematical ideas embedded in the cultural
artefacts from the out-of-school environment of the learners’ community was
observed and incorporated in the process of teaching and learning of school
mathematics.
The mathematical understanding is important for everyone and they are using mathematical ideas and knowledge to perform everyday work. The mathematical knowledge and ideas are implicitly used in out-of-school culture. My argument in this study is that cultural artefacts and the ethnomathematical ideas embedded in different cultural activities mediate to the understanding of school mathematics. This framework is based on the theory of conceptual metaphor that indicates the connection between the source domain and the target domain for meaningful mathematics teaching and learning. The source domain is the cultural artefacts and the associated practices, which are always familiar, known, and concrete to the learners. The knowledge to be learnt is the target domain, which is considered as abstract and difficult. The framework speaks that the incorporation of ethnomathematical ideas, embedded in the cultural artefacts, in the classroom teaching can facilitate the understanding of school mathematics. The connections of these concepts and ideas in the teaching and learning can enhance school mathematics.
 Figure 1
Connecting cultural
artifacts and school mathematics
(Author1s personal file)
Figure 1
Connecting cultural
artifacts and school mathematics
(Author1s personal file)
The learners'
culture and everyday activities regarding ethnomathematical ideas are an
integral part of education in general and learning mathematics in particular.
This framework highlighted the integration of the mathematical concepts which
are practiced in the learner’s culture with those of school mathematics (ADAM,
2004;ALANGUI, 2017). It is believed that classrooms and other learning
environments cannot be isolated from the communities in which they are
embedded, and students come to school bringing with them values, norms, and
concepts they have acquired from their culture and environment. The students’
home culture and ethnomathematical ideas provide opportunities to connect to
school mathematics. Figure 1 depicts a conceptual framework to connect the
students’ out-of-school knowledge, embedded mathematical ideas in their
cultural activities to school mathematics. This framework allows for a wider
set of cultural artefacts has the possibility in the discussion of formal
mathematical ideas. This suggests that it is possible to connect school
mathematics through the ethnomathematical ideas and the out-of-school context
of the learners.
The understanding of learners’ culture, their everyday activities and experiences not only enables teachers to gain a greater understanding of their students, but also provides rich material to incorporate into classroom learning activities (STRINGER, CHRISTENSEN & BALDWIN, 2010). It also provides an opportunity for teachers to understand their students in a richly meaningful way, and in the process, develop relationships that enable them to accomplish their work more effectively. In this framework, cultural artefacts and mathematical ideas embedded in it were the source domain, which mediates teaching and learning of the target domain, the abstract concepts of mathematics. The contextualization of school mathematics enables them to successfully accomplish the rewarding task of facilitating their students’ learning.
5 Methods and Procedures
This study was intended to explore the ethnomathematical ideas embedded in cultural artefacts and their role in the teaching and learning of school mathematics. To answer my research questions, I resolutely situated myself as a qualitative researcher. Choosing the most appropriate methodology, that reflective process led me to select ethnography. I choose ethnography as the methodology because it looks at mathematical ideas in different cultural artefacts constructed by the group of people as a socio-cultural process (TAYLOR & BOGDAN, 1998). Ethnography can be a primary methodology for collecting empirical data from the field regarding the mathematical ideas, knowledge, and practices in different cultural artefacts.
I used ethnography to describe, interpret, and reveal the meaning of cultural activities regarding ethnomathematical ideas embedded in cultural artefacts and activities. While conducting this research, I continuously addressed the questions of interest involving mathematical ideas embedded in the process of constructing cultural artefacts and their ways of teaching and learning in their cultural settings. The implicit mathematical ideas used by the group of people in the process of performing their everyday job positioning myself to engage in the research techniques as described within an ethnographic paradigm.
To obtain the answer to my research questions, I purposively selected five people involving in different income generating cultural activities. The cultural artefacts regarding mathematical ideas embedded in the surrounding of the public secondary school of sample school were captured by using ethnographic tools. A total of five school mathematics teachers and 12 students from the school level were selected for the study. The data regarding the mathematical ideas embedded in different cultural artefacts were collected through observation and in-depth interviews with a group of people in a natural setting. Focused Group Discussion (FGD) of teachers and students were conducted separately in order to examine the contribution of cultural artefacts in the process of teaching and learning of mathematics. This was done with the help of interview guidelines and observation checklist.
With regarding the data recording, the researcher chooses from several classical and contemporary positions and records the behavior and activities of the people in a natural setting through field notes (ANGROSINO & ROSENBERG, 2011). These field notes included paper-pencil, photographs, video or audio recorders with the consent permission of the research participants which can capture the lived experiences of the person or group within the context of the social setting. I carefully recorded all the possible conservations with the help of the video camera and took field notes as much as I could. I collected the data from multiple sources during the course of my study. I reviewed all of the data gathered from the multiple sources (CRESWELL, 2009) and then organized them into categories or themes that cut across all of the data sources. After observing the data, I linked them with many possible theories to interpret them.
I triangulated the data and the theoretical closures and gave meaning to my findings. In this process, I tried to produce accurate descriptions of the contents. Interpretation involved attaching meaning and significance to the analysis, explaining descriptive patterns, and looking for relationships and linkages among descriptive dimensions. In my study, the cultural artefacts and its associated practices in the students’ community and their ways of understanding the natural phenomena, and their ethnomathematical knowledge embedded in it were analyzed with the notions of pluralism. In this study, the analysis of the research was validated and made more reliable by triangulating the statements among the research participants, their ways of presenting the text in the several times of data collection periods.
6 Metaphors for Teaching and Learning
Mathematics
In this paper, I have discussed some cultural artefacts and practices associated with those artefacts that can be mediated for the development of mathematics ideas. One of my objectives was to explore the mathematical ideas embedded in cultural artefacts in the out-of-school environment. It was also intended to assess the contribution of cultural artefacts and associated practices in the process of teaching and learning of school mathematics. Cultural artefacts can be viewed as a series of mathematical ideas and concepts organized in an implicit manner. They practice their own mathematics within the cultural artefacts and activities associated with it. The emic knowledge of learners’ community embedded in different cultural artefacts and practices exhibit a lot of ethnomathematical ideas.
The ethnomathematical ideas embedded in the familiar context of the learners’ could be the source domain for the teaching and learning of school mathematics. In my study, the familiar context of the learner that can be facilitated to understand abstract and different concepts is viewed as a source domain of conceptual metaphor. Thus, ethnomathematical ideas embedded in different cultural artefacts and practices associated with it are the source domain of the conceptual metaphor. My study argued that the conceptual metaphor is a powerful tool that assists to communicate the abstract mathematical ideas through familiar and meaningful objects. From the interaction with my research participants, there are a lot of informal mathematical ideas observed in the out-of-school environment.
The cultural artefacts observed in the surrounding of the out-of-school environment has a great potential to communicate school mathematical ideas. The ethnomathematical ideas embedded in cultural artefacts are effective metaphors to communicate the abstract concepts of school mathematics. I found that the teachers were using ethnomathematical ideas of different groups of people as a metaphor in the process of teaching and learning of school mathematics. In the following sections, I have discussed the ethnomathematical ideas practiced by different groups of people in their everyday activities and cultural artefacts constructed by those groups of people and their contribution to the process of teaching and learning of school mathematics.
6.1 Money and Teaching Place Value
Money is one of
the cultural artefacts familiar to everyone from children to old aged people.
It has a strong connection with all
culture and it has been highly valued in
this physical world. Everyone, even illiterate, recognizes
the denominations of different currencies in terms of size, color,
image, print, and texture. Nepalese currency and its denominations are probably
unique since we find every denomination varied in terms of length, breadth,
color and portrait in it. The most familiar denominations are one, five, ten,
twenty, fifty, hundred, five hundred and thousand. Each has important cultural
value and importance. Each note has its own definition as we can see in table
1.
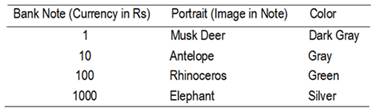 Table 1
Nepalese Bank Note and its Features
Author’s personal
file
Table 1
Nepalese Bank Note and its Features
Author’s personal
file
In Nepal, whenever there is a talk about Rs 100, the imprinted image Rhino, and its green color comes in mind or just vice-versa. Even it is common in conversations like when my son needs to ask for some money, he tells me “Pa, I need two Hatti (Elephant).” He was asking me for two thousand rupees (1USD = NRs.113.9, 15 aug. 2019). It might sound insane but it is a common interaction seen between people from a teen to the oldies. It is the same for other denominations. As a whole, we can easily understand 10 Musk Deer equaling to 1 Antelope, or 10 Rhinoceros equaling to 1 Elephant. This is equivalent to an understanding of 10 ones as 1 ten and 10 hundreds as 1 thousand. In the same way, 10 green notes equal 1 silver, which can equivalently be understood for 10 hundreds as 1 thousand.
In this regard, money can be a real-life example to teach different concepts in mathematics. Particularly this can be a powerful metaphor to conceptualize place value. During my survey, I asked some students if 2 or 8 had greater value in number 28, alas they replied that 8 was greater. The blunder they made was within the limit of my expectations, in fact, a chance for my research to experiment the efficiency of money as a metaphor. I took out the denominations of 2 tens, and 8 ones and asked them what was the total amount. They calculated them to be Rs. 28 in total. I again asked them whether 2 or 8 had a higher value. They finally answered the 2 had a higher value with a sight of realization. The use of money for developing the concept of place value can give it an actual significance.
The cultural artefacts can be used as a motivating stepping-stones to launch new mathematical knowledge (BONOTTO, 2007). He further explained that cultural artefacts offered the opportunity of making connections between mathematics incorporated in real-life situations and school mathematics. These artefacts are relevant to children; they are meaningful because they are part of their real-life experience, offering significance references to concrete situations. About the use of metaphors in teaching and learning of place value at the primary level, one of my research participant T4 used a money metaphor to teach place value. As money is familiar to each student, its connection to the mathematical ideas of place value seems to be very fruitful. To teach the place value at primary grades, she used the note of rupee one to represent the one's units, the 10 rupees to represent the tens unit and the hundred rupees to represent the hundred of the unit.
I took a post-class interview with two teacher participants who used a money metaphor to teach the place value at primary grades seems to be satisfied and happy. The use of place value during the counting of numbers seemed to be really appealing with the positive response from both teachers and the students. They gained the value of each digit from the numbers. About the use of metaphors in teaching and learning of place value at the primary level, one of my teacher participant T4 speaks:
After I joined the collaborative action
research, I got wonderful ideas and opportunities to teach place value using
money metaphors. As money is familiar to each student, its connection to the
mathematical ideas of place value seems to be very fruitful. To teach the place
value at primary grades, I used the note of 1 rupee to represent the ones
units, the 10 rupees to represent the tens units and the hundred rupees to
represent the hundreds units.
My other research
participant agreed with the views of T4, Further, T5 speaks,
Money is a powerful metaphor
as students seem to like talking about and playing with money. So I started
using the money metaphor to teach the concepts of place value at the basic
level of education. So I took the ones, 10 ones for a ten, 10 tens for a
hundred and 10 hundred for a thousand and so on.
Realizing this view, it
was found that the use of money metaphor to teach the concepts of place value
at the basic level of education really
made a difference in the learning process. From the observation of class, it was found that the concepts of ones, tens,
hundreds, thousands through money mediated to conceptualize the ideas of place
value for ones, 10 ones for a ten, 10 tens for a hundred and 10 hundred for a
thousand and so on. The classroom activities of the teacher and the interaction
supported the lines of Hutchens (2015) who viewed that the beauty of money with
place value is that it gives place value a real meaning. Thus, it is concluded
that money is a powerful metaphor to teach and learn one of the most important
ideas of arithmetic because the concept of place value is very
fundamental which helps to teach the mathematical operations of addition, subtraction,
multiplication, and division.
The household ideas and knowledge,
which students experience in their everyday activities in their familiar
context provides the opportunities to learn school mathematics. The students’
familiar context facilitates a systematic and powerful tool to represent the
abstract concepts of mathematics. In this connection, I always advocate for
Cummins (1996) “No learner is a blank slate” cited in Gonzalez, Moll and Amanti (2005, p. ix). It is believed that the students
bring some sort of mathematical ideas and knowledge into the classroom. The
ideas and knowledge possessed by the
children help to unlock difficult and abstract concepts of mathematics.
Mathematics lessons can be made interesting and effective from the students’ point of view if it is relating to the real-life context of the students. If we relate a mathematics lesson to the real life of the students, the attitude of students towards mathematics is positive and student interest in learning of mathematics increases. Money is one of the real-life examples to teach different concepts of mathematics. It has a strong connection to all cultures and given high valued. Therefore, the concept of place value could be the linking metaphor for the teaching and learning of other concepts of arithmetic.
6.2 Money and
Conceptualizing Integers
The concept of integers is introduced at grade VI in the school mathematics curriculum. It is a very important part of the curriculum and it symbolizes a move from concrete to abstract thinking. Even the secondary level students have misconceptions in tackling the problems regarding the negative integers. When I asked to identify the greater number in -5 and -8, most of the seventh-grade students have an incorrect answer. For making the concept of integers more easily understandable, there can be the use of many metaphors, which are familiar to the students’ out-of-school context. However, it becomes a difficult task for the teacher to figure out which metaphor would suit best to teach contents in the classroom teaching with good conceptual understanding.
When analyzing discussion during a workshop in a teacher support program in my sample school, different metaphors were proposed for the teaching and learning of integers. One of my research participants gave the MONEY is INTEGER as a metaphor to conceptualize integers. Many researches have been done in the area of integers about how can students of basic level be conceptualized with the notion of negative integers thereby students developed conceptual understanding in the subject. While teachers are going to deliver new abstract mathematical concepts, the metaphors are the effective tools to communicate the concepts. However, mathematics teachers are not always aware of the metaphors they use (FONT, BOLITE & ACEVEDO, 2010).
In the classroom observation of one of my research participants, I found that the teacher used several metaphors in the process of teaching the concept integers. But she was unaware of the question of what type of metaphor did she use. Most of the teachers used metaphors without noticing it as if they were the metaphors. I analyzed that the metaphors used by T3 in her study of teaching integers at grade six was MONEY is INTEGER metaphor. She told me that she generally used some familiar examples that students encounter in their everyday lives.
Teachers use money metaphor as the basis of integer that was compared with having or not having the money. The winning of money signified positive integers, the loss of money signified negative integers and the situation of neither a loss nor gain signified zero. The feeling of win, lose and neither win nor lose are well-known to every student of this age group which can act as the source domain to understand abstract concepts of positive, negative and zero integers. Therefore, money, a cultural artefact, could be the grounding metaphor for the teaching and learning of integers.
Money, as a metaphor, can be used as a very effective tool in the teaching of integers as it holds a great impact in this physical world. There is probably no child who lags the idea of earning and spending money. One of my teacher participant T5 speaks:
Students have a misconception about
the negative integers. Even a number of seventh graders have no clear ideas
about the identification of larger and smaller negative integers, say -10 and
-3. In my class on integers, I always give the example of assets and
liabilities to conceptualize the content. People who have more liabilities are
considered as small negative numbers and vice versa. For example, people are
less poor who have to pay a small amount than the people who have to pay more
amount. Therefore, -10 is smaller than the number -3.
The assets and
liabilities can also be the metaphor for the understanding of positive and
negative integers. Assets add positive income each period and liabilities
(debt) require payment to service it. From the interview with students and
teachers, I found that the money metaphor was equally significant in the course
of teaching integers. The metaphors ASSETS is POSITIVE INTEGER and LIABILITIES
is NEGATIVE INTEGERS used by teacher participant T5 have been a
powerful metaphor to conceptualize the integers. As per my observation of the T5
class
about integers, I found the connection of money with the teaching of integers
very graceful. She had connected the earning, spending and owing of money
directly with concepts of integers. The students’ participation in the task,
their facial expression during the classroom teaching was entertaining and
happy. They actively participated in classroom activities. The students’
familiar out-of-school context and their experiences and practices enhance to
understand the concept easily.
6.3 Clock Metaphor for Conceptualizing
Rounding off Numbers
Rounding off numbers is an important skill in every sector of human lives in general and particular in mathematics. Estimation of skill gives an idea about possible answers without doing a lot of work. This skill allows us to estimate numbers and make them easier to understand. Rounding off numbers to the nearest multiple of 10, 100, 1000, or million has great significance. In Nepal, the Central Bureau of Statistics (CBS) conducted a widespread national census in 2011. The CBS determined that the population of the country was 26,494,504. That number is hard to remember and if we say the population of Nepal is 30 million it is a good estimation because it doesn't make any real difference with what the exact number is.
In daily life, estimation is great for giving intelligent guesses about the possible amounts. The rounding of numbers in the nearest ten, hundred and thousand are introduced in the mathematics curriculum at the basic level of education. There are different metaphors to communicate the abstract concepts of rounding off numbers. The common metaphors used in the discussion of the contents were clock metaphor, number line metaphor, path, and fictive motion metaphor. In this paper, the clock metaphor is put forward to teach the concept of rounding off numbers.
The concept of rounding off numbers is used in everyday activities and basically used to describe the situations like morning, day and night. Any nonprofessional can also usually conceptualize the time in these three states of time. We eventually say that its morning, it's already a day and its night and so on. Which time is belonging to the morning, day and night? That is not a great deal here. The important thing is that our everyday interaction involves the rounding-off the time like morning, day and night. Anyone who says, its morning! It is not difficult to understand that he is rounding the interval of time in the morning.
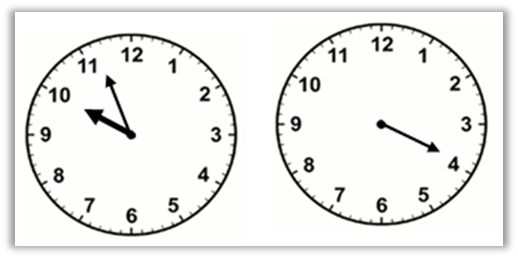 Figure 3
Analogue Watch as a Metaphor for Rounding-off Numbers
(Author’s
personal file)
Figure 3
Analogue Watch as a Metaphor for Rounding-off Numbers
(Author’s
personal file)
If we ask a person with a watch about what time is it
in the clock, then the person probably answers the time to be 10 o’clock even
when the exact time in the clock would have been 10:03 or 9:56 or any nearest
digits. This is because; people divide an hour into
four-fifteen minutes viz. an hour, quarter past, half past and quarter to-. The
concept of rounding of time is common in everyday interaction of the group of
people. Even when the exact time is 10:57, the time is told to be 11 o’clock or
even when it is 10:19, the time is told to be quarter past 10 which is
equivalent to 10:15. The minute here is rounded off to its nearest one-fourth
of a complete rotation. Thus, the watch can be a grounding metaphor for the
teaching and learning of the concept “Rounding off Numbers” inside the
classroom. We can conceptualize the concept for the rounding off numbers
implicitly in course of viewing the time in an analogue watch.
6.4 Mat and Embedded Mathematical Ideas
Weaving is one of the common cultural activities practiced in different communities in Nepal. The weaving of textiles, sitting mat, sleeping mat, basket, and other stuff reflects the cultural values and identities. Various mathematical ideas and thinking are inherited in the process of construction of the mat. Indigenous people have implicit mathematical knowledge with the ability to perform a task but without the ability to explain their deeds (PRADHAN, 2017). This implicit mathematical knowledge is embedded tacitly in their activities. Mosimege and Lebeta (2000) also reported that indigenous people use different mathematical concepts like estimation, tessellations, and symmetry in the construction of traditional artifacts and in various other cultural activities. I observed that the mat weavers exhibited sophisticated geometrical ideas in the process of construction of a net of the mat. The knowledge they practiced in the process of construction of a net of the sleeping mat used the theorems of Euclidean geometry implicitly.
Mat weavers practice mat
Mat weavers practice mathematical ideas and knowledge implicitly in the process of construction of mat. They use sophisticated geometrical ideas while constructing rectangular frames. Two poles are fixed in accordance with the length of mat required and the third pole is adjusted as per the breadth of the mat. To adjust the fourth pole, they use the X-test that is the process of constructing the frame of the mat involving tacit geometrical ideas that two diagonals of a rectangle are equal in length. In a cultural village of Nepal, a rectangular form of sitting or sleeping mat may be rolled up when it is not in use. Some people use sleeping mats to larder for the purpose of reserve paddy. It then takes approximately the form of a cylinder. From the observation of the situations, this cultural experience provides an opportunity for students to obtain an idea of calculation of the curved surface area, the total surface area and the volume of a cylinder.
The finished product is analysed to assess the embedded mathematical ideas in the mat and other cultural artefacts. We have a mat ABCD of length L and breadth H. Let us transform the mat ABCD into a cylinder by rolling up such that AC and BD are just in contact.
Here, Area of initial mat
ABCD = Surface area of the cylinder = L. H
It is evident that the circumference of the base of cylinder (C) = L
This implies that gives
Let A be the area of the cross-section area of the circular cylinder,
Also
From the
observation of the situations, this cultural experience provides an opportunity
for students to obtain the idea of calculation of the volume of a cylinder and
the study of different geometrical properties inherited in it. It is argued
that it is possible to use indigenous mat weaving as a metaphor for the
teaching and learning of mathematics at
different levels of education.
 Figure
4
Folding a mat: a model for cylinder
(PRADHAN, 2019, 136)
Figure
4
Folding a mat: a model for cylinder
(PRADHAN, 2019, 136)
The
incorporation of weaving activities in the process of teaching and learning
enhance mathematical understanding of the students. The teacher, in his
classroom, connected this concept by measuring the dimensions of the mat and
rolling it to conceptualize the concepts of curved surface area, total surface
area and volume of the cylinder formed. Then I took a post-class interview with
the students. I asked the students about how they felt about the teaching with
activity-based pedagogy. Regarding the effectiveness of introducing cultural
activities in the mathematics classroom, one of the student participant S1
viewed
I have learned most of the mathematical concepts through rote and memorization just with an aim to solve problems and score good marks without any level of understanding. Now, the abstract concepts and ideas of curved surface area, total surface area and volume of a cylinder were visualized easily through these activities.
From the
interaction of my student participants, I came to know that, the students’
everyday activities and experience play a vital role in the development of
mathematical concepts. One of the students S2 replied
Before the use of this teaching model, we were just
made to memorize the formula for the purpose of solving common problems. Later,
when this model was taken in action for teaching, we could easily visualize the
abstract concepts and visualize it as a mathematical object.
Another student
S3 viewed
After this class, I was surprised to know that
mathematics could even be linked with the cultural activities that we were
performing just for household jobs. Now, I think that everything that we study
can be linked with cultural activities making even these boring classes
interesting. This lecture really proves it.
The use of
cultural artefacts and everyday activities of learners in classroom teaching
seems to be really appealing and the outcome of the understanding as per the
students was quite appreciable. The use of ethnomathematical practices of mat
weavers as a pedagogical tool shows the importance of the contextualization of
problems (ROSA & OREY, 2012). Mathematical thinking and methods are quite
different in various cultures (GERDES, 2001). The mathematical ideas hidden in
the process of constructing the frame to weave a mat in the rural community in
Nepal is mostly equivalent to the methods that the Mozambican peasantry used
for constructing rectangular bases of houses (GERDES, 1999). Further, Gerdes
(1997) explored that the construction techniques of the housebuilders
facilitate to formulate the rectangle axiom. From the observation of the
different processes of mat weaving, it was found that it includes a lot of mathematical ideas, implicitly and
tacitly embedded in it.
6.5 Carving and Exploration of Geometry
The notion of
symmetry has an important role in the
development of mathematical concepts and science. In everyday life, the most common case of
symmetry is associated with a mirror
reflection. In this vein, Capra (1975) defines a symmetric figure as that which
one can draw a line through it and thereby divide the figure into two parts which
are exact mirror images of each other. By understanding the role of symmetry in the visual recognition process,
we can better recognize its frequency throughout a number of cultural domains.
The mirror symmetry, or bilateral symmetry, is the symmetry with respect to
reflection. A figure, which is indistinguishable from its mirror image, is
called mirror symmetric. A way to think about this symmetry is to fold the
image in the middle and check if the two
halves are identical (SPARAVIGNA, 2000). The rotational symmetry is different because it is quite natural for us to
follow the image in its rotation in the space. This symmetry produces a feeling
of motion and evolution. A breaking of symmetry,
in this case, enhances the idea of interpenetration
or contrast.
One of my research participants Biru (Pseudo name), who carve stone, said that “people love to buy the item if it looks attractive. So my effort is to make an image in the stuff more beautiful”. The image will be more beautiful, and eye-pleasing if the images are symmetric in the pattern. It exists not only in art and design, but it also exerts its strong presence in mathematics, in the physical world of science, in history, and even in story plots and character development. They construct different geometrical patterns in their works. They use rectangular coordinate axes while start to draw a pattern. The symmetries are found in their activities.
Every beautiful thing in the world possess mathematical properties, and the images possess the golden ratio. From the observation of the workplace of the carver, it was found that the coordinate axes, symmetry, reflection are the mathematical ideas embedded in their drawing a pattern. The stone they bring to make different stuff was more likely to rectangular form. I asked him “why do you make the stuff in circular shape even though it is difficult and time-consuming?” Regarding the answer to this, Biru says that the image that he carved possess mathematical properties of symmetry tacitly in order to make the stuff more beautiful and fascinating. He further said that the circular object seems to be more fascinating rather than of rectangular form. In this regard, a circle is a perfect geometrical figure than the rectangle and/ or square because the circle has an infinite number of symmetry axes (FRANCOIS, 2019). The carver had implicit and tacit knowledge of symmetry that helps to make the images more beautiful and eye-pleasing. They construct different geometrical patterns and designs in their works.
In the village of Nepal, symmetrical images are painted on either wall of the door in a house. The wonderful mathematical ideas and concepts which are practiced in the construction of different patterns in stone carving. The stone carver uses the emic view of the mathematical knowledge in the process. The mathematical knowledge they practiced since long complimented to their everyday lives and developed across generations verbally. So, it is impossible for a researcher to go through the emic approach because they all have preconceived perspectives, ideas, and theories. In this regard, Fetterman (2010) viewed that “most ethnographers start collecting data from the emic perspective and then try to make sense of what they have collected in terms of both the native’s view and their own scientific analysis” (p. 22).
This implicit mathematical knowledge is embedded in
their activities tacitly. Mosimege and Lebeta (2000) also reported that indigenous people use
different mathematical concepts like estimation, and tessellations, and
symmetry in the construction of the traditions artefacts
and cultural activities. The stone carver uses a lot of mathematical concepts
and knowledge. This knowledge is sufficient for performance that is consistent
with rules, even though the person might not be aware of the rules. The field
data also supported the findings of Millroy
(1992) that the stone carver uses tacit mathematical knowledge in the process of constructing different stuffs
as Millroy (1992) observed that the carpenters’
physical act of designing and building furniture involved tacit mathematical
knowledge. In this situation, they practice the mathematical ideas of the
circular shape, center, and radius of the
circle; the coordinate axes, reflection
and symmetry of different geometric patterns.
The indigenous language pattern of the speakers reflects mathematical concepts and ideas (OWENS, 2012) who observed how the most indigenous languages of Papua New Guinea (PNG) possess mathematical concepts like volume, mass, area, and length. The children from indigenous communities are deeply immersed in their own cultural world. Their home language reflects the mathematical thinking of the people in own ways (BARTON, 2008; OWENS, 2012) and I also observed that stone carver have tacit mathematical knowledge of circle, identification of center, diameter in the various stage of construction of geometrical pattern and in their conversation. Stone carver use circle in designing the different pattern in the stone.
The circular pattern helps them to make a pattern in symmetrical form. Symmetry in its various forms was found in the designs on the arts and artifacts constructed in a different community of Nepal. Rosa and Orey (2006) viewed that one of the major objectives of the ethnomathematical research is to look for possibilities of incorporating the mathematical ideas embedded into the cultural context of students and teachers for improving the teaching and learning of school mathematics. There is a prevalence of symmetry in designing textiles, sand painting, wall painting, pottery, arts, and artifacts of the people in different cultures.
6.6 Bell and Exploration of Geometry
Nepal is a secular country. The main religion of Nepali is
Hindu. They worship Brahma, Bishnu, and Maheshwar
and they are taken as the Trimurti
(Three God) in Sanskrit. The three forms are the supreme divinity in Hinduism.
They are considered as the cosmic functions of creation, maintenance, and
destruction. Particularly, they are leveled as Brahma the creator, Bishnu the preserver, and Maheshwar the destroyer or
regenerator. Hindu people often visit temples to worship god and goddess. We
did encounter the bells to enchant the prayers and to symbolize the presence of
the devotee in the temple to worship the god. The term geometry may be evolved
as a tool to measure the land. It is thus known as a measurement of “Geo”. However, our school geometry really does not
measure the associated problem regarding
the measurement of the distance between
different two places. It is also insufficient to measure the land area of different landscapes. Thus, Euclidean geometry
is the geometry of plane.
The mathematics teaching and learning would be more interesting and effective if the appropriate connection is made between out-of-school contexts to the school mathematics. The study of cultural artefacts and ethnomathematical ideas embedded in it are the sources for teaching and learning of school mathematics. Ultimately, I decided prehistoric Guheshwori temple as the study location for the field visit with the aim to connect cultural artefacts as the metaphor for teaching-learning mathematics. After reaching the field place, all the students were requested to observe the temple and its surroundings and note down the geometrical objects and the probable mathematical concept that they could identify.
After some time of observation, each group was requested to present their observations and findings. Each group involved in the common task serially presented their findings. The common observation made by the students were the 2D shaped objects like triangle, square, quadrilateral, circle, oval, octagon, trapezium, parallelogram and rectangle. They also observed 3D shapes like hemisphere, cone, frustum, sphere, cube, cuboid, cylinder, prism and pyramid. They sorted out the concepts of concentric circles, transformation, reflection, rotation, symmetry, pattern, and tessellations.
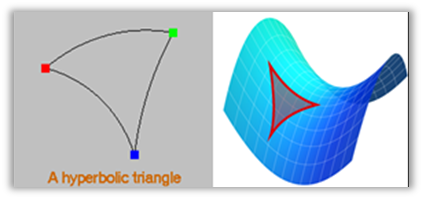
One of the objects they encountered was bell and they were unaware of the surface of it. In this vein, while observing the temple bell, it is possible to describe the distinctive features of hyperbolic geometry and was the metaphor to contextualized the notion of it. The different types of triangles can be drawn on the surface of the bell. It is considered that the inclusion of ethnomathematical ideas in school mathematics valued students’ cultural backgrounds and experiences. The observation of different cultural artefacts in the surrounding of the temple would motivate students to take mathematics relevant to their lives outside the classroom.
From the above
hyperbolic triangle, it is seen that the sum of the angles of a triangle is
always less than 180 degrees, which contradicts the notion that the sum of the
angles of the triangle in Euclidean plane is always equal to 180 degrees. Bell
is one of the interesting artefacts that have
many properties of non-Euclidean geometry. The various property of hyperbolic
geometry can be found in the bell. The parallel lines meet at a point, the sum
of the internal angles of a quadrilateral is less than 360 degree and other
related properties also can be found from the observation of bell. To
distinguish the different types of planes, we would like to draw three
different planes which may be helpful to generalise
the different types of geometrical figures of Euclidean plane, Hyperbolic plane
(surface) and Elliptic plane (surface). The bell can be described
metaphorically as a bell-shaped curve to normal distribution. The bell was
found to be an effective tool to conceptualize the notion of hyperbolic
geometry at a higher level than a basic level.
6.7 Rangauli Mandala and Geometrical Pattern
Nepal has rich cultural traditions and peculiar rituals. Rangauli mandala is constructed on
the occasion of Dipawali. It is drawn using the rice flour including seven
different colors and seen on the floors
of buildings and in front of the worship room during the festival. This drawing
requires different geometrical patterns and spatial reasoning (PRADHAN, 2018).
The number of concentric circles, the number of symmetries both bilateral and
rotational are found in the Rangauli mandala. Different colorings are also associated with this
drawing. Regarding the construction of Rangauli mandala, I asked one of my
research participants Sushila (Pseudo name), how is
the mandala pattern drawn. She replies that the:
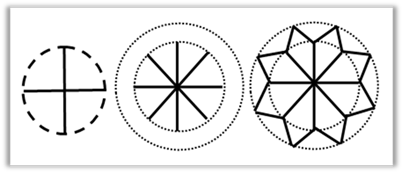
(…) mental image of the pattern helps to draw
a Rangauli mandala. The cognitive map of the mandala is important thing for that. We
start from a point and draw some concentric circles. Anyone can draw any shapes
inside the regions in concentric circles. Some may draw an eight-pointed star or eight petals of a lotus
as per their choices.
From the interview with Sushila, I came to
know that the construction of mandala is a mental construction. The different
geometrical pattern found in their construction is largely hidden from the participants. And the ways of drawing
of such cultural arts and artefacts are craft model approach. Image 6 is the
mandala constructed by Sushila herself in front of
the main doorways of the house. I asked
her how did she draw the eight-pointed star. She had already completed drawing
the mandala.
After my intense request, she chose to sketch it out as shown in Figure 3. The process of her drawing was that first, she drew concentric circles and divided the smaller circle into four equal parts by drawing two mutually perpendicular diameters. Then she further divided each part into two more halves forming eight parted circle. Finally, she retraced the consecutive lines by making them converge at the circumference of the larger concentric circle forming pointed triangles.
From the observation of her sketch of an eight-pointed star, I have come to know that they are practicing sophisticated mathematical ideas in the process of constructing mandala. The Asta Matrika or eight-pointed star has great significance and has religious meaning in Hindu culture. Every creation and perception of the pattern has a logical as well as aesthetic component (ASCHER, 1991). The Rangauli drawing involves complex mathematical activity and a strategic understanding of spatial reasoning. It is important to explore the hidden mathematical ideas in the process of constructing such cultural artefacts. For that, I have conducted interviews with some other people who are constructing such artefacts as their cultural tradition. In this regard, I asked another research participant Kamala (Pseudo name) about the knowledge they learned to construct such beautiful artefacts and her mathematical ideas associated with it. She replies:
I learned to make this artefact by observing
the ways of drawings of my mother as in the same of how these children
observing patiently to my activities here. First I draw a sitting place for
goddess Laxmi at the center as we are going to worship the goddess.
Then I drew some larger circle and eight petals of lotus as we believe that she likes to lye over the pleasant lotus flower.
Rangauli is a symbol of good fortune. Rice flour used for Rangauli drawings provides nourishments for smaller animals, such as birds and ants. This is a symbolic act of showing the necessity of sharing and maintaining proper relationships with others. It also reinforces the respect for nature and relationships with other human beings and animals. Hindu women almost exclusively practice this form of art. Rangauli is being constructed as cultural product from generation to generation in a process of craft model learning approach. It is consistent and perfection in their drawings of the mandala. Though they lack formal education, they possess sophisticated mathematical ideas in mandala construction. From the observation and interview with them, I have come to know that the indigenous people have had their own mathematical ideas and thinking in order to perform their everyday job.
Teaching mathematics becomes more interesting if the contents are related to the students’ familiar environments. Students’ everyday interaction with the cultural environment provides more opportunities to interact and conceptualise mathematical ideas. The cultural activities and artefacts of the students involve a lot of mathematical knowledge and ideas. These mathematical ideas embedded in the students’ cultural environment, which is familiar to the students, provide a good environment to learn. This environment acts as an important tool to communicate mathematical ideas.
The elders,
generally female personals, blissfully draw out the celebratory artefact, the Rangauli, where
they pour their intense ideas and creativity in it. In addition, for any
creation to look striking there is the definite use of mathematical ideas either
implicitly or explicitly. In this view, I interacted with some students
regarding their experiences with the Rangauli construction with their elders. To this note, my
student participants speak:
One of the reasons for me to like Dipawali is that my mother and sister draw the Rangauli and even I can put in
some colors in it. I get so fascinated to make use of so many colors and the
final art always looks so beautiful that I can just see and mesmerize its
beauty for hours.
Looking at her excitement it was sure that the connection of such out-of-school ideas inside the classroom could develop a positive attitude towards the subject, which definitely boosts the understanding of the mathematical concepts. Another participant added, “I patiently observed my mother’s work when it’s about the Rangauli. At the start, she sketched the pattern of the mandala. Then she carved it to a beautiful object by filling it with different shapes and colors in it.” I asked them to sketch the pattern of the mandala from their memory. I observed the same perfection of the outline in their workbook. I asked them if they could see any sort of mathematics in it, a student answered after an unusual pause that there were some shapes like circle, curves and lines.
From the observation of students’ workbook and interaction with them, I came to know that they are performing their cultural activities rather than doing some mathematical tasks. However, there are many mathematical ideas embedded in their construction. The main problem for easy understanding of concepts is that there is a lack of connection between the two mathematical worlds- school mathematics and cultural mathematics. The mathematical ideas practiced in students’ environmental context may be used as a (cultural) metaphor for the teaching and learning of school mathematics. The informal mathematical ideas and knowledge practiced and used in everyday activities are the sources domain for the understanding of abstract mathematical ideas. Thus, the ethnomathematical system of the cultural group can enable a better understanding of school mathematics.
7 Possibilities
of Incorporation of Cultural Artefacts in Mathematics Teaching
Teaching mathematics becomes more interesting if the
contents are related to the students’
familiar environments and ethnomathematical ideas they practice in the
out-of-school context. Students’ everyday interaction with the cultural environment provides more opportunities to
interact and conceptualise mathematical
ideas. They construct mathematical knowledge with the help of
their prior knowledge, experience, active participation in their environmental
activities and cultural artefacts surrounding them. The household activities of
the children and cultural artefacts involved many implicit mathematical ideas.
However, our school mathematics curriculum and teacher training is largely
ignoring the learners’ cultural activities and their ethnomathematical ideas
(PRADHAN, 2017;EZEIF, 2002).
Rosa and Gavarrete (2017) also viewed that children’s
ethnomathematical knowledge and learning approaches are not taken into
consideration in the formal school mathematics curricula. The mathematical
ideas from the group of working-class
people culture, the acknowledgment of
their ways of knowledge generation and transmission, and students’ experiences
should be blended with formal mathematics in the classrooms (PRADHAN, 2017). The mathematical ideas embedded in
the students’ cultural environment, which is familiar to the students, provide a
good environment to learn. This type of environment/ context provides a good
opportunity for students to explore and communicate mathematical ideas.
Mathematical ideas and thinking are embedded
in every environmental activity of a group of people. However, the mathematical
ideas they possess in order to perform
their everyday job remains largely hidden for them. Mathematical anthropology
uses mathematical modeling in historic,
ethnographic, and material culture studies to describe the material and cognitive
patterns of a certain group of people
(EGLASH, 2001). In this vein, Rosa and Orey (2010) viewed that mathematical modeling is a methodological
tool that may be used in the ethnomathematical program. Ethnomathematics can
reshape our greater cultural identity in a positive
way by requiring the inclusion of a greater representation of the true
mathematical practices and problems for a students’ own community (D’AMBROSIO,
1998; ZASLAVSKY, 1996). Symmetry in
designing textiles, sand painting, wall painting, pottery, arts, and artefacts
is prevalent in the people of different cultures
around the world.
The mathematical ideas practiced in students’ environmental context
may be used as a cultural metaphor for the teaching and learning of school
mathematics. The informal mathematical ideas and knowledge practiced and used
in the day-to-day activities are the source
domain for the understanding of abstract mathematical ideas. Thus, the
ethnomathematical system of the cultural group can enable a better
understanding of school mathematics. Regarding the possibilities of
incorporation of cultural artefacts for the teaching of school mathematics, one
of my research participants T1 says:
I believe that mathematics is evolved from the
culture. The different groups of people are using mathematical ideas implicitly
in their profession. Their children are also doing the same work what their
parents do. Children are also using same kind of mathematics. But the real
problem is to connect their mathematics to school mathematics.
Most of the research participants reported that mathematics originated from the cultural activities of different society, from different racial groups around the world. Different professional groups of people are using mathematical concepts and ideas in their own ways. My data in the construction of different cultural artefacts claim the embeddedness of hidden mathematical ideas on it. Their implicit mathematics knowledge of the group of people provides an opportunity for their children to learn mathematics in the classroom. Our school pedagogy has given much importance to rote learning and it is not converged with the ways of knowledge generation and distribution of the local people (PRADHAN, 2017). Thus, I observed that the pedagogy we adopt in school does not acknowledge the out-of-school knowledge of the students.
However, the pedagogy used in out-of-school context was the craft model approach, which is common to the knowledge generation and distribution. This involves participatory and cooperative approaches in which they learn with the help of their parents as Vygotsky (1978) sees learning as an activity in which shared mathematical meanings are constructed socially. Thus, the mathematical ideas embedded in the out-of-school context and the pedagogy they use could be powerful metaphors for the teaching and learning of school mathematics. Teachers who have children's cultural backgrounds and funds of knowledge can link in the classroom.
Other research
participant T3 opined that “We teachers do not have time to think
about to make mathematics teaching more culture friendly because of the
overloaded curricula and over duties in classroom teaching”. Connecting with
the same question, other research participant T2 questioned, “How
can teachers think their lesson more culture friendly if they do not have
sufficient time to manage?” But, another participant T4 gives
serious limitations of the teachers to make their class more culture friendly.
Time is not a problem at all to use cultural artefacts
in the teaching and learning of school mathematics. Attitude and knowledge of
the teachers about the cultural artefacts for teaching school mathematics are
more problematic. But the problem is the lack of ideas on the selection of
cultural artefacts for the teaching of the particular content of school
mathematics.
They believe
that incorporation of culture friendly pedagogy needs more time and extra
effort to classroom teaching. Regarding the use of cultural metaphors for the
teaching of school mathematics, my research participant T2 opined
that:
The use of cultural artefacts in mathematics teaching
is evident. But we are unable to use it in our classroom teaching. How can a
teacher who have the responsibility of taking five to six periods in a day can
manage their own class from culture friendly pedagogy? How to prepare class
with the view of cultural friendly pedagogy for certain mathematical content?
If a teacher has one or two periods of responsibility, then s/he can think
about which cultural metaphor fitted most appropriately.
Most of my research participants agreed with the view of T2. They all accept the importance of cultural artefacts for the conceptual understanding of the mathematical concepts. The incorporation of cultural artefacts in the process of teaching and learning of mathematics enhances mathematical understanding to the students. From the interaction of my research participants, it was found that there are a lot of informal mathematical ideas present in the construction of different cultural artefacts. Those mathematical ideas are effective metaphors to develop spatial reasoning and communicate the abstract mathematical a. I found that the teachers were using ethnomathematical ideas of different groups of people as a metaphor in the process of teaching and learning of classroom teaching.
Teachers are the main agents to deliver formal mathematical content knowledge to their students. Their attitudes, beliefs and values determine how classroom teachers demonstrate alignment for the most effective and meaningful teaching practice (BEARDEN, 2012). Regarding the role of cultural metaphor in the teaching of school mathematics, one of my research participant T1 viewed the cultural metaphor as a powerful tool for the development of mathematical concepts. Most of the participants viewed that the culture friendly pedagogy and the funds of knowledge for teaching and learning of school mathematics are effective for teaching mathematics. Almost all of my research participants agreed that cultural artefacts are potentially a very powerful tool for teaching-learning of the mathematical concepts. The incorporation of metaphor in the process of teaching and learning of mathematics enhances mathematical understanding of the students and eases to transfer abstract mathematical ideas.
8 Concluding Remarks
Metaphors are common to everyone in their everyday communication. Even a child uses metaphors in their gameplay without noticing it. Metaphor is one of the powerful mediated tools that give a real meaning of objects in view of observers. In my study, the ethnomathematical ideas that are practiced in everyday activities of different groups of people, the mathematics embedded in different arts and artifacts in the out-of-school environment, the cultural games, and gestural activities that contributed to conceptualizing the abstract mathematical ideas were considered as metaphors. The culturally relevant pedagogy bridges students’ home culture with school culture in the process of teaching and learning of mathematics. The people outside the classroom use sophisticated mathematical ideas to perform their everyday activities. For example, a mason uses the 3-4-5 method to construct the rectangular shape. Mat weavers use implicit knowledge of Euclidean geometry while they construct the frame for the mat.
Their indigenous knowledge and skills are sufficient for maintain their living. The ideas of estimation and approximation are fundamental and critical in the development of mathematical concepts. The major characteristics of home mathematics are estimation and approximation. The measuring system of the carpenter, estimation of Chundara in the process of constructing wooden stuffs, the ratio of different ingredients in the preparation of tea and the different mathematical ideas embedded in the kitchen involves the estimation and approximation. The mat weavers, textile weavers, stone carvers, wood carvers, small-scale businessperson and different groups of people possess highly sophisticated mathematical ideas in their everyday activities.
The people in the out-of-school environmental context use mathematical ideas implicitly for long. Their mathematical ideas and knowledge have practical validity but are neither acknowledged nor utilized in the school mathematics curriculum. In my study, different cultural activities and cultural artifacts provide an opportunity to explore the mathematical ideas embedded in the cultural context and help to connect school mathematics. The ethnomathematical ideas embedded in everyday activities of different groups of people can also be linked while teaching in the classroom to make it lively. Further, culturally relevant pedagogy builds on students’ home culture as a means to foster success in the learning of school mathematics.
The students’ out-of-school culture and embedded ethnomathematical ideas help to learn school mathematics. From the interaction to teachers and students, it was concluded that the cultural artefacts as metaphors substantially contribute to the process of teaching and learning of mathematics. For instance, the money metaphor contributes to teaching and learning of place value and to conceptualize integers; clock metaphor help to understand rounding off numbers; weaving mat, stone and woodcarving and other cultural activities facilitate understanding various mathematical concepts. This enabled me to conclude that the teachers need to figure out the cultural artefacts as metaphors and use them to teach and help students learn abstract concepts of mathematics. Most of the participants viewed that the culture friendly pedagogy for teaching and learning of school mathematics is effective for teaching mathematics. They agreed that the use of cultural artefacts and its incorporation in classroom teaching creates a positive attitude towards mathematics. They themselves enjoyed the approach of teaching and learning through the use of cultural artefacts and culture friendly pedagogy in the process of teaching and learning of school mathematics.
Acknowledgement
This paper is the outcome of the result of my Ph. D.
study. I would like to acknowledge my supervisor Prof. Dr. Hari Prasad
Upadhyay, Co-supervisor Prof. Dr. Bidya Nath Koirala
for their continuous and untiring support until this stage. I would also like
to give special thanks to community members engaged in different cultural
activities for their cooperation in gathering the necessary information. I
would like to extend my sincere thanks to the head teacher of the sample school
for providing me a huge space to conduct this study, and the participated
teachers and students for their cooperation and support.
References
ADAM, Shehenaz. Ethnomathematical ideas in the curriculum. Mathematics Education Research Journal, v. 16, n. 2, 49-68, jun. 2004.
ALANGUI, Wilfredo V. Ethnomathematics and culturally relevant mathematics education in the Philippines. In ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.), Ethnomathematics and its diverse approaches for Mathematics Education. Cham, Switzerland: Springer, 2017, p. 183-208.
ANGROSINO, Michael; ROSENBERG, Judith. Observations on observation: continuities and challenges. In: DENZIN, Norman K.; LINCOLN, Yvonna K. (Ed.). The SAGE handbook of qualitative research. Thousand Oaks: Sage, 2011, p. 467-478.
ASCHER, Marcia. Ethnomathematics: a multicultural view of mathematical ideas. Pacific Grove, California: Brooks/ Cole Publishing Company, 1991.
BARTON, Bill. Making sense of ethnomathematics: Ethnomathematics is making sense. Educational Studies in Mathematics, v. 31, n. 1/2, p. 201-233, sep. 1996.
BARTON, Bill. The language of mathematics: telling mathematical tales. New York: Springer, 2008.
BEARDEN, Lorrie Ogle. An examination of the relationship between high school mathematics teachers’ dispositions and their metaphors for teaching. 2012. 208f. Dissertation (Doctor of Education in Teacher Leadership) – Bagwell College of Education. Kennesaw State University. Kennesaw.
BISHOP, Alan John. Mathematics education in its cultural context. In: HARRIS, Mary (Ed.). Schools, mathematics and work. London: Falmer Press, 1991, p. 29-41.
BONOTTO, Cinzia. How to replace word problems with activities of realistic mathematical modelling. In: GALBRAITH, Peter L.; HENN, Hans-Wolfgang; NISS, Mogens. (Ed.). Modeling and Applications in Mathematics Education: The 14th ICMI Study. New York: Springer, 2007, p. 185-192.
CAPRA, Fritjof. The Tao of physics: an exploration of the parallels between modern physics and eastern mysticism. Boulder: Shambala Publications, 1975.
CRESWELL, John W. Research design: qualitative, quantitative and mixed methods approaches 3rd ed. New Delhi: Sage, 2009.
CUMMINS, Jim. Foreword. In Book, Affirming diversity: the sociopolitical context of multicultural education. Boston, MA: Allyn & Bacon, 1996, p. xiv-xviii.
D’AMBROSIO, Ubiratan. Ethnomathematics: the art or technique of explaining and knowing. Las Cruces: ISGEm, 1998.
D'AMBROSIO, Ubiratan. Etnomatemática: elo entre as tradições e a modernidade. 2 ed. Belo Horizonte: Autêntica, 2006.
DANESI, Marcel. A conceptual metaphor framework for the teaching of mathematics. Studies in Philosophy and Education, v. 26, n. 3, 225-236, mar. 2007.
EGLASH, Ron. Rethinking symmetry in ethnomathematics. Symmetry: Culture and Science, v. 12, n. 1-2, p. 159-166, 2001.
ENGLISH, Lyn D. Children's reasoning processes in classifying and solving computational word problems. In: ENGLISH, Lyn D. (Ed.). Mathematical reasoning: analogies, metaphors, and images. Mahwah: Lawrence Erlbaum Associates, 1997, p. 117-147.
EZEIF, Anthony N. Mathematics and cultural nexus: The interactions of culture and mathematics in an aboriginal classroom. International Educational Journal, v. 3, n. 3, p. 176-187, 2002.
FETTERMAN, David M. Ethnography: step by step. Thousand Oaks: Sage, 2010.
FONT, Vicenc; BOLITE, Janete; ACEVEDO, Jorge. Metaphors in mathematics classrooms: Analyzing the dynamic process of teaching and learning of graph functions. Educational Studies in Mathematics, v. 75, n. 2, p. 131-152, 2010.
FRANCOIS, Karen. Values and beauty in math education. In: TENTH INTERNATIONAL MATHEMATICS EDUCATION AND SOCIETY CONFERENCE, 2019, Hyderabad. University of Hyderabad, 2019.
FREIRE, Paulo. Pedagogy of the oppressed. New York: Seabury Press, 1970.
FYHN, Anne Birgitte. Sami culture as basis for mathematics teaching. In: BERGSTEN, Christer; GREVHOLM, Barbro; MASØVAL, Heidi Strømskag; RØNNING, Frode. (Ed.). Relating practice and research in Mathematics Education. Proceedings of NORMA 05, Fourth Nordic Conference on Mathematics Education. Trondheim: Tapir Academic Press, 2007, p. 245-256.
GERDES, Paulus. Geometry from Africa: mathematical and educational explorations. Washington: The Mathematical Association of America, 1999.
GERDES, Paulus. On culture, geometrical thinking and mathematics education. In: POWEL, Arthur Belford; FRANKENSTEIN, Marilyn. (Ed.). Ethnomathematics: challenging eurocentrism in Mathematics Education. New York: State University of New York, 1997, p. 223-247.
GERDES, Paulus. Symmetry aspects of Mavuku baskets among the Makhuwa (Mozambique). Symmetry: Culture and Science, v. 12, n. 1-2, p. 87-114, 2001.
GONZALEZ, Norma, MOLL, Luis C.; AMANTI, Cathy. Funds of knowledge: theorizing practices in households, communities and classrooms. Mahwah: Lawrence Erlbaum Asociates Publishers, 2005.
GUEUDET, Ghislaine; TROUCHE, Luc. Towards new documentation systems for mathematics teachers? Educational Studies in Mathematics, v. 71, n. 3, p. 199-218, 2009.
HUTCHENS, Mercedes. Using dollar bills to teach place value. 2015. Retrieved from http://surfingtosuccess.org/2015/08/using-dollar-bills-to-teach-place-value.html.
LAKOFF, George; NUNEZ, Rafael E. Where mathematics comes from: how the embodied mind brings mathematics into being. New York: Basic Books, 2000.
MILLROY, Wendy Lesley. An ethnographic study of the mathematics of a group of carpenters. Journal for Research in Mathematics Education, v. 5, p. i-210, 1992.
MOSIMEGE, Mogege David; LEBETA, Vicent. An ethnographic study of mathematical concepts at the Basotho cultural village. In: MAHLOMAHOLO, Sechaba; NKOANE, Milton; SMIT, K. (Ed). Proceedings of the 8th Annual Conference of the Southern African Association for Research in Mathematics and Science Education. Port Elizabeth: University of Port Elizabeth, 2000, p. 336-341.
OWENS, Kay. Papua New Guinea indigenous knowledge about mathematical concepts. Journal of Mathematics and Culture, v. 6, n. 1, p. 20-50, 2012.
PRADHAN, Jaya Bishnu. Cultural metaphor for mathematical understanding in Nepalese context. 2019. Dissertation (Doctor of Education) – Faculty of Education. Tribhuvan University. Kathmandu.
PRADHAN, Jaya Bishnu. Mathematical ideas in Chundara culture: Unfolding Nepalese teaching and learning system. In ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.), Ethnomathematics and its diverse approaches for Mathematics Education. Cham, Switzerland: Springer, 2017, p. 125-152.
PRADHAN, Jaya Bishnu. Mathematical ideas in cultural artefacts: A metaphor for teaching of school mathematics. International Journal of Scientific and Research Publications, v. 8, n. 9, p. 335-341, 2018.
PRADHAN, Jaya Bishnu. Mathematical knowledge generation and distribution of Chundaras: communalities and disparities from school pedagogy. University Grants Commission, Bhaktapur: 2012.
ROSA, Milton & OREY, Daniel Clark. Ethnomodelling as a pedagogical tool for the ethnomathematics program. Revista Latinoamericana de Ethnomatheamtica, v. 3, n. 2, p. 14-23, 2010.
ROSA, Milton; GAVARRETE, Maria Elena. An ethnomathematics overview: an introduction. In ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.), Ethnomathematics and its diverse approaches for Mathematics Education. Cham, Switzerland: Springer, 2017, p. 3-19.
ROSA, Milton; OREY, Daniel Clark. Ethnomathematics: cultural assertions and challenges towards pedagogical actions. The Journal of Mathematics and Culture, v. 1, n. 1, p. 57-78, 2006.
ROSA, Milton; OREY, Daniel Clark. The field of research in ethnomodelling: emic, etic, and dialectical approaches. Educação e Pesquisa, São Paulo, v. 38, n. 4, p. 865-879, oct./dec. 2012.
SPARAVIGNA, Amelia C Symmetries in images on ancient seals. International Journal of Sciences, v. 2, n. 8, p. 14-20, 2013.
STRINGER, Ernest Thomas; CHRISTENSEN, Lois McFadyen; BALDWIN, Sheila C. Integrating teaching, learning, and action research: enhancing instruction in the K-12 classroom. Thousand Oaks: Sage, 2010.
TAYLOR, Steven J.; BOGDAN, Robert. Introduction to qualitative research methods: a guidebook and resources. 3rd ed. New York: John Wiley & Sons, 1998.
VYGOTSKY, Lev Semenovich. Mind in society: the development of higher psychological processes. Cambridge: Harvard University Press, 1978.
ZASLAVSKY, Claudia. The multicultural mathematics classroom: bringing in the world. Portsmouth: Heinemann, 1996.
Alternative link
https://periodicos.ufop.br/revemop/article/view/2464/3166 (pdf)