1 Introduction
Mathematical activity is a cultural activity (GERDES,
2007) and mathematical knowledge should be understood as a knowledge that all
cultures produce (BISHOP, 1988). D'Ambrosio (2002)
called 'ethnomathematics' to the mathematics practiced by various cultural
groups, which are identified by common objectives and traditions. D’Ambrosio (2009) stated that “in all cultures, we find
manifestations related to and even identified with what we today call
mathematics (processes of organization, classification, counting, measurement,
inference)” (p. 38). Bishop (1986,1988)
determined the existence of six universal basic activities — counting,
locating, measuring, designing, playing, and explaining — by which
mathematics has developed in different cultures and which have contributed to
multiple significant ideas that integrate current mathematics. For Barton
(2008), “ethnomathematics can be regarded as the study of the different fibers
of mathematical knowledge” (p. 107). According to the author, such an image
calls into question the universal origin of mathematics: “There is no reason to
assume that, at the beginning of the braid, there was only one strand. Indeed,
(…), the more likely scenario is that mathematics had multiple origins (BARTON,
2008, p. 108).
The ethnomathematical study of mathematical practices
of particular communities makes us aware of new ideas, concepts and processes
that should not be seen as trivial or simple, and may even contribute to new
mathematics, capable of enriching our mathematical field (BARTON, 2009).
Ethnomathematics is the research area that studies the multifaceted
relationships and interconnections between mathematical ideas and other
cultural elements (GERDES, 2007). In this context, Moreira (2008) notes that in
today's multicultural society, it is essential to develop a conception of
mathematical education that shows it as sensitive to social factors, and as a
knowledge built on social processes. In accordance to this approach,
ethnomathematics allows educational approaches based on culturally relevant
pedagogies (ROSA & GAVARRETE, 2017, p. 26). As claimed by Shirley and Palhares (2017), ethnomathematics provide enrichment and
new topics to students, “demonstrating that mathematical applications can be
found not only in many areas of science, business, and everyday life, but also
that we can see mathematics in cultural practices around the world” (p. 13).
According to Rosa and Orey (2006), the establishment of cultural connections is a fundamental aspect in the development of new teaching-learning strategies, because it allows students to realize that mathematics is a significant part of their own cultural identity. For D'Ambrósio (2001), “beyond boosting minority interests, it is necessary to prepare majority students to work in a diverse, multicultural world, with recognition that not only the majority has or can make contributions to mathematics” (p. 69). “Ethnomathematical approaches are intended to make school mathematics more relevant and meaningful to students in order to increase the overall quality of education and assert more culturally relevant views of mathematics” (ROSA & GAVARRETE, 2017, p. 26).
2 Research Objectives
This investigation in ethnomathematics aims to uncover
the mathematical structure inherent in various elements that constitute folk
dances of Northern Portugal and Galicia, specifically choreography, music and
accessories (RIBAS, 1983). Galicia is an autonomous region of Spain, bordering
with the North of Portugal. Its language is very similar to Portuguese and
before Portugal and Spain existed as such, the two regions together formed an
independent kingdom. Concerning choreography, we intend to represent and
describe the movements that dancers perform during dances, as well as the
system through which they determine their location and thus organize
themselves. About music, we pretend to recognize repetitive phrases in the
musical pieces that accompany folk dances and identify their connection with
geometric transformations. Regarding accessories, we expect to identify
symmetries that the dancers’ costumes admit and classify some plane patterns
present on these costumes. This investigation also aims to construct
mathematical tasks related to the ethnomathematical study carried out, moving
from research to school practice.
3 Methodology
The first objective of research is to study three elements that constitute the folk dances: choreography, music and accessories (RIBAS, 1983). Therefore, from the point of view of the research strategy, this is a study with ethnographic characteristics, because it is a descriptive study of the fundamental aspects of the culture of a community (BAZTÁN, 1995), which is folk dances. Ethnography attempts to describe the culture or certain aspects of it (BOGDAN & BIKLEN, 1994).
Data collection has been carried out in a natural environment through several methods (described below) and complemented by information obtained through direct contact of the researcher with this environment (BOGDAN & BIKLEN, 1994). We studied the dance repertoire of one folk group from a city of Northern Portugal: Braga (Grupo Folclórico de Vila Verde) and another folk group from a city of Galicia: Santiago de Compostela (Agrupación Folclórica Cantigas e Agarimos).
Concerning choreography, we used video equipment to film under different perspectives the movements that dancers perform on the floor throughout the folk dances. We obtained dancers informed consent for recordings. From the video recordings, data has been transcribed (JOHNSON & CHRISTENSEN, 2000), and we made diagrams and numerical schemes representing the successive positions that from the dancers or pairs of dancers occupy during dances. Still in relation to choreography, interviews will be used to collect descriptive data in the language of the subjects (BOGDAN & BIKLEN, 1994) on how dancers determine their location and thus organize themselves.
About music, we collected scores to recognize repetitive phrases in the pieces of music that accompanies folk dances. According to Garland and Kahn (1995), to achieve cohesion, sequences of tones restate again and again in a piece of music, in variations of course, and the musical transformations that bring transformed restatements are closely related to the four basic geometric transformations — translation, reflection, glide reflection and rotation. As so, we intend to find out this particular application of geometric transformations to music in folk songs.
Regarding accessories, we used photographic equipment to photograph and catalog the costumes used by dancers in order to identify figure symmetries (WASHBURN & CROWE, 1988;CROWE, 2004;TAPP, 2012) and classify, according to the notation of the same authors, some plane patterns present on these costumes, specifically friezes or one-dimensional patterns. We obtained dancers informed consent for images. We intend to return and disseminate to participants and local communities the results obtained from this ethnomathematical research.
The second objective of this investigation is to construct mathematical tasks from the ethnomathematical study developed. According to Mason (2002), in a sense, teaching mathematics is mostly about constructing tasks for students, which makes it very important to construct tasks that really promote learning. Therefore, the tasks we will construct will be analyzed by professors for scientific validation and by elements of the folk groups for cultural validation. Then, the tasks will be analyzed by teachers and will be tested and applied in the classroom at the most appropriate educational levels. For this, we will take into account the contents/topics that must be taught at each grade level according to the school mathematics curriculum. The research strategy to be used for the second objective will be design-based research, because it is intended to explore possibilities for creating, using and researching new learning and teaching environments, in real contexts, through continuous cycles of design, analysis and redesign. Importantly, design-based research “goes beyond merely designing and testing particular interventions. Interventions embody specific theoretical claims about teaching and learning, and reflect a commitment to understanding the relationships among theory, designed artifacts, and practice (DESIGN-BASED RESEARCH COLLECTIVE, 2003, p. 6). At this moment, we are still working on this second objective, so this article does not incorporate possibilities for pedagogical practice in schools. This will be the goal of future work.
4 Results
The beginning of the study of choreography, music, and
accessories (costumes) has already allowed us to move towards the analysis of
“forms of mathematics that vary as they are embedded in cultural activities”
(ROSA & SHIRLEY, 2017a, p. 1). Several mathematical aspects arising from
folk dances have been identified. In this article, we will focus on the results
obtained in the study of choreography, to discover the 'hidden' or 'frozen'
mathematics, using the words of Gerdes (1988).
4.1 Choreography
types
Various types of choreography were identified in folk dances of folk groups from Northern Portugal and Galicia, based on dispositions that, although dancers may not remain fixed during the dances, are those to which they end up returning. The types of choreography imply the arrangements in space that dancers predominantly occupy in such dance.
In folk dances of Grupo Folclórico de Vila Verde (Braga, Northern Portugal), we found three types of choreography: circumference; parallel rectilinear axes; and perpendicular rectilinear axes.
In circumference choreography type, dancers are arranged in a
circumference and their movements are realized around the central point that
defines this circumference, sometimes occupying the area of the circle. As an example of these circle dances,
which are the most frequent in this Portuguese folk group, we have the dance Regadinho (Figure 1).
In parallel rectilinear axes choreography type, dancers have two
parallel rows and despite their movements they return to this initial
arrangement. An example of this type of choreography is the dance Chula de Ir à Frente(Figure 2).
 Figure 2
Parallel
rectilinear axes choreography type in the dance Chula de Ir à Frente
(GFVV, 2008, p.
42)
Figure 2
Parallel
rectilinear axes choreography type in the dance Chula de Ir à Frente
(GFVV, 2008, p.
42)
In perpendicular rectilinear axes choreography type(Figure 3),
one or two groups of four pairs are arranged in a cross shaped disposition
considering two perpendicular imaginary lines across every two pairs facing
each other. This configuration becomes even more visible when, in each group,
two of the pairs facing each other advance towards each other and then the
other two pairs emulate it. So, the execution of these kind of movements is
repeated twice, either by one of the two pairs facing each other (one of the
axes), or by the other (the other axis, perpendicular to the previous one).
This is what occurs in dance Vira ao Castelo(Figure 3).
 Figure 3
Perpendicular
rectilinear axes choreography type in the dance Vira ao Castelo
(GFVV, 2008, p. 39)
Figure 3
Perpendicular
rectilinear axes choreography type in the dance Vira ao Castelo
(GFVV, 2008, p. 39)
In folk dances of Agrupación Folclórica Cantigas e Agarimos (Santiago de Compostela, Galicia), we found three types of choreography: circumference; parallel rectilinear axes; and mixed. Note that the first two types of choreography coincide with two types of choreography identified in the Portuguese folk group.
In mixed choreography type, which did not appear in the choreographies of the Portuguese folk group, dancers combine at least two of the choreography types already mentioned. For example, in the dance Maneo de Verdillo, dancers begin the choreography arranged in two parallel rows and, at a certain moment of the plastic development of the movements, they gradually arrange themselves in a circumference (Figure 4). This transposition is repeated multiple times during the dance. Thus, in the dance Maneo de Verdillo, there is a combination of two types of choreography: parallel rectilinear axes and circumference. This type of choreography appears most frequently in folk dances of this Galician group.
 Figure
4
Mixed choreography type in the dance Maneo
de Verdillo
Figure
4
Mixed choreography type in the dance Maneo
de Verdillo
4.2 Diagrams
and numerical schemes
According to Feuillet (2010) “dancing is composed of positions, steps, sinkings, risings, springings, capers, fallings, slidings, turnings of the body, cadence or time, figures” (p. 2). Notwithstanding the complexity of elements that form the 'art of dancing', our analysis focus on 'positions', described as “the different placings of the feet in dancing” (FEUILLET, 2010, p. 2).
In the analytical method, we made diagrams, considering the number of dancers or pairs, the arrangement they assume at the beginning of the dance, and the changes of positions that occur between them. With appropriately and sufficiently detailed data in terms of such characteristics, folk dances were notated in terms of dancers’ changes of positions.
The notation we use is 'pictorial' or 'graphical', in which “indications of positions and movements tend to resemble those actually occurring” (THIE, 2018, p. 35). Therefore, in the diagrams, the vertices represent the positions of the dancers or the pairs — when the pairs dance together all the time — and they are indicated with capital letter. The directional arcs represent the movements of the dancers in relation to the previous positions, being disregarded the movements that do not include alteration of the relative positions. This means that, for example, the rotational movements that the dancers or pairs make around themselves are not assumed in the diagrams.
Each movement of the dancers is represented in a diagram. Therefore, the diagrams show how the choreography is performed, based on the initial position of the dancers and the sequence of changes of positions that occurs.
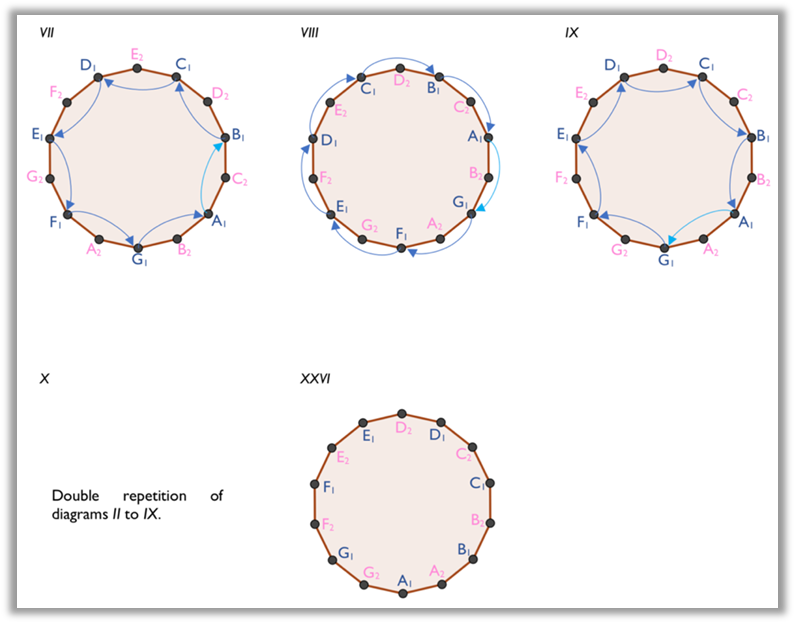
As an example, the analysis of the folk dance Regadinho (circumference choreography type)
is shown in figure 5. The diagrams represent the sequence of movements that
fourteen dancers (A1, A2, B1, B2, C1,
C2, D1, D2, E1, E2, F1,
F2, G1, and G2) do during the dance, starting
from their initial positions. Note that the directional arcs that represent the
movements of dancers A1 and A2 are marked with a slightly
different color, because if the reader wants to focus his attention only on the
changes of positions made by one pair, it becomes easier to follow their
movements. The other pairs make the same movements.
 Figure 5A
Diagrams of the analysis of the dance Regadinho
Figure 5A
Diagrams of the analysis of the dance Regadinho
 Figure
5B
Diagrams of the analysis of the
dance Regadinho
Figure
5B
Diagrams of the analysis of the
dance Regadinho
As another example, the analysis of the folk dance Vira
Velho de Vila Verde (parallel rectilinear axes choreography type) is
shown in Figure 6A-B.
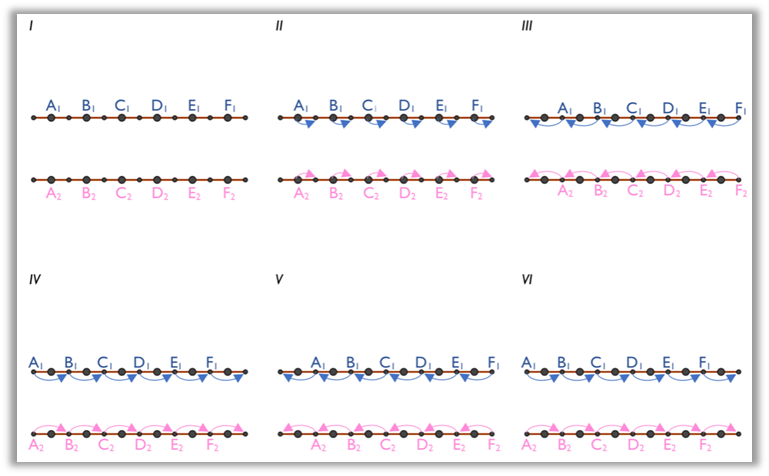 Figure 6A
Diagrams of the analysis of the dance Vira Velho de Vila Verde
Figure 6A
Diagrams of the analysis of the dance Vira Velho de Vila Verde
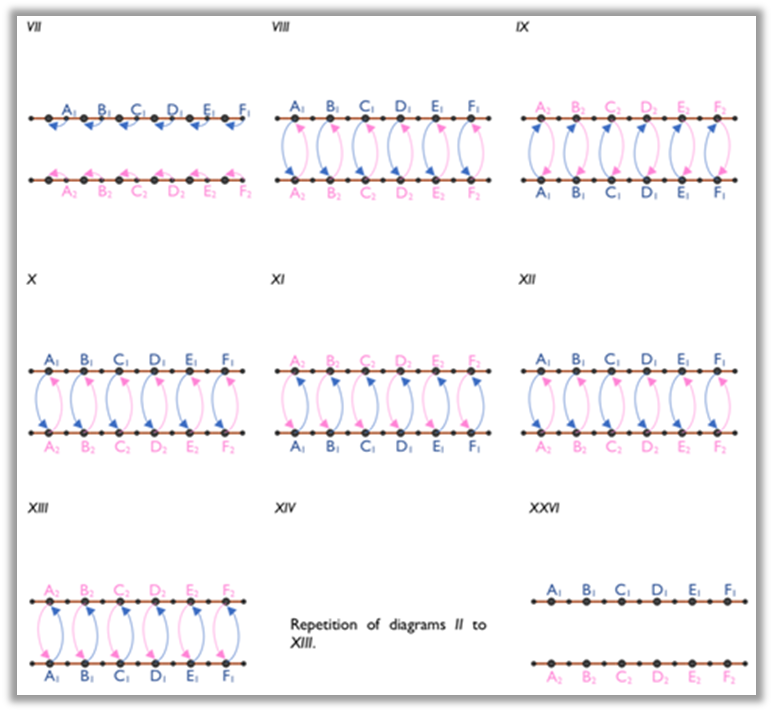 Figure 6B
Diagrams of the analysis of the dance Vira Velho de Vila Verde
Figure 6B
Diagrams of the analysis of the dance Vira Velho de Vila Verde
The distinct examples of dance analysis shown in Figures 5A-B and 6A-B use the same method of notation, already described. Nevertheless, the diagrams are noticeably different, because of the types of choreography implicated. Even with such differences, it was possible to apply the same pictorial notation to describe folk dances in terms of dancers’ changes of position.
Supported on the diagrams of the analysis of folk dances, we then made numerical schemes, advancing to a 'numerical' notation, which “uses abbreviations or characterizations of movements” (THIE, 2018, p. 35). For this purpose, we gave a number to each position of the dancers or the pairs on the initial configuration of the dances (first diagram of dance analysis). Accordingly, the location of dancer A1 corresponds to position number 1, the location of dancer A2 corresponds to position number 2, and so on, following an alphabetical order.
As an example, Figure 7 shows the position numbers (right side image) assigned to the dancers on the initial configuration of the dance Regadinho (left side image).
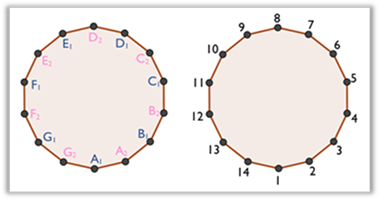 Figure
7
Positions of the dancers on the initial configuration of the dance Regadinho
Figure
7
Positions of the dancers on the initial configuration of the dance Regadinho
As another example, Figure 8 shows the position numbers (right side
image) assigned to the dancers on the initial configuration of the dance Vira Velho de Vila Verde (left side image).
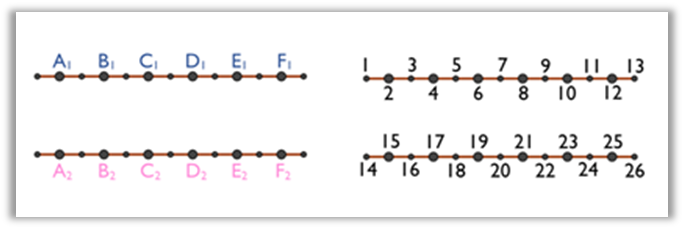 Figure 8
Positions of the dancers on the initial configuration of the dance Vira Velho de Vila Verde.
Figure 8
Positions of the dancers on the initial configuration of the dance Vira Velho de Vila Verde.
Based on the position numbers assigned to the dancers on the initial configuration of the folk dances’ analysis, the dancers’ changes of positions already represented in the diagrams are now described in a numerical scheme. For each diagram, a row of the numerical scheme is filled, giving the dancer A1, A2, B1, B2, C1, C2, … the appropriate position number (1, 2, 3, 4, 5, 6, …). This method repeats for all diagrams of the dance analysis.
As an example, Figure 9 shows the numerical scheme corresponding to the diagrams of the analysis of the folk dance Regadinho.
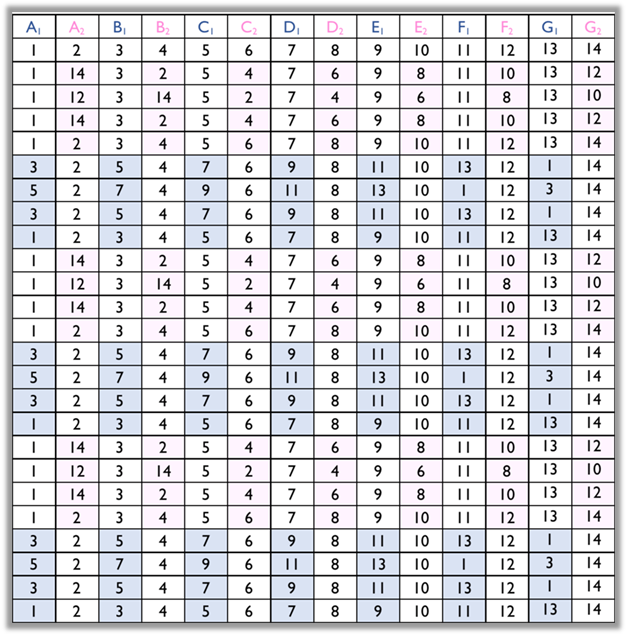 Figure 9
Numerical scheme of the dance Regadinho
Figure 9
Numerical scheme of the dance Regadinho
Another example, Figure 10 presents the numerical scheme corresponding
to the diagrams of the analysis of the folk dance Vira
Velho de Vila Verde.
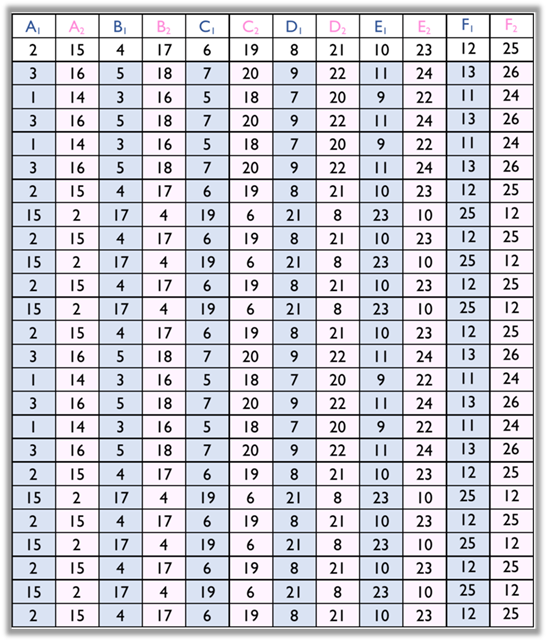 Figure 10
Numerical scheme of the dance Vira Velho de Vila Verde
Figure 10
Numerical scheme of the dance Vira Velho de Vila Verde
It is important to mention that the numerical schemes, based on the
diagrams, support and facilitate the identification of many mathematical
patterns, easily revealing the existence of mathematical aspects in folk
dances.
5 Final
reflections
Our investigation in ethnomathematics aims, on one hand, to analyze three elements that constitute folk dances of Northern Portugal and Galicia, specifically choreography, music, and accessories. On the other hand, it aims to construct mathematical tasks related to the ethnomathematical study carried out.
According to Rosa and Shirley (2017b) “In order to perceive the connection between culture and mathematics, it is crucial to underscore the importance of doing the ethnomathematical work first. This approach leads to a good understanding of the mathematical aspects of culture and a clear purpose of pedagogical activity” (p. 39). Therefore, our investigation began by studying the mathematical aspects present in folk dances. We studied the dance repertoire of one folk group from a city of Northern Portugal (Braga) and another folk group from a city of Galicia (Santiago de Compostela).
In this article we focused on the results obtained in the study of choreography. In our mathematical synthesis of dances, different types of choreography were identified in folk dances of folk groups from Northern Portugal and Galicia. The notion of circumference, center of circumference and circle, as well as the parallelism and perpendicularity of lines in the plane, associated with the different types of choreography found, appear as the mathematical contents emerging from the cultural practice under research.
In addition, we described and notated folk dances in terms of dancers’ changes of positions, making diagrams and numerical schemes, which represent the entire sequence of changes of positions that occurs in a dance, starting from the initial position of the dancers. The method of notation was successfully applied in the different types of choreography, although the diagrams were noticeably different. We believe that diagrams and numerical schemes corresponds to a possible method of mathematical modeling of choreography, that could be associated with combinatorial analysis next.
Our goal now is actually to advance to the second objective of research, which is to use the mathematical aspects emerged from the choreography, as well as music and accessories of folk dances, to construct tasks for students to work with. We think this culturally embedded knowledge can be very useful in school practice. After all, mathematical contents such as isometries, symmetry, geometric shapes, relative lines position and patterns, that emerge from the three elements of folk dances studied, are part of the mathematics curriculum in Portugal and Spain.
Acknowledgements
- This work was funded by FCT through SFRH/BD/131162/2017 and as part of a project of Research Centre on Child Studies from University of Minho, with the reference UID/CED/00317/2019.
- This work was also funded by FEDER/Ministerio de Ciencia, Innovación y Universidades –Agencia Estatal de Investigación/_Proyecto EDU2017-84979-R.
References
BARTON, Bill. Prefácio. In: PALHARES, Pedro. (Coord.). Etnomatemática: um olhar sobre a diversidade cultural e a aprendizagem matemática. Vila Nova de Famalicão: Edições Húmus, 2009, p. 7-10.
BARTON, Bill. The Language of Mathematics: telling mathematical tales. New York: Springer, 2008.
BAZTÁN, Ángel Aguirre. Etnografía. In: BAZTÁN, Ángel Aguirre. (Ed.). Etnografía: metodología cualitativa en la investigación sociocultural. Barcelona: Marcombo, 1995, p. 3-20.
BISHOP, Alan John. Mathematics education as cultural induction. Nieuwe Wiskrant, v. 6, n. 1, p. 27-32, oct. 1986.
BISHOP, Alan John. Mathematics Education in its cultural context. Educational Studies in Mathematics, v. 19, n. 2, p. 179-191, may. 1988.
BOGDAN, Robert C.; BIKLEN, Sari Knopp. Investigação qualitativa em Educação: uma introdução à teoria e aos métodos. Tradução de Maria João Alvarez, Sara Bahia dos Santos e Telmo Mourinho Baptista. Porto: Porto Editora, 1994.
CROWE, Donald W. Introduction to the Plane Symmetries. In: WASHBURN, Dorothy K.; CROWE, Donald W. (Ed.). Symmetry comes of age: the role of pattern in culture. Seattle: University of Washington Press, 2004, p. 3-18.
D’AMBRÓSIO, Ubiratan. Etnomatemática: elo entre as tradições e a modernidade. Belo Horizonte: Autêntica, 2002.
D’AMBRÓSIO, Ubiratan. General remarks on Ethnomathematics. ZDM, v. 33, n. 3, p. 67-69, jun. 2001.
D’AMBRÓSIO, Ubiratan. Globalização, educação multicultural e o programa etnomatemática. In: PALHARES, Pedro. (Coord.). Etnomatemática: um olhar sobre a diversidade cultural e a aprendizagem matemática. Vila Nova de Famalicão: Edições Húmus, 2009, p. 23-46.
DESIGN-BASED RESEARCH COLLECTIVE. Design-based research: an emerging paradigm for educational inquiry. Educational Researcher, v. 32, n. 1, p. 5-8, jan./feb. 2003.
FEUILLET, Raoul-Auger. Orchesography. Or, the Art of Dancing, by Characters and Demonstrative Figures. Wherein the Whole Art Is Explain'd; ... An Exact and Just Translation from the French of Monsieur Feuillet. by John Weaver, ... Translation of John Weaver. Gale ECCO Print Editions, 2010.
GARLAND, Trudi Hammel; KAHN, Charity Vaughan. Math and Music: harmonious connections. Palo Alto: Dale Seymour Publications, 1995.
GERDES, Paulus. Etnomatemática: reflexões sobre Matemática e diversidade cultural. Vila Nova de Famalicão: Edições Húmus, 2007.
GERDES, Paulus. On culture, geometrical thinking and mathematics education. Educational Studies in Mathematics, v. 19, n. 2, p. 137-162, 1988.
GRUPO FOLCLÓRICO DE VILA VERDE (GFVV). Grupo Folclórico de Vila Verde – mensageiro da sua terra ontem, hoje e sempre. Vila Verde: ATAHCA, 2008.
JOHNSON, R. Burke; CHRISTENSEN, Larry. Educational research: quantitative and qualitative approaches. Boston: Allyn & Bacon, 2000.
MASON, John H. Mathematics Teaching Practice: a guide for university and college lectures. Chichester: Horwood Publishing, 2002.
MOREIRA, Darlinda. Educação Matemática para a sociedade multicultural. In: PALHARES, Pedro. (Coord.). Etnomatemática: um olhar sobre a diversidade cultural e a aprendizagem matemática. Vila Nova de Famalicão: Edições Húmus, 2009, p. 47-65.
RIBAS, Tomaz. Danças populares portuguesas. Lisboa: Instituto de Cultura e Língua Portuguesa, 1983.
ROSA, Milton; GAVARRETE, Maria Elena. Polysemic Interactions between Ethnomathematics and Culturally Relevant Pedagogy. In: ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.), Ethnomathematics and its diverse approaches for Mathematics Education. Cham, Switzerland: Springer, 2017, p. 23-30.
ROSA, Milton; OREY, Daniel Clark. Abordagens atuais do Programa Etnomatemática: delineando um caminho para a ação pedagógica. Boletim, Rio Claro, v. 19, n. 26, p. 19-48, jul./dez. 2006.
ROSA, Milton; SHIRLEY, Lawrence. In Guise of Conclusion. In: ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.), Ethnomathematics and its diverse approaches for Mathematics Education. Cham, Switzerland: Springer, 2017b, p. 39-40.
ROSA, Milton; SHIRLEY, Lawrence. Introduction. In: ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.), Ethnomathematics and its diverse approaches for Mathematics Education. Cham, Switzerland: Springer, 2017a, p. 1-3.
SHIRLEY, Lawrence; PALHARES, Pedro. Ethnomathematics and its Diverse Pedagogical Approaches. In: ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.), Ethnomathematics and its diverse approaches for Mathematics Education. Cham, Switzerland: Springer, 2017, p. 13-17.
TAPP, Kristopher. Simmetry: a mathematical exploration. New York: Springer, 2012.
THIE, Joseph A. Dance Mathematics: rhythms & dances; analysis & synthesis. Createspace Independent Publishing Platform, 2018.
WASHBURN, Dorothy K.; CROWE, Donald W. Symmetries of culture: theory and practice of plane pattern analysis. Seattle: University of Washington Press, 1988.
Alternative link
https://periodicos.ufop.br/revemop/article/view/2194/3165 (pdf)

















