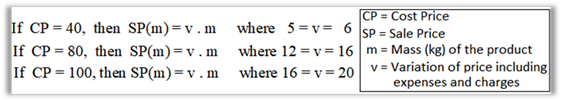1 Introduction
In this article we share our ideas related to the
pedagogical and sociocultural aspects gleaned from master's research entitled: Re-signifying the concepts of Function: A
Mixed Methods Study to Understand the Contributions of the Dialogic Approach of
Ethnomodelling, the Professional Master's in Mathematics Education at the
Universidade Federal de Ouro Preto (UFOP). Through a dialogic approach we
looked at what kind of contributions, if any, that ethnomodelling might offer
function concepts for second year of high school students. From a sociocultural
perspective, this study was directed towards the understanding of student etic[1]
knowledge when interacting with the emic[2]knowledge of a vendor in a dialogic[3]
perspective (CORTES, 2017a).
Perhaps a little context maybe in order here. Over
many years Professor Orey has observed the intersection of math and culture in
a variety of environments, most notably in New Mexico, México, Guatemala, Nepal
and Brasil. In 1998 he was invited as a Fulbright Scholar to work with
Professors Ubiratan D´Ambrosio and Rodney Bassanezi in a unique and creative
collaboration between the two scholars that had created a teacher specialist
certificate program linking ethnomathematics and mathematical modelling at the Pontifícia Universidade Católica de Campinas
(PUCCamp).
Orey was invited by Prof. D´Ambrosio by way of his questions about how Orey might work with teachers to create mathematical activities from an ethnomathematical context, perspective and paradigm. During his semester at PUCCamp he first observed groups of teachers working on a diversity of culturally-based ethnomathematics explorations that allowed them to develop mathematical models. It was there, that he began to look at how to apply ethnomathematics and create data that could be explored and examined through mathematical modelling.
It was Bassanezi (2002) who spoke to this possibility when he said and later wrote, "many interesting models are formulated through knowledge and data obtained in studies and research linked to the ethnosciences or more particularly to ethnomathematics" (p. 54). Therefore,
(...) ethnoscience proposes the rediscovery of
knowledge systems adopted by other cultures. When this knowledge uses, even if
intrinsically, some mathematical procedures then, through modelling it can
arrive at its origin more efficiently. In this way, many situations from
ethnomathematics have produced good results, in relation to teaching-learning,
when worked through mathematical modelling (BASSANEZI,
2002, p. 54).
Since 1998, the ongoing exploration between modelling,
ethnomathematics and mathematics education continued, first in California, and
later from Brasil. This took Orey to Nepal (as a Fulbright Scholar) and later
back to Brasil —
via CNPq[4] — as a visiting professor. Then in 2011, Orey became a
faculty member at the Universidade Federal de Ouro Preto (UFOP) where he has
continued to work along with Prof. Milton Rosa and students in both
undergraduate and graduate levels using mathematical modelling, ethnomathematics
and now, ethnomodelling.
Together we began working with students using modelling and ethnomathematics, and this soon melded into the concept of ethnomodelling. Over time, as Orey and Rosa participated in a number of congresses and meetings and came into contact with numerous scholars both here in Brasil and from abroad, we developed and observed a number of concerns in relation to ethnomathematics.
Diego graduated high school in 2005 and in 2009 was admitted into the Licentiate Mathematics Program at the Fundação Helena Antipoff in what is now called Universidade Estadual de Minas Gerais (UEMG). During his undergraduate studies, he had his first contact with research and with the rigor of academic mathematics and that identified him with the field of mathematics education.
In 2012 he finished his studies and in 2013 he became a teacher in the Secretaria Estadual de Educação de Minas Gerais (SEE-MG) system, where he has been teaching elementary and secondary students near Belo Horizonte ever since. During Diego’s ongoing work as a mathematics teacher he has encountered many of the difficulties of the teaching practice, he said,
I felt the need to specialize, so between 2013 and
2014 I participated in three consecutive modules of the Programa de Aperfeiçoamento
para Professores de Matemática do Ensino Médio — PAPMEM — offered by the Universidade Federal de Minas Gerais (UFMG) in
partnership with the Instituto de Matemática Pura e Aplicada (IMPA). Also in
2013 I studied a single discipline called Ambientes Educacionais Informatizados
the Mestrado Profissional de Educação Matemática da Universidade Federal de
Ouro Preto (UFOP) when I met my research line and also the studies of
Professors Daniel Clark Orey and Milton Rosa. (CORTES, 2017a, p. 16).
When he came across the work on ethnomathematics and
mathematical modelling he, elaborated a research project that allowed him to be
accepted into the masters in mathematics education at UFOP, his research
culminated in his master’s thesis: Re-significando
os conceitos de Função: Um Estudo Misto para entender as contribuições da
Abordagem dialógica da Etnomodelagem[5] (CORTES, 2017a).
His research investigated the following question that will be discussed below: What are the possible contributions that ethnomodelling can offer to the process and re-signification of the concept of function to second year students of a high school in a public school in the metropolitan area of Belo Horizonte through a dialogical approach?
His results have provided a serious advance to the understanding and the re-signification of concepts of function, most notably because his work detailed the integration between emic and etic knowledge through the use of a dialogical approach. In addition, his research has allowed us to develop a better understanding related to the inherent difficulties of mathematical teaching practices that can be better understood if they are observed from the point of view of ethnomodelling through a dialogue between academic and cultural knowledge.
First, to our minds, much of ethnomathematics research seems stuck in what can be referred to as the philosophical, with little work being undertaken in how to actually apply it in practical school/learner contexts. This is what led Prof. Orey initially to PUCCamp as a Fulbright Scholar in ethnomathematics/mathematical modelling and forms a very real and major criticism by many, especially in the mathematics education community, of what constitutes ethnomathematics. As well, many ethnomathematicians have come to confuse either what many non-ethnomathematicians see as indigenous, primitivist, or exotic forms of mathematics.
More importantly, being mindful in sharing new forms
of ethnomathematics and not falling into a colonization trap of the
non-academic mathematics as exotic but irrelevant forms of thinking and doing.
That is, often non-academic forms of mathematics are considered as mere curiosities and not respected or given
alternative forms of mathematics experienced by including the attention it
deserves, as is the traditional scientific-modern-western academic mathematics
that is taught in most universities and schools.
And finally, a question that is asked frequently goes
along the following line: “This is all good, but how do I do this with my
students?”. This is related to a famous and universal question by all students
everywhere: “When will I ever use this?”. It is a serious question, and as a
former public-school teacher himself, Orey deeply understood it. Needless to
say, something had to be done, as one of the academic dangers of most any
discipline are influenced by our own cultural blinders that are easily applied,
and difficult to remove, when we begin to interact with those that are diverse or different than ourselves.
These blinders are the basis to concerns related to the colonization of curriculum. So it is that the same goes with new and divergent ideas such as mathematical modelling and ethnomathematics. At the same time, especially in regard to the PUCCamp Project, Orey observed teachers in different contexts, looking at real problems in their lives with the tools of modelling and ethnomathematics, he began to see the real potential for this.
When Orey moved to Ouro Preto, he was given the course that is now is named EMA512 — Seminário I: Modelagem Matemática in which students in over 30 Polos (educational centers) representing a diversity and varied regions and contexts (urban, rural, poor, middle class etc.) of Brasil. During one semester, the country was gripped by a nation-wide strike and demonstrations by millions of protesters in the streets, because the government suddenly decided to raise bus fares.
At this opportunity, Orey stopped his class (taught
online) and it was decided that everyone should look at the transportation
crisis, through modelling. His modelers formed groups and developed interesting
models in relation to the fares, distance of busses needed to travel, number of
trips by the passengers, combustibles, salaries, etc. Again, he could see
potential in mathematical modelling, and ethnomathematics as a possibility of
great importance, and as a way towards peace (D'AMBROSIO,
2018). Thus, it is necessary to empower people to move away from emotion and
focus on the data in order to allow them to solve the problem under discussion.
What was most interesting, was the models that emerged, looked to us like mathematical poems. Like most any collection of poetry, some were better, more profound than others, more meaningful others. The feedback from the students ranged from gratefulness for the opportunity to safely connect what they know and what they were learning to teach, to what they saw happening in their own community. Most importantly, many students gave feedback related to this being the first time that they could feel free to express themselves mathematically.
Other students mentioned how the course and activity
allowed them to look at data and assist friends and family to look at the
problem, by focusing on the data, and less on the emotional or political
aspects of the bus fare debacle. This was powerful for all of us concerned, we
now saw how we as mathematics educators could use the tools, we had to make a
difference in our own communities. About this time, Orey was invited to give
TEDx talk in Sacramento about his work in Brasil, entitled What I Want to be When I Grow up[6](OREY, 2013).
Over time, we have enjoyed learning more about how to get individuals to share how they do, think and interact with a problem using ethnomathematics and modelling. We are mindful as well and very careful indeed to interfere as little as possible with our own cultural biases (background) on our part and that of the students and the community under which we are working. The more freedom and trust we extend to our students, the better many of the models are.
So it was that we began looking deeper into anthropological tools for assisting us in keeping mindful of our own built in biases and that might allow me to empower new voices of those we were working with. The best strategy was found by both Professors Rosa and Orey in looking first at both at day to day aspects of mathematics and the conflict/dialogue developed with the insider-outsider (emic/etic) dynamic.
And this has become what we now call ethnomodelling and will be outlined in detail below. So it was that Diego approached us and wanted to examine and test ethnomathematics and ethnomodelling ideas in the context of his own community and school. As we looked at the possibilities, it was decided that he would look at how a farmer market vendor of vegetables he had observed worked and then apply it to getting his students to explore his work and translate and connect it to functions and the formal curriculum.
The following is a description of his work and experience, in hopes that the reader might apply this in their communities and schools as a way to undercover, apply and, most importantly, apply ethnomodelling to assist leaners to value what is being done in your context with ethnomathematics. In agreement with this perspective, the mathematical practices locally developed in the market, by the vendors of vegetables or other objects, were incorporated dialogically with the academic knowledge of Diego´s students, thus reinforcing dimensional aspects of ethnomathematics, especially in the conceptual, cognitive and educational dimension.
Through the methodology of a mixed methods study, Diego developed an understanding that used both qualitative and quantitative aspects of cultural practices of the market vendor that could contribute to a re-signification of academic concepts related to functions. In order to achieve these objectives, his research was structured in such a way as to include the epistemology of ethnomathematics, mathematical modelling, ethnomodelling, as well etic, emic, and dialogic ethnomodels.
2 Ethnomathematics
What is important overall is that for us, shared knowledge and behaviors used by members of distinct cultural groups are configured as forms of understanding in the context of their own cultures (D'AMBROSIO, 2001). From this perspective, the study focused on the participation of members belonging to two specific cultural groups: one composed of 38 high school students while the other is formed by what mathematics is used in market setting. In this context, Rosa & Orey (2017) argue that through cultural dynamism[7], members share their knowledge in a symmetrical way in a dialogue performed with a sense of otherness.
D´Ambrosio´s Ethnomathematics Program recognizes that members of distinct cultural groups in their diverse environments develop their own means of mathematizing[8] their own daily practices. This facilitates the development of lively, dynamic pedagogies in response to their environmental, social and cultural needs, and gives space to imagination and creativity (D'AMBROSIO, 2008). In this study, the conception of the mathematization of reality was adopted, since it corroborates to how we come to understand the importance of mathematical thinking within our own school and community context; this by enabling the exploration of their own mathematical conceptions (D'AMBROSIO, 1993).
In this way, an
Ethnomathematics Program has important pedagogical implications for the valorization
of student cultural knowledge in relation to their own mathematical
knowledge/doing that they experience in school, and allows the development of a
sense of mindfulness, criticality, reflection and awareness so that they are
able to make better decisions about events in their own world (ALVES, 2014). Since it aims to analyze
the sociocultural roots of mathematical knowledge, the ethnomathematics program
has six important dimensions called: Cognitive, Educational, Conceptual,
Historical, Political, and the Epistemological, which are
interrelated (D'AMBROSIO, 2001).
However, in this
study, we opted for, and used a more detailed description of the Conceptual,
Cognitive and Educational dimensions (D’AMBROSIO, 2001), which were directly
related to the objectives of this discussion.
-
Conceptual Dimension: this dimension is related to the survival process of cultures, because it depends on immediate behaviors in response to the routines and problem situations inherent to the members that constitute them. Faced with this fact, mathematical knowledge emerges as a response to the survival and transcendental needs of members of these cultural groups.
-
Cognitive Dimension: this dimension is
related to the study of characteristics of human thought that are driven by
universal mathematical ideas, such as comparing, classifying, quantifying,
measuring, explaining, generalizing, inferring, evaluating,
and modelling present in all cultural groups.
-
Educational Dimension: this dimension also
considers academic mathematical knowledge that is developed in school
environments through its improvement with the incorporation of "values of
humanity, synthesized in an ethic of respect, solidarity and cooperation"
(D'AMBROSIO, 2001, p. 43). In
this dimension, this knowledge must be used in a critical and reflective way by
the members of distinct cultural groups so that they can meet the daily demands
faced daily.
Consequently, the
Ethnomathematics Program offers possibilities for multicultural education[9]
through which the learning of students in the classroom provides meaning and
re-signification of problems faced by school communities and societies.
3 Modelling
In Brasil, over the
last three decades, the amount of research related to mathematical modelling
has increased dramatically. However, the conduction of this particular study
was mainly based on the work developed by Rosa & Orey (2003, 2017), which
seeks to strengthen the process of teaching and learning mathematics in its
sociocultural aspect by considering possibilities of the use of the
Ethnomathematics Program and modelling in education.
The pedagogical action between ethnomathematics and modelling (ROSA & OREY, 2012) fosters an awakening of new possibilities for the exploration of related issues found in social, cultural, political, environmental and economic contexts. The objective is to help students to find a sense of contextualization and significance between the school and community mathematical content. This can be modeled through translation[10] and between different systems of mathematical knowledge.
The translation of mathematical knowledge among members of distinct cultural groups, such as found in the case of a farmer market vendor and local high school students; can be understood and/or improved on by the use of mathematical modelling. In this context, modelling can be considered as a form of access for the development of understanding of formal mathematical ideas, notions, procedures, and practices while ethnomathematics is a pedagogical action that facilitates the understanding of the mathematical potentialities developed by members of a particular cultural group (ROSA & OREY, 2006).
Thus, the possibility for the translation of cultural knowledge makes modelling an important tool to help students understand, analyze, and reflect on their own sociocultural context. Therefore, being efficient in the development of mathematical modelling becomes essential so that members of distinct cultural groups can actively develop and understanding and even transform their own reality where they live by enabling the inclusion of their perspectives in a critical and reflexive way (ROSA & OREY, 2006).
In this sense, it is necessary that activities developed in the classroom have their origins in systems[11] found in the context of a students' daily life and/or is very close to their socio-cultural reality as they learn to reflect on the aspects involved in problem situations to be modeled. Because it is related to the local economy of the region in which the students live, this study contemplated and valued the system (sales) of vegetables produced by local farmers and provided a certain familiarity with the sociocultural aspects of the school and community.
4 Ethnomodelling
While conducting explorations and research in mathematics education, it is common for both researchers and teachers to come across mathematical ideas and procedures rooted in diverse cultural contexts. This is often in line with the diversity of mathematical practices developed by the members of distinct cultural groups found around us.
In this context, ethnomodelling can be considered as a powerful pedagogical action, since it adopts a more comprehensive conception of locally developed mathematical practices (ROSA& OREY, 2010). Mathematical concepts developed academically can be remembered or reemphasized when connected with diverse mathematical and cultural realities and contexts (CORTES, 2017a).
Ethnomodelling enables a (general) holistic understanding of knowledge practiced by members of distinct cultural groups and broadens the understanding of academic mathematical concepts (ROSA & OREY, 2017). In this pedagogical action, the local knowledge developed by members of distinct cultural groups is related to a set of mathematical characteristics implicit in the ideas, procedures and mathematical practices different from those studied in school. Interesting sets of characteristics found outside of school is translated through ethnomodelling(ROSA & OREY, 2010)
It is important to emphasize the mathematical knowledge developed when members of distinct cultural groups share and exchange their own interpretation of their culture (an emic approach) as opposed to the interpretation of researchers and researchers (an etic approach). Therefore, Rosa & Orey (2012) state that one of the objectives of ethnomodelling is to study potential models developed by members of distinct cultural groups, yet do not exclude academic ethnomodels developed in educational institutions that can be deepened or improved through an ethnomathematical perspective.
In this way, the diversity of dimensions presented by applying ethnomathematics and modelling techniques helps and directs researchers and educators in valuing the models developed by members of distinct cultural groups. We argue that the pedagogical approach that connects the cultural aspects of mathematics (ethnomathematics) to the aspects of academic mathematics (modelling) is called ethnomodelling (ROSA & OREY, 2010).
From this direction, ethnomodelling seeks to use the ethnomathematical knowledge and modelling techniques to translate problem situations drawn from students’ own reality with the objective of consolidating sociocultural perspectives of this process. Local knowledge is related to a set of mathematical features implicit in the procedures and practices often different from those frequently studied in school institutions.
Global knowledge is associated with the ideas, notions, or what is thought of as universal mathematical procedures that are global constants and are considered as invariant practices that can be developed by members of distinct cultural groups. Local mathematical knowledge is developed when members of distinct cultural groups have their own interpretation of their culture (emic) in counterpart to the interpretation of external researchers and educators who use a global/outsider knowledge (etic) (ROSA & OREY, 2017).
In this context, Rosa
& Orey (2012) argue that an ethnomathematical and academic knowledge can be
used in teacher pedagogical practices through dialogical processes by applying
modelling. Thus, ethnomodelling is supported by using a dialogic approach,
where the encounters with and between other cultures, points of view, and
contexts allow for the members of distinct certain cultural groups to share the
characteristics, even create new ways of doing by using the knowledge,
experiences, and point of views of the others.
5 Ethnomodels
A mathematical model
can be defined as a set of symbols and mathematical relations that somehow
represent the object studied (BASSANEZI,
2002). However, models derived from cultural practices are formed by units of
information originating in and from ethnomathematical perspectives. These
models are rooted in sociocultural traits[12],
called ethnomodels that are
representations considered as small units of information used in the
interpretation and understanding of the reality of the members of distinct
cultural groups. The translation between emic and etic approaches can be
carried out with the elaboration of dialogic ethnomodels that consider
sociocultural influences in the process of ethnomodelling.
5.1 Emic ethnomodels
Ethnomodels that are elaborated from and by the perspective of local experiences and knowledge are referred to as emic ethnomodels, since they are based on mathematical conceptions rooted in cultural aspects and are internal to the specific cultural perspective as, for example, are religion, the clothes, the ornaments, the architecture, and other markers related to styles of life and often unique ways of counting, measuring, comparing, classifying etc. (ROSA & OREY, 2012).
Due to different relations with climate, colonization, trade, and power or religion, the members of distinct cultural groups may have developed unique ways of synthesizing mathematical knowledge, such as "drawings and sketches, artistic or written representations, as well explanatory and descriptive rhetorical expositions which present mathematical ideas and/or procedures proper to their culture" (CORTES, 2017b, p.17).
From the point of
view of ethnomodelling, Lett (1996) mentions that emic knowledge must be
validated consensually by members of the cultural group themselves, who must be
in agreement with the shared perception that portrays the characteristics of
their own culture and ways of doing.
In addition, this approach must consider "the whole complex and particular
characteristics intertwined with the whole cultural milieu" (ROAZZI, 1987, p. 37), which without a
doubt favors an appreciation of the mathematical knowledge of these members.
5.2 Etic ethnomodels
Etic ethnomodels can
be considered as a mathematical representation based on conceptions of external
observers in relation to members of a particular cultural group. Thus, in the
elaboration of ethnomodels it is common for us to use comparison techniques
between mathematical practices that were developed by members of the group
understudy and with the use of certain metric categories common to external
cultures (ROSA & OREY, 2012b).
It is necessary that an elaboration of ethnomodels is related to the objectives of what ethnomodellers consider external features when describing cultural contexts being observed, since reflections and validations of proposed ethnomodels are in accordance with their own mathematical conceptions. Etic knowledge can be obtained through sharing, elucidation and observation, so that members of a given cultural group present their scientifically valid knowledge (ROSA & OREY, 2017).
The ethnomodels developed from global conceptions present descriptive characteristics that demonstrate an analytical perception of behavioral and sociocultural structures of the observed group. Lett (1996) argued that these representations are based on metric and mathematical categories as developed by observers coming from outside the observed cultural group.
5.3 Dialogic ethnomodels
Dialogic ethnomodels are mathematical representations constituted holistically from both etic and emic perceptions. Thus, in the context of ethnomodelling a cross-cultural contrast is used (NICOLESCU, 1999), which ensures a translation of knowledge acquired during the meeting of external observers with members of a group under observation. This is why investigations must be based on a sense of complementarity between the etic and emic approaches that provide holistic understanding of the mathematical knowledge developed by the members of different cultural groups (ROSA & OREY, 2012a).
In general, an emic approach seeks to elucidate internal cultural distinctions (how we do it) while an etic approach aims to study the objectivity of the external observers with respect to the mathematical practices developed by the members of distinct cultural groups (how we think they do it). For example, Rosa & Orey (2017) affirm that dialogic ethnomodels make possible both the translation and sharing of sociocultural aspects of mathematics, through a symmetrical dialogue and with alterity between the observers and the observed. Thus, a dialogue between different perceptions of otherness enables the valorization of distinct sociocultural characteristics of members of the groups, which often complements each other in their diversities, reciprocally enriching both worldviews (emic and etic) through ethnomodelling.
6 Methodological approach
The methodological approach used in this research was a Mixed Methods Study (CRESWELL & CLARK, 2007) that prioritized a QUAN+QUAL methodological design by relating qualitative and quantitative approaches to the development of data collection, analysis, and interpretation processes simultaneously. Again, the population that participated in this study was composed of a group of 38 high school students in a public school near Belo Horizonte and by a farmer market vendor in an open-air vegetable market, who shared the same sociocultural context in the school community.
The instruments of data collection used in this study were: a) two questionnaires: one initial and one final; b) documentary record activities related to the elaboration of the emic, etic, and dialogic ethnomodels; c) teacher-researcher's field diary; d) visit to a free market; e) seminar with the participation of the farmer market vendor; and f) semi-structured interview with the farmer market vendor.
The data were organized, analyzed, and interpreted through the use of descriptive statistics with the elaboration of graphs and tables. The activities were filmed and later transcribed so that the researchers could verify the development of the students in relation to the re-signification of the functions concepts. In relation to data analysis, the interpretation of results through a data triangulation was performed as well as a dense description of the methodological procedures (GEERTZ, 1973).
The qualitative data were then quantified, and coded by using words, terms, phrases, and expressions (CRESWELL & CLARK, 2007). In order to allow for a better understanding of the research question of this study, the codes were grouped into similar themes that originated the categories of analysis.
7 Results and discussions
The systematic
analysis of the research instruments discussed above and the quantification of
qualitative data provided substantial elements in the description of three
categories: School Environment, Out-of-School Environment, and Dialogical
Environment, which are respectively associated with etic, emic, and
dialogic approaches related to ethnomodels developed by the students in this
study. The School Environment category was composed of three subcategories
named Function, Academic Mathematics, and School. The
analysis of the data showed that, according to the quantification of the
qualitative data; 26.2% of the words and terms and 23.5% of the phrases and
expressions codified in the collection instruments revealed characteristic
elements of the School Environment(CORTES, 2017a).
This result
corroborates with the conceptualization of the educational dimension of
Ethnomathematics Program (D'AMBROSIO,
2001), which also values school mathematical knowledge. Thus, one of the
objectives of this program is to incorporate behaviors and values, such as
emotional, social, cultural, affective, political, and economic, in the process
of teaching and learning mathematics so that students can become active
subjects of their educational process (OREY & ROSA, 2007). In this context, figure 1 highlights the etic
characteristics present in an ethnomodel developed by one of the students who
performed a translation of both the price and weight of a given commodity
through the concepts of domain and function image.
 Figure 1
An etic
ethnomodel relating the price and weight of a given commodity to the concept of
domain and image of a function
(CORTES, 2017a, p. 144)
Figure 1
An etic
ethnomodel relating the price and weight of a given commodity to the concept of
domain and image of a function
(CORTES, 2017a, p. 144)
With respect to figure 1, this example shows that there was a re-signification of the concepts of domain and image of the function, as well as of the notion of one-to-one correspondence through the interaction between the scholastic and etic knowledge present in the school community. Therefore, it is important to emphasize that ethnomodels are elaborated according to the view of the external observers (students) who represent them in the way that the ethnomodelers imagine that the systems taken from the inner reality (markets) work. These ethnomodels are related to the academic mathematical knowledge that predominates in the curricular activities developed in the schools (ROSA & OREY, 2012).
Data analysis showed that the Out-of-School Environment category comprised 63% of words and terms and 50.1% of phrases and expressions. Thus, reflecting on the importance of emic knowledge present in the work practices of the farmer market vendor. This category was composed of five subcategories: market, products, farmer market vendor, instruments, and packaging. It should be emphasized that these categories are related to the technical knowledge of the farmer marker vendor himself, as well to a transition between the scholarly and etic knowledge of the students. Thus, this category presented descriptively both emic and dialogic ethnomodels that were elaborated during the cultural dynamism between the members of these two distinct cultural groups (students and farmer market vendors).
Emic knowledge of the farmer market vendor emerged during an interview, whose main objective was to understand specificities of the vendor's culture, as well to understand the issues related to the use of his mathematical practices in daily life. Another objective was related to the elaboration of rhetorical emic ethnomodels derived from his everyday labor practices. Thus, when analyzing the level of schooling of the farmer market vendor, the working time for the commercialization of the products, and his experience with variety of mathematical knowledge used in the market, the researcher inferred that the knowledge of how the farmer market vendor used addition, subtraction, multiplication, and division were developed in the market context, and contributed to satisfactory performance of his activities in the market (CORTES, 2017a).
Because it is important to consider the relevance and articulation of the mathematics in the market with other forms of knowledge, such as reading, writing and, above all, the social roles played by the members of that particular cultural group, activities carried out in the market are not limited to the domain of elementary mathematical operations. According to this context, it is important to emphasize that commercial activities present in the market provide an environment full of ideas, notions, procedures, and mathematical practices that can be translated by actions of "comparing, classifying, quantifying, measuring, explaining, generalizing, inferring and in some way, to evaluate, are ways of thinking, present in the whole human species" (D'AMBROSIO, 2005, p. 30).
Through the analysis of the answers given in the interview, it can be inferred that there are indications for the application of local mathematical practices (emic), which emerged when the farmer market vendor mentioned that he also made sales using plastic packages. For example, for sales, the vendor made the products available in packages or per kilo for the choice of the customers. Generally, the packages weigh one kilogram, being weighed on a scale. According to the farmer market vendor, this type of weighing enables him to make a profit from sales, because "I put half a kilo in the package to give profit and weigh everything in the balance".
Thus, this know-how
is related to the development of mathematical thinking that seeks to explain,
understand, and comprehend the various ways farmer market vendor has to deal
with his work environment, for examples, he commented that "I make a
package to facilitate the customer, because he arrives in a hurry in need to be
attended quickly" For example, table 1 presents an excerpt from the
interview between the researchers and the farmer market vendor that shows the
development of the first emic ethnomodel.
Table 1
Excerpt from the
interview between the researchers and the farmer market vendor that shows the
development of the first emic ethnomodel
 Cortes (2017a, p. 151-152)
Cortes (2017a, p. 151-152)
The excerpts from this dialogue shows that mathematical practices are locally developed (an emic approach), since they are used in the daily life of members of distinct cultural groups for the contextualization of a sociocultural environment defined according to their history, language, and culture. These excerpts also show how the activities performed by the farmer market vendor in his daily work tasks contemplated the skills of mental and estimative calculations, which can serve as a starting point for the elaboration of problem situations for the materialization of a pedagogical proposal that can dialogue with the formal mathematical knowledge used in the everyday classroom.
On the other hand, it is important to observe that the position of the vendor interfered directly in the development of his ethnomodels, because he felt safer being in his own sociocultural context. He justified this discomfort because "when I'm there, in the market, I already have the prices in my head". Hence, Dwyer (1982) points out that in research contexts, it is necessary to develop an awareness of the researchers regarding an understanding of the positionality of the interviewees so that the contrasts of the coming and going between the academy and the fieldwork can be reduced. Then, Creswell & Clark (2007) argue that the positionality of members of local culture facilitates the description of the phenomena of their sociocultural reality.
During the visit to the market, the vendor said that at the beginning of the activity, the sale of the products is "more expensive due to the expenses with gasoline, plastic (packaging), food, and with the helper", whose argument is complemented by the following example:
Let's assume that you
buy tomatoes, it will come out at 40 reais a box, it will come out at 40 cents
for each 100 grams, I cannot sell at that price because of expenses. That way,
I put the five reais a kilo. Because it should be more expensive because you do
not go to CEASA to buy and sell at the same price. You go for 100 percent, 50
percent, or 60 percent more; it depends on the price I buy the product. This
system is used on any product. If I buy the product at 80 reais or 100 reais
its price should be 10 reais or 12 reais a kilo.
According to the
perspective provided by the farmer market vendor, it is inferred that this an
emic model is related to multiplicative thinking, in which the sale price is
approximately one-tenth of the purchase price. In addition, in some situations,
the farmer market vendor adds a higher value, which is intended to cover
expenses and charges on goods sold. For example, the farmer market vendor
explained that:
A product whose cost is 50 reais will have a sale price between 5 and 6 reais a kilo. Other product, whose cost price is 80 reais will have a sale price between 8 and 10 reais a kilo. And a third product whose cost price is 100 reais will have a selling price between 10 and 12.00 reais and so on. However, it is important to note that this selling price may be added to other expenses related to the market expenditures.
Figure 2 shows the
elaboration of a possible etic model developed by the students based on the
information given by the farmer market vendor.
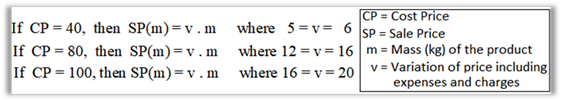 Figure 2
A possible etic ethnomodel approximation
of the marketer
(CORTES, 2017a, p. 167)
Figure 2
A possible etic ethnomodel approximation
of the marketer
(CORTES, 2017a, p. 167)
According to these results, it is inferred that the determination of the sale price, besides being related to the quantity of products purchased, is also linked to an emic construct developed by the work experience of the farmer market vendor. Thus, in accordance with an etic point of view, Figure 3 shows the elaboration of a possible etic ethnomodel representing this sales process developed by the merchant himself.
The interpretation of these emic and etic models allows us to infer that the sale price is comprised in an interval whose parameter of variation is approximately 10% of the cost price, since 10% of 50 equals 5, 10% of 80 is equal to 8, and 10% of 100 is equal to 10, which is a good approximation for the parameters highlighted above. However, in addition to this parameter, the farmer market vendor also adds an increase of costs related to the expenses of the vendor that are included in the final price of his products.
The category, Dialogic Environment, was composed of
two subcategories: Pedagogical Action for
Ethnomodelling and Connecting the
School and Out-of-School Environments. This category originated from the
quantification of the qualitative data that comprised 10.8% of the words and
terms and 26.4% of the phrases and expressions. It is worth noting here that
the development of dialogic ethnomodels helped the students in the
re-signification process of the concepts of function, since it connected the
students' school contexts with the out-of-school teacher. Figure 3 shows one of
the dialogic ethnomodels developed by the students, which presents
characteristics of a discrete function.
 Figure 4
Dialogical ethnomodel with discrete
function characteristic
(CORTES, 2017a, p. 145)
Figure 4
Dialogical ethnomodel with discrete
function characteristic
(CORTES, 2017a, p. 145)
The dialogic ethnomodel as represented in Figure 3 shows that the students transcended the concepts of function, since initially they could only represent a continuous function of the first degree and present it in the construction of the graph, the characteristics of a discrete linear model, whose content was unknown.
It is very important for us to emphasize here that the concept of discrete functions emerged naturally during the contact of student etic mathematical knowledge with a scholar's mathematical knowledge of the farmer market vendor. It was organic and emerged out of the context they observed and experienced. This was evidenced with the programmatic content referred to as the study of functions that did not introduce the concept of discrete functions. Thus, the elaboration of discrete ethnomodel was related to varied and different forms of sale used by the vendor, especially those related to the different forms of the packaging he used.
Since students
realized that the sale of products in boxes was related to the understanding of
a non-continuous (discrete) function domain, their interest and curiosity
regarding different types of packaging led them to the development of their
ethnomodel. In this way, the students restructured and re-signified knowledge
about function, and offered an innovative meaning that best interpreted this
problem-situation. Therefore, this model resulted from the dynamic of the
cultural encounter between these two distinct groups (students and markets),
which, through cultural dynamism, enabled the intertwining of the formal (etic)
and informal (emic) knowledge of these individuals.
8 Final Considerations
This research is related to ethnomodelling based on the understanding of mathematical labor practices developed by a vendor and his connections with the re-signification of the concept of function. An important contribution of ethnomodelling in this process was to provide an analysis of the informal and labor strategies used by the farmer market vendor as well the formal techniques employed by the students, in each cultural context, since these environments constitute spaces of effective exchange of mathematical knowledge. These spaces have principles based on cultural dynamism, with emphasis on dialogic communication that is based on mutual respect and individual differences, as well as on the valuation of individuals and their subjectivities.
The specific ethnomodels outlined here, allowed for the organization and presentation of the farmer market vendor’s mathematical practices (emic) to facilitate their communication, transmission, and diffusion in the school environment. The representation of local mathematical knowledge of the farmer market vendor was translated by means of scientific methods (etic) that were related to the re-signification of the concept of function. In this particular and powerful dynamic between these two cultural groups, students and farmer market vendor, it was possible to re-signify mathematical concepts of function that had not yet been contemplated or found in conventional academic methodologies.
Consequently, we found that the sociocultural perspectives in the ethnomodels contributed to the appreciation and know-how of the farmer market vendor who performs his own mathematical practices, such as counting, measuring, comparing, classifying and modelling. These are activities carried out in the market unveiled an environment full of ideas, notions, procedures and mathematical practices, inherent to the marketing process, which became obvious, indeed implicit in this context and which are different from those practiced in the academic school environment.
Ethnomodelling has allowed for an insertion and reconceptualization of function concepts in the mathematical curriculum by means of the elaboration of mathematical activities originating in the sociocultural context of the school and the community. This approach made possible a dialogic development between ideas, notions, procedures, and mathematical practices intrinsic to the farmer market vendor mathematical processes (emic) and the school mathematical contents (etic) with the use of problem situations that emerged from the context of a market free.
In this regard, the use of a common context, that of daily shopping in a market, can be used to teach mathematics, and reveals practices found outside the school environment and which is a true and real form of ethnomathematics (D'AMBROSIO, 2002). Thus, it is important to emphasize that academic mathematical knowledge is related to the function concepts and was adjusted to the farmer market vendor´s daily life in order to elaborate classroom activities based on these experiences.
Finally, ethnomodelling and its sociocultural perspective provided an integrative approach to school curriculum, which in addition to considering it as an etic approach to mathematical knowledge, recognizes what is as necessary as the emic characteristics of this knowledge. Through this, teachers and students might come to understand, a more respectful, connected, real and holistic (dialogic) way for the cultural information of the members of distinct cultural groups that make up their school community.
References
ALVES, Gelindo Martineli. As contribuições da Etnomatemática e da perspectiva sociocultural da história da Matemática para a formação da cidadania dos alunos de uma turma do 8.º ano do Ensino Fundamental por meio do ensino e aprendizagem de conteúdos da Educação Financeira. 2014. 357f. Dissertação (Mestrado em Educação Matemática) — Departamento de Matemática. Universidade Federal de Ouro Preto. Ouro Preto.
BANKS, James A. Educating citizens in a multicultural society. New York: Teachers College Press, 1997.
BASSANEXI, Rodney Carlos. Ensino-aprendizagem com Modelagem Matemática. São Paulo: Contexto, 2002.
CORTES, Diego Pereira de Oliveira. Etnomodelos como uma ação pedagógica: sugestões para a prática docente em sala de aula. Produto Educacional (Mestrado em Educação Matemática) 2017a. (Mestrado em Educação Matemática) — Departamento de Educação Matemática. Universidade Federal de Ouro Preto. Ouro Preto.
CORTES, Diego Pereira de Oliveira. Re-significando os conceitos de função: um Estudo Misto para entender as contribuições da abordagem dialógica da Etnomodelagem. 2017b. 226f. (Mestrado em Educação Matemática) — Departamento de Educação Matemática. Universidade Federal de Ouro Preto. Ouro Preto.
CRESELL, John W.; CLARK, Vicki L Plano. Designing and conducting mixed-methods research. Thousand Oaks: Sage Publication, 2007.
D’Ambrosio, U. Etnomatemática e Educação. In: KNIJNIK, Gelsa; OLIVEIRA, Claudio José; WANDERER, Fernanda. (Org.). Etnomatemática: currículo e formação de professores. Santa Cruz do Sul: EDUNISC, 2005, p. 39-52.
D'AMBROSIO, Ubiratan. Etnomatemática, justiça social e sustentabilidade. Estudos Avançados, São Paulo, v. 32, n. 94, p. 189-2014, set./dez. 2018.
D’AMBROSIO, Ubiratan. Etnomatemática: elo entre as tradições e a modernidade. Belo Horizonte: Autêntica, 2001.
D’AMBROSIO, Ubiratan. Etnomatemática: um programa. Educação Matemática em Revista, v. 1, p. 5-11, 1993.
D’AMBROSIO, Ubiratan. O Programa Etnomatemática: uma síntese. Acta Scientiae, Canoas, v. 10, n, 1, p. 7-16, jan./jun. 2008.
D’AMBROSIO, Ubiratan. Que Matemática deve ser aprendida nas escolas hoje? Teleconferência no programa PEC. Formação Universitária. São Paulo. SP: Secretaria de Educação do Estado São Paulo, 2002.
DWYER, Kevin. Moroccan dialogues: anthropology in question. London: J. Hopkins Press, 1982.
GEERTZ, Clifford. (Ed). The interpretation of culture: selected essays. New York: Basic Books, 1973.
LETT, James. Emic-etic distinctions. In: Levinson, David; Ember, Melvin. (Ed.). Encyclopedia of cultural anthropology. New York: Henry Holt and Company, 1996, p. 382-383.
NICOLESCU, Basarab. O manifesto da transdisciplinaridade. Tradução de Lúcia Pereira de Souza. São Paulo: Triom, 1999.
OREY, Daniel Clark. What I want to be when I grow up. TEDx Sacramento. Sacramento, CA: TEDx, 2013. Available in: https://www.youtube.com/watch?feature=player_embedded&v=anZNPNEgmUs#at=36. Accessed in: September 21st, 2019.
OREY, Daniel Clark; ROSA, Milton. A dimensão crítica da Modelagem Matemática: ensinando para a eficiência sociocrítica. Horizontes, Itatiba, v. 25, n. 2, p. 197-206, 2007.
ROAZZI, Antonio. Pesquisa e contexto: métodos de investigação e diferenças sócio-culturais em questão. Cadernos de Pesquisa, São Paulo, v. 62, p. 35-44, 1987.
ROSA, Milton; OREY, Daniel Clark. Abordagens atuais do programa etnomatemática: delineando um caminho para a ação pedagógica. Bolema, Rio Claro, v. 19, n. 26, p. 19-48, jul./dez. 2006.
ROSA, Milton; OREY, Daniel Clark. Alho e sal: Etnomatemática com Modelagem. Perspectivas da Educação Matemática, Campo Grande, v. 2, n. 4, p. 149-162, jul./dez. 2010.
ROSA, Milton; OREY, Daniel Clark. Etnomodelagem: a arte de traduzir práticas matemáticas locais. São Paulo: Livraria da Física, 2017.
ROSA, Milton; OREY, Daniel Clark. O campo de pesquisa em Etnomodelagem: as abordagens êmica, ética e dialética. Educação e Pesquisa, São Paulo, v. 38, n. 4, p. 865-879, out./dez. 2012a.
ROSA, Milton; OREY, Daniel Clark. The Mathematics of the curves on the wall of the Colégio Arquidiocesano and its mathematical models: a case for ethnomodeling. Journal of Mathematical Modelling and Application, Blumenau, v. 1, n. 8, p. 42-62, 2012b.
ROSA, Milton; OREY, Daniel Clark. Vinho e queijo: Etnomatemática e Modelagem! Bolema, Rio Claro, v. 16, n. 20, p. 1-16, jul./dez. 2003.
SAMOVAR, Larry A.; PORTER, Richard E.; McDANIEL, Edwion R.; ROY, Carolyn Sexton. (Ed.). Communication between cultures. Beijing: Foreign Language Teaching and Research Press, 2000.
Notes
[1] An etic approach refers to the interpretation of the characteristics of the mathematical knowledge of a given culture from the categories of those who observe it as researchers, researchers and educators (Rosa & Orey, 2017).
[2] The
emic approach seeks to understand the mathematical characteristics of culture
based on the frameworks and categories developed by its members (Rosa & Orey, 2017).
[3] The concept of dialogic is triggered from the recognition of the coexistence of many logics in the same system, which are complementary, being able to integrate the same phenomenon. There is a complementarity in the relationships between members of distinct cultural groups and researchers and researchers regarding locally developed ideas, procedures and mathematical practices (Rosa & Orey, 2017).
[4] CNPq (National Council for Scientific and Technological Development) is the Brazilian Ministério da Ciência, Tecnologia, Inovações e Comunicações (Ministry of Science, Technology, Innovation and Communications).
[5] Re-signifying Function Concepts: A Mixed Study to Understand the Contributions of the Dialogic Approach to Ethnomodelling.
[6] Orey, Daniel Clark. What I want to be when I grow up. TEDx Sacramento. Sacramento, CA: TEDx. Available in: https://www.youtube.com/watch?feature=player_embedded&v=anZNPNEgmUs#at=36; accessed in September 1st, 2019.
[7] In cultural dynamism, local knowledge interacts dialogically with the knowledge globally consolidated by the academy, developing a reciprocal relationship between the knowledge developed etically and emically (Rosa & Orey, 2017).
[8] Mathematics is the process by which individuals from different cultural groups use different tools that can help them to organize, analyze, understand, model and solve specific problems faced in everyday life. These tools enable the identification and description of ideas, procedures and mathematical practices specific to a cultural context, aimed at assisting the members of these groups in understanding relationships and regularities, in schematizing, formulating and visualizing problem situations in different ways , transferring them from the real world to the conceptualization and mathematical abstraction (Rosa & Orey, 2006).
[9] Multicultural education refers to any form of education or teaching that incorporates the stories, values, beliefs, and perspectives of students who have different cultural backgrounds. This type of education can also be considered as an instrument of social change through the educational system, which seeks the development of the students' imagination, creativity and critical and reflective thinking. In this sense, multicultural education is based on the principle of educational equity for students, regardless of culture, as it seeks to eliminate obstacles to educational opportunities for students of different cultural backgrounds (Banks, 1997).
[10] The translation process allows dialogic interaction between members of distinct cultural groups. In this process, global and local mathematical knowledge are mutually influenced, and particularly in relation to the influences of local knowledge development on globalization (Rosa & Orey, 2017).
[11] Systems are sets of interconnected elements for the formation of a whole, which are constantly changing. In these systems, we might find different forms of logic that may intertwine and overlap, leading to a complexity and even being irreducible to cause and an effect. Often this might be inseparable because they are connected. In this way, the work with several forms of logic aims at a better understanding of everyday phenomena through the use of dialogue (Rosa & Orey, 2017).
[12] A sociocultural trait can be considered as a socially learned system of beliefs, values, traditions, symbols and meanings that members of a particular cultural group acquire throughout history. These traits identify members of a specific culture because they are deposits of knowledge, experiences, actions, attitudes, hierarchies, religion, notions of time, roles, spatial relationships, universe concepts and artifacts developed by members of distinct cultural groups from generation to generation through individuals and their collective efforts (Samovar et al., 2000).
[13] Real, plural reais, is the Brazilian currency.
Alternative link
https://periodicos.ufop.br/revemop/article/view/2209/3162 (pdf)