1 Introduction
In 2001 the Minister of Sports and Recreation in South Africa launched the indigenous games at the Basotho Cultural Village in the northern part of the Free State Province. This was a culmination of one of the phases of the project by the South African Sports Commission (SASC) to revive indigenous games in South Africa. The SASC had identified 23 indigenous games in the different regions of South Africa that had been played over centuries by various communities.
The SASC argued that the games were linked to “traditions of a cultural group, being of a local origin and requiring physical skill, strategy and/or chance” (SASC, 2001, p. 3). After a process to reduce on the number of games a total number of seven games were selected which were found to be generic in the different Provinces of the country. These seven games are:
-
(i) Dibeke
(ii) Kho-kho
(iii) Kgati
(iv) Diketo
(v) Jukskei
(vi) Moruba
(vii) Morabaraba
The SASC notes that these games were grossly neglected in historical and anthropological accounts of indigenous peoples in South Africa (SASC, 2001).
Since the launch of these indigenous games the South African Department of Sport and Recreation decided to celebrate and preserve these games in the form of the Indigenous Games Festival which is held annually in September to celebrate Heritage Month.
The number of the games that are played at the Indigenous Games Festival has increased and now includes the following games which were used for competition at the 2017 Games held in Seshego in the Limpopo Province: Dibeke, Diketo, Drie Stokkies, Intonga, Juskei, Kgati, Kho-Kho, Morabaraba as well as Ncuva.
The Figures below show examples of participants participating in some of
the indigenous games at the different Festivals. In Figure 1, the players are
concentrating on the Morabaraba Game. Even though the picture shows only young men
and boys participating in the game, this is not a male game as females can also
play the game.
 Figure 1
Players
participating in the Indigenous Games Festival — Morabaraba Games
(Department of Sports and Recreation, South Africa)
Figure 1
Players
participating in the Indigenous Games Festival — Morabaraba Games
(Department of Sports and Recreation, South Africa)
In Figure 2, a
team comprising of girls and boys demonstrate the playing of the Kgati game. While the girls are skipping the rope, the boys
are also playing a part in the movements of the rope. This is a game that
clearly illustrates that both boys and games can play the game
 Figure 2
Players
participating in the Indigenous Games Festival — Kgati
Game
(Department of
Sports and Recreation, South Africa)
Figure 2
Players
participating in the Indigenous Games Festival — Kgati
Game
(Department of
Sports and Recreation, South Africa)
Figure 3 shows two men (one of them
elderly) playing the Intonga Game. Although this game
features prominently at the Indigenous games Festival, it is a game that is
dominant in the Eastern Cape Province of South Africa, especially among the
IsiXhosa speaking people.
 Figure 3
: Players
participating in the Indigenous Games Festival — Intonga
Game
(Department of
Sports and Recreation, South Africa)
Figure 3
: Players
participating in the Indigenous Games Festival — Intonga
Game
(Department of
Sports and Recreation, South Africa)
The Indigenous Games Festival are aimed at building a diverse society by embracing common national identity and celebrating a shared heritage. The annual Indigenous Games Festival has also assisted that the identified games — and other games not in the List that was launched — become the focus of research studies in Mathematics Education and other disciplines like Psychology of Education in South Africa, including other countries in Southern Africa.
Examples of research studies that have been conducted since the launch include: The ethnomathematical approach to the study on indigenous games from Southern Africa (Mosimege & Ismael 2004); Masekitlana: South African traditional play as a therapeutic tool in child psychology (Kekae-Moletsane, 2008); and the incorporation of the indigenous game of Morabaraba in the learning of mathematics (Nkopodi & Mosimege, 2009).
The importance of the indigenous games among the Ba-Phalaborwa of the Limpopo Province (Malesa, 2012); Using indigenous games to teach problem-solving in mathematics in rural learning ecologies (MOLOI, 2015); Using indigenous games and knowledge to decolonise the school curriculum (Nxumalo & Mncube, 2019). These are just a few of the examples of studies on indigenous and traditional games that have been undertaken following the launch of the Indigenous Games Project.
In addition to studies on indigenous games, studies have been conducted on the exploration of the role and use of indigenous materials and activities in the teaching and learning of school mathematics. Some examples of these studies are: The use of a cultural activity in the teaching and learning of mathematics through the use of twill weaving with a Weaving Board in a Mozambican classroom (Cherinda, 2002); The ethnomathematical approach to teaching and learning of some geometrical concepts (Mogari, 2002); and the student teachers’ exploration of beadwork as a resource for dealing with mathematical concepts (Dabula, 2000).
Most of these studies reveal that learners have a variety of experiences related to indigenous activities. Their experiences are largely influenced and determined by the socio-cultural milieu and the environments in which they live and interact. These are made up of playing and interacting with siblings and friends; lessons taught by parents and grandparents and other members of the community; engaging in daily activities at home and surroundings; observing others engage in a variety of socio-cultural activities etc. Masingila (1995) specifically refers to mathematical knowledge that students bring to school in relation to knowledge gained from everyday situations that the students have experienced.
Malloy (1997) adds the historical context (in addition to the sociocultural context) in which the learners live as defining these experiences. These experiences which occur to a greater extent outside the classroom, which may not necessarily be mathematical in nature, can be brought to bear on activities within the mathematics classroom. These authors found that the learners did not only see themselves as contributing to the discovery of new mathematics (in this case Geometry) but their interest towards mathematics was renewed. Unfortunately these experiences and knowledge do not always find much use by the educators in the classroom.
Some educators may not only find any use for it, but they may even consciously and intentionally discourage it (Lester; 1989) and in the process the students come to regard their experiences and knowledge as less important or not relevant at all. This creates an impression and strengthens the view that what they learn in their mathematics classrooms has got nothing to do with the environments in which they live and function. In the same way, many experiences that learners have gone through outside the classroom are largely viewed as having no relevance to what happens in the mathematics classroom.
The relevance of such experiences is a major area of concern in any classroom activity that brings everyday experiences to bear upon such classroom activity. If all there is to relevance is for pupils to enjoy the activities, then one wonders what mathematical competences are being derived from the activities (Nyabanyaba, 1999). Here Nyabanyaba joins many people who have criticised the use of games (and other daily experiences) as serving to a greater extent the affective component of fun. However, if we redefine the role of both learners and teachers when such activities are used in mathematics classrooms, then this problem will become less of a factor.
Orth (2018) further argues that whether you live in rural or urban areas, all you need to enjoy these games are your friends and easily accessible items such as pebbles, tin cans and your grandmother’s old stockings. She also indicates that’s besides being fun activities to entertain children, these games have significant value in promoting physical prowess, communication skills, teamwork and cognitive skills. Furthermore, each game serves to promote certain African values. Mosimege (2016) emphasizes the importance of indigenous games in reclaiming African pride in the teaching and learning of mathematics.
2 Indigenous Games in other African Countries
These indigenous games are not unique to South Africa. Some of the indigenous games launched in South Africa are also found to be played in other African countries. However, some of the versions and rules of the games differ from one country to another. Many Board Games have been played for centuries in different countries on the African continent.
One of the most popular Board Games that is played in many African countries is Mancala (Figure 4). Zijlma (2019) indicates that there are in fact more than 200 versions of this "count and capture" game, played throughout Africa, all with slightly different rules In North and West Africa it's common to use two rows of pits, in Ethiopia they play with 3 rows, and in East and Southern Africa, they play with four rows. Some games have "stores" at the end of each board, others do not.
The version of
this game in Kenya is called Bao.
UNESCO is working with the National Museums of Kenya in releasing an animation
of the game (UNESCO, 2018). The digitization process of the local traditional
games by UNESCO has encouraged and fostered creative thinking, innovation and
teamwork especially among young people in Kenya. It has also helped raise
public awareness and impact the preservation of traditional knowledge to
connect and improve the world in an innovative way.
3 Examples of the use of Indigenous Games in
Mathematics classrooms
Two
indigenous games have been selected in this paper to demonstrate how they can
be used in mathematics classrooms and how to teach various mathematical
concepts. The first game, Morabaraba Game, is one of
the indigenous mentioned in the Indigenous Games Festival. The second
indigenous game of Malepa has not been mentioned
above nor included as part of the Indigenous Games Festival. However, this game
has been studied by various scholars and the different studies have
demonstrated how it can be used to teach various mathematical concepts.
3.1 The Indigenous Game of Morabaraba
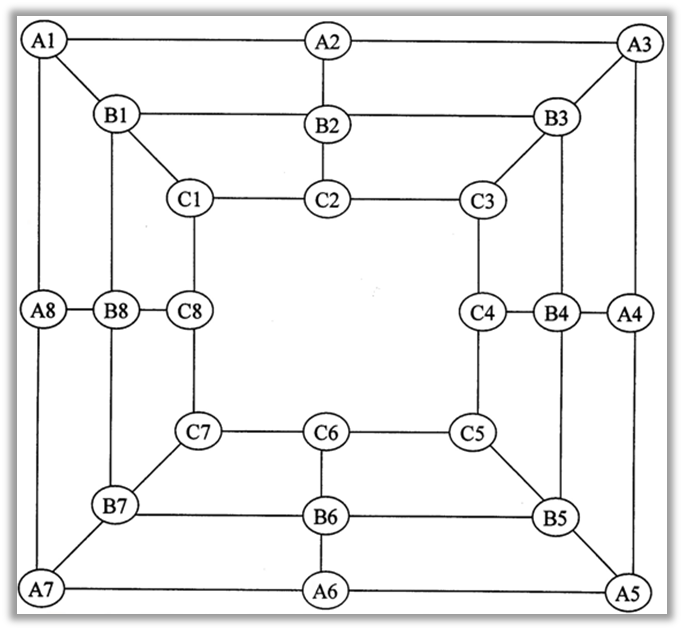
A mathematical analysis (applying mathematical concepts, principles and processes) of any game reveals the extent to which mathematical concepts are embedded in the game. Figure 5 shows the Indigenous Game of Morabaraba.
The following mathematical concepts are found in the
analysis of morabaraba:
-
- Identification of various quadrilaterals (squares) and the similarities and differences between them
- Ratio and proportion between the lines and the squares making the complete morabaraba board
- Symmetry: Symmetry is observed in at least three different instances, namely, (1) the various sides of the board; (2) within each side of the board; (3) the placement of tokens and repetitive movements of the tokens on the board
- Logical deductions in the execution of the various steps of the game
- Counting of the tokens
- Addition and subtraction of the tokens until a game is won on the basis of the remaining number of tokens.
When a Morabaraba Game is introduced in the mathematics class, the following observations may be made:
(i) As learners play together, most of them tend to be very quiet to concentrate on the moves they are going to make. Whenever any verbalisation takes place, it is in hushed tones, with verbal expressions few and far between. As a result, it is generally very difficult to follow the reasoning behind the learners’ moves without asking them questions. The following episode illustrates that even when the researcher continuously requested the learners to speak loudly so that he can hear, the learners still struggled to do so.
3.2 School A, Grade 10 B — Morabaraba game between
two male players at the back of the classroom
R: Le boleleleng godimo, le boleleleng godimonyana because ke batla gore ke lekwe mo, akere?
[Speak loudly, speak loudly because I need to hear you here, isn’t it?]
L2: Ja [Yes] {The second
learner looks at me and nods his head slightly in agreement with the first
learner}.
R: Le boleleleng godimonyana. [Speak loudly]. {The learners then
continue to place the tokens on the board, 7 remaining tokens by each player.
They still speak in hushed tones. However they place
most of the tokens without saying anything. The first learner then finishes
to place the tokens and rubs his hands together as a sign of a completed
activity and a job fairly well done}
R: Le boleleleng godimonyana. Le boleleleng godimonyana, ke nyaka go lekwa, nna ke nyaka
go lekwa. [Speak a bit louder. Speak a bit louder, I would like to hear you, I
would like to hear you] {This was done by the researcher upon the realisation that despite requesting the learners at the
beginning to speak louder, they did not do so. All the remaining tokens were
placed without any explicit attempt to increase the level of verbalisation}.
(ii) Some of the learners displayed actions physically
to signify a particular activity (placement, movement, formation of
three-in-a-row) in the game. For instance, after capturing a token, a learner
would show this by moving a hand in a sign that signifies beating. When this
action is signified physically, players move a pointing index finger downwards,
such that at the end of the movement the finger makes a striking sound against
the other fingers, particularly the third finger. This results in a striking
sound made by the two fingers, giving a feeling that something has been beaten.
3.3 Errors observed during the learners
interactions
The following observations were noted as errors that take place during the interaction in the Morabaraba game. It should however be noted that some of them may not necessarily be errors as the two players may have agreed about the adaptation of the rules which the researcher may not be aware of. The errors take place between all groups of learners who are in games between male players, female players, male — female players, and even between three players taking turns playing against each other.
Despite the repeated request by the researcher that the learners should speak a bit louder and the agreement by both learners (one of them verbally and the other through the physical action of nodding the head) the learners still continued to speak so softly that the researcher could not hear the exact expressions by the learners. This instance and many similar instances seem to indicate that Morabaraba is a game which is not characterised by speaking loudly but is characterised by either quietness and some thinking as it relates to the tokens and the related movements.
(iii) A few
learners verbalised some of their actions. When these
were done, they were more expressions of a good move made and a token captured
or an expression of desperation on the part of the losing player but not of why
a particular move was made. The expressions were mostly made in the learners’
home language. For instance a learner would express
the capturing of a token by saying ‘mamo’, (short for ‘mamola’)
meaning either removing or beating.
-
(i) Moving a token to an occupied junction either by the same player or the opponent.
(ii) Capturing an opponent’s token that is forming a three-in-a-row.
(iii) Capturing a token when no three-in-a-row has been formed.
(iv) Placing an opponent’s token on the board in an attempt to place own.
(v) Forming a three-in-a-row without capturing the opponent’s token.
(vi) Not ending the game when the opponent is not able to move any of the tokens.
4 Reference to the rules
On a number
of occasions, learners were video recorded studying the rules of the game
before starting to play the game (Figure 6).
 Figure 6
Learners referring to Morabaraba
rules
(MOSIMEGE, 2000, p. 235)
Figure 6
Learners referring to Morabaraba
rules
(MOSIMEGE, 2000, p. 235)
Reference
to the rules may be interpreted in a number of ways. For instance, it may be
interpreted to mean that learners who do not know the rules are studying them
so that they can engage in the game. It may also be interpreted that the
learners know the game but are reminding themselves about the rules which they
have possibly forgotten. However, since the learners who referred to the rules
were not questioned on their reference to the rules at the time of play, it is
not possible to verify whether these reasons that I have advanced are correct
or not.
4.1 The Indigenous Game of Malepa
In figure 7
there is a demonstration of Figure Gate Two, which is a Malpea
a bobedi, performed by a female student.
In figure
8, there is a demonstration of Figure Gate Six, which is a Malepa
a borataro, performed by a female student.
The indigenous game of Malepa
(String Figure Gate) can be analysed to reveal a
variety of mathematics concepts. Such an anlysis
reveals mathematical concepts such as geometric shapes and figures; patterns,
relations and functions expressed through various linear and quadratic
equations, and symmetry — some of the gates exhibit reflection symmetry, while
others have rotational symmetry, it is also possible to show radial symmetry;
translational symmetry; and antisymmetry. However,
the analysis of these mathematical concepts is not a focus of this paper[1].
Using indigenous game of Malepa (String Figure Activities) in classrooms shows that the learners bring to class various levels of knowledge of the games. These range from a complete lack of knowledge to the ability to perform a variety of intricate manipulations with the strings. When afforded an opportunity to explore and share their knowledge, spontaneous groups get formed, groups in which learners who know some string activities play a leading role.
Although in the study in which Malepa Games were trialled in the classrooms I did not necessarily isolate gender as an important factor to investigate, female learners seemed to be more conspicuous in engaging in string activities as most of them were selected to give demonstrations. Despite the instructions given to the learners on how to interact in some of the activities pertaining to the worksheets that were constructed on the game, the learners do not necessarily follow these as they arrive at specific activities more on their own than as a team working together.
4.2 Five distinct groups of learners
During the
period of Free Play, different learners became engaged in a variety of string
activities that they knew and able to exhibit in the first few minutes after
each learner was given a string. As the learners became engaged in these
activities, it was possible to notice that learners did not have the same
levels of knowledge of activities in strings. A further analysis of the
involvement of learners in these activities led to the identification of five
distinct groups:
-
(i) Learners who did not know any String Figure Activity (String Figure Gates or String Figure Configurations).
(ii) Learners who did not know String Figure Gates but other String Figure Constructions such as the Saw, Cup and Saucer or even Magic i.e. disentangling of the string around a mouth.
(iii) Learners who knew only one String Figure Gate. The majority could only construct one String Figure Gate especially String Figure Gate 2. Some of the learners could construct only one of the following Gates — Gate 1 and Gate 3. However, they were fewer than those who could construct Gate 2. An even a smaller number could construct string in figure gate 4.
(iv) Learners who were able to construct a maximum of two String Figure Gates. This group also includes learners who could use more than one method to make the same gate and these methods differ from those used by most of the learners or the standard method for constructing the gate.
(v) Learners who can construct more than two gates and other string figure configurations. They were also able to generate other string sates from those already made.
It is
necessary to emphasize that the numbers here are extremely low, at most two
learners in each school.
4.3 Spontaneous interaction
The different levels of knowledge of Malepa activities resulted in learners moving from their seating positions to nearer those who knew different string activities. I have classified this as spontaneous interaction among the learners as those who knew very little or knew nothing approached those who knew some of the activities and request them to show them (those who don’t know) how the activities are done.
This happened without the researcher telling them how to interact or specifying in which aspects of the string activities to interact. In some instances the learner who knew certain activities moved nearer to those who did not know a particular activity to give a demonstration and assist them with a variety of aspects of that activity, including the manipulation of the string on the fingers.
This spontaneous formation of groups was not only limited to learners in proximity as in some instances learners moved from their seating positions across the classroom to get nearer those who knew the different activities. The groups varied from individual learners working on their own to a group of about 8 learners gathered together and actively working together and in some cases talking loudly among themselves. Talking loudly happened mostly when a number of learners gathered around a few learners who knew certain activities and were trying to follow the instructions of making a particular activity.
The interaction varied from one classroom to another, ranging from very little participation to very noisy and the formation of big groups in some classrooms. Noisy classrooms seemed to result mostly from learners grouped together and all trying to follow what was being shown by one of the learners either with very little success in following the demonstrations and therefore all trying to get assistance from the knowledgeable learner. Sometimes learners who knew a little more about the particular activity talked loudly among themselves about how that activity could be successfully done.
4.4 Trends in terms of numbers of demonstrators according to gender
A number of learners were selected to give demonstrations to the rest of the learners in the classroom. Selection was based on the following criteria:
(i) Those who were able to show a complete String Activity — Gate, Saw, Magic, Monatlana, Cup and Saucer — either in the first group or second group (when Morabaraba was used together with strings in the classroom, the classroom was divided into two groups to concentrate on one of the two games at a time), so that those who are knowledgeable could come from any of the two groups.
However most learners who gave demonstrations came from the first group, that is, those who started with string activities first and then followed with Morabaraba game. This happened because by the time those in the second group made some activities with strings, some learners had already been selected from the first group of the learners to demonstrate the same activity, and there would not be sufficient time for more learners to give a demonstration of the same activity in one period.
(ii) Those who either used a different method for the same activity for which a demonstrator had already been selected or included different steps in their procedures of making a particular gate.
4.5 Demonstration of the String Figure Gate Two by
the Learners
This
demonstration was given by a female learner in Grade 10 in one of the schools
that participated in the research:
-
1. Re tsea string se ra se lokela mo monwaneng o mogolo le o monnyane. [We take this string and put it in the big and the small fingers]
2. Ra goga ka monwana wa boseven [We pull with the seventh finger]
3. Ra ntsha mo menwaneng e khi e megolo. [We remove on the big fingers]
4. Ra goga e khi ka mo mafelelong ka e khi e megolo... Ja. [We pull these ones at the end with the big ones]
5. Ra tsea e khi mo monwaneng wa boseven ra e lokela mo o mogolo. [We take the one on the seventh finger and put it in the big finger]
6. Le kamo [And this side]
7. And then ra isa e khi e megolo ka fatshe. [And then we take the big ones to the bottom]
8. Ra lokela e khi mo squareng, go nale disquarenyana mo gauswi le menwana e megolo. [We put these ones in the square, there is a small square near the big fingers]
9. Ra entsha mo menwaneng e khi e mennyane. [We remove on the small fingers]
This is just one of the examples in which a learner
was given an opportunity to give a demonstration of what she knows. The
advantage of using such an indigenous game in the mathematics classroom is that
learners get an opportunity to share their knowledge of what they know about
the game with others. This has got an added benefit of empowering learners to
teach others about their own knowledge. It also affords an opportunity for the
learners to learn from others. Using indigenous games in mathematics is
therefore not just dependent on what the teacher knows about the game
4.6 The importance of inclusion of indigenous games
in the teaching and learning of mathematics
Indigenous games have a great potential to change how
mathematics teaching and learning is viewed in classrooms. They do not only
make it possible for learners to engage in activities that are enjoyable, they
have a great potential to help open avenues for the connection between concrete
and abstract concept, between classroom environments and activities outside
classroom.
References
CHERINDA, Marcos. The use of a cultural activity in the teaching and learning of Mathematics: exploring twill weaving with a weaving board in Mozambican classrooms. 2002. Thesis. University of the Witwatersrand. Johannesburg.
DABULA, Nomonde Patiense. Student Teachers’ exploration of beadwork: cultural heritage as a resource for mathematical concepts. 2000. 154p. Dissertation (Master of Education) — Faculty of Education. Rhodes University, Grahamstown.
GIBBS, William; SIHLABELA, Mprophet. String figures. Mathematics in School, v. 25, n. 3, p. 24-27. 1996.
KEKAE-MOLETSANE, Mokgadi. Masekitlana: South African traditional play as a therapeutic tool in child psychotherapy. South African Journal of Psychology. v. 38, n. 2, p. 367-375. 2008.
LESTER, Frank K. The role of metacognition in mathematical problem solving: a study of two Grade Seven Classes. Final Report. Bloomington, 1989.
MALESA, Mohlago Tracey. The importance of the indigenous games among the Ba-Phalaborwa of the Limpopo Province. 2012. 78f. Dissertation (Master of Arts in Folklore Studies) – Faculty of Humanities. University of Limpopo. Limpopo.
MALLOY, Carol E. Challenges in the Mathematics Education of African-American children. Reston: NCTM, 1997.
MASINGILA, Joanna. Carpet laying: an illustration of everyday mathematics. In: HOUSE, Peggy A.; COXFORD, Arthur F. (Ed.). Connecting mathematics across the curriculum. Reston: NCTM, 1995, p. 163-169.
MOGARI, David. An ethnomathematical approach to teaching and learning of some geometrical concepts. 2002. Thesis. University of the Witwatersdrand, Johannesburg.
MOLOI, Tshele John. Using indigenous games to teach problem-solving in mathematics in rural learning ecologies. JHEA/RESA, v. 13, n. 1-2, p. 21-32, 2015.
MOSIMEGE, Mogege. Methodological challenges in doing ethnomathemtical research. International journal of African Renaissance Studies – Multi-, Inter- and Transdisciplinarity, v. 7, n. 2, p. 59-78, 2012.
MOSIMEGE, Mogege. Reclaiming our African pride through the integration of ethnomathematical studies in mathematics teaching and learning. Plenary Address given at the Association of Mathematics Education of South Africa (AMESA) Conference. 2016.
MOSIMEGE, Mogege David. Exploration of the games of Malepa and Morabaraba in South African secondary school mathematics education. 2000. 674p. Thesis. University of the Western Cape. Cape Town.
MOSIMEGE, Mogege David; ISMAEL, Abdulcarimo. Ethnomathematical studies on indigenous games: Examples from Southern Africa. In: INTERNATIONAL CONGRESS OF MATHEMATICS EDUCATION, 10, 2004, Copenhagen. Proceedings of the ICME-10. Copenhagen: Roskilde University, 2004, p. 107-118.
NKOPODI, Nokopodi; MOSIMEGE, Mogege David. Incorporating the indigenous game of morabaraba in the learning of mathematics. South African Journal of Education, v. 29, n. 3, p. 377-392. 2009
NXUMALO, Abednego Sabelo; MNCUBE, Dumisani Wilfred. Using indigenous games and knowledge to decolonise the school curriculum. Perspectives in Education. v. 36, n. 2, p. 103-118. 2019.
Nyabanyaba, Thabiso. Whither relevance? Mathematics teachers' discussion of the use of'real-life' contexts in school mathematics. For the Learning of Mathematics, v. 19, n. 3, p. 10-14, 1999.
ORTH, Zaida. Indigenous Games festival: preserving traditional African childhood games in South Africa. 2018. Found at https://www.africamattersinitiative.com; accessed on 7 sep. 2019.
SOUTH AFRICAN SPORTS COMMISSION (SASC). South African Indigenous Games: a Report on Indigenous Games in South Africa. 2001.
UNESCO. UNESCO digitalizes traditional African games to preserve and expose traditional culture. 2018. UNESCO Office in Nairobi.
ZIJLMA, Anouk. Guide to traditional African Board Games. 2019. Available in: https://www.tripsavvy.com.games.
Notes
[1] For references to this form of analysis and use in mathematics classroom see Gibbs & Sihlabela (1996), Nkopodi & Mosimege (2009) and Mosimege (2012).