1 Introduction
Forty years ago, ethnomathematics was beginning to be
recognised more widely (BISHOP, 1979;LANCY, 1978; VAN DER WAERDEN & FLEGG,
1975;WILDER, 1974;WOLFERS, 1971; ZASLAVSKY, 1973). Many linguists were
recording the counting systems of the people whose language(s) they were
learning (PANOFF, 1970;PUMUGE, 1975); Wurm and his colleagues (WURM et al.,
1975) were documenting the languages in New Guinea, and others were considering
Oceania (LYNCH, 1977; ROSS, 1988). Anthropologists were incorporating counting
into the various complex activities and beliefs of people (STRATHERN, 1977)
while cognitive, developmental psychologists (e.g., SAXE, 1979) were
considering how cultural context affected concepts. Papua New Guinea University
of Technology had a Mathematics Education Centre and the University of Papua
New Guinea had an Education Research Unit, both of which supported research that
took account of cultural difference in mathematics learning. Some of this work
was focused on difference using Piagetian studies and some on cognitive
development for mastery of concepts. It would be another decade before
ethnomathematics was widely discussed (ASCHER, 1994; BISHOP, 1988;D’AMBROSIO,
1990).
2 Counting
System Diversity and How They Developed
With written records of number, there are symbols used
in the various languages for numbers. These reflect the ways that the people
combined numeral words to make new number names. For example, the Romans, at
least in their later history, said four was IV, that is, one before five. In
one sense, place or position was important. We are also cognisant that the
Arabs used and modified the original Indian ways of recording numbers to give
us our current Hindu-Arabic system of base-10 with place value and a zero. But
what happened before this? In the second half of the 18th century, it was
considered that numerals were a hallmark of civilisation (CRAWFURD, 1863), and
then there was a debate about whether different civilisations invented their
counting and numerals or whether there was a diffusion from either Egypt around
4 000 BCE (SMITH, G.E, 1933) or the Sumerians (RAGLAN, 1939). The diffusionist
ideas prevailed and Seidenberg (1960) suggested that counting systems diffused
from Western Asia or Mediterranean civilisations starting with two-cycle
systems having one and two as frame words around 3 500 BCE “spread out over the
whole earth; later, other methods of counting arose and spread over almost all,
but not quite all, of the world” (p. 218). His view was based on the
anthropological evidence that suggested these two-cycle systems only occur on
the vestiges of the world in southern Africa, southern America, and Australia.
Some systems with numerals for three and perhaps four, but without combinations
for higher numbers he claimed as systemless and an aberration of the two-cycle
system. Seidenberg then suggested that paired systems developed; he called them
neo-2 systems in which 6 = 2 × 3
and 7 = 2 × 3 + 1 and so on. One
example was the Motu and Roro systems close to Port Moresby in Papua New
Guinea. Then, he said the base-10 system developed in conjunction with these
paired systems spreading around the world. Seidenberg went on to suggest that
the North American Inuits that have a (5, 20) cycle system came after the
10-cycle and there was a fusion, slurring (his term), or modification made with
the (2, 10) cycle system resulting in (10, 20), or 20-cycle systems. He
suggested that when the 10-cycle system developed in different places it was
diffused, unlike the two-cycle system that began in the Middle East (Western
Asia). From African systems, he suggested that the (2, 10) and (5, 20) systems
came together to make the second pentad (6 to 9) as five plus one to four or
another word plus one to four. Finally, Seidenberg believed that the body-part
tallying was a combining of the two-cycle system with the (5, 20) system as
they linked the idea of body part tallying to represent numbers when tabu
(society discouraged its use) prevented them from using counting words.
There are cases, for example, Duna which truncated a body-part tally system for
the sound of 14 was similar to a word that was tabu.
Glendon Lean began collecting the counting systems of his students from across Papua New Guinea (PNG) and Oceania in the late 1960s until the late 1970s. Importantly, these first university students were still well connected to their cultures and languages. Unknown by most educators or politicians at the time, he located first contact records in linguistic and government records and in research journals since the Pacific was an “exotic” place to visit for the enlightenment of the 1800s. Thus he was collecting records of what were until that time oral counting systems. The Summer Institute of Linguistics had also recording in their language surveys many language words including some counting words. University linguists were finding Papuan (non-Austronesian) languages in PNG had fascinating language patterns unknown in other parts of the world and so they too began to study more complex aspects of the languages. Surprisingly some of these languages were spoken by few people while others were spoken by thousands and some had numerous dialects. Interesting too were the similarities of the Austronesian languages spoken by Melanesians across the Pacific. Linguists were studying these languages and from these records, Lean was able to obtain counting words for analysis. In total, Lean collected the counting systems of 1 200 languages and we have added several further languages to this collection from field visits, students, and other papers.
Through careful collation and analysis, Lean was able to publish these data in 1988 for each province of PNG. These data formed part of his doctoral thesis (LEAN, 1992) together with counting system data for Oceania (West Papua — the name refugees use — then called Irian Jaya, Indonesia; Island Melanesia; Micronesia; and Polynesia). Geoffrey Smith (1984,1988) had also studied the systems in Morobe Province. Both used Salzmann’s (1950) method of ascertaining the frame words with which all other numerals were named, deciding the operative patterns by which the frame words were combined to make the other numbers and then deciding on the primary and superordinate cycles. For example, if a system has frame words of 1, 2, 5, and 20 by which all other numbers were named then the system was a (2, 5, 20) cycle system. In an earlier paper (OWENS, 2001), much of Lean’s work was summarised. It is extended in Owens, Lean, Paraide and Muke (2018).
3 Countering
the Diffusionist Theory
Seidenberg
claimed the two-cycle system was once widespread, but Lean found that there
were few systems that were pure two-cycle systems in PNG, and they have not
been found en route to South America (e.g., in North America although a paper
on California contradicts this (DIXON & KROEBER, 1907). In PNG, as
elsewhere, most two-cycle systems, in fact, went on to have a (2, 5) or (2, 5,
20) cycle system and these existed well before the 10-cycle systems introduced
mainly by Austronesian (AN) Oceanic speakers. Furthermore, the paired system
was a variation of the AN Oceanic speakers on the southern coast of PNG and generally
not found in the non-Austronesian (NAN) systems although there is evidence of
different group counting. These Oceanic languages spread from their homeland
near New Britain (OWENS et al., 2018;ROSS, PAWLEY & OSMOND, 2003).
Seidenberg thought 10 cycles preceded (5, 20) and body-tally systems, but Lean
countered this by recognising that finger gestures while counting are so
widespread among Indigenous people that digit-tally systems would have
developed across the world and not after base-10 systems were in place. It is
not commonly considered that the body tally systems were older than (5, 20)
systems as they are more complex and in many cases, there is no evidence that
this practice was linked to sharing body parts in rituals, as Seidenberg
claimed. Furthermore, Seidenberg has not explained how the systems with 1, 2, 3
and/or 4 evolved into a system with 10. Finally, having a system that is
efficient such as the base 10 system may not be the only reason for a group to
take up a counting system from a neighbour. A few AN 10-cycle systems in PNG
changed to a two-cycle system when the people moved inland along a major river
valley, the Markham, and were building relationships with people using
two-cycle systems, including variants like (2, 5) cycle systems (HOLZKNECHT,
1989;OWENS et al., 2018). There are many other reasons for systems to
be the same or different from others: friendliness, trade, length and intensity
of contact, desire to be separate or similar, or for what is valued such as multilingual
skills, care, confounding others, extravagance or prestige (JETT, 1971).
4 Extending
Our Understanding of How Counting Systems Develop
Not only does
Lean’s (1992) evidence contradict Seidenberg on a number of major issues but
his analysis also found several other factors of interest in discussing the
spread of counting systems. First, it was found that in West Papua, PNG, and
the Solomon Islands that NAN and older languages had borrowed some words,
mostly in the second pentad from Austronesian (AN) languages. Similarly, some
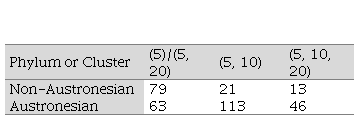
AN languages borrowed words from NAN languages. Table 1 indicates these
phenomena. However, these borrowings are not particularly common and more
significant is where a whole system is adopted as mentioned above in the Markham
Valley (OWENS et al., 2018).
Table 1
Summary of 5-Cycle
and 10-Cycle Systems in Austronesian and Non-Austronesian PNG Languages
 Owens et al. (2018)
Owens et al. (2018)
|
Phylum
or Cluster
|
(5)/(5, 20)
|
(5, 10)
|
(5, 10, 20)
|
|
Non-Austronesian
|
79
|
21
|
13
|
|
Austronesian
|
63
|
113
|
46
|
The majority of
(5)/(5,20) cycle systems are found in the NAN Sepik-Ramu and Trans New Guinea
(TNG) Phyla. There are many other systems in these phyla but there seems to be
some connections between the languages with some innovations in other languages.
It should be noted that the (5, 10) cycles are found in the NAN East Papuan
Phylum; and (5, 10, 20) in West Papuan Phylum where these languages had contact
with AN languages. Among the AN languages, the majority of languages that have
reverted from 10-cycle systems to incorporate features of 5-cycle are in North
New Guinea, Papuan Tip, Vanuatu and New Caledonia. The (5, 10) cycle systems
are found in Vanuato and (5, 10, 20) cycle systems are found in New Caledonia.
This evidence suggests contact with existing NAN languages or some diffusion
perhaps through on-going trade or displacement or they occurred spontaneously.
5 Evidence
of Large Numbers
5.1 Non-Base-10 Systems
In order to
illustrate how these Indigenous systems without a base 10 developed large
numbers, three language groups are selected:
-
- Yu Wooi (Mid-Wahgi) from the Jiwaka Province in the PNG western highlands that displays a digit tally system with vestiges of a four-cycle and from some informants, a body-tally system;
- Iqwaye from the Eastern Highlands Province bordering Morobe (a coastal province) that is a digit-tally system with (2, 5, 20) cycles; and
- six-cycle systems from a large island off the southern coast of West Papua and languages around the border of West Papua and Western Province, PNG.
Yu-Wooi.Muke
(2000) obtained data from a number of people from his four tribal groups that
have different dialects. The system is a typical (2, 5, 20) cycle system. For
example, 27 is angek yem yemsi simb yem yemsi, angek yemsi, tak (both
hands both legs half hand and two). For another example, 40 is hi tak simb
angek yemeyem (two men’s both legs and hands). However, they also count
items by twos and in hundreds by grouping them in tens and then tally each ten
using their fingers and toes to reach 200. Thus, as one participant said, “for
six hundred pigs, they would say that they will kill pigs equal to the hands
and legs of three man” (MUKE, 2000, p. 134). For the larger thousands, people
used the fingers and toes for groups of ten and when they had ten groups of
ten, they referred to a specific body part, starting from the head towards the
legs, aiding memory of giving for reciprocity.
One variation of
this was the use of the names of fingers for adding almost as a vestige of a
body-part tally system. Furthermore, when it came to counting and having the
opportunity to use hands, people often counted in twos. They would fold down
two fingers at a time saying eraksi meaning “take two” each time: two
then two on one hand followed by two and two on the other and bringing the four
folded fingers of each hand together being mam erak followed by the two
thumbs with the words angek yem yem “together hands” (some also folded
two, two, then thumb eraksi eraksi el and then two and two and thumb
repeated before bringing together and saying angek yem yem). When
deciding the number of pigs to be given by each person in a compensation claim,
the leader asked people to take the number that they would give from a bunch of
small banana fruit. When everyone had offered as they wished, the banana fruit
were put together and tallied in groups of 10, each group matched with a digit
tally part starting with the fingers.
Table 2
Yu
Wooi (Mid-Wahgi) Counting System for Large Numbers
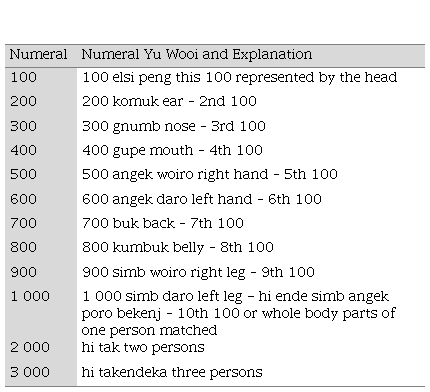 From Muke recorded in Owens, Lean & Muke (2018, p. 56)
From Muke recorded in Owens, Lean & Muke (2018, p. 56)
|
Numeral
|
Numeral Yu Wooi and Explanation
|
|
100
|
100 elsi
peng this 100 represented by the head
|
|
200
|
200 komuk
ear – 2nd 100
|
|
300
|
300 gnumb
nose – 3rd 100
|
|
400
|
400 gupe
mouth – 4th 100
|
|
500
|
500 angek
woiro right hand – 5th 100
|
|
600
|
600 angek
daro left hand – 6th 100
|
|
700
|
700 buk
back – 7th 100
|
|
800
|
800 kumbuk
belly – 8th 100
|
|
900
|
900 simb
woiro right leg – 9th 100
|
|
1 000
|
1 000 simb
daro left leg - hi ende simb angek poro bekenj – 10th 100 or whole
body parts of one person matched
|
|
2 000
|
hi tak two
persons
|
|
3 000
|
hi
takendeka three persons
|
Iqwaye. Building
on a binary system of relationships in which a pair is one or where another
number is linked to one (the whole), it seems that PNG and Oceania cultures
have a richer understanding of number. There is order in the counting, but
temporality related to this order may not be of the Western kind but pulsating
back and forth (MIMICA, 1988). One such group, Iqwaye, has a digit-tally system
starting with the thumb of either open hand, then the index finger, etc.,
moving to the other hand, then counting the toes. (Most language groups seem to
count by bending the fingers down starting with the little finger.) Twenty is
two hands and two legs or a person. Iqwaye refer to the link between the
creator and each of the five children represented by a finger as one child or
one to five children so one can be one or five can be one. Using this
digit-tally counting system, by which each digit represents a counting word in
order, the man standing up becomes one denoted by the thumb again. So, each
digit then represents a multiple of 20. Three fingers could represent three persons
or 3 × 20. The next iteration is for the digits to represent
202 counted off by the crouching man with fingers touching the toes.
Thus, two groups of 20 men (20 × 20 = 400) is represented by the thumb and index
finger so 1 000 is represented by two fingers and then 10 fingers (each finger
representing 20).
400 is Aa’ ’mnye, aa’mnye, toqwotni tepu hyelaqa kokoloule hyule hwolye hyelaqapu
Person person this-me this that-all their leg hand that-all ‘[as] this many persons [as] me this [one] person [speaker] all their legs and hands’ 1,000 is ‘two persons [as] me this [one] person all their legs and hands and to another person’s two hands (= ten persons) all their legs and hands’ (MIMICA, 1988, pp. 35-36)
Thus, the notion
of infinity is generated (MIMICA, 1988). This self-generating system of numbers
is reminiscent of some modern Western mathematical and binary systems. He
suggested that a study of the system shows an intuitive non-Western origin of
number, capable of developing into a system and purpose for counting (BROUWER,
1975).
Six-Cycle
Systems Near the Border of West Papua and PNG. Donohue’s (2008) study of the languages of Kolopom
Island has shown that languages like Kanum have developed an interesting
variety of counting systems to manage their base-six system for large numbers.
There are in fact three systems: for small numbers, moderate numbers, and a
complex system for one to large numbers, 65. Some number words occur
in more than one system, but the complex system is well established except that
the Indonesian currency note for 1 000 has brought confusion: Some younger
speakers are reinterpreting ntamnao ‘1296’ as ‘1 000’, ... ntamnao
tamp is effectively ambiguous between ‘5 000’ (1 000 × 5; new reading) or
‘6 480’ (1 296 × 5; old reading), although only the latter is prescriptively
correct (DONAHUE, 2008, p. 427). Evans (2009) has shown that languages of the
Morehead-Maro language group in Western Province, PNG and further west also
have large numbers for six-cycle languages. For example, Nen count to 65
or 66. The counting in these languages seems to relate to counting
yams (three in one hand and three in the other) that are then bundled in groups
of six (62) and then counted. In fact, in 1936, Williams recounted
that in Keraakie with two counters, one counted each of the bundles of 36 while
the other placed a yam representing 36 yam to form a daisy pattern.
Interestingly, different groups represented six by different parts or gestures
of the hand.
5.2 Base-10 Systems of the Region
The AN
languages, and in some places neighbouring NAN languages such as Nasioi and
Uisai on Bougainville, used numeral classifiers for large numbers. In most
cases, classifying prefix or suffix were for counting specific groups of
objects such as single bananas, a hand of bananas, long thin objects, food
items and so on (OWENS et al., 2018). However, in many languages there
are also numerical classifiers, that is a prefix or suffix that represents 100
or 1 000 or 10 000 or some other large number. Fisher (2006) on a Manus
language noted, for example, the prefix po- for 100 000. Bender &
Beller (2006; 2011) provided several different examples. For example, the
Samoan expression that refers to just 2 coconuts has a corresponding article
for “2” in Tongan that multiplies 10-score (thus 2 ×
20 = 400), thus yielding 400 coconuts. It is only when numeral and classifier
change their position (as infua-lua) in Samoan that a numerical change
occurs (from 2 to 20). Rennelles, a Polynesian Outlier, in the Solomon Islands
also shows multiplication for large numbers so the practice was widespread.
Examples also
illustrate the importance of alternative ways of representing or displaying
large numbers in base 10 and in mixed systems of composite groupings. For
example, the Tolai display their shell money in recognised ways. First, a
fathom is shown with the string of shell money generally looped and not taught
between the outstretched hands to display generosity and value. The fathoms are
then bundled in tens and tens of these and then tens of these are bundled and
wrapped together to form large hoops of shell. These are highly valued hoops
displayed during exchange ceremonies such as marriage (PARAIDE, 2018). Others
display in heaps of say yams such as in Kilivila, or amounts are spread out
upon the ground as in Loboda. Thus large numbers can be represented and recognised
in different ways Owens et al. (2018).
6 Evidence
for the Longevity of Counting Systems in Our Region
Lean (1992) drew
heavily on linguistic data and archaeological linguistics, and his thesis is
supported by more recent evidence. For example, the dating of the spread of
Oceanic languages is based on Proto Oceanic language and the cultural complex
associated with the Lapita-style ceramic tradition found throughout Island
Melanesia and western Polynesia (ALLEN, 1996; ADDISON & MATISOO-SMITH,
2010; PAWLEY & GREEN, 1985; SPRIGGS, 2011). The deep conceptual structure
of counting systems, namely their cyclic nature, rather than just loanwords
suggests a long-standing existence of these counting systems and their
connectivity. The cycle of 10 is common across these languages as shown in
Table 3 although the older NAN languages with whom they were in contact has
influenced many languages resulting in other cycles.
Table 3
Distribution of Counting System and Tally Types Among the AN Clusters
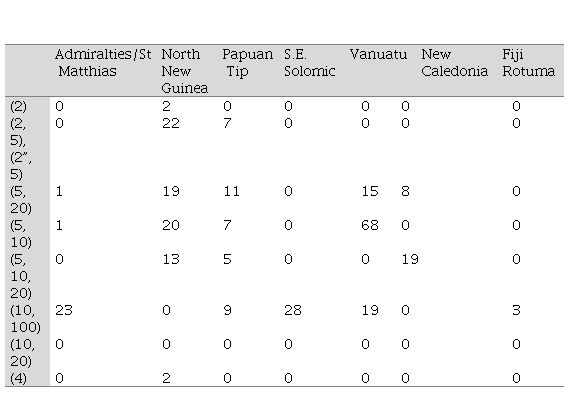 (2”,
5) are systems with a distinct numeral for 3 but 4 = 2+2. S.E. South-East
(2”,
5) are systems with a distinct numeral for 3 but 4 = 2+2. S.E. South-East
|
Admiralties/St Matthias
|
North New Guinea
|
Papuan Tip
|
S.E. Solomic
|
Vanuatu
|
New Caledonia
|
Fiji
Rotuma
|
|
(2)
|
0
|
2
|
0
|
0
|
0
|
0
|
0
|
|
(2, 5), (2”, 5)
|
0
|
22
|
7
|
0
|
0
|
0
|
0
|
|
(5, 20)
|
1
|
19
|
11
|
0
|
15
|
8
|
0
|
|
(5, 10)
|
1
|
20
|
7
|
0
|
68
|
0
|
0
|
|
(5, 10, 20)
|
0
|
13
|
5
|
0
|
0
|
19
|
0
|
|
(10, 100)
|
23
|
0
|
9
|
28
|
19
|
0
|
3
|
|
(10, 20)
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
(4)
|
0
|
2
|
0
|
0
|
0
|
0
|
0
|
| | | | | | | | | | |
Proto Oceanic
contained at least terms for 100 and 1 000 with some northern areas losing
these for various reasons, perhaps due to NAN influence with other languages
inventing further systems. Higher powers are common in Polynesian languages
sometimes as 2 × powers of ten and probably due to tributes to chiefs.
According to Harrison & Jackson (1984), higher powers, at least for
Micronesia, may have a later history and several innovations. For Polynesia and
Micronesia, Owens, et al., 2018 following Lean, suggests that there are 39 with
cycles of 10 and higher powers, six having (10, 20) cycles and one with a (5,
20) cycle system. Nevertheless, Tryon (1995) suggests Proto Oceanic has a
beginning 6 000 years ago.
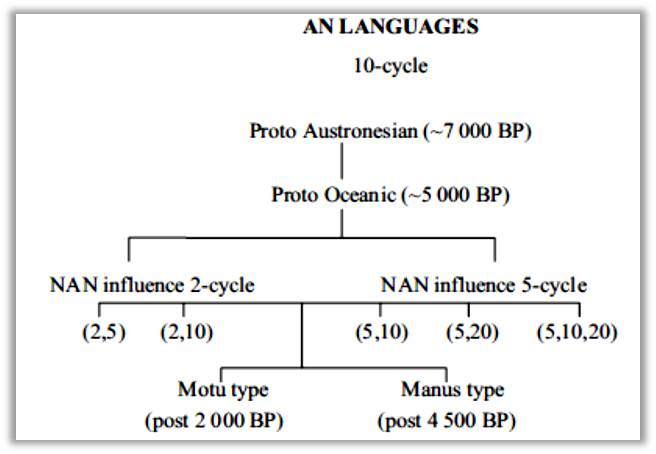
The genealogy
suggested for the age of the systems is given in Figure 1. This figure
indicates some of the spread of the languages as summarized by Addison and
Matisoo-Smith (2010) and other studies of obsidian spread and pottery sources,
trade and similarities in certain areas together with likely settlement in
different areas (MAY & TUCKSON, 2000; PARAIDE et al., forthcoming).
By contrast, the
older NAN languages show surprising diversity although some main systems tend
to dominate different phyla suggesting again some long-standing systems. Table
4 indicates the diversity. TNG Phylum accounts for most of the mainland of New
Guinea outside of the coastal areas and has a diversity of types of systems.
Eighty percent of body-part systems are found in one of the sub-phylum. There
is also a cluster of four-cycle systems but they are quite diverse in
themselves and so seem to be localised innovations. The majority are variants
of two-cycle systems and mainly (5, 20) cycle systems. The Sepik-Ramu Phylum
tend to have body-part tallies as well as 2-cycle, 5-cycle, and (5, 20) cycle
systems with some variation mainly due to the nearby AN languages. There are
also body-tally systems in south-east Australia (a considerable distance from
PNG) and Torres Strait Islands lying between Australia and Papua New Guinea and
possibly not in other parts of the world. The southernmost languages of the
Sepik Hill Stock, especially Hewa, have been influenced by East New Guinea
Highlands Stock of the Trans New Guinea (TNG) Phylum and other TNG Stock (WURM,
1982). Body-part tallies may have been introduced into the Sepik-Ramu Phylum
languages by such influence and not been an original feature (LEAN, 1992) but
this is not clear. The two branches (Kanum and Moro) of Morehead-Wasur
languages have six-cycle systems with large numbers suggesting the
Proto-Morehead-Wasur language contained a six-cycle system, thousands of years
ago (EVANS, 2009). Some East Papuan and Bougainville languages have classifiers
and most have features suggesting influence from AN languages.
Table 4
Distribution of Counting System and Tally Types Among the NAN Phyla
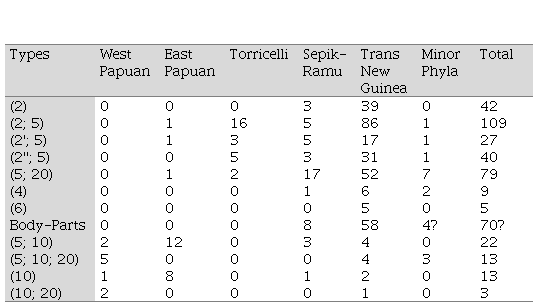 These are numbers from Lean’s (1992) collected data,
which are most languages but not all languages in PNG and Oceania. They exclude
11 West Papuan languages in North Halmahera.
These are numbers from Lean’s (1992) collected data,
which are most languages but not all languages in PNG and Oceania. They exclude
11 West Papuan languages in North Halmahera.
|
Types
|
West Papuan
|
East Papuan
|
Torricelli
|
Sepik- Ramu
|
Trans New Guinea
|
Minor Phyla
|
Total
|
|
(2)
|
0
|
0
|
0
|
3
|
39
|
0
|
42
|
|
(2; 5)
|
0
|
1
|
16
|
5
|
86
|
1
|
109
|
|
(2'; 5)
|
0
|
1
|
3
|
5
|
17
|
1
|
27
|
|
(2''; 5)
|
0
|
0
|
5
|
3
|
31
|
1
|
40
|
|
(5; 20)
|
0
|
1
|
2
|
17
|
52
|
7
|
79
|
|
(4)
|
0
|
0
|
0
|
1
|
6
|
2
|
9
|
|
(6)
|
0
|
0
|
0
|
0
|
5
|
0
|
5
|
|
Body-Parts
|
0
|
0
|
0
|
8
|
58
|
4?
|
70?
|
|
(5; 10)
|
2
|
12
|
0
|
3
|
4
|
0
|
22
|
|
(5; 10; 20)
|
5
|
0
|
0
|
0
|
4
|
3
|
13
|
|
(10)
|
1
|
8
|
0
|
1
|
2
|
0
|
13
|
|
(10; 20)
|
2
|
0
|
0
|
0
|
1
|
0
|
3
|
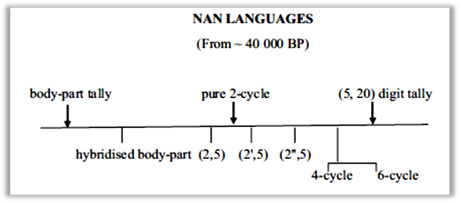
Unlike
Seidenberg, Lean proposed that the body-part tally and pure 2-cycle and (5, 20)
digit tally all developed independently across Papua New Guinea given the
places where these occurred and in the phyla or sub-phyla where they occur.
There is no evidence to suggest that one preceded and developed into the other
type.
Then there were modifications and new cycles developed. The various (2, 5) cycles appear to come afterwards as did the hybridized body-part tally systems and 4- and 6- cycle systems.
7 Implications
for Changing our Teaching on the History of Number
One of the most significant aspects of this research is that a complex connection between archaeological linguistics, an understanding of counting systems and their cycles, and an acceptance of oral knowledge and histories has resulted in new insights into how counting began and was used.
There are also important educational benefits:
-
- Learning about these systems extends students’ understanding of counting systems, respects Indigenous cultures, and provides a global mathematics perspective;
- It counters limited conceptions of history including the development of number and mathematics;
- It values archaeological linguistics of which Australia, Papua New Guinea and the Pacific countries are rich;
- The importance of groups in early arithmetic and higher levels of mathematics and relationships between numbers can be enriched; and
- For some students, the link to culture will be a critical way of engendering an interest and understanding in mathematics.
Each of these will be further discussed.
If the history of numbers is taught in the school environment, it diminishes the Indo-Western Asia-European Centred view about mathematics. Mathematics is no longer viewed as having developed in Western Asia and Europe and perceived to be mainly that of western culture. Even though school mathematics has originated from diverse cultures, the absence of any history of number implies mathematics is not connected to culture and society. For instance, the base 10 system is perceived to have western origins, even though other cultures such as Indian and the Austronesian cultures, had base 10 systems but then it is taken as the only system ever used. If history of number is taught, it would help students perceive that number systems have diverse human contribution and does not have a single western origin. Further, if systems that are not base 10 from different cultures are acknowledged by examples, then the actual underlying concepts inherent in the base 10 system such as composite groups will be further appreciated.
When the history of number is taught, it will show the trend and potential of cultural evolution. All cultures have the potential to evolve and develop, responding to change and exposure of the culture to new ideas and practices. Cultural counting systems were established to sensibly meet the immediate social and physical need to quantify at a particular time and context. However, as cultures changed due to exposure to other cultures, there seem to be a natural mechanism that enables cultures to respond and go through change to accommodate aspects from other cultures. This includes exposure to other counting practices. This evolution is often illustrated with the base 10 system and the use of zero but it would be strengthened by realizing that in places like Papua New Guinea when groups traded they often changed their systems to incorporate features of a neighbouring partner with whom they traded. For example some base 10 systems developed characteristics of base 5 systems while some who had (5, 20) cycle systems included a 10 rather than two fives. Such history will provide an understanding that all cultural knowledge and practice could go through evolution process to improve mathematics. Such a view could help students aim to reflect on their cultural counting practice, take an interest to understand their own cultural practices, compare with others and initiate ways to make their own culture better. This is a process that could build and maintain culture instead of destroying it when the evolution process described earlier is promoted.
When the history of number is taught, it will promote value of all cultural counting systems. Currently, the absence of history of cultural counting systems promotes devaluing of these knowledges and assumes base 10 counting system as superior and the only valued system. All counting knowledge and practices were equally important because they managed to meet the need to quantify cultural purposes successfully. In most indigenous cultures, there was no need to quantify large numbers of items, thus reflected on their counting practices. If there was a new need to quantify large numbers of items, these cultures had potential to initiate additional practices of counting systems to meet the need to quantify large numbers. Most cultures have shown signs of making changes to meet the new modern need, but with connection and continuation from the existing practices (OWENS et al., 2018). The base 10 counting system used at school may have been an advanced system, promoted for its modern convenience to quantify large numbers of items, but it was of no higher value compared to those counting systems as described earlier in indigenous cultures (PARAIDE, 2018). People often recognised and compared large quantities but not necessarily by counting. For example, the space that the objects take up can be used and the size of the bundles of shell money in Tolai and other Oceanic cultural groups. Numbers served the purpose they meant to serve within the context for which they were established. Therefore, through history of counting systems, it will help promote and emphasise how and why each counting system was of equal value in their respective cultures. It will show that no cultural counting practices was better off than the other because all conveniently served cultural needs to quantify. This valuing of culture encourages the identity with culture to influence and strengthen the mathematical thinking identity of the student (OWENS, 2015).
When the history
of number is taught, it will establish the connection between mathematics and
human reality. The school mathematics is often taught in such a way that it has
no connection to reality of life, particularly in cultural groups who have
strong non-Western ways of living. In this case, when base 10 counting system
is taught without history, it seem to have no human face to the number system
and no connection to cultures that contributed. When history of different
counting practices and their application in all indigenous culture are taught
and compared, it will put a human face to number systems; it will value
indigenous cultures which is very important for indigenous societies who have
been seriously impacted by colonial influences, invasion and alienation from
their land (KNIJNIK & WANDERER, 2010). Furthermore, when comparing
different counting systems, it will promote appreciation of counting systems of
other cultures. This includes the understanding and appreciation of using base
10 system taught at school, in relations to students’ foundational cultural
counting systems. The students, especially indigenous or minority students, not
only establish a connectivity with their culture and school mathematics, but
also realise how the school counting system is related to their cultural
counting systems (PARAIDE & OWENS, 2018). It gives them an opportunity to
appreciate how their cultural counting system could be used together with the
base 10 counting system in their cultural life and to better understand number
systems in general. For example, understanding that their system was based on a
5-cycle system rather than a 10-cycle system emphasises that the grouping
variable is significant whether it is 5 or 10. If a hand is used to represent 5
in their oral counting which is often associated with gestures, then
representing ten in writing as 10 is just another way of representing. If the
number 2 in a (5, 20) cycle system is also used to represent 2 men or 2
twenties then this can be compared to representing twenty as 20 with the 2
carefully placed to the left, in English and European languages, of the zero
that is showing no ones. The order of two frame words can be linked to the
order of the digits when writing the numeral. Rinsveld et al. (2016)
have shown how bilingual students learn other mathematical systems more easily.
Finally, the history of number would not only change
views and perspectives of mathematics, but it would impact both teaching and
learning of school mathematics. If history of number is taught, the students
are given the opportunity to learn from known knowledge in their home culture
and language which is real in their life to unknown knowledge of school and
thus provide a transition that is meaningful from one language and culture to
another. The students will be learning mathematics by first using their known
counting systems and leading them into learning unknown mathematics using base
10 counting system. From a constructivist view, the known cultural counting
knowledge will play a major role in learning new mathematics using base 10
counting system. There will be a stronger conceptual understanding of counting
as a system and of composite groups as an important notion in mathematics.
Therefore, if history of number is taught, students make necessary and
important connections to base 10 counting system at school, enabling effective
learning.
References
ADDISON, David; MATISOO-SMITH, Elizabeth. Rethinking Polynesians origins: a West-Polynesia Triple-I Model. Archaeology in Oceania, v. 45, n. 1, p. 1-12, 2010.
ALLEN, Jim. The pre-Austronesian settlement of Island Melanesia: implications for Lapita archaeology. Transactions of the American Philosophical Society, v. 86, n. 5, p. 11-27, 1996.
ASCHER, Marcia. Ethnomathematics: a multicultural view of mathematical ideas. New York: Chapman & Hall, 1994.
BENDER, Andrea; BELLER, Seighard. Cultural variation in numeration systems and their mapping onto the mental number line. Journal of Cross-Cultural Psychology, v. 42, n. 4, p. 579-597, 2011.
BENDER, Andrea; BELLER, Seighard. Numeral classifiers and counting systems in Polynesian and Micronesian languages: common roots and cultural adaptations. Oceanic Linguistics, v. 45, n. 2, p. 380-403, 2006.
BISHOP, Alan John. Mathematical enculturation: a cultural perspective on Mathematics Education. Dordrecht: Kluwer, 1988.
BISHOP, Alan John. Visualising and mathematics in a pre-technological culture. Educational Studies in Mathematics, v. 10, n. 2, p. 135-146, 1979.
BROUWER, Luitzen Egbertus Jan. Guidelines of intuitionistic mathematics. In: HEYTING, Arend. (Ed.). Philosophy and foundations of mathematics. Amsterdam: North Holland, 1975, p. 123-138.
CRAWFURD, John. On the numerals as evidence of the progress of civilization. Transactions of the Ethnological Society of London, v. 2, p. 84-111, 1863.
D’AMBROSIO, Ubiratan. The history of Mathematics and Ethnomathematics: how a native culture intervenes in the process of learning science. Impact of Science on Society, v. 40, n. 4, p. 369-378, 1990.
DIXON, Roland; KROEBER, A. L. Numerical systems of the languages of California. American Anthropologist, v. 9, p. 663-690, 1907.
DONOHUE, Mark. Complexities with restricted numeral systems. Linguistic Typology, v. 12, n. 3, p. 423-429, 2008.
EVANS, Nicholas. Two pus one makes thirteen: senary numerals in the Morehead-Maro region. Linguistic Typology, v. 13, n. 2, p. 321-335, 2009.
FISHER, John. Enriching students' learning through ethnomathematics in Kuruti elementary schools in Papua New Guinea. In: International Conference on Ethnomathematics, 3, 2006, Auckland. Proceedings ICEM-3: Cultural Connections and Mathematical Manipulations. Auckland: The University of Auckland, 2006, p. 1-17.
HARRISON, Sheldon; JACKSON, Frederick. Higher numerals in several Micronesian languages. In BENDER, Byron (Ed.). Studies in Micronesian Linguistics. Canberra: Pacific Linguistics: 1984, p. 61-79.
HOLZKNECHT, Susanne. The Markham languages of Papua New Guinea. Canberra: School of Pacific Research Studies, Australian National University, 1989.
JETT, Stephen. Diffusion versus independent development: the bases of controversy. In RILEY, Carroll; KELLEY, J. Charles; PENNINGTON, Campbell; RANDS, Robert (Ed.). Man Across the Sea: problems of pre-columbian contacts. Austin & London: University of Texas Press, 1971, p. 5-53.
KNIJNIK, Gelsa; WANDERER, Fernanda. Mathematics Education and differential inclusion: a study about two Brazilian time-space forms of life. ZDM Mathematics Education, v. 42, n. 3-4, p. 349-360, 2010.
LANCY, David. Indigenous mathematics systems: an introduction. Papua New Guinea Journal of Education, v. 14, p. 6-15, 1978.
LEAN, Glendon. Counting systems of Papua New Guinea and Oceania.1992. Thesis (Doctorate in Mathematics). Papua New Guinea University of Technology. Lae.
LYNCH, John. On the history of the Tanna numerals and number markers. Te Reo: Journal of the Linguistic Society of New Zealand, v. 20, p. 3-28, 1977.
MAY, Patricia; TUCKSON, Margaret. The traditional pottery of Papua New Guinea. rev. ed. Adelaide: Crawford House Publishing, 2000.
MIMICA, Jardin. Intimations of infinity: the mythopoeia (cultural meanings) of the Iqwaye counting and number systems. Oxford: Berg, 1988.
MUKE, Charly. Ethnomathematics: Mid-Wahgi counting practices in Papua New Guinea, 2000. Thesis (Masters in Mathematics Education). University of Waikato, Waikato.
OWENS, Kay. The work of Glendon Lean on the counting systems of Papua New Guinea and Oceania. Mathematics Education Research Journal, v. 13, n. 1, p. 47-71, 2001.
OWENS, Kay. Visuospatial reasoning: an ecocultural perspective for space, geometry and measurement education. New York: Springer, 2015.
OWENS, Kay; LEAN, Glendon, with PARAIDE, Patricia; MUKE, Charly. The history of number: perspective from Papua New Guinea and Oceania. New York: Springer, 2018.
OWENS, Kay; LEAN, Glendon; MUKE, Charly. 2-cycle systems including some digit-tally systems. In OWENS, Kay; LEAN, Glendon; PARAIDE, Patricia; MUKE, Charly. (Ed.). History of number: evidence from Papua New Guinea and Oceania. New York: Springer, 2018, p. 41-60.
PANTOFF, Michel. Father arithmetic: numeration and counting in New Britain. Ethnnology, v. 9, n. 4, p. 358-365, 1970.
PARAIDE, Patricia. Indigenous and western knowledge. In OWENS, Kay; LEAN, Glendon; PARAIDE, Patricia (Ed.). History of number: Evidence from Papua New Guinea and Oceania. New York: Springer, 2018, p. 223-242.
PARAIDE, Patricia; OWENS, Kay. Integration of Indigenous knowledge in formal learning environments. In OWENS, Kay; LEAN, Glendon; PARAIDE, Patricia; MUKE, Charly (Ed.). History of number: evidence from Papua New Guinea and Oceania. New York, NY: Springer, 2018, p. 243-269.
PARAIDE, Patricia; OWENS, Kay; CLARKSON, Philip; MUKE, Charly; OWENS, Chris. History of Mathematics Education in Papua New Guinea. New York: Springer (forthcoming).
PAWLEY, Andrew; GREEN, Roger. The Proto-Oceanic language community. In KIRK, Robert; SZATHMARY, EmOke. (Ed.). Out of Asia: peopling the Americas and the Pacific. Canberra: Australian National University, 1985, p. 161-184.
PUMUGE, Hilary. The counting system of the Pekai-Alue tribe of the Topopul village in Ialibu sub-district in the Southern Highlands District, Papua New Guinea. Science in New Guinea, v. 3, n. 1, p. 19-25, 1975.
RAGLAN, Lord B. How came civilization? London: Methuen and Company, 1939.
RINSVELD, Amandine Van; SCHILTZ, Christine; LANDERL, Karin; BRUNNER, Martin; UGEN, Sonja. Speaking two languages with different number naming systems: what implications for magnitude judgments in bilinguals at different stages of language acquisition? Cognitive Processing, v. 17, n. 3, p. 225-241, 2016.
ROSS, Malcolm. Proto Oceanic and the Austronesian languages of western Melanesia. Canberra: School of Pacific Research Studies, Australian National University, 1988.
ROSS, Malcolm; PAWLEY, Andrew; OSMOND, Meredith. The lexicon of Proto Oceanic: The culture and environment of ancestral Oceanic society. 2: The physical environment. Canberra, Australia: Pacific Linguistics, Research School of Pacific and Asian Studies ANU, 2003.
SALZMANN, Zdeněk. A method for analyzing numerical systems. Word, 6, p. 78-83, 1950.
SAXE, Geoffrey. A comparative analysis of the acquisition of numeration: studies from Papua New Guinea. The Quarterly Newsletter of the Laboratory for Comparative Human Cognition, v. 1, n. 3, p. 37-43, 1979.
SEIDENBERG, Abraham. The diffusion of counting practices. University of California Publications in Mathematics, v. 3, 1960.
SMITH, Geoffrey P. S. Morobe counting systems. In: Papers in New Guinea Linguistics. Series A, n. 76. Canberra: Pacific Linguistics, 1988, p. 1-132.
SMITH, Geoffrey P. S. Morobe counting systems: an investigation into the numerals of the Morobe Province, Papua New Guinea, 1984. Thesis (Masters in Language and Communication). Papua New Guinea University of Technology, Lae.
SMITH, Grafton Elliot. The diffusion of culture. London: Watts and Company, 1933.
SPRIGGS, Matthew. Archaeology and the Austronesian expansion: where are we now? Antiquity, v. 85, n. 328, p. 510-528, 2011.
STRATHERN, Andrew. Mathematics in the moka. Papua New Guinea Journal of Education, v. 13, n. 1, p. 16-20, 1977.
TRYON, Darrell (Ed.). Comparative Austronesian dictionary. Berlin: Mouton de Gruyter, 1995.
VAN DER WAERDEN, Bartel Leendert; FLEGG, Graham. Counting 1: primitive and more developed counting systems. Milton Keynes: Open University, 1975.
WILDER, Raymond. Evolution of mathematical concepts. London: Transworld, 1974.
WILLIAMS, Francis. Papuans of the Trans-Fly. Oxford: Clarendon Press, 1936.
WOLFERS, Edwards. The original counting systems of Papua and New Guinea. Arithmetic Teacher, v. 18, n. 1, p. 77-83, 1971.
WURM, Stephen. Papuan languages. In: MAY, Ronald James; NELSON, Hank (Ed.), Melanesia: Beyond diversity. Canberra: Research School of Pacific Studies, Australian National University, 1982, pp. 225-240.
WURM, Stephen; LAYCOCK, David; VOORHOEVE, Clemens; DUTTON, Thomas. Papuan linguistic prehistory, and past language migrations in the New Guinea area. New Guinea area languages and language study. Vol. 1: Papuan languages and the New Guinea linguistic scene, Pacific Linguistics v. C-38. Canberra: Research School of Pacific Studies Australian National University, 1975, p. 935-960.
ZASLAVSKY, Claudia. Africa counts: number and pattern in African culture. Boston: Prindle, Weber and Schmidt, 1973.