



International perspectives on Ethnomathematics: from research to practices
Revising the history of number: how Ethnomathematics transforms perspectives on indigenous cultures
Revisando la historia de los números: cómo las Etnomatemáticas transforma las perspectivas sobre las culturas indígenas
Revisando a história do número: como a Etnomatemática transforma perspectivas sobre culturas indígenas
Revemop
Universidade Federal de Ouro Preto, Brasil
ISSN-e: 2596-0245
Periodicity: Frecuencia continua
vol. 2, 2020
Received: 06 September 2019
Accepted: 20 November 2019
Published: 04 March 2020

Abstract: Many accounts of the history of number rely on written evidence such as clay, stone, and wood engravings or paintings. However, some of the oldest cultural groups (between 5 000 and 30 000 years old) have had only recent contact with the rest of the world, namely between 80 and 140 years ago but these were oral cultures without written records. Finding out about their understanding of number has involved analysis of the types of counting but also how counting related to the rest of their cultural relationships. There is some surprising evidence of diversity of number systems, longevity of the systems, and the interplay with cultural practices that begs respect for Indigenous cultures. Brief summaries of this history of number in Papua New Guinea and Oceania and the diversity of systems is followed by how this new knowledge can inform school mathematics learning in any part of the world.
Keywords: History of number, Indigenous mathematics, Papua New Guinea, Melanesia, Pacific, Longevity of number systems.
Resumen: Muchos relatos de la historia de los números se basan en pruebas escritas como grabados o pinturas de arcilla, piedra y madera. Sin embargo, algunos de los grupos culturales más antiguos (entre 5 000 y 30 000 años) solo han tenido contacto reciente con el resto del mundo, es decir, hace entre 80 y 140 años, pero se trataba de culturas orales sin registros escritos. Conocer su comprensión del número ha implicado el análisis de los tipos de conteo, pero también cómo el conteo se relaciona con el resto de sus relaciones culturales. Hay alguna evidencia sorprendente de la diversidad de sistemas numéricos, la longevidad de los sistemas y la interacción con prácticas culturales que exigen respeto por las culturas indígenas. Breves resúmenes de esta historia del número en Papua Nueva Guinea y Oceanía y la diversidad de sistemas es seguida por cómo este nuevo conocimiento puede informar el aprendizaje matemático escolar en cualquier parte del mundo.
Palabras clave: Historia de los Números, Matemáticas indígenas, Papua Nueva Guinea, Melanesia, Pacifico, Longevidad de sistemas numéricos.
Resumo: Muitos relatos da história do número dependem de evidências escritas como em argila, em pedra, em gravuras, em madeira ou em pinturas. No entanto, alguns dos grupos culturais mais antigos (entre 5.000 e 30.000 anos) tiveram apenas um contacto recente com o resto do mundo, nomeadamente entre 80 e 140 anos atrás, mas esses tinham culturas orais sem registos escritos. Descobrir a compreensão do número envolveu a análise dos tipos de contagem, mas também como a contagem se relacionava com o restante de suas relações culturais. Há algumas evidências surpreendentes da diversidade de sistemas numéricos, longevidade dos sistemas e interação com as práticas culturais que imploram respeito pelas culturas indígenas. Breves sumários desta história de números em Papua Nova Guiné, Oceânia e numa diversidade de sistemas são seguidos por uma reflexão sobre como esse novo conhecimento pode informar a aprendizagem de Matemática escolar em qualquer parte do mundo.
Palavras-chave: História do número, Matemática indígena, Papua Nova Guiné, Melanésia, Pacífico, Longevidade de sistemas numéricos.
1 Introduction
Forty years ago, ethnomathematics was beginning to be recognised more widely (BISHOP, 1979;LANCY, 1978; VAN DER WAERDEN & FLEGG, 1975;WILDER, 1974;WOLFERS, 1971; ZASLAVSKY, 1973). Many linguists were recording the counting systems of the people whose language(s) they were learning (PANOFF, 1970;PUMUGE, 1975); Wurm and his colleagues (WURM et al., 1975) were documenting the languages in New Guinea, and others were considering Oceania (LYNCH, 1977; ROSS, 1988). Anthropologists were incorporating counting into the various complex activities and beliefs of people (STRATHERN, 1977) while cognitive, developmental psychologists (e.g., SAXE, 1979) were considering how cultural context affected concepts. Papua New Guinea University of Technology had a Mathematics Education Centre and the University of Papua New Guinea had an Education Research Unit, both of which supported research that took account of cultural difference in mathematics learning. Some of this work was focused on difference using Piagetian studies and some on cognitive development for mastery of concepts. It would be another decade before ethnomathematics was widely discussed (ASCHER, 1994; BISHOP, 1988;D’AMBROSIO, 1990).
2 Counting System Diversity and How They Developed
With written records of number, there are symbols used in the various languages for numbers. These reflect the ways that the people combined numeral words to make new number names. For example, the Romans, at least in their later history, said four was IV, that is, one before five. In one sense, place or position was important. We are also cognisant that the Arabs used and modified the original Indian ways of recording numbers to give us our current Hindu-Arabic system of base-10 with place value and a zero. But what happened before this? In the second half of the 18th century, it was considered that numerals were a hallmark of civilisation (CRAWFURD, 1863), and then there was a debate about whether different civilisations invented their counting and numerals or whether there was a diffusion from either Egypt around 4 000 BCE (SMITH, G.E, 1933) or the Sumerians (RAGLAN, 1939). The diffusionist ideas prevailed and Seidenberg (1960) suggested that counting systems diffused from Western Asia or Mediterranean civilisations starting with two-cycle systems having one and two as frame words around 3 500 BCE “spread out over the whole earth; later, other methods of counting arose and spread over almost all, but not quite all, of the world” (p. 218). His view was based on the anthropological evidence that suggested these two-cycle systems only occur on the vestiges of the world in southern Africa, southern America, and Australia. Some systems with numerals for three and perhaps four, but without combinations for higher numbers he claimed as systemless and an aberration of the two-cycle system. Seidenberg then suggested that paired systems developed; he called them neo-2 systems in which 6 = 2 × 3 and 7 = 2 × 3 + 1 and so on. One example was the Motu and Roro systems close to Port Moresby in Papua New Guinea. Then, he said the base-10 system developed in conjunction with these paired systems spreading around the world. Seidenberg went on to suggest that the North American Inuits that have a (5, 20) cycle system came after the 10-cycle and there was a fusion, slurring (his term), or modification made with the (2, 10) cycle system resulting in (10, 20), or 20-cycle systems. He suggested that when the 10-cycle system developed in different places it was diffused, unlike the two-cycle system that began in the Middle East (Western Asia). From African systems, he suggested that the (2, 10) and (5, 20) systems came together to make the second pentad (6 to 9) as five plus one to four or another word plus one to four. Finally, Seidenberg believed that the body-part tallying was a combining of the two-cycle system with the (5, 20) system as they linked the idea of body part tallying to represent numbers when tabu (society discouraged its use) prevented them from using counting words. There are cases, for example, Duna which truncated a body-part tally system for the sound of 14 was similar to a word that was tabu.
Glendon Lean began collecting the counting systems of his students from across Papua New Guinea (PNG) and Oceania in the late 1960s until the late 1970s. Importantly, these first university students were still well connected to their cultures and languages. Unknown by most educators or politicians at the time, he located first contact records in linguistic and government records and in research journals since the Pacific was an “exotic” place to visit for the enlightenment of the 1800s. Thus he was collecting records of what were until that time oral counting systems. The Summer Institute of Linguistics had also recording in their language surveys many language words including some counting words. University linguists were finding Papuan (non-Austronesian) languages in PNG had fascinating language patterns unknown in other parts of the world and so they too began to study more complex aspects of the languages. Surprisingly some of these languages were spoken by few people while others were spoken by thousands and some had numerous dialects. Interesting too were the similarities of the Austronesian languages spoken by Melanesians across the Pacific. Linguists were studying these languages and from these records, Lean was able to obtain counting words for analysis. In total, Lean collected the counting systems of 1 200 languages and we have added several further languages to this collection from field visits, students, and other papers.
Through careful collation and analysis, Lean was able to publish these data in 1988 for each province of PNG. These data formed part of his doctoral thesis (LEAN, 1992) together with counting system data for Oceania (West Papua — the name refugees use — then called Irian Jaya, Indonesia; Island Melanesia; Micronesia; and Polynesia). Geoffrey Smith (1984,1988) had also studied the systems in Morobe Province. Both used Salzmann’s (1950) method of ascertaining the frame words with which all other numerals were named, deciding the operative patterns by which the frame words were combined to make the other numbers and then deciding on the primary and superordinate cycles. For example, if a system has frame words of 1, 2, 5, and 20 by which all other numbers were named then the system was a (2, 5, 20) cycle system. In an earlier paper (OWENS, 2001), much of Lean’s work was summarised. It is extended in Owens, Lean, Paraide and Muke (2018).
3 Countering the Diffusionist Theory
Seidenberg claimed the two-cycle system was once widespread, but Lean found that there were few systems that were pure two-cycle systems in PNG, and they have not been found en route to South America (e.g., in North America although a paper on California contradicts this (DIXON & KROEBER, 1907). In PNG, as elsewhere, most two-cycle systems, in fact, went on to have a (2, 5) or (2, 5, 20) cycle system and these existed well before the 10-cycle systems introduced mainly by Austronesian (AN) Oceanic speakers. Furthermore, the paired system was a variation of the AN Oceanic speakers on the southern coast of PNG and generally not found in the non-Austronesian (NAN) systems although there is evidence of different group counting. These Oceanic languages spread from their homeland near New Britain (OWENS et al., 2018;ROSS, PAWLEY & OSMOND, 2003). Seidenberg thought 10 cycles preceded (5, 20) and body-tally systems, but Lean countered this by recognising that finger gestures while counting are so widespread among Indigenous people that digit-tally systems would have developed across the world and not after base-10 systems were in place. It is not commonly considered that the body tally systems were older than (5, 20) systems as they are more complex and in many cases, there is no evidence that this practice was linked to sharing body parts in rituals, as Seidenberg claimed. Furthermore, Seidenberg has not explained how the systems with 1, 2, 3 and/or 4 evolved into a system with 10. Finally, having a system that is efficient such as the base 10 system may not be the only reason for a group to take up a counting system from a neighbour. A few AN 10-cycle systems in PNG changed to a two-cycle system when the people moved inland along a major river valley, the Markham, and were building relationships with people using two-cycle systems, including variants like (2, 5) cycle systems (HOLZKNECHT, 1989;OWENS et al., 2018). There are many other reasons for systems to be the same or different from others: friendliness, trade, length and intensity of contact, desire to be separate or similar, or for what is valued such as multilingual skills, care, confounding others, extravagance or prestige (JETT, 1971).
4 Extending Our Understanding of How Counting Systems Develop
Not only does Lean’s (1992) evidence contradict Seidenberg on a number of major issues but his analysis also found several other factors of interest in discussing the spread of counting systems. First, it was found that in West Papua, PNG, and the Solomon Islands that NAN and older languages had borrowed some words, mostly in the second pentad from Austronesian (AN) languages. Similarly, some AN languages borrowed words from NAN languages. Table 1 indicates these phenomena. However, these borrowings are not particularly common and more significant is where a whole system is adopted as mentioned above in the Markham Valley (OWENS et al., 2018).
| Phylum or Cluster | (5)/(5, 20) | (5, 10) | (5, 10, 20) |
| Non-Austronesian | 79 | 21 | 13 |
| Austronesian | 63 | 113 | 46 |
The majority of (5)/(5,20) cycle systems are found in the NAN Sepik-Ramu and Trans New Guinea (TNG) Phyla. There are many other systems in these phyla but there seems to be some connections between the languages with some innovations in other languages. It should be noted that the (5, 10) cycles are found in the NAN East Papuan Phylum; and (5, 10, 20) in West Papuan Phylum where these languages had contact with AN languages. Among the AN languages, the majority of languages that have reverted from 10-cycle systems to incorporate features of 5-cycle are in North New Guinea, Papuan Tip, Vanuatu and New Caledonia. The (5, 10) cycle systems are found in Vanuato and (5, 10, 20) cycle systems are found in New Caledonia. This evidence suggests contact with existing NAN languages or some diffusion perhaps through on-going trade or displacement or they occurred spontaneously.
5 Evidence of Large Numbers
5.1 Non-Base-10 Systems
In order to illustrate how these Indigenous systems without a base 10 developed large numbers, three language groups are selected:
- Yu Wooi (Mid-Wahgi) from the Jiwaka Province in the PNG western highlands that displays a digit tally system with vestiges of a four-cycle and from some informants, a body-tally system;
- Iqwaye from the Eastern Highlands Province bordering Morobe (a coastal province) that is a digit-tally system with (2, 5, 20) cycles; and
- six-cycle systems from a large island off the southern coast of West Papua and languages around the border of West Papua and Western Province, PNG.
Yu-Wooi.Muke (2000) obtained data from a number of people from his four tribal groups that have different dialects. The system is a typical (2, 5, 20) cycle system. For example, 27 is angek yem yemsi simb yem yemsi, angek yemsi, tak (both hands both legs half hand and two). For another example, 40 is hi tak simb angek yemeyem (two men’s both legs and hands). However, they also count items by twos and in hundreds by grouping them in tens and then tally each ten using their fingers and toes to reach 200. Thus, as one participant said, “for six hundred pigs, they would say that they will kill pigs equal to the hands and legs of three man” (MUKE, 2000, p. 134). For the larger thousands, people used the fingers and toes for groups of ten and when they had ten groups of ten, they referred to a specific body part, starting from the head towards the legs, aiding memory of giving for reciprocity.
One variation of this was the use of the names of fingers for adding almost as a vestige of a body-part tally system. Furthermore, when it came to counting and having the opportunity to use hands, people often counted in twos. They would fold down two fingers at a time saying eraksi meaning “take two” each time: two then two on one hand followed by two and two on the other and bringing the four folded fingers of each hand together being mam erak followed by the two thumbs with the words angek yem yem “together hands” (some also folded two, two, then thumb eraksi eraksi el and then two and two and thumb repeated before bringing together and saying angek yem yem). When deciding the number of pigs to be given by each person in a compensation claim, the leader asked people to take the number that they would give from a bunch of small banana fruit. When everyone had offered as they wished, the banana fruit were put together and tallied in groups of 10, each group matched with a digit tally part starting with the fingers.
| Numeral | Numeral Yu Wooi and Explanation |
| 100 | 100 elsi peng this 100 represented by the head |
| 200 | 200 komuk ear – 2nd 100 |
| 300 | 300 gnumb nose – 3rd 100 |
| 400 | 400 gupe mouth – 4th 100 |
| 500 | 500 angek woiro right hand – 5th 100 |
| 600 | 600 angek daro left hand – 6th 100 |
| 700 | 700 buk back – 7th 100 |
| 800 | 800 kumbuk belly – 8th 100 |
| 900 | 900 simb woiro right leg – 9th 100 |
| 1 000 | 1 000 simb daro left leg - hi ende simb angek poro bekenj – 10th 100 or whole body parts of one person matched |
| 2 000 | hi tak two persons |
| 3 000 | hi takendeka three persons |
Iqwaye. Building on a binary system of relationships in which a pair is one or where another number is linked to one (the whole), it seems that PNG and Oceania cultures have a richer understanding of number. There is order in the counting, but temporality related to this order may not be of the Western kind but pulsating back and forth (MIMICA, 1988). One such group, Iqwaye, has a digit-tally system starting with the thumb of either open hand, then the index finger, etc., moving to the other hand, then counting the toes. (Most language groups seem to count by bending the fingers down starting with the little finger.) Twenty is two hands and two legs or a person. Iqwaye refer to the link between the creator and each of the five children represented by a finger as one child or one to five children so one can be one or five can be one. Using this digit-tally counting system, by which each digit represents a counting word in order, the man standing up becomes one denoted by the thumb again. So, each digit then represents a multiple of 20. Three fingers could represent three persons or 3 × 20. The next iteration is for the digits to represent 202 counted off by the crouching man with fingers touching the toes. Thus, two groups of 20 men (20 × 20 = 400) is represented by the thumb and index finger so 1 000 is represented by two fingers and then 10 fingers (each finger representing 20).
400 is Aa’ ’mnye, aa’mnye, toqwotni tepu hyelaqa kokoloule hyule hwolye hyelaqapu
Person person this-me this that-all their leg hand that-all ‘[as] this many persons [as] me this [one] person [speaker] all their legs and hands’ 1,000 is ‘two persons [as] me this [one] person all their legs and hands and to another person’s two hands (= ten persons) all their legs and hands’ (MIMICA, 1988, pp. 35-36)
Thus, the notion of infinity is generated (MIMICA, 1988). This self-generating system of numbers is reminiscent of some modern Western mathematical and binary systems. He suggested that a study of the system shows an intuitive non-Western origin of number, capable of developing into a system and purpose for counting (BROUWER, 1975).
Six-Cycle Systems Near the Border of West Papua and PNG. Donohue’s (2008) study of the languages of Kolopom Island has shown that languages like Kanum have developed an interesting variety of counting systems to manage their base-six system for large numbers. There are in fact three systems: for small numbers, moderate numbers, and a complex system for one to large numbers, 65. Some number words occur in more than one system, but the complex system is well established except that the Indonesian currency note for 1 000 has brought confusion: Some younger speakers are reinterpreting ntamnao ‘1296’ as ‘1 000’, ... ntamnao tamp is effectively ambiguous between ‘5 000’ (1 000 × 5; new reading) or ‘6 480’ (1 296 × 5; old reading), although only the latter is prescriptively correct (DONAHUE, 2008, p. 427). Evans (2009) has shown that languages of the Morehead-Maro language group in Western Province, PNG and further west also have large numbers for six-cycle languages. For example, Nen count to 65 or 66. The counting in these languages seems to relate to counting yams (three in one hand and three in the other) that are then bundled in groups of six (62) and then counted. In fact, in 1936, Williams recounted that in Keraakie with two counters, one counted each of the bundles of 36 while the other placed a yam representing 36 yam to form a daisy pattern. Interestingly, different groups represented six by different parts or gestures of the hand.
5.2 Base-10 Systems of the Region
The AN languages, and in some places neighbouring NAN languages such as Nasioi and Uisai on Bougainville, used numeral classifiers for large numbers. In most cases, classifying prefix or suffix were for counting specific groups of objects such as single bananas, a hand of bananas, long thin objects, food items and so on (OWENS et al., 2018). However, in many languages there are also numerical classifiers, that is a prefix or suffix that represents 100 or 1 000 or 10 000 or some other large number. Fisher (2006) on a Manus language noted, for example, the prefix po- for 100 000. Bender & Beller (2006; 2011) provided several different examples. For example, the Samoan expression that refers to just 2 coconuts has a corresponding article for “2” in Tongan that multiplies 10-score (thus 2 × 20 = 400), thus yielding 400 coconuts. It is only when numeral and classifier change their position (as infua-lua) in Samoan that a numerical change occurs (from 2 to 20). Rennelles, a Polynesian Outlier, in the Solomon Islands also shows multiplication for large numbers so the practice was widespread.
Examples also illustrate the importance of alternative ways of representing or displaying large numbers in base 10 and in mixed systems of composite groupings. For example, the Tolai display their shell money in recognised ways. First, a fathom is shown with the string of shell money generally looped and not taught between the outstretched hands to display generosity and value. The fathoms are then bundled in tens and tens of these and then tens of these are bundled and wrapped together to form large hoops of shell. These are highly valued hoops displayed during exchange ceremonies such as marriage (PARAIDE, 2018). Others display in heaps of say yams such as in Kilivila, or amounts are spread out upon the ground as in Loboda. Thus large numbers can be represented and recognised in different ways Owens et al. (2018).
6 Evidence for the Longevity of Counting Systems in Our Region
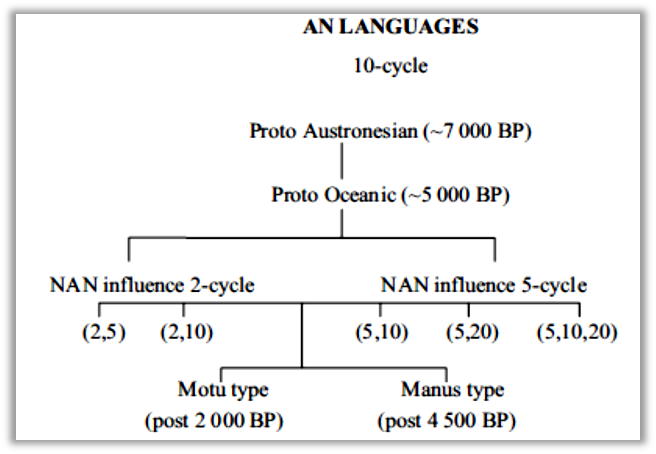
Lean (1992) drew heavily on linguistic data and archaeological linguistics, and his thesis is supported by more recent evidence. For example, the dating of the spread of Oceanic languages is based on Proto Oceanic language and the cultural complex associated with the Lapita-style ceramic tradition found throughout Island Melanesia and western Polynesia (ALLEN, 1996; ADDISON & MATISOO-SMITH, 2010; PAWLEY & GREEN, 1985; SPRIGGS, 2011). The deep conceptual structure of counting systems, namely their cyclic nature, rather than just loanwords suggests a long-standing existence of these counting systems and their connectivity. The cycle of 10 is common across these languages as shown in Table 3 although the older NAN languages with whom they were in contact has influenced many languages resulting in other cycles.
| Admiralties/St Matthias | North New Guinea | Papuan Tip | S.E. Solomic | Vanuatu | New Caledonia | Fiji Rotuma | ||||
| (2) | 0 | 2 | 0 | 0 | 0 | 0 | 0 | |||
| (2, 5), (2”, 5) | 0 | 22 | 7 | 0 | 0 | 0 | 0 | |||
| (5, 20) | 1 | 19 | 11 | 0 | 15 | 8 | 0 | |||
| (5, 10) | 1 | 20 | 7 | 0 | 68 | 0 | 0 | |||
| (5, 10, 20) | 0 | 13 | 5 | 0 | 0 | 19 | 0 | |||
| (10, 100) | 23 | 0 | 9 | 28 | 19 | 0 | 3 | |||
| (10, 20) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| (4) | 0 | 2 | 0 | 0 | 0 | 0 | 0 | |||
Proto Oceanic contained at least terms for 100 and 1 000 with some northern areas losing these for various reasons, perhaps due to NAN influence with other languages inventing further systems. Higher powers are common in Polynesian languages sometimes as 2 × powers of ten and probably due to tributes to chiefs. According to Harrison & Jackson (1984), higher powers, at least for Micronesia, may have a later history and several innovations. For Polynesia and Micronesia, Owens, et al., 2018 following Lean, suggests that there are 39 with cycles of 10 and higher powers, six having (10, 20) cycles and one with a (5, 20) cycle system. Nevertheless, Tryon (1995) suggests Proto Oceanic has a beginning 6 000 years ago.
The genealogy suggested for the age of the systems is given in Figure 1. This figure indicates some of the spread of the languages as summarized by Addison and Matisoo-Smith (2010) and other studies of obsidian spread and pottery sources, trade and similarities in certain areas together with likely settlement in different areas (MAY & TUCKSON, 2000; PARAIDE et al., forthcoming).
By contrast, the older NAN languages show surprising diversity although some main systems tend to dominate different phyla suggesting again some long-standing systems. Table 4 indicates the diversity. TNG Phylum accounts for most of the mainland of New Guinea outside of the coastal areas and has a diversity of types of systems. Eighty percent of body-part systems are found in one of the sub-phylum. There is also a cluster of four-cycle systems but they are quite diverse in themselves and so seem to be localised innovations. The majority are variants of two-cycle systems and mainly (5, 20) cycle systems. The Sepik-Ramu Phylum tend to have body-part tallies as well as 2-cycle, 5-cycle, and (5, 20) cycle systems with some variation mainly due to the nearby AN languages. There are also body-tally systems in south-east Australia (a considerable distance from PNG) and Torres Strait Islands lying between Australia and Papua New Guinea and possibly not in other parts of the world. The southernmost languages of the Sepik Hill Stock, especially Hewa, have been influenced by East New Guinea Highlands Stock of the Trans New Guinea (TNG) Phylum and other TNG Stock (WURM, 1982). Body-part tallies may have been introduced into the Sepik-Ramu Phylum languages by such influence and not been an original feature (LEAN, 1992) but this is not clear. The two branches (Kanum and Moro) of Morehead-Wasur languages have six-cycle systems with large numbers suggesting the Proto-Morehead-Wasur language contained a six-cycle system, thousands of years ago (EVANS, 2009). Some East Papuan and Bougainville languages have classifiers and most have features suggesting influence from AN languages.
| Types | West Papuan | East Papuan | Torricelli | Sepik- Ramu | Trans New Guinea | Minor Phyla | Total |
| (2) | 0 | 0 | 0 | 3 | 39 | 0 | 42 |
| (2; 5) | 0 | 1 | 16 | 5 | 86 | 1 | 109 |
| (2'; 5) | 0 | 1 | 3 | 5 | 17 | 1 | 27 |
| (2''; 5) | 0 | 0 | 5 | 3 | 31 | 1 | 40 |
| (5; 20) | 0 | 1 | 2 | 17 | 52 | 7 | 79 |
| (4) | 0 | 0 | 0 | 1 | 6 | 2 | 9 |
| (6) | 0 | 0 | 0 | 0 | 5 | 0 | 5 |
| Body-Parts | 0 | 0 | 0 | 8 | 58 | 4? | 70? |
| (5; 10) | 2 | 12 | 0 | 3 | 4 | 0 | 22 |
| (5; 10; 20) | 5 | 0 | 0 | 0 | 4 | 3 | 13 |
| (10) | 1 | 8 | 0 | 1 | 2 | 0 | 13 |
| (10; 20) | 2 | 0 | 0 | 0 | 1 | 0 | 3 |
Unlike Seidenberg, Lean proposed that the body-part tally and pure 2-cycle and (5, 20) digit tally all developed independently across Papua New Guinea given the places where these occurred and in the phyla or sub-phyla where they occur. There is no evidence to suggest that one preceded and developed into the other type.
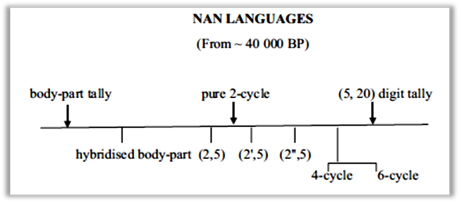
Then there were modifications and new cycles developed. The various (2, 5) cycles appear to come afterwards as did the hybridized body-part tally systems and 4- and 6- cycle systems.
7 Implications for Changing our Teaching on the History of Number
One of the most significant aspects of this research is that a complex connection between archaeological linguistics, an understanding of counting systems and their cycles, and an acceptance of oral knowledge and histories has resulted in new insights into how counting began and was used.
There are also important educational benefits:
- Learning about these systems extends students’ understanding of counting systems, respects Indigenous cultures, and provides a global mathematics perspective;
- It counters limited conceptions of history including the development of number and mathematics;
- It values archaeological linguistics of which Australia, Papua New Guinea and the Pacific countries are rich;
- The importance of groups in early arithmetic and higher levels of mathematics and relationships between numbers can be enriched; and
- For some students, the link to culture will be a critical way of engendering an interest and understanding in mathematics.
Each of these will be further discussed.
If the history of numbers is taught in the school environment, it diminishes the Indo-Western Asia-European Centred view about mathematics. Mathematics is no longer viewed as having developed in Western Asia and Europe and perceived to be mainly that of western culture. Even though school mathematics has originated from diverse cultures, the absence of any history of number implies mathematics is not connected to culture and society. For instance, the base 10 system is perceived to have western origins, even though other cultures such as Indian and the Austronesian cultures, had base 10 systems but then it is taken as the only system ever used. If history of number is taught, it would help students perceive that number systems have diverse human contribution and does not have a single western origin. Further, if systems that are not base 10 from different cultures are acknowledged by examples, then the actual underlying concepts inherent in the base 10 system such as composite groups will be further appreciated.
When the history of number is taught, it will show the trend and potential of cultural evolution. All cultures have the potential to evolve and develop, responding to change and exposure of the culture to new ideas and practices. Cultural counting systems were established to sensibly meet the immediate social and physical need to quantify at a particular time and context. However, as cultures changed due to exposure to other cultures, there seem to be a natural mechanism that enables cultures to respond and go through change to accommodate aspects from other cultures. This includes exposure to other counting practices. This evolution is often illustrated with the base 10 system and the use of zero but it would be strengthened by realizing that in places like Papua New Guinea when groups traded they often changed their systems to incorporate features of a neighbouring partner with whom they traded. For example some base 10 systems developed characteristics of base 5 systems while some who had (5, 20) cycle systems included a 10 rather than two fives. Such history will provide an understanding that all cultural knowledge and practice could go through evolution process to improve mathematics. Such a view could help students aim to reflect on their cultural counting practice, take an interest to understand their own cultural practices, compare with others and initiate ways to make their own culture better. This is a process that could build and maintain culture instead of destroying it when the evolution process described earlier is promoted.
When the history of number is taught, it will promote value of all cultural counting systems. Currently, the absence of history of cultural counting systems promotes devaluing of these knowledges and assumes base 10 counting system as superior and the only valued system. All counting knowledge and practices were equally important because they managed to meet the need to quantify cultural purposes successfully. In most indigenous cultures, there was no need to quantify large numbers of items, thus reflected on their counting practices. If there was a new need to quantify large numbers of items, these cultures had potential to initiate additional practices of counting systems to meet the need to quantify large numbers. Most cultures have shown signs of making changes to meet the new modern need, but with connection and continuation from the existing practices (OWENS et al., 2018). The base 10 counting system used at school may have been an advanced system, promoted for its modern convenience to quantify large numbers of items, but it was of no higher value compared to those counting systems as described earlier in indigenous cultures (PARAIDE, 2018). People often recognised and compared large quantities but not necessarily by counting. For example, the space that the objects take up can be used and the size of the bundles of shell money in Tolai and other Oceanic cultural groups. Numbers served the purpose they meant to serve within the context for which they were established. Therefore, through history of counting systems, it will help promote and emphasise how and why each counting system was of equal value in their respective cultures. It will show that no cultural counting practices was better off than the other because all conveniently served cultural needs to quantify. This valuing of culture encourages the identity with culture to influence and strengthen the mathematical thinking identity of the student (OWENS, 2015).
When the history of number is taught, it will establish the connection between mathematics and human reality. The school mathematics is often taught in such a way that it has no connection to reality of life, particularly in cultural groups who have strong non-Western ways of living. In this case, when base 10 counting system is taught without history, it seem to have no human face to the number system and no connection to cultures that contributed. When history of different counting practices and their application in all indigenous culture are taught and compared, it will put a human face to number systems; it will value indigenous cultures which is very important for indigenous societies who have been seriously impacted by colonial influences, invasion and alienation from their land (KNIJNIK & WANDERER, 2010). Furthermore, when comparing different counting systems, it will promote appreciation of counting systems of other cultures. This includes the understanding and appreciation of using base 10 system taught at school, in relations to students’ foundational cultural counting systems. The students, especially indigenous or minority students, not only establish a connectivity with their culture and school mathematics, but also realise how the school counting system is related to their cultural counting systems (PARAIDE & OWENS, 2018). It gives them an opportunity to appreciate how their cultural counting system could be used together with the base 10 counting system in their cultural life and to better understand number systems in general. For example, understanding that their system was based on a 5-cycle system rather than a 10-cycle system emphasises that the grouping variable is significant whether it is 5 or 10. If a hand is used to represent 5 in their oral counting which is often associated with gestures, then representing ten in writing as 10 is just another way of representing. If the number 2 in a (5, 20) cycle system is also used to represent 2 men or 2 twenties then this can be compared to representing twenty as 20 with the 2 carefully placed to the left, in English and European languages, of the zero that is showing no ones. The order of two frame words can be linked to the order of the digits when writing the numeral. Rinsveld et al. (2016) have shown how bilingual students learn other mathematical systems more easily.
Finally, the history of number would not only change views and perspectives of mathematics, but it would impact both teaching and learning of school mathematics. If history of number is taught, the students are given the opportunity to learn from known knowledge in their home culture and language which is real in their life to unknown knowledge of school and thus provide a transition that is meaningful from one language and culture to another. The students will be learning mathematics by first using their known counting systems and leading them into learning unknown mathematics using base 10 counting system. From a constructivist view, the known cultural counting knowledge will play a major role in learning new mathematics using base 10 counting system. There will be a stronger conceptual understanding of counting as a system and of composite groups as an important notion in mathematics. Therefore, if history of number is taught, students make necessary and important connections to base 10 counting system at school, enabling effective learning.
References
ADDISON, David; MATISOO-SMITH, Elizabeth. Rethinking Polynesians origins: a West-Polynesia Triple-I Model. Archaeology in Oceania, v. 45, n. 1, p. 1-12, 2010.
ALLEN, Jim. The pre-Austronesian settlement of Island Melanesia: implications for Lapita archaeology. Transactions of the American Philosophical Society, v. 86, n. 5, p. 11-27, 1996.
ASCHER, Marcia. Ethnomathematics: a multicultural view of mathematical ideas. New York: Chapman & Hall, 1994.
BENDER, Andrea; BELLER, Seighard. Cultural variation in numeration systems and their mapping onto the mental number line. Journal of Cross-Cultural Psychology, v. 42, n. 4, p. 579-597, 2011.
BENDER, Andrea; BELLER, Seighard. Numeral classifiers and counting systems in Polynesian and Micronesian languages: common roots and cultural adaptations. Oceanic Linguistics, v. 45, n. 2, p. 380-403, 2006.
BISHOP, Alan John. Mathematical enculturation: a cultural perspective on Mathematics Education. Dordrecht: Kluwer, 1988.
BISHOP, Alan John. Visualising and mathematics in a pre-technological culture. Educational Studies in Mathematics, v. 10, n. 2, p. 135-146, 1979.
BROUWER, Luitzen Egbertus Jan. Guidelines of intuitionistic mathematics. In: HEYTING, Arend. (Ed.). Philosophy and foundations of mathematics. Amsterdam: North Holland, 1975, p. 123-138.
CRAWFURD, John. On the numerals as evidence of the progress of civilization. Transactions of the Ethnological Society of London, v. 2, p. 84-111, 1863.
D’AMBROSIO, Ubiratan. The history of Mathematics and Ethnomathematics: how a native culture intervenes in the process of learning science. Impact of Science on Society, v. 40, n. 4, p. 369-378, 1990.
DIXON, Roland; KROEBER, A. L. Numerical systems of the languages of California. American Anthropologist, v. 9, p. 663-690, 1907.
DONOHUE, Mark. Complexities with restricted numeral systems. Linguistic Typology, v. 12, n. 3, p. 423-429, 2008.
EVANS, Nicholas. Two pus one makes thirteen: senary numerals in the Morehead-Maro region. Linguistic Typology, v. 13, n. 2, p. 321-335, 2009.
FISHER, John. Enriching students' learning through ethnomathematics in Kuruti elementary schools in Papua New Guinea. In: International Conference on Ethnomathematics, 3, 2006, Auckland. Proceedings ICEM-3: Cultural Connections and Mathematical Manipulations. Auckland: The University of Auckland, 2006, p. 1-17.
HARRISON, Sheldon; JACKSON, Frederick. Higher numerals in several Micronesian languages. In BENDER, Byron (Ed.). Studies in Micronesian Linguistics. Canberra: Pacific Linguistics: 1984, p. 61-79.
HOLZKNECHT, Susanne. The Markham languages of Papua New Guinea. Canberra: School of Pacific Research Studies, Australian National University, 1989.
JETT, Stephen. Diffusion versus independent development: the bases of controversy. In RILEY, Carroll; KELLEY, J. Charles; PENNINGTON, Campbell; RANDS, Robert (Ed.). Man Across the Sea: problems of pre-columbian contacts. Austin & London: University of Texas Press, 1971, p. 5-53.
KNIJNIK, Gelsa; WANDERER, Fernanda. Mathematics Education and differential inclusion: a study about two Brazilian time-space forms of life. ZDM Mathematics Education, v. 42, n. 3-4, p. 349-360, 2010.
LANCY, David. Indigenous mathematics systems: an introduction. Papua New Guinea Journal of Education, v. 14, p. 6-15, 1978.
LEAN, Glendon. Counting systems of Papua New Guinea and Oceania.1992. Thesis (Doctorate in Mathematics). Papua New Guinea University of Technology. Lae.
LYNCH, John. On the history of the Tanna numerals and number markers. Te Reo: Journal of the Linguistic Society of New Zealand, v. 20, p. 3-28, 1977.
MAY, Patricia; TUCKSON, Margaret. The traditional pottery of Papua New Guinea. rev. ed. Adelaide: Crawford House Publishing, 2000.
MIMICA, Jardin. Intimations of infinity: the mythopoeia (cultural meanings) of the Iqwaye counting and number systems. Oxford: Berg, 1988.
MUKE, Charly. Ethnomathematics: Mid-Wahgi counting practices in Papua New Guinea, 2000. Thesis (Masters in Mathematics Education). University of Waikato, Waikato.
OWENS, Kay. The work of Glendon Lean on the counting systems of Papua New Guinea and Oceania. Mathematics Education Research Journal, v. 13, n. 1, p. 47-71, 2001.
OWENS, Kay. Visuospatial reasoning: an ecocultural perspective for space, geometry and measurement education. New York: Springer, 2015.
OWENS, Kay; LEAN, Glendon, with PARAIDE, Patricia; MUKE, Charly. The history of number: perspective from Papua New Guinea and Oceania. New York: Springer, 2018.
OWENS, Kay; LEAN, Glendon; MUKE, Charly. 2-cycle systems including some digit-tally systems. In OWENS, Kay; LEAN, Glendon; PARAIDE, Patricia; MUKE, Charly. (Ed.). History of number: evidence from Papua New Guinea and Oceania. New York: Springer, 2018, p. 41-60.
PANTOFF, Michel. Father arithmetic: numeration and counting in New Britain. Ethnnology, v. 9, n. 4, p. 358-365, 1970.
PARAIDE, Patricia. Indigenous and western knowledge. In OWENS, Kay; LEAN, Glendon; PARAIDE, Patricia (Ed.). History of number: Evidence from Papua New Guinea and Oceania. New York: Springer, 2018, p. 223-242.
PARAIDE, Patricia; OWENS, Kay. Integration of Indigenous knowledge in formal learning environments. In OWENS, Kay; LEAN, Glendon; PARAIDE, Patricia; MUKE, Charly (Ed.). History of number: evidence from Papua New Guinea and Oceania. New York, NY: Springer, 2018, p. 243-269.
PARAIDE, Patricia; OWENS, Kay; CLARKSON, Philip; MUKE, Charly; OWENS, Chris. History of Mathematics Education in Papua New Guinea. New York: Springer (forthcoming).
PAWLEY, Andrew; GREEN, Roger. The Proto-Oceanic language community. In KIRK, Robert; SZATHMARY, EmOke. (Ed.). Out of Asia: peopling the Americas and the Pacific. Canberra: Australian National University, 1985, p. 161-184.
PUMUGE, Hilary. The counting system of the Pekai-Alue tribe of the Topopul village in Ialibu sub-district in the Southern Highlands District, Papua New Guinea. Science in New Guinea, v. 3, n. 1, p. 19-25, 1975.
RAGLAN, Lord B. How came civilization? London: Methuen and Company, 1939.
RINSVELD, Amandine Van; SCHILTZ, Christine; LANDERL, Karin; BRUNNER, Martin; UGEN, Sonja. Speaking two languages with different number naming systems: what implications for magnitude judgments in bilinguals at different stages of language acquisition? Cognitive Processing, v. 17, n. 3, p. 225-241, 2016.
ROSS, Malcolm. Proto Oceanic and the Austronesian languages of western Melanesia. Canberra: School of Pacific Research Studies, Australian National University, 1988.
ROSS, Malcolm; PAWLEY, Andrew; OSMOND, Meredith. The lexicon of Proto Oceanic: The culture and environment of ancestral Oceanic society. 2: The physical environment. Canberra, Australia: Pacific Linguistics, Research School of Pacific and Asian Studies ANU, 2003.
SALZMANN, Zdeněk. A method for analyzing numerical systems. Word, 6, p. 78-83, 1950.
SAXE, Geoffrey. A comparative analysis of the acquisition of numeration: studies from Papua New Guinea. The Quarterly Newsletter of the Laboratory for Comparative Human Cognition, v. 1, n. 3, p. 37-43, 1979.
SEIDENBERG, Abraham. The diffusion of counting practices. University of California Publications in Mathematics, v. 3, 1960.
SMITH, Geoffrey P. S. Morobe counting systems. In: Papers in New Guinea Linguistics. Series A, n. 76. Canberra: Pacific Linguistics, 1988, p. 1-132.
SMITH, Geoffrey P. S. Morobe counting systems: an investigation into the numerals of the Morobe Province, Papua New Guinea, 1984. Thesis (Masters in Language and Communication). Papua New Guinea University of Technology, Lae.
SMITH, Grafton Elliot. The diffusion of culture. London: Watts and Company, 1933.
SPRIGGS, Matthew. Archaeology and the Austronesian expansion: where are we now? Antiquity, v. 85, n. 328, p. 510-528, 2011.
STRATHERN, Andrew. Mathematics in the moka. Papua New Guinea Journal of Education, v. 13, n. 1, p. 16-20, 1977.
TRYON, Darrell (Ed.). Comparative Austronesian dictionary. Berlin: Mouton de Gruyter, 1995.
VAN DER WAERDEN, Bartel Leendert; FLEGG, Graham. Counting 1: primitive and more developed counting systems. Milton Keynes: Open University, 1975.
WILDER, Raymond. Evolution of mathematical concepts. London: Transworld, 1974.
WILLIAMS, Francis. Papuans of the Trans-Fly. Oxford: Clarendon Press, 1936.
WOLFERS, Edwards. The original counting systems of Papua and New Guinea. Arithmetic Teacher, v. 18, n. 1, p. 77-83, 1971.
WURM, Stephen. Papuan languages. In: MAY, Ronald James; NELSON, Hank (Ed.), Melanesia: Beyond diversity. Canberra: Research School of Pacific Studies, Australian National University, 1982, pp. 225-240.
WURM, Stephen; LAYCOCK, David; VOORHOEVE, Clemens; DUTTON, Thomas. Papuan linguistic prehistory, and past language migrations in the New Guinea area. New Guinea area languages and language study. Vol. 1: Papuan languages and the New Guinea linguistic scene, Pacific Linguistics v. C-38. Canberra: Research School of Pacific Studies Australian National University, 1975, p. 935-960.
ZASLAVSKY, Claudia. Africa counts: number and pattern in African culture. Boston: Prindle, Weber and Schmidt, 1973.

