1 Introduction
Acknowledging children’s linguistic,
intellectual, cultural and social resources is deemed as central in the process
of developing an educational environment that is inclusive of students’
experiences at home and in their communities (MOLL, 1992). In mathematics
education, besides considering children’s funds of knowledge, it is
important to include open tasks offering students multiple ways of engaging in
mathematics, as well as to make sense of these tasks by engaging in
mathematical meaning-making activity (LESH et al., 2000;NGACBP, 2010). Integrating these perspectives in the
preparation of pre-service teachers represents both a great potential and a
challenge.
This paper describes Ethnomathematics as an
important approach in teacher preparation to support this link, since
Ethnomathematics represents a “way that
members of various cultural groups mathematize their own reality because it
examines how both mathematical ideas and practices are processed and used in
daily activities” (D’AMBROSIO &
ROSA, 2017, p. 288). More specifically, this manuscript describes the
challenges and affordances that a group of pre-service teachers (PSTs),
participating in a mathematics teaching methods course, faced creating and
developing tasks that were sensitive to their students’ culture, language,
interests and experiences. The analysis of PSTs’ work on ethnomathematical
approaches provides an insight of how PSTs’ are bridging children’s funds of
knowledge and mathematics during their design of ethnomathematical
activities.
Ethnomathematics
is a term introduced by Ubiratan D’Ambrosio
(1991) to describe the techniques used to explain, understand and cope with
reality in order to survive across diverse communities. Ethno
relates to the members of distinct groups identified by cultural traditions,
codes, symbols, myths and specific ways of reasoning and inferring (D’AMBROSIO,
1985). As Ethnomathematics centers on the mathematizing of frequent activities
in specific communities (D’AMBROSIO
& ROSA, 2017), such stance highlights mathematics as a cultural practice
existent in human activity and challenges the perspectives that present
mathematics mainly as a Western — Roman, Greek — knowledge, commonly taught at
school.
An
ethnomathematical approach helps us understand mathematics from a wider
perspective than traditional school mathematics, seeing mathematics as a human
act. As a result, Ethnomathematics can help us renovate the way we teach
mathematics (LANGE, 1996;D’AMBROSIO & ROSA,
2017). In mathematics teaching and learning, Ethnomathematics helps us:
expand, affirm and redistribute mathematical authorship and
empowerment; draw from and expand resources to teach and learn mathematics;
recognize and challenge spaces of marginality of knowledges of many
communities; and strengthen the relationship between learners and mathematics (AGUIRRE,
INGRAM-MAYFIELD & MARTIN, 2013; KOKKA, 2015).
Such approach should “perpetuate and foster — to sustain — linguistic,
literate and cultural pluralism that are part of schools” (PARIS, 2012, p. 93). Thus,
when students and teachers use their real world as a starting point for conceptual
development, mathematics teaching and learning become more complex (LANGE,
1996) as they also become doers of mathematics (NCTM, 2000) by engaging in
problem solving, multi-modal representations and communication to develop
mathematical meaning making and mathematize through their own perspectives (NGACBP, 2010;FREUDENTHAL, 1973).
2 Context of the Study
This study includes the work with PSTs in a mathematics teaching methods
course within a teacher-preparation initiative named TECLA (Teacher Education Collaborative in Language
Diversity and Arts Integration) project. TECLA project is the result of the
collaboration of seven professors in a United States (US) southwestern
university across two different colleges and three different departments.
Professors worked with the group of PSTs at different times along the three
semesters that PSTs spent in TECLA as part of their Elementary Education
undergraduate degree program.
The project focuses on a collaboration process among the professors that
designed the program structure for the PSTs by integrating the content of their
courses and field experiences. This collaboration is also extended to the
relationship developed between the Cooperating Teachers at the hosting school
and the PSTs planning and co-teaching since the first day of the PSTs’ field
work. There were also an Arts and Curriculum teacher and a graduate student,
who collaborated with the Cooperating Teachers, PSTs and professors, bridging
together the work of everyone in the project and guaranteeing the extended
integration of all activities in the project. Although the project’s general
approach relates to an Arts-Integration (FALTIS, 2019;MARSHALL & DONAHUE,
2014), at the center of there is a social-justice goal that focuses on the
linguistic and cultural diversity of the students’ background at the hosting
school.
The project hosted at an Elementary School, La Montañita,
which is a community school that has Spanish-English, Navajo-English bilingual
programs and welcomes a great diverse student population. According to the
school district data, this school includes students who are 86% Hispanic, 7%
American Indian, 3.5% African American, 2.6% White and 0.8% Asian.
Additionally, a great influx of refugees and immigrants and also languages
characterize students’ population at this school. The PSTs’ program in TECLA
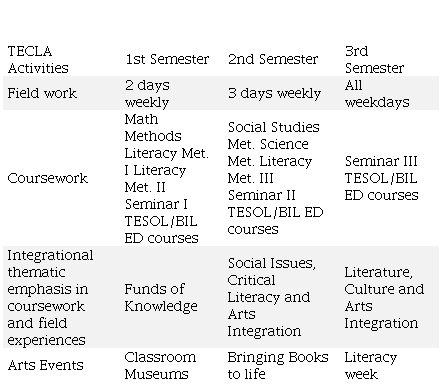
project is described in Table 1 below.
Table 1
Timeline of PSTs’ expected work and activities in TECLA
 Elaborated by the
Author
Elaborated by the
Author
|
TECLA
Activities
|
1st
Semester
|
2nd
Semester
|
3rd
Semester
|
|
Field work
|
2 days weekly
|
3 days weekly
|
All weekdays
|
|
Coursework
|
Math Methods
Literacy Met. I
Literacy Met. II
Seminar I
TESOL/BIL ED courses
|
Social Studies Met.
Science Met.
Literacy Met. III
Seminar II
TESOL/BIL ED courses
|
Seminar III
TESOL/BIL ED courses
|
|
Integrational thematic
emphasis in coursework and field experiences
|
Funds of Knowledge
|
Social Issues, Critical
Literacy and Arts Integration
|
Literature, Culture and
Arts Integration
|
|
Arts Events
|
Classroom Museums
|
Bringing Books to life
|
Literacy week
|
As shown in Table 1, PSTs
in the Mathematics Methods course focused on “Funds of Knowledge” as a
generative and integrative topic across coursework and field experiences. The
group of PSTs described in this manuscript includes: 4 male (1 Hispanic and 3
White) and 18 female (10 Hispanic and 8 White) college students in the
Elementary Education Program. Only 6 PSTs were bilingual (Spanish and English).
All PSTs were their first semester of the program and fieldwork, which includes
two full days at school. PSTs taught in K-5 grades: 5 in Kindergarten, 4 in
first grade, 6 in third grade, 4 in fourth grade and 3 in fifth grade. Funds of
Knowledge served as a framework/theme integrated across the methods courses
during the first semesters; this thematic emphasis varied in the next two
semesters. This study reports PSTs’ work only during the first semester.
Consequently, language and
culture were explored along the entire mathematics methods course, though this
course curricular structure addressed aspects related to: mathematics reform
such as mathematics processes and teaching standards (NCTM, 2000), mathematical
practices and emphasis on problem solving (NGACPB, 2010;VAN DE WALLE, KARP
& BAY-WILLIAMS, 2013), Cognitively
Guided Instruction, valuing and building on children’s thinking and reasoning
(CARPENTER et al., 2014;FOSNOT & DOLK, 2001), facilitation of mathematics instructional conversations
(CHAPIN, O’CONNOR & ANDERSON, 2013;PARRISH, 2014), promotion and development of mathematical discourse (MOSCHKOVICH, 2002), collaborative learning (LOTAN, 2003), planning and
selecting worthwhile mathematical tasks (STEIN et al., 2000).
This curricular structure was aligned with the generative topic
supported by TECLA and the course content integrated language and culture
perspectives as follows. In the first module: perspectives of English learners
(ELs) (RAMÍREZ & CELEDÓN-PATTICHIS, 2012), different mathematics algorithms
in Latin America (PERKINS & FLORES, 2002), suggestions for working with ELs
(BRESSER, 2003;GARRISON & MORA, 1999;MOSCHKOVICH, 2013), applications of
mathematics to real-life events and community (LO CICERO, FUSON & ALLEXSAHT-SNIDER,
1999;SIMIC-MULLER, TURNER & VARLEY,
2009), students’ mathematical identities (BOALER & GREENO, 2000), walk
through the community and charlas (forums)
with mothers of students at La Montañita.
Then, two consecutive modules address the mathematical educational concepts
described above, always focusing on students and their community.
Consequently, students’ funds of knowledge in mathematics were addressed by PSTs through reading, thinking about, observing and reflecting on the community. PSTs often need to learn about both the mathematics reform ideas and funds of knowledge. The process of bridging these topics seems overwhelming, so the class conversations and reflections took more time than expected. As an instructor, I worry about integrating students’ funds of knowledge in mathematics teaching (GONZÁLEZ et al., 2001), ethnomathematics, through the development of community mathematization projects, and the “mathematical” teaching practices described in Principles to Actions’ (2014), mainly problem solving and their relevance in nurturing children’s reasoning and understanding.
Nevertheless, once PSTs engaged with these integrated perspectives, they started making clear connections across course modules and in their teaching practices construction they collaborated with each other and encouraged peers to incorporate children’s thinking, language, funds of knowledge, self-perception in mathematics and problem-solving strategies. As a result, PSTs helped me to realize that in a mathematics-methods course the focus is on children — who they are, where they come from, what they care about, what they know, what is going on around them. This is the essential foundation of all academic and pedagogical content knowledge for teaching mathematics.
3 Mathematics Teaching, Funds
of Knowledge, and PSTs’ Preparation
Investigations about students’ funds of knowledge highlight the
relevance of an education that actively includes students’ community,
backgrounds and language in the teaching and learning of school contents and
languages. Funds of knowledge(MOLL &
GREENBERG, 1990) include “the knowledge base that underlies the productive and
exchange activities of households” (MOLL & GONZALEZ, 2004, p. 700). Funds of knowledge are not possessions
of people in the family; instead they are “part of what people do in activities”
(MOLL, 1992, p. 222); they refer “to the content and the social relationships
that facilitate the exchange” (p. 231). Such knowledge and social relationships
are flexible and adaptive, so they can be mobilized across contexts and
activities, including mathematics learning and teaching (GONZÁLEZ et al.
2001; MOLL & GREENBERG, 1990; MOLL, 1992).
Students’ funds of knowledge are linked to pedagogies valuing
diverse students’ life experiences and communities which were deemed from
deficit views. Culturally Relevant Pedagogy (CRP) is defined ‘‘as using the
cultural knowledge, prior experiences, frames of reference and performance
styles of ethnically diverse students to make learning encounters more relevant
and effective for them’’ (GAY, 2000, p. 29). CRP encompasses a process through
which all students have the opportunity to experience academic success, develop
and/or maintain cultural competence and develop a critical consciousness
through which the status quo of the current social order is challenged
(LADSON-BILLINGS, 1995). CRP perspectives have evolved into complex constructs
that acknowledge societal power structures, so that the emphasis is placed on
an integrated and sustainable
development of cultural and academic competences of students:
The term culturally sustaining requires
that our pedagogies be more than responsive of or relevant to the cultural
experiences and practices of young people — it
requires that they support young people in sustaining the cultural and
linguistic competence of their communities while simultaneously offering access
to dominant cultural competence (PARIS, 2012, p. 95).
Several approaches in
mathematics education specifically addressing the link between minoritized and
dominant cultural competences have emerged. For example, Gonzalez et al.
(2001) describe a ‘Zone of Mathematical Practice’ as an interactional space
where the following processes take place: (a) the development of
inter-subjectivity, sense making in joint activities with others, (b) equalized
social interaction, equal validation of participants, (c) a kind of mathematics
that is playful, accessible and ‘natural’, and (d) funds of knowledge
are transformed into meaningful activity in mathematics. Many of these
approaches have highlighted the role of parents and community members in
mathematics education of children from cultural and linguistical diverse
communities (CIVIL & BERNIER, 2009;CIVIL, BRATTON & QUINTOS, 2005;
CIVIL & QUINTOS, 2006).
Aguirre (2012) suggests a Culturally Responsive Mathematics Teaching (CRMT) approach with two main goals: (a) students’ development of mathematics thinking and (b) equity in mathematics classroom. As so, for the implementation of a CRMT approach teachers need to develop specific pedagogical knowledge, dispositions and practices that mobilize students’ funds of knowledge, nurture their mathematical thinking and promote social justice in mathematics education.
In consequence, this study’s theoretical framework is founded on the explicit acknowledgment of the participants’ linguistic, intellectual, cultural and social knowledge in mathematics education. For example, Moschkovich (1999) recommends that when working with Latinx[1] students, mathematics teachers should: (a) honor the diversity of Latinx students’ experiences, (b) know the students, (c) avoid deficit models, and (d) provide opportunities for mathematical discussions. Regarding the preparation of PSTs, it means that they need to engage in an explicit work and understanding on how to bridge students’ funds of knowledge and mathematics. This means that PSTs need to work at the borderlands or liminal spaces of thinking about both their students and mathematics, linkage which is mediated by PSTs themselves.
Thus, who PSTs are is a crucial element to this linking process.
PSTs need to work as Nepantler@s. Nepantler@s,
according to Anzaldúa, travel in many disciplines to “invent holistic,
relational theories and tactics enabling them to reconceive or in other ways
transform the various worlds in which they exist” (KEATING, 2006, p. 9) to
support bridges between students’ lives and school. Only a careful ethnographic
analysis of the transmission of these resources at home and their application
into school instruction will support a convincing demonstration of children's
knowledge in their academic performance (MOLL, 1992). Moreover, besides PSTs’
inclusion of children’s funds of knowledge, in mathematics education
designing open tasks is also important since they offer students a context to
engage with mathematics, to make sense of it and engage in mathematical
activity (LESH et al., 2000; NCTM, 2000;NGACPB, 2010).
In my opinion, it is through the inclusion of the learner’s prior
perspectives that school mathematics becomes integrated with the learner’s
knowledge basis. In mathematics education several approaches have targeted the
link between school and community mathematics; for example, Ethnomathematics
(D’AMBROSSIO, 1991), Realistic Mathematics Education (RME) approach (WEBB, VAN
DER KOOIJ & GEIST, 2011) and mathematization processes (GRAVEMEIJER, 1997).
In RME, “students connect prior knowledge to new mathematical representations,
concepts and skills.
As a result, a more robust way of knowing and doing mathematics is constructed from the student’s perspective” (WEBB, VAN DER KOOIJ & GEIST, 2011, p. 48). The realistic portion does not necessarily imply connections “with real world contexts, but it is related to the emphasis that RME puts on offering students problem situations which are imaginable” (WEBB, VAN DER KOOIJ & GEIST, 2011, p. 48) or realistic in the view of the students. When students engage in mathematical tasks that blur borders and become relevant to students and their social interactions, then tasks promote the emergence of a “zone of mathematical practice” (GONZÁLEZ et al., 2001).
Holistically, the conceptual framework in this study centers on how PSTs mathematize their own reality and their students’ reality in order to promote mathematical tasks that overcome the borders that school mathematics often places between students’ daily life and mathematical activities and practices (D’AMBROSIO & ROSA, 2017).
Some works in mathematics education have explored how PSTs have grappled in linking mathematics and the community. For example, Drake and Norton-Meier (2007) promoted PSTs’ awareness of family and community resources by integrating mathematics and literacy and by linking family and community funds of knowledge with school-based content in the methods course. They describe how 51 PSTs learned, experienced and enacted these overlaps by interacting with parents during the planning and lessons implementation.
Authors found that for PSTs there are evident links between mathematics and literacy but the “boundaries between funds of knowledge and academic content proved to be quite rigid and very difficult to cross in the context of a one-semester course” (D’AMBROSIO & ROSA, 2017, p. 188). Nonetheless, the authors describe that the overlap of contexts created potential connections across contexts for PSTs to promote better connections between the community and school mathematics.
Also, Aguirre, Zavala and Katanyoutanant (2012) described how a mathematics methods course emphasizes the connections among mathematics, children's mathematical thinking, children's funds of knowledge and mathematics for social justice. Through mixed methods the authors found that PSTs has given more explicit attention to issues associated with children's mathematical thinking and their academic language by integrating cultural funds of knowledge, than issues related to mathematics for social justice. Nevertheless, those issues were possibly linked to pedagogical rather than ideological challenges.
Finally, Aguirre et al. (2013) describe how 70 PSTs from three universities visited community settings and developed problem-solving mathematics lessons that linked mathematical practices to the community settings. In this analysis, the authors identified three levels of these connections (i.e., emergent, transitional and meaningful). These connections showed different levels of consistency in addressing both children’s mathematical thinking and funds of knowledge in their teaching.
4 Methods and Data Sources
Content analysis process is a “technique for making inferences by objectively and systematically identifying specified characteristics of messages” (HOLSTI, 1969, p. 14). In order to explore the processes of integrating children’s funds of knowledge with school mathematics, as well as how the 22 PSTs understood these processes as part of their mathematics teaching practices with bilingual and bicultural students, I used content analysis.
I qualitatively analyzed the first-semester PSTs’ assignments, such as module reflections, the community-based lesson (CBL) paper and their journal reflections, taken during course classes and fieldwork experiences, as well as the instructors’ field notes. The CBL paper was developed by PSTs through interviews with their students and observations of them during class and breaks. Some of them also consulted the cooperating teachers.
The initial themes of the
analytical process were related to the content either of the task/problem that
PSTs developed or their reflections linking students’ funds of knowledge with
mathematics teaching and learning. A second level coding yielded overarching
themes that are described in this paper and which are illustrated through
examples that come from PSTs’ work. While PSTs’ gender did not represent a
major variable for these patterns, PSTs’ cultural and linguistic backgrounds
had a more significant but still not consistent role across cases.
5 Results
Three themes permeated
PSTs’ transformative knowledge and actions in mathematics education: (a) finding links between students’ funds of
knowledge and mathematics- PSTs’ investigations about their students’ funds
of knowledge revealed various potentially-rich contexts and practices that
could support links between school and community mathematics; (b) developing
these links based on PSTs’ personal experiences-while some PSTs
acknowledged the identified contexts or practices related to the students’
funds of knowledge or community wealth, PSTs used their ideas and experiences
to present these links; and (c) developing these links by mathematizing
student-centered experiences-PSTs used student-relevant potentially
rich-mathematical contexts as sources for students’ mathematical
investigations and problem solving, The
inclusion of students’ experiences linked more directly students’ personal
identities and funds of knowledge and to seeing themselves as doers of
mathematics. Each of these themes is described below with examples of PSTs’
work.
5.1 Finding Links Between
Students’ Funds of Knowledge and Mathematics
Through interviews and
classroom activities, PSTs’ developed an inquiry about their students’ funds of
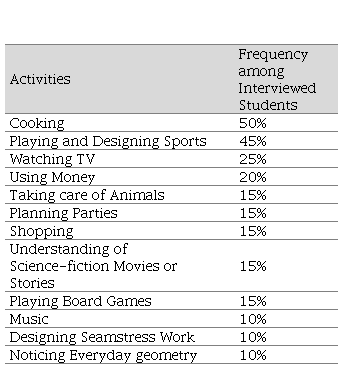
knowledge, which served as a foundation to develop mathematical tasks. Table 2
presents a list of twelve activities that PSTs identified as potential sources
to establish connections between students’ funds of knowledge and
mathematics. This list describes human activities that resemble Bishop’s (1988)
list of mathematical activities across cultures, which include: Counting,
Locating, Measuring, Designing, Playing and Explaining. For example, cooking
includes measuring, sports can include several of these activities, using money
includes counting, etc. The activities that children reported engaging in at
home include thinking and actions that while not explicitly and deliberately
linked to school mathematics, they are still mathematical.
Table 2
Activities
PSTs’ Found to Link Mathematics and Funds of Knowledge
 Survey Data
Survey Data
|
Activities
|
Frequency among
Interviewed Students
|
|
Cooking
|
50%
|
|
Playing and Designing
Sports
|
45%
|
|
Watching TV
|
25%
|
|
Using Money
|
20%
|
|
Taking care of Animals
|
15%
|
|
Planning Parties
|
15%
|
|
Shopping
|
15%
|
|
Understanding of
Science-fiction Movies or Stories
|
15%
|
|
Playing Board Games
|
15%
|
|
Music
|
10%
|
|
Designing Seamstress Work
|
10%
|
|
Noticing Everyday
geometry
|
10%
|
Learning about students’ funds
of knowledge started PSTs’ borderlands’ journey to start developing links
between school and community mathematics. Thus, PSTs were challenged to design
mathematical tasks that could mobilize these community activities and
knowledges into school mathematics concepts. Among the repertoire of funds
of knowledge that PSTs recognized in their students related to ideas
described in the course readings. For example, the fact that algorithms and the
writing of numerical symbols vary across cultures and countries. Marta, in her
reflection of module 1, made connections to the course reading of Perkins &
Flores (2002), describing algorithms in Latin America:
Marta: This was very surprising
to me, but I was able to see firsthand some of these important differences. A
girl in my assigned classroom is new to the United States from Ecuador, and
while I was helping her with math I wrote a 7 (uncrossed) and she read it as
a one, I am still getting used to the way she writes her 1s, which, to me,
look sometimes like 7s. Respect means that teachers will not negatively view
the knowledge (or funds of knowledge) that students bring to the classroom,
but will instead use them to aid the education process. Respect also means
eliminating “the notion that methods used in schools in the United States are
inherently better” (Perkins and Flores, p. 124).
PSTs’ reflections on
students’ funds of knowledge were extended, not only through readings, but
also through their own experiences with their students. These reflections
included also the process of devising and designing responsive mathematical
tasks. Andrea reflected on how she envisioned the possible mobilization of
students’ funds of knowledge in mathematics by addressing beyond the
content of her students’ funds of knowledge:
Andrea: The perfect way to
motivate students and create a complexity of literature is by learning how to
mobilize funds of knowledge in a classroom. The way I plan to mobilize funds
of knowledge in my class is by pulling each student own experiences to help
them like math. For example, if a student comes from a family where they own
a business then this child must know some type of math. I can relate back to
him and say for example, “Well Johnny you know how your dad owns a store, how
does he add up all the money in the cash register? Maybe you can help us
teach addition today.” Another great idea would be to invite Johnny’s dad
into the class as a guest speaker so that he can briefly explain how he
conducts such task. By creating social interactions, funds of knowledge can
easily be mobilized to benefit our students.
Andrea’s argument supports
the notion that funds of knowledge are not simply related to “what” or
the content of an activity in the life of a student, but also to the kind of
social relations that both generated and mobilize those ideas. In this way,
empty uses of “whats” would be insufficient if they
are not supported by social interactions that nurture them to get into the new
context of learning school mathematics.
Although PSTs developed stances about how they would address the bridging of student experiences and mathematics, PSTs’ prior experiences in mathematics also affected how they conceptualized a mathematical task. Then, the levels of risks they took to mathematize a -potentially-rich-mathematical activity related to students’ funds of knowledge was constrained by how PSTs self-received in relation to mathematics. These relations were informed by their experiences with school mathematics.
Thus, I find it crucial to consider PSTs’ emotional landscape as a baseline to engage in the design of mathematical tasks. As a result, PSTs’ lived experiences in school mathematics had a major influence in their level of freedom to go beyond traditional school mathematics. 90% of PSTs argued to have experienced a memory-based mathematics instruction and not being able to develop positive identities as doers of mathematics. Their idea about what mathematics teaching and learning was partly renovated as they took mathematics content courses in their Elementary Education Program. Viviana’s excerpt describes her experience as a student:
Viviana: I struggled a lot.
Information just did not stick. Math was the only subject that I did not
excel in, which made for a very sad, young little girl. I felt unintelligent
and that my input, opinion or thoughts were not necessary or needed. Instead
of being the student who felt confident to raise her hand and answer
questions, be the Math group leader, or the student who was happy to see her
test scores; I was the one who sat passively year after year, dreading Math
class, being so nervous the night before a test that I could not sleep.
Experiences such as
Viviana’s were not uncommon among PSTs. These situations highlight that at the
borderland of linking school and community mathematics, PSTs grapple with more
than just establishing a link. They need to face who they think they are in relation
to mathematics. Furthermore, as these borderlands also include the linking of
cultural practices, the connection that PSTs noted between their experiences
and their students’ was affected by their perceived
connections between self and the students’ community. It is further described
next.
5.2 Developing Links between
School and Community Mathematics Based on PSTs’ Experiences
As PSTs developed of
mathematical tasks related to what they had learned about their students’ funds
of knowledge, these tasks were not always directly linked to the students’
but rather PSTs’ experiences. For example, some PSTs identified music and
sports as important activities related to their students’ funds of knowledge;
however, during the development of mathematical tasks some PSTs drew from their
own funds of knowledge and experiences instead of from their students’.
The work of Daniel and Diane represent this situation.
They made use of their
prior experiences and knowledge to link what they found about their students’ funds
of knowledge. Daniel — a PST who enjoys music very much, after realizing
that the students he interviewed enjoy music also — developed
a task linking music and mathematics. He worked in Kindergarten and needed to
teach about patterns. Daniel linked the concept of patterns with music through
a task of using pattern blocks and linking each shape to an action or sound, so
that the shapes could be sequenced in different patterns to create patterns of
shapes and rhythms or ‘music’.
 Figure 1
Pattern blocks used to explore mathematical and rhythmic
patterns
Figure 1
Pattern blocks used to explore mathematical and rhythmic
patterns
Daniel: The activity will have
students to understand what a sequence is. For example, I will say clap,
clap, legs, legs, feet and feet. I will repeat this sound sequence twice and
students will try to remember this pattern of counting. Another example could
be feet, clap, clap and feet, also repeated twice. This task allows students
to learn the importance of counting in the rhythm of songs. Notice that if
one student forgets to count the sequence correctly, he will lose the rhythm
of the song. However, it doesn’t mean that he can’t figure out the sequence
in the right order after he got lost.
When Daniel implemented this task, he modeled to students how to create rhythms. Students were able to decide the arrangement of the shapes and what they represented. In this way, students “wrote” different patterns and rhythms. This task promoted student participation and motivation in pre-algebraic thinking. While this task related to music, the task itself did not directly align to students’ experiences with mathematics, but to Daniel’s adaptation of musical rhythm represented through shapes.
In the case of Diane, she found out that her students like soccer, used the idea of soccer not to create a soccer embedded mathematical task. Instead she developed a task/game in which students imagined that they were playing soccer and annotated a goal by responding to a question related to a mathematical operation, like “what is 5 times 5?”. Another PST also used a golf game board in which students could move along the board by responding to subtraction operations. In the two cases students did not engage in the games as expected by PSTs. It is not sure whether students viewed the tasks as related to the sports they like.
Some PSTs could not find ways to link more directly their students’ funds of knowledge with mathematics; and instead they developed mathematical tasks that were superficially related to funds of knowledge and required low levels of cognitive mathematical reasoning. This lack of social and mathematical authenticity relates to the fact that the activity of playing soccer or golf is not the same as playing a board game that relates to golf or soccer; even the mathematics involved in soccer does not relate to answering to basic facts fluently. A board game is another activity that might not always be significant to the students. Funds of knowledge are to be transformed into meaningful activity in mathematics, these include activities people do in a community and to the content and the social relationships in those activities (GONZALEZ et al., 2001;MOLL, 1992).
It is not only to be
responsive or relevant to a cultural content, experiences or practices of a
community, a culturally sustaining approach requires to sustain the
cultural and linguistic competence of the communities while simultaneously offering
access to academic competence (PARIS, 2012). This situation makes one wonder
about what needs to happen so that PSTs find relevance between their students’ funds
of knowledge and their own? How does this connection facilitate the process
of establishing these nuanced links? What is the actual issue? Drake and
Norton-Meier (2007) have found rigid boundaries between funds of knowledge
and academic content. Daniel was able to find links between music and
mathematics due to his familiarity with both, but he was not as successful in
bridging this familiarity with his students’.
Diana on the other hand was
not familiar with soccer but instead she was more familiar with game boards,
which is what she used. She also could not find a direct mathematical connection
to the game, so she resourced on basic mathematical facts. These ideas speak to
situations when adaptations of mathematical problems to make them culturally
responsive by simply changing some names or words in the word problem. This
adaptation focuses on what without acknowledging the social dimension of those
activities that characterize the meaningfulness of the activity to the
community.
Further, familiarity with
mathematical content and what helps students learn mathematics are important
knowledges that can better support PSTs’ development of mathematical tasks.
Diana reflected on these points in her following assignment as she focused more
on the mathematics and less on the cultural responsiveness of a mathematical
task. It takes explicit reflection and experience with who students are and
their ways of learning. More studies exploring bridges between PSTs’ funds
of knowledge and their students’, especially how PSTs cope with these
differences as well as the quality of connections established between the
mathematical task and the activity related to the students’ funds of
knowledge are needed.
6 Developing Links between
School and Community Mathematics Based on Students’ Experiences
The relevance of a
Culturally Responsive Mathematics Teaching (CRMT), which is based on the need
of a genuine exploration of students’ funds of knowledge; especially of those
from minoritized groups, was evident to all PSTs. This relevance had different
connotations. Some PSTs have had personal experiences that informed them
directly about the importance of addressing student’s diversity in the teaching
of mathematics. PSTs wanted to
make a difference and effect changes in education, so that education would be
more inclusive of students’ experiences, cultures and languages. Laura’s
comment extends this argument beyond mathematics education:
Laura: This is something I
always struggled with in school because it felt like in every class the material always focused on my white counterparts’
lives and it was just something that made me not interested in school.
However, one thing I might add and caution future teachers, even myself, is
to not try and make the problem without finding out about students’ lives,
meaning don’t just add a problem about making tamales because you have a
Latino student and assume he makes them on his spare time.
To Laura, knowing students is of great importance to guide teachers’ teaching and curricular adaptations away from essentialist cultural perspectives based on their students’ backgrounds. Instead, Laura called for a more authentic process of getting to know her students. Laura’s insights derived from her own experiences as a Latina student. Her familiarity with this issue granted her with awareness about important aspects of being a teacher with this student population.
Such stance has been documented with Chicana teachers whose identities and previous experiences contribute to how they define their professional role in relation to students from a similar cultural minority background as well as their awareness of the challenges that minoritized students face (GALINDO, 1996). As a result, Laura’s adaptation of mathematical tasks, drew from non-essentialistic students’ funds of knowledge of Latinx students. She worked with a group of girls mathematizing formations and positions for a cheerleader presentation. Students used mathematical activities such as measuring time and designing symmetric formations
Brisa’s teaching experience speaks
to a similar situation. Nevertheless, as she was working on perimeter and
diameter of geometric shapes, she wanted her students to apply and reinforce
such concepts and ideas. Looking for challenging experiences for 5th
graders and having mathematical explorations outside of the classroom, she
noted maple trees around the school playground. Furthermore, aware of students’
funds of knowledge reports on exploring geometry in nature and that students
needed to study plants in Science. She developed a task — ‘how much a maple
leaf measures?’ —, in which
students had to find the area and perimeter of a leaf.
To solve the task, students had to
use unconventional unit measures. When, Brisa asked how they would measure the
leaf’s perimeter and area, students resourced to using the squares on a sheet
of grid paper as unit of measurement. Arguing that the edge or margin of the
leaf is the perimeter, and the area is the lamina or blade of the leaf. Figure
2 below presents an example of students’ work on this task. Note that students
differentiated between the two-dimensional aspect of the measuring of area as
it covers entire squares, while the perimeter related only to the length of a
side of the square.
 Figure 2
Brisa’s task, finding the area and perimeter of a maple leaf
Figure 2
Brisa’s task, finding the area and perimeter of a maple leaf
In a personal reflection about
teaching field experiences, Brisa mentioned: “I enjoyed my math methods class
because it was at La Montañita. It gave me a
real feeling of being in a classroom with kids that put myself out of my
comfort zone”. In Brisa’s reflection, we observe how PSTs’ self-concept in mathematics serves
as a starting platform in the borderline to start developing sensitive links
between the students’ ideas and mathematics. Further, as Brisa took risks and
engaged in developing mathematical experiences more tangible and meaningful for
her students, students participated more enthusiastically and genuinely to the
point that they learned and showed their learning and desire in completing the
task in the best way possible. In turn, Brisa’s confidence in doing and teaching
mathematics also increased. Thus, I think that as we attempt to blur boundaries
between school mathematics and our students, we also blur those boundaries for
ourselves as mathematics teachers. Both students and Brisa remarked feeling
more competent in mathematics by engaging in such application of
mathematics.
Another daily activity that
was very common among students from the school was the watching of TV programs.
However, the pool of TV programs that they had watched was very diverse. For
example, Surama found that students from Mexican
background in her class enjoyed watching the program “El Chavo
del 8”. Consequently, Surama decided to use this
context to design a mathematics problem. Knowing that El Chavo
is always hungry and that divind chocolate bars can
lead into thinking about fraction, she had students think of the characters
wanting to share a chocolate bar, so students came up with the following
problem:

This problem presents multiple entry points to solve it, but it also
requires a high level of cognitive reasoning because students are engaged in
“doing mathematics” (STEIN et al., 2000). Students mathematized the
division of the chocolate bar by either dividing it into fractions or using the
already embedded structure of this composite unit. Although the mathematical
concepts embedded in this problem were rich, the content and social
interactions of the problem also showed the type of jokes and interactions that
exist in El Chavo program.
This speaks that the
content of the program was left and used as it is, but it served as a context
to creating a problematic situation that resembles common situations in the
practice or TV program that students are familiar with. Further, the use the
characters’ gender in Spanish, as in the case of El Profesor Jirafales and La Popis, was
the result of students knowing and liking the show. Surama
herself was familiar with both the TV program and fractions. As a result, we
note how PSTs make use of their own funds of knowledge to design
mathematical tasks that were culturally responsive to their students’ funds of
knowledge.
I learned that while PSTs
from similar linguistic and cultural backgrounds as their students’ had a
critical awareness, PSTs from mainstream, White backgrounds, also developed
responsiveness (LADSON-BILLINGS, 1999) by intentionally learning about these
students and developing a genuine commitment to implementing teaching practices
that supported who the students are. Most of PSTs successfully integrated
student’s funds of knowledge and mathematical concepts such as basic
operations, fractions, measurement, geometry, money value and exchange, number
sense, modeling, patterns, estimation and decimals. However, this integration
also showed the establishment of links with PSTs’ funds of knowledge.
For example, Hispanic PSTs had similar experiences to those from Hispanic
students they interviewed.
7 Concluding Remarks
“Successful cases of integration are characterized by ‘transformative
practice zones’ that ‘provide spaces to share and listen to others’ ideas,
visions and commitments, and to build relationship in collaboration across
disciplines” (BRESLER, 2003, p. 24). I learned through the PSTs I worked with
that when we take risks working to blur the borders between mathematics and
students’ experiences, we also blur those borders for and within ourselves.
Therefore, we are contributing to a renovation of how we see ourselves as
mathematics’ doers and especially as mathematics’ teachers. A stronger and
closer relationship with our students and mathematics is revealed in our eyes
and in our heart, just as Brisa described.
Moll (1992) and colleagues have argued that the ultimate goal of these
innovations “depends on when and how teachers become part of the decision to
initiate change” (p. 229). This study describes an evolving commitment of PSTs
towards educational changes that place students’ own knowledge at the center of
mathematical education. Although PSTs’ efforts to support their students’
mathematical learning in their students’ funds of knowledge were
evident, it was also clear that in the process of developing the mathematical
tasks PSTs’ funds of knowledge played an important role too. Most of the
PSTs (20/22) were actually able to bridge school mathematics, realistic
mathematics applications and students’ funds of knowledge.
At a certain point, PSTs found some kind of familiarity during the design of the mathematical tasks because their prior experiences as students somehow resembled their students’ activities, although the content could not exactly be the same. For example, Daniel’s familiarity with music, not necessarily the same type of music of his students like, helped him to see potential links between sounds, rhythm and mathematical patterns.
Nevertheless, some PSTs with least familiarity with students’ funds of knowledge faced greater challenges trying to establish these links. They designed tasks with less realistic applications and with lower levels of cognitive reasoning(STEIN et al., 2000). Like Aguirre, Zavala & Katanyoutanant (2012), questions related to these shortcomings should be explored in relation to pedagogical issues. Perhaps, it might be helpful for PSTs’ to engage in a more ethnographic approach to understand the diverse community practices and activities that are unfamiliar to them, so they can get better ideas to establish these links.
Mathematics methods courses could help PSTs to develop this type of
awareness and also strategies to develop mathematical tasks that are inclusive
in terms of their students’ funds of knowledge. One way to establish
connections with unfamiliar activities perhaps could be through engaging in an
Extended Related Activity (see LÓPEZLEIVA, 2014) that could help us to become
more familiar with the diverse community activities and mathematize them.
Another way to get to know students better (MOSCHKOVICH, 1999) could be
by developing a mutual learning process between PSTs and students they work
with. That way PSTs learn about their students through the development of a
closer relationship with one student or more. This resembles Moll’s household
visits and interviews with parents, so that PSTs could learn more about
community practices and knowledges.
The goal of Mathematics Teacher Education is to take an
ethnomathematical perspective, so PSTs can learn about their students’ funds
of knowledge. The first step would be to identify a border that needs to be
overcome and blur (KEATING, 2006) through ‘transformative practice zones’
(BRESLER, 2003) of working and the development of closer relationships with
students. We need mathematics teaching practices that recognize and challenge
spaces of marginalized knowledges of many communities; and strengthen the
relationship between students and mathematics (AGUIRRE, INGRAM-MAYFIELD &
MARTIN, 2013).
We need mathematics teachers — and mathematics teacher educators — critical and smart enough to notice and identify borders, but most of all, sensitive and creative enough to make breakthroughs that promote knowledge and relationships among students, teachers and mathematics.
Furthermore, PSTs’ understanding of funds of knowledge was also crucial in the development of empathy and commitment helping them to integrate students’ identities in mathematics teaching. PSTs’ understanding of both concepts and their relevance was promoted through a system that transcended the mathematics methods course and reached a system of support provided by the TECLA program through the Literacy courses and the fieldwork seminar. This confirms that an integrated approach in PSTs’ preparation provides a rich conceptual, pedagogical and practical context to teaching and learning mathematics.
Acknowledgment:
The TECLA (Teacher Education Collaborative in Language
Diversity and Arts Integration) project was developed by seven faculty at
the University of New Mexico from three programs and two colleges that include,
Drs. Rebecca Sanchez, Sylvia Celedon-Pattichis,
Carlos LópezLeiva, Nancy Pauly, Leila Flores-Dueñas, Karla Kingsley, Eileen Waldschmidt,
and Amy Sweet (Arts Teacher). TECLA is funded partly by a private donor.
References
AGUIRRE, Julia M. Developing culturally responsive Mathematics teaching. Fall 2012 TODOS Newsletter TODOS — Mathematics For All.
AGUIRRE, Julia M.; TURNER, Erin E.; BARTELL, Tonya Gau; KALINEC-CRAIG, Crystal; FOOTE, Mary Q.; ROTH MCDUFFIE, Amy; DRAKE, Corey. Making Connections in Practice: How Prospective Elementary Teachers Connect to Children’s Mathematical Thinking and Community Funds of Knowledge in Mathematics Instruction. Journal of Teacher Education, v. 64, n. 2, p. 178-192, 2013.
AGUIRRE, Julia M.; ZAVALA, Maria del Rosario; KATANYOUTANANT, Tiffany. Developing Robust Forms of Pre-Service Teachers' Pedagogical Content Knowledge through Culturally Responsive Mathematics Teaching Analysis. Mathematics Teacher Education and Development, v. 14, n. 2, p. 113-136, 2012.
AGUIRRE, Julia; MAYFIELD-INGRAM, Karen; MARTIN, Danny Bernardo. The impact of identity in K-8 mathematics: Rethinking equity-based practices. Reston: NCTM, 2013.
BISHOP, Allan John. Mathematical enculturation: a cultural perspective on Mathematics Education. Boston: Kluwer, 1988.
BOALER, Jo; GREENO, James G. Identity, agency, and knowing in mathematics worlds. In: BOALER, Jo (Ed.). Multiple perspectives on mathematics teaching and learning. Westport: Ablex, 2000, p. 171-200.
BRESLER, Liora. Out of the trenches: the joys (and risks) of cross-disciplinary collaborations. Council of Research in Music Education, n. 152, p. 17-39, 2003.
BRESSER, Rusty. Helping English language learners develop computational fluency. Teaching Children Mathematics, v. 9, n. 6, p. 294-300, feb. 2003.
CARPENTER, Thomas P.; FENNEMA, Elizabeth; FRANKE, Megan Loef; LEVI, Linda; EMPSON, Susan B. Children’s mathematics: Cognitively Guided Instruction. 2nd ed. Portsmouth: Heinemann, 2014.
CHAPIN, Suzanne H.; O’CONNOR, Catherine; ANDERSON, Nancy Canavan. Classrooms discussions in Math: a teacher’s guide for using talk moves to support Common Core and more. 3rd ed. Sausalito: Scholastic, Math Solutions, 2013.
CIVIL, Marta; BERNIER, Emily. Exploring images of parental participation in mathematics education: Challenges and possibilities. Mathematical Thinking and Learning, v. 8, n. 3, p. 309-330, nov. 2009.
CIVIL, Marta; BRATTON, Jill; QUINTOS, Beatriz. Parents and Mathematics Education in a Latino Community: redefining parental participation. Multicultural Education, v. 13, n. 2, p. 60-64, 2005.
CIVIL, Marta; QUINTOS, Beatriz. Engaging families in children's mathematical learning: Classroom visits with Latina mothers. New Horizons for Learning Online Journal, v. 12, n. 1, 2006.
D’AMBROSIO, Ubiratan. Matemática, Ensino e Educação: uma proposta global. Temas e Debates, São Paulo, v. 4, n. 3, p. 1-16, 1991.
D’AMBROSIO, Ubiratan; ROSA, Milton. Ethnomathematics and Its Pedagogical Action in Mathematics Education. In: ROSA, Milton; SHIRLEY, Lawrence; GAVARRETE, Maria Elena; ALANGUI, Wilfredo V. (Ed.). Ethnomathematics and its Diverse Approaches for Mathematics Education. Cham, Switzerland: Springer International Publishing, 2017, p. 285-305.
D'AMBROSIO, Ubiratan. Ethnomathematics and its place in the history and pedagogy of mathematics. For The Learning of Mathematics, v. 5, n. 1, p. 44-48, feb. 1985.
DRAKE, Corey; NORTON-MEIER, Lori A. Creating Third Spaces: Integrating Family and Community Resources into Elementary Mathematics Methods. In: 29th Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education. Lake Tahoe, Nevada, 2007.
FALTIS, Christian. Arts‐Based Pedagogy for Teaching English Learners. In: OLIVEIRA, Luciana (Ed). Handbook of TESOL in K-12. Hoboken: Wiley, 2019, p. 323-338.
FOSNOT, Catherine T.; DOLK, Maarten. Young mathematicians at work: Constructing number sense, addition, and subtraction. Portsmouth: Heinemann, 2001.
FREUDENTHAL, Hans. Mathematics as an Educational Task. Dordrecht: D. Reidel Publishing Company, 1973.
GALINDO, Rene. Reframing the past in the present: Chicana Teacher Role Identity as a Bridging Identity. Education and Urban Society, v. 29, n. 1, 85-102, nov. 1996.
GARRISON, Leslie; MORA, Jill Kerper. Adapting mathematics instruction for English language learners: The language-concept connection. In: ORTIZ-FRANCO, Luis N.; HERNANDEZ, Norma G.; DE LA CRUZ, Yolanda. (Ed.). Changing the faces of mathematics: Perspectives on Latinos. Reston: NCTM, 1999, p. 35-47.
GAY, Geneva. Culturally responsive teaching: theory, research, and practice. 2nd ed. New York: Teachers College Press, 2010.
GONZALEZ, Nora; ANDRADE, R.; CIVIL, Marta; MOLL, Luis C. Bridging funds of distributed knowledge: Creating zones of practices in mathematics. Journal of Education for Students Placed at Risk, v. 6, n. 1 and 2, p. 115-132, 2001.
GRAVEMEIJER, Koeno. Commentary solving word problems: a case of modelling. Learning and Instruction, v. 7, n. 4, p. 389-397, 1997.
HOLSTI, Ole R. Content analysis for the social sciences and humanities. Reading: Addison-Wesley, 1969.
KEATING, Ana Louise. From Borderlands and New Mestizas to Nepantlas and Nepantleras: anzalduan theories for social change. Human Architecture: Journal of the Sociology of Self-Knowledge, v. 4, n. 3, p. 5-16, 2006.
KOKKA, Kari. Addressing dilemmas of social justice mathematics through collaboration of students, educators, and researchers. Educational Considerations, v. 43, n. 1, p. 13-21, 2015.
LADSON-BILLINGS, Gloria. But that’s just good teaching! A case for culturally relevant pedagogy. Theory into Practice, n. 34, p. 159-165, 1995.
LANGE, Jan de. Using and Applying Mathematics in Education. In: BISHOP, Alan John; CLEMENTS, Ken; KEITEL, Christine; KILPATRICK, Jeremy; LABORDE, Colette. (Ed.). International handbook of Mathematics Education. Kluwer Academic Publisher, 1996, p. 49-97.
LESH, Richard A.; HOOVER, Mark; HOLE, Bonnie; KELLY, Anthony Edward; POST, Thomas. Principles for developing thought-revealing activities for students and teachers. In: KELLY, Anthony Edward; LESH, Richard A. (Ed.). Handbook of research design in Mathematics and Science Education. Mahwah: Lawrence Erlbaum Associates, Inc., 2000, p. 591-646.
LO CICERO, Ana Maria; FUSON, Karen C.; ALLEXSAHT-SNIDER, Martha. Mathematizing children’s stories, helping children solve word problems, and supporting parental involvement. In: ORTIZ-FRANCO, Luis N.; HERNANDEZ, Norma G.; DE LA CRUZ, Yolanda. (Ed.). Changing the faces of mathematics: Perspectives on Latinos. Reston: NCTM, 1999, p. 59-70.
LÓPEZLEIVA, Carlos. A. Bilingual Latina/o students model community practices using familiar resources. In: CIVIL Marta; TURNER, Erin E. (Ed.). The Common Core State Standards in Mathematics for English Language Learners, Grades K-8. New York: Teachers College, Columbia University, 2014, p. 95-109.
LOTAN, Rachel A. Group-worthy tasks. Educational Leadership, v. 60, n. 6, p. 72-75, mar. 2003.
MARSHALL, Julia; DONAHUE, David M. Art-centered learning across the curriculum: Integrating contemporary art in secondary school classroom. New York: Teachers College, 2014.
MOLL, Luis C. Literacy research in community and classrooms: a sociocultural approach. In: BEACH, Richard; GREEN, Judith L.; KAMIL, Michael L.; SHANAHAN, Timothy. (Ed.). Multidisciplinary perspectives on literacy research. National Council of Teachers of English, 1992, p. 211-244.
MOLL, Luis C.; GONZÁLEZ, Nora. Engaging life: a funds of knowledge approach to multicultural education. In BANKS, James A.; BANKS, Cherry A. McGee. (Ed.). Handbook of research on multicultural education. New York: Macmillan, 2004, p. 628-634.
MOLL, Luis. C.; GREENBERG, James B. Creating zones of possibilities: Combining social contexts for instruction. In: MOLL, Luis. C. (Ed.). Vygotsky and Education. New York: Cambridge University Press, 1990, p. 319-348.
MOSCHKOVICH, Judit. A situated and sociocultural perspective on bilingual mathematics learners. Mathematical Thinking and Learning, n. 4, n. 2-3, p. 189-212, 2002.
MOSCHKOVICH, Judit. Principles and guidelines for equitable mathematics teaching practices and materials for English language learners. Journal of Urban Mathematics Education, n. 6, p. 45-57, 2013.
MOSCHKOVICH, Judit. Understanding the needs of Latino students in reform-oriented mathematics classrooms. In: ORTIZ-FRANCO, Luis N.; HERNANDEZ, Norma G.; DE LA CRUZ, Yolanda. (Ed.). Changing the faces of mathematics: Perspectives on Latinos. Reston: NCTM, 1999, p. 5-12.
NCTM. National Council of Teachers of Mathematics. Principles and standards for school mathematics. Reston: NCTM, 2000.
NGACBP. National Governors Association Center for Best Practices. Common Core State Standards for Mathematics. Washington, 2010.
PARIS, Django. Culturally Sustaining Pedagogy: A Needed Change in Stance, Terminology, and Practice. Educational Researcher, v. 41, n. 3, p. 93-97, 2012.
PARRISH, Sherry. Number talks: Helping children mental math and computation strategies, grades K-5. Sausalito: Scholastic, Math Solutions, 2014.
PERKINS, Isabel; FLORES, Alfinio. Mathematical notations and procedures of recent immigrant students. Mathematics Teaching in the Middle School, v. 7, n. 6, p. 346-351, feb. 2002.
RAMIREZ, Nora; CELEDÓN-PATTICHIS, Sylvia. Second language development and implications for math classroom. In: CELEDÓN-PATTICHIS, Sylvia; RAMIREZ, Nora (Ed.). Beyond Good Teaching: Advancing Mathematics Education for ELLs. Reston: NCTM, 2012, p. 19-38.
SIMIC-MULLER, Ksenjia; TURNER, Erin E.; VARLEY, Maura C. Math club: problem posing. Teaching Children Mathematics, v.16, n. 4, p. 206-212, nov. 2009.
STEIN, Mary Kay; SMITH, Margareth. S.; HENNINGSEN, Marjorie A.; SILVER, Edward A. Implementing standards-based mathematics instruction: a casebook for professional development. New York: Teachers College Press, 2000.
VAN DE WALLE, John A.; KARP, Karen S.; BAY-WILLIAMS, Jennifer M. Elementary and Middle School Mathematics: Teaching Developmentally (8th ed). Upper Saddle River: Pearson, 2013.
WEBB, David; VAN DER KOOIJ, Henk; GEIST, Monica. R. Design research in the Netherlands: introducing logarithms using Realistic Mathematics Education. Journal of Mathematics Education at Teachers College, v. 2, n. 1, p. 47-52, 2011.
Notes
[1] I use the term Latinx acknowledging gender diversity and fluidity rather than a dichotomized view.










