1 Introdução
A pandemia do novo coronavírus fez com que os meios de comunicação divulgassem, diariamente, os números da contaminação do vírus no Brasil e no Mundo. Nas aulas de Cálculo Diferencial, que lecionamos na universidade, fomos questionados pelos estudantes, em meados de abril, de como era possível obter a curva de contaminação que era apresentada nos veículos de comunicação, tal questionamento motivou-nos a escrever este artigo.
Isso posto, revelamos ao longo do trabalho como respondemos a essa interrogação dos alunos e aguçamo-los a pensar de que maneira poderíamos encontrar a expressão matemática que representava a curva e como, por meio desta fórmula, poderíamos utilizar a Derivada para calcular o tempo em que o Brasil ocuparia a segunda posição em número de contaminados. Ressaltamos que, em meados de abril, essa posição era ocupada pela Rússia.
A fim de respondermos tais indagações, dividimos o trabalho em quatro seções: Introdução, Referencial Teórico-Metodológico, A Aula e Considerações Finais.
Na seção Referencial Teórico-Metodológico, apresentamos nossas teorias e metodologias empregadas ao longo deste trabalho: Registros de Representação Semiótica, Sentido Holístico da Derivada (teorias), Modelagem Matemática, Excel e GeoGebra (metodologia), já na seção A Aula, revelamos a operacionalização e respostas da nossa problemática. Finalizamos a pesquisa com as nossas Considerações Finais.
A seguir, apresentaremos as ideias que julgamos essenciais do nosso referencial teórico-metodológico: Registros de Representação Semiótica, Sentido Holístico da Derivada, Modelagem Matemática, Excel e o GeoGebra.
2 Referencial Teórico-Metodológico
Nesta seção, apresentaremos os nossos referenciais teórico-metodológicos utilizados ao longo deste estudo. A posse dessas referências possibilitou-nos fazer conversões entre as representações do objeto matemático Derivada, assim como o seu entendimento como uma medida de taxa de variação que, em no nosso trabalho, denominamos velocidade de contaminação.
Além disso, modelamos e criamos gráficos que foram nomeados de Evolução da Contaminação no Brasil e Evolução da Contaminação na Rússia.
2.1
Registros de Representação Semiótica e o Sentido Holístico da Derivada
Nesta seção, apresentaremos algumas ideias pontuais, que julgamos necessárias para o desenvolvimento deste trabalho sobre os Registros de Representação Semiótica e o Sentido Holístico da Derivada. Começaremos com os Registros de Representação Semiótica.
De acordo com Duval (2009), para ocorrerem os processos pedagógicos do ensino e aprendizagem da matemática, necessitamos de representações, pois seus objetos são apresentados de forma abstrata, por meio das propriedades, teoremas, axiomas, estruturas algébricas e relações que podem ser expressas em diferentes situações.
Portanto, para o ensino e a aprendizagem da matemática, precisamos levar em consideração diferentes formas de representações de um mesmo objeto matemático.
Acerca das representações semióticas, Duval (2009) define semiósis como a presentação ou a produção, e a nóseis como a apreensão conceitual de um objeto. Então, para haver a apreensão de um objeto matemático é necessário que a nóseis ocorra por meio de representações semiósis, ou seja, quando o mesmo objeto matemático a ser apreendido tiver maior número de registro de representação, maior será a possibilidade de apreensão do objeto.
Segundo Duval (2009), um registro de representação é um sistema semiótico que tem as funções cognitivas fundamentais de apontar o funcionamento cognitivo consciente em que a situação é apresentada ao aluno, por meio de registros de representações, facilitando, assim, a compreensão ou a descoberta a respeito do objeto matemático.
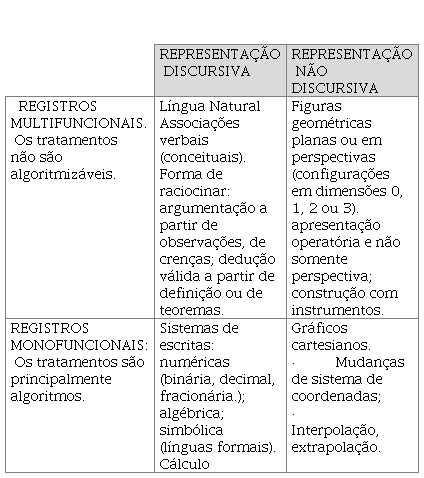
Segundo Duval (2011), os registros mobilizados no aprendizado dos objetos matemáticos são classificados em:
· representação discursiva que é subdividida em língua natural e os sistemas de escritas;
· representação não discursiva que é subdividida em figuras geométricas planas ou em perspectivas e os gráficos cartesianos.
Essa classificação pode ser resumida no Quadro 1.
1
Quadro 1:
Classificação dos diferentes registros mobilizáveis no funcionamento matemático
(fazer matemático, atividade matemática)
 Fonte:
Duval (2011, p. 14)
Fonte:
Duval (2011, p. 14)
|
REPRESENTAÇÃO
DISCURSIVA
|
REPRESENTAÇÃO
NÃO DISCURSIVA
|
|
REGISTROS
MULTIFUNCIONAIS.
Os
tratamentos não são algoritmizáveis.
|
Língua Natural
Associações verbais
(conceituais).
Forma de raciocinar:
argumentação
a partir de observações, de crenças;
dedução válida
a partir de definição ou de teoremas.
|
Figuras geométricas planas ou
em perspectivas (configurações em dimensões 0, 1, 2 ou 3).
apresentação
operatória e não somente perspectiva;
construção
com instrumentos.
|
|
REGISTROS
MONOFUNCIONAIS:
Os tratamentos
são principalmente algoritmos.
|
Sistemas de escritas:
numéricas
(binária, decimal, fracionária.);
algébrica;
simbólica
(línguas formais).
Cálculo
|
Gráficos cartesianos.
·
Mudanças de sistema de coordenadas;
·
Interpolação, extrapolação.
|
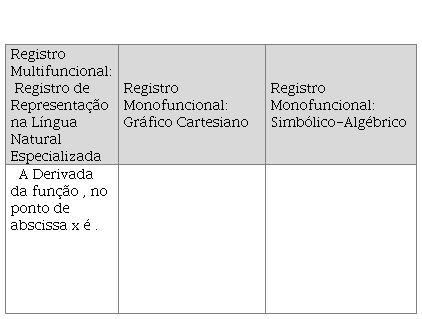
No Quadro 2, a seguir,
apresentamos alguns exemplos de registros de representação semiótica para o
objeto matemático Derivada. Neste quadro, revelamos que a Derivada em um ponto
pode ser representada por registro de representação língua natural
especializada, o registro de representação gráfico cartesiano e o registro de
representação simbólico-algébrico.
2
Quadro 2: Exemplos de Registros
 Fonte:
Lobo (2017, p. 101)
Fonte:
Lobo (2017, p. 101)
|
Registro Multifuncional:
Registro de Representação na Língua Natural Especializada
|
Registro Monofuncional: Gráfico Cartesiano
|
Registro Monofuncional: Simbólico-Algébrico
|
|
A Derivada da função , no ponto de abscissa x é .
| | |
De acordo com Duval (2009), nossa perspectiva dos objetos matemáticos não é imediatamente ou diretamente acessível, a não ser através de sua representação. Segundo o mesmo autor, as representações matemáticas são significativas porque permitem uma comunicação entre os sujeitos e as atividades cognitivas do pensamento, e esses vários registros da representação são necessários para o aprendizado. Exemplificando: uma expressão, um símbolo e uma figura são representações dos objetos matemáticos: derivada, número, função, um ponto, entre outros.
Ainda de acordo como estudioso, em relação aos registros de representação semiótica, existem dois tipos de transformações: os tratamentos e as conversões.
Os tratamentos são transformações no interior de um mesmo registro, ou seja, uma transformação interna a um registro e são ligados à forma, não a
Os tratamentos são transformações no interior de um mesmo registro, ou seja, uma transformação interna a um registro e são ligados à forma, não ao conteúdo dos objetos matemáticos.
Dois exemplos de tratamento encontram-se a seguir, em que o cálculo da função Derivada das funções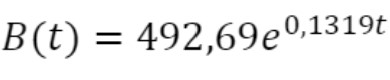 e
e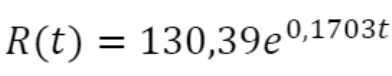 em relação à variável é feito conservando o mesmo registro de representação simbólico-algébrico:
em relação à variável é feito conservando o mesmo registro de representação simbólico-algébrico: 
Outro tipo de transformação são as conversões. Conversões são transformações de representações que consistem na mudança de registro, conservando os mesmos objetos matemáticos. Dessa forma, converter implica coordenar registros mobilizados. Portanto, segundo Duval (2009), fundamental no trabalho com as representações semióticas e no aprendizado da matemática.
Na sequência, damos dois exemplos de conversão do registro de representação simbólico-algébrico para o registro de representação língua natural especializada:
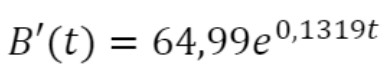 · e a Derivada da função que representa a velocidade de contaminação do Brasil no instante qualquer;
· e a Derivada da função que representa a velocidade de contaminação do Brasil no instante qualquer;
·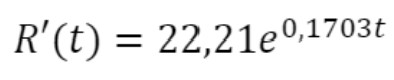 e a Derivada da função que representa a velocidade de contaminação da Rússia no instante qualquer.
e a Derivada da função que representa a velocidade de contaminação da Rússia no instante qualquer.
Agora, apresentaremos as ideias essenciais de Pino-Fan et al. (2013) sobre o Sentido Holístico da Derivada. A apropriação dessa noção permitiu-nos fazer conversões entre o registro de representação simbólico-algébrico da Derivada e a Velocidade no registro de representação língua natural especializada.
A palavra holística foi formulada a partir do termo holos, um termo grego que significa todo ou inteiro. Dessa forma, o Sentido Holístico da Derivada procura entender o fenômeno na sua totalidade e globalidade.
De acordo com Stigar (2008), o holismo considera o sistema completo, comportando-se de um modo diferente da soma das suas partes e ressalta a importância do todo. O estudioso destaca ainda a importância da correlação das parcelas, as quais não podem existir de forma independente, e o todo é maior que a soma dessas interações.
Nesta teoria filosófica, o todo e cada uma das partes encontram-se ligados com interações constantes, estabelecendo uma relação de interdependência e a convergência. Devido a essas questões, este conceito é, frequentemente, aplicado à Educação.
O pesquisador Pino-Fan et al (2013) utilizou essa teoria filosófica para reconstruir o que chamou de Sentido Holístico da Derivada. Para isso, identificou o todo (Derivada) e as partes (significados parciais da Derivada) e, então, após uma revisão bibliográfica a partir da matemática grega até o século XX, o investigador criou a noção de configuração epistêmica (CE), tais configurações epistêmicas foram responsáveis por reconstruir o Sentido Holístico da Derivada.
Segundo Pino-Fan et al (2013), existem nove configurações epistêmicas associadas aos seguintes problemas: traçados de tangentes na Matemática grega (CE1), problemas sobre taxas de variação na Idade Média (CE2), cálculo de subtangentes e tangentes utilizando álgebra (CE3), traçados de tangentes mediante considerações cinemáticas (CE4), cálculo de máximos e mínimos mediante a ideia intuitiva de limite (CE5), cálculo de tangentes e subtangentes mediante métodos infinitesimais (CE6), cálculo de fluxões (CE7), cálculo de diferenças (CE8), derivada como um limite (CE9).
Nosso trabalho está imerso na configuração epistêmica CE4, que, segundo Pino-Fan et al (2013), parte dos traçados de tangentes mediante considerações cinemáticas para o entendimento da Derivada como Taxa de Variação e Velocidades.
A seguir, na Figura 1, apresentamos as interações possíveis para o ensino e para aprendizagem da Derivada. Na base da figura, definem-se as configurações primárias, que possuem caráter extensivo e são ativadas na resolução de situações-problema, que envolvem as diversas configurações epistêmicas.
Assim, observamos que, por exemplo, as configurações epistêmicas CE2 e CE4 são ativadas para resolver situações-problema que envolvem a Velocidade.
A seguir, abordaremos alguns princípios que avaliamos fundamentais da Modelagem Matemática e apresentaremos uma justificativa de adotarmos o modelo matemático exponencial para o nosso estudo
2.2
Modelagem Matemática
Estudos em Educação Matemática indicam que a utilização da Modelagem Matemática no ensino da Matemática é uma alternativa ao método tradicional (BASSANEZI, 2002). Assim, o autor defende a sua utilização aliada à necessidade de professores desenvolverem intervenções inovadoras em salas de aulas para, possivelmente, produzir um ensino eficaz.
Desse modo, aplicaremos, nesta pesquisa, a metodologia da Modelagem Matemática, que, segundo Bassanezi (2002), é um processo dinâmico, utilizado para a obtenção e validação de modelos matemáticos, uma forma de abstração e generalização com a finalidade de previsão de tendência; além disso, consiste na arte de transformar situações da realidade em problemas matemáticos cujas soluções devem ser interpretadas na linguagem usual. E, ainda, segundo o estudioso, essas repostas dos problemas possuem alto grau de confiabilidade.
Bassanezi (2002) concebe o processo de modelagem matemática em seis etapas:
· Experimentação: este é o passo inicial e é um processo laboratorial ou estatístico utilizado para obtenção dos dados do problema;
· Abstração: nesta fase, identificamos e selecionamos as variáveis da situação-problema e, em seguida, formulamos o problema na língua natural para posterior formulação matemática;
· Resolução: neste ponto, resolvemos o problema com as ferramentas matemáticas;
· Validação: nesta etapa, comparamos a solução obtida com os dados reais e optamos pela aceitação ou não do modelo matemático;
· Modificação: nesta parte, caso não ocorra a validação, deve-se modificar as variáveis ou a lei de formação do modelo. Após as mudanças, o processo reinicia-se;
· Aplicação: neste o último passo, é possível entender, explicar, fazer previsões e tomar decisões, por exemplo, do mundo real, sugerindo mudanças ou não no panorama da situação-problema.
Ainda, segundo Bassanezi (2002), a metodologia da Modelagem Matemática é uma arte que fornece um conjunto de equações ou funções matemáticas elaboradas para corresponder a algum fenômeno que pode ser físico, biológico, social ou outro qualquer.
Na sequência, apresentaremos nosso modelo matemático à luz da Modelagem Matemática.
2.2.1
Crescimento e Decrescimento Populacional
Nesta seção, apresentaremos a justificativa de termos escolhido a modelagem matemática exponencial para a construção das funções que medem a evolução da contaminação do novo coronavírus no Brasil e na Rússia.
Segundo Zill et al (2001), o problema de valor inicial 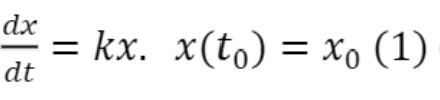 em que é uma constante de proporcionalidade, ocorre em muitas teorias científicas envolvendo crescimento ou decrescimento populacional.
em que é uma constante de proporcionalidade, ocorre em muitas teorias científicas envolvendo crescimento ou decrescimento populacional.
Ainda de acordo com o autor,
em biologia, é frequentemente observado que a taxa de crescimento de certas bactérias é proporcional ao número de bactérias presentes no dado instante. Durante um certo intervalo de tempo, a população de pequenos animais, tais como roedores, pode ser prevista com alto grau de precisão pela solução para (1). Em física, um problema de valor inicial (1) proporciona um modelo para cálculo aproximado da quantidade remanescente. (Zill, 2001, p. 102).
Isso posto, temos que 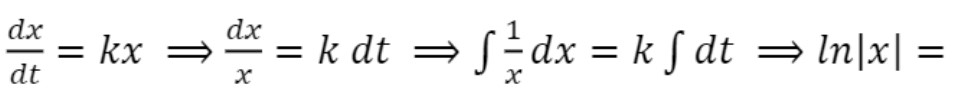
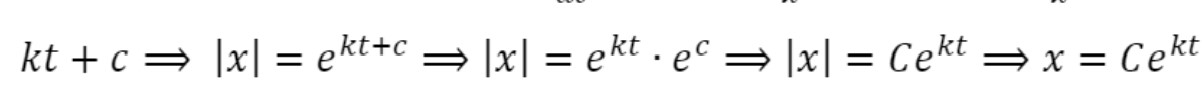 , em que C é uma constante real.
, em que C é uma constante real.
Dessa forma, encontramos uma função exponencial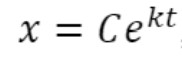 , que é solução da equação diferencial
, que é solução da equação diferencial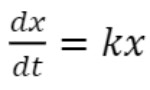 que mede o crescimento ou decrescimento populacional.
que mede o crescimento ou decrescimento populacional.
Como nosso trabalho envolve modelar o crescimento populacional das contaminações por coronavírus no Brasil e na Rússia, adotaremos tal modelo exponencial para o nosso estudo.
Na sequência, apresentaremos as justificativas de utilizarmos os softwares Excel e GeoGebra.
2.3
Excel e o GeoGebra
Diversos pesquisadores, por exemplo, Cury (2006) e Ferreira et al. (2009) afirmam que o uso de softwares computacionais aplicados podem viabilizar a construção do conhecimento, por parte dos estudantes, de maneira autônoma e independente, além de possibilitar uma inovação no ensino, pois são considerados ferramentas auxiliares na construção de conceitos e aplicações relacionados ao ensino de matemática, permitindo criar situações de aprendizagem estimulante.
Em nossas aulas de Cálculo, ministradas nos cursos de primeiro semestre de engenharia, procuramos utilizar softwares, como o GeoGebra e o Excel.
O GeoGebra é um software matemático livre (para uso não comercial), com base na GPL (GNU General Public License), desenvolvido por Markus Hohenwarter no início de 2001, na University of Salzburg, na Áustria, para ser utilizado em ambiente de sala de aula. Por se tratar de um software livre, os colaboradores podem realizar alterações em seus códigos fontes, atualizando ou acrescentando novas ferramentas, a fim de disponibilizarem melhoramentos a todos que o utilizem.
O GeoGebra possibilitou-nos utilizar o registro de representação gráfico cartesiano para, a partir dos gráficos das funções, encontrarmos o ponto de encontro entre as curvas de Evolução de Contaminação do novo Coronavírus no Brasil e na Rússia.
O software Excel foi desenvolvido pela empresa americana Microsoft a partir da década de 1980. Escolhemos esse aplicativo por ser muito popular entre os estudantes e por rodar em sistemas operacionais como Windows e Android, por exemplo.
Ele possui diversas ferramentas, e destacamos que, entre elas, é possível fazer os gráficos das funções e encontrar as expressões algébricas das funções que representam tais gráficos, ou seja, encontramos o registro de representação simbólico-algébrico e, assim, fizemos a conversão deste último registro para o registro de representação gráfico cartesiano e vice-versa.
Ressaltamos que o Excel oportunizou-nos escrever o registro simbólico algébrico das funções evolução de contaminação do Brasil e da Rússia.
Finalizamos esta seção, ressaltando que, na nossa percepção, os estudantes são bastante conectados às tecnologias, assim, utilizando o computador como método de ensino, eles sentem-se mais motivados pelas aulas e fixam os conceitos mais rápido do que pelos métodos convencionais (CAMPOS, 2009).
Na próxima seção, apresentaremos a operacionalização deste trabalho.
3 A Aula
Nesta seção, apresentaremos o relato de como procedemos na aula. Pedimos aos estudantes que consultassem os dados da Jonhs Hopkins Universty, essa instituição, em seu site, mantém os dados de contaminação do novo Coronavírus pelo mundo. Notamos que os meios de comunicação o utilizam constantemente.
Assim foi feito, fizemos a consulta ao site https://coronavirus.jhu.edu/map.html do dia 17/03/2020 até o dia 23/04/2020. Selecionamos o dia 17/03/2020 como marco inicial dos nossos estudos, e o dia 23/04/2020 foi escolhido como o ponto final, já que, nesta data, terminamos a aula, iniciada no dia 02/04/2020.
Ressaltamos que, de acordo, com o site Jonhs Hopkins Universty, o Brasil, no dia 23/04/2020, ocupava a oitava posição em número de contaminações, e a Rússia era a segunda colocada.
Sendo assim, operacionalizamos esses dados utilizando o software Excel. Com o auxílio do aplicativo, obtemos funções que representam o número de contaminados no Brasil e na Rússia. Essas funções foram representadas graficamente (registro de representação gráfico cartesiano) e algebricamente (registro de representação simbólico-algébrico).
Portanto, para encontrarmos tais funções, pedimos aos estudantes que, inicialmente, abrissem o aplicativo, Figura 2 a seguir:
 Figura 2. Excel
Fonte: O pesquisador (2020)
Figura 2. Excel
Fonte: O pesquisador (2020)
Em seguida, digitamos os dados
obtidos em duas planilhas: uma para o Brasil e outra para a Rússia e, para
encontrarmos o gráfico das funções, selecionamos o botão inserir e, em seguida,
gráfico de dispersão. Podemos acompanhar estes feitos na Figura 3 e na Figura
4, reproduzidos em seguida:
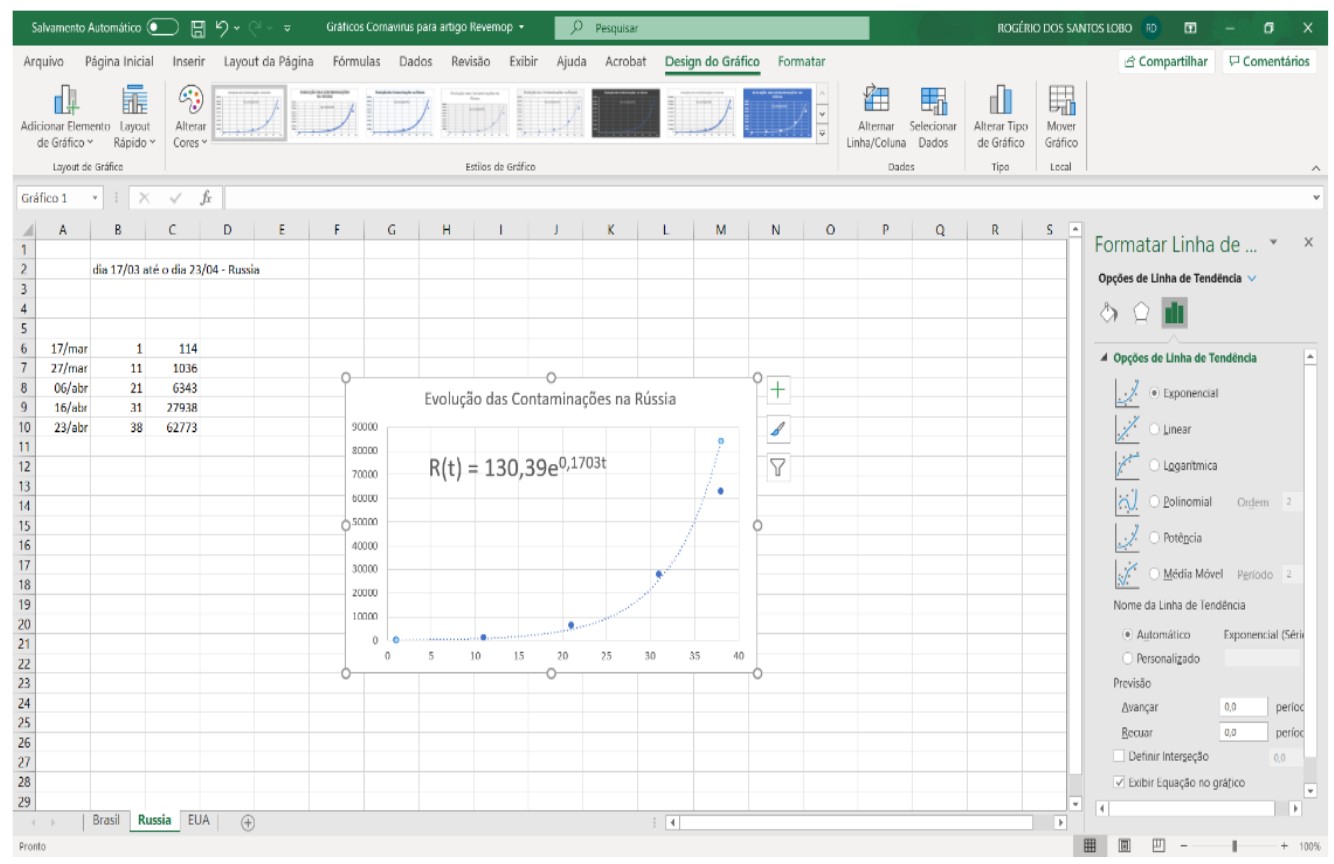 Figura 3. Plotando o
Gráfico
Fonte: O pesquisador (2020)
Figura 3. Plotando o
Gráfico
Fonte: O pesquisador (2020)
Agora, para obtermos o registro
de representação simbólico-algébrico das funções, utilizamos a guia: “Adicionar
Linhas de Tendência”, exponencial (justificamos esta escolha na seção
referencial teórico-metodológico). Para finalizar, selecionamos o box: Exibir Equação no gráfico”.
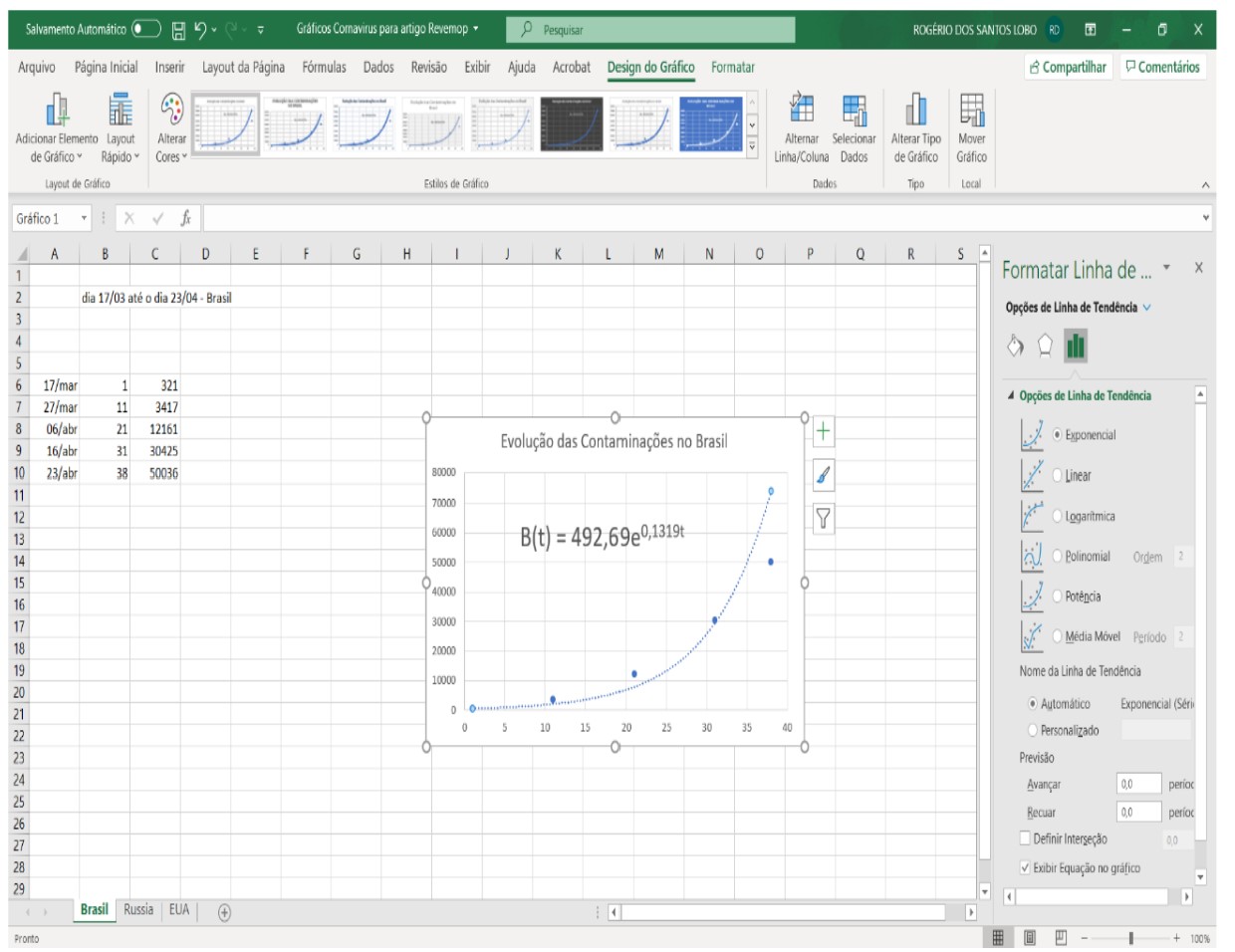 Figura 4. Adicionando
Linha de Tendência
Fonte: O pesquisador (2020)
Figura 4. Adicionando
Linha de Tendência
Fonte: O pesquisador (2020)
Isso posto, construímos as representações das funções algebricamente e graficamente, Figura 5 e Figura 6; nelas, colocamos, no eixo horizontal, o tempo; e, no eixo horizontal, o número de infectados. Estas figuras revelam a evolução da contaminação do novo Coronavírus no Brasil e na Rússia no período de 17/03/2020 até 23/04/2020.
Nas duas figuras, chamamos o eixo horizontal de t e construímo-lo assim: dia 17/03/2020 equivale a t = 1 , dia 27/03/2020 equivale a t = 11 , dia 06/04/2020 equivale a t = 21, dia 16/04/2020 equivale a t = 31e no dia 23/04/2020 equivale a t = 38.
No eixo horizontal, colocamos, nas duas figuras, o número de contaminados, no caso do Brasil, chamamos esse número de B e, no caso da Rússia, chamamos esse número de R .
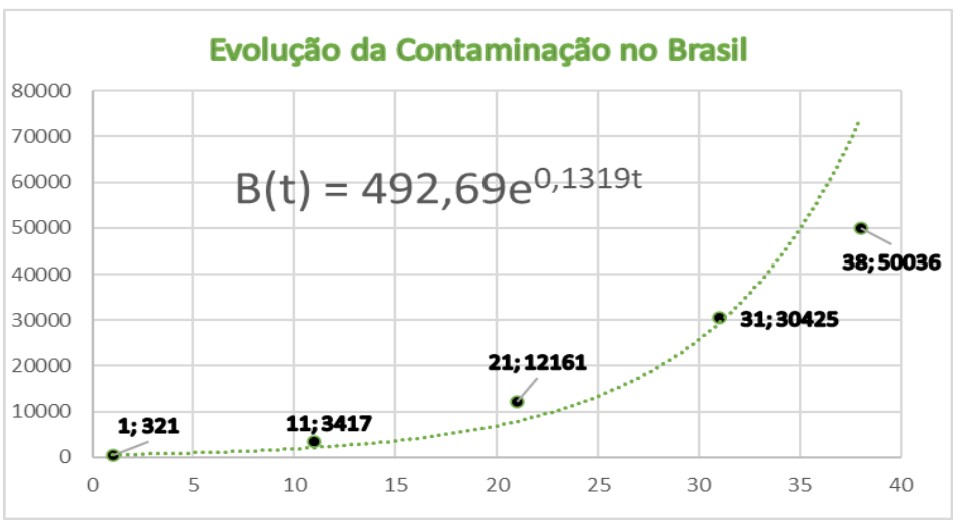 Figura 5. Evolução da
Contaminação no Brasil
Fonte: O pesquisador (2020)
Figura 5. Evolução da
Contaminação no Brasil
Fonte: O pesquisador (2020)
Então, na Figura 5, 1;321 significa que para t = 1 (dia 17/03/2020), no Brasil, o número de
infectados era 321,
matematicamente, B(1) = 321 .
Analogamente, na Figura 6, 31;27938 significa que para t = 31 (dia 16/04/2020); na Rússia, o número de contaminados era 27938, matematicamente, R(31) = 27938 .
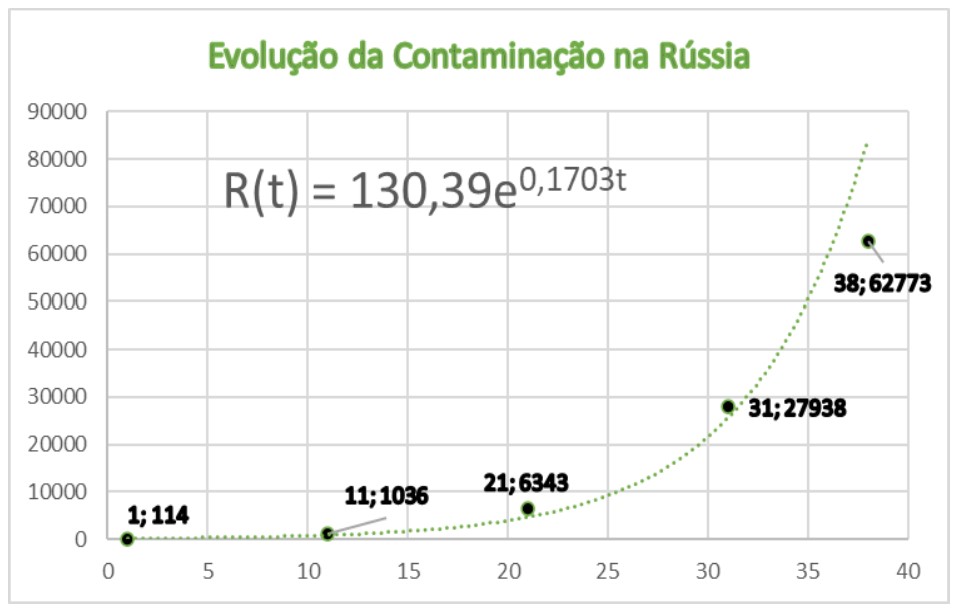 Figura 6. Evolução da
Contaminação na Rússia
Fonte: O pesquisador (2020)
Figura 6. Evolução da
Contaminação na Rússia
Fonte: O pesquisador (2020)
Dessa forma, utilizamos o aplicativo para encontrar funções que medem o número de infectados em qualquer instante que desejarmos. A saber: para o Brasil, a fórmula é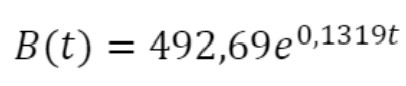 e; para a Rússia,
e; para a Rússia, 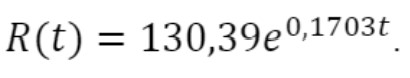 .
.
Assim sendo, com a posse das duas funções e , podemos calcular a velocidade de contaminação para o Brasil (B' ) e Rússia (R'), por meio da Regra da Cadeia para Derivação, da seguinte maneira:
•
Sendo assim, encontramos o tempo em que o Brasil igualaria a Rússia, em número de contaminações, de duas formas, utilizando os registros: registro de representação simbólico-algébrico e o registro de representação gráfico cartesiano.
Iniciaremos pelo registro de representação simbólico-algébrico, para isto, 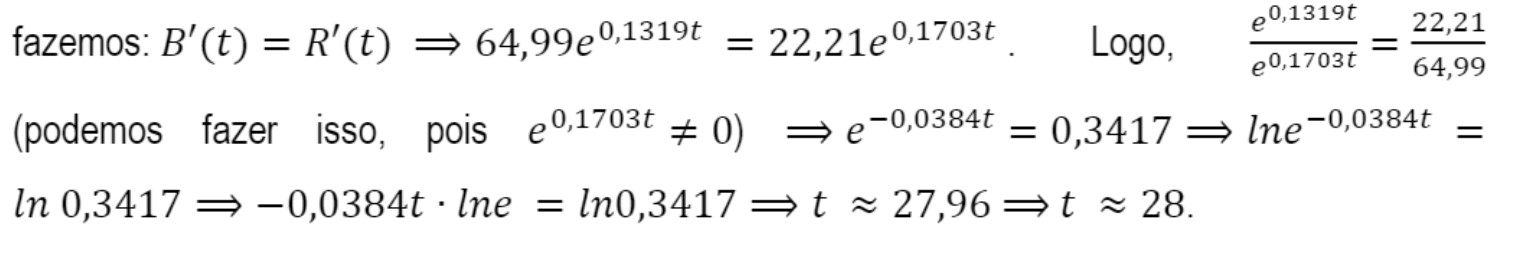
Poderíamos chegar a esse resultado pelo registro de representação gráfico cartesiano, para isto, utilizaremos o GeoGebra. Durante a aula, pedimos aos estudantes abrirem o aplicativo e digitar, na entrada, a função velocidade de contaminação para o Brasil (B') e para a Rússia (R'), Figura 7, a seguir.
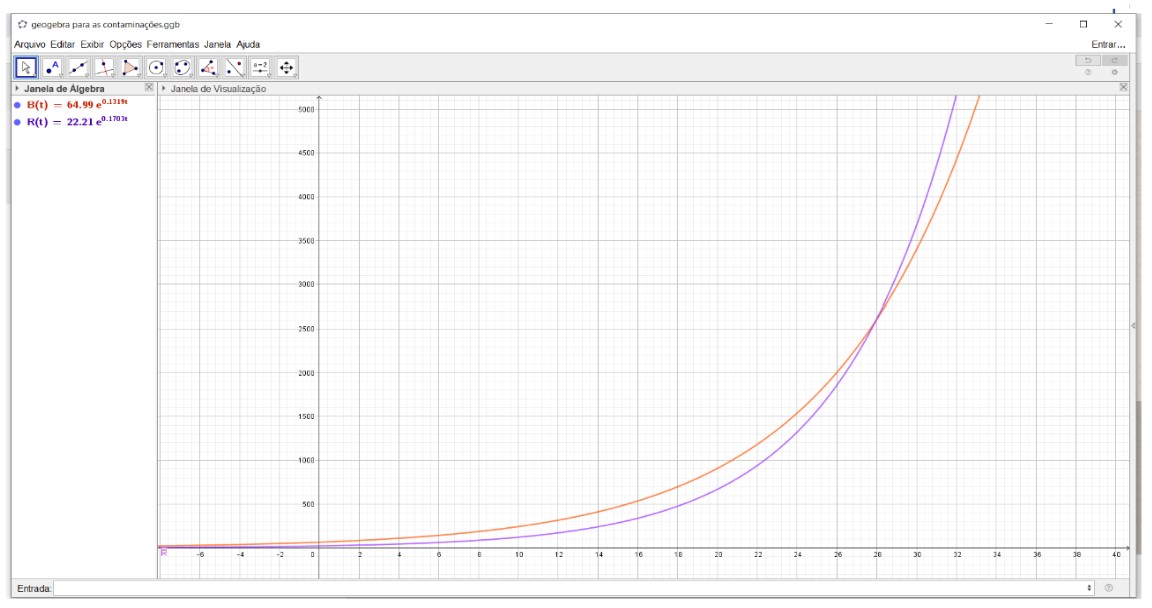 Figura 7: Plotando
Curvas no GeoGebra
Fonte: O pesquisador (2020)
Figura 7: Plotando
Curvas no GeoGebra
Fonte: O pesquisador (2020)
Nesta Figura 7, observamos que as
duas funções se encontram, então precisamos encontrar este ponto. Para isto,
recorremos ao ícone interseção de Dois Objetos, Figura 8 a seguir.
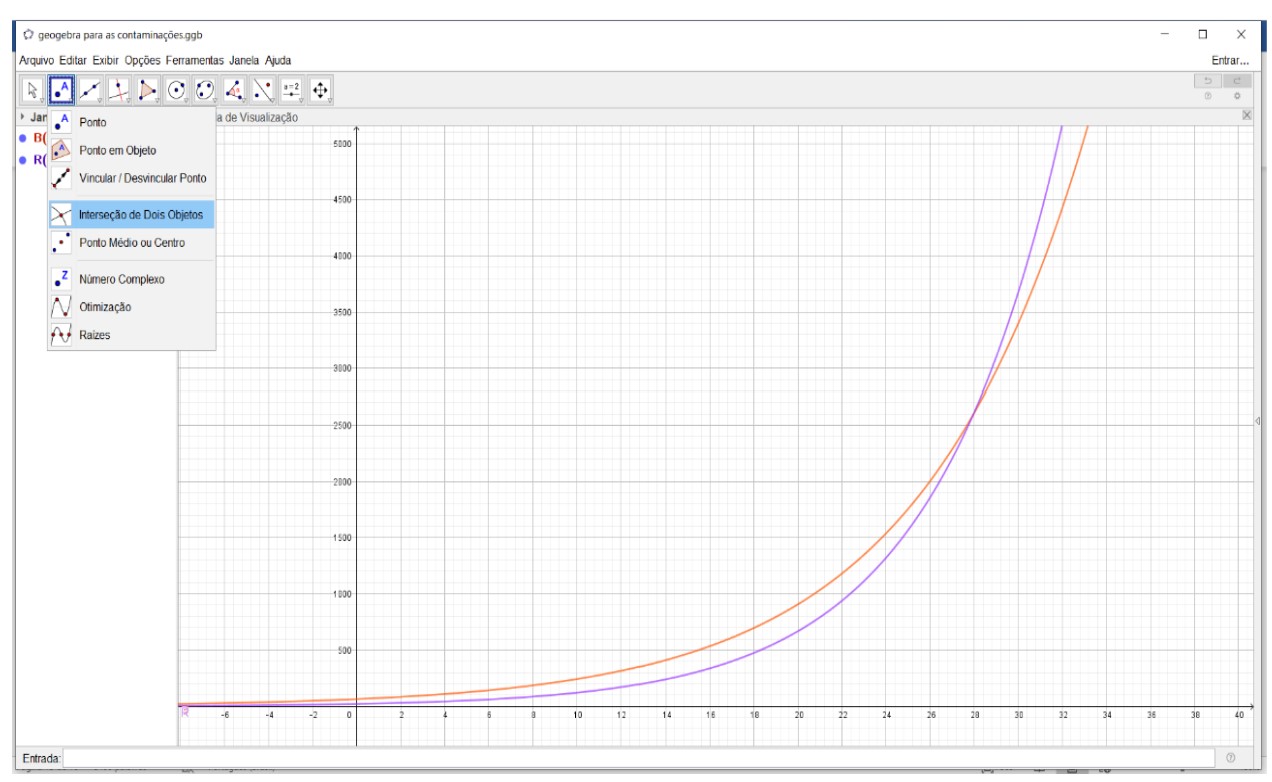 Figura 8: Intersecção de
Pontos no GeoGebra
Fonte: O pesquisador (2020)
Figura 8: Intersecção de
Pontos no GeoGebra
Fonte: O pesquisador (2020)
E, assim, construímos o ponto P, Figura 9.
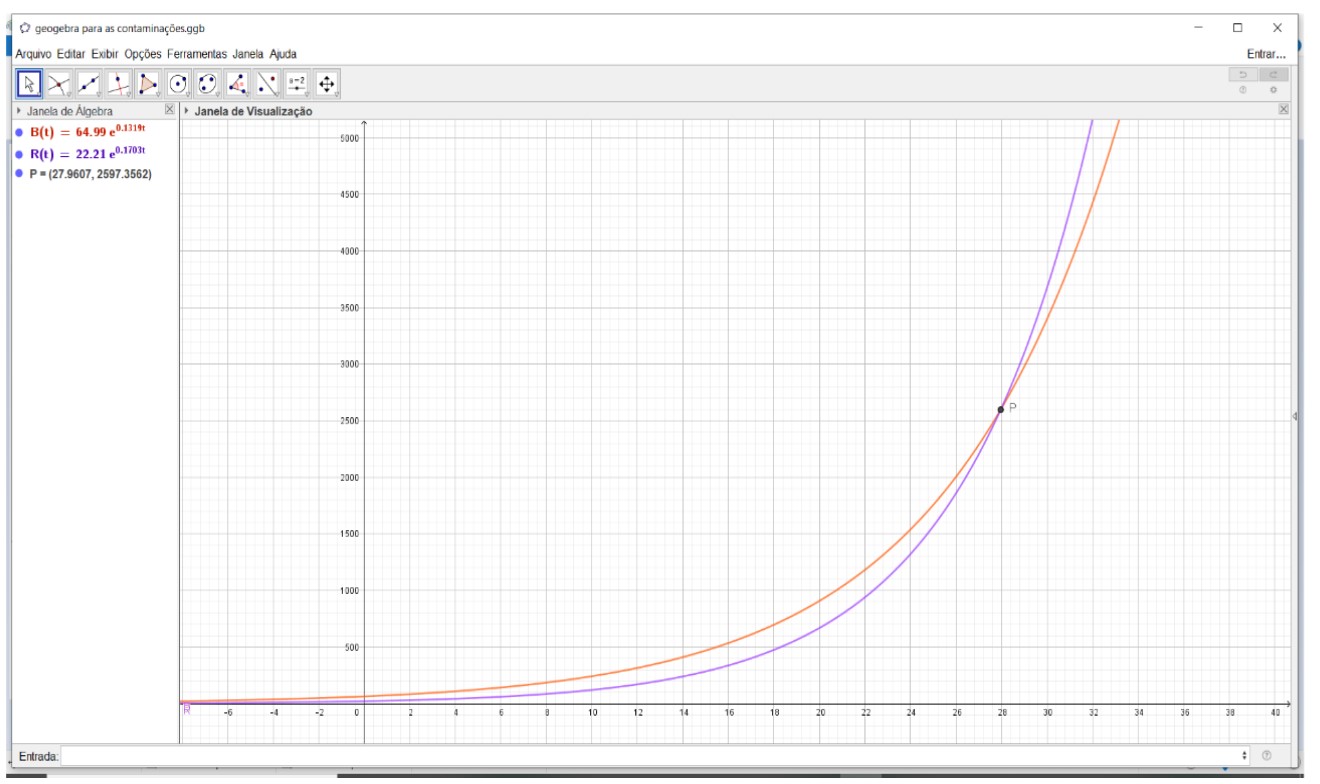 Figura 9. Localizando o Ponto de Intersecção
Fonte: O pesquisador (2020)
Figura 9. Localizando o Ponto de Intersecção
Fonte: O pesquisador (2020)
Agora, ainda, na Figura 9, observamos a abscissa do ponto P, que é 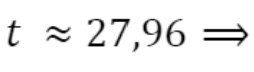
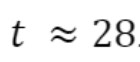 .
.
Esse número 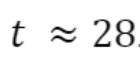 que encontramos, nas duas formas de resolução do problema, significa que o Brasil igualaria a Rússia em 28 dias, aproximadamente, a partir do dia 23/04/2020, ou seja, dia 21/05/2020, então, no dia 22/05/2020, ocuparia a vice-liderança mundial nos números de contaminações
que encontramos, nas duas formas de resolução do problema, significa que o Brasil igualaria a Rússia em 28 dias, aproximadamente, a partir do dia 23/04/2020, ou seja, dia 21/05/2020, então, no dia 22/05/2020, ocuparia a vice-liderança mundial nos números de contaminações
Ressaltamos que, segundo o site https://noticias.uol.com.br, o Brasil ultrapassou a Rússia e ocupou o posto de segundo lugar em contaminações no dia 19/05/2020.
Na próxima seção, apresentaremos nossas considerações finais.
4 Considerações Finais
Iniciamos nossa pesquisa com um questionamento dos estudantes, em uma aula de Cálculo Diferencial, ministrada para uma turma de primeiro semestre, sobre como encontrar a curva de contaminação do novo Coronavírus, pois tal curva aparecia com frequência nos meios de comunicação.
Propusermos responder esta indagação e acrescentamos algumas hipóteses: em que dia o Brasil ultrapassaria a Rússia, que, até então, era a segunda colocada e tornar-se-ia o segundo colocado no nível de contaminação; e outras inquietações: seria possível encontrar a expressão matemática que descrevesse a curva de contaminação.
Sabíamos que os alunos já tinham tomado conhecimento da Derivada e dos softwares Excel e GeoGebra, então aceitamos o desafio, pois, devido a nossa formação em Educação Matemática, conhecemos que as indagações dos estudantes podem proporcionar uma aprendizagem eficaz e também que essa intervenção poderia ser um exemplo a ser seguido pelos demais professores, que se apropriando dessas ideias do artigo, com as devidas adaptações às situações-problema, que queira estudar, criaríamos um bom ambiente de aprendizado nas aulas de Cálculo Diferencial.
Aproveitamos, então, esse ensaio para reforçar, nos estudantes, uma ideia fundamental da Derivada, que é a Taxa de Variação e que, neste trabalho, foi focado no cálculo da Velocidade.
Nossa experiência revela que os alunos são capazes de “decorar” o fato de que é possível utilizar a Derivada para obtermos a Velocidade, mas fazem isso apenas para se submeterem às provas e também sabemos que muitos, com o decorrer dos dias, acabam esquecendo essa relação.
Pensamos, então, em romper isso, pois diversos estudos, em Educação Matemática, revelam que uma aula feita a partir de questionamentos deles e aliada ao nosso referencial teórico-metodológico pode possibilitar um aprendizado eficaz em relação ao ensino tradicional.
Neste artigo, aplicamos a teoria do Sentido Holístico da Derivada, que proporcionou ao pesquisador a possível ativação da configuração epistêmica CE4 que leva ao entendimento da Derivada como Velocidade e, assim, aliado aos Registros de Representação Semiótica, podemos fazer tratamentos e, principalmente, a conversão do registro de representação simbólico-algébrico da Derivada com a Velocidade no registro de representação língua natural especializada.
Finalmente, o Excel e o GeoGebra foram fundamentais para operacionalizarmos esta proposta de aula, eles nos oportunizaram a construção dos gráficos, aquisição das expressões matemáticas e, assim, obtivemos respostas numéricas.
No final do processo, percebemos os estudantes engajados e com o “brilho no olhar” por terem entendido, associado e inferido em uma área do Cálculo Diferencial que, geralmente, é motivo de inúmeros problemas de aprendizagem por parte eles.
Alguns alunos mostraram-se interessados em atuar fora da vida acadêmica com a Modelagem Matemática, ou seja, nas empresas, e outros ficaram seduzidos a entrarem no programa de iniciação científica para aplicarem nas suas áreas a Modelagem Matemática.
Finalizamos observando o grau de precisão que o nosso estudo obteve, pois ele revelou que o Brasil igualaria a Rússia após 28 dias, aproximadamente, a partir do dia 23/04/2020, ou seja, dia 21/05/2020. Logo, no dia 22/05/2020, ocuparia a vice-liderança mundial nos números de contaminações. Ressaltamos que o Brasil ultrapassou a Rússia e ocupou o posto de segundo lugar em contaminações no dia 19/05/2020.
Esperamos que este artigo contribua para o bom aprendizado do Cálculo Diferencial e possa desmitificar certas questões que permeiam o ambiente da universidade.
Para os estudos futuros, sugerimos associar a Derivada a uma das outras configurações epistêmicas a uma situação-problema tal qual fizemos com o número de contaminados pelo novo Coronavírus.





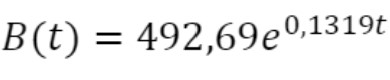 e
e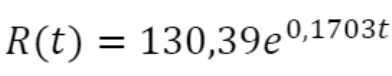 em relação à variável é feito conservando o mesmo registro de representação simbólico-algébrico:
em relação à variável é feito conservando o mesmo registro de representação simbólico-algébrico: 
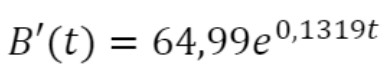 · e a Derivada da função que representa a velocidade de contaminação do Brasil no instante qualquer;
· e a Derivada da função que representa a velocidade de contaminação do Brasil no instante qualquer; 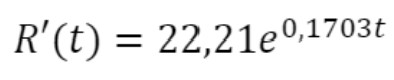 e a Derivada da função que representa a velocidade de contaminação da Rússia no instante qualquer.
e a Derivada da função que representa a velocidade de contaminação da Rússia no instante qualquer. 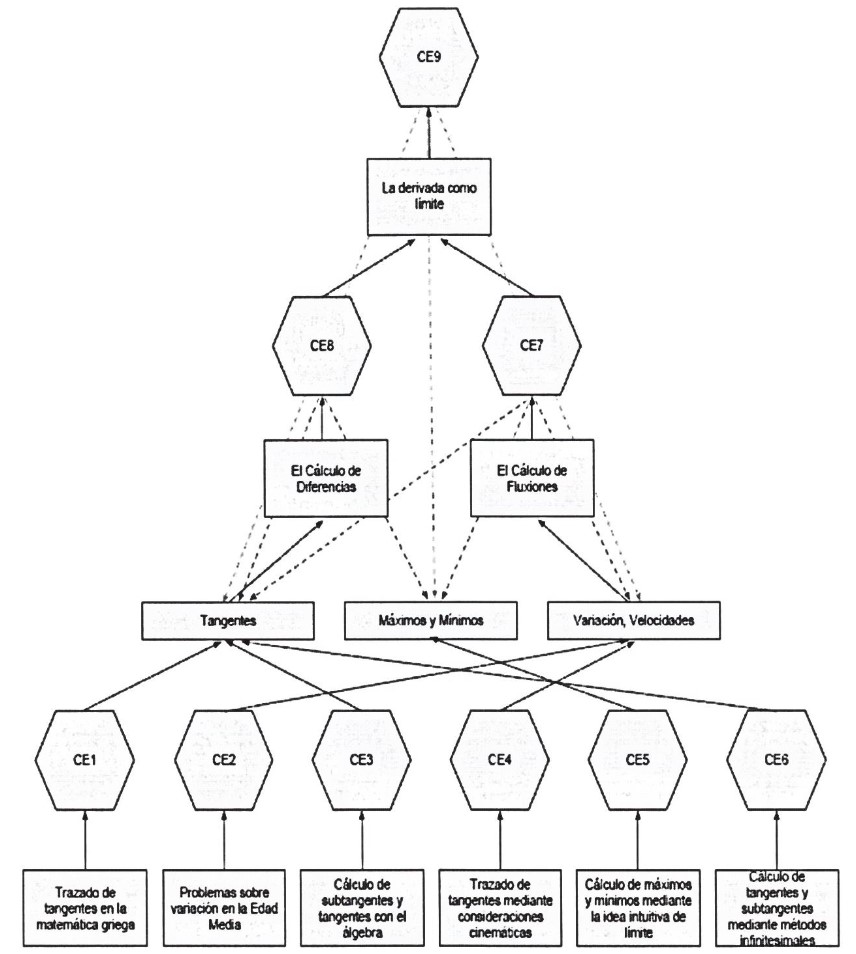
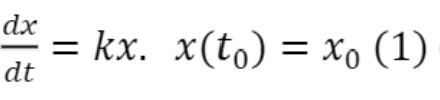 em que é uma constante de proporcionalidade, ocorre em muitas teorias científicas envolvendo crescimento ou decrescimento populacional.
em que é uma constante de proporcionalidade, ocorre em muitas teorias científicas envolvendo crescimento ou decrescimento populacional. 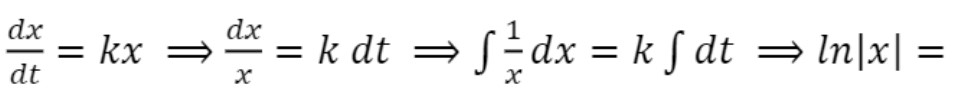
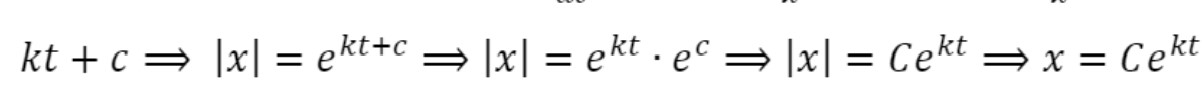 , em que C é uma constante real.
, em que C é uma constante real. 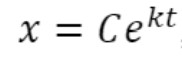 , que é solução da equação diferencial
, que é solução da equação diferencial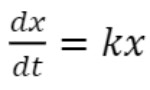 que mede o crescimento ou decrescimento populacional.
que mede o crescimento ou decrescimento populacional. 




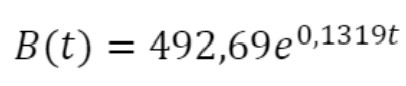 e; para a Rússia,
e; para a Rússia, 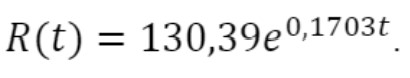 .
. 
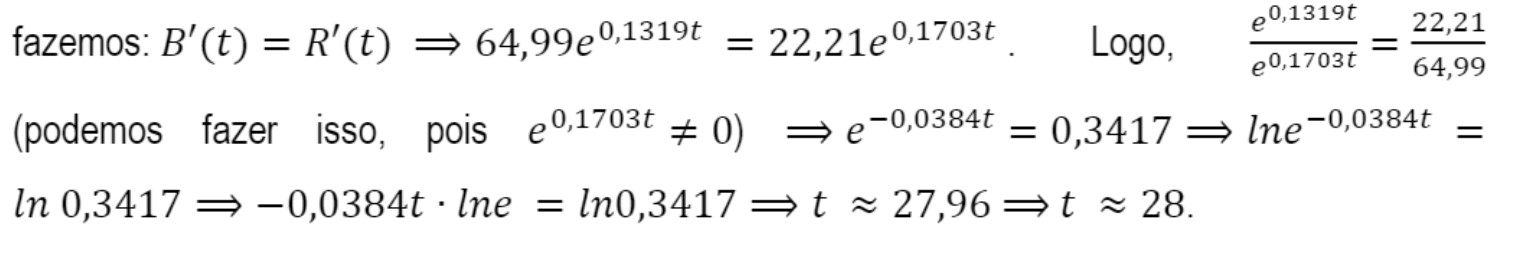



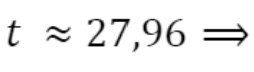
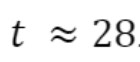 .
. 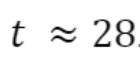 que encontramos, nas duas formas de resolução do problema, significa que o Brasil igualaria a Rússia em 28 dias, aproximadamente, a partir do dia 23/04/2020, ou seja, dia 21/05/2020, então, no dia 22/05/2020, ocuparia a vice-liderança mundial nos números de contaminações
que encontramos, nas duas formas de resolução do problema, significa que o Brasil igualaria a Rússia em 28 dias, aproximadamente, a partir do dia 23/04/2020, ou seja, dia 21/05/2020, então, no dia 22/05/2020, ocuparia a vice-liderança mundial nos números de contaminações 

