INTRODUCCIÓN
La manera en que se enseñan los conceptos y la resolución de problemas que involucran fracciones es una de las tareas más difíciles para los docentes de Matemática que abordan este contenido en la educación primaria, debido a que, según Morales (2014), “se prioriza el fraccionamiento de la unidad o se centra en la mecanización de algoritmos, que dejan de lado el razonamiento y la comprensión del concepto que permitirían el planteamiento y solución de diferentes problemas matemáticos”.
En algunos sectores se considera que aprender a resolver problemas es aprender a aprender y que el enfoque más conveniente con respecto a alcanzar este objetivo en entornos de enseñanza y aprendizaje es el aprendizaje basado en problemas (Tandogan, & Orhan, 2007) citados por Gonzales y Maz (2018). El propio currículum de quinto grado de educación primaria de Nicaragua lo establece como una de las competencias que todo estudiante debe desarrollar.
Sin embargo, los problemas que involucran alguna aplicación de la matemática escolar se dejan para el final de una unidad o para el final del programa, por lo cual la mayoría del tiempo los estudiantes aprenden matemáticas formales y abstractas fuera de contexto. Este hecho fue puntualizado por Morales (2014), el cual manifiesta que estos problemas suelen ser omitidos por falta de tiempo. Esto conlleva a que la competencia de resolución de problemas no sea desarrollada por los estudiantes.
En el contexto educativo nicaragüense ese fenómeno se manifiesta debido a que se prioriza cumplir la programación de los contenidos en un tiempo establecido. Por ello el interés del presente artículo es identificar los errores que cometen una muestra de estudiantes de quinto grado de educación primaria al resolver problemas aditivos de agregación y agrupación. Para lograr esta identificación de errores, aplicamos un cuestionario, compuesto por 4 ítems, que evalúa aspectos de desarrollo procedimental, traducción del lenguaje natural al aritmético y procesos de carácter conceptual en la resolución de problemas aditivos. El análisis lo efectuamos a partir de dos metodologías: análisis minucioso de las producciones de los estudiantes y mediante herramientas de la estadística descriptiva. Esto nos permitió una clasificación de errores que están dentro de los propuestos en la literatura y otros errores que no habían sido clasificados.
METODOLOGÍA
La presente investigación, según su enfoque es mixta. Cuantitativa porque hace uso de herramientas de la estadística para al tratamiento de la información de los datos a través de la categorización y la descripción de las propiedades, características y los perfiles de las personas, grupos, comunidades, procesos y objetos o cualquier otro fenómeno que se someta al análisis (Hernández, Fernández y Baptista, 2010). Cualitativa ya que es una actividad sistemática orientada a la comprensión en profundidad de fenómenos educativos y sociales (en nuestro caso los errores cometidos por estudiantes de 5˚en la resolución de problemas aditivos de enunciado verbal con fracciones), a la transformación de prácticas y escenarios socioeducativos, a la toma de decisiones y también hacia el descubrimiento y desarrollo de un cuerpo organizado de conocimiento (Bisquerra, 2009). En cuanto a su nivel es descriptiva porque trata de la caracterización de un hecho, fenómeno, individuo o grupo, con el fin de establecer su estructura o comportamiento (Fidias, 2012), además, tiene como punto primordial la identificación de los errores cometidos por estudiantes de educación primaria en la resolución de problemas aditivos de enunciado verbal tanto de agregación como de agrupación. Para Bisquerra (2009) los estudios prospectivos avanzan en la recopilación de los datos, a la vez que se van sucediendo los hechos, luego la investigación es transversal y prospectiva porque la recogida de datos fue en un único período de tiempo, específicamente en el II semestre del año lectivo 2020, y toda la información se recogió, de acuerdo con los criterios del investigador y para los fines específicos de la investigación, después de la planeación de ésta.
Objetivos
- 1.
Identificar
los errores cometidos por estudiantes de 5˚ grado de Educación Primaria en la
resolución de problemas aditivos de enunciado verbal.
- 2.
Identificar
la familia de problemas (agregación o agrupación) que genera la mayor cantidad
de errores en los estudiantes durante el trabajo con problemas aditivos de
enunciado verbal.
Participantes
En la investigación participaron 20 de los 37 estudiantes matriculados en el quinto grado C de Educación Primaria del Colegio Público Maestro Calixto Moya de Masatepe. La edad de los participantes oscila entre 10 y 13 años, además, 8 de los participantes fueron niñas y los 12 restante fueron niños. No fue necesario aplicar alguna fórmula para calcular el tamaño de la muestra, ya que se seleccionó el quinto grado C porque fue al que se tuvo acceso, y la muestra final fue de 20 debido a que eran los que asistían a clase de forma regular. Para finalizar, destacar que el tipo de muestreo empleado fue el muestro no probabilístico causal o accidental, que es aquel en el cual el investigador selecciona directa e intencionalmente la muestra, debido fundamentalmente a que tiene fácil acceso a la misma y es representativa de la población (Gil, Rodríguez y García, 1995; Albert, 2006).
Instrumentos
Para el levantado de la información se empleó como técnica la encuesta y de instrumento un cuestionario, el cual estuvo constituido de 4 problemas aditivos de enunciado verbal, de los cuales 2 eran de agrupación y 2 de agregación. Los dos primeros problemas involucran fracciones con iguales denominadores y los últimos dos fracciones con distintos denominadores. Los problemas fueron extraídos del libro de texto de quinto grado El poder de las Matemáticas, de Avendaño D. (2019). y luego adecuados al nivel de segundo ciclo de la educación primaria nicaragüense. Este instrumento fue validado en cuanto a contenido y pertenencia por el profesor titular y la directora del Colegio Público.
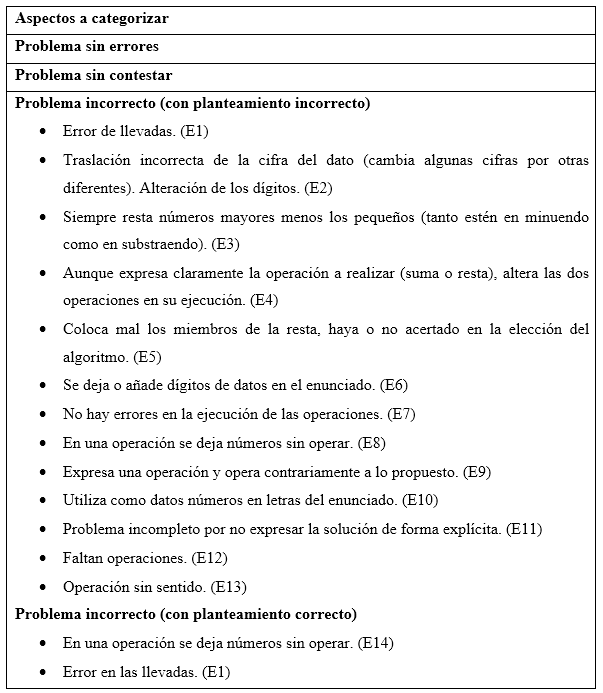
En cuanto a los criterios de análisis para la identificación de los errores, se tomó la clasificación que recoge el conjunto de todos los errores aritméticos en problemas verbales (Tabla 1) propuesta por Casajús (2005) y empleado recientemente en Del Rosal, Gutiérrez y Maz-Machado (2018) y Maz-Machado, González de Quevedo Herranz y Argudo-Osado (2018). Además, se recogieron y contabilizaron todos los errores evidenciados en las producciones de los estudiantes según la clasificación referida. Cuando el planteamiento era incorrecto, se continuaba corrigiendo para verificar si existían errores en la ejecución de las operaciones. De igual forma, en un planteamiento correcto, no se acababa el análisis hasta recolectar todos los errores cometidos.
Tabla 1
Código de
error
RESULTADOS
Con el fin de reportar de forma clara y sencilla los hallazgos producto de la investigación, hemos dividido este acápite en dos partes: En la primera, reportamos todos los errores evidenciados en las producciones de los estudiantes durante el trabajo con los problemas presentes en el instrumento. En la segunda, presentamos la descripción de la distribución de la totalidad de los errores según el tipo de error, la familia de problemas (agrupación o agregación) y el sexo.
Errores evidenciados en las producciones de los estudiantes.
De los 15 errores presentes en la clasificación de Casajús (2005) solo se logró obtener evidencia de 4 de ellos: Siempre resta los números mayores menos los pequeños (E3), No hay errores en la ejecución de las operaciones (E7), Problema incompleto por no expresar la solución de forma explícita (E11), Operación sin sentido (E8). Además, se identificó 10 errores que no pertenecen a la clasificación de Casajús, a saber, Traducción incorrecta de datos a un lenguaje aritmético (D1), No respeta la estructura de resolución de problemas (D2), Inventa datos (D3), Opera únicamente los numeradores (D4), Aplica operación contraria (D5), Simplificación incompleta (D6), Sin simplificar (D7), Simplificar de manera inadecuada (D8), Aplica incorrectamente el algoritmo de la suma de fracciones con distintos denominadores (D9), Escribe como respuesta datos del enunciado (D10); de estos D6 y D9 pertenecen a una clasificación presente en Gonzales (2015), el error D1 aparece planteado en Morales (2014) como una posible dificultad de los estudiantes al momento de resolver un problema verbal, los demás errores constituyen el primer hallazgo del presente trabajo.
A continuación, presentamos dos ejemplos que evidencian los errores cometidos por los estudiantes en la resolución de problemas aditivos sobre fracciones.
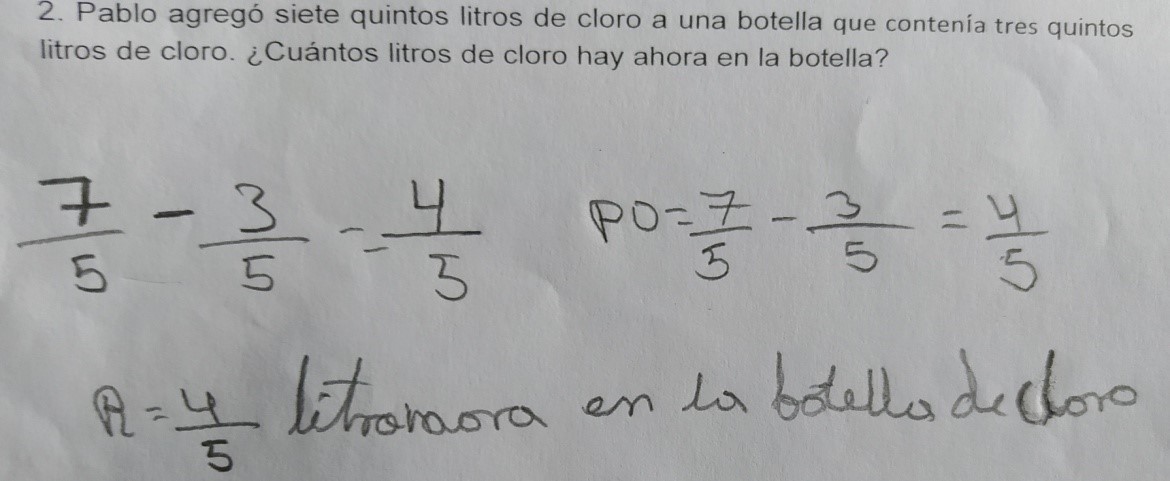
No hay errores en la ejecución de las operaciones (E7).
Podemos
observar que el estudiante plantea incorrectamente los datos del problema al no
identificar correctamente la operación que se requería aplicar, sin embargo,
ejecuta correctamente la resta planteada.
No respeta la estructura de resolución de
problemas (D2).
Referente a
la estructura de resolución de problemas podemos observar que el estudiante no
escribe datos, al planteamiento de operaciones lo nombra como Re y a la
respuesta como Po. Esto se puede atribuir al poco aprendizaje adquirido sobre
la estructura de resolución de problemas.
Distribución total de los errores
Una vez identificados los errores que los estudiantes cometen durante el trabajo con problemas aditivos de enunciado verbal que involucren fracciones, resulta interesante saber qué tan frecuentes son estos errores, lo cual nos permitirá inferir acerca de su persistencia.
En total se encontró que el 100% de los problemas presentan al menos un error en su resolución. Además, todos los problemas fueron trabajados por los estudiantes, lo cual nos indica que tenían ideas y/o estrategias para abordar los problemas.
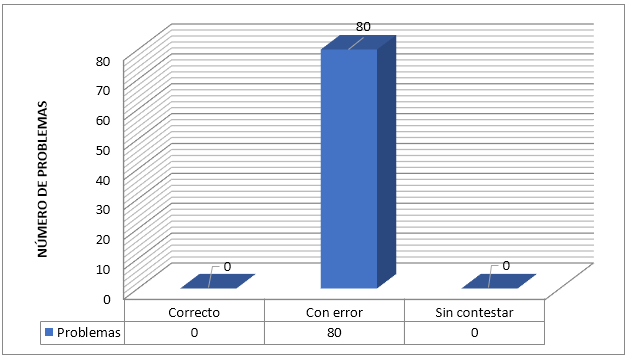 Gráfico 1
Frecuencia de problemas según
respuestas de los estudiantes.
Gráfico 1
Frecuencia de problemas según
respuestas de los estudiantes.
Al tener en cuenta la frecuencia con
la que ocurren cada uno de los errores evidenciados se tiene que, globalmente
de los 15 tipos de errores considerados en la clasificación de Casajús (2005),
4 de ellos están presentes en las producciones de los estudiantes. De estos el más frecuentes es E7 con un porcentaje del
7.11% respecto al total. De los errores que no están considerados por Casajús
los más frecuentes son: D1,
D2 y D9
con un porcentaje de 14.13%, 30.04% y 12.25%, respectivamente.
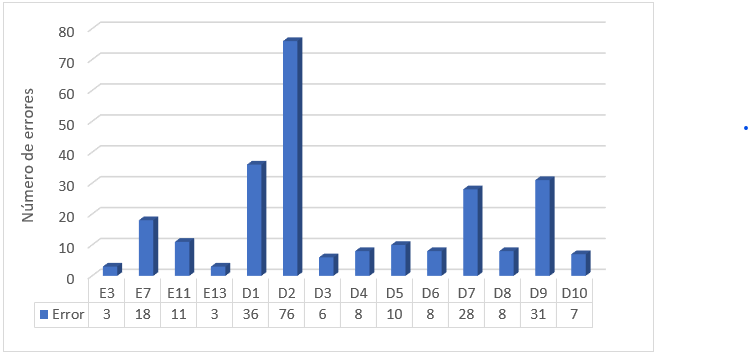 Gráfico 2
Frecuencia de los errores presentes
en el estudio.
Gráfico 2
Frecuencia de los errores presentes
en el estudio.
Atendiendo a la familia de problemas,
para la familia de agregación se cometieron 13 tipos de errores de los 14
identificados, siendo los más frecuentes: No
respeta la estructura de resolución de problemas (D2), Sin simplificar (D7), Traducción
incorrecta de datos a un lenguaje aritmético (D1) y Aplica incorrectamente el
algoritmo de la suma de fracciones con distintos denominadores (D9).
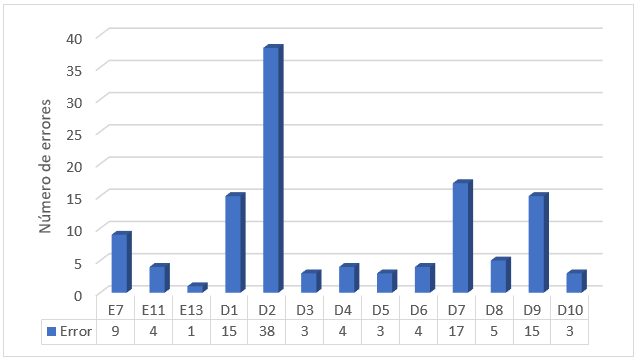 Gráfico 3
Frecuencia de los errores
presentes en los problemas de agregación.
Gráfico 3
Frecuencia de los errores
presentes en los problemas de agregación.
En los problemas de la familia de
agrupación se identificaron los 14 errores, siendo los más frecuentes: No
respeta la estructura de resolución de problemas (D2), Traducción incorrecta de datos a
un lenguaje aritmético (D1)
y Aplica incorrectamente el algoritmo de la suma de fracciones con
distintos denominadores (D9).
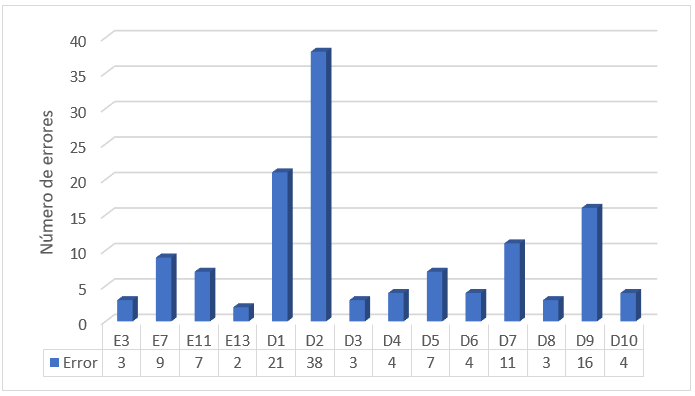 Gráfico 4
Frecuencia de los errores presentes
en los problemas de agrupación.
Gráfico 4
Frecuencia de los errores presentes
en los problemas de agrupación.
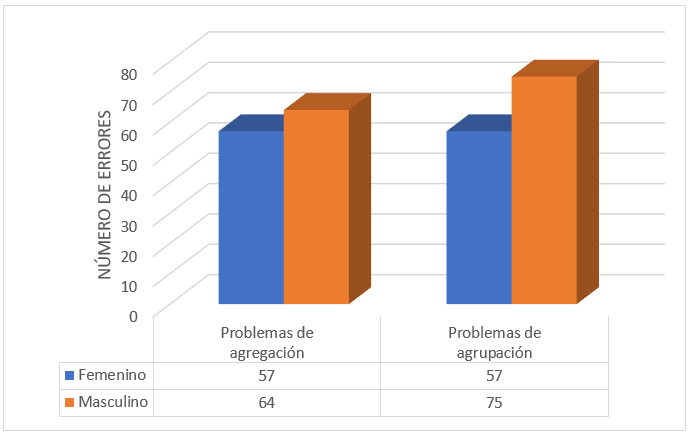
Al revisar los errores por familia de
problemas y por sexo se obtiene que los varones cometieron más errores que las
mujeres, con porcentajes de 54.94% y 45.06%, respectivamente. Además, para las
mujeres, ambas familias generan la misma dificultad, mientras que los varones cometen
más errores en la familia de agrupación, lo cual significa que les genera mayor
dificultad.
CONCLUSIONES
Después de haber realizado el proceso investigativo, con los datos obtenidos, podemos confirmar que los estudiantes presentan dificultades en la interpretación correcta del enunciado de un problema y al operar fracciones de distintos denominadores.
Se logró identificar que los errores más cometidos por estudiantes fueron: No respeta la estructura de resolución de problema (D2), Traducción incorrecta de datos a un lenguaje aritmético (D1) y Aplica incorrectamente el algoritmo en la suma de fracciones de distintos denominadores (D9), los cuales representan el 30.04%, 14.13% y 12.25% del total de errores cometidos en el estudio, respectivamente. Es importante destacar que ninguno de los estudiantes intentó encontrar fracciones equivalentes para sumar fracciones de distintos denominadores, esto quiere decir que no conocen o no dominan el algoritmo de la suma de fracciones vía ampliación de fracciones.
Los datos obtenidos muestran que se cometieron más errores en los problemas de Agrupación (52.17%), sin embargo, los porcentajes de errores cometidos en cada familia de problemas respecto al total de errores cometidos en el estudio, son similares.
En el contexto nicaragüense, la clasificación de Casajús (2005) resulta insuficiente para realizar una clasificación de errores en educación primaria sobre fracciones, por lo cual nos proponemos como trabajo futuro el diseño y validación de un instrumento que permita identificar los errores que cometen los estudiantes durante sus producciones en la resolución de problemas aditivos de enunciado verbales que involucren fracciones.
Además, se pone en evidencia que los estudiantes, aunque tienen ideas para resolver problemas, estas presentan inconsistencia y no logran concretizarla por fallas en las operaciones con fracciones y la poca práctica en la traducción del problema verbal al lenguaje aritmético.
BIBLIOGRAFÍA
Albert, M. (2006). La investigación educativa. Claves Teóricas. Madrid: McGraw-Hill.
Bisquerra, R. (2009). Metodología de la investigación educativa. Madrid: La Muralla.
Del Rosal, A., et al (2018). Errores en la resolución de problemas aritméticos de cambio y combinación en alumnos de 2do grado de primaria.
Fidias, G. (2012). El proyecto de investigación: Introducción a la metodología científica (ed.). República Bolivariana de Venezuela: EDITORIAL EPISTEME, C.A.
Gonzales, D. (2015). Errores comunes en el aprendizaje de las fracciones: Un estudio con alumnos de 12/13 años en Cantabria.
Gonzales, M., Maz, A. (2018). Análisis de errores en resolución de problemas aditivos de enunciado verbal en educación primaria.
Gil, J., Rodríguez, G., y García, E. (1995). Estadística básica aplicada a las ciencias de la educación. Sevilla: Kronos.
Hernández, R., Fernández, C., & Baptista, M. (2010). Metodología de la investigación. México: McGra-Hill.
León, C., Maz, A., Madrid, M., Casas, J. (2013). Errores de los estudiantes a maestro cuando trabajan con fracciones.
Morales, R. (2014). Dificultades y errores en la solución de problemas con números racionales.
Rodríguez, C., Navarro, C., Castro, A., García, M. (2019) Estructuras semánticas de problemas aditivos de enunciado verbal en libros de textos mexicanos.
Salgado, J., et al, (2019), Matemática 5to grado, Managua, Nicaragua, MINED.
Zubieta, J. (2018). Tipificación de errores y dificultades en el desarrollo de las funciones trigonométricas de estudiantes de grado décimo.