Introducción

El proceso de enseñanza de las matemáticas ha sido a lo largo de la historia uno de los aspectos educativos más cuestionados debido a los problemas que sistemáticamente enfrentan los estudiantes en todos los niveles del sistema educativo venezolano. Trabajos de hace algunos años como el de Planchart (1990), indicaban profundas brechas entre lo deseado y la realidad en la enseñanza matemática, al punto de considerar para ese año que Venezuela era un país numéricamente analfabeta. Esta afirmación hecha hace casi cuatro décadas reclamaba la atención sobre una situación que protagonizaban directamente los docentes de Matemática y sus estudiantes; e indirectamente otros factores institucionales (Estado, las instituciones educativas, las familias, entre otros).

Posteriormente los focos de atención sobre el problema, que en principio estuvieron orientados al rendimiento académico estudiantil como un indicador de la calidad de la educación y del sujeto en situación de aprendizaje, se han trasladado a aspectos tecnológicos poco atendidos como las estrategias de enseñanza y la interacción docente estudiante. La incorporación de estos elementos se funda en la aceptación de la complejidad del problema. González (2014), en la búsqueda de información relevante para contribuir a mitigar la situación logró identificar algunos aspectos que caracterizan al estudiante universitario venezolano en el campo de las matemáticas: (a) presentan fallas en capacidades y conocimientos correspondientes a los niveles educativos anteriores; (b) estudian memorística y mecánicamente; (c) tienen dificultades para el análisis y la comprensión de hechos y fenómenos; (d) carecen de criticidad; (e) carecen de hábitos de estudio adecuados; y, (f) poseen una deficiente base formativa y analítica.

Sin embargo, en este campo del saber poco se ha investigado acerca del docente venezolano y los factores inherentes a su desempeño y actitudes hacia la enseñanza. Estos aspectos resultan de interés para explorar las relaciones que se establecen con la enseñanza de la matemática, puesto que pueden orientar la conducta y justificar los comportamientos que se realizan en dicha praxis. Una manera de explorar la complejidad de la enseñanza pasa por intentar comprender el significado o significados del término enseñar. Martínez y Arellano (2011), han abordado el proceso desde la búsqueda del conocimiento de sentido común y sus dimensiones con base en la participación de las personas en contextos sociales. De allí se desprende que el conocimiento de sentido común de la enseñanza y el aprendizaje puede constituir un factor explicativo de la vida cotidiana de los estudiantes.

La búsqueda de las expresiones del sentido común puede ser emprendida desde el punto de vista de las representaciones sociales que los docentes y estudiantes guardan sobre los procesos inherentes a la marcha del sistema didáctico de las matemáticas; de sus actores y elementos (conocimiento, estrategias, recursos, docente, estudiante). De la identificación de las representaciones sociales pueden surgir las explicaciones que realizamos sobre los hechos y los objetos sociales y sus procesos atributivos. Por tanto conocer tales representaciones contribuirá a comprender los procesos de elaboración y construcción de conocimiento matemático y las prácticas didácticas en las matemáticas.

Con base en estas premisas interaccionistas se concibe la posibilidad de considerar las matemáticas, y sus procesos de enseñanza y aprendizaje como objetos sociales dinámicos cuyo abordaje permitirá develar el funcionamiento del sistema didáctico propio de esta área del saber.

En este artículo pretendemos identificar las representaciones sociales de los docentes sobre la enseñanza de los contenidos de Matemática II en los programas de Ingeniería de la Universidad Nacional Experimental Francisco de Miranda (UNEFM).

En la UNEFM, en la administración de la unidad curricular Matemática II que se dicta en los programas de ingeniería, se propicia la enseñanza y aprendizaje a través de procedimientos que luego son reproducidos por los estudiantes. Tal unidad es cursada por los estudiantes de los diferentes programas de Ingeniería, en ella se requiere al docente el uso de estrategias que faciliten la comprensión y aplicación de la integral de Riemman en situaciones acordes al perfil profesional, a la resolución de problemas, y al empleo de la terminología básica que pondrá en práctica cuando profundice en los contenidos específicos de las unidades curriculares de semestres posteriores.

Antecedentes y Revisión Teórica

Martínez (2008), explica que hay quienes piensan que la matemática es difícil de aprender, que solo gusta a un reducido grupo de estudiantes porque tiende a ser misteriosa, aburrida, compleja y por tanto tiende a ser aborrecida u odiada por quienes no la entienden generando, en consecuencia, frustración, angustia y aversión casi colectiva, en vez de satisfacciones por los logros obtenidos. Una situación así hace difícil tanto su enseñanza como su evaluación, pues, seguramente, los resultados serían deficientes y generarían gran preocupación entre los actores involucrados en esos procesos.

Otra crítica se centra en el estilo tradicional de ejercer la enseñanza (González, 2008), que se caracteriza por utilizar casi exclusivamente el método expositivo, el cual ha sido cuestionado ampliamente porque presenta inconvenientes tales como la poca involucración del alumno en su actividad de aprendizaje y desmotivación por el papel pasivo del mismo durante las sesiones.

Para Álvarez y Ruiz (2008), los docentes continúan utilizando en el área de matemática metodologías apoyadas en la exposición de reglas y principios con contenidos orientados hacia la ejecución de procedimientos, métodos, reglas y algoritmos. Así mismo, se observa en carreras como la ingeniería, que la prioridad del desempeño docente se orienta hacia la transmisión dogmática de unos contenidos reflejados en el programa de la asignatura.

Martínez (2008), indica que la problemática se torna aún más grave cuando, por ejemplo, se hace referencia a la formación matemática y didáctica de los docentes que actualmente enseñan matemática en los centros educacionales, pues, se han encontrado casos donde la misma ha sido catalogada como muy deficiente. En algunos casos se ha determinado que la mayoría de los enunciados de los problemas de matemática que elaboran los docentes para que sean desarrollados por sus estudiantes tienen problemas de construcción; además existen docentes de matemática que tienen tanto problemas de conocimiento como deficiencias para gestionar las dificultades que se le presentan con los estudiantes, evidenciándose cuando estos cometen errores similares a los de sus estudiantes y cuando dan muestras de no poseer suficientes recursos cognitivos para responderles.

Una visión más amplia del problema es provista por Morales et al (2010), quienes señalan que además de los factores cognitivos, socioculturales y socioeconómicos, existen factores de tipo psicológico, como la motivación y la actitud, que pueden afectar al aprendizaje de la matemática. Por lo tanto, no solo tener el conocimiento es válido, siendo la desmotivación uno de los obstáculos que generan dificultades en la comprensión y resolución en matemática y a este aspecto afectivo debería prestarse atención en el aula. Sobre este particular, Suárez (2014) establece que en la enseñanza de la matemática, existen dos problemas que deberían ser el asunto eje a resolver de cualquier docente: el primero radica en convencer a los estudiantes de que dicho saber puede ser aprendido con facilidad pero con esfuerzo y dedicación, el segundo, que tal conocimiento es y será útil e importante en su vida cotidiana, académica o profesional.

Algunos autores reportan que existen desfases derivados de la utilización de métodos pedagógicos inadecuados, de la organización de las instituciones educativas, de las dificultades de adaptación del diseño curricular al ritmo de los cambios científicos, tecnológicos, sociales, económicos y culturales, así como docentes confundidos, apáticos y desilusionados (Álvarez y Ruiz, 2008).

Montes y Machado (2011) a su vez aseguran que desde el punto de vista educativo es necesario, entonces, utilizar cada vez más en las aulas herramientas propias de esta generación, para motivarlos y desarrollar sus habilidades a partir de sus estilos, los modos y formas en que aprenden. Por su parte, González (2008) indica que una forma de mejorar la praxis docente es examinar la manera de practicar la enseñanza. De acuerdo a nuestro interés es posible a partir de allí encontrar respuestas enriquecedoras para el desarrollo de los contenidos en Matemática II de los futuros ingenieros de la UNEFM.

Sobre la base de las ideas expuestas y en concordancia con lo que establece Martínez (2008), se pretende explorar la práctica docente de la unidad curricular Matemática II de los programas de ingeniería de la UNEFM, con la intención de identificar sus representaciones sociales en al menos tres dimensiones básicas (a) lo cognitivo: referido al contenido matemático, (b) lo metodológico: relacionados con los factores técnicos, metodológicos y docentes inherentes al contenido y (c) el afectivo: creencias, emociones y actitudes hacia la matemática y del contenido en particular; todo ello en el marco de las innovaciones educativas.

Dentro de esta última dimensión tienen cabida las representaciones sociales, que son una expresión del conocimiento de sentido común, cuya naturaleza reside en el carácter social de los procesos que las producen.

Moscovici (1979) considera a las Representaciones Sociales (RS) como el conjunto de ideas y explicaciones que tienen su origen en la vida cotidiana a partir de la interacción y comunicación entre los sujetos, resultando una forma del conocimiento de sentido común típico, tal como señalan Banchs (2001), Villarroel (2007) y Jodelet (2007). Para Moscovici las RS se pueden conformar a partir de la reinterpretación de las ideas científicas a las cuales se tiene acceso por medio de los procesos de educación formal o informal, o a través de los procesos de socialización, lecturas o de información audiovisual disponible en los mas media. Jodelet (2007), considera que estos constructos permiten a los sujetos reconstruir y manifestar, dar sentido y clasificar las situaciones, los fenómenos y los sujetos, para así poder actuar a posteriori.

Las representaciones sociales tienen una dimensión cognoscitiva, quien las considera como “sistemas cognoscitivos en los que es posible reconocer la presencia de estereotipos, opiniones, creencias, valores y normas que suelen tener una orientación actitudinal positiva o negativa" (Araya, 2001, p.11).

Esta concepción es compartida por Moscovici (1979, p. 57) quien expresa bajo una adopción de un esquema hereditario, que la lógica causal de las representaciones sociales se reduce a la siguiente frase: “Dime con quién andas y te diré quién eres”.

La construcción de una representación social requiere de dos procesos que son el “anclaje” y la “objetivación” (Moscovici, 1979; Araya, 2002). El primero consiste en un proceso de categorización en el cual se le asigna un nombre a sujetos, grupos o cosas; la acción consiste en integrar cognitivamente el objeto al sistema de pensamiento preexistente. La “objetivación” se concibe como el proceso de transformar categorías abstractas en algo concreto, realidades físicas o imágenes.

Para Ponte y Tineo (2013) y Rondón (2014), las RS están formadas por tres ejes: la información, la actitud y la representación. Esta última, expresa la organización del contenido de la representación en forma jerarquizada; puede variar inter o intra grupalmente. Se organiza en torno al núcleo figurativo (simbólico) que es la parte más sólida y estable de la representación. Éste se construye a través del proceso de objetivación y proviene de la transformación de contenidos conceptuales heterogéneos en imágenes que permiten construir una visión más concreta del objeto representado, así las ideas abstractas se convierten en formas icónicas.

Estructura y Teoría del Núcleo Central

Para Larrañaga (2005), la variabilidad de las RS se explica con base en la estructura de sus contenidos. Jodelet (1991) y Abric (2001), están de acuerdo en el hecho de que la representación presenta un contenido estructurado. Señala Larrañaga que recientes investigaciones se refieren a la existencia de un núcleo representativo, aunque recibe denominaciones diferentes por parte de los investigadores: núcleo figurativo (Moscovici, 1979), núcleo central (Abric, 2001) y principios organizadores (Doise, 1991).

Para Abric (2001), el núcleo central está conformado por elementos fuertemente conectados entre ellos que le dan a la representación su significado. Tiene una determinación marcadamente social y está vinculado a normas y valores, lo que le hace permanecer en la memoria colectiva del grupo que la elabora y ser bastante estable y rígido. Se corresponde con la parte más consensual y homogénea de una representación social.

Los elementos del sistema periférico (SP) son dependientes del núcleo central, pero son más accesibles, vivos, comunicables, dinámicos y variables, además de ser flexibles permitiendo la adaptación a las circunstancias particulares. Para Ponte y Tineo (2013), estas incluyen informaciones resguardadas, seleccionadas e interpretadas, juicios, estereotipos y creencias. Los elementos periféricos pueden estar jerarquizados y aquellos más próximos al núcleo tienen un rol en la concreción del significado de la RS; mientras que los más lejanos ilustran, aclaran, justifican la RS.

Estrategia metodológica

El lugar donde se llevó a cabo la investigación fue el Complejo Académico El Sabino de la Universidad Nacional Experimental Francisco de Miranda, en el Departamento de Física y Matemática en el lapso académico III-2016.

Para el logro del objetivo se planteó el procedimiento descrito por Moscovici (1961/1979) sobre la teoría de las representaciones sociales y de Abric (1996) acerca de la teoría del núcleo central. Respecto a la investigación, se pretende identificar las representaciones sociales del proceso de enseñanza de los contenidos de Matemática II, información de primera mano tomada de los propios docentes que han dictado la unidad curricular a los estudiantes que cursan los distintos programas de ingeniería de la UNEFM que proviene de su experiencia dentro del ambiente social donde se desenvuelven y del intercambio de comunicaciones de su grupo social.

En el caso particular sobre el proceso de enseñanza de los contenidos de la unidad curricular Matemática II, los docentes poseen una representación fundamentada de su quehacer educativo y esa información pasa a ser significante como se mencionó anteriormente, debido a sus experiencias académicas desde sus inicios hasta la actualidad, a la pertinencia en los acuerdos establecidos con la universidad, a sus relaciones con las autoridades; pares y los propios estudiantes, su participación docente en el aula de clases y fuera de ella, a la afectividad asociada con la praxis docente y la repercusión social de la misma.

El paradigma que sustenta este apartado es de tipo cualitativo cuya metodología fue apoyada en el análisis cuantitativo para la estructuración de las representaciones sociales sustentado en el modelo de Moscovici (1961/1979), además se fundamenta en ambos enfoques ya que se analiza y caracteriza las dimensiones de la representación social y se hizo énfasis en la estructura del campo de la representación desde la teoría del núcleo central; todo esto con la finalidad de identificar las representaciones sociales sobre el proceso de enseñanza de los contenidos de la unidad curricular Matemática II en la UNEFM.

En el caso particular, los ciento seis códigos que surgieron como resultado de las entrevistas aplicadas a los docentes se agruparon en categorías en un proceso de codificación axial, puesto que la idea es relacionar los códigos entre sí para avanzar a niveles cada vez más complejos en cuanto a las posibles categorías a considerar. Durante el proceso se generaron veinte metacódigos y con ello se logra la identificación del contenido de la representación a través de un conjunto de conceptos relacionados entre sí utilizando como criterio las cualidades descritas por Moscovici (1961/1979) que permiten dar cuenta de las cualidades del objeto de estudio.

Con los metacódigos se procedió a diseñar una matriz de doble entrada que fue llenada por cada docente, simplemente marcando con una equis si considera que los códigos se corresponden, con la finalidad de estudiar las relaciones entre los mismos. Con la información recolectada por medio de estas técnicas se procedió al análisis estructural a técnicas cuantitativas como la técnica de escalerización con la finalidad de obtener una mayor profundización y ampliación de las representaciones sociales sobre el proceso de enseñanza de los contenidos de Matemática II.

Según Ponte y Caballero (2005), para la técnica de escalerización se construye una matriz de implicación (F) donde cada elemento Fij de la matriz, corresponde al número de respondientes que proponen la meta i como la fuente de la meta. En la matriz, por cada meta se definen dos medidas en “grados de entrada” y “grados de salida”. La primera indica la frecuencia de la meta al final de la relación entre las metas. Los grados de salida indica la frecuencia de la meta en el medio. Con estas dos medidas, por cada meta, se calcula el índice de “Abstracción” (rango de 0-1). Para evaluar la importancia de una simple meta en la representación mental, además del índice de “Abstracción”, se calcula el índice de “Prestigio” que permite determinar la razón más profunda que implica la práctica docente en la enseñanza de los contenidos de Matemática II en los programas de ingeniería de la UNEFM y el índice de “Centralidad” que expresa el grado en el cual una meta está involucrada en uniones con otras metas.

Hallazgos

De las entrevistas aplicadas a los docentes surgieron ciento seis códigos que luego se agruparon en categorías considerando su coincidencia, similitud y relaciones en un proceso de codificación axial. Para la consolidación de las categorías, se utilizaron criterios basados en el conocimiento sobre el proceso de enseñanza y dominio de los contenidos académicos de la unidad curricular Matemática II que se posee como investigadores del área para finalmente obtener veinte metacódigos

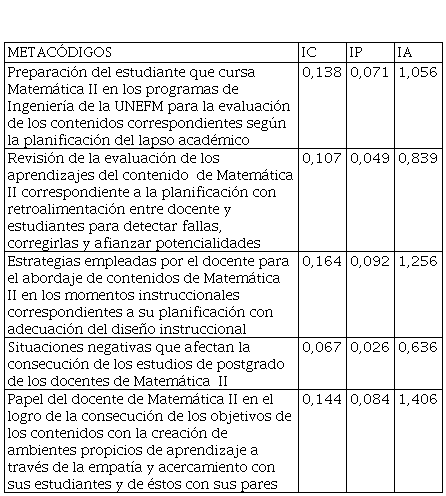
El eje de las representaciones sociales que pretendemos abordar lo constituye la dimensión del campo de representación. En el cuadro 1 se presenta los metacódigos y los resultados del cálculo de los índices de “centralidad” (IC); “prestigio (IP) y “abstracción” (IA), según Millán (2010) con éstos se profundiza en los significados de los contenidos de la representación social. Además se procedió al cálculo de los percentiles, técnica cuantitativa que permite determinar las categorías que pertenecen al núcleo central y a los periféricos en la representación social.

Cuadro 1
Índice de Centralidad, Prestigio y Abstracción de los metacódigos

METACÓDIGOS	IC	IP	IA
Preparación del estudiante que cursa Matemática II en los programas de Ingeniería de la UNEFM para la evaluación de los contenidos correspondientes según la planificación del lapso académico	0,138	0,071	1,056
Revisión de la evaluación de los aprendizajes del contenido de Matemática II correspondiente a la planificación con retroalimentación entre docente y estudiantes para detectar fallas, corregirlas y afianzar potencialidades	0,107	0,049	0,839
Estrategias empleadas por el docente para el abordaje de contenidos de Matemática II en los momentos instruccionales correspondientes a su planificación con adecuación del diseño instruccional	0,164	0,092	1,256
Situaciones negativas que afectan la consecución de los estudios de postgrado de los docentes de Matemática II	0,067	0,026	0,636
Papel del docente de Matemática II en el logro de la consecución de los objetivos de los contenidos con la creación de ambientes propicios de aprendizaje a través de la empatía y acercamiento con sus estudiantes y de éstos con sus pares	0,144	0,084	1,406

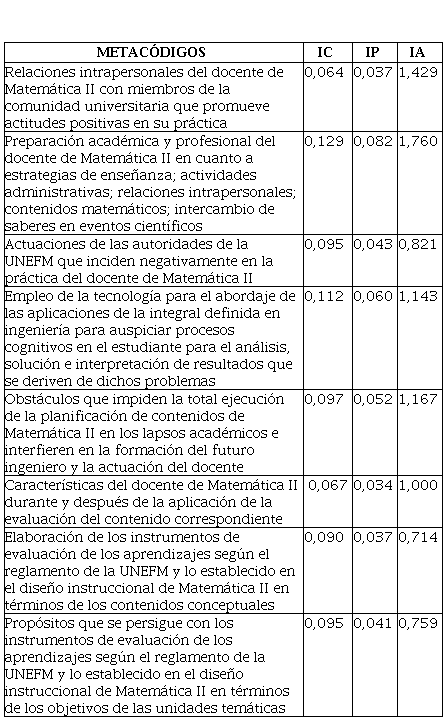
Cuadro 1. (Cont.)

METACÓDIGOS	IC	IP	IA
Relaciones intrapersonales del docente de Matemática II con miembros de la comunidad universitaria que promueve actitudes positivas en su práctica	0,064	0,037	1,429
Preparación académica y profesional del docente de Matemática II en cuanto a estrategias de enseñanza; actividades administrativas; relaciones intrapersonales; contenidos matemáticos; intercambio de saberes en eventos científicos	0,129	0,082	1,760
Actuaciones de las autoridades de la UNEFM que inciden negativamente en la práctica del docente de Matemática II	0,095	0,043	0,821
Empleo de la tecnología para el abordaje de las aplicaciones de la integral definida en ingeniería para auspiciar procesos cognitivos en el estudiante para el análisis, solución e interpretación de resultados que se deriven de dichos problemas	0,112	0,060	1,143
Obstáculos que impiden la total ejecución de la planificación de contenidos de Matemática II en los lapsos académicos e interfieren en la formación del futuro ingeniero y la actuación del docente	0,097	0,052	1,167
Características del docente de Matemática II durante y después de la aplicación de la evaluación del contenido correspondiente	0,067	0,034	1,000
Elaboración de los instrumentos de evaluación de los aprendizajes según el reglamento de la UNEFM y lo establecido en el diseño instruccional de Matemática II en términos de los contenidos conceptuales	0,090	0,037	0,714
Propósitos que se persigue con los instrumentos de evaluación de los aprendizajes según el reglamento de la UNEFM y lo establecido en el diseño instruccional de Matemática II en términos de los objetivos de las unidades temáticas	0,095	0,041	0,759

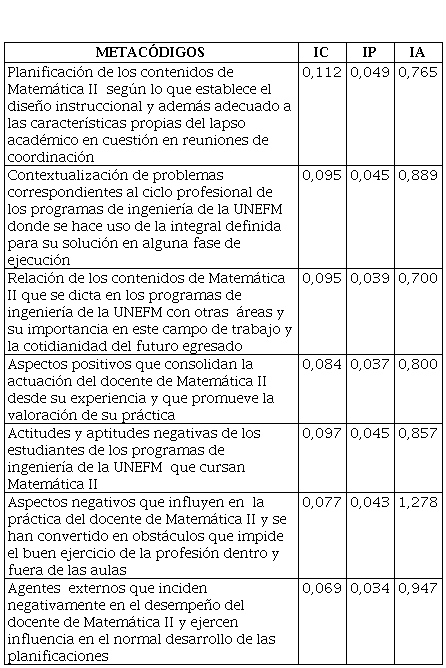
Cuadro 1. (Cont.)

METACÓDIGOS	IC	IP	IA
Planificación de los contenidos de Matemática II según lo que establece el diseño instruccional y además adecuado a las características propias del lapso académico en cuestión en reuniones de coordinación	0,112	0,049	0,765
Contextualización de problemas correspondientes al ciclo profesional de los programas de ingeniería de la UNEFM donde se hace uso de la integral definida para su solución en alguna fase de ejecución	0,095	0,045	0,889
Relación de los contenidos de Matemática II que se dicta en los programas de ingeniería de la UNEFM con otras áreas y su importancia en este campo de trabajo y la cotidianidad del futuro egresado	0,095	0,039	0,700
Aspectos positivos que consolidan la actuación del docente de Matemática II desde su experiencia y que promueve la valoración de su práctica	0,084	0,037	0,800
Actitudes y aptitudes negativas de los estudiantes de los programas de ingeniería de la UNEFM que cursan Matemática II	0,097	0,045	0,857
Aspectos negativos que influyen en la práctica del docente de Matemática II y se han convertido en obstáculos que impide el buen ejercicio de la profesión dentro y fuera de las aulas	0,077	0,043	1,278
Agentes externos que inciden negativamente en el desempeño del docente de Matemática II y ejercen influencia en el normal desarrollo de las planificaciones	0,069	0,034	0,947

Ahora bien, a partir del gráfico 1 se puede observar que el núcleo central está formado por seis categorías según el percentil 75 e indicadas por el índice de “centralidad” que expresa el grado en que una categoría está implicada con otra, siendo “estrategias empleadas por el docente para el abordaje de contenidos de Matemática II en los momentos instruccionales correspondientes a su planificación con adecuación del diseño instruccional” la que reflejó el valor más elevado con un índice de “centralidad” de 0.164 seguido de “papel del docente de Matemática II en el logro de la consecución de los objetivos de los contenidos con la creación de ambientes propicios de aprendizaje a través de la empatía y acercamiento con sus estudiantes y de éstos con sus pares” con 0.144 y de “preparación del estudiante que cursa Matemática II en los programas de Ingeniería de la UNEFM para la evaluación de los contenidos correspondientes según la planificación del lapso académico” con 0.138 de índice de “centralidad”.

La “centralidad” de estas categorías reflejan el hecho de que los docentes de Matemática II se preocupan por lograr en el estudiante aspectos concretos de la integral definida que serán útiles en las unidades curriculares y basan el desarrollo de los contenidos en estrategias que puedan aplicar dentro y fuera del aula en atención a los recursos con que cuenta las cuales emplean durante los momentos instruccionales según su plan de clases sin dejar a un lado los recursos tradicionales.

Continuando con lo relativo, una estrategia que emplea el docente es el aprendizaje basado en problemas, pues según sus comentarios, promueve la participación de los estudiantes en cada una de las etapas de ejecución otorgando la oportunidad que ofrezca alternativas que permitan dar una solución lógica al problema planteado y que se sienta capaz de hacerlo, hecho que estaría en concordancia con los nuevos modelos de enseñanza, donde se pone de manifiesto lo cognitivo a través de las estructuras mentales que se formarían los estudiantes respecto a la integral definida y de lo afectivo, pues entra en juego el papel del docente en crear ambientes de aprendizaje donde hay involucración de todos los estudiantes por igual, sin dejar a un lado los modos y estilos de aprendizaje.

Las siguientes tres categorías que formarían parte del núcleo central son “preparación académica y profesional del docente de Matemática II en cuanto a estrategias de enseñanza; actividades administrativas; relaciones intrapersonales; contenidos matemáticos; intercambio de saberes en eventos científicos” con un índice de “centralidad” de 0.129.

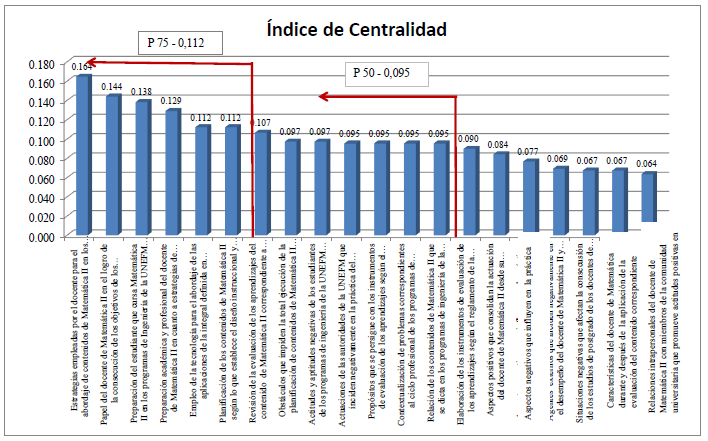Gráfico 1
Índice de Centralidad

Por otro lado se observa las categorías “empleo de la tecnología para el abordaje de las aplicaciones de la integral definida en ingeniería para auspiciar procesos cognitivos en el estudiante para el análisis, solución e interpretación de resultados que se deriven de dichos problemas” y “planificación de los contenidos de Matemática II según lo que establece el diseño instruccional y además adecuado a las características propias del lapso académico en cuestión en reuniones de coordinación”, éstas últimas con 0.112 de índice de “centralidad”.

Estas categorías evidencian que los docentes de Matemática II no se han quedado detenidos en el tiempo y en el espacio, tal como manifestaron en sus entrevistas, han realizado sus estudios de postgrado para afianzar y ampliar los conocimientos en cuanto a contenidos matemáticos; la institución ha podido brindarles cursos y talleres de formación académica y humana; sus conocimientos han sido expandidos más allá de las aulas de clases y en concordancia con las categorías anteriores están siempre en la búsqueda de ampliar su arsenal de estrategias de enseñanza para el abordaje de los contenidos de Matemática II. Entre esa búsqueda, el uso de la tecnología es la que consideran está acorde con el momento educativo en primer lugar porque sus estudiantes cursan programas de ingeniería, en segundo lugar porque los programas académicos están adscritos al área de la universidad con el mismo nombre y en tercer lugar porque es la tecnología la que da dinamismo al crecimiento e interacción de las civilizaciones.

Es en este punto donde el docente centra su atención al hecho de aprovechar recursos tecnológicos para el abordaje de la integral definida, más aún al empleo de las aplicaciones en ingeniería que hacen uso de la misma para la solución de problemas.

Ahora bien, en el gráfico 2 se puede observar que las primeras cinco categorías correspondientes al percentil 75 son las que tienen los mayores índices de “prestigio”. Con valores de 0.092; 0.084; 0.082; 0.071 y 0.060 indican la razón más profunda del proceso de enseñanza de los contenidos de Matemática II en los programas de ingeniería de la UNEFM y además coinciden con las primeras cinco categorías que forman parte del núcleo central de la representación según los índices de “centralidad”. Estas categorías son “estrategias empleadas por el docente para el abordaje de contenidos de Matemática II en los momentos instruccionales correspondientes a su planificación con adecuación del diseño instruccional”, “papel del docente de Matemática II en el logro de la consecución de los objetivos de los contenidos con la creación de ambientes propicios de aprendizaje a través de la empatía y acercamiento con sus estudiantes y de éstos con sus pares”, “preparación académica y profesional del docente de Matemática II en cuanto a estrategias de enseñanza; actividades administrativas; relaciones intrapersonales; contenidos matemáticos; intercambio de saberes en eventos científicos”, “preparación del estudiante que cursa Matemática II en los programas de Ingeniería de la UNEFM para la evaluación de los contenidos correspondientes según la planificación del lapso académico” y “empleo de la tecnología para el abordaje de las aplicaciones de la integral definida en ingeniería para auspiciar procesos cognitivos en el estudiante para el análisis, solución e interpretación de resultados que se deriven de dichos problemas”.

Evidentemente estos resultados atribuyen características del docente de Matemática II que van más allá de una entrega de contenidos en una sola dirección, es decir, que ya no solo se está preocupando por desarrollarlo tal como lo establece el diseño instruccional, sino que en la adecuación de los mismos y en atención a la dinámica de los lapsos académicos y de los grupos de estudiantes son capaces de adaptar situaciones que no afecten tan severamente al estudiante.

Esto se lo ha dado su experiencia; su preparación académica y profesional. Sin embargo y a pesar de las limitaciones busca la manera de sobrevivir con los agentes externos que últimamente solapan el trabajo que a bien quiere desempeñar y se han convertido en obstáculos para la práctica docente. El efecto negativo es que no se da la oportunidad de explorar en nuevas estrategias que salgan de lo común y lo tradicional, bien sea por factor tiempo (generalmente para no escapar de su zona de confort), por falta de recursos; por los espacios académicos o por actitudes propias y/o de los estudiantes. Para el docente de Matemática II, las estrategias de enseñanza son pilares en la consolidación de los contenidos y en la promoción de la participación, tal es el caso del aprendizaje basado en problemas.

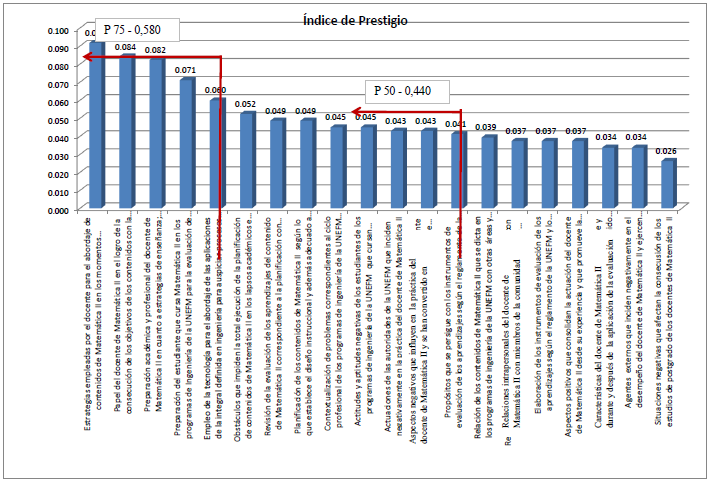Gráfico 2
Índice de Prestigio

Por otro lado, la tecnología es una herramienta que también pudiera aprovechar para lograr los objetivos que se persiguen con la unidad curricular tal como lo manifestaron en las entrevistas, para ello debería realizar un buen diseño del propósito de la misma y unificar aspectos que garanticen la significancia y durabilidad del conocimiento en miras de enfocar la clase, aparte de los contenidos conceptuales, en la utilidad y aplicación de los mismos en el campo de la ingeniería y la valoración de las integrales en la cotidianidad. En otro orden de ideas, el gráfico 3 muestra la representación de los índices de abstracción de las categorías asignadas y tomadas en consideración para el análisis las cinco primeras según el percentil 75.

En el gráfico se evidencia que se mantienen tres categorías obtenidas en los índices anteriores para el mismo percentil, solo que aquí el docente hace énfasis en la preparación académica y profesional; siendo válida esta abstracción puesto que el mismo estará ganado a nuevas estrategias para el abordaje de los contenidos de Matemática II y como bien lo establece la otra categoría, éste obtendrá un buen papel en la consecución del logro de los objetivos.

Aparece entonces una nueva categoría con un índice de “abstracción” de 1.429 en el segundo lugar según el orden de jerarquización, esta es “relaciones intrapersonales del docente de Matemática II con miembros de la comunidad universitaria que promueve actitudes positivas en su práctica”, coincide con la categoría de mayor frecuencia en el conteo simple y como indica la misma se presenta el valor del compañerismo, la amistad y se pone de manifiesto su lado humano.

Es de hacer mención que la actitud del docente en el aula se verá reflejado en sus estudiantes, al igual si el ambiente de trabajo no es agradable también influirá en éste, es decir, toda la comunidad universitaria debería estar en armonía para que los objetivos personales y colectivos se dirijan hacia un propósito común.

Con un índice de “abstracción” de 1.278 aparece en el cuarto lugar la categoría “aspectos negativos que influyen en la práctica del docente de Matemática II y se han convertido en obstáculos que impide el buen ejercicio de la profesión dentro y fuera de las aulas” en contraposición a la categoría anterior y en concordancia con lo descrito en el párrafo antepuesto.

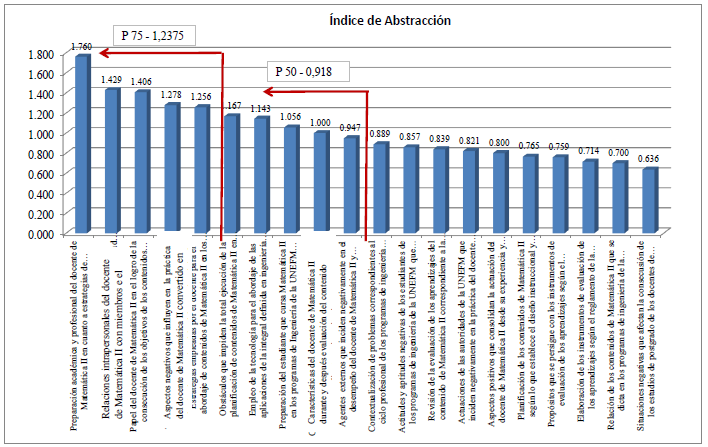Gráfico 3
Índice de Abstracción

Los docentes de Matemática II pueden tener muy buenas intenciones para con los estudiantes, estar abiertos a los nuevas estrategias de enseñanza, estar ganados al uso de la tecnología, ser constantes en su preparación académica y profesional, entre otras variables positivas en su quehacer educativo, pero si las limitaciones son recurrentes y no evidencia cambios o soluciones entonces influirá muy al contrario de lo que exige la institución y él mismo como docente.

En otro orden de ideas, el sistema periférico estará formado por las catorce categorías restantes descartadas como núcleo central de la representación social según el índice de centralidad y los percentiles los cuales generan dos grupos. Según el gráfico 1, el primer grupo evidencia que aunque los docentes pretendan mejorar su práctica y sus estrategias estén basadas en la contextualización de problemas de ingeniería que hagan uso de la integral definida así como hacer del conocimiento a los estudiantes de la relación de Matemática II con otras áreas, su desempeño se verá opacado por los agentes externos que impiden la total ejecución de los contenidos.

Según los índices de prestigio para las categorías del percentil 50 en el gráfico 2, se presenta nuevamente aspectos negativos que influyen en la buena práctica docente, donde se incluye la actuación de las autoridades frente a situaciones propias de la institución, los agentes externos que impiden el desarrollo normal de un lapso académico, las actitudes y aptitudes negativas de los estudiantes y se añade además la poca disponibilidad de espacios para los trabajos de docencia, investigación, extensión así como consultas y preparación de clases.

Según los índices de abstracción para las categorías del percentil 50 en el gráfico 3, se perfila el uso de la tecnología, la preparación del estudiante en la evaluación de contenidos y las implicaciones del docente frente a las mismas y se presentan nuevamente los factores que influyen negativamente en la práctica del docente de Matemática II.

El segundo grupo de categorías son los elementos más lejanos al núcleo central lo cual indica que constituyen elementos periféricos en un segundo nivel. A su vez presentan los niveles más bajo de índice de abstracción que expresa que dichas categorías forman parte de sus experiencias negativas tal como lo reflejan los índices de “prestigio” donde se evidencia además son los componentes sociales que influyen en la práctica docente.

En el gráfico 4 se presentan los tres grupos de categorías en la representación social del proceso de enseñanza de los contenidos de Matemática II en los programas de ingeniería de la UNEFM, el primero que conforma el núcleo central y los otros dos el nivel periférico.

Reflexiones finales

Los docentes manifestaron la revisión y actualización de los diseños instruccionales donde se priorice las aplicaciones de la integral definida en problemas de ingeniería y además se incluyan prácticas de laboratorio donde se pueda evidenciar el uso de los contenidos de la unidad curricular Matemática II. También señalaron la creación de ambientes tecnológicos y el manejo de software que bien pudieran ser diseñados por los mismos estudiantes.

Según ellos y lo que marca el núcleo central de su representación social, el empleo de la tecnología para el abordaje de las aplicaciones de la integral definida en ingeniería auspiciaría procesos cognitivos en el estudiante, la idea es dedicar más tiempo al análisis de los datos del problema y a la interpretación de los resultados.

Además hicieron énfasis en aspectos negativos que influyen en su práctica como las limitaciones en la universidad en cuanto a espacios como cubículos, salas de lectura y de investigación que coartan su preparación académica y el pleno ejercicio de sus funciones de docencia; investigación y extensión por lo cual solicitan la mejora u optimización de dichos espacios. Si se quiere avanzar con la tecnología la universidad no dispone de equipos para la revisión y preparación de materiales didácticos y por ello las limitaciones para la adquisición de equipos no permiten el avance de los contenidos matemáticos a la par con dichas tecnologías. Respecto a las representaciones sociales sobre los procesos de enseñanza y aprendizaje de los contenidos de Matemática II, los docentes señalaron que aparte de los descrito anteriormente, el uso de la tecnología debe ser complemento de las actividades que se planifican y el estudiante pueda articular desde sus conocimientos previos y los adquiridos, un procedimiento analítico visto en clase con una herramienta que provea el mismo resultado otorgando importancia al análisis e interpretación en el sistema o entorno de estudio.

Gráfico 4.
Representaciones sociales sobre la enseñanza de los contenidos de la unidad curricular Matemática II en los programas de ingeniería de la UNEFM

Referencias bibliográficas

Abric, J. C. (1996). Specific processes of social representations. Papers on social representations, 5 (1):77-80.

Abric, J. C. (2001). Prácticas sociales y representaciones. México: Coyoacán. Disponible en: http://datateca.unad.edu.co/contenidos/401514/401514_AVA_14B/Entorno_Conocimiento/Unidad_3_Aplicabilidad_e_Investigacion_Social/Lecturas_Complementarias/Abric_JC_Practicas_Sociales_y_Representaciones.pdf [consulta: 2018, febrero 14].

Álvarez, Y. y Ruiz-Soler, M. (2008). Actitudes hacia el docente de matemáticas en estudiantes de ingeniería. IV Jornadas De Investigación e Innovación Educativa “Creatividad e Innovación en Contextos Socioeducativos de Cambios”. UCLA. Consultado el 29/11/2015 de http://www.ucla.edu.ve/viacadem/redine/jornadas

Araya, S. (2001). La equidad de género en la educación. La Ventana, 13, 159–187.

Banchs, M. (2001). Jugando con las ideas en torno a las representaciones sociales desde Venezuela. Fermentun. 30:11-32.

Doise, W. (1991). Identidad social e identidad individual en las relaciones intergrupales. Anthropos, 27, 154-161.

González, D. (2008). Rasgos de la práctica docente sobresaliente en los cursos de Matemáticas para Ingeniería. Revista Iberoamericana de Educación Matemática, Nº 14, páginas 49 – 60. Consultado el 08-11-2015 de http://www.fisem.org/www/union/revistas/2008/14/Union_014.pdf#page=49

González, F. (2014). Procesos cognitivos y metacognitivos que activan los estudiantes universitarios venezolanos cuando resuelven problemas matemáticos. ARJÉ Revista de Postgrado FACE-UC. Vol. 8 Nº 14. Edición Especial / 51-68.

Jodelet, D. (1991). Representaciones sociales: Un área de expansión. En D. Páez, C. San Juan, I. Romo y A. Vergara, Sida: Imagen y prevención (pp. 25-30). Madrid: Fundamentos.

Jodelet, D. (2007). El movimiento de retorno al sujeto y enfoque de las representaciones sociales. Cultura y representaciones sociales. 3(5):32-63.

Larrañaga, E. (2005). La lectura en los estudiantes universitarios: variables psicosociales en la formación de los hábitos lectores. Castilla – La Mancha: Ediciones de la UCLM.

Martínez, O. (2008). Actitudes hacia la matemática. Sapiens. Revista Universitaria de Investigación, vol. 9, núm. 1, pp. 237-256. Universidad Pedagógica Experimental Libertador Caracas, Venezuela. Consultado el 06/11/2015 de http://www.redalyc.org/articulo.oa?id=41011135012

Martínez, G., & Arellano, Y. (2011). Representaciones sociales que del aprendizaje de las matemáticas tienen estudiantes de nivel medio superior. Sinéctica, (36), 1-14. Recuperado en 14 de marzo de 2018, de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665109X2011000100001&lng=es&tlng=es.

Millán, Z. (2010). Internet y su uso educativo: representaciones sociales de docentes de la Escuela de Educación. Universidad Central de Venezuela. Trabajo de ascenso no publicado, Escuela de Educación, Universidad Central de Venezuela, Caracas

Montes, N. y Machado, E. (2011). Estrategias docentes y métodos de enseñanza-aprendizaje en la Educación Superior. Revista de Humanidades Médicas, Volumen 11, Nº 3. Ciudad de Camaguey. Consultado el 06-11-2015 de http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S172781202011000300005

Morales, L., Sánchez, J. y Roldán, H. (2010). Influencia de la actitud en el rendimiento académico en matemática con estudiantes universitarios. Universidad Nacional Autónoma de México. Consultado el 06-11-2015 de http://funes.uniandes.edu.co/4602/1/MoralesInfluenciaALME2010.pdf

Moscovici, S. (1961/1979). El Psicoanálisis su imagen y su público. Buenos Aires.

Planchart, E. (1990). Realidad de la enseñanza de la matemática en la educación básica y media diversificada y profesional en Venezuela. Acta Científica Venezolana, 41(5-6), 279-282.

Ponte de Ch, C. y Caballero, C. (2005). Representaciones sociales de la práctica del reciclaje de los estudiantes del Instituto Pedagógico de Caracas. Enseñanza de las Ciencias [Revista en línea]. Consultado el 18-11-2016 de http://ddd.uab.cat/pub/edlc/edlc_a2005nEXTRA/edlc_a2005nEXTRAp203repsoc.pdf

Ponte C. y Tineo E. (2013). Representaciones Sociales de la enfermedad de Chagas: Dimensiones y estructura. Revista de investigación [Revista en línea], Nº 78 Vol. 37. ISSN 0798-0329. Disponible en: https://dialnet.unirioja.es/servlet/articulo?codigo=4414138 [consulta: 2018, febrero 02].

Rondón, A (2014). Representaciones Sociales que poseen los estudiantes del Instituto Pedagógico de Miranda José Manuel Siso Martínez – Extensión Nueva Cúa sobre las plantas Medicinales. Revista de Investigación [Revista en línea], Nº 81 Vol. 38. Disponible en: http://revistas.upel.edu.ve/index.php/revistadeinvestigacion/article/view/2582 [consulta: 2018, febrero 14].

Suárez, J. (2014). Factores que generan miedo, apatía y desinterés frente al estudio de las matemáticas. Universidad Tecnológica de Pereira, Facultad de Ciencias Básica. Consultado el 17-11-2015 de http://hdl.handle.net/11059/5253

Villarroel, G. (2007). Las representaciones sociales: una nueva relación entre el individuo y la sociedad. Fermentum, Año 17, Nº49, 434-454.