1. Introducción

.

El exponencial crecimiento de las aplicaciones de las comunicaciones inalámbricas en los últimos años ha hecho que se requiera un continuo estudio y desarrollo de las técnicas de transmisión. Es por ello que para las futuras redes móviles de quinta generación (5G), las aplicaciones requerirán mejores características como en su rendimiento, en la tasa de transmisión de datos, en el retardo y en el uso eficiente del espectro en contraste con las redes móviles de cuarta generación (4G) como LTE/LTE Advanced y Wi-Fi [1]. Dichos sistemas de comunicaciones actuales han adoptado OFDM (Orthogonal Frequency Division Multiplexing) como formato de señal básico para realizar el transporte de los datos por el aire.

OFDM es extremadamente ventajoso en algunos aspectos; por ejemplo, OFDM tiene una relativa protección contra el ISI (Inter Symbol Interference), puede sobrellevar el desvanecimiento por multitrayecto utilizando técnicas de ecualización en el dominio de la frecuencia, también utiliza operaciones FFT/IFFT (Fast Fourier Transform / Inverse Fast Fourier Transform) eficientes para la modulación y demodulación de la señal OFDM y ofrece una alta eficiencia espectral. Además, OFDM puede adaptarse fácilmente para ser usado en sistemas inalámbricos MIMO (Multiple-Input, Multiple-Output). Sin embargo, todas estas ventajas de OFDM solo pueden lograrse bajo un nivel estricto de sincronización en tiempo y frecuencia entre el transmisor y el receptor [2]. Este enfoque estricto por hacer cumplir el sincronismo no es probable que cumpla de manera eficiente los desafíos de los sistemas de comunicaciones futuros como IoT (Internet Of Things) y las Comunicaciones MTC (Machine Type Communications) [3]. Por lo tanto, para superar estos inconvenientes, se han considerado y estudiado nuevas técnicas de modulación como FBMC (Filter Bank Multicarrier) y UFMC (Universal Filtered Multi-Carrier).

FBMC es una técnica multiportadora, en donde se aplica un filtrado a cada una de las subportadoras. Así, los lóbulos laterales del espectro son más débiles y, por lo tanto, el ICI (Inter Carrier Interference) se reduce significativamente. Sin embargo, para filtrar eficazmente, FBMC requiere longitudes de filtros muy altos [1]. Además, las rampas de los filtros hacen que FBMC sea vulnerable a las transmisiones de ráfagas cortas en una comunicación uplink[4]. Por otro lado, a diferencia de FBMC, UFMC divide todo el ancho de banda en sub-bandas y filtra dichas sub-bandas individualmente. En consecuencia, la longitud del filtro disminuye significativamente y, por lo tanto, se generarán símbolos con duraciones más cortas al mismo tiempo que, los requerimientos estrictos de sincronización de tiempo y frecuencia se reducen. Además, también se disminuye los altos niveles espectrales de los lóbulos laterales [5, 6]. UFMC combina la simplicidad de OFDM y la robustez de FBMC [7], considerándose una técnica atractiva para 5G.

Otra tarea importante en los sistemas de comunicación inalámbrica es la estimación de canal. La estimación de canal asistida por pilotos para el sistema OFDM emplea símbolos pilotos cuyos valores y posiciones son conocidos tanto en el transmisor como receptor. Por lo tanto, el canal se puede estimar en el receptor fácilmente en sus correspondientes posiciones de tiempo y frecuencia, siempre y cuando no exista ISI. En OFDM, el ISI puede ser mitigado en el receptor eliminando el CP (Cyclic Prefix) insertado en el transmisor, siempre que el CP sea más largo que la duración de la respuesta impulsiva del canal. Por otro lado, UFMC no hace uso de CP para tener una mejor eficiencia espectral y esto podría hacer que la estimación de canal asistida por pilotos usada en OFDM no sea aplicable en UFMC.

En este artículo se presenta un análisis del efecto de una canal multitrayecto con un retardo máximo variable en el rendimiento del sistema UFMC. El objetivo de este análisis es constatar si un sistema UFMC es robusto contra un canal multitrayecto a pesar de no utilizar el CP. Además, se muestra que el método de estimación de canal asistido por pilotos del sistema OFDM, es completamente aplicable en los sistemas UFMC, a pesar de la falta de CP [8, 9]. El resto de este artículo es organizado de la siguiente manera: la Sección 2 presenta un análisis del estado del arte del sistema UFMC. Luego, la Sección 3 presenta un análisis de la técnica UFMC, su comportamiento en un canal multitrayecto, el proceso de estimación de canal y los parámetros utilizados en la simulación de Matlab implementada. En la Sección 4 se discuten los resultados obtenidos de la simulación Finalmente, en la Sección 5 se presentan las conclusiones alcanzadas con este trabajo.

2. Estado del arte

En [8] se presenta la estimación de canal basada en subportadoras piloto para UFMC. Se muestra que la estimación de canal utilizada en OFDM también se puede aplicar a un sistema UFMC obteniendo un buen resultado. La estimación de canal de las subportadoras de datos se realiza usando interpolación lineal y usando un algoritmo de ventana deslizante. En los resultados se muestra la efectividad de la estimación usando un canal con desvanecimiento plano y un canal con desvanecimiento selectivo en frecuencia. Una de las limitaciones es que la estimación no se analiza para canales multitrayecto con diferente retardo máximo, tampoco se presentan resultados usando diferente tamaño para la FFT.

El trabajo descrito en [10] investiga sobre la optimización de las señales piloto para diferentes técnicas de estimación de canal en UFMC: LSLI (Least Square linear Interpolation), DFT (Discrete Fourier Transform), MMSE (Mínimum Mean Square Error) y RMMSE (Relaxed MMSE). Se propone un algoritmo para la estimación de canal y las fórmulas para las señales óptimas de pilotos para cada una de las técnicas mencionadas previamente. En los resultados se presentan gráficas del MSE considerando UFMC con un filtro de longitud 60, 1200 subportadoras y en canales UMa (Urban Macrocell) y UMi (Urban Microcell). Los resultados muestran que con el algoritmo propuesto se puede obtener una buena estimación de canal. Sin embargo, no se presentan resultados de la tasa de bits errados ni con diferente número de subportadoras totales.

En [11] se presenta la estimación de canal para UFMC en canales con desvanecimiento variante en el tiempo usando un filtro adaptivo. Este artículo propone una estimación de canal basada en la combinación de un filtro Kalman con un modelo autoregresivo. Los resultados de la estimación muestran el rendimiento del esquema de estimación de canal propuesto para canales variantes en el tiempo con diferente nivel de efecto Doppler y una distribución Rayleigh. Sin embargo, este trabajo no considera canales multitrayecto ni prueba con diferentes tamaños de ventana FFT.

El trabajo presentado en [12] muestra un análisis de UFMC en canales con desvanecimiento multitrayecto. Este estudio se enfoca en el rendimiento de UFMC, que no utiliza un prefijo cíclico como OFDM, en un canal con desvanecimiento multitrayecto. Las simulaciones se realizan para los canales: EPA (Extended Pedestrian A), EVA (Extended Vehicular A) y ETU (Extended Typical Urban) con diferentes frecuencias Doppler. Los resultados muestran que UFMC puede obtener un rendimiento similar a OFDM usando canales con desvanecimiento multitrayecto. Sin embargo, este trabajo no considera la estimación de canal requerida en UFMC.

En [13] se estudia la estimación de canal para sistemas UFMC. Se investiga sobre los estimadores LS (Least Square) y MMSE como también técnicas de interpolación lineal y spline. Los resultados muestran la tasa de errores de los diferentes estimadores en canales AWGN y Rayliegh, dando buenos resultados. Las limitaciones de este trabajo son que no considera canales multitrayecto ni tampoco presenta resultados del rendimiento de UFMC para diferentes tamaños de ventana FFT.

3. Materiales y métodos

3.1. Sistema UFMC

UFMC realiza una división de todo el ancho de banda en sub-bandas. Cada sub-banda puede estar conformada por subportadoras consecutivas, en donde posteriormente dichas sub-bandas son procesadas individualmente. Existen casos particulares en la manera en que se pueda dividir la banda completa en UFMC, es decir, si el número de sub-bandas es igual al número de subportadoras por sub-banda ( ) se entraría al caso de la técnica de modulación FBMC. Pero, si el número de subportadoras por sub-banda es igual número total de subportadoras de datos del sistema se estaría hablando de un sistema OFDM [14].

Figura 1.
Forma de filtrado según la forma de onda [15].

En la Figura 1 se muestra las diversas formas de filtrar a las subportadoras dependiendo de la técnica de modulación que se desee utilizar. Se tiene un filtrado completo de banda, un filtrado por subportadora y un filtrado por sub-banda, correspondientes a las técnicas de modulación OFDM, FBMC y UFMC, respectivamente.

En la Figura 2 se muestra un diagrama de bloques de un transmisor UFMC y en la Figura 3 un diagrama de bloques de un receptor UFMC. El sistema UFMC inicia con la subdivisión de toda la banda en múltiples sub-bandas con un tamaño fijo de subportadoras. Los bits de información de cada sub-banda son modulados usando cierto esquema de modulación. Posteriormente, las sub-bandas de manera individual se someten a IFFT de puntos generando una señal () en el dominio del tiempo y con una longitud muestras.

Figura 2.
Diagrama de bloques del transmisor UFMC [16].

Figura 3.
Diagrama de bloques del receptor UFMC [16].

Luego, esta señal para a través de un filtro prototipo FIR con ventana Dolph Chevyshev de longitud . Esto genera una señal de longitud debido al resultado de la convolución lineal (denotado con ) entre la señal () y el filtro prototipo (). Finalmente, todas las sub-bandas filtradas se suman para conformar la señal que será transmitida. Matemáticamente, la operación del transmisor UFMC está expresada como [4].

(1)

donde $\textcolor{red}{}i$ representa el índice de las diferentes sub-bandas, $\textcolor{red}{}B$ es el número total de sub-bandas y $\textcolor{red}{}{f}_i$ es la respuesta impulsiva del filtro FIR usado en la sub-banda $\textcolor{red}{}i$ .

Después de que la señal pase por el canal multitrayecto, cuyos efectos se aclararán en detalle más adelante, la señal recibida será transformada del dominio del tiempo al dominio de la frecuencia por medio de la FFT de puntos, ya que la señal no puede ser demodulada por una FFT de puntos por la operación de filtrado realizada en el transmisor. Por lo tanto, la señal es rellenada de ceros con longitud para ser demodulada usando una FFT de puntos. A la salida de la operación FFT de puntos, los valores de frecuencia de índices impar generados son adicionalmente descartados debido a que son frecuencias con distorsión y, las frecuencias de índice par se mantienen ya que corresponden al lóbulo principal de la subportadora [4, 12, 13]. La señal que ingresará al siguiente bloque contendrá valores de símbolos complejos correspondientes a los generados por el transmisor.

Luego de que la señal se transformó al dominio de la frecuencia, se ecualiza los efectos de distorsión que ocasionó el proceso de filtrado en el transmisor. Por lo tanto, se aplica una ecualización por subportadora con un filtro prototipo inverso al usado en la parte transmisora con el fin de igualar el efecto conjunto del canal y mejorar la calidad de la señal [18]. Finalmente, se recuperan los datos originales realizando la demodulación de los símbolos complejos.

3.2. Efectos de un canal multitrayecto en UFMC

Las comunicaciones inalámbricas sufren el efecto de la propagación por múltiples trayectorias. En OFDM, el ISI causado por el canal multitrayecto puede eliminarse mediante la introducción de un CP, haciendo que la estimación de canal sea muy sencilla. Para mitigar el efecto multitrayecto en UFMC, el CP también puede ser empleado, pero afectaría la ventaja del uso eficiente del espectro [8]. Por lo tanto, se debe considerar una transmisión sin CP en UFMC para garantizar una mejor eficiencia espectral.

En la Figura 4, se observa las formas básicas del símbolo UFMC antes del filtrado, después del filtrado y posterior al paso a través de un canal multitrayecto. La señal antes de ser filtrada es una señal UFMC normal, es decir, es la señal resultante de la operación IFFT de una cierta sub-banda de tamaño con subportadoras consecutivas. Luego, un intervalo con longitud de muestras es insertado entre dos señales UFMC, siendo la longitud del filtro FIR. La señal UFMC se convoluciona linealmente con un filtro FIR produciendo señales UFMC con una longitud de símbolo de . Finalmente, cuando la señal filtrada pasa por un canal multitrayecto se genera interferencia entre símbolos UFMC consecutivos produciendo ISI e ICI.

Figura 4.
Forma del símbolo de la señal UFMC antes del filtrado, después del filtrado y después de pasar por un canal multitrayecto [8].

En este punto se espera dos efectos, ISI debido a la ausencia del CP e ICI debido a la pérdida de ortogonalidad de las subportadoras en UFMC. Si se considera un símbolo UFMC y que dicho símbolo pasa a través de un canal inalámbrico con una respuesta impulsiva , en recepción se espera una señal de llegada , representada en el dominio del tiempo como [8].

(2)

donde representa la respuesta impulsiva del canal, es el ruido gaussiano blanco aditivo con varianza y * representa la operación de convolución lineal.

En recepción, la señal de llegada entra a un proceso de relleno de ceros para poder convertir dicha señal al dominio de la frecuencia. A la salida del bloque FFT, la señal está dada por [8, 9].

(3)

Si los supuestos del sistema no se mantienen, es decir, si no se mantiene la suposición de tener un canal con una sola derivación o que el ISI e ICI son insignificantes, la señal en el demonio de la frecuencia se puede representar como [8, 9]

(4)

donde , , y son la DFT de 2N puntos de su correspondiente señal en el dominio del tiempo, es decir de , , y respectivamente. Además, es un factor de reducción de la amplitud de la señal debido a la pérdida de la ortogonalidad, es el ICI causado por las demás subportadoras en la subportadora y es el ISI causado por el símbolo anterior en la subportadora .

3.3 Estimación de canal en UFMC

Debido al enfoque de filtrado, las rampas de subida y de bajada del símbolo UFMC contienen relativamente menos energía y actúan como una protección suave contra la propagación del retardo del canal. Al diseñar adecuadamente el filtro FIR, tanto en su forma como en su longitud, el ISI e ICI ocasionado por el canal puede limitarse por debajo de cierto valor de MSE (Mean Square Error) de modo que no afecte significativamente el rendimiento del sistema [6, 8].

Si el sistema UFMC está diseñado de manera que el ISI asistido por el canal sea insignificante, las estimaciones de los símbolos en el receptor se pueden escribir como [8].

(5)

Se considera que la subportadora está asignada a la sub-banda y, que también se descartan todas las salidas de las subportadoras impares de la FFT de 2N en UFMC. Por lo tanto, la expresión se puede reducir aún más como [8, 9].

(6)

Con (6) se puede concluir que, la estimación del canal en el dominio de la frecuencia y los algoritmos de ecualización de canal para OFDM son reutilizables en los sistemas UFMC, excepto que la respuesta del filtro debe ecualizarse adicionalmente en UFMC. Como el símbolo piloto ya se conoce en el receptor, se puede realizar la estimación de . La representación de la estimación de canal para UFMC en la subportadora viene dada por [9].

(7)

Por lo tanto, la estimación de canal difiere de OFDM solo en la ecualización de la forma del filtro en UFMC. En la Figura 5, se muestra el esquema de ecualización de la forma del filtro antes de la estimación de canal para UFMC. En primer lugar, a la salida del bloque FFT de 2N-pt los símbolos se dividen por su respuesta del filtro en la posición de la subportadora correspondiente en UFMC. Una vez que la forma del filtro se iguala, UFMC es equivalente a los sistemas OFDM. Después de obtener la respuesta del canal en las posiciones de los pilotos conocidos, se puede realizar un algoritmo de interpolación para estimar la respuesta en las posiciones de los símbolos de datos.

La estimación de canal permite obtener su estado en las subportadoras piloto, pero para obtener el estado del canal en las subportadoras de datos se utiliza algún tipo de interpolación. Uno de los algoritmos de interpolación más utilizados es el lineal debido a su simplicidad y baja complejidad.

Considerando que las estimaciones iniciales en los símbolos piloto están corrompidas por el ruido y suponiendo que la respuesta del canal es constante dentro de una cierta longitud de subportadoras consecutivas, la varianza del ruido AWGN se puede reducir tomando la media de varias estimaciones consecutivas como las estimaciones finales. Este algoritmo se llama ventana deslizante [19] y su procedimiento se ilustra en la Figura 6.

Figura 5.
Ecualización de la forma del filtro UFMC [8].

Figura 6.
Algoritmo de ventana deslizante [9].

Una ventana de tamaño se desplaza una subportadora a la vez para obtener la estimación final de la subportadora central dentro de la ventana de selección. Se debe tomar en cuenta y dar un tratamiento especial a las subportadoras de borde.

Aplicando el enfoque de ventana deslizante en UFMC, la varianza del ruido se reduce pero las estimaciones de canal pueden ser muy inexactas si se elige un tamaño de ventana deslizante demasiado grande en un canal con desvanecimiento selectivo en frecuencia. Sin embargo, si el canal es plano en frecuencia se tiene mucha ventaja si el tamaño de la ventana es grande. Normalmente el tamaño de la ventana se elige como un número impar para que el estimador sea imparcial al momento de realizar la estimación final de la subportadora central de la ventana deslizante [9].

3.4. Configuración de la simulación en Matlab

Para el filtrado de cada sub-banda se utiliza un filtro digital FIR (Finite Impulse Response) de ventana Dolph Chevyshev. En la Tabla 1 se muestra un resumen de los parámetros y sus valores utilizados para las simulaciones de UFMC y OFDM que se implementaron. El objetivo de implementar también un sistema OFDM convencional es comparar el rendimiento de UFMC en un canal multitrayecto y usando estimación de canal versus un sistema OFDM tradicional. Los parámetros de la simulación son usados tanto para el sistema OFDM como para UFMC. La longitud del filtro en UFMC será igual a la longitud del prefijo cíclico utilizado en OFDM con el fin de tener una comparación justa entre ambos.

Por otro lado, se utilizarán en total 3 canales multitrayecto con desvanecimiento selectivo en frecuencia con una distribución de Rayleigh cuyos perfiles de retardos de potencias (PDP) se presentan en la Tabla 2. Los valores para el Canal – Recomendación ITU-R (nombrado CH1) se obtendrá de [16] y tiene un retardo máximo de 410 ns. También se implementan dos canales de prueba con el mismo número de rayos y potencia promedio que CH1 pero cambiando los retardos de los rayos canal. El canal de prueba CH2 tiene un retardo máximo de 750 ns y el canal de prueba CH3 tiene un retardo máximo de 1150 ns. Los tres canales servirán para analizar el rendimiento del sistema UFCM con diferentes canales multitrayecto.

Tabla 1.
Parámetros de la simulación en Matlab.

Parámetros	Valor
Número de puntos FFT	512, 128
Longitud del Filtro (UFMC) Longitud del CP (OFDM)	16, 32, 64
Modulación	16QAM
Separación de Subportadoras Piloto	Cada 5 subportadoras

Tabla 2.
PDP de los canales para la simulación.

	Rayo	Retardo Relativo [ns]	Retardo Normalizado	Potencia Promedio [dB]
Canal de Recomendación ITU – R (CH1)	1	0	0	0
	2	110	2	-9.7
	3	190	4	-19.2
	4	410	8	-22.8
Canal de Prueba (CH2)	1	0	0	0
	2	250	5	-9.7
	3	500	10	-19.2
	4	750	15	-22.8
Canal de Prueba (CH3)	1	0	0	0
	2	500	10	-9.7
	3	1000	20	-19.2
	4	1550	31	-22.8

4. Resultados

4.1.PSD de los Sistemas OFDM y UFMC

Dependiendo del número de puntos FFT, se tendrá el número de sub-bandas y el número de subportadoras por sub-banda. Con 512 puntos FFT se tendrá 10 sub-bandas con 20 subportadoras cada una, con 256 se tendrá 10 sub-bandas con 10 subportadoras cada una y con 128 se tendrá 5 sub-bandas con 10 subportadoras cada una.

En la Figura 7.a) se observa la gráfica de la PSD resultante de la técnica UFMC y en la Figura 7.b) del sistema OFDM, ambas con 512 puntos FFT y 200 subportadoras. En UFMC las 200 subportadoras se dividen en 10 sub-bandas de 20 subportadoras cada una. Comparando ambas gráficas, claramente se ve la reducción en la radiación fuera de banda de la PSD de UFMC respecto a la de OFDM. UFMC muestra un valor de aproximadamente -86 dB, mientras que OFDM muestra un valor de -21 dB. Por lo tanto, se comprueba que evidentemente UFMC presenta una mejora respecto a OFDM en la radiación fuera de banda.

4.2. BER vs Eb/No de UFMC y OFDM

Las curvas resultantes de BER vs Eb/No se obtuvieron para una FFT de 512 y 128 puntos. Se utilizó los 3 canales multitrayecto antes mencionados y con un esquema de modulación 16QAM.

4.2.1. BER vs Eb/No para FFT de 512 puntos

En la Figura 8 se observa las curvas de BER vs Eb/No de las estimaciones de canal de los sistemas UFMC y OFDM usando el canal de la recomendación ITU-R (CH1) para: a) una longitud de filtro y prefijo cíclico de 32 y b) longitud de filtro y prefijo cíclico de 64. Con los parámetros ya establecidos, se observa que las curvas de UFMC y OFDM son muy similares cuando L=CP=32. Además, se nota que el PDP del canal utilizado funciona igual para ambos sistemas. Pero es evidente que el mejor resultado es la curva de la estimación perfecta del canal puesto que se asume que se conoce perfectamente el canal que está siendo utilizado. La curva que le sigue es la curva de la estimación LS-SW y quedando al final la estimación de canal LS. La estimación LS-SW y la estimación LS se encuentran muy cercanas pero la estimación LS-SW tiene mejores valores de BER. En cambio, en la Figura 8.b) se observa que cuando L=CP=64 la técnica UFMC no tiene un buen resultado debido al incremento en la longitud del filtro. Se observa en las gráficas que la BER en el sistema UFMC se degrada cuando se tiene una longitud de filtro de 64 tanto para la estimación perfecta de canal como la estimación LS y LS-SW. Por otro lado, en el sistema de OFDM las curvas de las estimaciones no se ven afectadas y funcionan de forma similar a los casos mostrados anteriormente. Debido a que UFMC no funciona correctamente con una longitud de filtro de 64, en adelante solo se analizará la BER cuando se tengan longitudes de filtro de 16 o 32.

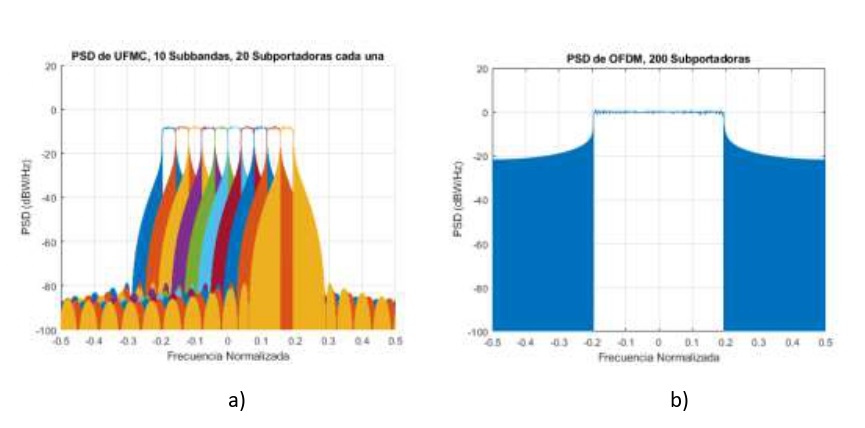Figura 7.
PSD (FFT = 512, L = 16 y modulación 16-QAM) de: a) UFMC, b) OFDM

Figura 8.
BER vs Eb/No de UFMC y OFDM (FFT = 512, CH1, 16-QAM). a) L = CP = 32, b) L = CP = 64.

En la Figura 9 se observa las curvas de BER vs Eb/No de las estimaciones de canal de los sistemas UFMC y OFDM para: a) CH2 y L=CP=16 y b) CH3 y L=CP=32. En el caso de la Figura 9.a), para las curvas de las tres estimaciones de UFMC se puede observar que para un Eb/No mayor a 15 dB existe una degradación comparada con OFDM. Este resultado muestra que al tener un canal con un máximo retardo muy cercano a la longitud del filtro en UFMC provoca una degradación de la BER en altas Eb/No. En el caso de la Figura 9.b), la degradación de la BER para valores de Eb/No mayores a 15 dB de las curvas de UFMC son más evidentes, es decir, tienen valores de BER más elevados que cuando se tenía una longitud de filtro de 16. También se puede observar que la estimación LS-SW tiene peor BER comparada con la estimación LS tanto para UFMC como para OFDM.

Figura 9.
BER vs Eb/No de UFMC y OFDM (FFT = 512, 16-QAM). a) CH2 con L = CP = 16, b) CH3 con L = CP = 32.

De todos los resultados obtenidos se puede concluir que las estimaciones de canal de UFMC, sin importar el canal que se esté utilizando, tienen mucha dependencia de la longitud del filtro que se elija. Mientras que para OFDM, la curva de la estimación perfecta de canal no depende de la longitud del prefijo cíclico ni del PDP del canal que se esté utilizando, pero las estimaciones LS y LS-SW si dependen del PDP del canal que se utiliza. En este caso, las estimaciones LS y LS-SW son mucho mejores cuando la PDP del canal es de la recomendación ITU-R M.1225. Por el contrario, cuando se haga uso de un canal en donde se modifican sus retardos acordes al prefijo cíclico que se utiliza, las curvas de dichas estimaciones tienen valores de BER altos para Eb/No mayores a 15 dB.

4.2.2 BER vs Eb/No para FFT de 128 puntos

En la Figura 10 se observa las curvas de BER vs Eb/No de los sistemas UFMC y OFDM usando el canal de la recomendación ITU-R (CH1) para: a) una longitud de filtro y prefijo cíclico de 16 y b) longitud de filtro y prefijo cíclico de 32. En la Figura 10.a) se puede observar que la BER con estimación de canal tanto para UFMC como para OFDM tiene una diferencia significativa respecto a la estimación perfecta. Además, se puede observar un rendimiento similar en la estimación de OFDM y UFMC siendo el estimador LS el que mejor resultado obtiene. En la Figura 10.b) se observa que cuando L=CP=32 el rendimiento del sistema UFMC no es bueno ya que la BER tiene una degradación considerable respecto al sistema OFDM. Esto se debe a que para el número de puntos FFT que se está utilizando, la longitud de filtro es muy grande y por lo tanto no se puede realizar una estimación adecuada. Otro factor que se involucra en el rendimiento de los dos sistemas de comunicaciones es la separación de los pilotos. Al tener un número relativamente pequeño de subportadoras, se tienen pocas subportadoras piloto y por lo tanto la estimación de canal no será muy precisa.

Figura 10.
BER vs Eb/No de UFMC y OFDM (FFT = 128, CH1, 16-QAM). a) L = CP = 16, b) L = CP = 32.

En la Figura 11 se observa las curvas de BER vs Eb/No de los sistemas UFMC y OFDM usando el canal de prueba CH2 para: a) una longitud de filtro y prefijo cíclico de 16 y b) longitud de filtro y prefijo cíclico de 32. En el caso de la Figura 11.a) se puede observar que la estimación de canal no tiene buen rendimiento tanto en UFMC como en OFDM, esto se debe a que el canal tiene una alta variación por lo que la interpolación no obtiene un buen resultado. Para la Figura 11.b) se puede observar que cuando L=CP=32 se tiene un comportamiento similar a la Figura 10.b) e inclusive un poco peor. Se puede observar que con una longitud de filtro de 32 usando FFT de 128 puntos el sistema UFMC no funciona correctamente y se degrada significativamente comparado con OFDM.

4.3. MSE vs Eb/No de UFMC Y OFDM

una configuración de 512 puntos FFT, con modulación 16-QAM, una longitud de filtro y de prefijo cíclico de 32 y 64 y con el canal de la recomendación ITU-R M.1225 (CH1). Se puede observar que en la Figura 12.a), con una longitud de filtro y prefijo cíclico de 32 respectivamente, las estimaciones de canal que presentan menor MSE tanto en UFMC como en OFDM son cuando se utiliza el algoritmo de ventana deslizante. En ambas gráficas, las curvas con dicho algoritmo son iguales. Por otro lado, en la Figura 12.b) se observa que la curva con mayor desempeño es la estimación LS con el enfoque de ventana deslizante de OFDM, seguido por la estimación LS-SW de UFMC. Esto se debe a la inestabilidad del filtro debido a que su longitud es muy grande. La tercera mejor estimación es la LS de OFDM y quedando finalmente la estimación LS de UFMC. Se nota que, con una longitud de filtro de 64 la estimación de canal en el sistema UFMC tiene más error comparado al sistema OFDM.

Figura 11.
BER vs Eb/No de UFMC y OFDM (FFT = 128, CH2, 16-QAM). a) L = CP = 16, b) L = CP = 32.

Figura 12.
MSE vs Eb/No de UFMC y OFDM (FFT = 512, CH1, 16-QAM). a) L = CP = 32, b) L = CP = 64.

5. Conclusiones

En este artículo se presentó un análisis de la técnica UFMC en canales multitrayecto y usando estimación de canal. Los resultados mostraron que debido al filtrado por sub-banda que realiza el sistema UFMC, los lóbulos laterales tienen una potencia más pequeña y, por lo tanto, se tendrá una mayor eficiencia en el uso del espectro. También la interferencia entre subportadoras será despreciable haciendo que no sea necesario el uso de un prefijo cíclico.

Usando una configuración de filtro adecuado, el sistema UFMC puede ofrecer niveles de rendimiento muy buenos y casi similares a los de los sistemas OFDM. Por otro lado, el método de la estimación de canal asistido por piloto, además de la ecualización de canales, son aplicables en el sistema UFMC, siempre y cuando se realice una previa compensación de la respuesta del filtrado.

Además, el sistema UFMC tiene un buen funcionamiento cuando se usa un canal multitrayecto con desvanecimiento selectivo en frecuencia. Sin embargo, cuando el retardo máximo del canal es cercano a la longitud del filtro utilizado, el BER se degrada. Por lo tanto, es necesario que para seleccionar la longitud del filtro también se tenga en cuenta el retardo máximo del canal y el tamaño de FFT que es utilizado.

El sistema UFMC tiende a obtener malos resultados en términos de BER cuando la longitud del filtro es demasiado grande. Por ello, además de realizar una selección adecuada del número de sub-bandas y el tamaño de dichas sub-bandas, es necesario que se establezca una longitud de filtro adecuado, puesto que estos parámetros influyen de manera directa en el nivel del rendimiento del sistema.

Finalmente, se pudo observar que la estimación de canal no tiene un buen resultado cuando se tiene un canal multitrayecto con un retardo máximo elevado ya que el canal tiene bastante variación y la interpolación no puede estimar correctamente la respuesta del canal en las subportadoras de datos. Por esta razón, como trabajo futuro se quiere implementar una estimación de canal usando pilotos tipo bloque para ver el rendimiento en canales con alta selectividad en frecuencia e inclusive con canales variantes en el tiempo.

6. Referencias

[1] Bochechka, G., Tikhvinskiy, V., Vorozhishchev, I., Aitmagambetov, A., Nurgozhin, B. (2017). Comparative analysis of UFMC technology in 5G networks. Trabajo presentado en International Siberian Conference on Control and Communications (SIBCON), Moscow.

[2] Van Nee, R., Prasad, R. (2000). OFDM for Wireless Multimedia Communications. Boston, MA: Artech House.

[3] Wunder, G., Kasparick, M., Brink, S. T., Schaich, F., Wild, T., Gaspar, I., Ohlmer, E., Krone, S., Michailow, N., Navarro, A., Fettweis, G., Ktenas, D., Berg, V., Dryjanski, M., Pietrzyk, S., Eged, B. (2013). 5GNOW: Challenging the LTE Design Paradigms of Orthogonality and Synchronicity. Trabajo presentado en IEEE 77th Vehicular Technology Conference Spring (VTC Spring), Dresden, Germany. doi: https://doi.org/10.1109/VTCSpring.2013.6691814

[4] Helwa, S. S., Ibrahim, M., Elramly, S. (2016). Universal Filtered Multi-Carrier Performance Analysis with Multipath fading Channels. Trabajo presentado en 10th International Conference on Next Generation Mobile Applications, Security and Technologies (NGMAST), Cairo.

[5] Schaich, F., Wild, T. (2014). Waveform contenders for 5G - OFDM vs. FBMC vs. UFMC. Trabajo presentado en IEEE 6th International Symposium on Communications, Control and Signal Processing (ISCCSP'14), Athens.

[6] Schaich, F., Wild, T., Chen, Y. (2014). Waveform contenders for 5G – suitability for short packet and low latency transmissions. Trabajo presentado en IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, South Korea. doi: https://doi.org/10.1109/VTCSpring.2014.7023145

[7] Farhang-Boroujeny, B. (2011). OFDM Versus Filter Bank Mulcarrier. IEEE Signal Processing Magazine, 28 (3), 92-112.

[8] Wang, X., Wild, T., Schaich, F., ten Brink, S. (2015). Pilot-aided Channel Estimation for Universal Filtered Multi-Carrier. Trabajo presentado en IEEE 82nd Vehicular Technology Conference (VTC Fall), Stuttgart.

[9] Wang, X. (2014). Channel Estimation and Equalization for 5G Wireless Communication Systems (Master’s thesis). University of Stuttgart.

10] Zhang, L., He, C., Mao, J., Ijaz, A., Xiao, P. (2017). Channel estimation and optimal pilot signals for universal filtered multi-carrier (UFMC) systems. Trabajo presentado en IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, Montreal, QC. doi: https://doi.org/10.1109/PIMRC.2017.8292777

[11] Jamoos, A., Hussein, M. (2018). Estimation of UFMC Time-Varying Fading Channel Using Adaptive Filters. Trabajo presentado en International Conference on Promising Electronic Technologies (ICPET), Deir El-Balah. doi: https://doi.org/10.1109/ICPET.2018.00014

[12] Helwa, S. S., Ibrahim M., Elramly S. (2016). Universal Filtered Multi-carrier Performance Analysis with Multipath Fading Channels. Trabajo presentado en 10th International Conference on Next Generation Mobile Applications, Security and Technologies (NGMAST), Cardiff. doi: https://doi.org/10.1109/NGMAST.2016.19

[13] Durga V., Anuradha, S. (2019). On Channel Estimation in Universal Filtered Multi-Carrier (UFMC) System. Trabajo presentado en PhotonIcs & Electromagnetics Research Symposium - Spring (PIERS-Spring), Rome, Italy. doi: https://doi.org/10.1109/PIERS-Spring46901.2019.9017701

[14] Rábanos, J. H., Mesquida, C. L., Burgos, J. M. (2018). TENDENCIAS: Modulación y multiacceso en 5G. BIT (Colegio Oficial de Ingenieros de Telecomunicación - COIT), 207, 57-67. Recuperado de: https://www.coit.es/sites/default/files/archivobit/pdf/bit-207-tendencias-modulacion-y-multiacceso-en-5g.pdf

[15] Borruel, H. M. (2016). Tecnología 5G y Formas de Onda de Acceso al Medio (Proyecto de Fin de Carrera). Universidad Politécnica de Madrid. Recuperado de: http://oa.upm.es/44166/

[16] Rani, P. N., Rani, C. S. (2016). UFMC: The 5G Modulation Technique. Trabajo presentado IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Chennai, India. doi: https://doi.org/10.1109/ICCIC.2016.7919714

[17] Wen, J., Hua, J., Lu, W., Zhang, Y., Wang, D. (2018). Design of Waveform Shaping Filter in the UFMC System. IEEE Access, 6, 32300-32309. doi: https://doi.org/10.1109/ACCESS.2018.2837693

[18] Gómez, A. V. (2017). Toward to design of 5G Optical Communications (Trabajo final de grado). Universitat Politècnica de Catalunya, Barcelona.

[19] Song, H.-K. (Julio 1999). A channel estimation using sliding window approach and tuning algorithm for MLSE. IEEE Communications Letters, 3 (7), 211-213.

[20] Guidelines for evaluation of radio transmission technologies for IMT-2000. (1997). Recommendation ITU-R M.1225.