1. Introducción

Desde un principio el uso de la palabra álgebra ha sido asociado con la resolución de ecuaciones, generalmente usando las operaciones de adición, sustracción, multiplicación, división y extracción de raíces; lo cual es conocido como resolución por radicales.

Uno de los resultados más fascinantes en el álgebra (y en general en toda la matemática) es el teorema que dice que el polinomio general de grado mayor o igual a cinco no es resoluble por radicales. Este resultado, descubierto a finales del siglo XVIII tuvo que esperar casi 300 años, después de la solución de la ecuación de cuarto grado, para su demostración (Ayoub, 1980), (Pierpony, 1896), (Van der Waerden, 2013). Su demostración sorprendió a los matemáticos de la época, los cuales no la aceptaron con mucho agrado, pues sus líneas de investigación estaban dirigidas a encontrar una solución de la misma (Katz y Parshall, 2014), (Kleiner, 2007), (Pierpont, 1898). Este resultado es atribuido a N. H. Abel y es generalmente identificado con la Teoría de Galois, pues es un corolario de la teoría general de resolubilidad desarrollada por Galois (Rothman, 1982). Sin embargo, los trabajos de Abel fueron en realidad antes que los de Galois (Katz y Parshall, 2014).

Las contribuciones valiosas del médico y matemático italiano Paolo Ruffini (1765 - 1822) al problema de la solubilidad de la ecuación general de quinto grado no son muy conocidas ni bien entendidas. En realidad, las contribuciones de Ruffini han tenido un reconocimiento limitado y fueron rápidamente opacadas por los trabajos de sus sucesores Abel, Cauchy y Galois (Ayoub, 1980), (Rothman, 1982), (Sorensen, 1999). Prácticamente el único matemático que valoró el trabajo de Ruffini fue Cauchy, y esto es sorprendente, pues Cauchy era el peor entre todos los matemáticos en dar crédito a los trabajos de los demás (Rothman, 1982).

En este trabajo se presentan las contribuciones de Ruffini al problema de solubilidad de la ecuación de quinto grado, haciendo notar que Ruffini fue el primero en establecer que la ecuación general de quinto grado no es soluble por radicales, a pesar de que sus cinco demostraciones tenían un vacío, pero eran correctas.

2. Paolo Ruffini

Ruffini nació el 22 de septiembre de 1765 en el pequeño pueblo de Valentano, estado Papal (ahora Italia). Su padre, Basilio Ruffini, era un médico en Valentano. Su familia se mudó a Reggio, cercano a la ciudad de Modena en la región Emilia – Ramana del norte de Italia.

Cuando joven, Ruffini era de temperamento místico y parecía destinado a ser sacerdote, pero en su lugar escogió estudiar medicina y matemática. Ruffini ingresó a la Universidad de Modena en 1783 donde estudió matemática, medicina, filosofía y literatura. Entre sus profesores de matemática en la Universidad de Modena figuraron Luigi Fantini que le enseñó geometría y Paolo Cassiani que le enseñó cálculo. En 1787 Paolo Cassiani fue nombrado cónsul y el curso de Fundamentos del Análisis dictado por él en la Universidad de Modena fue asignado a Ruffini en 1787-1788, aunque todavía no se había graduado para ese entonces. Ruffini se gradúo el 9 de junio de 1788 con títulos en filosofía y medicina y un poco después obtuvo el título de matemática.

Ruffini realizó un excelente trabajo en el curso de Fundamentos del Análisis dejado por Cassiani, ya que el 15 de octubre de 1788 fue nombrado como profesor de Fundamentos del Análisis en la Universidad de Modena. Luigi Fantini, quien le enseñó geometría a Ruffini cuando era estudiante, tuvo problema con la vista y tuvo que dejar su posición en la Universidad de Modena en 1791. Ruffini, fue seleccionado para la posición de profesor de Elementos de Matemática en 1791. Pero Ruffini no solo era matemático, fue entrenado como médico y también en 1791 obtuvo la idoneidad para practicar la medicina en el colegio de medicina de Modena. Posteriormente, Ruffini fue electo como representante del distrito de Parma y vivió en Milán por varios años.

Estos eran tiempos de levantamientos políticos, la influencia de la revolución francesa se sentía fuertemente y aunque Ruffini no abrigaba las nuevas ideas importadas, no fue doctrinado en su adherencia a la ideología tradicional. Por otro lado, por oponerse a un juramento civil fue privado de su posición en la Universidad de Modena y no fue restituido hasta 1799. En ese período Ruffini practicó la medicina y realizó sus investigaciones en matemática, publicando su primer trabajo sobre la teoría de ecuaciones, en el cual prueba el teorema sobre la imposibilidad de la solubilidad de la ecuación de quinto grado. Después de dejar la Universidad de Modena, Ruffini pasó siete años enseñando matemática aplicada en la Escuela Militar de Modena. Continuó practicando la medicina y atendía pacientes desde los más pobres hasta los más ricos en la sociedad. Después de la caída de Napoleón se convirtió en rector de la Universidad de Modena en 1814. La situación política era todavía

extremadamente compleja y a pesar de sus habilidades personales, el gran respeto que mantenía y su reputación de honestidad, sus tiempos de rector fueron muy difíciles.

Ruffini fue electo en la recién fundada Academia de Ciencia, llamada “La Sociedad de los Cuarenta” y fue un miembro muy activo.

En 1817-1818, había una epidemia de fiebre tifoidea. Ruffini descuidadamente atendía los enfermos y presos, contrajo la fiebre en 1818 y casi pierde la vida. En base a su experiencia escribió sobre el contagio de la tifoidea. Ruffini también se interesó en la religión y la filosofía y escribió sobre la definición de la vida, así como un discurso refutando la teoría Mecanicista de Laplace sobre los fenómenos morales.

A pesar de que Ruffini tuvo una recuperación parcial, nunca se recuperó del todo y en 1819 renunció de su cátedra de medicina clínica, pero nunca renunció de su trabajo científico.

Admirado por sus colegas y amado por sus pacientes, Ruffini muere a la edad de 57 años, el 10 de mayo de 1822 en la ciudad de Modena.

3. La noción de solubilidad por radicales

Una etapa fundamentalmente importante en la historia del álgebra se puede situar hacia la segunda mitad del siglo XVIII y está conectada con la teoría de ecuaciones algebraicas. Uno de los problemas centrales de este tiempo era el de encontrar las soluciones de la ecuación general de grado

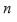
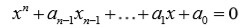
por medio de radicales; esto es a través de hacer operaciones aritméticas (suma, resta, multiplicación, división y extracción de raíces) con los coeficientes de la ecuación; es decir, encontrar una fórmula para las raíces del polinomio en términos de los coeficientes del polinomio, de tal manera que en la fórmula sólo aparezcan las operaciones de suma, resta, multiplicación, división y extracción de raíces.

La solución de la ecuación cuadrática por radicales ha sido conocida desde los tiempos de los babilonios. Al primer matemático que se le atribuye la solución de la ecuación cúbica es Scipione del Ferro (Gray, 2018), (Katz y Parshall, 2014), (Kleiner, 2007). En esos tiempos

los matemáticos parecían estar menos enfocados en cuanto se debiera saber, sino más bien en cuanto se debiera saber en comparación con sus adversarios. Debido a este ambiente fue que del Ferro decidió mantener su solución en secreto.

A finales de su vida del Ferro decidió revelar su secreto a sus estudiantes Antonio Maria Fiore y Annibale della Nave. Al mismo tiempo Niccolo Fontane (Tartaglia) estaba trabajando en el mismo problema. Algunos han comentado que posiblemente Tartaglia plagió el total o parte de la solución de del Ferro. Aunque esto pueda ser cierto o falso, lo que sí es cierto es que Tartaglia derrotó a del Ferro en un duelo matemático. Por lo tanto, Tartaglia tuvo que haber tenido una solución más general que la del Ferro.

Conociendo que Tartaglia tenía una solución de la ecuación cúbica, Cardano lo persuade para que le revelara la solución con la condición de que no lo publicaría. Cardano mantuvo su palabra, pero descubrió que del Ferro también tenía una solución; por lo tanto, decidió que la solución debía publicarse, a pesar de su compromiso con Tartaglia.

Cardano no deseaba publicar la solución de Tartaglia, sino una solución de la ecuación cúbica. Cardano y Ferrari tuvieron acceso a las notas de del Ferro por medio de della Nave y confirmaron que en efecto del Ferro tenía la misma solución que ellos tenían. Cardano presentó la solución de la ecuación cúbica (junto con la solución de la ecuación cuártica) con todos sus detalles en su libro Ars Magna, dándoles créditos tanto a del Ferro como a Tartaglia. Tartaglia se molestó cuando supo de esta publicación y le contó a todos sobre el asunto. Lodovico Ferrari, un sirviente y estudiante de Cardano desafió a Tartaglia a un duelo matemático. El duelo fue ganado por Ferrari, ya que él no sólo conocía la solución de la ecuación cúbica, sino que sabía aplicarla a la ecuación cuártica por lo que tenía más conocimiento del asunto.

Los métodos para resolver ecuaciones cúbicas y cuárticas de los algebristas italianos del siglo XVI es simplemente una extensión del método usado por los antiguos babilónicos para resolver la ecuación cuadrática. En notación moderna estas soluciones son prácticamente directas. La solución de la ecuación cúbica se basa en la completación del cubo, pero sorprendentemente, la ecuación cuártica es resuelta de una manera bastante similar a la cuadrática por lo tanto no es necesario la completación de un cuadrado –

cuadrado. Este procedimiento permite reducir la ecuación dada a otra ecuación de grado menor, la cual puede ser resuelta por métodos previos.

Los métodos desarrollados por los italianos en el siglo XVI fueron generalizados por varios matemáticos en los siglos subsiguientes; entre ellos se puede mencionar a Vieta, Descartes, Euler y Bézout. Debido al éxito que estos lograron en el análisis algebraico de las ecuaciones cúbicas y cuártica, muchos de los grandes matemáticos del siglo XVII y XVIII trataron con ahínco de encontrar un método para resolver por radicales la ecuación general de quinto grado; algunos de ellos fueron Newton, Leibniz, Tichirnhausen, D’Alembert y Euler (Katz y Parshall, 2014). Se tenía la idea de que dicho método, debía existir y en todo caso si no se había encontrado era debido a que no se era lo suficientemente ingenioso y/o hábil. Así el problema de la cúbica y la cuártica resultó ser bastante elusivo y no hubo avances significativos sino hasta 1770 con los trabajos de Vandermonde y Lagrange (Gray, 2018).

Euler encontró la forma de las raíces de una ecuación de quinto grado en el caso cuando la ecuación es soluble por radicales y presentó muchos ejemplos como el siguiente:

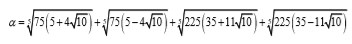
es raíz de la ecuación

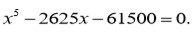
Sin embargo, Euler no fue capaz de visualizar el problema ni de encontrar condiciones para la solubilidad en dichos casos.

En 1770, Alexander - Théophile Vandermonde (1735 – 1796) presentó a la Academia de Ciencia de Paris un trabajo titulado Mémoire sur la resolution des equatione, en el cual enunciaba que toda ecuación de la forma

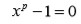
donde

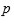
es un número primo, es soluble por radicales.

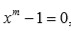
donde

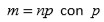
primo, entonces se tiene que

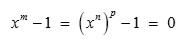
y haciendo

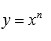
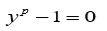
se obtiene que

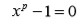
para la incógnita

y, la cual se podría resolver por radicales en caso de que la afirmación de

Vandermonde fuera correcta. Sin embargo, Vandermonde prueba el resultado solo para

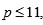
lo cual no permite resolver el caso general.

Vandermonde razona que si

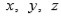
denotan las raíces de la ecuación cúbica general

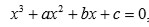
entonces podemos expresarlas en la forma:

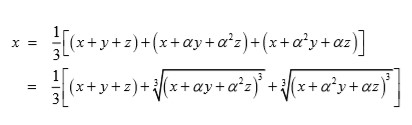
donde

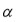
es una raíz cúbica primitiva de la unidad. Expresiones similares se obtienen para

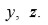
Por las propiedades de los polinomios simétricos en las raíces de una ecuación polinomial (Viéte) se tiene que

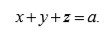
Vandermonde advierte que si

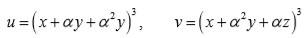
entonces

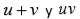
son polinomios simétricos en

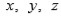
y por lo tanto son conocidos

ya que cualquier polinomio simétrico en las raíces se puede expresar en base a los polinomios simétricos elementales y estos a su vez están estrechamente ligados a los coeficientes de la ecuación cúbica (ecuaciones de Viéte).

Una vez conocidas las cantidades

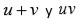
es posible obtener los valores de

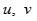
con lo cual queda determinada la raíz

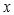
. Procedimientos análogos para

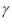
y para

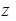
dará las tres raíces de la ecuación cúbica, probando así que es posible resolverla por radicales.

Vandermonde presenta también un método similar para encontrar las raíces de la

ecuación cuártica e incluso, analiza algunos casos de ecuaciones particulares de grado superior. Lamentablemente, su trabajo no fue publicado hasta 1774 y sus razonamientos serían opacados por el gran tratado de Lagrange sobre la teoría de las ecuaciones (Pierpont, 1896).

En 1771 se publica la memoria de Lagrange, Refléxions sur la résolution algébrique des equations, por la Academia Prusiana de Ciencias. En este tratado se analiza desde diferentes puntos de vista, varios de los métodos conocidos en ese tiempo para resolver por radicales las ecuaciones algebraicas de tercero y cuarto grado. En base a este análisis, Lagrange presenta un método que resume los anteriores y logra encontrar las características subyacentes en cada uno de los otros métodos: el hecho de que funcione se debe a que es posible reducir cualquier ecuación cúbica o cuártica a una ecuación auxiliar cuyo grado es menor, en uno, que el de las ecuaciones originales; estas, por lo tanto, admiten una solución por medio de radicales.

Para ilustrar el método de Lagrange, se supone que

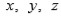
son las raíces de la ecuación cúbica general

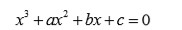
(las cuales se desean determinar). Considérese ahora la cantidad t dada por:

donde

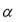
es una raíz cúbica primitiva de la unidad. (Las tres raíces cúbicas de la unidad son

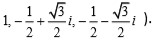
Si se permutan las raíces en (1), entonces se obtienen seis

valores posibles para

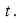
Sean

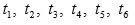
los distintos valores que se obtienen de (1) al permutar las raíces cúbicas. Estos seis

valores satisfacen la ecuación

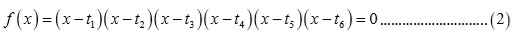
y es posible notar que los coeficientes de esta ecuación son polinomios simétricos en las

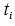
por la manera en que se definieron los

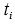
, también son simétricos en

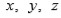
luego,

se pueden conocer en términos de los coeficientes de la ecuación cúbica que se intenta resolver. La ecuación (2)

es la ecuación auxiliar de la que se habló arriba y hoy en día es

llamada la resolvente de Lagrange para el caso de la ecuación cúbica.

La ecuación (2)

es una ecuación de sexto grado, considerablemente mayor que el

de la cúbica que se quiere resolver. Sin embargo, en este caso las cantidades

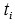
satisfacen las relaciones

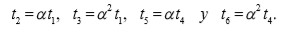
Esto se cumple para cierto orden de las permutaciones de las raíces en (1) . Si se permutan las raíces en otro orden, se obtienen relaciones similares a las anteriores. De esta manera,

(2) es una ecuación cuadrática en

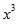
pues

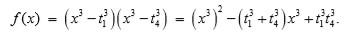
Si se toma

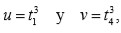
entonces los coeficientes de la ecuación son precisamente

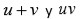
los cuales es posible expresarlos en términos de los coeficientes de la

cúbica original y se obtiene a través de ellos la solución como se comentó arriba. De esta manera, es posible obtener los seis valores para

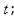
por consiguiente, las soluciones de la cúbica están dadas por:

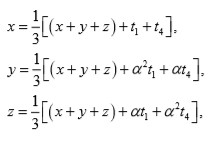
por lo que solo se necesita identificar bien a

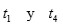
de entre las seis posibles soluciones

de la ecuación resolvente (2) . Recuérdese que la expresión

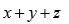
es un polinomio simétrico elemental de estas tres raíces y, por lo tanto, se conoce su valor pues

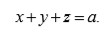
En este caso, Lagrange va más allá y da una manera explícita para calcular esos valores.

En el caso de la ecuación general de cuarto grado

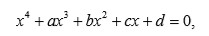
se denotan

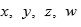
como sus raíces, entonces al definir la cantidad

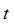
como

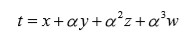
donde

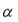
es una raíz cuarta primitiva de la unidad, la resolvente es una ecuación de grado

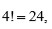
las posibles permutaciones de estas cuatro raíces. Sin embargo, en este caso se

simplifica mucho el procedimiento pues las raíces cuartas de la unidad son

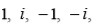
y tanto Vandermonde como Lagrange usaron este hecho para obtener las raíces de la bicuadrática; en este proceso es necesario resolver una cúbica como ecuación auxiliar. De hecho, Lagrange probó que las veinticuatro permutaciones de las raíces sólo producen seis valores distintos para

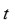
los cuales son

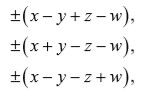
y cada uno de ellos ocurre cuatro veces. Si se denota por

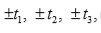
entonces la ecuación resolvente es

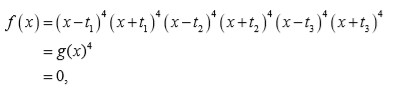
donde

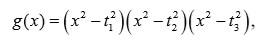
es un polinomio cúbico en

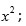
además

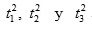
son las raíces de una ecuación cúbica conocida, pues los coeficientes de

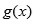
son simétricos en

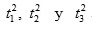
; luego, también son simétrico en

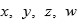
Dado que se puede resolver dicha ecuación cúbica, es

posible encontrar los valores para

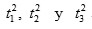
y por consiguiente, los de

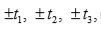
ya que solo basta extraer raíces cuadradas. De esta manera, las soluciones de la ecuación cuártica vienen dadas por

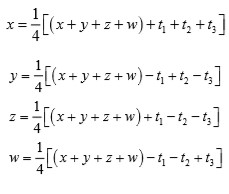
Es necesario observar que solo se necesitan escoger los signos adecuados a

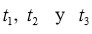
lo cual, en el peor de los casos se puede hacer por ensayo y error. También

es necesario señalar que

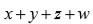
es un polinomio simétrico elemental de estas raíces

y es, por lo tanto, igual al coeficiente del término cúbico en la ecuación cuártica original; es decir

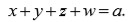
Lagrange aplicó el mismo método a la ecuación general de quinto grado

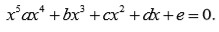
Al considerar

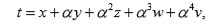
donde se supone a priori qu

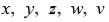
son las cinco raíces de la ecuación original y

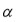
es una raíz quinta primitiva de la unidad, Lagrange observó que las posibles

permutaciones de estas raíces nos dan

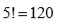
valores para

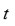
por lo que la ecuación resolvente

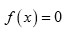
es de grado 120 . Sin embargo, Lagrange pudo probar que esta se

puede reducir a un polinomio de grado 24 en

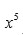
, pero no pudo obtener nada concluyente. Además, los “trucos” que se podían realizar en los casos anteriores no se pueden aplicar aquí, pues todas las raíces quintas de la unidad son primitivas, excepto la trivial

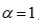
; así, no es posible hacer las reducciones de la resolvente como en el caso de la cúbica y la bicuadrática.

El trabajo de Lagrange sobre la resolución algebraica de ecuaciones es una parte fundamental en el desarrollo del álgebra moderna, no solo por las respuestas que obtuvo, sino por la gran influencia que ejerció en la comunidad matemática de finales del siglo XVIII y el siglo XIX. Antes de Lagrange nadie había contemplado la posibilidad de la no existencia de métodos generales para resolver por radicales las ecuaciones de grado superior al cuarto.

Más aún, es posible citar ejemplos de matemáticos que creyeron haber resuelto la ecuación de quinto grado. Tal es el caso del gran algebrista de siglo XVII, Tschirnhausen (1661-1708), quien desarrolló un método que se basaba en transformar la ecuación dada a una más simple, proceso en el cual era necesario resolver una ecuación auxiliar. Este método funcionaba muy bien para ecuaciones de segundo, tercero y cuarto grado; sin embargo, después se probó que, al aplicarlo a la ecuación general de quinto grado, la ecuación auxiliar que previamente se debía resolver resultaba ser de sexto grado.

Tschirnhausen comienza considerando un polinomio mónico de grado tres

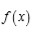
sobre el cuerpo de los racionales

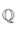
y trata de encontrar sus raíces. Luego extiende

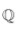
agregándole una raíz cúbica primitiva de la unidad y llama a esta cuerpo

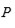
Luego lo que resta encontrar es un cuerp

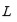
que contiene el cuerpo de ruptura

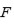
del polinomio dado.

A partir de aquí Tschirnhausen considera una extensión arbitraria

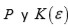
donde

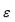
es una raíz de

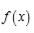
. De aquí, él prueba que la dimensión

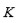
sobre

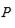
es dos, lo cual determinará el grado de la resolvente. En general la resolvente de un polinomio general de grado

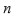
tiene grado

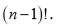
Fue necesario esperar hasta el siglo XIX para que el problema quedara completamente resuelto, aunque no en el sentido que la mayoría de los matemáticos hubiera deseado.

4. Ruffini y la ecuación de quinto grado

El primer intento serio por demostrar que era imposible resolver la ecuación general

de grado

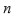
por medio de radicales, para

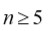
, fue hecho por Paolo Ruffini (Pierpont, 1896).

Ciertamente ningún matemático había publicado tal afirmación y aún Lagrange en su artículo famoso de 1771, Reflexions sur la resolution algebrique des equations, dice que él regresará a la pregunta de la ecuación de quinto grado, claramente él tenía la esperanza de resolver esta ecuación por medio de radicales. En 1799 Ruffini publica su libro titulado Teoría Generale delle Equazion, donde afirma que la ecuación de quinto grado no puede ser resuelta por radicales. En el mismo año, Gauss, en su disertación doctoral indica que él había considerado esta posibilidad, pero no publicó su intento.

Ayoub (1980), citando a Ruffini, señala que éste inicia la introducción de su libro como sigue:

La solución algebraica de ecuaciones generales de grado mayor que cuatro es siempre imposible. Observar un teorema muy importante el cual creo que soy capaz de afirmar (si no me equivoco) y presentar la demostración de esto es la principal razón de publicar este volumen. El inmortal Lagrange, con su sublime Refle

Ruffini usó la teoría de grupo en su trabajo, pero tuvo que inventarla. Lagrange había usado las permutaciones y uno puede argumentar que los grupos aparecen en los trabajos de Lagrange, pero como Lagrange nunca compuso permutaciones esta idea es muy vaga en sus artículos.

Ruffinii es el primero en introducir la noción de orden de un elemento, conjugado, la descomposición cíclica de elementos del grupo de permutaciones y la noción de primitivo e imprimitivo. Ruffini probó algunos teoremas fundamentales (con la notación moderna que se indica a continuación).

· El orden de una permutación es el mínimo común múltiplo de las longitudes en la descomposición de ciclos disjuntos.

· Un elemento de

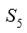
de orden 5 es un 5-ciclo.

· Si

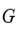
es un subgrupo de

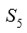
cuyo orden es divisible por 5, entonces

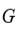
tiene un elemento de orden 5.

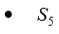
no tiene subgrupos de índice 3, 4, ó 8.

La demostración presentada por Ruffini es completa excepto por un pequeño, pero

significante vacío. Este vacío era tan evasivo que aún Cauchy, uno de los pocos matemáticos que respondieron favorablemente a Ruffini; no notó esto.

El problema fue que Ruffini asumió que todas las funciones algebraicas pueden ser expresadas en términos de funciones racionales de las raíces de una ecuación. En

terminología moderna si

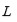
es contenido en una torre radical sobre

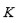
, entonces

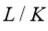
es

también una torre radical. Este resultado fue probado en el primero de los dos pasos de la demostración de Abel (Pierpont, 1898). No es claro si Ruffini sabía que esto era necesario para su demostración, pero parece que no, ya que ninguna de sus cinco demostraciones contiene una discusión precisa sobre este resultado. Lo que tampoco es claro es que si algún matemático de esa época notaría este vacío para no aceptar la demostración de Ruffini. Esto indica que la comunidad matemática simplemente no estaba preparada para aceptar este hecho. Hubo muchos matemáticos que respondieron con preocupación, pero la mayoría de ellos se basan en la falta de entendimiento de los argumentos de Ruffini, pero nunca mostraron que existía un vacío en la demostración. Otra razón porque su demostración fue muy poco aceptada es que ella era muy larga y difícil de entender; esto es debido a sus antecedentes como médico y matemático.

Ayoub (1980), citando a Ruffini, destaca que en 1801 Ruffini le envía una copia de su libro a Lagrange; pero al no recibir respuesta éste le escribe nuevamente diciendo:

Debido a la incertidumbre de que no haya recibido mi libro, le envío otra copia. Si tengo errores en alguna demostración o si he dicho algo que pensaba que era nuevo y el cual realmente no es nuevo, finalmente si he escrito un libro insignificante, le ruego que me lo indique sinceramente. (p.269)

Pero Lagrange no respondió. Nuevamente en 1802 Ruffini le escribe a Lagrange diciéndole:

Nadie tiene más derecho que usted en recibir el libro el cual me tomé la libertad de enviarle. Al escribir este libro tenía en mente principalmente presentar una demostración de la imposibilidad de resolver una ecuación de grado mayor que cuatro. (p.269)

En 1803 Ruffini publicó un artículo denominado

“Sobre la Solubilidad de Ecuaciones de Grado Mayor que Cuatro”.

Ayoub (1980), señala que Ruffini escribió:

“En la presente memoria trataré de probar la misma proposición (la insolubilidad de la ecuación de quinto grado) con menos razonamiento oscuros, y con completo rigor” (p. 269).

A esta demostración Gian Francisco Malfatti presentó cierta objeción, indicando que él no entendía la demostración de manera clara, especialmente el enunciado que dice que una resolvente es irreducible. Ruffini contesta sobre la objeción de Malfatti y prueba que una ecuación de quinto grado es soluble por radicales si su resolvente de Malfatti es irreducible.

En 1806 Ruffini publica otra demostración la cual no tuvo reacción visible. En 1813 publica un artículo “Reflexiones sobre la solución de ecuaciones algebraicas generales”. En la introducción, expresa su desacuerdo sobre la acogida que tuvo su trabajo.

Otro impulso para buscar el aprecio de su trabajo provino de una publicación de Jean Baptiste Joseph Delambre. Ayoub (1980), señala que en este artículo Delambre dice

“Ruffini propuso probar la imposibilidad de la solubilidad de la ecuación de quinto grado” (p. 270).

Ruffini contesto

“No solo propuse, sino en realidad lo probé y tengo en mente presentar la demostración al Instituto para que la examine y hacer que el Instituto se pronuncie sobre su validez” (p. 271)

A Ruffini se le informa que Lagrange, Legendre y Lacroix fueron nombrados para examinar su memoria. También se le informó que si una cosa era no importante no se informaba y que Lagrange con su frialdad encontró muy poco de valor en este trabajo.

Ruffini también envió sus memorias a la Royal Society en Londres. La Royal Society le responde que ellos no aprueban ningún trabajo, pero reportan lo que han dicho los que lo han leído y están satisfechos de lo que afirma.

El defensor más grande de Ruffini fue nada menos que Cauchy. Cauchy encontró en los trabajos de Ruffini una mina de oro. En 1813 - 1815, Cauchy escribió un artículo sobre la teoría de los grupos de permutaciones, generalizando algunos de los resultados de Ruffini. Este artículo fue aceptado por el comité de la Academia Francesa de Ciencias y este Comité menciona a Ruffini por su nombre. Cauchy reconoce su gratitud a Ruffini en una carta fechada en 1821, más o menos seis meses antes de la muerte de Ruffini.

La Sociedad matemática debe sentir pena por lo que le pasó a Ruffini. Si algún matemático le hubiese escrito mostrándole que había un error o que había una laguna en su demostración, por lo menos Ruffini hubiese tenido la oportunidad de corregirlo. Pareciera que en ese tiempo nadie estaba interesado en saber que la ecuación algebraica de quinto grado no podía ser resuelta por radicales. Finalmente, la pregunta es por qué Abel recibió el crédito de probar la insolubilidad de la ecuación de quinto grado y no Ruffini. Será que la comunidad matemática no estaba preparada para aceptar la idea revolucionaria de Ruffini, de que un polinomio no podía ser soluble por radicales y que el método de las permutaciones era muy exótico y difícil de entender.

5. La demostración de Ruffini

Aunque Gauss dijo que creía que la insolubilidad de la ecuación algebraica de quinto grado no era muy difícil de probar, Ruffini en 1799 fue el primer matemático en establecer la insolubilidad como un resultado y presentar una demostración. El estilo de presentación de Ruffini era largo, complicado y con algunas lagunas, por lo que obtuvo críticas inmediatas. Pero convencido de su resultado y demostración, Ruffini se mantuvo elaborando y clarificando su teoría en publicaciones por los próximos 20 años; y produjo un total de cinco versiones diferentes de su demostración. Las demostraciones fueron publicadas en Italia como monografía, en Bologna y en las memorias matemáticas de la Societa Italiana della Scienze en Modena.

Los escritos de Ruffini fueron inspirados por el análisis de Lagrange sobre la solubilidad de ecuaciones. Igual que Lagrange, Ruffini estudió ecuaciones de grados inferiores para establecer patrones sujetos a generalizaciones. Los argumentos de Ruffini

estaban basados en su clasificación de las permutaciones. Basado en los estudios de Lagrange sobre el comportamiento de las funciones cuando sus argumentos son permutados, Ruffini clasifica todas las permutaciones de los argumentos que dejan la función inalterable. El concepto de permutación según Ruffini difiere del concepto moderno y puede ser mejor entendido si se traduce a la concepción moderna introducida por Cauchy en 1840 como sistema de sustituciones conjugadas. Por lo tanto, una permutación para Ruffini es una colección de intercambios (transición de un arreglo a otro) que deja la función formalmente inalterable.

En notación moderna: Si

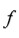
es la función dada con

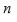
variable, una permutación para

Ruffini es un conjunto

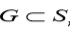
tal que

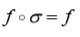
para todo

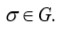
Ruffini dividió sus permutaciones en simples, las cuales eran generadas por iteraciones (o sea potencias) de un solo intercambio (en términos modernos grupos de permutaciones cíclicas) y en compuestas, las cuales eran generadas por más de un intercambio. Sus permutaciones simples que consistían en potencias de un solo intercambio fueron subdivididas en dos tipos, distinguiendo el caso en que el intercambio consistía de un sólo ciclo del caso en que el intercambio era el producto de más de un ciclo.

Las permutaciones compuestas de Ruffini fueron posteriormente subdivididas en tres tipos. Una permutación (o sea conjunto de intercambios) es del primer tipo si existen dos arreglos que están relacionados por un intercambio de la permutación (o sea que existen

dos arreglos

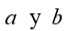
tal que

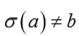
para todo s en el conjunto de intercambios).

Traducido a terminología de grupo de permutaciones, este tipo corresponde a los grupos intransitivo. Ruffini definió el segundo tipo como aquellas permutaciones que no pertenecen al primer tipo y para las cuales existe un conjunto de raíces

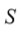
tal que, en

notación moderna,

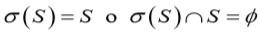
para todo intercambio que pertenece

a la permutación. Estos grupos transitivos fueron posteriormente llamados grupos imprimitivos. El último tipo consiste de las permutaciones que no pertenecen a ninguno de los tipos anteriores, y por lo tanto corresponde a los grupos primitivos.

En base a esta clasificación, Ruffini introduce su otro concepto básico “grado de equivalencia” de una función dada de las n raíces de una ecuación como el número de las diferentes permutaciones que no alteran el valor formal de

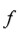
. Denotando el grado de equivalencia por

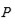
, Ruffini establece que

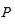
debe dividir a

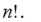
Después de un extensivo y laborioso estudio, ayudado por su clasificación, Ruffini fue capaz de establecer que sí

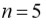
entonces el grado de equivalencia

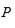
de una ecuación algebraica de grado cinco no puede asumir ninguno de los valores 15, 30 o 40.

Como el número de valores diferentes de la función

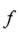
puede ser obtenido dividiendo

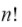
por

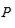
, Ruffini ha probado que ninguna función de las cinco raíces de la ecuación de grado cinco puede existir asumiendo.

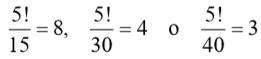
valores diferentes bajo permutaciones de las cinco raíces.

El resultado principal de Ruffini puede ser visto como determinación de los índices de todos los subgrupos de

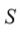
Para probar la imposibilidad de resolver la ecuación algebraica de quinto grado, Ruffini asumió sin demostrar que cualquier radical que ocurra en una supuesta solución puede ser racionalmente expresable en términos de las raíces de la ecuación. Él nunca revisó esta hipótesis y es considerada como una de las grandes ventajas de la demostración de Abel sobre la de Ruffini. Basado en este supuesto y en el resultado que ninguna función

de las raíces

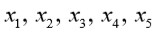
puede tener 3, 4 o 8 valores, Ruffini pudo probar que la

ecuación algebraica de quinto grado no era soluble por radicales

La primera demostración de Ruffini en 1799 sobre la insolubilidad de la ecuación algebraica de quinto grado fue basada en tres partes centrales:

1. La clasificación de las permutaciones en 5 tipos.

2. Una demostración, basada en (1) , que ninguna función de las cinco raíces de la ecuación general de quinto grado puede tener 3, 4 o 8 valores bajo permutaciones de las raíces.

3. Un estudio de los dos radicales más interiores en una supuesta solución de la ecuación de quinto grado, en la cual el resultado de (2) es usado para obtener una contradicción.

En la quinta y última publicación de su teorema en 1813, Ruffini recapituló importantes partes de la teoría de Lagrange, en la cual enfatizaba la diferencia entre igualdades formales e igualdades numéricas. Esta demostración puede ser dividida en las siguientes partes.

1. Si dos funciones

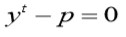
de las raíces

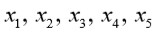
relacionados por una ecuación una ecuación algebraica están

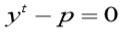
(para algún

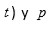
se mantiene inalterada por la permutación cíclica (12345), entonces

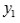
de

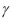
el cual cambia a

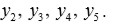
Consecuentemente,

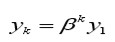
donde

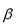
es una raíz quinta de la unidad.

2. Si ademá

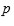
se mantiene inalterada por la permutación (123) , entonces

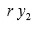
donde

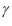
es una raíz cúbica de la unidad.

3. La permutación (13452) es comprimida en dos ciclos (12345)(123) y

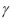
permanecer inalterada. Por lo tanto,

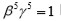
lo cual implica que

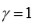
, probando que y no puede ser

alterada por ninguna de las permutaciones (123), (234), (345), (451) 0 (512) .

Combinando estos 3 - ciclos se puede obtener el 5 - ciclo (12345), y por lo tanto

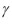
tampoco puede ser alterado por este 5 - ciclo.

4. Consecuentemente, es imposible mediante la extracción sucesiva de raíces describir funciones que tiene más de dos valores, y por ende la insolubilidad es probada.

En 1845, Pierre Laurent Wantzel (1814- 1848) presentó una fusión, incorporando los argumentos de la teoría de permutaciones presentados en la última demostración de Ruffini, dentro de la demostración de Abel.

Como se ha dicho anteriormente, el único problema en la demostración de Ruffini fue asumir que todas las funciones algebraicas pueden ser expresadas en términos de funciones

racionales de las raíces de una ecuación. En terminología moderna, si

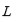
está contenida en una torre radical. Ruffini afirmó lo siguiente (en notación moderna):

Sea

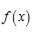
un polinomio general de quinto grado. Si

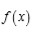
es soluble por radicales, entonces

existe una torre radical de cuerpos

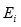
desde

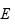
hasta

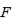
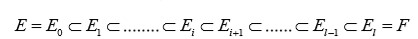
donde

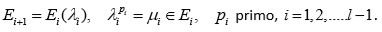
Resulta que esta afirmación es cierta. Por lo tanto, la demostración de Ruffini es correcta (aunque incompleta). Esta afirmación la prueba Abel en la primera parte de su demostración sobre la insolubilidad de la ecuación algebraica general de quinto grado.

A continuación, se muestra la forma como se prueba la laguna dejada por Ruffini y que es una de las mayores contribuciones de Abel, la cual depende de los siguientes muy bien conocidos resultados.

Lema 1: Sea

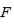
un cuerpo que contiene una raíz primitiva quinta de la unidad. Si

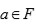
no es una

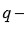
potencia, entonces

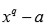
es irreducible.

Lema 2: Sean

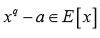
irreducible y a es una raíz de

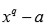
Sea

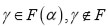
. Entonces existe un

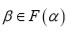
tal que

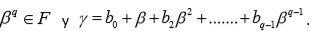
Lema 3: Sea

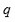
un número primo y

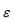
una raíz primitiva

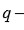
enésima de la unidad. Entonces cada unidad

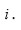
Lema 4: Sea

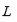
una extensión de

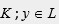
. Entonces el polinomio mínimo de

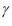
sobre

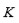
se factoriza completamente en

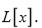
Lema 5: Sea

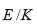
una extensión,

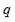
un número primo y

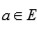
tal que

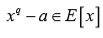
es irreducible. Sea

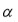
una raíz de

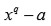
Sea

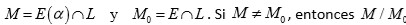
es una extensión radical. Más precisamente, existe un

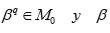
genera a

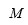
sobre

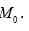
Teorema: Si

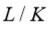
está contenido en una torre radical, entonces radical.

Demostración:

Supóngase que

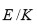
es una torre radical y que

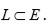
Luego

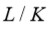
es una torre

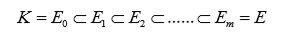
donde

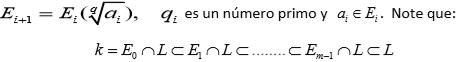
es una torre.

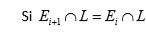
no hay nada más que decir.

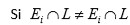
, entonces del Lema 5 se tiene que

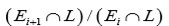
extensión radica

Por lo tanto, después de eliminar los términos que son

iguales en la torre anterior, se obtiene una torre radical para

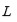
. Así pues

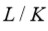
es una torre radical.

Con esta demostración elegante de Abel, la demostración de Ruffini sobre la insolubilidad de la ecuación algebraica de quinto grado queda completa

Referencias bibliográficas

Ayoub, R.G. (1980). Paolo Ruffini’s Contributions to the Quintic. Arch. Hist. Exact Sci., 23, 253-277.

Gray, J. (2018). A history of abstract algebra: from algebraic equations to modern algebra. Switzerland: Springer Undergraduate Mathematics Series.

Katz, V. J., Parshall, K.H. (2014). Taming the unknown: A history of algebra from antiquity to the early twentieth century. Princeton University Press.

Kleiner, I. (2007). A history of abstract algebra. Boston: Birkhäuser.

Pierpont, J. (1896). On the Ruffini-Abelian theorem. Bulletin of the American Mathematical Society, 2, 200-221.

Pierpont, J. (1898). Early history of Galois Theory of equations. Bulletin of the American Mathematical Society, 4, 332-40.

Rosen, M. (1995). Niels Hendrik Abel and Equations of the Fifth Degree. TheAmerican Mathematical Monthly, 102, 495-505.

Rothman, T. (1982). Genius and biographers: The fictionalization of Evariste Galois. The American Mathematical Monthly, 89, 84-106.

Sorensen, H.K. (1999). Niels Henrik Abel and the theory of equations. Denmark: History of Science Department University of Aarhus.

Van der Waerden, B.L. (2013). A history of algebra. From al-Khwarizmi to Emmy Noether. New York: Springer–Verlag.

IR