INTRODUCCIÓN
Las
torres de bandejas son cilindros verticales en los cuales el líquido y el gas
establecen contacto en un arreglo por etapas sobre bandejas o platos. El
líquido entra por el tope y fluye hacia abajo por gravedad. En su camino, el
líquido fluye a través de la bandeja y es dirigido hacia la bandeja inferior
por medio del tubo de bajada (downcomer). El gas, por su parte, transita
hacia arriba por el interior de aberturas colocadas en la bandeja, burbujeando
a través del líquido para formar una espuma y luego separarse de esta, para
luego transitar hacia la siguiente bandeja, ubicada encima. Se obtiene como
efecto global un contacto múltiple a contracorriente entre el gas y el líquido
que se caracteriza por el flujo cruzado de ambos fluidos. Cada bandeja de la
torre es considerada como una etapa debido a que los fluidos son puestos en
contacto íntimo entre sí, ocurriendo difusión interfacial entre ellos, para
luego ser separados. El número de etapas de equilibrio (bandejas teóricas) de
una torre depende solamente de la dificultad del proceso de separación y se
determina directamente a partir de los balances de masa y consideraciones de
equilibrio líquido-vapor (Benitez, 2009).
Las torres
de bandejas constituyen el tipo de equipo de transferencia de masa más empleado
en la actualidad para llevar a cabo operaciones de absorción y destilación. El
número de etapas o bandejas a utilizar en la torre dependerá del grado de
pureza deseado y de la dificultad de la operación de separación. Estos equipos
son más eficientes para efectuar un determinado proceso de separación en
comparación con las columnas empacadas (Eranda, 2016). Para ello, se emplean
diferentes tipos de bandejas, cuya selección depende del grado de pureza
requerido para el producto de interés, los tipos de fluidos manejados y sus
caudales y las dimensiones de los diferentes accesorios que contiene, entre
otros parámetros.
La
eficiencia de la etapa, y por tanto el número real de bandejas, se determina a
partir del diseño mecánico establecido y las condiciones de operación. El diámetro
de la torre, por su parte, depende de las cantidades de gas y líquido que
fluyen a través de la torre por unidad de tiempo y de las propiedades
físicoquímicas de los fluidos que se procesan.
Debido a su
simplicidad y bajo costo, las bandejas perforadas constituyen hoy en día los
tipos de bandejas más importantes en el área de la destilación y absorción
(Eranda, 2016). Estos mecanismos están conformados por placas de metal con
huecos de diversos números, tamaños y patrones de construcción, donde el vapor
es dirigido directamente hacia arriba a través del líquido que fluye por
encima de las bandejas. Durante el diseño de bandejas perforadas es necesario
definir un diámetro de la torre para acomodar los caudales a manejar. Así
mismo, se debe seleccionar los detalles del arreglo de las bandejas, estimar la
caída de presión del gas, el acercamiento a la inundación y asegurar el
equipo para que no ocurra arrastre y/o derrame excesivo (Benitez, 2009). Estas
bandejas ofrecen una elevada capacidad de procesamiento y eficiencia de
separación, baja caída de presión, facilidad de fabricación y limpieza y bajos
costos de capital (Eranda, 2016).
Las torres
de bandejas han sido objeto de estudio tanto en cuestiones relacionadas con su
diseño (Anand & Erickson, 1999; Pilling, 2006; Zavaleta-Aguilar &
Simões-Moreira, 2012), eficiencia (Cheng & Chuang, 1993; Lamprecht, 2017;
Zahedi et al., 2010), evaluación del rendimiento (Olivier &
Eldridge, 2002; Outili et al., 2013) y cálculo del número de bandejas
(Azizi et al., 2015), así como en lo relacionado con sus aplicaciones y
aspectos generales (Benitez, 2009; Kister, 1992; Lockett, 1986; Rose, 1985).
El presente
trabajo tiene como objetivo llevar a cabo el diseño de una torre de bandejas
perforadas para efectuar la absorción de etanol contenido en una corriente
gaseosa mediante el uso de agua como solvente. Para ello, se emplean
correlaciones y ecuaciones publicadas fundamentalmente por autores como
Treybal (1980), Lockett (1986), Seader y Henley (1998), Perry y Green (2008) y
Benitez (2009). Además, se determina el diámetro de la torre, la caída de
presión total, el flujo de arrastre, la eficiencia de Murphree de la
bandeja corregida por efectos del arrastre y el número total real de bandejas
o etapas. Por último, se establece el costo capital de la torre para el año
2018 y se compara el resultado obtenido con el valor de costo determinado durante
el diseño de una columna empacada (Pérez et al., 2019) para luego
seleccionar el equipo de menor costo económico.
MATERIALES Y MÉTODOS
Definición del problema
Debido a un
proceso fermentativo a escala industrial se obtienen 680 m3/h de una
mezcla gaseosa compuesta por 86 % mol de dióxido de carbono (CO2) y 14 %
mol de etanol, a una temperatura de 25 ºC (303 K) y 1,1 atm de presión. Se
desea recuperar el 98 % del etanol contenido en esta corriente gaseosa mediante
un proceso de absorción a contracorriente empleando agua como solvente, un
caudal disponible de 900 kg/h y una temperatura de 25 ºC (298 K). Por ello, se
requiere diseñar una torre de bandejas perforadas para cumplir con los
requerimientos señalados. La máxima caída de presión permisible para la
corriente gaseosa no deberá superar 1,0 kPa/bandeja. Así mismo, esta se deberá
operar bajo un 80 % de inundación bajo condiciones isotérmicas (figura 1).
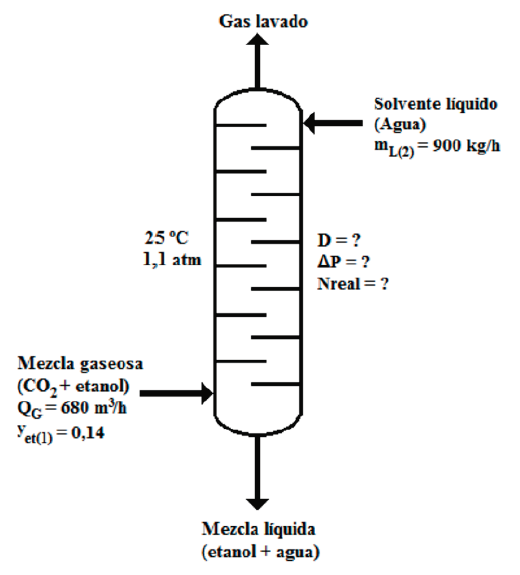 Figura 1
Esquema del proceso de absorción
Fuente: elaboración propia.
Figura 1
Esquema del proceso de absorción
Fuente: elaboración propia.
Debido a
que el sistema de absorción opera a baja presión y temperatura (1,1 atm y 298
K, respectivamente), el gas soluto se encuentra altamente diluido en la fase
líquida (esto es, la fase líquida puede clasificarse como una solución líquida
diluida), el sistema opera bajo condiciones isotérmicas y no existe reacción
química entre en soluto disuelto (etanol) y el solvente (agua). Por lo
anterior, se asume que el sistema obedece la Ley de Henry (Benitez, 2009; Perry
& Green, 2008; Rose, 1985; Treybal, 1980). Según Perry y Green (2008), el
valor de la constante de Henry para un sistema etanol/agua operando a 25 ºC es
H = 0,272. De esta manera, el coeficiente de distribución (φ) para el sistema
gas-líquido (sistema etanol-agua) a 25 ºC y 1,1 at es φ = H/P = 0,272/1,1 =
0,229.
Parámetros de diseño de la torre inicial
La tabla 1
muestra los parámetros de diseño de la torre inicial requeridos para efectuar
los cálculos de diseño del equipo.
Tabla 1
Parámetros de diseño de la torre inicial requeridos para realizar el diseño del equipo
 Fuente: elaboración propia.
Fuente: elaboración propia.
Características de la bandeja
La bandeja
tendrá las características señaladas en la tabla 2. Además, cada bandeja
presentará un arreglo equilateral-triangular y será elaborada en acero
inoxidable.
Tabla 2
Características de la bandeja
 Fuente: elaboración propia.
Fuente: elaboración propia.
Diámetro de la torre
El diámetro
de la torre de bandejas perforadas se determinará empleando correlaciones
establecidas por Treybal (1980) y Benitez (2009). El diámetro determinado, y
por consiguiente su área de sección transversal, deberá ser lo suficientemente
grande para manejar los diferentes caudales de líquido y gas dentro de
intervalos de flujo satisfactorios (Benitez, 2009).
En primer
lugar, se determinarán el peso molecular (MG), la densidad (ρG), la
viscosidad (μG) y el caudal másico (mG) de la mezcla gaseosa
mediante las ecuaciones 1, 2, 3 y 4, respectivamente.
A
continuación, se calcula la relación área de hueco de vapor/área activa de la
bandeja (Ah/Aa); el factor α; el factor β; el coeficiente CF y el factor
de tensión superficial (FTS) mediante las ecuaciones 5, 6, 7, 8 y 9,
respectivamente.
Luego, el
factor empírico C se determina mediante la ecuación 10.
Donde:
FE – Factor de
espuma = 0,9 para columnas que llevan a cabo la absorción de alcohol (Kister,
1992):
FHA = 1,0 cuando Ah/Aa ≥ 0,10, y= 5(Ah/Aa) + 0,5 cuando Ah/Aa < 0,10
La velocidad superficial del gas (vSG) será:
El diámetro de la torre de bandejas perforadas (Dtorre) se determinará según la siguiente correlación:
Donde:
El valor
obtenido de diámetro de la torre de bandejas perforadas deberá ser verificado
mediante la información presentada en la
tabla 3 (con respecto al valor de espaciado de las bandejas [eb] asumido
al inicio).
Tabla 3
Espaciado de bandeja recomendado según el valor del diámetro de la torre
 Fuente: Treybal (1980).
Fuente: Treybal (1980).
A
continuación, se determinarán otros parámetros de la torre de bandejas, tales
como ángulo del downcomer [θ] (ecuación 13); longitud del vertedero [Lvert] (ec. 14);
la distancia del vertedero desde el centro de la torre [rvert] (ec. 15);
el área de sección transversal total [AT] (ec. 16);
el área del downcomer [Atubo] (ec. 17);
el área activa sobre la bandeja [Aa] (ec. 18); y el área total
del hueco [Ah] (ec. 19).
Caída de presión
La caída de
presión típica para el flujo de vapor en una torre oscila entre 0,3 y 1.0
kPa/bandeja (Benitez, 2009). La caída de presión (expresada como pérdida de
carga) para las bandejas perforadas se debe a: (i) la fricción que ocasiona el
flujo de vapor a través de las perforaciones de la bandeja, (ii) la acumulación
de líquido en la bandeja y (iii) las pérdidas por tensión superficial.
Pérdida de carga de la bandeja seca (hS)
Se determina el coeficiente del orificio (C0) a través dela siguiente ecuación
La cual es válida solo si se cumple:
La velocidad del hoyo o hueco (vh) será:
Luego, la pérdida de carga de la bandeja seca (hd) se halla mediante la ecuación 22:
Donde ρH2O es la
densidad del agua a la temperatura del líquido utilizado para el lavado
[solvente] (kg/m3).
Pérdida de carga del líquido claro sobre la bandeja (hl)
La pérdida
de carga del líquido claro sobre la bandeja (hl) depende
de la altura del vertedero, la densidad del líquido y del vapor y de la
longitud del downcomer. De esta manera, la velocidad superficial del
gas con base en el área activa de la bandeja (va), el parámetro
de capacidad (KS), la densidad relativa efectiva de la espuma (ϕe), el
caudal volumétrico del líquido a través de la bandeja (QL(1)), el
coeficiente (Cl) y la carga equivalente del líquido claro en la bandeja [caída
de presión] (hl) serán calculadas mediante las ecuaciones 23, 24, 25, 26, 27 y
28, respectivamente.
Pérdida de carga debido a la tensión superficial (hσ)
Las
burbujas deben vencer la tensión superficial a medida que el gas emerge de las
perforaciones de la bandeja. La caída de presión debida a la tensión superficial
está dada por la diferencia entre la presión dentro de la burbuja y de aquella
del líquido, según la siguiente correlación teórica:
Donde σL se da en
N/m y d0 en m. Se asume que el tamaño máximo de la burbuja puede
tomarse como el diámetro de la perforación (d0).
Caída de presión total por bandeja (ht)
La caída de presión total por bandeja (ht) se expresa a través de la siguiente ecuación:
La cual también se puede expresar como:
Flujo o caudal de arrastre
Para que
una bandeja opere a una alta eficiencia, el goteo de líquido a través de las
perforaciones de la bandeja deberá ser pequeño en comparación con el flujo
sobre el vertedero de drenaje y hacia el downcomer. Así mismo, el
arrastre de líquido por el gas no deberá ser excesivo. El goteo de líquido
ocurre cuando existen bajas velocidades de vapor y/o elevados caudales de
líquido. Se reporta que el goteo de líquido no degrada de forma sustancial el
rendimiento de la bandeja, siempre y cuando se cumpla lo planteado por Benitez
(2009):
Donde hl se da en metros (m).
Una vez se
calcule el número de Froude del hueco u orificio mediante la ecuación
32, se procede a estimar la constante k (ec. 33), la altura de la región
bifásica en la bandeja [h2ϕ] (ec. 34), el arrastre fraccional [Af] (ec. 35)
y el caudal másico del arrastre [QA] (ec. 36).
Donde tanto hl como d0 se dan en milímetros (mm).
Donde tanto hl como d0 se dan en metros (m).
Donde hl y eb se dan en metros (m).
Eficiencia de Murphree de la bandeja
La
eficiencia de la bandeja es el acercamiento fraccional hacia una etapa en
equilibrio que es alcanzada por una bandeja real. Para determinar el número
real de etapas requeridas para lograr una separación dada, deberá ajustarse el
número de etapas de equilibrio con la eficiencia de la etapa o eficiencia de la
bandeja. De esta manera, se calcula el número de Reynolds fraccional (ReF), la
concentración molar del gas (cG), la concentración molar del líquido (cL) y la eficiencia
puntual de la bandeja en fase gaseosa (E0G) utilizando las ecuaciones
37, 38, 39 y 40, respectivamente.
Donde ML = 20,12 kg/kmol (Pérez et al., 2019).
Donde: DG = 8,21x10-6 m2/s y DL = 1,36x10-9 m2/s (Pérez et al.,2019).
A
continuación, se determina el grado de mezclado de la fase de vapor. Para ello,
se calcula el número de Peclet de la fase de vapor o gaseosa [PeG] (Katayama
& Imoto, 1972):
La cual es válida si se cumple que:
Donde: DEG – Difusividad de remolino del gas = 0,01 m2/s (Lockett,1986)
Si PeG > 50 puede considerarse el vapor como no mezclado
Por último,
se determinan la difusividad de remolino del líquido [DEL] (ecuación
42), el número de Peclet del líquido [PeL] (ec. 43), el coeficiente N
(ec. 44), el factor de absorción [λ] (ec. 45); la eficiencia de Murphree de
la bandeja [EMG] (ec. 46) y la eficiencia de Murphree de la
bandeja corregida por arrastre [EMGA] (ec. 47).
Donde: mG(1) = 0,376 kg/s y mL(1) = 0,302 kg/s (Pérez et al., 2019)
Número de etapas o bandejas
Primero, se
determinará el número de etapas o bandejas ideales (Nideal) mediante
la ecuación 48. Luego, se calculará la eficiencia total de la bandeja en
cascada (E0) a través de la ecuación 49. Por último, se hallará el número
real de bandejas (Nreal) según la ecuación 50.
Donde: yet(1) = 0,14
yet(2) = (1) (1 %Re ) et et c y
xet(2) = 0
A = 7,397 (Pérez et al., 2019).
Cálculos económicos
El costo de
la torre de platos perforados será calculado mediante la figura 14.84
presentada en el trabajo de Perry y Green (2008, pp. 14-88). En esta figura, el
costo establecido tiene como fecha de referencia el mes de enero de 1979. Para
actualizar dicho costo al año 2018 se empleará la siguiente ecuación (Peters
& Timmerhaus, 1991):
Donde:
En la
mencionada figura el costo de la columna está referido por bandeja (USD/bandeja).
RESULTADOS Y DISCUSIÓN
Las tablas
4, 5, 6, 7 y 8 muestran los resultados de las diferentes variables determinadas
durante el cálculo del diámetro de la torre, la caída de presión, el flujo de
arrastre, la eficiencia de Murphree de la bandeja y el número real total
de etapas, respectivamente.
Tabla 4
Resultados obtenidos durante la determinación del diámetro de la torre
 Fuente: elaboración propia.
Fuente: elaboración propia.
Tabla 5
Resultados obtenidos durante el cálculo de la caída de presión

* Como se cumple que d0/s > 1,0, se puede emplear la ecuación 20 para determinar el coeficiente de orificio (C0).Fuente: elaboración propia
Fuente: elaboración propia
Tabla 6
Resultados obtenidos al determinar el flujo de arrastre
 Fuente: elaboración propia.
Fuente: elaboración propia.
Tabla 7
Resultados obtenidos al determinar la eficiencia de la bandeja

* Como se cumple que h2ϕ/eb < 1,0, entonces se puede emplear la ecuación (41) para determinar el número de Peclet de la fase gaseosa o de vapor.
Fuente: elaboración propia.
Tabla 8
Resultados obtenidos al calcular el número real total de etapas o bandejas
 Fuente: elaboración propia.
Fuente: elaboración propia.
Según se
puede observar en las tablas anteriores, se obtuvo un valor del diámetro de la
torre (Dtorre) igual a 0,404 m, siendo menor que 1,0 m, por lo que el
espaciado de bandejas (eb = 0,50 m) asumido al inicio es el correcto o recomendado
para una torre con este valor de diámetro, de acuerdo con lo establecido por
Treybal (1980) y Benitez (2009). Por otra parte, la caída de presión total fue
de 0,783 kPa/bandeja, siendo inferior a la caída de presión máxima permisible
para este sistema de absorción (1,0 kPa/bandeja). También se obtuvo un flujo de
arrastre de 0,018 kg/s (64,8 kg/h), que puede considerarse aceptable, tomando
en cuenta los caudales manejados durante el proceso de absorción (Benitez,
2009). Se alcanzó además un valor de eficiencia de la bandeja de Murphree corregida
para flujo de arrastre igual a 0,829, mientras que se requiere un total de 11
etapas o bandejas, aproximadamente, para cumplir con los requerimientos de este
sistema de absorción.
Benitez
(2009) lleva a cabo el diseño de una torre de bandejas perforadas para la
absorción de etanol gaseoso utilizando agua como solvente, con un flujo de la
mezcla gaseosa de 180 kmol/h (7929,21 kg/h) y una composición molar de CO2 y etanol de
98 y 2 %, respectivamente. El caudal de agua utilizado es de 151,5 kmol/h
(2729,27 kg/h) cuando se desea recuperar el etanol en un 97 %. Para estas
condiciones de proceso se obtuvo un díametro de torre de 0,989 m, una caída de
presión de 0,817 kPa/bandeja, un flujo de arrastre de 0,110 kg/s (396 kg/h) y
una eficiencia de la bandeja de Murphree corregida para flujo de
arrastre igual a 0,811. Vale destacar que no se efectuó la determinación del
número de bandejas o etapas. En el trabajo de Benitez (2009) se obtuvieron
valores superiores de Dtorre, ΔPt y QA (en comparación con los estimados en este artículo)
debido a que se emplearon mayores caudales másicos tanto de gas como de
líquido.
El crédito
o mérito de este trabajo radica en que combina y aplica varias correlaciones y
ecuaciones publicadas por diversas fuentes (Benitez, 2009; Lockett, 1986;
Perry & Green, 2008; Seader & Henley, 1998; Treybal, 1980) con el fin
de elaborar una metodología coherente, lógica y abarcadora que permita llevar
a cabo el diseño de una columna de platos perforados para la absorción de un
componente contenido en una corriente gaseosa, empleando para ello un solvente
líquido. Con lo anterior, es posible determinar parámetros de importancia
tales como el diámetro de la torre, la caída de presión, el flujo de arrastre,
la eficiencia de Murphree y el número total de platos o bandejas
perforadas. El objetivo principal consiste, entonces, en elaborar una
metodología completa mediante la cual se pueda diseñar torres de platos perforados
para aplicaciones donde se realice la absorción gas-líquido.
Costo de la torre
Por medio de la ecuación (51) se tiene que:
Donde:
Sustituyendo estos valores en la ecuación 51, el costo de la torre por bandeja:
A continuación, tomando en cuenta el número total de bandejas que poseerá la torre, se obtiene un costo total de:
Por lo
tanto, se requieren alrededor de USD 15.315 para adquirir una torre de bandejas
perforadas conteniendo 11 bandejas y así cumplir con los requerimientos del
proceso de absorción. Al comparar este costo con aquel obtenido para la columna
de absorción con anillos Nor-Pac®, el cual fue de USD 22.000 (Pérez et al., 2019),
se concluye que resulta más económico adquirir la torre de bandejas perforadas
para efectuar el proceso de absorción propuesto, pues esta última registra un
costo 1,44 veces inferior al de la columna empacada, con lo cual se obtiene un
ahorro de USD 6.685.
CONCLUSIONES
Se efectuó
el diseño de una torre de absorción de bandejas perforadas utilizando
correlaciones y ecuaciones descritas por Treybal (1980), Locket (1986), Seader
y Henley (1998), Perry y Green (2008) y Benitez (2009), con lo cual se
determinan parámetros importantes como el diámetro de la torre, la caída de
presión del gas y el número total de bandejas o etapas reales que tendrá este
equipo.
Se obtuvo un diámetro de la torre de 0,404 m, por lo que el
espaciado de bandejas asumido al inicio (0,5 m) es el correcto.
La caída de
presión total del gas fue de 0,783 kPa/ bandeja, la cual se encuentra por
debajo del límite máximo permisible para este proceso de absorción (1,0
kPa/bandeja). Por otra parte, se obtuvo un flujo de arrastre de 0,018 kg/s
(64,8 kg/h), el cual se considera aceptable.
Se obtuvo
un valor de la eficiencia de la bandeja de Murphree corregida por flujo
de arrastre igual a 0,829 (la torre tendrá 11 bandejas o etapas en total).
Se elaboró
una metodolgía de cálculo completa e integral para llevar a cabo el diseño de
columnas de platos perforados que involucre aplicaciones donde se realice la
absorción gas-líquido.
La torre de
bandejas tuvo un costo aproximado de USD 15.315, siendo este valor 1,44 veces
inferior al costo de la columna empacada determinado por (Pérez et al.
2019). Teniendo en cuenta lo anterior, se concluye que resulta más factible,
desde el punto de vista económico, adquirir la torre de bandejas perforadas
para llevar a cabo este proceso de absorción.
Referencias
Anand, G., & Erickson, D. C. (1999). Compact sieve-tray distillation column for ammonia-water absorption heat pump: Part I. E design methodology. ASHRAE Trans, 105, 796-803.
Azizi, N. G., Ghomshe, S. M. T., & Vaziri, M. (2015). New calculation of the tray numbers for Debutanizer Tower in BIPC. International Journal of Engineering Science Invention, 4(8), 1-7.
Benitez, J. (2009). Principles and modem applications of mass transfer operations (2nd ed.). John Wiley & Sons,
Inc.
Chemical
Engineering’s Plant Cost Index [cepci] (2018). Economic indicators. Chemical
Engineering, 125(10), 76.
Cheng,
G. X., & Chuang, K. T. (1993). Prediction of point efficiency for sieve
tray in distillation. Chem. Eng. Commun, 189, 41-60.
Eranda, H. (2016). Design of
o-xylene plate/tray distillation column. University of Moratuwa.
Katayama, H., & Imoto, T.
(1972). Effect of vapor mixing on the tray efficiency of distillation columns. J.
Chem. Soc. Japan, 9, 1745-1751. https://doi.org/10.1246/nikkashi.1972.1745
Kister, H. Z. (1992). Distillation
design. McGraw-Hill.
Lamprecht, J. H. (2017). The
development of simplistic and cost-effective methods for the evaluation of tray
and packed column efficiencies (Master of Engineering thesis, Stellenbosch
University). Stellenbosch University Scholar Research Repository.
https://scholar.sun.ac.za/handle/10019.1/100887
Lockett, M. J. (1986). Distillation
tray fundamentals. Cambridge University Press.
Olivier, E., & Eldridge, R. B.
(2002). Prediction of the trayed distillation column mass transfer performance
by neural network. Ind. Eng. Chem. Res., 41, 3436-3446.
https://doi.org/10.1021/ ie010499l
Outili, N., Chegga, N., Elbahi, K.,
& Meniai, A. H. (2013). Effect of downcomers sizes on tray column
performance. Chemical Engineering Transactions, 32, 1981-1986.
Pérez, A., Pérez, E. J., &
Liaño, N. (2019). Diseño de una columna empacada y una torre de bandejas
perforadas para la absorción de etanol. 1. Diseño de la columna empacada. Mutis,
9(1), 50-64. https://doi.org/10.21789/22561498.1431
Perry, R. H., & Green, D.
(2008). Chemical Engineers’ Handbook (8th ed.). McGraw Hill.
Peters, M. S., & Timmerhaus, K.
D. (1991). Plant design and economics for chemical engineers (4th ed.).
McGraw-Hill.
Pilling, M. (2006). Design
considerations for high liquid rate tray applications. AIChE Annual
Meeting: Advances in Distillation Equipment and Applications, San Francisco,
U.S.A.
Rose,
L. M. (1985). Distillation design in practice. Elsevier.
Seader, J.
D., & Henley, E. J. (1998). Separation process principles. Wiley.
Treybal, R.
E. (1980). Mass-transfer operations (3rd ed.). McGraw-Hill.
Zahedi, G.,
Parvizian, F., & Rahimi, M. R. (2010). An expert model for estimation of
distillation sieve tray efficiency based on artificial neural network approach.
Journal of Applied Sciences, 10(12), 1076-1082. https://doi.org/10.3923/jas.2010.1076.1082
Zavaleta-Aguilar,
E. W., & Simões-Moreira, J. R. (2012). Thermal design of a tray-type distillation
column of an ammonia/water absorption refrigeration cycle. Applied Thermal
Engineering, 41, 1-9. https://doi.org/10.1016/j.applthermaleng.2011.12.009





 [Ec. 1]
[Ec. 1] [Ec. 2]
[Ec. 2] [Ec. 3]
[Ec. 3] [Ec. 4]
[Ec. 4] [Ec. 5]
[Ec. 5] [Ec. 6]
[Ec. 6] [Ec. 7]
[Ec. 7] [Ec. 8]
[Ec. 8] [Ec. 9]
[Ec. 9] [Ec. 10]
[Ec. 10] [Ec. 11]
[Ec. 11] [Ec. 12]
[Ec. 12]

 [Ec. 14]
[Ec. 14] [Ec. 15]
[Ec. 15] [Ec. 16]
[Ec. 16] [Ec. 17]
[Ec. 17] [Ec. 18]
[Ec. 18] [Ec. 19]
[Ec. 19] [Ec. 13]
[Ec. 13] [Ec. 20]
[Ec. 20]
 [Ec. 21]
[Ec. 21] [Ec. 22]
[Ec. 22] [Ec. 23]
[Ec. 23] [Ec. 24]
[Ec. 24] [Ec. 25]
[Ec. 25] [Ec. 26]
[Ec. 26] [Ec. 27]
[Ec. 27] [Ec. 28]
[Ec. 28] [Ec. 29]
[Ec. 29] [Ec. 30]
[Ec. 30] [Ec. 31]
[Ec. 31] [Ec. 32]
[Ec. 32] [Ec. 33]
[Ec. 33] [Ec. 34]
[Ec. 34] [Ec. 35]
[Ec. 35] [Ec. 36]
[Ec. 36] [Ec. 37]
[Ec. 37] [Ec. 38]
[Ec. 38] [Ec. 39]
[Ec. 39] [Ec. 40]
[Ec. 40] [Ec. 41]
[Ec. 41]
 [Ec. 42]
[Ec. 42] [Ec. 43]
[Ec. 43] [Ec. 44]
[Ec. 44] [Ec. 45]
[Ec. 45] [Ec. 46]
[Ec. 46] [Ec. 47]
[Ec. 47] [Ec. 48]
[Ec. 48] [Ec. 49]
[Ec. 49] [Ec. 50]
[Ec. 50] [Ec. 51]
[Ec. 51]





 [Ec. 51]
[Ec. 51]




