Introdução
Oh! Bendito o que semeia
Livros... à mão cheia...
E manda o povo pensar!
O livro, caindo n’alma
É germe – que faz a palma,
É chuva – que faz o mar!
Castro Alves – Espumas Flutuantes, 1870.
Em 1985, comprei, em uma livraria de Londrina – PR, meu primeiro livro do Malba Tahan: “O homem que calculava”. Recordo-me que foi uma leitura agradável e repleta de descobertas. A partir dessa leitura, adquiri muitos outros livros do autor, que me despertaram interesses em outros temas como problemas, jogos, curiosidades, recreações, histórias, filosofia da Matemática, entre outros.
A opção por discutir, neste artigo, o livro A Lógica na Matemática de Malba Tahan foi motivada pelo meu interesse sobre o tema e pelas linhas de pesquisa em que tenho atuado dentro da Educação Matemática.
No início do prólogo de A Lógica na Matemática, Malba Tahan deixa evidente a necessidade do professor de Matemática em compreender a estrutura lógica, as concepções epistemológicas e ontológicas presente na Matemática e não somente os conhecimentos específicos dessa ciência para desempenhar sua profissão e, em diferentes momentos, deixa explícito seu intuito de possibilitar ao professor uma compreensão abrangente e consistente sobre as correlações da Lógica, Matemática, Filosofia da Matemática e História da Matemática. Na introdução, elenca alguns tópicos que o professor deve conhecer e que estão relacionados com a arquitetura da Matemática: a Lógica, os atributos dos axiomas, o modelo axiomático, as demonstrações, os métodos de investigações, as definições, os sofismas e a História da Matemática.
Em vista disso, neste artigo, faço uma análise do livro A Lógica na Matemática com o objetivo de discutir, em uma concepção atual, os tópicos de Lógica Matemática que estão presentes nessa obra.
Para a elaboração do estudo optou-se pela pesquisa historiográfica proposta em Autor (2004). Assim, foram seguidas algumas etapas: verificação bibliográfica, com o propósito de encontrar obras relacionadas com a pesquisa; coleta de elementos referente ao tema pesquisado na obra de Malba Tahan; localização, nas referências bibliográficas, dos conteúdos pesquisados para estabelecer uma relação entre o que o autor expõe no texto e o planejamento do pesquisador.
Sobre a base lógica da Matemática
No primeiro capítulo Malba Tahan (1966, p. 1) trata da base lógica da Matemática, enfatizando a importância do estudo de métodos e de princípios empregados para distinguir o raciocínio correto do raciocínio incorreto. Assim, ao definir a Lógica, a sua importância e a sua relação com a Matemática, Malba Tahan serviu-se de autores importantes que lhe proporcionaram uma conceituação daqueles tópicos. Na atualidade, conforme Hurley:
A Lógica pode ser definida como o corpo organizado de
conhecimento, ou ciência, que avalia argumentos. Todos nós encontramos
argumentos na nossa experiência do dia a dia. Assim, nós os lemos em livros e
jornais, ouvimo-los na televisão e formulamo-los quando nos comunicamos com
amigos e outras pessoas. O escopo da Lógica é desenvolver um sistema de métodos
e princípios que possamos utilizar como critério para avaliar os argumentos dos
outros e como guias na construção de argumentos próprios. Consequentemente,
entre os benefícios que se esperam do estudo da Lógica é um aumento na
confiança de fazer sentido os argumentos quando criticamos os argumentos dos
outros e quando progredimos com os nossos próprios argumentos. (HURLEY, 2012,
p. 1)
Para descrever o arcabouço da Matemática e suas relações com os componentes fundamentais (termos, regras, axiomas, postulados, teoremas, etc), Malba Tahan os divide em dois grupos: os conceitos e as proposições. De fato, segundo Tahan:
Apesar da incrível e espantosa variedade dêsses elementos, podemos dividi-los em dois grupos:
1) os conceitos;
2) as proposições ou relações.
Para os conceitos, estabelece o matemático certos elementos fundamentais: têrmos, regras, coordenação, extensão, etc. Tudo isso vai formar a notável conceituação matemática.
Será inútil dizer que, no campo da Ciência, os conceitos não ficam soltos, mas se apresentam interrelacionados pelas proposições ou relações. Entre essas proposições ou relações, destacamos:
as definições;
os axiomas;
os postulados;
os teoremas, etc.
No trabalho de investigação da Verdade, passamos de uma relação para a outra com auxílio de certo raciocínio denominado demonstração.
O estudo da estrutura lógica, isto é, dos métodos, das conceituações, das proposições, das relações etc., constitui o objeto da Epistemologia da Matemática. (TAHAN, 1966, p. 4)
Neste momento, Malba Tahan, tenta estabelecer uma explicação simples sobre a noção de conceito por meio de algumas citações e, depois, estabelece sua definição. Atualmente, a definição de conceito adotada pelos lógicos é pouco diferente da estabelecida por Malba Tahan. De acordo com Cook (2009):
Um conceito (ou atributo ou propriedade) é um objeto
abstrato ou uma entidade mental (muitas vezes denominada de “ideia”) que é ou
corresponde ao significado de um predicado. No entanto, dentro da Lógica, os
conceitos são mais frequentemente considerados como o referente (se houver) de
predicados (note que este último entendimento poderia ser apenas um caso
especial do primeiro). Nesse sentido, o conceito de “vermelhidão” seria o
referente do predicado “é vermelho”. (COOK, 2009, p. 56)
Malba Tahan conceitua e exemplifica o que se entende em Lógica sobre conceitos individuais e conceitos específicos e exemplifica o que constitui a extensão de um conceito específico, ou seja, o aglomerado de elementos que constituem o conceito.
Em seguida, Malba Tahan apresenta a definição de conceitos coordenados. Ele apresenta um exemplo da geometria euclidiana em que aparecem diversos conceitos coordenados em ordem crescente de extensão. Por exemplo, os conceitos: trapézio, quadrilátero, polígono, figura geométrica. De fato, um trapézio é um quadrilátero plano convexo que tem dois lados paralelos; sejam A, B, e D quatro pontos em um mesmo plano, todos distintos e três quaisquer desses pontos não colineares com os segmentos de reta e que se intersectam apenas nas extremidades. A reunião desses quatro segmentos de reta é denominada quadrilátero plano convexo. Sejam P1, P2, P3, ... , Pn, uma sequência de pontos distintos num plano com . Suponha que os segmentos de reta e têm as seguintes propriedades: (i) nenhum par de segmentos de reta se intersecta a não ser nas suas extremidades; (ii) nenhum par de segmentos de reta com extremidade comum é colinear. Desse modo, a reunião dos segmentos de reta é denominada polígono plano convexo. E figura geométrica é a entidade abstrata primitiva que mediante a qual a Geometria e outros ramos similares da Matemática estão articulados.
Ainda sobre conceitos coordenados, Malba Tahan, salienta que podemos assinalar diferenças específicas entre conceitos, conceitos equivalentes, conceitos coordenados que se intersectam, conceitos contraditórios e conceitos contrários.
Para o caso de conceitos que se intersectam, por exemplo, Malba Tahan estabelece como exemplo o triângulo retângulo e o triângulo retângulo isósceles. Para os conceitos contraditórios, discute o exemplo de considerar que se A é um número natural qualquer, se afirmar que A é par, então A não é ímpar. E, para os conceitos contrários, Malba Tahan usa o exemplo dos conceitos maior do que, menor do que e igual, que são conceitos contrários, porém não contraditórios.
Para finalizar esse capítulo, Tahan (1966, p. 16) sublinha que: “Para o estudo da Matemática, precisamos conhecer certas noções conceituais básicas, fundamentais. Assim, o professor deve assegurar-se, na medida do possível, dos conceitos de número, de ordem, de operação, de forma, de relação, etc”. Além disso, Malba Tahan também enfatiza que ao investigar as origens, a formação e a utilização dos conceitos, no transcorrer da história, em especial, aqueles presentes na fundamentação da Matemática, formulados pelas inúmeras correntes filosóficas, percebem-se que existem divergências filosóficas sobre o modo de compreendê-los, explicá-los, expô-los e utilizá-los na constituição arquitetônica da Matemática.
Sobre a definição de conceito
No segundo capítulo, Malba Tahan aborda os seguintes temas: como definir um conceito, a definição e seus atributos, conceitos sem definição, elementos sem definição, Grupos de Jolivet, os indefiníveis de Le Roy e a impossibilidade de definir tudo.
Com o desejo de dissertar sobre o assunto, inicialmente, Tahan (1966, p. 21) deixa evidente qual é a intenção básica da definição; para isso, se remete a Aristóteles (384-322 a. C.): “Aristóteles, apontado como o criador da Lógica, tinha idéia bem nítida sôbre a finalidade precípua da definição. O objeto da definição é a essência do conceito definido. O problema fundamental em Matemática, em sua marcha ascencional, é obter, para os conceitos, definições lógicas e perfeitas”.
Para estipular uma correlação entre o conceito e a sua definição, Tahan (1966, p. 22) escreve a seguinte afirmação: “Definir um conceito é caracterizá-lo e determiná-lo por meio de outros conceitos conhecidos ou já definidos”. Em Lógica,
Um conceito (ou atributo ou propriedade) é um objeto
abstrato ou uma entidade mental (geralmente denominada de “ideia”) que é ou
corresponde ao significado de um predicado. Dentro da lógica, no entanto, os
conceitos são mais frequentemente considerados como o referente (se houver) de
predicados (note que este último entendimento poderia ser apenas um caso
especial do primeiro). Nesse sentido, o conceito de “vermelhidão” seria o
referente do predicado “é vermelho”. (COOK, 2012, p. 56)
Na constituição basilar da Matemática ou na construção de quaisquer ramos dessa ciência surgem conceitos que são admitidos na teoria sem definição. De fato, para sublinhar esse aspecto de conceitos que aparecem naquela área do conhecimento, Tahan (1966, p. 24) transcreve as observações de Manuel Amoroso da Costa (1885-1928) sobre esse assunto: “As noções primeiras são apresentadas sem definição. Nada impede que lhes atribuamos uma significação intuitiva e concreta, mas essa significação se conservará extensiva à dedução e aos enunciados dos teoremas”.
De maneira didática para o leitor e para o professor, Tahan (1966, p. 25-27) esclarece, mediante um exemplo da geometria euclidiana elaborado em ordem ascendente, a ideia de noções primeiras:. Em termos modernos, essas implicações são: (5) Quadrado é um quadrilátero convexo cujos os quatro lados são congruentes e os quatro ângulos são retos ou Quadrado é o paralelogramo que tem seus lados congruentes e os ângulos retos; (4) Paralelogramo é um quadrilátero convexo cujos pares de lados opostos são congruentes e paralelos dois a dois; (3) Quadrilátero é um polígono de quatro lados e quatro vértices; (2) Polígono plano convexo pode ser definido como consistindo de um número finito de pontos (denominados de vértices) e um número igual de segmentos de reta (denominados lados), ou seja, um conjunto de pontos ciclicamente ordenado em um plano, sem três pontos consecutivos colineares, juntamente com segmentos de reta que juntam com os pares consecutivos dos pontos; (1) Segmento de reta é o conjunto cujos pontos são e , juntamente com todos os pontos que estão entre e ; (0) Reta é um ente primitivo da geometria euclidiana.
Sobre os princípios para se definir um
objeto
No prelúdio do terceiro capítulo, Malba Tahan, previne e orienta o professor sobre a importância de compreender as inúmeras formas de definições que se apresentam nos conteúdos da disciplina de Matemática.
Em seguida, Malba Tahan, expõem as regras estabelecidas por Blaise Pascal (1623-1662) para formular com prudência definições: a primeira regra, conforme Tahan (1966, p. 34): “Aceitar sem definição os conceitos tão simples e tão claros por si mesmos que não existam outros mais simples ou mais claros para explica-los”. A segunda regra, (1966, p. 35): “Não admitir têrmos incertos ou obscuros numa definição”. E, a terceira regra (1966, p. 35): “Ao definir um conceito empregar, apenas, têrmos bem claros por si mesmos ou que já tenham sido prèviamente definidos”.
Tahan (1966, p. 36-49) apresenta e enuncia sete regras gerais para a formulação de definições. Para isso, considera as três regras de Pascal e os princípios formulados por François J. Thonnard (1896-1974). A primeira regra de reflexibilidade da definição é: A definição deve substituir rigorosamente o objeto definido; a segunda regra da clareza da definição: A definição deve ser mais clara do que o definido; a terceira regra da autenticidade da definição: O definido não deve entrar na definição; a quarta regra da concisão da definição: A definição deve ser breve; a quinta regra da legitimidade da definição: Na definição só podem figurar conceitos simples, já conhecidos, ou conceitos admitidos sem definição; a sexta regra do conteúdo da definição: A definição não deve ser deficiente nem deve ser superabundante; a sétima regra da determinação da definição: A definição deve convir ao definido e só ao definido.
Sobre as definições em Matemática
No quarto capítulo, Tahan (1966, p. 51) retoma as discussões sobre definição e enuncia, novamente, a regra aristotélica: “A definição deve caracterizar o ser definido pelo gênero próximo e pelas diferenças específicas”. Com o escopo de ilustrar para o professor de Matemática esse princípio, ele estabelece de forma didática alguns exemplos de conceitos da geometria euclidiana. Por exemplo, os paralelogramos podem-se apresentar sob as seguintes formas distintas: losango, retângulo e quadrado. Um losango é um paralelogramo cujos lados são todos congruentes. Conceito definido: Losango. Gênero próximo: Paralelogramo. Diferença específica: cujos lados são todos congruentes.
Sobre a natureza dos axiomas em Matemática
No quinto capítulo, Tahan (1966, p. 62) apresenta de forma elementar um estudo conciso e didático sobre axioma e postulado. Para isso, define e dá exemplos de axiomas e postulados. Para a primeira tem-se: “Axioma é uma verdade evidente por si mesma. É uma proposição na qual a verdade se manifesta pelo seu cunho de certeza universal”. E a origem desse termo, (1966, p. 62), “vem do grego axioma, através do latim axioma. Em grego significava estima, opinião, dogma”.
Neste ponto, é pertinente tecermos algumas observações em relação ao significado etimológico e a definição em Matemática e em Lógica do termo axioma, com o desejo de completar as informações apresentadas por Malba Tahan. Segundo Chantraine (1968, p. 94): “Verbo denominativo casual em – ovw: ajjxiovw, – ovomai “julgar digno de, acreditar” (jônico-ático), então ajxivwma “estima, dignidade”, e raramente “decisão, exigência, pedido” (jônico-ático), então “axioma” a partir de Aristóteles com os derivados”. Além disso, Mugler discute a acepção de axioma e seu emprego por Aristóteles de Estagira e Euclides de Alexandria (325-365 a. C.):
ajxivwma – Termo imputado por alguns geômetras após Euclides
para a afirmação de verdades gerais, sem demonstração, sobre a quantidade,
especialmente sobre as figuras geométricas. Euclides distingue cinco, que os
manuscritos apresentam, sob o título koinaiv e[nnoiai, já
no primeiro livro de Os Elementos,
entre os postulados e as proposições. Os sucessores de Euclides aumentaram o
número de axiomas para nove; a distinção entre postulados e axiomas, análoga à
estabelecida entre os problemas e os teoremas (cp. ai[tema, qewvrhma, provblhma), remonta às discussões sobre os fundamentos da
Geometria na Academia, especialmente entre Espeusipo
e Menêcmo. Aristóteles denomina esses primeiros
princípios da Matemática às vezes koinai; dovxai, às vezes ajxiwvmata. (MUGLER,
1958, p. 68)
Dessa maneira, uma proposição matemática cuja verdade é aceita sem demonstração é denominada axioma. Por fim, apresenta-se o sentido de axioma e seu emprego em Lógica estabelecida por Cook:
Um axioma é uma fórmula utilizada como uma suposição
inicial e da qual outras – teoremas – são derivadas. Dessa forma, muitas
declarações são demonstradas utilizando axiomas, mas os axiomas não precisam,
em virtude de sua definição, ser demonstrados. No passado, os axiomas deveriam
ser autoevidentes e, assim, não precisavam de suporte
adicional ou evidência. Agora, no entanto, um axioma é um princípio que é
assumido sem demonstração. (COOK, 2009, p. 21)
Para o vocábulo postulado, Tahan (1966, p. 66) estabelece a seguinte definição: “O postulado é um princípio, ou melhor, uma verdade que aceitamos sem demonstração”. Por conseguinte, se faz algumas reflexões sobre o significado etimológico de postulado. Para esse fim, consoante Chantraine (1968, p. 40): “aijtevw: – hvsw, etc., eólico ai[thmi (Píndaro, Fr. 155, Teócrito) “pedir”, etc. (Homero, jônico-ático). 2) ai[thma “pedido” (Platão. LXX, NT, etc.) no sentido do postulado em Lógica e Matemática. (Aristóteles, etc.)”.
Mugler apresenta a definição de postulado e seu emprego por Aristóteles e Euclides:
ai[thma – Um termo reservado para o enunciado de uma verdade
geométrica irredutível para outras e, consequentemente, o elemento final da
análise geométrica, stoicei`on
tw`n qewrhmavtwn, de acordo com a expressão
de Proclus. Euclides distingue cinco, os quais ele
coloca numa lista no início do primeiro livro de Os Elementos, entre as definições e os axiomas. (...) ai[thma é atestado como um termo técnico somente a partir de
Euclides, mas é provável que seu uso remonte à escola de Platão na discussão
entre Espeusipo e Menêcmo
como afirma Proclus. Aristóteles conhece bem a
distinção entre axiomas e postulados, mas usa uma terminologia diferente
daquela de Euclides. (MUGLER, 1958, p. 45)
Malba Tahan (1966, p. 68) deixa evidente que não há distinção entre os vocábulos axioma e postulado: “Dado o conceito moderno de teoria dedutiva, não há razão alguma para estabelecer distinção entre axioma e postulado. As proposições iniciais formam um corpo homogêneo, nenhuma delas sendo privilegiada pela sua maior ou menor evidência”.
Em seguida, Malba Tahan reserva um subcapítulo para descrever algumas proposições não demonstradas que se tornaram célebres na História da Matemática (os postulados de Euclides, Lobachevsky, Riemann, Goldbach, Arquimedes, Dedekind, Eudoxo, Schröder e Zermelo) e outros subcapítulos para examinar os postulados de Arquimedes, Dedekind, Eudoxo, Schröder e Zermelo.
Vale salientar que no prefácio do tratado Sobre a esfera e o cilindro, Arquimedes testemunha que Eudoxo conhecia essas ideias, porém o termo “axioma de Arquimedes”, empregado atualmente, foi proposto em 1882 por Otto Stolz (1842-1905) em seu artigo Zur Geometrie der Alten, insbesondere über ein Axiom des Archimedes. Em termos modernos, esse postulado pode ser formulado como segue: sejam e , então existe um número tal que .
Sobre o método axiomático
No sexto capítulo, Malba Tahan disserta sobre o método axiomático. Para isso, já no primeiro subcapítulo, expõe uma síntese desse esquema.
Ao iniciar o estudo de um ramo (ou de um capítulo) da
Matemática apresentaria o seu autor todos os axiomas, ou princípios fundamentais
(postulados) que iriam servir de base aos conhecimentos: definições, teoremas,
problemas, etc., relacionados com êsse ramo (ou êsse capítulo). Todos êsses
conhecimentos seriam tirados dos axiomas básicos, por meio de um número finito
de raciocínios lógicos bem coordenados. (TAHAN, 1966, p.79)
Um sistema axiomático comporta em sua constituição alguns elementos fundamentais: uma linguagem subjacente ao sistema axiomático, um sistema lógico, um vocabulário de palavras não definidas, um conjunto de proposições (axiomas) referente às palavras não definidas e um conjunto de definições derivadas desse conjunto de palavras não definidas e do conjunto de axiomas e novas proposições para serem demonstradas utilizando as regras de inferências da lógica.
Em sua discussão sobre o método axiomático, Malba Tahan enuncia, discute e exemplifica alguns princípios presentes numa teoria lógica ou axiomática, ou seja, uma teoria lógica consistente é aquela em que não é possível derivar uma proposição e sua negação do conjunto de proposições da teoria; uma teoria lógica independente é aquela para a qual uma proposição é independente em um conjunto de proposições quando não é implicada por alguma proposição de ; e uma teoria lógica completa é aquela quando todas as sentenças válidas da linguagem da teoria são proposições dela.
Sobre o método
axiomático na Geometria
No sétimo capítulo, Malba Tahan expõe a axiomática euclidiana. Ele analisa os grupos de axiomas e estabelece uma discussão sobre o número de axiomas que entram nessa teoria. Cabe explicar que Euclides estabelece, nesta ordem, três grupos de proposições: as vinte e três definições, os cinco postulados e as nove noções comuns (axiomas).
Malba Tahan discute cada um dos postulados euclidianos e se dedica em realizar um estudo sobre o quinto postulado. Para isso, o enuncia de três formas diferentes e o analisa com o intuito de possibilitar uma compreensão por parte dos professores. Também o exprimi de várias maneiras equivalentes àquelas propostas por diversos geômetras no transcorrer da história da geometria não-euclidiana.
Em seguida, de forma breve, Malba Tahan apresenta o postulado de Lobachevsky. O postulado das paralelas na geometria euclidiana declara que, para cada reta e para cada ponto fora dessa reta , a unicidade das paralelas é válida (dada a reta e o ponto não sobre , existe uma e somente uma reta através de paralela a ). Por outro lado, a negação dessa proposição, o postulado da geometria hiperbólica, afirma que para alguma reta e para algum ponto não nessa reta , a unicidade das paralelas não é válida (dada a reta e o ponto não sobre , existe pelo menos duas retas através de paralela a ). Assim como seus antecessores – Girolamo Saccheri (1667-1733), Johann Heinrich Lambert (1728-1777) e Adrien-Marie Legendre (1752-1833) – Lobachevsky esperava constatar uma contradição no modelo euclidiano modificado; entretanto, seu sistema não era incoerente e, em 1826, desenvolveu uma geometria diferente da euclidiana (denominada de geometria hiperbólica). Em 1899, David Hilbert (1862-1943) apresentou uma axiomatização da geometria euclidiana em cinco grupos de axiomas – oito de incidência, quatro de ordem, cinco de congruência, axioma das paralelas e dois de continuidade; em vista disso, pode-se formular com rigor o problema relativo ao quinto postulado – Ao aceitar os axiomas hilbertiano é possível deduzir deles o quinto postulado euclidiano? Em síntese, o resultado obtido por Lobachevsky é: O quinto postulado euclidiano não é consequência dos axiomas hilbertiano.
De forma concisa, Malba Tahan enuncia o postulado de Riemann; desse modo, pode-se tecer algumas considerações sobre a terceira geometria (geometria elíptica) que pode ser desenvolvida, na qual não há reta paralela a passando por um ponto fora dessa reta (dada a reta e o ponto não sobre , não existe reta alguma passando por paralela a ), isto é, uma geometria cujas retas paralelas não existem. Os postulados da geometria elíptica plana organizam-se com base nos postulados de incidência, de congruência e de continuidade da geometria euclidiana (com as formulações de novas definições de segmento de reta, ângulo, triângulo, quadrilátero, etc.) e o postulado das paralelas é substituído por aquele postulado descrito acima.
Sobre as diferentes axiomáticas para a geometria
euclidiana
No oitavo capítulo, Malba Tahan expõe os axiomas dos sistemas de Pasch, os cinco grupos de axiomas de Hilbert e os postulados de Veblen para a construção da geometria euclidiana e enuncia de forma didática os postulados de Peano para construção dos números naturais. Neste ponto são necessárias algumas explicações: em seu tratado, Peano, após seu prefácio, elabora duas tabelas (signos da Lógica e da Aritmética) e alguns signos compostos que serão utilizados em sua obra. Nessas listas aparecem os símbolos, os seus conceitos e as páginas em que aparecem no tratado. Por exemplo, conforme Peano (1889, p. VI): “signo – P; significado – proposição; página – VII. Desse modo, Peano elenca os seguintes sinais: K (classe), ∩ (e), ∪ (ou), - (não), = (é igual), (é, pertence), Th (teorema), Hp (hipótese), Ts (tese), L (lógica), (números inteiros positivos), R (números racionais positivos), -< (não é menor), =U> (igual ou maior)”.
Neste sentido, depois de apresentar uma sucessão de proposições lógicas, Peano, no capítulo sobre Arithmetices principia, estabelece algumas explicações e as interpretações dos signos: os números (inteiros positivos), a sequencia mais e (é igual). Em seguida, Peano (1889, p. 1), expõem os postulados de sua axiomática para construção dos números naturais:
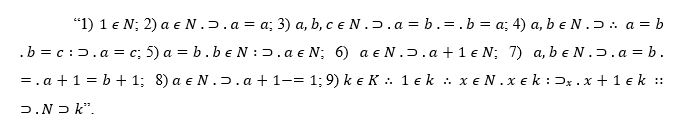
Dessa maneira, os axiomas 2), 3), 4) e 5) referem-se à igualdade de elementos do conjunto dos números naturais e os axiomas 1), 6), 7) e 8), 9) são os conhecidos postulados de Peano cuja interpretação respectivamente é: 1 é um número; a é um número, então o sucessor a + 1 é um número; a e b são números e se é igual a b, então os sucessores desses números a + 1 e b + 1 são iguais; a é um número, então o sucessor a + 1 não é o número 1; seja k uma classe pertencendo a uma classe k (de números) e 1 é um número da classe k, se x é um número de N (números inteiros positivos),x é um número da classe k, então o seu sucessor x + 1 é um número da classe k, então todo número k está em N.
Sobre a estrutura lógica de um sistema
dedutivo
No nono capítulo, Malba Tahan explicita a estrutura lógica de um sistema dedutivo. Para tanto, segmenta-o em proposições fundamentais (as noções conceituais, os axiomas e as definições) e em proposições secundária (teoremas, corolários, teoremas relacionados e condições restritivas).
Uma vez estudadas as proposições fundamentais, cumpre-nos, apenas, dirigir a nossa atenção para as proposições secundárias.
E quais são as proposições secundárias?
São várias as proposições secundárias dentro da Matemática. Apontemos as seguintes: 1) os teoremas; 2) os corolários dos teoremas; 3) os teoremas relacionados; 4) as condições restritivas; 5) os problemas; 6) as relações e fórmulas; 7) os sofismas e os paralelogismos; 8) os paradoxos. (TAHAN, 1966, p. 126)
Malba Tahan (1966, p. 127) estabelece a definição de teorema e o exemplifica: “Denomina-se teorema, de um modo geral, a uma verdade que é aceita, isto é, admitida como certa e legítima, depois de ter sido demonstrada”.
Consoante Chantraine, a acepção etimológica de teorema é:
qewrov" – jônico-ático, “alguém enviado para consultar um
oráculo”, (...) é a partir de Platão que aparece o significado de
“contemplação, consideração” e no grego helenístico, (contemplação e vida
contemplativa em Platão), “teoria, especulação” em oposição à prática. Verbo
denominativo: qewreVw “fazer teorias” (Aristóteles). (...)
mas geralmente qewvrhma “espetáculo, contemplação, teoria, teorema”,
(jônico-ático). CHANTRAINE (1968, p. 433)
A noção de teorema presente nos geômetras gregos, segundo Mugler (1970, p. 220), é: “qewvrhma
– Nome que o enunciado e a demonstração de uma propriedade geométrica. (...) Proclus: distinguem-se nos processos fundamentais da
geometria os problemas e os teoremas, os primeiros contêm a constituição de
figuras (...) ao passo que o segundo demonstra as propriedades de cada uma das
figuras”.
De acordo com Cook (2009, p. 287), em Lógica, “um teorema, em relação a uma teoria, é uma afirmação que pode ser comprovada utilizando, como pressupostos, apenas axiomas dessa teoria particular. Em outras palavras, um teorema de uma teoria é uma consequência dedutiva dessa teoria”.
Em Matemática, um teorema é qualquer afirmação matemática que possa ser demonstrada como verdadeira empregando os princípios de um sistema lógico e argumentos matemáticos aceitos.
A acepção etimológica de demonstrar, segundo Chantraine (1968, p. 257), é: “deivknmi – (...) Sentido: “fazer ver, mostrar, demonstrar, indicar” (Homero, jônico-ático, etc.); cf. também Mugler, Terminologie géométrique. Diversas formas para o pré-verbo no verbo e nas formas nominais: ajna- “mostrar, proclamar”, ajpo- “demonstrar”.
O significado de demonstração na geometria grega, consoante Mugler (1970, p. 74), é: “ajpovdeixi" – O nome da operação que
consiste em fundamentar uma propriedade geométrica, reduzindo-a as proposições
logicamente anteriores e, se necessário, ao primeiro princípio. (...) ajpovdeixi" é comum em Aristóteles, com
um sentido lógico muito geral, especialmente, nos Analíticos posteriores”.
Conforme Cook (2009, p. 230), “uma prova (ou demonstração) é uma sequência finita de declarações em que cada declaração na lista é um axioma ou o resultado da aplicação de uma regra de inferência para uma ou mais declarações precedentes. A declaração final é a conclusão da prova”.
Desse modo, em Matemática, uma demonstração de uma proposição matemática é uma sequência finita de afirmações matemáticas que em cada passo dessa sucessão expõem-nas empregando, não nesta ordem, definições, axiomas ou outras proposições anteriores reunidas pelas regras de inferências e nesse processo a afirmação da etapa final comprova a veracidade da proposição matemática.
Em seguida, Tahan (1966, p. 129) salienta que há duas partes (hipótese e tese) numa afirmação de um teorema: “A hipótese é a parte, contida no enunciado do teorema, que admitimos como verdadeira. A tese é a parte expressa no enunciado do teorema, que queremos, ou devemos, provar que é verdade”.
O significado de hipótese na geometria grega, para Mugler (1970, p. 440), é: “uJpovqesi" – Fato geométrico admitido no início de uma demonstração e cuja demonstração deduz as consequências”.
Em lógica, a acepção de hipótese, de acordo com Cook (2009, p. 13), é: “o antecedente de um condicional é a subfórmula do condicional que ocorre entre o “se” e o “então” ou, se o condicional não estiver na forma rigorosa “se ... então ...”, assim o antecedente é a subfórmula que ocorre entre “se” e “então” em “se ... então ...” declaração logicamente equivalente ao condicional original”.
O sentido etimológico de tese, em Chantraine (1968, p. 1117), é: “tivqhmi – (...) Diversos derivados que entram nos sistemas coerentes. Nome de ação: 1. qevdi" “ação de colocar, de estabelecer (leis), de depor, de adotar”, etc., com o sentido técnico na geometria, na lógica, na métrica (Alceu, Píndaro, jônico-ático); em muitos pré-verbos: ajvnav-, ajntiv-, (...), suvvn-, uJpo-, etc.;”.
Conforme Cook (2009, p. 62), tese em Lógica é: “O consequente de um condicional é a subfórmula do condicional que ocorre após o “então” ou, se o condicional não estiver em forma rigorosa “se ... então ...”, assim o consequente é a subfórmula que ocorre após o “então” em “se ... então ...” declaração logicamente equivalente ao condicional original”.
Malba Tahan (1966, p. 131) deixa evidente a noção de corolário e apresenta um exemplo, como segue: “De certo teorema podemos tirar outros teoremas – chamados corolários – que são consequências imediatas e lógicas do primeiro. Quando, portanto, o teorema B decorre como consequência lógica e imediata do teorema A, dizemos que o teorema B é um corolário do teorema A”.
Em conformidade com Chantraine (1968, p. 929), o significado etimológico de corolário é: “porismov": “maneira de ganhar, fato de procurar”, termo em geometria “corolário”. E, segundo Mugler (1970, p. 355), em geometria grega é: “povrisma – nome que designa uma proposição suplementar resultante como consequência acessória da prova de um teorema”.
Em seguida, Tahan (1966, p. 132) estabelece e exemplifica o conceito de teorema recíproco como descrito: “Consideremos um teorema A cuja hipótese é H e cuja tese é T. Consideremos outro teorema B cuja hipótese é T e cuja tese é H. Diremos, nesse caso, que o teorema B é a recíproca do teorema A”.
Malba Tahan (1966, p. 135) relata e exemplifica a ideia de teorema contrário: “Sendo dado um teorema A, cuja hipótese é H e cuja tese é T, podemos, em certos casos, formular outro teorema B cuja hipótese é a negação de H e cuja tese é a negação de T. diremos nesse caso, que o teorema B é o contrário do teorema A”.
Por fim, Malba Tahan (1966, p. 137) aborda sobre as condições restritivas de uma propriedade: “Sendo formulada uma propriedade, ou uma relação qualquer, pode acontecer que essa propriedade, ou relação, esteja sujeita a certas condições restritivas. As condições restritivas que se apresentam em Matemática são três: 1) Condição necessária, mas não suficiente; 2) Condição suficiente, mas não necessária; 3) Condição necessária e suficiente”.
Em Lógica, de
acordo com Cook (2009, p. 197-198), uma condição necessária e uma condição suficiente têm as seguintes acepções: “𝐴
é uma condição necessária para 𝐵 se,
e somente se, a verdade de 𝐵
for suficiente para garantir a verdade de 𝐴.
Assim, 𝐴
é uma condição necessária para 𝐵 se, e somente
se, o material condicional 𝐵 → 𝐴 é verdadeiro. Se 𝐴 é uma condição
necessária para 𝐵, então 𝐵 é
uma condição suficiente para 𝐴”.
Em Matemática as declarações presentes nas proposições
e nas suas demonstrações são afirmações
condicionais da forma 𝐻 implica 𝑇 (𝐻 → 𝑇)
cuja implicação condicional organiza algumas instruções àquelas declarações.
Com efeito, na asserção condicional 𝐻 → 𝑇 a asserção antecedente 𝐻 é uma condição suficiente
para 𝑇 e a asserção consequente 𝑇 é uma condição necessária para 𝐻.
Por isso, as proposições matemáticas podem ser expressas por: “𝐻, é
uma condição suficiente para 𝑇”,
“se 𝐻,
então 𝑇”,
“se 𝐻 é verdadeira, então 𝑇 é verdadeira”, “𝐻, somente
se 𝑇”, “𝑇, é uma condição necessária para 𝐻”, “
Sobre as alguns métodos
de demonstração em Matemática
No décimo capítulo, Tahan (1966, p. 146) apresenta várias formas de se provar um teorema – demonstração direta, por absurdo, pelo terço excluído, por indução e por analogia – e aponta algumas observações didáticas. Sobre demonstração direta, define: “Uma demonstração é chamada direta quando é obtida exclusivamente com auxílio de proposições anteriormente demonstradas ou aceitas sem demonstração”.
Em Lógica, o processo do método de demonstração direta
pode ser expresso pelo teorema que garante
a validade desse procedimento. Para as formas
proposicionais
Em Matemática, pode-se
estabelecer o seguinte
esquema para o método direto de demonstração: considere a proposição matemática “se 𝐻, então 𝑇”, a partir de sua hipótese,
constrói-se uma sequência finita de afirmações utilizando definições,
axiomas, corolário e outras asserções
matemáticas mediante inferência lógicas que resultarão na tese que é parte final da demonstração daquela
proposição. Dessa maneira,
um esboço simplificado desse processo de demonstração
direta tem este modelo: 𝐻
= 𝑝0 → 𝑝1 → ⋯ → 𝑝𝑛−2
→ 𝑝𝑛−1 = 𝑇 em que a
partir da hipótese 𝐻
mediante argumentos lógicos conduz-se à proposição 𝑝1, 𝑝1
mediante asserções lógicas
conduz-se à proposição 𝑝2, e assim consecutivamente até que a tese T.
Na demonstração por absurdo, Malba Tahan demonstra uma proposição da geometria euclidiana; após comprová-la expõe alguns inconvenientes desse método de prova.
Em Lógica, o processo do método de demonstração por reductio ad absurdum (ou reductio, ou reductio absurdum,
ou contradição) ou redução ao absurdo pode ser descrito pelo teorema que garante
a validade desse
procedimento: Para todas as formas proposicionais 𝑝, 𝑞, ¬𝑝 → (𝑝
𝖠 ¬𝑝) ⇒
𝑞.
Em Matemática, pode-se
estabelecer o seguinte
esquema: considere a proposição matemática “Se 𝐻 é
verdadeira, então 𝑇 é verdadeira”, começa por assumir
que a hipótese 𝐻 é
verdadeira e a tese 𝑇 é falsa. Em
razão disso, com base nessas duas declarações, constrói-se uma sequência
finita de afirmações utilizando definições, axiomas,
corolário e outras asserções matemáticas mediante inferência lógicas é
seguida até que uma contradição se desenvolva. Com efeito, agora, trabalhando valendo-se de 𝐻 e ¬𝑇, para uma contradição comprova a proposição
𝐻 → 𝑇 mostrando que 𝐻 𝖠 ¬𝑇 é sempre falsa,
e desde que 𝐻 𝖠 ¬𝑇 é logicamente equivalente a
¬(𝐻 → 𝑇) (por ¬(𝑃 → 𝑄) ⇔ 𝑃 𝖠 ¬𝑄), segue-se que a negação da proposição também é
falsa. Agora, se a negação da
proposição é sempre falsa, então se tem o caso que a proposição é sempre verdadeira. Portanto, o método de demonstração por redução ao absurdo comprova
𝐻 → 𝑇, demonstrando que ¬(𝐻 → 𝑇) nunca pode ser verdadeira.
Sobre a indução, analogia e dedução em
Matemática
No décimo primeiro capítulo, Malba Tahan estabelece a noção de indução e a indução matemática.
Em Lógica, conforme Cook:
A indução matemática (ou o esquema de indução, ou o
esquema de indução matemática) é o seguinte esquema de axioma da aritmética
(para qualquer predicado ): (em que é a função sucessora aritmética). A indução
matemática é um esquema de axioma da aritmética de Peano, mas não de muitos
sistemas mais fracos, incluindo a aritmética de Robinson. (COOK, 2009, p. 184-185)
Em Matemática, o princípio da indução matemática –
termo nomeado por Augustus De Morgan
em 1838, que segue do axioma da boa ordem que afirma que cada conjunto não
vazio de números naturais tem um
menor elemento – tem a seguinte formulação: Seja 𝑁 um
subconjunto do conjunto ℕ dos números
naturais; se 𝑁 possui as duas seguintes propriedades: (i) 1 ∈ 𝑁 e
(ii)
𝑘
+ 1 ∈ 𝑁 sempre que 𝑘
∈ 𝑁, então 𝑁 contém todos os números naturais. Além disso, na
maioria das aplicações desse
princípio, o matemático está interessado em demonstrar proposições para todos os números naturais. No entanto, há uma
possibilidade análoga daquele princípio enunciado acima: Seja 𝑁 um subconjunto do conjunto ℕ dos
números naturais; se 𝑁 possui as duas seguintes propriedades:
(i) 1 ∈ 𝑁 e (ii) 𝑘 + 1 ∈ 𝑁 sempre que 1, 2, 3, ⋯ , 𝑘
∈ 𝑁, então 𝑁 contém
todos os números naturais.
Em relação ao desenvolvimento histórico do conceito do princípio de indução Rashdi Rashed realizou uma investigação aprofundada sobre esse tema, consultando os tratados de Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji (953-1029), Ibn Yahya al-Maghribi Al-Samawal (1130-1180), Levi ben Gerson (1288-1344), Francesco Maurolico (1494-1575) e Blaise Pascal e concluiu que:
Em outras palavras, se começarmos com formulações após
Peano, encontramos vestígios fortes que nos permitem
descobrir o princípio da indução em Pascal. Mas se começarmos com Pascal, os
tipos de demonstrações de Al-Karaji e Al-Samawal será incluído como raciocínio matemático indutivo e
de regressão como uma forma arcaica de indução matemática, uma inclusão difícil
de alcançar a partir da formulação de Peano.
Portanto, em uma “história recorrente”, a tentativa de Pascal parece ser a
culminância das ideias de Al-Karaji e Al-Samawal, enquanto a tentativa de Peano
parece ser o culminar das tentativas que começaram com Pascal. Para evitar a
“recorrente” história comum, devemos escolher um ponto de partida no passado,
que é um ponto culminante, um ponto culminante que é necessariamente o ponto
culminante de um começo. A dupla referência, portanto, necessária para o
historiador nos permite concluir: os métodos de demonstração de Al-Karaji e Al-Samawal –
especialmente os tipos de demonstrações deles e da regressão de alguma forma –
constituem o início da indução matemática, se alguém começar com Pascal.
(RASHED, 1994, p. 81)
Malba Tahan exibe exemplos
de indução matemática, falsa indução e a falsa indução relacionada com a conjectura de Pierre de Fermat (1601-1665): todo número da forma 𝐹 = 22𝑛 +
𝑛
1, para 𝑛 ∈ ℕ, é primo;
ele mostrou que para 𝐹0 = 3, 𝐹1 = 5, 𝐹2 = 17, 𝐹3 = 257 e 𝐹4 = 65.537 são primos. Porém,
Euler provou em 1732 que 𝐹5 = 232 + 1 = 641 × 6.700.417 e Thomas
Clausen (1801-1885) antes de F. Landry (1799-1862) mostrou em 1855 que 𝐹6 = 264 + 1 =
274.177 × 67.280.421.310.721 são números compostos. De fato, consoante Krizek:
Em 1880, F. Landry, quando tinha
oitenta e dois anos, fatorou o sexto número Fermat em dois fatores. No entanto, Kurt-R. Biermann
afirma que, em uma carta de 1 de janeiro de 1855, a Gauss, que permanece na
biblioteca da Universidade de Göttingen, Thomas Clausen (que também era
conhecido como um astrônomo importante) apresentou a completa fatoração de em dois fatores primos, ou seja, antes de
Landry em 1880. (KRIZEK; LUCA; SOMER, 2001, p.3)
Malba Tahan elabora algumas considerações entre indução e dedução, método dedutivo e dedução e Matemática.
Em Lógica, conforme Cook, dedução tem a seguinte acepção:
Uma derivação (ou dedução) é uma sequência finita de
afirmações dentro de um sistema formal em que cada declaração na sequência é um
axioma, uma suposição ou o resultado da aplicação de uma regra de inferência em
uma ou mais declarações anteriores. A declaração final é a conclusão do
argumento que foi derivado, e cada suposição é uma premissa do argumento
derivado. (COOK, 2009, p. 88)
Em Matemática, o raciocínio dedutivo é um procedimento derivativo em que a tese é verificada mediante uma sequência finita de argumentos lógicos fundamentados em uma coleção de proposições – definições, axiomas, corolário ou outras premissas lógicas – não necessariamente nessa ordem.
Por fim, Tahan (1966, p. 172) estabelece algumas ponderações sobre analogia, analogia em Matemática, método por analogia e demonstração por analogia. Assim, define esse termo: “A palavra analogia vem do grego, através do latim, e significava proporção, semelhança. Em grego teríamos aná, conforme a, logos, razão. Analogia é qualquer relação entre coisas distintas”.
Em Chantraine (1968, p. 82), o significado etimológico de analogia é: “avnaj: (...) apresenta o emprego resultantes da noção de “de baixo para cima”, na qual “por meio de” em especial com um sentido temporal, finalmente com um valor distributivo “em razão de” ou “proporcionalmente”. E completa com (1968, p. 625): “lovgo" forma de um tipo antigo de grande importância, “conversas, palavras” (Ilíada. 15.393, Odisseia. 1,56); em jônico-ático com vários sentidos, “narrativa, relato, consideração, explicação, raciocínio, razão, palavra”, (...) Além disso, adjetivos derivados da hipóstase: ajvnavlogo" “proporcional”.
Em Matemática, conforme Polya (1968), uma analogia é uma comparação entre dois objetos, entre dois conceitos, entre duas proposições ou entre sistemas de objetos matemáticos em que se destacam alguns aspectos que podem ser examinados com o intuito de buscar semelhanças entre seus entes matemáticos.
Considerações
O intuito de Malba Tahan ao escreve um livro sobre a Lógica na Matemática ressalta sua preocupação como educador da necessidade do professor da Educação Básica, para exercer a docência, entender a estrutura e os aspectos da Lógica, as concepções epistemológicas e ontológicas presente na Matemática e não apenas nos conhecimentos específicos dessa ciência. Para realizar esse projeto, Malba Tahan emprega sua erudição crítica – de modo didático e organizado, numa leitura agradável – para abordar conteúdos correlacionados com a estrutura da Lógica, da Matemática e da Filosofia desses ramos do conhecimento.
Malba Tahan aborda assuntos pertinentes que têm conexão com a Lógica e a Matemática, tais como: as bases da lógica Matemática, a relação entre a Lógica e a Matemática, problemas da definição, definição de objetos matemáticos, objetos primitivos de algumas áreas da Matemática, utilidade dos axiomas, o método axiomático da Matemática, estrutura lógica dos sistemas dedutivos, proposições (lemas, teoremas e corolários) da Matemática, condições necessárias e suficientes patentes nas proposições, demonstração em Matemática, os diversos métodos de demonstração, indução, indução matemática, dedução em Matemática, analogia em Matemática, etc. Consequentemente, para construir seu texto, Malba Tahan, conforme consta na bibliografia (disponível em sua época), utiliza-se de publicações de inegáveis especialistas nas distintas áreas da Filosofia, Filosofia da Matemática, Lógica, Matemática e História da Matemática, para citar alguns, a saber: Amoroso Costa, Bell, Blanché, Borel, Bourbaki, Cabrera, Caraça, Castrucci, Catunda, Dedron, Dickson, Enriques, Fourrey, Gama, Heyting, Hilbert, Jolivet, Loria, Mieli, Nascentes, Pascal, Pastor, Poincaré, Polya, Russell, Silva, Titchmarsh, Vera, Whitehead, Young, etc. Além disso, Malba Tahan orienta seus leitores para que consultem outras publicações de sua autoria que podem complementar seus estudos nessa temática. Nesta perspectiva, considerando a vasta obra de divulgação da Matemática proclamada por Malba Tahan, pode-se afirmar que muitas gerações de professores da Educação Básica tiveram-no como inspiração e modelo de professor ideal e usufruíram de seus textos para desmitificar a Matemática e que a apreensão dessa não é para alguns privilegiados.
Dessa forma, pode-se considerar que o livro A Lógica na Matemática é um texto que poderia ser lido, consultado e utilizado, evidentemente, com algumas ressalvas de ordem técnica – filosófica, lógica, matemática e histórica –, em diversas disciplinas dos cursos de Licenciatura em Matemática para discutir, analisar, fundamentar e aprofundar aqueles conteúdos declarados anteriormente. Por fim, Malba Tahan figura entre os notórios – Walter William Rouse Ball, Italo Ghersi, Emile Fourrey, Yakov Perelman, Paul Karlson, Lancelot T. Hogben, Edward Kasner e James R. Newman, Martin Gardner, Raymond M. Smullyan, Philip J. Davis e Reuben Hersh, Miguel de Guzmán, John H. Conway, Ian N. Stewart, etc. – divulgadores da Matemática.