1. Introdução

Um dos objetivos do ensino da Matemática escolar é levar os alunos a aprenderem conceitos matemáticos (NCTM, 2000; BRASIL, 1998; 2018). Um caminho para tal envolve abordar a resolução de problemas, de modo que os alunos possam desenvolver habilidades matemáticas, compreender a estrutura matemática, bem como aprender a resolver problemas, o que implica na aprendizagem e na mobilização dos vários conceitos matemáticos (CAI; LESTER, 2012; PRUSAK; HERSHKOWITZ; SCHWARZ, 2013; ECHEVERRÍA; POZO, 1998; LESTER JR.; CAI, 2016; PROENÇA, 2018; TAMBUNAN, 2019; SCHOENFELD, 2020).

Envolver os alunos na resolução de problemas contribui para a aprendizagem conceitual no sentido de que, segundo Schroeder e Lester Jr. (1989), compreender Matemática é relacionar ideias matemáticas a uma variedade de contextos, relacionar certos problemas às ideias matemáticas que podem ser identificadas e relacionar as diversas ideias matemáticas presentes em um problema. Dessa forma, esses autores enfatizaram que a construção dessas relações pelos alunos permite-lhes ampliar suas compreensões de Matemática.

Schroeder e Lester Jr. (1989) indicaram três abordagens de ensino da resolução de problemas: ensinar sobre, para e via resolução de problemas. No caso do ensino via resolução de problemas, o qual implica o uso do problema como ponto de partida da atividade matemática, vários estudos mostraram que a sua implementação em sala de aula ajudou os alunos a aprender matemática (FI; D

Schroeder e Lester Jr. (1989) indicaram três abordagens de ensino da resolução de problemas: ensinar sobre, para e via resolução de problemas. No caso do ensino via resolução de problemas, o qual implica o uso do problema como ponto de partida da atividade matemática, vários estudos mostraram que a sua implementação em sala de aula ajudou os alunos a aprender matemática (FI; DEGNER, 2012; VALE, 2013; MATSUDA, 2017; SOUSA; PROENÇA, 2019). Por outro lado, no caso dos ensinos sobre e para resolução de problemas, ambos acabam dando enfoque ao uso do problema como aplicação de conteúdo que se acabou de aprender. Proença e Maia-Afonso (2020) mostraram que estudos que seguiram a abordagem do ensino para resolução de problemas acabaram evidenciando a ideia de apenas ‘resolver problemas’, de modo que os conceitos matemáticos foram exigidos como forma direta de aplicação sem ter foco na formação desses conceitos em meio aos problemas utilizados.

O estudo de Proença et al. (2020) chamou a atenção à possível falta desse foco em sala de aula, pois, ao analisar 111 alunos do nono ano do ensino fundamental na resolução de 10 situações contextualizadas, mostrou que a concentração de dificuldades ocorreu pelo desconhecimento do significado de conceitos matemáticos. Já Gonçalves e Proença (2020) justificaram a falta desse foco ao mostrar que, dos 26 alunos do primeiro ano do ensino médio, houve dificuldades em identificar e reconhecer uma equação de 2.º grau, sendo que na resolução de três situações contextualizadas não houve uso desse conceito, em que prevaleceu o alto índice de erros e respostas em branco. Isso indica a urgência de um trabalho voltado à aprendizagem conceitual em meio à resolução de problemas, pois os conteúdos matemáticos, utilizados nessas pesquisas, já foram estudados pelos alunos.

Diante do exposto, o uso do problema como ponto de partida tem grande potencial para abordar conceitos matemáticos. No entanto, quando há o uso do problema após o conteúdo, percebemos que falta realizar um trabalho de formação de conceitos, bem como de buscar estabelecer uma relação entre os conceitos aprendidos e os contextos dos ‘problemas’ (novas situações). Diante disso, buscamos refletir sobre o seguinte questionamento: Como poderíamos encaminhar uma integração entre a resolução de problemas e a aprendizagem de conceitos matemáticos?

Dessa forma, neste artigo, apresentamos uma proposta de organização do ensino para propiciar a aprendizagem de conceitos matemáticos em meio à resolução de problemas. Elaboramos uma estrutura para o artigo que é composta das seguintes seções: a) Definindo o que são conceitos; b) Aspectos teóricos da resolução de problemas e sua abordagem no ensino; c) Proposta de organização do ensino; d) Palavras finais.

2. Definindo o que são conceitos

Sobre o significado da palavra conceito, Klausmeier e Goodwin (1977) indicaram que pode se referir aos construtos mentais ou às entidades públicas. Os conceitos como construtos mentais são construídos de acordo com as aprendizagens de cada indivíduo. Já os conceitos como entidades públicas correspondem à informação organizada e que se encontram, por exemplo, em livros. Dessa forma, define-se um conceito como “informação ordenada sobre as propriedades de uma ou mais coisas – objetos, eventos ou processos – que torna qualquer coisa ou classe de coisas capaz de ser diferenciada de ou relacionada com outras coisas ou classes de coisas” (KLAUSMEIER; GOODWIN, 1977, p. 312).

Para favorecer a aprendizagem e o desenvolvimento de conceitos no movimento do construto mental à entidade pública, Klausmeier e Goodwin (1977) enfatizaram que o planejamento do ensino deve partir da entidade pública do conceito (definição matemática) para delinear os atributos envolvidos, ou seja, as características relevantes e irrelevantes, bem como tomar ciência dos exemplos e elencar não exemplos. Por exemplo, o conceito de função apresenta características relevantes que o diferencia de uma equação e, assim, determina exemplos como os vários tipos de funções, sendo que um não exemplo seria um tipo de equação. Diante disso, deve-se partir de alguns exemplos e não exemplos e elaborar uma atividade para envolver os alunos na identificação de características que fazem parte do conceito. Assim, após estabelecer a terminologia do conceito, de suas características e de seus exemplos, pode-se tratar de relações de inclusão que envolvem seus exemplos.

Na visão de Pozo (1998), os conceitos devem ser compreendidos pelos alunos, de modo que saibam dizê-los, segundo suas próprias palavras. Trata-se de uma compreensão gradual e qualitativa que “não se trata tanto de se o aluno o compreende ou não, mas de como o compreende” (POZO, 1998, p. 27, grifo do autor). Dessa forma, Pozo (1998) apontou que os conceitos que são ensinados aos alunos podem ser avaliados com foco na aprendizagem significativa, a saber: a) levá-los a elaborarem uma definição do significado do conceito; b) levá-los a reconhecerem a definição do conceito em meio a algumas possibilidades; c) levá-los a apresentarem uma escrita sobre um tema que envolve o conceito; d) levá-los a identificarem e a categorizarem os exemplos ou situações ligadas ao conceito; e) levá-los a utilizar o conceito na aplicação à solução de problemas.

No caso da aplicação do conceito à solução de problemas, isso envolve a transferência da aprendizagem, o que implicaria, em sala de aula, possibilitar aos alunos de fazer a transferência do que aprenderam a novas situações (GAGNÉ, 1973). Gagné (1973) ressaltava que uma capacidade intelectual como a aprendizagem conceitual depende de cada pessoa, no sentido de que “quanto mais sólidas forem as bases em que uma capacidade tiver sido aprendida, maior probabilidade terá de ser transferida a situações novas e diferentes. De acordo com isso, a utilidade de qualquer capacidade aprendida crescerá, se ela for utilizada em muitas situações, tantas quanto possível” (GAGNÉ, 1973, p. 211).

Como orientação ao ensino que vise à transferência da aprendizagem, Gagné (1973, p. 213) destacou que “é da maior importância observar que a transferência é um fenômeno que depende da aprendizagem prévia”. Nesse sentido, é possível compreender a importância de que os conceitos estejam bem formados no que se refere ao movimento do construto mental à entidade pública. Portanto, se isso ocorrer, será oportuno levar os alunos a ampliarem suas compreensões dos conceitos matemáticos quando da abordagem de novas situações e sob o olhar da perspectiva da resolução de problemas.

3. Aspectos teóricos da resolução de problemas e sua abordagem no ensino

Quando se fala em resolução de problemas, os aspectos teóricos envolvem definir o que seria um problema e, assim, como se resolve um problema. Desse modo, dentre as várias definições presentes na literatura, apontamos duas que acreditamos refletir sobre sua natureza:

Uma situação somente pode ser concebida como um problema na medida em que exista um reconhecimento dela como tal, e na medida em que não disponhamos de procedimentos automáticos que nos permitam solucioná-la de forma mais ou menos imediata, sem exigir, de alguma forma, um processo de reflexão ou uma tomada de decisões sobre a sequência de passos a serem seguidos. (ECHEVERRÍA; POZO, 1998, p. 16).

Nessa mesma direção, no que se refere à área específica da Matemática, Proença (2018) definiu que “[...] uma situação de Matemática se torna um problema quando a pessoa precisa mobilizar conceitos, princípios e procedimentos matemáticos aprendidos anteriormente para chegar a uma resposta. Não se trata, assim, do uso direto de uma fórmula ou regra conhecidas – quando isso ocorre, a situação tende a se configurar como um exercício” (PROENÇA, 2018, p. 17-18).

Para Echeverría (1998), o exercício tem função específica no ensino que pela repetição visa à memorização para consolidar procedimentos algorítmicos, técnicas e certas habilidades, de modo que seu uso não envolve a tomada de decisão, pois já estão definidos. Assim, “[...] dificilmente podem trazer alguma ajuda para que essas técnicas sejam usadas em contextos diferentes daqueles onde foram aprendidas ou exercitadas, ou dificilmente podem servir para a aprendizagem e compreensão de conceitos” (ECHEVERRÍA, 1998, p. 49).

Já quando a pessoa se depara com uma situação e encontra uma dificuldade em que a reconhece como um problema, de modo que não se está partindo de um procedimento automático, passamos a falar sobre como se resolve um problema, o que implica no envolvimento da pessoa no processo de resolução de problemas. “Além disso, essa dificuldade seria antes um impasse intelectual do que uma dificuldade de cálculo” (SCHOENFELD, 1985, p. 74).

Dessa forma, o processo de resolução de problemas implica a mobilização cognitiva pela pessoa de seus conhecimentos na busca de uma solução, correspondendo, segundo Brito (2010), a quatro etapas de pensamento, a saber: representação, planejamento, execução e monitoramento. Uma descrição sobre essas etapas foi apresentada por Proença (2018), conforme segue.

A etapa de representação corresponde à compreensão que o aluno terá do problema. Tal compreensão se dará por sua representação mental do contexto envolvido, o que dependerá do uso de seus conhecimentos linguísticos (da língua materna) e semânticos (matemáticos). Assim, o aluno deve “[...] realizar uma compreensão com base no que sua língua materna evidencia sobre a estrutura mais geral do problema (quem comete a ação, objetos envolvidos), isto é, reconhecer as palavras. E, no caso do conhecimento semântico, a compreensão se dá, justamente com base no conhecimento da pessoa sobre os termos matemáticos que aparecem no problema e também sobre as relações que se estabelecem entre esses termos” (PROENÇA, 2018, p. 27).

Caso o aluno realize uma representação adequada do problema a ser resolvido, terá condições de identificar a sua estrutura formal. Assim, terá condições de “[...] perceber se faltam informações no problema (informações incompletas) ou mesmo se há dados que não ajudam ou não precisam ser levados em consideração na busca da solução (informações supérfluas)” (PROENÇA, 2018, p. 28).

Na etapa de planejamento, o aluno deve apresentar uma estratégia, ou seja, um caminho que o ajude a obter uma solução. Essa estratégia vai depender da representação que fez do problema e seguirá suas preferências por um caminho ou outro. Em outras palavras, o aluno planeja um caminho que “[...] segue o uso de conhecimentos lógico-verbais, viso-pictóricos (desenhos, figuras, diagramas) ou ambos. Assim, essa etapa ajuda a evidenciar as habilidades da pessoa para, por exemplo, pensar com símbolos matemáticos, generalizar de forma rápida e abreviar o processo de raciocínio matemático” (PROENÇA, 2018, p. 28).

Na etapa de execução, Proença (2018, p. 28) explicou que “[...] a pessoa precisa executar a estratégia proposta. Implica executar os cálculos matemáticos necessários, bem como desenhar os elementos viso-pictóricos”. Por fim, a etapa de monitoramento implica em dois aspectos importantes: a) verificar a racionalidade da resposta encontrada em termos do contexto envolvido; b) rever o processo de resolução seguido, o que pode ocorrer não apenas quando se obtém a resposta, mas em qualquer momento do processo de resolução (PROENÇA, 2018).

Diante disso, ser um problema não é inerente de uma tarefa qualquer de Matemática (SCHOENFELD, 1985). Assim, para solucionar um problema, a pessoa deve “[...] combinar, na estrutura cognitiva, os conceitos, princípios, procedimentos, técnicas, habilidades e conhecimentos previamente adquiridos que são necessários para encontrar a solução com uma nova situação que demanda uma re-organização conceitual cognitiva” (BRITO, 2010, p. 19). Portanto, resolver um problema não é algo linear ou poderia ser tratado de forma linear no ensino, uma vez que se o aluno realizar uma compreensão inadequada de um problema, devido a má formação conceitual que apresenta, isso comprometerá todo o processo, resultando em uma resposta incorreta.

Diante dessa perspectiva da resolução de problemas, a sua abordagem no ensino é indicada, nos Parâmetros Curriculares Nacionais – PCN (BRASIL, 1998), para ajudar na compreensão de conceitos e procedimentos matemáticos. Como estratégia pedagógica, nesse documento, incentiva-se o uso do problema como ponto de partida e não a definição matemática, ideia essa que corresponde à abordagem de ensino via resolução de problemas (SCHROEDER; LESTER JR., 1989). Na visão de Lester Jr. e Cai (2016), essa abordagem, ao evitar que a resolução de problemas seja tratada apenas após o ensino de conceitos e habilidades matemáticas, gera um ambiente propicio para aprender Matemática. Para esses autores, adotar o ensino via resolução de problemas permite que se favorece a socialização de ideias entre os alunos, potencializando a compreensão conceitual ou mesmo a ideia a ser aprendida.

Depois que os alunos tiverem contato com o novo conteúdo, o uso do problema ocorreria, na visão de Schroeder e Lester Jr. (1989), por meio da abordagem de ensinar sobre e para resolução de problemas. Para esses autores, o ensinar sobre resolução de problemas está direcionado a primeiro explicar aos alunos como se resolve um problema (as quatro etapas de resolução) para que apliquem essa ideia nos ‘problemas’ a serem resolvidos, o que é um limite no ensino, porém acaba pelo menos envolvendo os alunos sobre como se resolve problemas. Já o ensinar para resolução de problemas foi denunciado por esses autores como o tipo de abordagem da resolução de problemas que apenas preza pela apresentação de conceitos matemáticos para que sejam aplicados diretamente em ‘problemas’, o que ocorre em detrimento da construção desses conceitos, correspondendo, assim, a um limite maior no ensino. Porém, esses autores ressaltaram que os ensinos via, sobre e para resolução de problemas acabam se tornando um conjunto necessário para a aprendizagem de Matemática e para aprender a resolver problemas.

Assim, como na Base Nacional Comum Curricular – BNCC (BRASIL, 2018) consta a necessidade de levar os alunos a desenvolverem suas habilidades de resolução de problemas, entendemos que isso é possível não apenas se problemas forem abordados, mas ainda se houver construção de conceitos em meio à perspectiva da resolução de problemas. Diante disso, passamos a apresentar uma proposta que visa a uma organização do ensino que envolve favorecer a aprendizagem de conceitos em meio à resolução de problemas.

4. Proposta de organização do ensino

A nossa proposta de organização de ensino foi estruturada, conforme mostra a Figura 1 a seguir, nas seguintes etapas que correspondem a uma sequência de aulas a ser desenvolvida em sala de aula: 1) Uso do problema como ponto de partida; 2) Formação do conceito; 3) Definição do conteúdo; 4) Aplicação em novos problemas. Essa proposta sequencial envolve a combinação do ensino via resolução de problemas (etapa 1) e dos ensinos sobre e para resolução de problemas (etapa 4), seguindo a perspectiva da resolução de problemas. Envolve, também, o trabalho com a formação do conceito (etapa 2) no sentido de levar os alunos a compreenderem as características do conceito (construto mental) e, assim, poderem se apropriar do conceito matemático (entidade pública) e de procedimentos algorítmicos quando da definição do conteúdo (etapa 3).

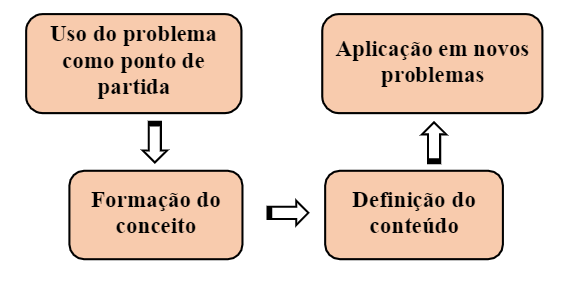Figura 1
Estrutura da organização de ensino.
O autor

1) Uso do problema como ponto de partida. Nesta etapa, deve-se utilizar uma situação de Matemática (possível problema) como ponto de partida para depois introduzir o conteúdo (novo conteúdo/conceito). Para ajudar o professor a planejar e orientar suas aulas nesta etapa, sugerimos que ele possa seguir a implementação da proposta de Proença (2018), denominada de Ensino-aprendizagem de Matemática via resolução de problemas, a qual sugere um trabalho baseado em cinco ações de ensino. Na primeira ação, de escolha do problema, deve-se selecionar uma situação (possível problema) e fazer a previsão de possíveis estratégias de resolução e da forma como poderia articular uma delas ao conteúdo a ser introduzido, enquadrando-se em um planejamento prévio. Na ação de introdução do problema, a qual ocorre em sala de aula, deve-se justamente apresentar a situação (possível problema) aos alunos, distribuídos em grupos, e indicar-lhes a resolverem pelo caminho que quiserem. É neste momento que podem reconhecer a situação como algo difícil, como um problema, sendo necessário tomar uma decisão sobre qual caminho poderia ajudar a encontrar uma resposta. Na ação de auxílio aos alunos durante a resolução, é o momento de o professor atuar como observador do que os alunos fazem, de modo a incentivar e direcionar a busca de uma solução e mesmo sugerir caminhos, baseados nas estratégias previstas na primeira ação. Na ação de discussão das estratégias dos alunos, o professor deve discutir coletivamente as resoluções dos alunos, buscando elucidar e explicar erros cometidos. Por fim, na quinta ação, de articulação das estratégias dos alunos ao conteúdo, deve-se utilizar uma estratégia que foi discutida na ação anterior e fazer sua articulação à forma matemática do conteúdo envolvido. Tomemos como exemplo o conteúdo Equação de 2.º grau. Essa articulação implica utilizar pontos cerne da estratégia de um grupo, tomada como referência, para elucidar/mostrar a representação simbólico-matemática dessa equação, seguido de algum procedimento algorítmico de resolução. Diante disso, esta primeira etapa da nossa proposta de organização do ensino é importante, porque, ao iniciar o ensino com uma situação, envolve os alunos no uso de seus conhecimentos matemáticos para encontrarem estratégias de resolução (algorítmicas e/ou heurísticas) que os ajudem a obter uma resposta. Uma vez que os alunos devem propor estratégias com base nas representações simbólicas que dominam, isso permite seguir o processo de abstração do contexto do problema para a forma matemática do conteúdo. Dessa forma, a introdução do conteúdo corresponde a relacionar as estratégias dos alunos a sua forma matemática, a qual deve ser estudada nas aulas seguintes.

2) Formação do conceito. Uma vez que os alunos tiveram contanto com um novo conteúdo, por meio de sua representação matemática, a etapa seguinte é a de levar os alunos a formarem o conceito, ou seja, aprenderem e desenvolverem a compreensão sobre o conceito. Do exemplo do conteúdo Equação de 2.º grau, abordaríamos nesta etapa justamente as representações simbólico-matemáticas de equações que o constituem. Dessa forma, o professor deve propor atividades que levem os alunos a compreenderem propriedades e/ou características do conceito, possibilitando que consigam diferenciá-lo de outros conceitos matemáticos. Isso é de suma importância porque o estudo de Gonçalves e Proença (2020) mostrou que alunos de primeiro ano de ensino médio tiveram dificuldades em reconhecer exemplos e não exemplos de equações de segundo grau, sendo que 11,53% (n=26) deles as confundiram com equações de primeiro grau. Diante disso, as atividades a serem desenvolvidas em sala de aula implicam em levar os alunos a: a) explorarem exemplos e não exemplos do conceito para explorar suas características; b) apresentarem uma definição para o conceito (construto mental), o que evidenciará as características do conceito que eles mencionam; b) apresentarem outros tipos ou variações do conceito, ou seja, apresentar exemplos do conceito; c) apresentarem não exemplos do conceito, o que permite ampliar a compreensão conceitual, pois, por exemplo, para saber o que é uma equação de segundo grau, também é importante saber o que não é. Uma proposta de formação de conceito que pode servir como ponto de referência foi sobre o conceito de polígono, indicada por Proença (2020), na vertente do processo de abstração. Este autor se baseou no processo de representação-generalização-síntese-abstração para que o professor possa envolver alunos de quinto ano do ensino fundamental a desenvolverem o conceito de polígono.

3) Definição do conteúdo. Nesta etapa, as aulas devem focar sobre a definição matemática do conteúdo, de modo a inserir os alunos no entendimento da linguagem simbólico-formal. Isso implica em abordar tanto a definição do conceito matemático (entidade pública) quanto os procedimentos algorítmicos de resolução. Sobre a definição do conceito, do nosso exemplo do conteúdo Equação de 2.º grau, seria definir matematicamente o que seria esse tipo de equação, evidenciando suas características e suas diversas representações. Nesta etapa, é importante o professor estabelecer a relação entre a linguagem matemática envolvida e a linguagem que foi utilizada pelos alunos quando das atividades de formação conceitual (etapa 2) no sentido de debater coletivamente sobre seus entendimentos da estrutura matemática e realizar a síntese entre as representações (exemplos e não exemplos) que foram utilizadas. O estudo de Proença e Pirola (2009) revela a importância desse debate, uma vez que chamaram a atenção, em sua fundamentação teórica, do fato de que encontraram definições do conceito de polígono com termos formais que levavam a apontar exemplos que em outras eram não exemplos. Sobre a abordagem dos procedimentos algorítmicos, do nosso exemplo Equação de 2.º grau, seria tratar da resolução para a obtenção das raízes, envolvendo procedimentos como o algoritmo da fórmula de Bhaskara e procedimentos como a fatoração (colocar a variável em evidência) e como a de completar quadrados. É importante que o aluno aprenda várias possibilidades algorítmicas para que sua compreensão do conteúdo seja ampliada, pois, no caso da equação de segundo grau, muitas vezes a fórmula de Bhaskara é a única trabalhada em sala de aula.

4) Aplicação em novos problemas. Nesta etapa, as aulas devem ser elaboradas com base na utilização de uma variedade de novas situações (‘novos problemas’ ou possíveis problemas), as quais visam à transferência da aprendizagem pelos alunos do conceito matemático, bem como dos procedimentos algorítmicos estudados. De alguma forma, isso envolve o ensinar para resolução de problemas, porém com o trabalho advindo da formação conceitual. As novas situações a serem trabalhadas devem ser situações contextualizadas (envolvendo aspectos da vida cotidiana (social, política e econômica), a história da Matemática e/ou outras áreas como a Física, Química, Biologia etc.). Além disso, sugerimos que não se aborde apenas situações com informações completas (todos os dados são utilizados), mas ainda, e sobretudo, situações com enunciados que contenham informações incompletas e informações supérfluas. Isso será importante para verificar como os alunos obtém e/ou utilizam a informação matemática presente nos contextos envolvidos. Nesse sentido, o trabalho em sala de aula deve ocorrer na perspectiva da resolução de problemas, de modo a avaliar os alunos nas quatro etapas do processo de resolução, bem como tornar-lhes cientes dessas etapas (ensinar sobre resolução de problemas). Seguir essa perspectiva resulta do fato de que ao longo dessas aulas é possível que os alunos encontrem dificuldades ao buscarem uma solução às novas situações, sendo que as reconheçam como um problema. Esse reconhecimento pode ocorrer devido ao fato de que, apesar de os alunos conhecerem o conceito e os procedimentos algoritmos a serem transferidos nas novas situações (avindo das etapas anteriores), os alunos devem não apenas mobilizar conhecimentos matemáticos (semânticos), mas ainda mobilizar conhecimentos linguísticos e os que derivam de sua visão de mundo. Dessa forma, ao se deparar com os contextos envolvidos, isso exigirá, certamente, uma reorganização cognitiva pelos alunos tanto do conceito a ser transferido quanto de outros conceitos anteriores, justamente porque cada contexto traz palavras/termos de uma realidade que necessitarão ser traduzidos em uma linguagem matemática, o que evidencia sua complexidade para tal. Portanto, o professor deve observar e sanar: a) as dificuldades dos alunos no processo de resolução de problemas (representação, planejamento, execução, monitoramento); b) suas dificuldades na relação entre os contextos das situações e a identificação e representação do conceito matemático, quando realizam a compreensão do problema (representação do problema). Trata-se, assim, de levar os alunos a realizar a ressignificação do conceito matemático em meio às situações contextualizadas que são trazidas para o ensino em sala de aula. Para exemplificar, ao explicar sobre o uso de inequações em uma situação contextualizada sobre a capacidade de um centro esportivo, Travassos e Proença (2020, p. 85) chamaram a atenção ao fato de que a seguinte passagem textual em seu enunciado “considerando a capacidade máxima de 6000 pessoas” é uma condicionante, de modo que o professor deve observar como os alunos a compreendem. Isso porque, segundo os autores, a palavra ‘máxima’ implica na ideia de ‘menor ou igual’ e o aluno pode não conseguir identificá-la. Nesse sentido, uma vez que Travassos e Proença (2020) explicaram que palavras que implicam em ‘menor e igual’ ou ‘maior ou igual’ podem vir, respectivamente, como ‘não exceder’ e ‘a partir de’ no enunciado de outras situações, observa-se que é necessário e muito importante abordar uma variedade de situações contextualizadas.

5. Palavras finais

Na nossa proposta de organização de ensino, situamos o trabalho com a aprendizagem de conceitos matemáticos em meio à resolução de problemas. Tratamos de envolver o uso do problema nas vertentes dos ensinos via, sobre e para resolução de problemas para que pudéssemos apresentar uma proposta de modo que o conteúdo a ser abordado também o fosse pela vertente da formação conceitual. A motivação para apresentar essa organização de ensino derivou do fato da necessidade de abordar o aspecto conceitual, de modo a evitar a forma tradicional de ensino em que conteúdos são aplicados diretamente em atividades, revelando o ato de apenas ‘resolver problemas’.

Dessa forma, como a BNCC (BRASIL, 2018) indica a necessidade de que alunos consigam desenvolver suas capacidades e habilidades para resolver problemas, entendemos que em sala de aula o trabalho do professor precisa ser feito de forma que contemple diversos momentos de ensino por meio da resolução de problemas. Propusemos o uso do problema como ponto de partida como primeira etapa para que se valorize os conhecimentos dos alunos e para que haja vínculo entre estes e o novo conteúdo, dando condições iniciais para desenvolver a abstração. Em seguida, propusemos realizar atividades de formação do conceito para que os alunos aprendam a reconhecer e a identificar suas características e as representações que fazem parte (exemplos) e as que não fazem parte (não exemplos). Este momento é crucial, pois ajuda a favorecer a compreensão dos conceitos pelos alunos, favorecimento esse que acaba sendo ampliado quando da terceira etapa que implica em discussão coletiva para levar os alunos a entenderem a linguagem simbólico-formal do conteúdo. Ao contrário disso, esse é um trabalho que notadamente não se verifica nas aulas nas escolas. Tudo fica na base do ensino tradicional (definição-exemplo-exercícios) e com isso fica prejudicada a transferência da aprendizagem a novas situações.

A última etapa que propusemos visa justamente levar os alunos a relacionarem os conceitos, aprendidos pelas atividades de formação conceitual, às novas situações (‘novos problemas’). A nossa preocupação foi a de que haja significado na aprendizagem, uma vez que os contextos das situações exigem vários conhecimentos por parte dos alunos e, por ser complexo, isso necessita de que os conceitos estejam bem formados e que ocorra sua ampliação e/ou ressignificação no envolvimento a vários outros contextos.

Contudo, podemos apontar que nossa proposta de organização do ensino promove uma contribuição, direcionada à reflexão sobre um trabalho em sala de aula que vise à aprendizagem e à ressignificação dos conceitos matemáticos. Esse trabalho propicia um continuum que envolve o ato de não apenas resolver problemas para aprender Matemática, mas ainda o ato de aprender a resolver problemas. Portanto, esperamos que essa estrutura de ensino que apresentamos auxilie no ensino e na aprendizagem de Matemática, bem como sirva de referência a novas propostas, sobretudo àquelas que busquem integrar a atividade de elaboração/proposição de problemas (problem posing) por parte dos alunos.

6. Referências

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Educação Infantil, Ensino Fundamental e Ensino Médio. (versão final). Brasília: MEC, 2018.

BRASIL. Secretaria de Ensino Fundamental. Parâmetros curriculares nacionais: 3º e 4º ciclos. Brasília, DF, 1998.

BRITO, M. R. F. Alguns aspectos teóricos e conceituais da solução de problemas matemáticos. In: BRITO, M. R. F. (Org.). 2. ed. Solução de problemas e a matemática escolar. Campinas: Alínea, 2010, p. 13-53.

CAI, J.; LESTER, F. Por que o ensino com resolução de problemas é importante para a aprendizagem do aluno? Boletim GEPEM, v. 36, n. 60, p. 147-162, jan./jun. 2012.

ECHEVERRÍA, M. P. P.; POZO, J. I. Aprender a resolver problemas e resolver problemas para aprender. In: POZO, J. I. (Org.). A solução de problemas: aprender a resolver, resolver para aprender. Porto Alegre: ArtMed, 1998, p. 13-42.

ECHEVERRÍA, M. P. P. A solução de problemas em matemática. In: POZO, J. I. (Org.). A solução de problemas: aprender a resolver, resolver para aprender. Porto Alegre: ArtMed, 1998, p. 43-65.

FI, C. D.; DEGNER, K. M. Teaching through problem solving. Mathematics Teacher, v.105, n. 6, february, p. 455-459, 2012.

GAGNÉ, R. M. Como se realiza a aprendizagem. (Tradução de Therezinha Maria Ramos Tovar). 1. ed. Rio de Janeiro: Ao Livro Técnico S/A, 1973.

GONÇALVES, B. M.; PROENÇA, M. C. Análise dos conhecimentos conceitual e procedimental de alunos do primeiro ano do ensino médio sobre equação do 2.º grau. Revista Sergipana de Matemática e Educação Matemática, v. 5, n. 2, p. 209-228, 2020.

Klausmeier, H. J.; Goodwin, W. Manual de psicologia educacional: aprendizagem e capacidades humanas. Tradução de M. C. T. A. Abreu. São Paulo: Harper & Row, 1977.

LESTER JR., F. K., CAI, J. Can mathematical problem solving be taught? preliminary answers from 30 years of research. In: FELMER, P., PEHKONEN, E., KILPATRICK, J. (Eds.). Posing and Solving Mathematical Problems. Springer: Cham, 2016, p. 117-135.

MATSUDA, F. F. S. Um ensino de equação de 1º grau com uma incógnita via resolução de problemas. 2017. 131f. Dissertação (Mestrado em Ensino de Ciências e Matemática) – Universidade Estadual de Maringá, Maringá, 2017.

NATIONAL COUNCIL OF TEACHERS OF MATHEMATICS. Principles and standards for school mathematics. Reston, VA: NCTM, 2000.

POZO, J. I. A aprendizagem e o ensino de fatos e conceitos. In: COLL, C.; POZO, J. I.; SARABIA, B.; VALLS, E. Os conteúdos na reforma: ensino e aprendizagem de conceitos, procedimentos e atitudes. Trad. Beatriz Affonso Neves. Porto Alegre: Artes Médicas, 1998, p. 17-71.

PROENÇA, M. C. O processo de abstração do conceito de polígono: uma proposta de ensino para o 5.º ano do ensino fundamental. In: PROENÇA, M. C. (Org.). Formação de conceitos matemáticos: propostas de ensino aos anos iniciais e finais do ensino fundamental. Campo Mourão-PR.: Editora Fecilcam, 2020, 173p., p. 63-77.

PROENÇA, M. C. Resolução de Problemas: encaminhamentos para o ensino e a aprendizagem de Matemática em sala de aula. Maringá: Eduem, 2018.

PROENÇA, M. C.; MAIA-AFONSO, E. J.; TRAVASSOS, W. B.; CASTILHO, G. R. Resolução de Problemas de Matemática: análise das dificuldades de alunos do 9.º ano do ensino fundamental. Amazônia: Revista de Educação em Ciências e Matemáticas, v.16, n. 36, p. 224-243, 2020.

PROENÇA, M. C.; MAIA-AFONSO, E. J. Resolução de problemas: análise de propostas de ensino em dissertações de mestrado profissional. Revista Paranaense de Educação Matemática, v.09, n.18, p.180-201, jan./jun., 2020.

PROENÇA, M. C.; PIROLA, N. A. Um estudo sobre o desempenho e as dificuldades apresentadas por alunos do ensino médio na identificação de atributos definidores de polígonos. Zetetiké, Bauru, v, 17, n.31, p. 11-45, 2009.

PRUSAK, N.; HERSHKOWITZ, R.; SCHWARZ, B. B. Conceptual learning in a principled design problem solving environment. Research in Mathematics Education, v. 15, n. 3, p. 266-285, 2013.

SCHOENFELD, A. H. Mathematical practices, in theory and practice. ZDM: The International Journal on Mathematics Education, v. 52, n. 2, p. 01-13, 2020.

SCHOENFELD, A. H. Mathematical problem solving. Orlando: Academic Press, 1985.

SCHROEDER, T. L.; LESTER, F. K., JR. Developing understanding in mathematics via problem solving. In: TRAFTON, P. R.; SHULTE, A. P. (Eds.). New directions for elementary school mathematics. Reston: NCTM, 1989, p. 31-42.

SOUSA, A. C.; PROENÇA, M. C. Uma proposta de ensino de equação de 1.º grau com uma incógnita via resolução de problemas. Revista Prática Docente, v. 4, n. 2, p. 431-451, 2019.

TAMBUNAN, H. The effectiveness of the problem solving strategy and the scientific approach to students’ mathematical capabilities in high order thinking skills. International Electronic Journal of Mathematics Education, v. 14, n. 2, p. 293-302, 2019.

TRAVASSOS, W. B.; PROENÇA, M. C. Ensino-aprendizagem de inequações: uma proposta envolvendo congruência semântica. In: PROENÇA, M. C. (Org.). Formação de conceitos matemáticos: propostas de ensino aos anos iniciais e finais do ensino fundamental. Campo Mourão-PR.: Editora Fecilcam, 2020, 173p., p. 78-101.

VALE, I. Padrões em contextos figurativos: um caminho para a generalização em matemática. Revista Eletrônica de Educação Matemática, v. 8, n. 2, p. 64-81, 2013.

Ligação alternative

https://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/359 (pdf)