1. Introdução
Durante o ano de 2018, a licencianda em Matemática, Andressa Rubim, que, à época, era aluna do curso de Licenciatura em Matemática do Instituto de Matemática e Estatística da Universidade São Paulo, desenvolveu seu trabalho de conclusão de curso, o qual foi orientado pela professora doutora Raquel Milani, junto à sala de aula da professora Maíra Fernandes, a qual lecionava em uma turma do 5ºano do Ensino Fundamental I da Escola Estadual Prudente de Moraes, na cidade de São Paulo. As três professoras aqui citadas são autoras do presente texto.
O objetivo do trabalho de conclusão de curso foi caracterizar uma aula em que os alunos estivessem envolvidos em situações de investigação, exploração e descobrimento, no contexto particular da turma do 5º ano da professora Maíra. Justifica-se esta escolha, sobretudo, porque a aula de Matemática, muitas vezes, é marcada pelo modelo usual em que o professor expõe o conteúdo, mostra alguns exemplos da teoria e, em seguida, os alunos resolvem exercícios do tipo “calcule…”, “resolva as operações…”, semelhantes aos mostrados pelo professor, caracterizando a educação matemática tradicional (SKOVSMOSE, 2000).
No que se refere a este modelo e suas implicações, D’Ambrósio (1989, p. 16) afirma que “[...] na matemática escolar o aluno não vivencia situações de investigação, exploração e descobrimento”. Esta afirmação de D’Ambrósio continua atual quando olha-se para muitas salas de aula de Matemática, e, além disso, nos motivou a tentar caracterizar uma aula em que os alunos estivessem envolvidos em tais situações.
Algumas atividades de exploração e investigação foram implementadas na referida turma de 5º ano do Ensino Fundamental. Dentre estas atividades, uma delas era sobre polígonos, a qual daremos ênfase neste texto, uma vez que, durante seu desenvolvimento, observamos que situações imprevisíveis ocorreram, fazendo com que a licencianda Andressa e a professora Maíra procurassem por uma forma de lidar com elas para dar continuidade à proposta da aula. Este texto é um relato de experiência a respeito da implementação desta atividade sobre polígonos, tendo como objetivo, para além de descrever os fatos, refletir sobre as aprendizagens das professoras em situações de imprevisibilidade.
Na próxima seção, trataremos de uma caracterização possível para as tarefas nas aulas de Matemática, a fim de esclarecer o porquê a atividade dos polígonos tem potencial exploratório ou investigativo e diferencia-se de um exercício ou problema. Em “Procedimentos metodológicos”, explicamos de que forma a atividade foi implementada e como foi feita a recolha dos dados para análise. Já na seção “O que é mesmo um polígono?” descreveremos os principais momentos da implementação da atividade na turma do 5º ano, com ênfase nas situações de imprevisibilidade que afetaram o planejamento da aplicação da atividade. Na penúltima seção, “Análise da aplicação da atividade", apresentaremos nossas reflexões sobre tais situações e, por fim, em “Considerações finais”, conclui-se o presente texto com ênfase na aprendizagem das autoras sobre a definição de polígono.
2. As tarefas
de Matemática
De acordo com
Ponte (2003), uma tarefa de Matemática assume quatro dimensões básicas, sendo
elas categorizadas por: grau de dificuldade, estrutura (aberta ou fechada),
contexto referencial e tempo para resolução. Para as duas primeiras, pode-se
organizar o diagrama abaixo:
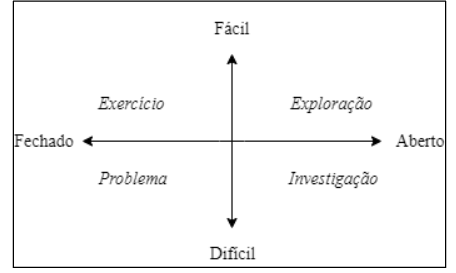
Os exercícios, tal
como no diagrama da Figura 1, encaixam-se no 2º quadrante pelo fato de serem
caracterizados por uma estrutura fechada, isto é, só admitem uma resposta
correta, assim como os problemas, e em ambos há uma clareza entre o que é dado
e o que é pedido no enunciado. Nota-se que a diferença entre eles está no grau
de dificuldade. Alguns autores abordam esta diferença mais a fundo, tais como Pólya (1995) e Echeverría e Pozo (1998). Estes últimos enfatizam que “[...] um problema
se diferencia de um exercício na medida em que, neste último caso, dispomos e
utilizamos mecanismos que nos levam de forma imediata, à solução” (ECHEVERRÍA;
POZO, 1998, p. 16). Ao passo que um problema não exige só mecanismos para resolvê-los imediatamente, mas também é preciso uma
estratégia para utilizar tais mecanismos (ECHEVERRÍA; POZO, 1998).
Tal como ocorre com os exercícios e os problemas, as tarefas de investigação e exploração também têm proximidades quanto à estrutura. Ambas são abertas, isto é, a questão não é tão bem definida no enunciado, como ocorre com os exercícios e problemas. Ponte (2003), no entanto, afirma que, muitas vezes, chama-se as duas tarefas de investigação e isso se dá por conta do grau de dificuldade que as duas podem assumir. A investigação, no 4º quadrante, é considerada mais difícil do que uma atividade de exploração. Contudo, “[...] é complicado saber à partida qual o grau de dificuldade que uma tarefa aberta terá para um certo grupo de alunos” (PONTE, 2003, p. 30). Em vista disso, é razoável que não se saiba distinguir uma atividade da outra em certos casos, isto tanto para investigação e exploração quanto para exercícios e problemas, já que também pode acontecer que um determinado problema seja proposto e um aluno consiga resolvê-lo de forma imediata sem precisar de estratégias, reduzindo-o, então, a um exercício (ECHEVERRÍA; POZO, 1998).
No que se refere à dimensão chamada de contexto referencial, como o nome sugere, a mesma está relacionada a contextos sobre os quais as tarefas fazem referência. Em síntese, segundo Skovsmose (2000) há diferentes tipos de referências, sendo elas puramente matemáticas, semirreais e reais. Como exemplo de contextos puramente matemáticos, pode-se destacar aqueles cujo enunciado começa com “calcule” ou “resolva”. A semirrealidade, por sua vez, está relacionada a contextos em que a situação parece ter vínculo com a realidade. Por exemplo, em um enunciado que coloque a situação de uma compra em um mercado, pode não ser possível afirmar que trata-se de um mercado real.
O que Skovsmose (2000) chama atenção é que os exercícios, mesmo fazendo referência a contextos matemáticos puros, podem conduzir a questões exploratórias e investigativas, desde que o professor convide os alunos a pensarem em outras possibilidades. Ponte (2003, p. 32) mostra um exemplo interessante que pode ser trabalhado quando os alunos estiverem resolvendo exercícios sobre potências. Seu exemplo seria o seguinte: “[...] Repara que 42= 16 e 24= 16. Será sempre verdade que an=na ?”. Veja que o professor de Matemática pode propor aos alunos investigarem para quais outros números essa igualdade vale e começar então um trabalho de investigação.
Tal exemplo mostra que, através de um exercício, outras questões podem emergir, sendo que estas podem ser de exploração e até mesmo de investigação. Isto evidencia que, partindo de um exercício, pode-se chegar a um cenário de investigação. De acordo com Skovsmose (2000, p. 69), um cenário de investigação é “[...] um ambiente que pode dar suporte a um trabalho de investigação” de tal forma que através dele os alunos sejam convidados a formularem questões, bem como explicações (SKOVSMOSE, 2000).
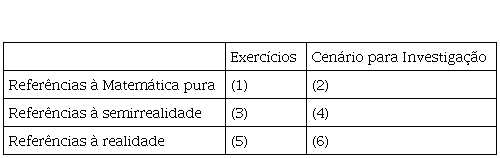
Com o que foi apresentado sobre a dimensão contexto referencial de uma tarefa, e agora com essa definição de cenário de investigação, pode-se, então, perceber que, assim como um exercício pode fazer referência à matemática pura, semirrealidade e realidade, um cenário de investigação também pode partir desses diferentes contextos referenciais. Skovsmose (2000, p. 73) chama de “ambiente de aprendizagem” cada uma das seis combinações possíveis de exercícios e cenários de investigação com as diferentes referências, conforme o Quadro 1 abaixo:
Quadro 1
Ambientes de aprendizagem
 Skovsmose (2000, p. 73).
Skovsmose (2000, p. 73).
|
Exercícios
|
Cenário para Investigação
|
|
Referências à
Matemática pura
|
(1)
|
(2)
|
|
Referências à
semirrealidade
|
(3)
|
(4)
|
|
Referências à
realidade
|
(5)
|
(6)
|
Mover-se por estes
diferentes ambientes é o que propõe o autor Skovsmose
(2000) com a expectativa de que os alunos se envolvam de forma mais ativa,
reflexiva e crítica nas aulas de Matemática. Ir dos exercícios aos cenários de
investigação nestes ambientes também pode propiciar outras possibilidades para
que o professor trabalhe com seus alunos questões cuja estrutura seja aberta,
as quais abrem margem para aprofundar os assuntos que estão sendo estudados. O
autor também explica que pode fazer sentido propor exercícios após o trabalho
dos alunos nos cenários de investigação a fim de “consolidar” algumas ideias.
3. Procedimentos metodológicos
O presente relato de experiência faz parte de um trabalho de conclusão de curso cujo objetivo foi caracterizar uma aula de Matemática em que os alunos estivessem envolvidos em situações de investigação, exploração e descobrimento. Para tal caracterização, foram elaboradas algumas atividades, dentre elas a que será descrita neste texto, com potencial exploratório ou investigativo sobre polígonos, as quais foram implementadas em uma turma do 5º ano do Ensino Fundamental. Tal atividade foi escolhida juntamente com a professora da turma, Maíra, de modo que houvesse conexão entre os conteúdos que estavam sendo trabalhados por ela e seus alunos à época. Cabe destacar que a professora vinha trabalhando assuntos relacionados à Geometria, como perímetro de figuras, por exemplo. O objetivo de aprendizagem relacionado à atividade escolhida era fazer com que os alunos percebessem que podemos ter polígonos de mesma área e perímetros diferentes.
Para a implementação da atividade, foram pensados três momentos para o desenvolvimento, sendo eles: explicação da atividade e entrega de eventuais materiais necessários; realização da atividade por parte dos alunos; e uma discussão final para que os alunos comentassem suas soluções. É importante destacar que o tempo reservado para a atividade foi de duas horas-aula, incluindo o intervalo dos alunos.
O método de
recolha de dados foi feito por meio de observação participante da professora da
turma e da licencianda, as quais, logo após a
realização da aula, anotavam, num diário de campo, os relatos sobre o que
ocorria ao longo da implementação das atividades. Outra fonte de dados foi o
registro escrito dos alunos nas folhas em que desenvolveram a atividade
proposta. Os pais dos alunos autorizaram, mediante assinatura do termo de
consentimento livre e esclarecido, o uso dos registros, desde que os nomes dos
alunos fossem omitidos. Por conta disso, o nome de nenhum aluno será
explicitado neste texto. Para análise qualitativa das situações percebidas em
sala de aula, como por exemplo a imprevisibilidade, a ser destacada neste
texto, utilizou-se os trabalhos de Skovsmose (2000),
Ponte (2003) e Ponte, Brocardo e Oliveira (2016). Existem diferenças teóricas
entre as abordagens de Ponte e Skovsmose quando
tratam de atividades de caráter investigativo nas aulas de Matemática. No
entanto, para este relato de experiência, trouxemos a contribuição de ambos
para a atividade desenvolvida com os alunos.
4. “O que é mesmo um polígono?”
Na aula Matemática da
professora Maíra, tínhamos dois períodos para desenvolver uma atividade a
respeito de polígonos. A atividade foi iniciada com a licencianda
Andressa apresentando a primeira parte do enunciado aos alunos, o qual continha
a seguinte situação:
 Figura 2
Enunciado da atividade
Acervo
do CAEM (2018).[4]
Figura 2
Enunciado da atividade
Acervo
do CAEM (2018).[4]
Após a
apresentação, ela perguntou aos alunos se existiam outros polígonos com área
igual a e perímetro diferente destes das duas figuras
apresentadas. Um aluno quis ir à lousa tentar encontrar tal polígono. Tentou
algumas vezes, mas o polígono tinha sempre o perímetro igual à ou .
Depois de algumas tentativas, o aluno chegou à seguinte Figura:
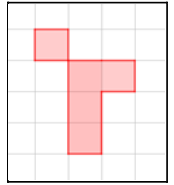 Figura 3
Desenho do
aluno na lousa.
Elaboração própria
(2018)
Figura 3
Desenho do
aluno na lousa.
Elaboração própria
(2018)
Neste momento, a licencianda Andressa e a professora Maíra não perceberam que a figura não representava um polígono. A aula continuou. A licencianda explicou aos alunos a segunda parte do enunciado da atividade que dizia que Rosana havia decidido montar novos polígonos, só que agora com área e todos os perímetros diferentes. A questão a ser respondida seria: “Quais perímetros Rosana pode ter encontrado?”. Para que os alunos realizassem esta etapa da atividade, foi entregue um papel quadriculado com quadrados de lado . Cabe enfatizar que a atividade caracteriza-se como sendo exploratória ou investigativa, uma vez que admite mais do que uma solução e pode ser acessível para alguns alunos, por isso exploratória, mas também pode ser difícil para outros, sendo nesse caso investigativa.
Enquanto a licencianda Andressa entregava as folhas, começou a pensar nas possibilidades de figuras que poderiam surgir. Refletiu sobre o exemplo que o aluno havia desenhado na lousa. Se algum dos quadradinhos que compunham a figura 3 fosse deslocado, poderia-se ter muitas possibilidades de figuras. Foi nesse momento que a licencianda deu-se conta que a figura desenhada na lousa não representava um polígono. Prontamente, foi compartilhar esse fato com a professora Maíra. Logo em seguida, a professora falou aos alunos: “pessoal, figuras como essas da lousa não podem, porque não são polígonos”. A partir disso, os alunos ficaram com dúvidas sobre o que seria um polígono. Consequência disso foi que, toda vez que desenhavam um “polígono” na folha quadriculada, perguntavam para a licencianda ou para a professora se estava certo ou não.
Faltava, então, discutir com os alunos um critério para saber quais figuras poderiam ser consideradas polígonos e quais não. Embora a licencianda Andressa soubesse identificar alguns polígonos, ela não se recordava, naquele momento, da definição por completo. Enquanto os alunos estavam no intervalo, a licencianda e a professora pesquisaram, primeiramente, no material EMAI[5] utilizado pelos alunos, o qual embora abordasse o conteúdo de polígonos, não exibia exemplos de não-polígonos. Depois, recorreram à internet, mas não obtiveram sucesso, pois suas buscas retornavam conceitos de polígono convexo e não-convexo, e não necessariamente a definição que elas precisavam no momento. Depois de um certo tempo, encontraram um site[6] com a seguinte definição formal:
 Figura 4
Definição de polígono.[7]
Retirado de Clube da Matemática OBMEP.
Figura 4
Definição de polígono.[7]
Retirado de Clube da Matemática OBMEP.
Tal definição ajudou a elaborar uma explicação com alguns exemplos para que os alunos compreendessem a definição de forma clara, a partir de uma linguagem já conhecida por eles. Sabíamos que não seria adequado apresentar tal definição, uma vez que a mesma envolvia uma linguagem não adequada para os alunos e alguns termos matemáticos ainda desconhecidos por eles quando a atividade foi aplicada, tais como: colinear e intersecção.
Quando os alunos voltaram do intervalo, a licencianda Andressa desenhou algumas figuras na lousa, conforme a Figura 5 abaixo, e explicou que, para ser polígono, primeiro era necessário no mínimo três lados retos. Depois explicou que esses lados não poderiam se cruzar, pois, se houvesse cruzamento, já não se tratava mais de um polígono. A respeito do critério sobre os pontos não serem colineares, disse-lhes que não poderíamos ter três pontos alinhados, e desenhou um exemplo de pontos alinhados e não-alinhados. Após isso, com os exemplos colocados no quadro (Figura 5), pediu para que eles classificassem quais eram polígonos. Em geral, eles demonstraram que entenderam, pois acertaram os exemplos colocados. Neste momento, também foi retomado o exemplo inicial que foi desenhado pelo aluno (Figura 3) e os alunos compreenderam por que não se tratava de um polígono. Em seguida, continuaram a atividade, explorando os polígonos de mesma área e perímetros diferentes.
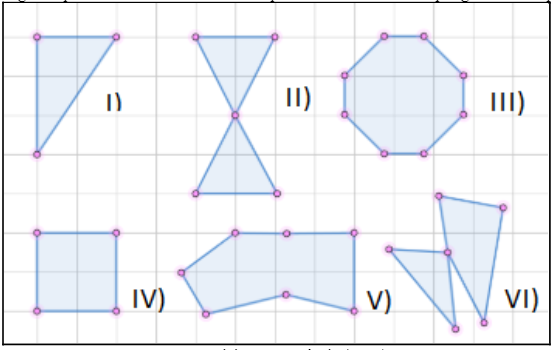 Figura 5
Figuras que
foram desenhadas na lousa para classificá-las como polígonos e não-polígonos.[8]
Elaboração própria (2018)
Figura 5
Figuras que
foram desenhadas na lousa para classificá-las como polígonos e não-polígonos.[8]
Elaboração própria (2018)
Em outro momento da aula, dois alunos perguntaram se a diagonal do quadrado de lado 1cm da folha quadriculada tinha medida igual a 1cm, assim como o lado do quadrado, e se eles poderiam considerar que sim para então desenharem outros polígonos. A licencianda perguntou o que eles achavam, pois falar √2 (ou Pitágoras!) não faria muito sentido para os alunos nesse momento da aprendizagem, já que este assunto correspondia aos anos posteriores ao 5ºano. Um dos alunos lhe disse que parecia sim, mas que dava a impressão de ser um pouquinho maior. Ela então pediu emprestada a régua de um aluno que estava próximo e mediu junto com eles para verificar que a medida era maior que 1cm. A partir disso, os alunos concluíram que não media 1cm e prosseguiram a atividade. Evidentemente, a licencianda Andressa não perdeu a oportunidade de contar que em anos futuros eles iriam descobrir que tal medida era o número √2. Um dos alunos ficou um pouco impressionado, e por fim exclamou: “Nossa! Isso existe?!”.
Por fim, os alunos foram convidados à lousa para desenhar os perímetros que haviam encontrado quando desenharam os polígonos na folha quadriculada, conforme o exemplo abaixo:
 Figura 6
Exemplo de
uma atividade feita pelos alunos.
Dados
da pesquisa (2018).
Figura 6
Exemplo de
uma atividade feita pelos alunos.
Dados
da pesquisa (2018).
Cabe comentar que
na Figura 6 acima, é possível notar que o aluno estabeleceu uma correspondência
biunívoca, um risquinho para cada unidade de comprimento, e este foi seu
processo para saber o perímetro dos polígonos desenhados. Além disso, é
possível perceber que o aluno não indica quais os vértices dos polígonos, e
isto faz diferença na definição de polígonos. Na Figura 7 abaixo, o triângulo
ABC é um polígono, mas a outra figura não o é, uma vez que os pontos E, F e G
são colineares.
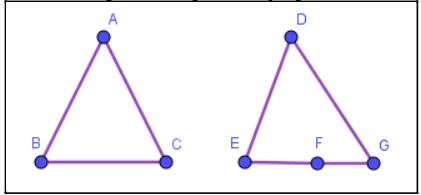 Figura 7
Polígono e
não polígono.
Elaboração própria (2018).
Figura 7
Polígono e
não polígono.
Elaboração própria (2018).
Por fim, os alunos compararam quantos polígonos com área e perímetro diferentes cada dupla havia encontrado e assim encerrou-se a atividade. É importante destacar que parece-nos que, para os alunos, ficou clara a diferença entre área e perímetro e, para explicar isto, utilizamos os exemplos dos próprios alunos na discussão final, concluindo que podemos ter polígonos de mesma área e perímetros diferentes.
5. Análise da aplicação da
atividade
Observando como os alunos desenvolveram a atividade apresentada anteriormente, foi possível notar que não houve muitas dificuldades para explorarem o que foi proposto sobre polígonos e a atividade foi acessível a todos da sala. Para a licencianda e a professora a atividade em questão proporcionou dois momentos que não haviam sido previstos durante seu planejamento. O primeiro deles foi o momento em que se fez necessário abordar a definição de polígono. Tal situação fez com que, tanto a licencianda quanto a professora, rapidamente pensassem em como abordar essa definição com os alunos. O segundo momento foi quando um aluno perguntou se poderia considerar 1 cm como a medida da diagonal do quadrado de lado 1cm.
Na primeira situação, sobre a definição de polígono, o uso dos celulares da licencianda Andressa e da professora Maíra ajudou muito a pesquisar na internet um bom site que apresentasse a definição, uma vez que a mesma não constava no material de Educação Matemática nos Anos Iniciais (EMAI) utilizado pelos alunos. As duas tiveram um tempo curto, de aproximadamente 15 minutos, para selecionar um site e planejar como explicar aquele conteúdo aos alunos. O modo escolhido para lidar com este imprevisto gerou aprendizagens para todos.
Pode-se notar isso quando Andressa e Maíra escolheram abordar a definição com os alunos, ao não se conformarem em “deixar de lado” algo que não estava correto do ponto de vista matemático. Os alunos tinham direito a saber o que era um polígono e isso foi feito via exploração. É fato que uma mudança no enunciado resolveria a questão de forma breve se, ao invés de “polígonos”, estivesse escrito “figuras”, mas percebeu-se um momento oportuno para estudar este novo assunto com os alunos. Segundo Ponte (2017), isto deve fazer parte das preocupações do professor ao propor atividades desta natureza, uma vez que atividades exploratórias e investigativas podem constituir bons pontos de partida para o estudo de novos conceitos.
No caso da situação da diagonal do quadrado, também foi percebido um momento propício para explicar que a medida da diagonal do quadrado de lado não era 1cm. Foi uma situação imprevisível que fez com que a licencianda e a professora prestassem mais atenção se outros alunos estavam considerando essa medida como 1 cm também e explicassem que não era o caso. Elas queriam que os alunos se convencessem e, por isso, utilizaram a régua quando o primeiro aluno perguntou sobre a medida da diagonal. Ficou claro que um dos papéis do professor é mediar o desenvolvimento de uma tarefa, de modo a “[...] compreender como o trabalho dos alunos se vai processando e prestar o apoio que for sendo necessário” (PONTE; BROCARDO; OLIVEIRA, 2016, p. 29).
A resposta para a pergunta do aluno parecia não ser difícil de ser dada, embora, no momento em que ele perguntou, tenha sido difícil, para a licencianda, pensar rapidamente em como conseguir explicar que tal medida não era 1cm para alunos que ainda não haviam estudado o Teorema de Pitágoras e nem os números irracionais. Em outros casos, a depender da atividade de investigação ou exploração que os alunos estiverem envolvidos, nem sempre essas perguntas podem ser fáceis de serem respondidas e, por essa razão, a atividade pode até mesmo “[...] impor novos requisitos às competências do professor”, como afirmam Ponte et al. (1999, p. 134).
Essas duas situações apontadas evidenciam o que Skovsmose (2000) diz ocorrer quando há o trabalho nos cenários para investigação, o qual é uma das possibilidades para os ambientes de aprendizagem nas aulas de Matemática (Quadro 1). Quando se está num cenário de investigação, há incertezas sobre o que os alunos vão perguntar e os caminhos que vão percorrer no desenvolvimento da atividade, podendo até mesmo colocar questões que o professor não pensou antecipadamente. Essas incertezas são maiores do que quando professor e aluno estão em um ambiente do paradigma do exercício, o qual é caracterizado pela dualidade de respostas (certas ou erradas) e possui apenas uma resposta correta, pois, em tarefas assim, é mais fácil para o professor prever o que os alunos podem perguntar, bem como as dificuldades que terão.
A imprevisibilidade sobre o que pode ocorrer durante o desenvolvimento das atividades em um cenário de investigação é característica por uma zona de risco (SKOVSMOSE, 2000). Para o autor, propor atividades de caráter investigativo implica em não conhecer de antemão os caminhos que os alunos seguirão para desenvolvê-la e isso representa uma responsabilidade compartilhada entre professor e alunos pela aprendizagem. Eliminar esse risco pode significar um recuo ao paradigma de exercícios e a abdicação de ricas oportunidades de aprendizagem para professor e alunos.
Na perspectiva de Skovsmose (2000, p. 83), sobre as incertezas que eventualmente emergirem num cenário de investigação, o autor reitera que essas não devem ser vistas como ameaças ao professor, mas como um “[...] desafio a ser enfrentado”. Mais ainda, tais situações podem fazer com que o professor e o aluno pensem juntos, pois a partir do momento que ambos elaboram questões como “o que acontece se…?” hipóteses podem ser levantadas, e um novo cenário de investigação pode ser proposto. É também nesse sentido que “[...] ser um cenário para investigação é uma propriedade relacional” (SKOVSMOSE, 2000, p. 72), pois depende do convite do professor, do aceite dos alunos e também da própria natureza do cenário que pode não chamar atenção e não interessar os alunos.
Em síntese, prever se os alunos vão se interessar ou não pela atividade investigativa, pode ser algo incerto de se saber de antemão, já que, ao considerar essa propriedade relacional do cenário de investigação, fica evidente que os alunos podem aceitar ou não o trabalho investigativo. Contudo, se o professor nem sequer realizar o convite aos alunos, mesmo que por uma simples pergunta ou observação, ele pode deixar de oportunizar uma experiência, tanto para ele mesmo quanto para seus alunos, de aprender algo novo.
6. Considerações finais
Conclui-se que atividades de natureza exploratória e investigativa podem possibilitar um aprendizado mútuo, para professor e aluno, em que, nessas circunstâncias, o professor não é mais o sujeito que explica e passa atividades para os alunos resolverem, mas aquele que está pensando para resolver junto com eles. Isso pode ocorrer de tal modo que se a zona de risco for vista por ele como um desafio a ser enfrentado, segundo Skovsmose (2000), ela pode propiciar que ambos os sujeitos passem a intervir nesta zona, estabelecendo assim uma nova forma de trabalho colaborativa entre alunos e professor.
Andressa e Maíra aceitaram fazer parte da zona de risco e aprenderam que algumas decisões que precisam ser tomadas rapidamente e estrategicamente em sala de aula ao implementar uma atividade podem gerar aprendizagens para os alunos e para o professor. No caso, elas tiveram que aprender a definição de polígono e imediatamente adaptar a linguagem formal da definição para que a mesma fosse compreensível aos alunos. A decisão foi estratégica porque a atividade permitia que a definição fosse oportunamente trabalhada e, por isso, escolheu-se não substituir o termo “polígono” por “figura”. Perder-se-ia uma rica discussão se isso tivesse sido feito e elas talvez sequer teriam aprendido a definição de polígono.
Tudo isso evidencia que o professor não é aquele que “sabe de tudo”, pelo contrário, é o que está sempre aprendendo enquanto ensina e para ensinar. Inclusive, durante a escrita deste texto, a licencianda e a professora descobriram que existem os polígonos chamados Polígonos complexos[9], e que o polígono desenhado pelo aluno (Figura 3) encaixa-se em sua definição. Mais ainda, a definição de polígono que foi trabalhada, Figura 4, é a definição de Polígono simples e como a atividade não especificou de qual tipo se tratava, seria possível seguir em frente, afinal, o aluno estava correto. Para esclarecer, um polígono complexo é um polígono que não é simples, isto é, num polígono complexo a interseção de dois lados não consecutivos é diferente do vazio, conforme o exemplo abaixo:
 Figura 8
Exemplo de
um polígono complexo.
Elaboração própria (2020)
Figura 8
Exemplo de
um polígono complexo.
Elaboração própria (2020)
De todo modo,
seria muito importante discutir com os alunos, em algum momento, o que
caracteriza um polígono simples, visto que eles seguirão estudando sobre o
conceito ao longo de suas trajetórias escolares e também para evidenciar que
definições são importantes em Matemática e fazem diferença quando se está
explorando e investigando soluções para uma tarefa. Consideramos, então, que a
atividade proposta propiciou um bom momento para essa discussão e para as
aprendizagens da licencianda e da professora, as
quais puderam ampliar seus conhecimentos sobre polígonos. Quando forem tratar
novamente este tema com outras turmas, ficarão mais atentas às sutilezas das
definições e ao caso dos polígonos complexos.