1. Introdução
Este artigo é parte de uma pesquisa de Doutorado no Ensino de Matemática que está em andamento. Sua realização aconteceu em uma escola privada com alunos de 1º e 2º anos do Ensino Fundamental com crianças entre 6 e 8 anos.
O tema da pesquisa está fundamentado no objetivo de investigar a necessidade de compreender a evolução do conhecimento de crianças dos Anos Iniciais do Ensino Fundamental no Campo Multiplicativo no processo ensino-aprendizagem, ou seja, quais conceitos eles já haviam se apropriado e quais eles precisavam saber sobre as ideias do campo multiplicativo.
Para corroborar com as análises realizadas dos dados coletados dessa investigação matemática, foi realizada uma revisão de literatura, a qual abarca a teoria dos Campos Conceituais de Vergnaud (2009), os estudos de Nunes e Bryant (1997) e parte da pesquisa realizada por Castro (2016).
Sendo assim, para que se pudesse evidenciar o que é discutido por Vergnaud (2009), Nunes e Bryant (1997) foi utilizada como metodologia com abordagem investigativa a qual associa dados qualitativos e quantitativos, de acordo com Creswell (2010), através da análise documental de protocolos e de vídeo-filmagem das resoluções, propiciando uma gama de dados minuciosos de como se dá o desenvolvimento do raciocínio multiplicativo para os estudantes de 1º e 2º anos do Ensino Fundamental.
O uso de vídeo segundo Hall (2000, p.247, apud Powell; Francisco; Maher, 2004, p. 85) na Educação Matemática tem uma história importante e crescente, pois apresenta um leque diversificado de investigações relacionado às interrogações que emergem sobre as práticas de ensino e as dificuldades detectadas na aprendizagem dos estudantes.
De acordo com estudos de vídeo-filmagem, este pode ser uma das fontes com maior riqueza de detalhes, pois permite captação de comportamento verbal e não verbal, os quais são analisados a partir das perspectivas de pesquisa estabelecida pelos pesquisadores em ação, sejam elas quantitativas ou qualitativas, permitindo ao pesquisador ver e rever as atividades, tantas vezes achar necessário.
2. Embasamento Teórico
A teoria dos Campos Conceituais foi desenvolvida pelo psicólogo francês Gérard Vergnaud (1996), a qual está focada em estudos sobre atividades cognitivas, e supõe que o núcleo de desenvolvimento cognitivo seja a conceitualização do real Segundo o autor, tem o intuito de proporcionar subsídios para estudos da aprendizagem de competências complexas, atendendo, em especial, atividades de formação de conceitos matemáticos (VERGNAUD, 1982; 1990; 1996).
Vergnaud (1988, 1990) define o Campo Conceitual como um conjunto de situações em que seu domínio requer a noção de situações e ações dos sujeitos em tantos outros conceitos distintos, bem como, nos conceitos matemáticos, não os reduzindo a uma única definição, mas, possibilitando uma ruptura entre os conhecimentos prévios e os novos (VERGNAUD, 2012).
A teoria dos Campos Conceituais visa à construção de princípios, que permitem articular competência e concepções constituídas tanto em situações de natureza teórica quanto de natureza prática.
No campo das estruturas aditivas caracterizam-se situações que requerem para a sua resolução uma operação de adição ou uma operação de subtração ou as duas operações combinadas. No campo das estruturas multiplicativas caracterizam-se situações que requerem para a sua resolução uma operação de divisão ou multiplicação ou a combinação de ambas (VERGNAUD 1982; 1990; 2009).
Sendo assim, o autor define estes conceitos como três conjuntos indissociáveis, um conjunto de situações que dá sentido ao conceito (S), um conjunto de ações dos sujeitos diante uma situação (I) e representações simbólicas (R), ou seja, uma função tríplice, distinta, mas interligada. Sua representação simbólica apresenta-se pela sigla: C = (S, I, R).
Segundo Vergnaud (1990), o uso simultâneo dessa função tríplice é essencial para se estudar um determinado conceito no processo ensino aprendizagem. Afirma, ainda, que essas situações não são biunívocas, pois, não se relacionam a um único conceito, assim como, um conceito não se resume a uma única situação.
De acordo com a teoria dos Campos Conceituais, todos os conceitos só se tornam significativos a partir de situações naturais, assim como, o conjunto de situações requer o domínio de vários conceitos de naturezas distintas (VERGNAUD, 1988; 1990).
Segundo Vergnaud (1994), as relações multiplicativas apresentam vários tipos de multiplicação e várias classes de problemas. O autor destaca que se faz necessário analisá-los com muito cuidado para que se possam distinguir estas classes, proporcionando às crianças possibilidades para que reconheçam os procedimentos adequados e apropriados para a solução dos problemas propostos.
De acordo com Vergnaud (1996), as relações multiplicativas mais simples não são as ternárias (relações que ligam três elementos entre si), mas sim quaternárias (relação que liga quatro elementos entre si), onde os problemas de multiplicação ou divisão implicam em uma proporção simples de duas variáveis, uma em relação à outra.
Segundo o autor, as relações quaternárias são utilizadas para introduzir a multiplicação no ensino básico.
Vergnaud (2009), em seus estudos afirma que no Campo Conceitual das Estruturas Multiplicativas encontramos um conjunto de problemas que envolvem duas grandes categorias: Isomorfismo de Medidas e Produto de Medidas.
Será exemplificada nesse trabalho a categoria Isomorfismo de Medidas envolvendo as ideias de proporcionalidade, multiplicação comparativa e a categoria Produto de Medidas envolvendo as ideias de configuração retangular e combinatória, usando números naturais, para uma melhor compreensão da ideia dos problemas.
Vale ressaltar que essas categorias foram essenciais para que fundamentássemos a elaboração dos instrumentos da nossa pesquisa de doutorado.
3. Categoria Isomorfismo de Medidas
Na categoria Isomorfismo de Medidas, Vergnaud (2009) apresenta problemas de proporcionalidade e de multiplicação comparativa, destaca uma relação quaternária envolvendo duas quantidades de um tipo e as outras duas de outro tipo. Nos problemas mais simples uma dessas quantidades é igual a um e outra quantidade é aquela a ser buscada. É o que alguns autores como Nunes e Bryant (1997), denominam de relação de “um a muitos”.
Entretanto, o autor reitera que a relação quaternária pode apresentar uma correspondência entre os dois tipos de quantidades em que nenhuma delas é unitária. Esse tipo de situação é mais complexo do que o anterior. É o que Nunes e Bryant (1997), denominam de relação “muitos a muitos”.
Vergnaud (2009) faz dois tipos de análise: uma análise vertical (escalar) e outra horizontal (noção de função linear).
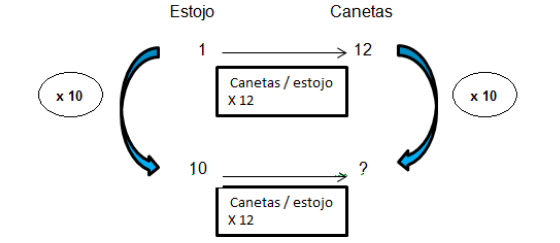
Segundo Vergnaud (2009) os números um e três apresentados no exemplo 1 representam quantidades de pacotes de iogurtes e são considerados como medidas, enquanto o número quatro e o termo desconhecido representam a quantidade de iogurtes, considerados também como medidas, porém de outra natureza. Neste exemplo, os operadores verticais (x 3) são escalares (não tem dimensão) que permitem passar de uma linha à outra na mesma categoria de medidas. Os operadores horizontais (x 4), representam funções, e expressam a passagem de uma categoria de medidas à outra, para que o emprego da forma verbal possa expressar uma relação iogurte por pacote ou iogurte/ pacote.
O autor conclui que existem duas formas de encontrar o termo desconhecido. A primeira aplica o operador 3 à quantidade de 4 iogurtes. A segunda aplica a função iogurte/pacote e multiplica 4 pelos 3 pacotes. Portanto, as duas formas são equivalentes, mas também são distintas por tratarem uma delas de uma multiplicação simples e a outra da aplicação de uma função.
Essa análise permite compreender que se efetuando 4 x 3 ou 3 x 4 não se multiplica iogurtes por pacotes ou pacotes por iogurtes, (por que resultariam então iogurtes e não pacotes?).
O autor apresenta ainda algumas classes de problemas do tipo multiplicativo de isomorfismo de medidas. Essas classes podem ser identificadas segundo o caráter discreto ou contínuo das quantidades envolvidas, ou segundo as propriedades dos conjuntos numéricos utilizados, ou ainda a posição do termo desconhecido.
Vergnaud (1994), aponta um caso especial do isomorfismo de medidas que envolve expressão como, por exemplo, “três vezes mais” ou “três vezes menos” no enunciado. O autor exemplifica as variações desse tipo de problema e a operação que pode ser usada para resolvê-lo:
Exemplo 1 - Multiplicação
“São necessários 2 m de tecido para fazer uma saia. São necessários três vezes mais para fazer um conjunto. Quanto de tecido é necessário para fazer esse conjunto?” (VERGNAUD, 2009, p. 263)
Exemplo 2 – Divisão: busca de uma medida
“São necessários três vezes mais tecido para fazer um conjunto do que uma saia. São necessários 6 m para um conjunto. Quanto de tecido é necessário para fazer uma saia?” (VERGNAUD, 2009, p. 263)
Exemplo 3 – Divisão: busca de um escalar
“São necessários 2 m de tecido para fazer uma saia e 6 m para um conjunto. Quantas vezes mais de tecido são necessárias para fazer um conjunto em relação a uma saia?” (VERGNAUD, 2009, p. 263)
A forma verbal da pergunta “quanto de tecido” e “quantas vezes mais” marca a diferença entre a noção de medida e de escalar. Todos os problemas de isomorfismo de medidas envolvem a noção de proporcionalidade.
Portanto, segundo o autor, a análise dimensional permite estabelecer a relação multiplicativa de forma simples e a utilizar o operador-função na solução de problemas, como acontece no isomorfismo de medidas, o qual permite encontrar o produto de medidas como uma segunda forma de solução.
4. Categoria Produto de Medidas
Segundo Vergnaud (2009), o produto de medidas não é bem compreendido pelas crianças por se tratar de uma dupla proporcionalidade (duplo isomorfismo de medidas), em que a criança precisa identificar uma dimensão a um produto de dimensões mais simples que possam ser medidas.
De acordo com o autor, as relações multiplicativas se remetem a um conjunto de composições numéricas (multiplicações, divisões, regras de três simples e composta etc.), e às composições relacionadas a dimensões (dimensões simples, dimensões-produto, dimensões-quociente).
De acordo com Vergnaud (2009), não podemos nos limitar aos conceitos ou aspectos elementares ao tratarmos das relações de multiplicação e de divisão, uma vez que as crianças apresentam várias formas de solução para os problemas matemáticos.
Portanto, a intervenção do professor deve ter um cunho pedagógico a fim de ajudar as crianças e não as limitar ao conhecimento de determinadas soluções, acreditando que os alunos devam aprender algumas noções apenas ao final do Ensino Fundamental. Na verdade, essas noções devem ser abordadas ao longo de toda escolaridade e não em uma determinada fase.
5. Outros
estudos sobre as Estruturas Multiplicativas
De acordo com Nunes e Bryant (1997), a multiplicação e divisão são operações vistas como operações aritméticas, que deveriam ser ensinadas somente após as crianças aprenderem a adição e subtração, pois, dessa forma as crianças não precisariam passar por nenhuma transformação no raciocínio para desenvolver cálculos multiplicativos e divisíveis.
Em 1965 Piaget já discutia que as operações de multiplicação e divisão promoviam uma transformação qualitativa para o pensamento das crianças.
Os estudos de Nunes e Bryant apresentam análises para que se possam entender os muitos passos que as crianças dão em direção ao entendimento e compreensão progressiva do raciocínio multiplicativo, as operações de pensamento, sistemas de sinais e situações que possam estar conectadas aos conceitos de multiplicação e divisão. Bem como, entender por que as crianças que desenvolvem com grande destreza algumas formas do raciocínio multiplicativo, em alguns outros problemas propostos falham ao tentar resolvê-los mesmo que estejam no mesmo nível de dificuldade.
Os autores apontam situações primordiais para que possamos compreender o raciocínio multiplicativo: 1) situações de correspondência um-para-muitos; 2) situações que envolvem relações entre variáveis; 3) situações que envolvem distribuição, divisão e divisões ao meio (NUNES e BRYANT, 1997, p. 143).
De acordo com os autores as situações multiplicativas envolvem uma relação constante de correspondência um-para-muitos entre dois conjuntos. Esta relação, por sua vez, é uma constante invariável na situação, algo que não acontece no raciocínio aditivo.
Segundo Nunes e Bryant (1997), a correspondência de um-para-muitos, torna-se a base para um novo conceito matemático, o conceito de proporção, o que contrasta com a situação aditiva. Este raciocínio quanto à proporção invariável não quer dizer unir/ separar, mas, sim replicar, a cada conjunto a unidade correspondente para que a correspondência um-para-muitos seja mantida. A proporção permanece constante quando a replicação é efetuada.
Os autores afirmam que essa relação pode dar um novo sentido ao número, pois tudo acontecerá de acordo com o número de replicações efetuadas em uma dada situação, número este que denominam como fator escalar. Assim, para que a proporção seja uma constante, o fator escalar deve ser aplicado a cada conjunto (NUNES e BRYANT, 1997).
Entretanto, os autores afirmam que podemos encontrar um tipo diferente de sentido de número no raciocínio multiplicativo, ou seja, quando duas ou mais variáveis co-variam como uma consequência de convenção ou causa. Para Nunes e Bryant convenção, significa “co-variação concordada” passível de alterações.
Dentre os exemplos citados em sua obra, os autores apontam a existência de semelhanças e diferenças entre duas situações multiplicativas apresentadas por eles. O que assemelham estas situações é a replicação e seu inverso, problemas com relações entre duas variáveis e os que envolvem correspondência um-para-muitos entre conjuntos.
Exemplo 4 - Correspondência um-para-muitos
“...um carro tem quatro rodas (1-para-4), uma criança tem dois pés (1-para-2), em uma mesa podem sentar 6 pessoas (1-para-6), etc...” (NUNES e BRYANT, 1997, p. 143).
Quanto à diferença citada pelos autores é bem significativa, pois os números no segundo tipo de situação se referem a valores sobre variáveis e não a conjuntos, uma vez que conjuntos são compostos por elementos descontínuos e as variáveis são contínuas. Portanto, valores fracionais emergem naturalmente no contexto de variáveis enquanto somos confinados a números inteiros ao falar sobre conjuntos (NUNES e BRYANT, 1997).
Referente à questão de distribuição e divisão, Nunes e Bryant (1997) apresentam um terceiro conceito de situação que envolve o raciocínio multiplicativo, ou seja, a distribuição equitativa de um conjunto, relações parte-todo. No entanto, os autores ressaltam que há três elementos a serem considerados: o tamanho do todo, o número das partes e o tamanho das partes, os quais devem ser o mesmo para todas as partes.
Exemplo 5 – Distribuição e divisão
“... se há 20 doces (o todo) e 4 crianças para partilhá-los (4 partes), há 5 doces por criança (o tamanho da parte ou quota)” (NUNES e BRYANT, 1997, p. 148).
Para a criança, a situação de partição parece bastante diferente da correspondência de um-para-muitos, uma vez que a proporção não é fixa desde o início, pois os mesmos terão que lidar com a relação entre três conjuntos (ou variáveis). Estas relações novas a serem entendidas, como o caso da distribuição ou cortes sucessivos permite entender a relação inversa como um passo básico para avançar nas atividades mais simples de distribuir até a compreensão da divisão (CORREA E BRYANT, 1994).
Os autores Nunes e Bryant ainda apresentam uma terceira razão para estabelecer uma linha. Afirmam que uma divisão pode naturalmente resultar em frações, enquanto a correspondência de um-para-muitos está conectada diretamente a números inteiros.
Quanto à divisão, os estudos de Nunes e Bryant (1997) utilizam os termos cortes sucessivos e divisões sucessivas, ideia desenvolvida por Confrey (1994) o qual usa a expressão splits – cortes com um sentido mais amplo do que divisão.
Afirmação que podemos esclarecer melhor visualizando o processo de divisão, utilizando o diagrama de árvore sugerido por Confrey (1994).
O autor especifica seu raciocínio:
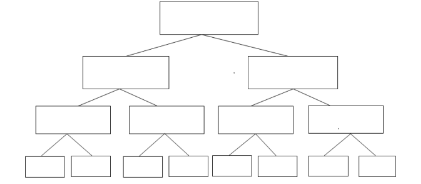Figura 2
Cortes e divisões sucessivas
Confrey, 1994. Adaptado pela pesquisadora
Segundo Nunes e Bryant (1997), a proposta de cortes sucessivos desenvolvida por Confrey (1994) difere das situações multiplicativas, primeiro porque indica uma taxa de transformação, segundo estes cortes diferem do resultado da replicação, uma vez que a replicação gera uma progressão aritmética, enquanto na divisão ocorre uma transformação na relação parte-todo.
Anteriormente, Correa e Bryant (1994) classificaram a distribuição como uma ação da divisão, pois acreditavam que a divisão ia muito mais além, envolvendo relação inversa entre receptores e o tamanho de sua quota.
Diante de uma reflexão muito cuidadosa levantada pelos autores, eles constataram que o conceito do raciocínio multiplicativo não se sustentava no conceito de uma mera repetição aditiva, nem a divisão como uma repetição da subtração.
Em suma, relações entre variáveis correspondem a frações de unidades de medidas, pois, as variáveis correspondem às quantidades contínuas, além de ser representada por um fator, uma função ou uma quantidade intensiva.
Nunes e Bryant (1997) afirmam que os diferentes contextos possibilitam compreender relações proporcionais entre variáveis, pois as crianças relacionam situações de correspondência acreditando que possam aplicar nos problemas que envolvem relações entre variáveis. No entanto, os autores apontam a correspondência um-para-muitos como ponto de partida para que as crianças consigam desenvolver as relações entre variáveis, compreendendo, assim, as relações proporcionais, como também novos conceitos diante do raciocínio multiplicativo que não dependem da compreensão das situações aditivas. São eles:
-Proporção – uma nova forma de dar sentido ao número em uma situação de correspondência um-para-muitos e muitos-a-muitos.
-Replicar/ Fator Escalar – é a ação de replicar a ser efetuada e não apenas juntar.
-Fator/ Função/ Quantidade intensiva conectando as duas variáveis – situação multiplicativa que envolve uma relação entre duas variáveis, relação horizontal de Vergnaud.
-Distribuição – uma nova visão das relações parte-todo, diferenciando-se das relações aditivas, pois apresenta três valores novos: o total, o número de receptores e a quota (medida).
Os autores concluem que estes novos sentidos de números ainda precisam ser dominados pelas crianças para que possam desenvolver o raciocínio multiplicativo (NUNES e BRYANT, 1997).
6. Procedimentos
metodológicos
Com base nos procedimentos de diferentes concepções definidos por Creswell (2010), definimos nossa pesquisa como métodos mistos por ser uma abordagem investigativa que combina ou associa a pesquisa qualitativa e quantitativa em um único estudo, a escolha do método misto nos permitiu perceber que a coleta de dados realizada não era meramente analítica ou quantitativa, sua aplicação revelou dados importantes ao se cruzarem, tornando-se robusta e com maior propriedade para as análises.
A pesquisa fora realizada com crianças escolhidas aleatoriamente, com auxílio das professoras polivalentes e anuência formal dos pais.
Para este artigo foram selecionadas 4 crianças do primeiro ano e 5 crianças do segundo ano, em que cada criança recebeu 5 protocolos contento as ideia de proporcionalidade envolvendo as correspondências “um a muitos” e muitos a muitos” do Campo Multiplicativo, bem como trechos dos resultados encontrados.
Devido às crianças do primeiro ano não serem leitoras fluentes, os problemas foram apresentados pela pesquisadora, realizando a leitura, por vezes dando pistas para encontrarem o melhor raciocínio para a resolução, após tal intervenção não fora realizada nenhuma outra por parte da pesquisadora.
Para o desenvolvimento da pesquisa optamos em dividi-la em três etapas.
1ª etapa da pesquisa
Aplicação dos problemas do Campo Multiplicativo aos alunos de 1º ao 5º ano do Ensino Fundamental e gravações de vídeo-filmagem.
2ª etapa da pesquisa
Com a recolha dos protocolos na 1ª etapa, todos foram organizados em um portfólio separado por ano de escolaridade, criança a criança denominadas como E1, E2, E3, E4 e E5 para os anos de escolaridade, tendo como primeira página o termo de consentimento livre e esclarecido de cada uma. Optamos em chamar as 9 crianças pela mesma nomenclatura citada acima, por entender que facilitaria o movimento de manuseio do portfólio a cada necessidade de retomada para análise, outro fator agregado ao portfólio como facilitador foram os separadores adesivos com cores estabelecidas para cada nomenclatura dada as crianças (E1 – azul; E2 – verde; E3 – amarelo; E4 – laranja; E5 – rosa).
Após toda organização dos protocolos e identificação das crianças, foram realizadas as análises das resoluções dos problemas com base nos registros das crianças, para que assim pudéssemos categorizá-los em acertos e qual tipo de procedimento a criança usou para a resolução dos problemas, se por raciocínio aditivo ou multiplicativo, se fez por representação pictórica, cálculo mental ou algoritmo.
Dentre os 70 problemas aplicados, foram analisados 62, pois houve faltas de alunos ou não souberam fazer, não tentando qualquer tipo de resolução.
3ª etapa da pesquisa
De posse dos instrumentos da 2ª etapa da pesquisa preenchidos e organizados, iniciamos a transcrição das vídeo-filmagens, a fim de encontrarmos respostas para tudo aquilo que não estava explicito nas resoluções das crianças.
Portanto, a partir desse momento inicia-se um trabalho detalhado de horas e dias, para que não perdêssemos nenhum dado importante para compreender o desenvolvimento do pensamento multiplicativo das crianças, para tal as análises de interpretação dos problemas nos apoiamos na técnica de análise do uso de dados de vídeo.
Segundo Hall (2000, p.247, apud Powell; Francisco; Maher, 2004, p. 85) afirma ser uma metodologia pouco conhecida e escrita, sobre o uso da mídia para “coletar, assistir e interpretar o vídeo com uma fonte estável de dados para a pesquisa e para propósitos de apresentação”.
Trata-se de uma abordagem de capturar e arquivar dados para ambas as classes de pesquisas, sejam elas qualitativas ou quantitativas, por permitir analisar fenômenos sejam em sala de aula ou outro ambiente de pesquisa. O vídeo é um instrumento flexível, traz uma coleta de dados muito rica em áudio, expressões e comportamentos valiosos e interações importantes entre estudantes e professor, permitindo ao pesquisador reexaminar continuamente os dados coletados.
Para a análise e transcrição do vídeo procuramos seguir o modelo analítico: Observar atentamente aos dados do vídeo; Descrever os dados do vídeo; Transcrever; Codificar; Construir o enredo; Compor a narrativa (POWELL; FRANCISCO; MAHER, 2004, p. 98).
Por se tratar de uma pesquisa de doutorado em andamento, selecionamos apenas a transcrição do vídeo de um aluno.
O quadro abaixo traz a transcrição do vídeo.
Quadro 1
Ciclo de Alfabetização/ 1º ano - Protocolo 1
Fonte: Elaboração
da pesquisadora
|
Parte
A
|
Ideia de Proporcionalidade (Um a
muitos)
|
|
0:00–0:01:52
|
A pesquisadora cumprimenta a aluna E1
e pergunta: “você sabe ler?”
E1 – Sei e balança a cabeça para
confirmar.
Pesquisadora:
Aponta com o
dedo onde a aluna deve começar a leitura.
E1 – Faz a leitura do protocolo 1 com
fluência, ao terminar olha para pesquisadora com o olhar, “o que eu faço
agora?”.
Pesquisadora: Você sabe resolver esse problema?
E1 – Balança a cabeça com sentido de não,
com um sorriso tímido diz “Não”. Permanece o tempo todo mexendo no cabelo,
como se estivesse insegura.
Pesquisadora: Não sabe!!! Então, vamos lá... a
pesquisadora faz a leitura do problema para a aluna.
E1 – 1 por cada dia?
Pesquisadora: Quantos dias são?
E1 – Pensa, pensa...
Pesquisadora:
Quantos dias
estão marcados no protocolo?
E1 – Abaixa a cabeça lendo novamente o
problema acompanhado com a ponta do lápis e diz: 5, olhando para a
pesquisadora.
Pesquisadora: Então, quantos copos ela vai tomar?
E1 – Rapidamente responde 5 e representa
com a mãozinha.
Pesquisadora:
Muito bem!!! E
como você vai representar?
E1 – Representar ela tomando (sempre com o
lápis em movimento ou mexendo no cabelo).
Pesquisadora:
Então, coloca
o total e me diz como você vai fazer para achar esses 5 copos?
E1 – Vou vendo!
Pesquisadora: Faz, pode fazer.
E1 – Começa a fazer a representação
pictórica e há todo momento olhando para a pesquisadora, (fez uma menina
segurando um copo) olha para a pesquisadora como se tivesse concluído.
Pesquisadora: Aí ela está tomando quantos copos?
E1 – 5.
Pesquisadora: 5 copos? Você desenhou 5 copos?
E1 – Não (dá início ao desenho novamente,
complementando).
Pesquisadora: Muito bem, parabéns!
|
|
Parte
B
|
Ideia
de Proporcionalidade (Muitos a muitos)
|
|
0:00:00 – 0: 03:37
|
Pesquisadora: E1 você entendeu o segundo problema?
E1- Eu entendi, (olhando para o
protocolo e segurando o lápis).
Pesquisadora:
O que você vai
ter que fazer?
E1 – Eu vou ter que desenhar ela com
bolachas (mexe no cabelo).
Pesquisadora: É?
E1 – Aham
(balança a cabeça)
Pesquisadora: Então, faz. Quantas bolachas você
vai ter que desenhar? São bolachas ou são pacotes?
E1 – Para, faz a leitura silenciosa,
solta o lápis, rola para cá e para lá e diz: pacotes!
Pesquisadora: Muito bem! Então faz, eu quero ver!
E1 – Quantos?
Pesquisadora: Então, você leu direitinho o que
você vai ter que fazer?
E1 – Faz a leitura novamente em voz alta.
Vou desenhar 2.
Pesquisadora: Tá.
E1 – Inicia a representação pictórica, ao
concluir olha para a pesquisadora, mexe no cabelo, como se dissesse terminei.
Pesquisadora: O que você fez?
E1 – Eu fiz ela aqui comendo bolacha!
Pesquisadora: Quantos pacotes você desenhou?
E1 – 3
Pesquisadora: Porque 3?
E1 – Dá um sorriso, põe o dedinho na boca
como se estivesse afirmando errei, e diz: porque eu esqueci que era 2.
Pesquisadora: Ahhh, você
tem borracha, você pode apagar.
E1 – Apaga o pacote que desenhou a mais.
Pesquisadora: Muito bem, ela fala o quê? Que numa
promoção 2 pacotes custam R$5,00, certo? E ele quer saber quanto custam 8
desses pacotes, se 2 custam R$ 5,00? Quanto custam 8? Você sabe descobrir?
E1 – Balança a cabeça, afirmando não e
entorta a boquinha do lado decepcionada.
Pesquisadora: Não sabe???
E1 – Continua balançando a cabeça e
mexendo incessantemente no lápis.
Pesquisadora:
Nem desenhando?
Não? Nem imagina? (E1 permanece o tempo todo balançando a cabeça afirmando
que não e balançando o corpo e remexendo o lápis). Muito bem, então, vamos
pensar, 2 (E1 sinaliza com os dedinhos) é igual a 5 (E1 sinaliza com os
dedinhos) né, e 8? Como nós conseguiríamos contar?
E1 – Mexe no cabelo com o lápis
incessantemente e se balança tentando encontrar uma resposta.
Pesquisadora:
Ele está
contando de quanto em quanto aí?
E1 – 2, 5 e 8.
Pesquisadora:
Mas os pacotes
de bolachas estão sendo contadas de 2 em 2, não é isso?
E1 – 4, Balança a cabeça confirmando, mas fica com o olhar vazio olhando
para o nada.
Pesquisadora:
Então pensa,
seriam 2, 4, 6, 8
E1 – 4
Pesquisadora:
Quanto daria
todas essas bolachas?
E1 – 4, fica olhando para a pesquisadora,
remexendo no cabelo com o lápis, esboçando muitas dúvidas.
Pesquisadora:
Percebo medo e
insegurança, nesse momento pergunto: Você não quer fazer?
E1 – Balança a cabeça afirmando não.
Pesquisadora:
Não quer
fazer?
E1 – Balança novamente a cabeça afirmando
não.
Pesquisadora:
Tá bom então,
vamos tentar fazer outro.
E1 – Esboça um sorriso de alívio.
Pesquisadora:
Pode dar
tchau!!!
E1 – Acena dando tchau com um sorriso
aliviado.
|
Ressaltamos que não foi
uma tarefa fácil, pois trazer para o documento detalhes de um vídeo requer
destreza e habilidade em saber ouvir, observar e acima de tudo não se envolver
emocionalmente na análise.
7. Resultados
Apresentamos os resultados da tabela 1 com os dados quantitativos do 1º ao 2º ano dos problemas aplicados envolvendo a categoria de isomorfismo de medidas, segundo Vergnaud (2009), utilizando as duas subcategorias indicadas no embasamento teórico do nosso trabalho, proporcionalidade.
A tabela sintetiza o ano de escolaridade, a quantidade de acertos, e os raciocínios explicitados pelas crianças (raciocínio aditivo, raciocínio multiplicativo e representação pictórica).
Tabela 1
Problemas de
Isomorfismo de medidas - Ciclo de Alfabetização
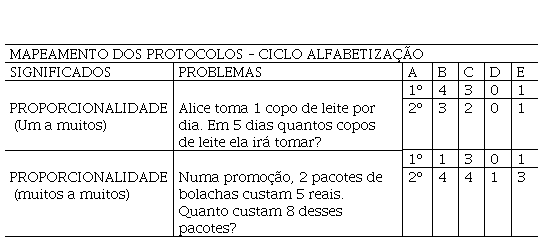Fonte: Elaboração da pesquisadora.
|
MAPEAMENTO
DOS PROTOCOLOS – CICLO ALFABETIZAÇÃO
|
|
SIGNIFICADOS
|
PROBLEMAS
|
A
|
B
|
C
|
D
|
E
|
| |
1º
|
4
|
3
|
0
|
1
|
|
PROPORCIONALIDADE
(Um a muitos)
|
Alice toma 1 copo de leite por dia. Em 5 dias
quantos copos de leite ela irá tomar?
|
2º
|
3
|
2
|
0
|
1
|
| |
1º
|
1
|
3
|
0
|
1
|
|
PROPORCIONALIDADE
(muitos a muitos)
|
Numa promoção, 2 pacotes de bolachas
custam 5 reais. Quanto custam 8 desses pacotes?
|
2º
|
4
|
4
|
1
|
3
|
Legenda: A(Ano de escolaridade); B(Acertos); C(Raciocinio aditivo); D(Raciocinio multiplicativo); E(Representação pictórica).
Protocolos/ ciclo alfabetização (1º e 2º ano):
Figura 3
Protocolo 1/ parte A – Proporcionalidade - Um
a muitos – 1º ano
Fonte: Elaboração
da pesquisadora
As análises dos dados dos alunos do primeiro ano na tabela mostram têm quatro resoluções as quais estão demonstradas na figura 3 e um aluno faltante. Todas as crianças acertaram a resolução do problema 1 envolvendo proporcionalidade (um a muitos). É predominante o uso do raciocínio aditivo. Três crianças usaram o raciocínio aditivo e uma delas apenas a representação pictórica. Há outra criança que usou o raciocínio aditivo e parece precisar da representação pictórica para conseguir resolver adequadamente.
Ao nos debruçarmos nas resoluções das crianças do primeiro ano envolvendo o significado de proporcionalidade (um a muitos), as alunas, em sua maioria, não apresentaram dificuldades de interpretação do texto do problema para a resolução. No entanto nenhuma delas usou o raciocínio multiplicativo. Como o problema relaciona uma quantidade a muitas, facilita a contagem por unidade. Essa ação segundo Treffers (1987) não pode ser considerada como uma ação da multiplicação, mas trata-se de uma estratégia ou “esquematização progressiva”, que permeia por diversos estágios do desenvolvimento da multiplicação para a aplicação da mesma.
Figura 4
Protocolo 1 /parte B – Proporcionalidade -
Muitos a muitos – 1º ano
Elaboração
da pesquisadora
Na análise dos dados referentes à relação “muitos a muitos” temos 4 resoluções, sendo 1 aluno faltante, os dados detalhados em relação acertos, erros, faltas, e tipos de resoluções realizadas pelas crianças.
A proporcionalidade envolvendo a ideia de muitos a muitos para as alunas E1 e E3, não estava clara, mesmo utilizando a contagem por unidade não conseguiram estabelecer uma resolução que pudesse chegar ao esperado. O vídeo revela que faltam elementos matemáticos para que as alunas compreendam o sentido da relação que deveria ser usada.
A aluna E4, lança mão do desenho para realizar o cálculo por contagem, logo após passa para o cálculo formal, utilizando a estrutura aditiva. Em sua verbalização percebemos os conceitos de proporcionalidade muito claros para a aluna, quando diz que se 2 pacotes são iguais a 5, precisava agrupar os demais em dois em dois até chegar em oito pacotes e para cada dois pacotes estabeleceu 5 e realizou a adição chegando ao resultado.
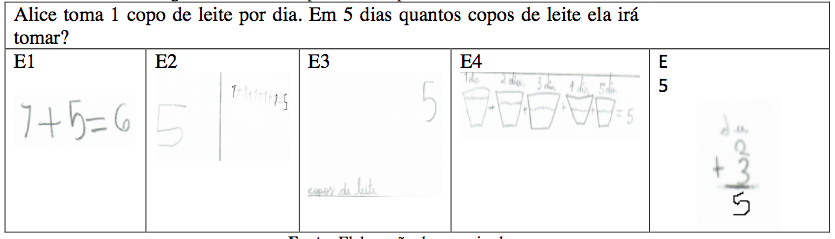Figura 5
Protocolo 1/ parte A – Proporcionalidade -
Um a muitos – 2º ano
Elaboração
da pesquisadora
No segundo ano, nesse mesmo problema, a situação não evolui. Temos 4 resoluções corretas de crianças do 2º ano e a predominância do raciocínio aditivo é evidente, temos 3 crianças usando o raciocínio aditivo corretamente e uma delas usando o raciocínio pictórico.
Porém, destacamos a resolução da aluna E3, a qual faz o uso do cálculo mental, na vídeo-filmagem conseguimos detectar que a ideia da proporcionalidade é clara para a aluna. No entanto, explica sua resolução por repetição, mas não é explicito se fez por parcelas iguais, pois em sua fala subentende-se que é uma repetição multiplicativa, pois mostra 5 dedinhos sem fazer contagem, achando desnecessário fazer a conta por ser muito fácil e rápido para se encontrar o resultado.
Entendemos nesse momento que a aluna está no processo de desenvolvimento do pensamento multiplicativo, assim como, Nunes e Bryant (1997) explicam, afirmando que a correspondência de um-para-muitos, é a base para um novo conceito matemático contrastando com a situação aditiva.
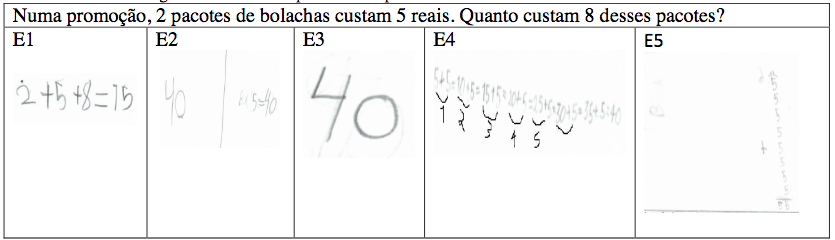Figura 6
Protocolo 1/ parte B – Proporcionalidade -
Muitos a muitos – 2º ano
Elaboração
da pesquisadora
As análises do 2º ano evidenciam que as resoluções das crianças ao tange a ideia de proporcionalidade “muitos a muitos” relativa às operações de multiplicação e divisão, foram desenvolvidas por agrupamentos, pelo significado da ideia aditiva de parcelas iguais, o desenvolvimento das ideias por meio da linguagem pictórica e pela ideia multiplicativa, assim como revelam os dados da tabela 1.
Destacamos o pensamento multiplicativo desenvolvido pela aluna E3 no problema 1/parte A fazendo o uso do cálculo mental. Segundo Nunes e Bryant (1997) explicam, afirmando que a correspondência de um-para-muitos, é a base para um novo conceito matemático contrastando com a situação aditiva.
Dessa forma pudemos perceber esse processo na fala da aluna, quando explica como pensou no problema 1/ parte B, entende que se faz necessário multiplicar as quantidades de pacotes de bolachas pelo valor aplicado a dois pacotes de bolachas, no entanto, estabeleceu o valor para 1 pacote e não para 2 pacotes.
Queremos chamar a atenção para as resoluções em que os alunos acertaram a primeira parte, ou seja, conseguiram chegar ao resultado igual a 40, mas em suma as crianças não conseguiram compreender que esse resultado não se tratava do final da proporção a ser buscada. De acordo com Nunes e Bryant (1997), para que essa relação onde à proporção seja uma constante, o fator escalar deve ser aplicado a cada conjunto.
Portanto, diante das resoluções e falas transcritas dos vídeos, entendemos que as crianças compreenderam não se tratar de uma unidade, mas ao registrarem seus raciocínios matemáticos não perceberam a possibilidade de um fator escalar/divisão, onde o valor em reais estava atribuído a 2 pacotes de bolachas, devendo continuar com outra operação para encontrarem o valor em reais para 8 pacotes.
Mediante a essas revelações se confirma a afirmação de Vergnaud (2009), que a correspondência muitos a muitos, nessa fase de escolaridade é mais complicada para ser compreendida pelas crianças, por se tratar de uma dupla proporcionalidade.
8. Considerações finais
Com a categorização e análises dos protocolos e dos vídeos, foi possível reconhecer e classificar o desenvolvimento do pensamento matemático dos estudantes envolvendo os problemas envolvendo as estruturas multiplicativas aplicadas a eles.
Vimos à importância do contexto aplicado aos problemas propostos aos estudantes, pois se tornou um facilitador na compreensão e elaboração dos procedimentos matemáticos, os quais deveriam ser aplicados nas resoluções dos problemas e no estabelecimento de novas estratégias.
Nossa pesquisa detectou que mesmo as crianças sem saber as tabuadas ou algoritmos da multiplicação conseguem resolver os problemas do Campo Multiplicativo, seja por raciocínio pictórico, estratégias pessoais, raciocínio aditivo ou multiplicativo, desmistificando os princípios de que a criança precisa ser um leitor fluente ou estar alfabetizado.
Conclui-se que alguns alunos estão no processo de desenvolvimento do pensamento multiplicativo, porém a ideia de proporcionalidade envolvendo a correspondência muitos a muitos, está em construção, pois, alguns lançam mão de vários caminhos para conseguir manter a proporção adequada, mas acaba por resolver o problema aditivamente.
De acordo como nosso aporte teórico, nesse momento de alfabetização a criança está passando pelo processo de construção de novas estratégias para explorar situações matemáticas e assim construí-las seja por manipulação, estimativa ou cálculo.
Todos os detalhes dos resultados estão em construção devido a tese estar em andamento.
