Introdução
A sala de aula de Matemática na Educação Básica nem sempre tem sido um espaço possível de desenvolvimento e de aprendizagem de modos matemáticos de pensamento. Isso, pois os estudantes passam grande parte do tempo realizando tarefas e atividades matematicamente escolarizadas que, muitas vezes, pouco fazem sentido em suas práticas não escolarizadas. O objetivo deste texto é discutir os processos de ensino e de aprendizagem em matemática escolar, buscando estabelecer situações didáticas em que se possa propor um fazer matemático “com sentido”. Nessa perspectiva, o texto tece considerações sobre a sala de aula como um ambiente social de interações, buscando atribuir sentido à Matemática, em atividades com tarefas envolvendo jogos e resolução de problemas, de forma a utilizar o pensamento probabilístico nas práticas matemáticas escolares.
A literatura sobre os processos de aprendizagem matemática destaca a importância de se fomentarem, na Educação Básica, situações em que os jogos e os desafios sejam vivenciados nas aulas de Matemática, em uma perspectiva de resolução de problemas, para possibilitar que as crianças desenvolvam estratégias, antecipem, experimentem, analisem jogadas e resolvam problemas. Em muitas dessas estratégias e análises, a Matemática está presente, contribuindo para a resolução de problemas no jogo (GRANDO, 1995, 2000, 2004; LUVISON; GRANDO, 2018).
Dessa forma, neste texto, discute-se o movimento de ideias relacionadas à metodologia de resolução de problemas, indicando as perspectivas de um ensino de Matemática para resolver problemas, pela resolução de problemas, de forma a dar sentido a essa tarefa. A partir dessa discussão sobre tal metodologia, buscamos compreender uma prática pedagógica problematizadora, desenvolvida com estudantes de um 7.º ano do Ensino Fundamental, ao explorar situações que envolvem o pensamento e a linguagem probabilísticos. Os dados apresentados fazem parte de pesquisa de Mestrado de Santos (2010). No primeiro momento, as tarefas foram realizadas com 28 estudantes do 7.º ano de uma escola pública no interior do estado de São Paulo. A professora pesquisadora, segunda autora desse texto, desenvolveu uma sequência de 18 tarefas abordando o desenvolvimento do pensamento e da linguagem probabilísticos dos estudantes. Para tanto, a sequência de tarefas contemplou as diferentes concepções de probabilidade: subjetivista, frequentista, clássica e axiomática (SANTOS, 2010).
Depois da resolução desse coletivo de tarefas pelos estudantes, quatro deles se dispuseram a participar de um segundo momento da pesquisa, a fim de que se identificasse “o que ficou” do conhecimento sobre probabilidade desenvolvido em aula. Foram realizadas sete tarefas consideradas resíduos (HIEBERT et al., 1997) e, em seguida, entrevistas individuais com os estudantes sobre a resolução das tarefas.
Para este artigo trazemos um recorte de duas delas: uma no primeiro e outra no segundo momento, envolvendo o jogo. A escolha desse recurso de ensino se dá porque a teoria das probabilidades, historicamente, é construída a fim de explicar, compreender e atribuir sentido ao jogo. Assim, praticamos uma matemática que é produzida para dar sentido aos jogos “Corrida de cavalos” e “A travessia do rio”.
Movimento de ideias relacionadas à metodologia de
resolução de problemas
O movimento de ideias relacionadas à metodologia de resolução de problemas é impulsionado por uma primeira perspectiva, que vem ao encontro da necessidade de ensinar os estudantes a resolver problemas. As primeiras manifestações dessa perspectiva estão sistematizadas por George Pólya (1995, prefácio, tradução nossa), em seu clássico livro A arte de resolver problemas (tradução de How to solve it?), com a promessa de ser “um sistema de pensamento que pode ajudar você a resolver qualquer problema”. Ali Pólya (1995) descreve uma porção de heurísticas de raciocínio que considerava fundamentais para que os estudantes saíssem da condição de resolvedores de exercícios para resolvedores de problemas. Esse, sem dúvida, é um livro clássico na pesquisa e na prática de resolução de problemas em Matemática. O grande objetivo do autor era tornar os estudantes mais competentes nessa tarefa, o que o levou a propor uma Matemática para resolver os problemas. Pólya (1995) determinou “passos” para a resolução de problemas: compreensão do problema, elaboração de um plano, execução do plano e avaliação (retrospecto).
Durante muitos anos e até hoje, muitos professores utilizam essas orientações e as heurísticas de Pólya (1995) para ensinar os estudantes a solucionar problemas. É importante pensar o papel da Matemática nesse processo. De certa forma, o problema é proposto para que certa Matemática seja utilizada, com o intuito de tornar os estudantes bons revolvedores de problemas. Embora essa perspectiva já esteja, sem dúvida, superada do ponto de vista da pesquisa em Educação Matemática (ENGLISH; LESH; FENNEWALD, 2008), cursos de licenciatura e bacharelado em Matemática ainda reproduzem tais práticas em disciplinas como Resolução/Solução de Problemas. Entende-se a importância de encontrar caminhos para os estudantes aprenderem a resolver problemas com as orientações de Pólya (1995) e reproduzi-las como práticas escolares na Educação Básica. Em geral, os problemas escolhidos para essa exploração são oriundos de Olimpíadas de Matemática ou de avaliações externas. Há que se considerar que essa perspectiva, embora avance no sentido de pensar em estratégias e heurísticas de resolução do problema, ainda está vinculada a um paradigma do exercício que, segundo Skovsmose (2000), representa o ensino tradicional da Matemática: preso a fórmulas, regras, manipulação simbólica e repetição.
Uma outra perspectiva de resolução de problemas foi marcada, a partir da década de 1980, por um movimento disparado pelo Conselho Nacional de Professores de Matemática (NCTM) norte-americano, quando publicou um documento denominado Uma agenda para a ação (An agenda for action), que propunha uma série de recomendações ao ensino de Matemática, apresentando como primeira: “O National Council of Teachers of Mathematics recomenda que: 1. A resolução de problemas seja o foco (focus) da Matemática escolar nos anos 80” (NCTM, 1980, p. 1, tradução nossa).
De certa forma, esse documento coloca a metodologia de resolução de problemas como o foco central do ensino de Matemática, o que influenciou, posteriormente, os currículos escolares em grande parte dos países ocidentais da Europa, da América Latina, além dos EUA. A proposta era de que os problemas provocassem a necessidade de um conteúdo, de conceitos e habilidades matemáticas. Dessa forma, podemos caracterizar essa perspectiva como um ensino de matemática pela resolução de problemas. As alterações nos currículos implicaram diretamente nas alterações dos manuais e dos livros didáticos nas escolas. Assim, é comum observarmos, nos livros didáticos baseados nos Parâmetros Curriculares Nacionais – PCN (BRASIL, 1995) e, atualmente, na Base Nacional Comum Curricular para o Ensino Fundamental (BRASIL, 2017), propostas de problemas aos estudantes, incentivando-os a resolvê-los por meio de estratégias pessoais, a fazer pesquisas e observações. Em seguida, propõe-se uma solução possível, utilizando estratégias, recursos e procedimentos de resolução, como observamos no livro (Figura 1):
Muitas pesquisas e práticas desenvolvidas nos últimos 30 anos estão baseadas nessa perspectiva, assim como os trabalhos envolvendo investigações matemáticas, jogos, resolução de problemas, modelagem matemática etc. Os problemas a serem resolvidos são de naturezas distintas, podendo ser internos à própria matemática (explorações, investigações), situações reais (modelagem), situações de jogos e lúdicas, brincadeiras, etc. O entendimento sobre essa perspectiva foi bastante variado nas práticas escolares. Assim, muitas vezes, os problemas se mostravam pouco “abertos” ou, mesmo, com poucas possibilidades de produção de uma matemática com sentido para a resolução do problema.
No campo da pesquisa, os trabalhos desenvolvidos pela Profa. Dra. Lourdes de la Rosa Onuchic, por seus orientandos e participantes do grupo de pesquisa destacam essa perspectiva, ao trabalhar com a Metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas. Onuchic (2008, p. 8) assim conceitua:
A opção de utilizar a palavra composta Ensino-Aprendizagem-Avaliação tem o objetivo de expressar uma concepção em que ensino e aprendizagem devem ocorrer simultaneamente durante a construção do conhecimento, tendo o professor como guia e os alunos como co-construtores desse conhecimento. Além disso, essa metodologia integra uma concepção mais atual sobre avaliação. Ela, a avaliação, é construída durante a resolução do problema, integrando-se ao ensino com vistas a acompanhar o crescimento dos alunos, aumentando a aprendizagem e reorientando as práticas de sala de aula, quando necessário.
Para a autora, o Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas “reflete uma tendência de reação a caracterizações passadas como um conjunto de fatos, domínio de procedimentos algorítmicos ou um conhecimento a ser obtido por rotina ou por exercício mental” (ONUCHIC, 1999, p.203). O problema é ponto de partida, e a aprendizagem da matemática acontece por meio da sua resolução. Na prática escolar, a dimensão colaborativa é ressaltada como um espaço em que professores e estudantes, juntos, desenvolvem um trabalho em que ambos aprendem. Essa perspectiva propicia uma concepção mais ampla do processo de ensino e de aprendizagem matemática, em que a avaliação é compreendida como um aspecto-chave no processo de resolução.
Neste texto, buscamos pensar em uma terceira perspectiva de resolução de problemas, que vem impulsionada pelo movimento norte-americano de buscar uma aprendizagem “com sentido” nos diferentes campos de conhecimento. É em trabalhos como revela o texto denominado Making Sense: teaching and learning mathematics with understanding, dos pesquisadores Hiebert et al. (1997), que encontramos essa perspectiva. Ali a Matemática é vista como dando sentido à resolução dos problemas. Ou seja, é possível a resolução de problemas por diferentes estratégias e procedimentos, e a Matemática é um caminho possível à resolução. Assim, a Matemática faz sentido na resolução do problema. O objetivo não é restringir a aprendizagem a conceitos somente “aplicáveis”, mas garantir que o conhecimento matemático produzido tenha, para os estudantes, uma justificação, uma aplicação, uma construção significativa e seja compartilhado em uma comunidade de aprendizagem – a sala de aula de Matemática.
A proposta do fazendo matemática com sentido acontece em um ambiente de problematização em que são considerados os seguintes aspectos: a natureza da tarefa proposta, o papel do professor, os recursos didáticos, uma cultura social de sala de aula de Matemática e a acessibilidade da Matemática para todos os estudantes. Quanto à natureza da tarefa proposta, há que se considerar a variabilidade na proposição das tarefas. Que elas possam ser abertas também no sentido de mobilizar conhecimentos matemáticos dos estudantes e que sejam tarefas coerentes, com sentido. Por exemplo, um livro didático apresentava em uma de suas propostas a situação de que uma pessoa arremessou uma moeda 500 vezes e perguntava quantas caras e quantas coroas provavelmente sairiam. O objetivo era trabalhar com a ideia de equiprobabilidade. A tarefa sugerida poderia ser repensada e alterada. Propor aos estudantes que fizessem o experimento e que cada um deles arremessasse a moeda 10 vezes. E, em seguida, somassem os resultados da turma. Provavelmente teríamos o resultado de 300, 400 arremessos, e a análise poderia ser realizada diante desse conjunto de lançamentos. Esse é apenas um exemplo de como podemos pensar nos cuidados que, algumas vezes, necessitamos ter, quando buscamos propor uma tarefa em que a matemática faça sentido na resolução.
Quanto ao papel do professor, os autores sugerem uma postura problematizadora, investigadora, nas aulas de Matemática: que o professor possa ser o mediador das interações em sala de aula, colocando novos problemas, ajudando os estudantes a refletir e analisar possibilidades. Que os auxilie a organizar e registrar ideias; observar regularidades; levantar hipóteses; experimentar; antecipar resultados; fazer estimativas; produzir sínteses e construir conceitos. Enfim, que o professor possa ser uma referência de letramento matemático para os estudantes.
Para a resolução dos problemas podem ser propostos variados recursos, cuja escolha tem a ver com a natureza da tarefa. Assim, podem ser oferecidos recursos tecnológicos, livros, jogos, materiais manipulativos, instrumentos de medida e recursos corporais (cenas, teatros, imagens), dentre outros. Há que considerar os cuidados na proposição dos recursos, para que eles possibilitem atribuir sentidos à Matemática na resolução dos problemas e para que eles não representem empecilhos, nem gerem uma conceitualização matematicamente inadequada ou errônea.
Os autores defendem uma cultura de aula de matemática problematizadora, em que a sala de aula seja um ambiente social de interações em matemática escolar e de compartilhamento de experiências e ideias matemáticas na resolução de problemas. Uma sala de aula como essa oferece possibilidades de: discussão matemática, construção de uma matemática oralizada/escrita, produção colaborativa entre os atores do processo educacional, mobilização de conhecimentos, variabilidade de recursos de ensino, avaliação durante o processo e o desenvolvimento de projetos interdisciplinares. Até mesmo a forma de organização dos estudantes em torno da resolução de problemas necessita ser repensada. O trabalho em pequenos grupos, seguido de processos de socialização e compartilhamento de resoluções no coletivo, possibilita que os estudantes estejam envolvidos colaborativamente na resolução e na produção matemática.
Talvez um dos aspectos mais importantes tratados por Hiebert et al. (1997) seja a acessibilidade do conhecimento matemático a todos os estudantes, de forma que os problemas sejam escolhidos, as interações na sala de aula e as problematizações propostas pelo professor sejam capazes de criar nesse ambiente uma comunidade de investigação, para que todos participem e possam compreender o sentido da matemática para a resolução dos problemas. Não é necessário que todos os estudantes gostem de matemática, mas é importante que todos tenham acesso a um conhecimento matemático produzido historicamente e com significado nas práticas sociais. Esse é um direito do estudante, assim como é também seu direito não gostar de matemática, e isso deve ser respeitado.
É possível que aqueles que se interessam por um ambiente colaborativo de produção de conhecimento matemático construam formas diferenciadas de resolver problemas, que se sintam protagonistas de sua aprendizagem matemática e produtores de conhecimento. Essa perspectiva prevê um ensino de matemática voltado ao sucesso, e não ao fracasso. Os processos de resolução construídos significativamente em cada grupo representam importantes soluções a serem compartilhadas, validadas, discutidas. Eventualmente, encontrar um erro em uma solução de problema é um exercício mais interessante do que resolvê-lo corretamente. De acordo com Hiebert et al. (1997), em um ambiente de aprendizagem, tarefas que possibilitem a interação social em sala de aula são essenciais para a compreensão conceitual, mas esse contexto precisa deixar resíduos. Ou seja, os conceitos desenvolvidos precisam ser incorporados à prática dos estudantes na resolução de outros problemas também em contextos diferentes. Isso contribui para que o conhecimento não seja exclusivamente local, aplicável a uma situação particular, e que as estratégias e os conhecimentos mobilizados e construídos possam ser utilizados em outras situações, em outros contextos. Conforme apontam Lopes e Socha (2020, p. 17)
Percebemos que problematizar situações para aprendizagem matemática e estatística, por meio de uma ação docente que encoraje os alunos a pensar, questionar, levantar hipóteses, estabelecer conjecturas, debater suas ideias e estratégias, proporciona-lhes compreender conceitos e procedimentos construídos conjunta e colaborativamente.
É louvável que alguns estudantes busquem saber mais, conhecer mais, que se sintam desafiados por exames de avaliação, olimpíadas, etc. Entretanto, o nosso compromisso como educadores matemáticos é com uma aprendizagem matemática com sentido por todos os estudantes. E isso é uma questão política, cidadã, de pertencimento. Que os estudantes saibam matemática para tomar decisões, analisar situações matematicamente e que a matemática possa contribuir para não serem enganados e para que ajam conforme suas escolhas, matematicamente esclarecidos. Isso é uma atitude cidadã.
O aspecto da acessibilidade da Matemática aos estudantes também pode ser compreendido como as adaptações para que as tarefas sejam acessíveis aos estudantes com deficiências ou mesmo a construção de novas tarefas acessíveis a todos. Nas salas de aula de Matemática, principalmente na Educação Básica, há estudantes que apresentam diferentes especificidades. Apesar do suporte de especialistas na área, como o intérprete de Libras para o estudante surdo, ainda é um desafio ao professor de matemática lidar com as diferentes formas de ensinar matemática em contextos inclusivos. Quando pensamos no ensino e na aprendizagem matemática com sentido estamos também focados na acessibilidade da Matemática para todos os estudantes, independente de suas especificidades.
Acreditamos e defendemos que essas propostas relacionadas a uma aprendizagem matemática com sentido na resolução de problemas possam acontecer em sala de aula, para que os conceitos, os processos e a linguagem matemática, mobilizados e construídos para atender a resolução de um determinado problema ou conjunto de problemas, possam ser mobilizados em outras situações, possibilitando a produção de resíduos. Essa será nossa discussão na próxima seção.
Metodologia da pesquisa
Tínhamos como hipótese inicial nesta pesquisa que as estratégias utilizadas no cotidiano escolar não vêm promovendo o desenvolvimento do pensamento probabilístico dos estudantes e que uma metodologia diferenciada, com uma prática problematizadora, voltada aos cenários de investigação (SKOVSMOSE, 2000), e a mediação do professor poderiam mobilizar tal pensamento, uma vez que os estudantes atuariam no seu processo de aprendizagem, em um contexto de resolução de problemas organizado de forma que a comunicação de ideias fosse estabelecida.
Para tanto, desenhamos esta pesquisa com o objetivo de investigar os processos de ensino e de aprendizagem em matemática escolar, mais especificamente, o pensamento probabilístico, buscando estabelecer um fazer matemático “com sentido”. Nessa perspectiva, tecemos considerações sobre um ambiente social de interações, buscando atribuir sentido à Matemática, em tarefas na perspectiva da problematização. Investigamos os estudantes de uma sala de aula de 7º ano do Ensino Fundamental de uma escola pública em uma cidade no interior do estado de São Paulo. A pesquisa foi desenvolvida no âmbito de um mestrado acadêmico (SANTOS, 2010) e foi aprovada pelo comitê de ética em pesquisa da Universidade de origem. A segunda autora desse texto era a professora regular da turma e assumiu o trabalho de produção de dados. Os dados foram registrados por meio de áudio gravações dos momentos de discussão nos grupos e dos momentos de socialização de estratégias de jogo, produção escrita dos estudantes e diário de campo da pesquisadora.
Todas as atividades foram realizadas em sala de aula. Os estudantes foram divididos em grupos de quatro pessoas (cinco grupos). Foram realizadas, incialmente, tarefas com o jogo “A travessia do rio” com resolução de problemas envolvendo a análise probabilística a partir do jogo e, posteriormente foram realizadas tarefas com um jogo semelhante denominado “corrida de cavalos” a fim de identificar os “resíduos” (Hiebert et al, 1997) das aprendizagens probabilísticas dos estudantes. Para esse segundo jogo foram realizadas entrevistas individuais com os estudantes.
A análise dos dados foi qualitativa por meio da descrição e interpretação dos modos de pensar probabilísticos dos estudantes em situações de jogos.
Problematizações em aulas de matemática
Em uma perspectiva de cultura de aula de matemática problematizadora, o jogo pode ser utilizado como um recurso de ensino. No caso da situação escolar analisada a seguir, a professora pesquisadora explora as ideias relacionadas à probabilidade por meio do jogo “A travessia do rio”, que em seu contexto envolve análise de possibilidades, medida de chance e discussões sobre aleatoriedade.
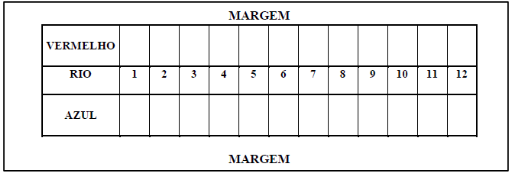
O jogo consiste na disposição e na “travessia” de peças de cores diferentes (Figura 2)
No início do jogo cada jogador coloca as suas 12 peças (apostando nos números) numa das margens do rio, podendo pôr mais do que uma na mesma casa e deixar outras vazias. Alternadamente, lançam dois dados e calculam a soma. Se a soma corresponder a uma casa onde estejam peças suas na respectiva margem, uma delas passa para o outro lado do rio. Ganha quem conseguir passar primeiro todas as peças para o outro lado.
Com o intuito de envolver os estudantes em um movimento de construção de sentidos, o jogo foi realizado com estudantes do 7.º ano do Ensino Fundamental em uma dinâmica organizada em quatro etapas, nas quais a disposição das fichas era alterada. Na primeira etapa, todas as fichas foram dispostas de forma injusta: a equipe azul tinha suas fichas colocadas nos números com maior probabilidade de sair, ao somar dois dados; e a equipe vermelha possuía fichas nos números que ou tinham menores probabilidades de sair ou tornavam isso impossível, como o número 1, que não pode resultar da soma entre dois dados. O objetivo era provocar a curiosidade do aluno quanto à (des) vantagem em relação à outra equipe. Na segunda etapa, também prevalecia o critério de as fichas de uma equipe estarem dispostas nos números que tinham mais probabilidade de sair, ao passo que, na outra equipe, a situação era contrária. O que mudava é que as equipes tinham a liberdade de escolher o número para colocar 3 fichas, e não havia fichas dispostas no número 1. A terceira etapa era semelhante à segunda, mas nessa fase eles escolhiam a posição de 6 fichas. Na última etapa, os estudantes escolhiam o número em que colocariam as 12 fichas, porém precisavam anotar os números sorteados e as somas obtidas.
Os integrantes dos grupos formaram duplas para jogar entre si, e, em seguida, ao final de cada etapa, foram propostas discussões sobre o jogo, com o objetivo de que os estudantes percebessem regularidades, ou não, durante as jogadas e assim mobilizassem conhecimentos matemáticos.
De imediato, nenhuma equipe descobriu que não era possível obter o número 1, somando dois dados na primeira etapa; no entanto, à medida que foram jogando, foram descobrindo. Alguns ficavam furiosos. Assim que percebiam, chamavam a professora-pesquisadora para falar sobre a descoberta, e ela perguntava: “Quem ganhou o jogo?”. Muitos diziam que não era justo; não se referiam ao jogo todo, mas à ficha que estava no número um. Alguns grupos jogavam até o final, sem perceber que o resultado do jogo já estava definido. Essa discussão foi estendida à classe depois que todos os grupos concluíram a jogada. A professora pesquisadora pedia que registrassem a cor da equipe vencedora.
Ao receberem o tabuleiro da segunda etapa, os estudantes logo verificavam se não havia fichas no número 1, antes de iniciar a jogada. Isso se repetiu na terceira etapa. Apesar de dizerem, durante o jogo, que algumas somas saíam mais, alegavam que a sorte determinava os resultados. E comentavam que o número que estavam esperando saía para o adversário. Ao receber a última cartela, ficaram felizes, pois escolheriam a posição de todas as fichas. O jogo transcorreu em duas aulas, mas não no mesmo dia.
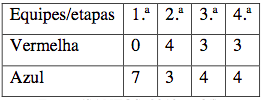
Na socialização final, a professora colocou
na lousa o seguinte quadro (Figura 3), com o resultado das equipes vencedoras
em cada etapa, do qual surgiram o diálogo e as considerações acerca da tarefa:
Prof.ª: - Na primeira etapa, somente a equipe azul ganhou. Por que será?
Flávio: - Foi injusto, não valeu!
Prof.ª: - Por quê?
Vinícius: - Não tinha como sair 1 com dois dados! Só com um dado.
Breno: - Quebrei a cabeça.
Prof.ª: - Por quê?
Breno: - Fiquei jogando e não saía.
Prof.ª: - E a segunda etapa?
Flávio: - Estava legal, não tinha ficha no 1.
Prof.ª: - O jogo iniciou com a cartela cheia, depois foi aumentando a possibilidade de escolha das fichas, certo? Eu percebi que na última etapa vocês ficaram felizes ao receberem a cartela vazia, pois poderiam completá-la colocando suas fichas nos números que desejassem. Por quê?
Flávio: - A gente poderia colocar nos números que saía mais, de seis para cima.
Carla: - Colocar em números maiores.
Prof.ª: - Espera aí! O Flávio disse que poderia colocar nos números que saíam mais, de seis para cima, e a Carla, nos números maiores. Por quê?
Carla: - Porque saíam mais.
Flávio: - Não, o 12 não saía.
Henrique: - No nosso saía toda hora.
Prof.ª: - Eu pedi para vocês anotarem a quantidade de vezes que caiu cada soma. Vamos ver. Até que número eu devo colocar na tabela?
Flávio: - Até o doze.
Os grupos foram falando a quantidade de vezes que saiu cada soma, os estudantes foram somando esses valores, e a professora-pesquisadora anotou os resultados no quadro na lousa (Figura 4), o que provocou discussão:
Nelson: - Olha só, começou menor, foi aumentando e depois voltou a diminuir. Veja
as pontas. Começou do menor e foi até o 70, depois começou a diminuir.
Prof.ª: - Será que tem uma explicação?
Nelson: - É jogo, é sorte.
Prof.ª: - Vocês me falaram que os números maiores tinham mais chance de sair?
Breno: - Nada “a ver”, do número 10 para baixo sai mais.
Prof.ª: - Qual foi o número que mais saiu?
Classe: - O sete.
Prof.ª: - Mas vocês falaram que os maiores tinham mais chance?
Rodrigo: - Cai nos números mais altos.
Prof.ª: - Por quê?
Flávio: - Porque para sair o 2 tem que ser 1 e 1.
Maicon: - Tem dois dados para somar.
Prof.ª: - Mas também tem números pequenos no dado.
Nelson: - Só se fosse com um só.
Prof.ª: - Mas tinha números pequenos nos dois dados.
Carla: - Mas era difícil de sair.
Nelson: - Como que ia dar o 1?
Carla: - Não tem como sair o 1!
Prof.ª: - E o 2?
Classe: - O 1 e o 1.
Henrique: - Só que é muito raro!
Prof.ª: - E o 3?
Flávio: - 2 e 1, só.
Prof.ª: - E o 1 e o 2?
Alunos: - É a mesma coisa!
Flávio: - Poderia ser dois dados.
Nelson: - Poderia no branco cair 1 e no vermelho cair 2 e depois no branco cair 2 e no vermelho cair 1.
Prof.ª: - E o 4?
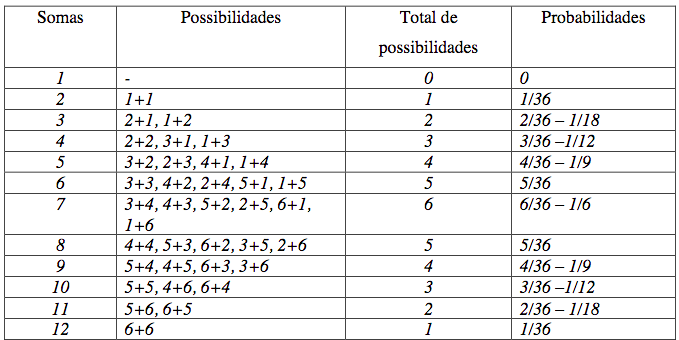
Classe: - 2+2, 3+1, 1+3.
Depois disso, os estudantes foram falando as possibilidades, e a professora foi anotando na lousa, da seguinte forma:
Quando a socialização estava por encerrar, surgiu uma nova observação:
Nelson: - Olha só, diminui. Do número 2 ao 7 aumenta e depois vai diminuindo, igual ao outro.
Prof.ª: - Por que será que isso acontece?
Breno: - É mesmo!
Prof.ª: - Mas por que será que isso aconteceu, tanto nos números que saíram nas jogadas de vocês, como nas possibilidades?
Aline: - Porque são dois dados.
Prof.ª: - Vamos analisar o 7, nas nossas jogadas foi o que mais caiu!
Carla: - Ele é porque ele está no meio dos números de lá e daqui.
Maicon: - É que tem mais combinações para dar 7.
Prof.ª: - Quando um número tem mais combinações, ele tem mais chance?
Classe: - Sim.
Prof.ª: - Eu poderia usar outra palavra para expressar isso?
Nelson: - Que ele tem mais possibilidades.
Prof.ª: - E tem como eu saber qual a probabilidade de sair o número 7?
Marco: - Tem. Doze é o inteiro, então ele tem metade [pensou nas seis possibilidades de cair o 7 e pensou no inteiro como as possíveis somas].
Prof.ª: - Por que 12 é o inteiro?
Nelson: - Porque 6 é a metade, então vai para o número maior.
Prof.ª: - Não entendi!
Nelson: - Tem 12, dividi ao meio, vai 6 para cada lado, não pode ser 14, né!
Prof.ª: - Marco, quando você diz inteiro, a que você se refere?
Marco: - Ao número máximo de possibilidades.
Prof.ª: - Qual o número máximo de possibilidades que temos?
Breno: - Doze.
Prof.ª: - Doze são os possíveis resultados, não o total de possibilidades.
Vinícius: - Só somando.
Prof.ª: - Vamos somar para ver.
Somaram juntos, depois a professora acrescentou uma linha no final da tabela e colocou o total de possibilidades.
Prof.ª: - Qual a probabilidade de sair o número 2?
Breno: - 1/36.
Prof.ª: - E o 3?
Classe: - 2/36.
A professora acrescentou outra coluna como a probabilidade, e os estudantes foram falando.
Prof.ª: - Pessoal! Qual é o número que tem maior probabilidade de sair?
Classe: - É o 7.
Prof.ª: - Será que existe uma relação com os números que obtivemos no nosso jogo?
Breno: - É a sorte.
Júlia: - Não é, senão daria diferente em algum número.
Carla: - São as combinações.
Prof.ª: - Por que será que ele não sai em todas as jogadas?
Maicon: - O 7 tem mais probabilidade de sair, mas isso não quer dizer que vai sair toda hora!
Bruno: - Boa!!!
A classe aplaudiu e a aula foi encerrada.
A discussão realizada sobre o jogo constituiu um momento importante na partilha de conhecimentos. Os estudantes colocaram em confronto suas estratégias, conjecturas e justificações. O papel desempenhado pela professora, tanto na organização da tarefa como no momento de discussão, foi fundamental para que os estudantes fossem mobilizados para a investigação; para que cada um refletisse sobre o trabalho realizado, não só por ele, mas por outros estudantes e, consequentemente, desenvolvesse o seu poder de argumentação, assim como sua capacidade de comunicar-se matematicamente.
Quanto às concepções de pensamento probabilístico envolvidas, acreditamos que a concepção subjetivista faça parte desse universo do jogo, em que a aleatoriedade, o risco e a esperança se entrelaçam. No entanto, as ideias surgidas na socialização quanto ao número que tem mais chance de se repetir possibilitaram a descoberta da simetria entre os resultados, o que pressupõe que o aluno tenha sido provocado pela regularidade observada, ou seja, por uma frequência. Em virtude disso, foi possível estimar formalmente a probabilidade de cada evento. Isso não significa que os estudantes tenham se apropriado desses conceitos, mas que buscaram um critério para suas concepções pessoais.
Acreditamos que essa percepção seja muito significativa na construção do pensamento probabilístico, pois partimos da ideia de que uma situação problemática pode ou não oferecer um problema a ser resolvido, e os problemas podem não ser os mesmos para todos os estudantes; portanto, o modelo de probabilidade que será empregado em cada situação precisa ser definido pelo aluno. Favorecer uma determinada concepção de tarefas não significa esperar que os estudantes a utilizem, mas que reflitam sobre ela ou sobre o contexto em que está inserida. Dessa forma, compreendemos essa busca de um critério como uma tentativa de adequação da hipótese à situação que está sendo vivenciada, o que poderá contribuir para o desenvolvimento do pensamento probabilístico e a atribuição de sentido à Matemática.
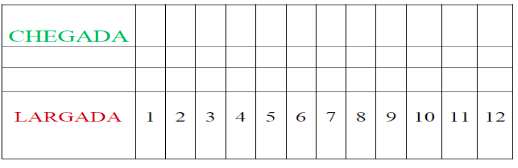
Em momento posterior, os estudantes foram convidados a realizar um jogo semelhante ao proposto, o “Corrida de cavalos”. O objetivo era analisar se havia resíduos das discussões coletivas na concepção individual dos estudantes. A ideia do resíduo, segundo Hiebert et al. (1997), diz respeito à identificação e à compreensão sobre o que ficou, para os estudantes, do conteúdo desenvolvido. Nesse caso, situações semelhantes são realizadas com eles, a fim de identificar os conhecimentos apropriados.
Na “Corrida de cavalos” (Figura 6), os estudantes jogaram individualmente e para isso recebiam três fichas, as quais deveriam apostar em cavalos. As apostas poderiam ser feitas em apenas um cavalo, dois ou três. O cavalo avança quando a soma dos números extraídos de dois dados lançados é igual ao número do cavalo. O avanço é marcado com um x no diagrama em frente ao número obtido. Vence o cavalo que primeiro se colocar na linha de chegada.
De uma maneira geral, as apostas dos estudantes e suas respectivas justificativas se assemelham às seguintes:
Humberto dividiu sua aposta em três cavalos, de números 7, 10 e 12, e fez as seguintes considerações:
Prof.ª: - Por que escolheu esses números?
Humberto: - O 7, pelos números que estão do lado dele. Acho que ele tem mais chance que o 6 e o 8. Ele [o número 7] poderia sair o 5 com 2 ou 6 com 1 ou 4 com 3. O 6 eu achava que não tinha tanta chance e o 8 também porque seriam 4 e 4, 6 e 2. O 10 é mais fácil: 5+5 e 6+4. O 12, porque eu poderia ter uma chance de acontecer de sair o 6 e 6.
Prof.ª: - Por que escolheu dividir sua aposta em três cavalos?
Humberto: - Para ter mais chance de ganhar.
Maicon também dividiu suas fichas em três cavalos, nos números 5, 6 e 7, e justificou da seguinte forma:
Maicon: - Eu aposto mil (uma ficha) em cada um.
Prof.ª: - Em quais?
Maicon: - No 5, 6 e 7.
Prof.ª: - Por que escolheu esses números?
Maicon: - Porque tinham mais possibilidades.
Prof.ª: - Por que dividiu sua aposta em três números?
Maicon: - Não sei, eu achei que os três poderiam ganhar.
Júlio, da mesma forma que os colegas descritos anteriormente, apostou em três cavalos, de números 6, 7 e 8. Suas explicações foram as seguintes:
Prof.ª: - Por que escolheu os números: 6, 7, 8?
Júlio: - Porque eu penso que o 7 e 8, eles têm mais possibilidades de soma.
Prof.ª: - E o 6?
Júlio: - Não tem muita.
Prof.ª: - Por que dividiu sua aposta em três cavalos?
Júlio: - Porque daí eu tinha mais chance.
Júlia, diferentemente de seus colegas, apostou em dois cavalos, ou seja, duas fichas no número 6 e uma no número 7. Seus comentários foram os seguintes:
Prof.ª: - Por que apostou nestes números?
Júlia: - No 6, porque eu gosto; e no 7, porque tinha mais possibilidades.
Prof.ª: - Por que não apostou em um só?
Júlia: Eu fiquei com medo de escolher um e o outro ganhar; como estava em dúvida com eles, apostei nos dois.
Prof.ª: - Por que apostou mais no número que gosta?
Júlia: - Por impulso.
Prof.ª: - Quanto você gastou com apostas?
Júlia: - Com ele, mil. [Estava se referindo ao cavalo vencedor]
Prof.ª: - Você acha que teve sorte neste jogo?
Júlia: - Sim.
Percebemos, nas explicações individuais dos estudantes, vestígios residuais das discussões coletivas realizadas anteriormente. Eles apresentam certa compreensão do modelo matemático para o tratamento da incerteza e de sua aplicação em situações de jogo. Entretanto, em muitas explicações os estudantes estiveram vinculados a uma concepção experimental de probabilidade. A frequência com que observaram os resultados anteriores influenciou na escolha das apostas na corrida de cavalos. Para além disso, ainda reconhecemos a presença da concepção subjetivista de probabilidade, quando Júlia justifica que apostou no 6 porque gosta do número. As análises matemáticas realizadas com as possibilidades e as chances nem sempre são apropriadas ou são consideradas como solução. O jogo envolve o risco, o que é possível em apostas sem muito sentido.
Considerações sobre a Resolução de Problemas com
sentido nas práticas de matemática escolar
Os estudantes puderam compreender, nos jogos realizados, que, mesmo com fatores que envolvem a aleatoriedade, como o lançamento dos dados, há um estudo possível matematicamente que “controla” possíveis resultados. As respostas dos estudantes, tanto na situação coletiva quanto nas entrevistas individuais, evidenciam que o movimento de pensamento probabilístico não é linear. Há oscilações entre as concepções subjetivistas, as frequentistas e a clássica. Todas elas fazem sentido no contexto do jogo. Nas situações de resíduo notamos uma apropriação, principalmente da linguagem probabilística. Os estudantes são capazes de expressar modos de pensar matematicamente, por meio de uma linguagem apropriada das situações vivenciadas anteriormente.
Durante a entrevista, nos diálogos entre os estudantes e a professora-pesquisadora, eles se mostravam confiantes, ao expressar ideias probabilísticas, e revelavam refletir e superar alguns equívocos apresentados. Essa postura conduz ao fazer matemático e apresenta uma cultura social em sala de aula que torna a Matemática acessível para todos os estudantes.
O jogo, como recurso de ensino utilizado pela professora pesquisadora, tanto nas situações de aprendizagem sobre probabilidade como no momento de avaliação (resíduo), possibilitou um contexto favorável à construção de conceito e de linguagem probabilísticos. Para resolver os problemas de jogo, analisando situações de jogo justo, injusto, chance, possibilidade e cálculo de probabilidades, os estudantes se apropriam de uma Matemática que estamos chamando neste artigo de Matemática com sentido.
Um trabalho escolar na perspectiva de resolução de problemas com sentido possibilita formar o cidadão para lidar com a incerteza, com as possibilidades, com a tomada de decisões e contribui para a sua emancipação. Defendemos a ideia de um letramento matemático que possibilite uma leitura também matemática de mundo, ou seja, que torne o estudante proficiente para analisar uma mesma situação-problema a partir de um ponto de vista afetivo, social, motor, científico, linguístico e, por que não dizer, matemático (LOPES; GRANDO; D’ AMBROSIO, 2017).