Introdução
A resolução de problemas tem sido uma área forte de investigação na Educação Matemática em Portugal desde os últimos trinta anos. Na década de noventa do século passado, importantes estudos foram produzidos, como sejam os de Pires (1992), Boavida (1993), Porfírio (1993), Oliveira (1993), Vale (1993), Fonseca (1995) e Graça (1995). Esses estudos privilegiaram o campo da comunicação matemática e abordaram outros aspetos tão distintos, como (a) os processos de resolução de problemas, (b) as representações pessoais dos professores, (c) a formulação de problemas, (d) as conceções e as práticas dos professores e (e) a avaliação em resolução de problemas.
Também nesse período temporal foram realizados estudos em que se associava a temática da resolução de problemas ao tema da metacognição, de onde destacamos os de Borralho (1990), Santos (1993) e Afonso (1995).
A relevância a dar ao tema da resolução de problemas e à comunicação matemática teve o seu culminar no Programa de Matemática do Ensino Básico, de 2007, de onde se podem ler os seguintes objetivos gerais:
Os alunos devem ser capazes de resolver problemas. Isto é, devem ser capazes de:
• compreender problemas em contextos matemáticos e não matemáticos e de os resolver utilizando estratégias apropriadas;
• apreciar a plausibilidade dos resultados obtidos e a adequação ao contexto das soluções a que chega;
• monitorizar o seu trabalho e reflectir sobre a adequação das suas estratégias, reconhecendo situações em que podem ser utilizadas estratégias diferentes;
• formular problemas.
A resolução de problemas é uma actividade privilegiada para os alunos consolidarem, ampliarem e aprofundarem o seu conhecimento matemático. Neste processo, os alunos devem compreender que um problema matemático, frequentemente, pode ser resolvido através de diferentes estratégias e dar atenção à análise retrospectiva da sua resolução e apreciação das soluções que obtêm (PONTE; SERRAZINA; GUIMARÃES; BREDA; GUIMARÃES, SOUSA; MENEZES; MARTINS, OLIVEIRA, 2007, p. 6).
Os alunos devem ser capazes de comunicar as suas ideias e interpretar as ideias dos outros. Isto é, devem ser capazes de:
• interpretar enunciados matemáticos formulados oralmente e por escrito;
• usar a linguagem matemática para expressar as ideias matemáticas com precisão; • descrever e explicar, oralmente e por escrito, as estratégias e procedimentos matemáticos que utilizam e os resultados a que chegam;
• argumentar e discutir as argumentações de outros;
• organizar e clarificar o seu pensamento matemático através da comunicação.
Os alunos devem ser capazes de, oralmente e por escrito, descrever a sua compreensão matemática, os procedimentos matemáticos que utilizam, e explicar a sua argumentação, o seu trabalho e o seu raciocínio, bem como interpretar e analisar a informação que lhes é transmitida por diversos meios. Estas capacidades desenvolvem-se comunicando por uma variedade de formas e reflectindo sobre processo de comunicação (PONTE; SERRAZINA; GUIMARÃES; BREDA; GUIMARÃES, SOUSA; MENEZES; MARTINS, OLIVEIRA, 2007, p. 5).
Passados seis anos, o atual programa de Matemática do Ensino Básico (2013) voltou a enfatizar explicitamente o tema da comunicação matemática e o da resolução de problemas:
Comunicação matemática – Oralmente, deve-se trabalhar com os alunos a capacidade de compreender os enunciados dos problemas matemáticos, identificando as questões que levantam, explicando-as de modo claro, conciso e coerente, discutindo, do mesmo modo, estratégias que conduzam à sua resolução. Os alunos devem ser incentivados a expor as suas ideias, a comentar as afirmações dos seus colegas e do professor e a colocar as suas dúvidas. Sendo igualmente a redação escrita parte integrante da atividade matemática, os alunos devem também ser incentivados a redigir convenientemente as suas respostas, explicando adequadamente o seu raciocínio e apresentando as suas conclusões de forma clara, escrevendo em português correto e evitando a utilização de símbolos matemáticos como abreviaturas estenográficas (BIVAR; GROSSO; OLIVEIRA; TOMÓTEO, 2013, p. 5).
Resolução de problemas – A resolução de problemas envolve, da parte dos alunos, a leitura e interpretação de enunciados, a mobilização de conhecimentos de factos, conceitos e relações, a seleção e aplicação adequada de regras e procedimentos, previamente estudados e treinados, a revisão, sempre que necessária, da estratégia preconizada e a interpretação dos resultados finais. Assim, a resolução de problemas não deve confundir-se com atividades vagas de exploração e de descoberta que, podendo constituir estratégias de motivação, não se revelam adequadas à concretização efetiva de uma finalidade tão exigente. Embora os alunos possam começar por apresentar estratégias de resolução mais informais, recorrendo a esquemas, diagramas, tabelas ou outras representações, devem ser incentivados a recorrer progressivamente a métodos mais sistemáticos e formalizados. Em particular, no 1.º ciclo, solicita-se explicitamente que o número de passos necessários à resolução dos problemas vá aumentando de ano para ano. É fundamental que os alunos não terminem este ciclo de ensino conseguindo responder corretamente apenas a questões de resposta imediata. Estudos nacionais e internacionais recentes, como o Trends in International Mathematics and Science Study (TIMSS), mostram que, em 2011, 60% dos alunos portugueses do 4.º ano não conseguem ultrapassar esse patamar (Intermediate International Benchmark) (BIVAR; GROSSO; OLIVEIRA; TOMÓTEO, 2013, p. 5).
Mais recentemente (2017) surgiu uma obra de referência da Associação de Professores de Matemática, numa tradução para Portugal dos Princípios para a Ação do NCTM sobre o que deve ser feito para se assegurar a todos o sucesso em Matemática. Um desses princípios é, precisamente, “propor tarefas que promovam o raciocínio e a resolução de problemas” (APM., p. 17).
Os problemas propostos
Os nove problemas que a seguir analisamos, da autoria dos autores deste artigo, podem ser associados aos seguintes blocos temáticos: Geometria e Medida, Números e Cálculo e em Lógica Matemática. O critério que presidiu à sua seleção foi, precisamente, o facto de possibilitarem mais do que uma solução, permitindo, assim, a troca de opiniões entre resolvedores e o desenvolver o conhecimento que o indivíduo tem sobre os seus próprios processos cognitivos, tomando consciência da sua existência (metacognição) no que respeita às estratégias de resolução a utilizar e à mobilização de conhecimentos que as mesmas exigem.
As várias resoluções que iremos apresentar são da autoria dos autores deste artigo e visam evidenciar a riqueza pedagógica que estes problemas podem suscitar ao serem utilizados em contexto de sala de aula ou em contexto da formação inicial ou contínua de professores de Matemática. As resoluções apresentadas não esgotam a riqueza pedagógica destes recursos de aprendizagem, porque outras resoluções poderão surgir quando implementados e explorados em contexto formativo ou de sala de aula de Matemática.
A – Problemas de Geometria e Medida:
Figura 1
A
ampulheta como medidor de tempo
autores (2019)
O problema da Figura 1 poderá ser resolvido utilizando-se, por exemplo,
uma argumentação do tipo: usam-se as ampulhetas de 8 minutos e de 2 minutos em
simultâneo e quando a de 2 esgotar sabemos que faltam 6 à de 8 e põe-se o bolo
no forno. Assim que terminar os 6 minutos (da ampulheta do 8) vira-se a de 5 e
no final perfaz 11 minutos. Mas esta não é a única resposta possível, face ao
desafio colocado. Outra possibilidade poderia ser a seguinte: usam-se a de 5 e
a de 2. Quando faltarem 3 minutos à de 5 põe-se o bolo no forno e a seguir
conta-se com a dos 8 minutos. O total será 11 minutos.
Eis outra possibilidade de resposta: usa-se a de 2, duas vezes
simultaneamente com a de 5. Depois usa-se 1 minuto restante da de 5, a de 2 e
por fim a de 8. O total será 11 minutos.
Não se usando a ampulheta dos 8 minutos, o problema também é possível ser
resolvido com a utilização apenas das outras duas ampulhetas. Vejamos: usa-se
três vezes a de 2 minutos e, de seguida, uma vez a de 5 minutos, o que dá um
total de 11 minutos gastos.
O mesmo também é possível se não se usar a ampulheta dos 2 minutos e apenas se usarem as restantes ampulhetas: antes de se ligar o forno, colocam-se as duas ao mesmo tempo. Quando passarem 5 minutos liga-se o forno pelos 3 minutos que faltam da de 8 e depois usa-se novamente a de 8.
Este tipo de problema possibilita que em contexto de sala de aula estas ou outras propostas de resolução possam ser apresentadas por vários estudantes, gerando-se a necessidade de justificarem as suas propostas e, simultaneamente, analisarem se as que são propostas pelos colegas são ou não igualmente válidas.
Em termos metacognitivos, este problema desafia o próprio resolvedor a
“dialogar” consigo mesmo, no sentido de analisar se a sua resolução é ou não
única, é ou não válida, antes mesmo de a apresentar à restante turma e ao
docente.
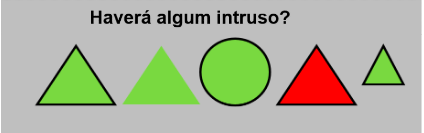Figura 2
Haverá
algum intruso?
autores (2019).
O problema da Figura 2 também poderá gerar várias respostas, pois cada um dos elementos do conjunto pode ser intruso, dependendo do critério que se utilize para se fazer essa avaliação, seja ele a altura das figuras, a cor das mesmas, a forma de cada uma ou o seu contorno. Assim, quanto à cor, a figura vermelha é a única que não é verde; quanto à forma, o círculo é o único que não é triângulo, em termos de contorno só há uma figura que não tem linha de contorno bem definida e quanto à altura, apenas existe uma figura mais pequena que as demais. Assim, este problema possibilitava esta resposta completa ou cada um dos 4 aspetos em separado.
Além destes aspetos, também era possível avançar com a ideia da distância das figuras à pessoa que as observa, havendo apenas uma posicionada a uma maior distância do observador do que as outras.
Dado que há apenas uma figura que, aparentemente, não é referenciada como sendo intrusa, que é a primeira do lado esquerdo, esta também poderá ser considerada intrusa precisamente por isso mesmo, isto é, todas as outras destoam das demais em alguma coisa menos esta. Assim sendo, será legítimo que cada uma das cinco figuras possa ser considerada intrusa, o importante é que quem as propuser como tal, seja capaz de justificar muito bem a sua tomada de decisão. Obviamente que com esta postura de resolvedor estar-se-á a promover a capacidade de comunicação matemática.
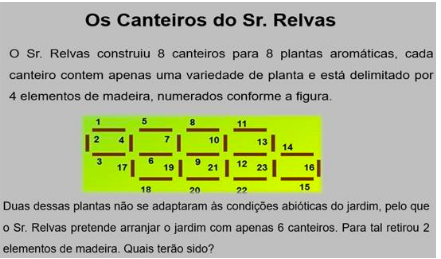Figura 3
Os Canteiros do Sr. Relvas
autores (2019)
O problema da Figura 3 é mais um problema que permite mais do que uma resposta. Uma delas é mencionarem-se os elementos n.º 23 e o n.º 4, sendo que os 6 canteiros resultantes não mantêm todos a forma original. O mesmo se passa se os elementos de madeira selecionados forem o n.º 7 e o n.º 21 ou o n.º 6 e o n.º 12.
Por outro lado, no caso de os canteiros resultantes continuarem a manter o formato dos canteiros originais, então, também aqui há várias possibilidades de resposta, pois podem ser: (a) os elementos n.º 20 e n.º 8; (b) os elementos n.º 5 o n.º 22, (c) o n.º 5 e o n.º 18, (d) o n.º 8 e o n.º 18 e (e) o n.º 8 e o n.º 22.
Trata-se, pois, de um problema muito rico, que obriga à necessidade de se analisarem as várias figuras planas que, ao nível do espaço são representações dos canteiros do Sr. Relvas. A justificação de, no final, os canteiros ficarem ou não com o formato original também é necessário ser referido e justificado. Além de tudo isto, uma vez mais os resolvedores terão de ter a capacidade de avaliarem as outras propostas de resolução a serem apresentadas, provenientes de outros estudantes, e assumir que poderão ser tão válidas quanto as que por si forem apresentadas.
B – Problemas de Números e Cálculo
Figura 4
Olhando mais do que que uma
vez, descobrimos coisas novas
autores (2019)
Uma vez mais, o problema da Figura 4 é propício à apresentação de mais do que uma resposta possível para a sua resolução. O intruso poderá ser o 100, por ser o único cuja soma dos dígitos que o forma não pertencer à sequência numérica resultante das somas dos dígitos que formam os outros números:
1 + 2 + 5 = 8
2 + 1 + 6 = 9
6 + 4 = 10
Por outro lado, alguém poderá responder que o 100 é o número intruso, mas devido a outra razão, ser o único que não é um número cúbico. De facto, os restantes três números são números cúbicos:
64 = 4 x 4 x 4
125 = 5 x 5 x 5
216 = 6 x 6 x 6
Dependendo da criatividade do resolvedor, poderão surgir sugestões mais ou menos complexas do ponto de vista do conhecimento matemático envolvendo os números e o cálculo. Assim, duas respostas bem simples e, igualmente corretas, seriam as que referissem que o 64 é o único número que na sua composição não contempla o algarismo 1, ou o 125 por ser o único número ímpar.
Já uma resposta mais complexa, que denota o conhecimento dos tipos de números, designadamente os figurados, seria a seguinte: Pode ser o 216, já que se ordenarmos os números por ordem crescente, é o único número cuja diferença para o anterior não é um número quadrado. De facto:
125 – 100 = 25 = 5 x 5
100 – 64 = 36 = 6 x 6
Por outro lado, também poderia ser referido o 125 como sendo o intruso, por ser o único que não é divisível por 4.
Em síntese, o confronto desta variedade de respostas possíveis face ao problema colocado permitiria, uma vez mais, gerar o debate de ideias, a análise metacognitiva das propostas dadas por cada resolvedor e permitiria, em última análise, o desenvolvimento da capacidade de se comunicar matematicamente.
Figura 5
Descoberta Numérica
autores (2019)
O problema da Figura 5 tira partido do conhecimento de vários conceitos matemáticos, como seja o conceito de “parte de”, número ímpar, média aritmética, número ordinal e permite estabelecer a diferença entre algarismo e número.
Apresentamos algumas respostas possíveis, dependendo da interpretação dada à posição do 1.º algarismo. Se este for colocado à esquerda, as respostas possíveis poderão ser as seguintes: (a) 204682 e (b) 202886. Dado que nada é referido sobre a possibilidade ou não de se repetirem algarismos, então a opção (b) também é válida. Se o 1.º algarismo for o da ordem das unidades do número, então poderá haver as seguintes soluções: (c) 286402 e (d) 688202. Neste problema valerá a pena solicitar justificação para a colocação do último algarismo, porque ele depende da opção que se tomar para o 3.º e para o 4.º algarismo. Haverá, pois, a necessidade de, em particular, se justificar qual o número a colocar na 6.ª posição.
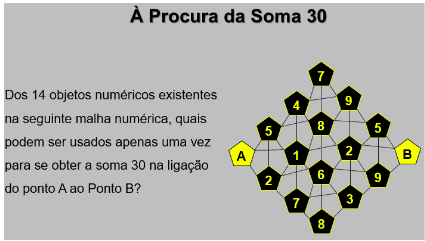Figura 6
À
Procura da Soma 30
autores (2019).
O problema da Figura 6 relaciona-se com o tema da decomposição do número em parcelas. No caso vertente, a soma procurada é o valor 30. Usando-se a malha numérica existente no enunciado do problema e partindo-se do pressuposto que só é possível unir dois algarismos adjacentes, então eis algumas respostas possíveis usando-se apenas 5 parcelas:
1 + 8 + 7 + 9 + 5
2 + 5 + 8 + 6 + 9
2 + 6 + 8 + 9 + 5
5 + 4 + 7 + 9 + 5
5 + 8 + 2 + 6 + 9
5 + 8 + 6 + 2 + 9
Usando-se 6 parcelas, de entre as respostas corretas possíveis, destacamos as seguintes:
1 + 2 + 7 + 8 + 3 + 9
1 + 5 + 4 + 7 + 8 + 5
1 + 5 + 8 + 9 + 5 + 2
1 + 7 + 8 + 3 + 2 + 9
2 + 6 + 8 + 2 + 3 + 9
2 + 7 + 6 + 2 + 8 + 5
2 + 7 + 6 + 8 + 2 + 5
5 + 1 + 4 + 7 + 8 + 5
5 + 1 + 8 + 2 + 5 + 9
5 + 1 + 8 + 2 + 9 + 5
5 + 2 + 1 + 7 + 6 + 9
Com o recurso à decomposição do 30 em 7 parcelas há mais algumas respostas corretas, das quais destacamos as seguintes:
1 + 2 + 6 + 7 + 3 + 9 + 2
1 + 2 + 7 + 6 + 3 + 2 + 9
1 + 2 + 7 + 6 + 3 + 9 + 2
2 + 1 + 6 + 7 + 3 + 2 + 9
Fica, pois, evidente que este problema é excelente para o desencadear de troca de opiniões e das respetivas justificações das tomadas de decisão que tiverem que ser feitas.
C – Problemas de Lógica Matemática
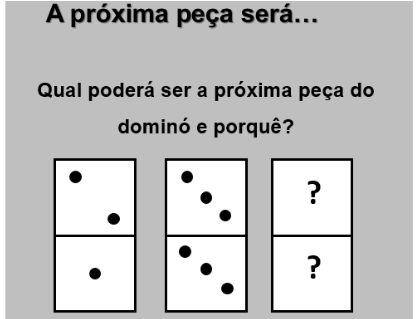Figura 7
A
próxima peça será…
autores (2019).
O problema da Figura 7 implica dar resposta à frase “se …, então…”, pelo que se trata de um bom exemplo para que os resolvedores expliquem como pensaram. Eis algumas respostas corretas que este problema poderá admitir:
– 4 e 5, pois o 4 dá continuidade à sequência 2, 3,.. e o 5 dá continuidade à sequência 1, 3, …
– Outra possibilidade poderia ser uma peça cuja soma dos dois valores numéricos aí existente fosse 9, pois a soma das pintas da 1.ª peça é 3, a soma das pintas na 2.ª peça é 6, pelo que a terceira peça poderia ser (1,8); (8,1); (2,7); (7,2); (3,6); (6,3) ou (4,5); (5,4).
- Do modo análogo, a soma das pintas da 3.ª peça poderia ser 12, dobrando esta soma a soma da 2.ª peça, pois a soma da 2.ª peça dobra a soma da 1.ª peça. Assim, a peça seria formada pelo 6 e 6.
- Existe, também, a possibilidade de ser a peça 5 e 4, sendo o 5 a soma de 2 com 3 e 4 a soma de 1 com 3 ou a peça 6 e 3, sendo o 6 o produto de 2 por 3 e o 3 o produto de 1 por 3.
– Contudo se se imaginar que o número de pintas na parte de cima da peça é o número dessa posição da peça anterior mais uma unidade e o número de pintas do monominó de baixo é soma de todas as pintas da peça anterior, então a peça seguinte poderá ser a peça 4 e 6.
Haja, pois, criatividade por parte dos resolvedores e outras soluções possíveis serão suscetíveis de ocorrer e estarem, igualmente, corretas.
Figura 8:
Os Mealheiros do João e da
Joana
autores (2019)
O problema da Figura 8 poderá ter uma resolução teórica, baseada no domínio de procedimentos de cálculo algébrico, como evidenciamos a seguir:
Dado que 10 é o dobro de 5, poder-se-á inferir que a quantidade de notas do João é um múltiplo de 5, isto é, 5x. Por sua vez a quantidade de notas do mealheiro da Joana será um múltiplo de 20, isto é, 20y.
A Joana só pode retirar dois terços das suas notas quando tiver no mínimo 3 notas e nessa altura ficaria no mealheiro apenas uma nota (20€). Este valor corresponde a metade da poupança do João, o que nos leva a concluir que a sua poupança seria de 40€. De facto esta poupança seria possível apenas com notas de 5€ e 10€.
Poder-se-á então concluir que a poupança mínima do João seria 40€ (dobro de 20€) e a poupança da joana seria 60€ (triplo de 20€).
O mesmo será verdade se o valor total do dinheiro do João for 80 euros e o da Joana for 120 euros, pois metade de 80 é igual a um terço de 120. Por este motivo, o mealheiro do João poderia ter 80 euros e o da Joana 120 euros.
Seria interessante se os alunos concluíssem que este problema terá sempre solução se a quantidade de dinheiro do mealheiro do João for um múltiplo de 40 e a quantidade de dinheiro do mealheiro da Joana for um múltiplo de 60 euros.
O Quadro 1 permite estabelecer a respetiva relação algébrica entre os dois montantes:
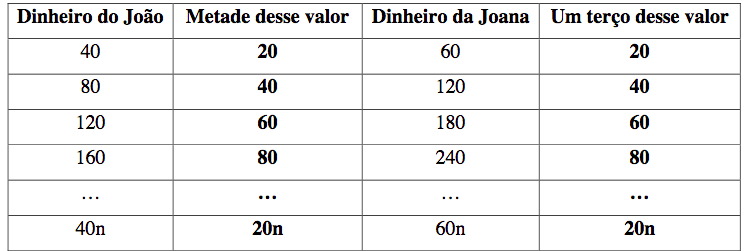Quadro 1
Relação
entre o dinheiro do João e da Joana
autores (2019)
Em síntese, trata-se de um problema com um número infinito de soluções,
possibilitando um debate interessante entre as várias propostas de solução que
poderão surgir.
Figura 9
As Gaiolas do Sr. João
autor (2019)
O problema da Figura 9 é mais um problema que permite a existência de várias soluções, pois os números de aves da 1.ª e da 2.ª gaiolas estarão sempre dependentes do número de aves existentes na 3.ª gaiola. Sabendo-se, ainda, que 2 (x + 3) + (x + 3) + x, sendo x o número de aves existentes na 3.ª gaiola, tem de ser um número quadrado e que existem apenas 8 números quadrados maiores que 1 e menores que 100 (4, 9, 16, 25, 36, 49, 64, 81), então 4x + 9 terá de ser um desses números quadrados. Isto implica que o número quadrado tenha de ser o quadrado de um número ímpar, maior que 3.
Assim, existem 3 possíveis soluções, os quadrados de 5, 7 e 9:
(a) – a 3.ª gaiola tem 4 aves;
– a 2.ª gaiola tem 7 aves;
– a 1.ª gaiola tem 14 aves.
Total de aves: 4 + 7 + 14 = 25, que é o quadrado de 5.
(b) – a 3.ª gaiola tem 10 aves;
– a 2.ª gaiola tem 13 aves;
- a 1.ª gaiola tem 26 aves.
Total de aves: 10 + 13 + 26 = 49, que é o quadrado de 7.
(c) – a 3.ª gaiola tem 18 aves;
– a 2.ª gaiola tem 21 aves;
– a 1.ª gaiola tem 42 aves.
Total de aves: 18 + 21 + 42 = 81, que é o quadrado de 9.
Em síntese, este problema possibilita rever o conceito de número quadrado e desenvolve a capacidade de os resolvedores relacionarem logicamente as premissas entre si, de modo a que possam comunicar as suas tomadas de decisão.
Considerações finais
O conjunto dos nove problemas analisados permite, de facto, que se possa concluir que poderão ser desencadeadores de resoluções diversas por parte de quem os tentar resolver. Em contexto de sala de aula de Matemática poderão permitir a troca de opiniões entre colegas, sendo que cada um deve ser encorajado a justificar as suas resoluções, quer seja oralmente, quer seja por escrito. Cabe aos professores incutir nos estudantes o hábito de metacognitivamente avaliarem as suas resoluções e motivá-los para procurarem identificar se os problemas lhes possibilitam a obtenção de mais do que uma solução. Este tipo de atitude poderá contribuir para que os estudantes possam aumentar e desenvolver o conhecimento que têm sobre os próprios processos cognitivos, bem como tomarem consciência desses processos (VALENTE, 1989).
Deixamos aqui o desafio de a totalidade ou alguns destes problemas poderem ser explorados em contexto de sala de aula de Matemática no sentido de se recolher informação sobre qual ou quais e quantas serão as resoluções que os alunos apresentam, bem como os argumentos que utilizam para justificarem essas mesmas resoluções.
