1. Introdução
De maneira geral, os documentos oficiais sobre o ensino de Matemática no Brasil apontam desde 1997 que o professor adote a resolução de problemas em sala de aula, buscando com que o aluno possa desenvolver habilidades e competências necessárias não apenas para resolver problemas que envolvem Matemática mas ainda para desenvolver processos mentais, relacionados, por exemplo, à capacidade de generalização (BRASIL, 1997, 1998; BNCC, 2017).
Na Base Nacional Comum Curricular-BNCC (BRASIL, 2017, p. 263), pode-se encontrar que o ensino em sala de aula deve conduzir os alunos a estabelecerem relações entre o mundo real e representações que culminem na aprendizagem de conceitos e propriedades, de modo que possam utilizar a “[...] matemática para resolver problemas, aplicando conceitos, procedimentos e resultados para obter soluções e interpretá-las segundo os contextos das situações”.
De acordo com vários autores que investigaram sobre a resolução de problemas no ensino de Matemática (KRULIK; RUDNICK, 1982; CHARLES, 1985; SCHOENFELD, 1990; POZO; ANGÓN, 1998; FI; DEGNER, 2012; CAI; LESTER, 2012), é possível verificar que abordar a resolução de problema nas aulas tem potencial para favorecer aos alunos o desenvolvimento do pensamento matemático, uma vez que auxilia: a) na construção de processos dedutivos; b) no levantamento de hipóteses quando se busca compreender o problema; c) em análise da racionalidade da resposta encontrada, segundo o contexto do problema; d) na construção de pensamento indutivo, relacionado ao processo de generalização para formulação de padrões (expressões matemáticas).
Dessa forma, considerando a importância do trabalho em sala de aula que adote a resolução de problemas, buscando desenvolver o pensamento matemático dos alunos da escola, o presente artigo teve como objetivo analisar o conhecimento de professores recém-formados de cursos de Licenciatura em Matemática sobre o ensino de matemática via resolução de problemas.
Uma vez que os documentos oficiais do Brasil, citados anteriormente, recomendam que seja feito um trabalho envolvendo a resolução de problemas, buscamos investigar os estudantes que acabaram de concluir o curso de Licenciatura em Matemática porque entendemos ser importante revelar o quão construídos e desenvolvidos estavam seus conhecimentos sobre a resolução de problemas no ensino de Matemática.
Entendemos que o ensino de Matemática via resolução de problemas corresponde a um conhecimento de cunho pedagógico para abordar conteúdos matemáticos. Conforme apontou Shulman (1986), o conhecimento pedagógico do conteúdo, ou seja, as formas de abordar determinados conteúdos, é um dos que precisam ser desenvolvidos na formação de professores.
Segundo Imbernón (2011, p. 60-61), é preciso favorecer conhecimento pedagógico consistente ao futuro professor como, por exemplo, para ensinar Matemática via resolução de problemas, ou seja, “[...] deve capacitá-lo a assumir a tarefa educativa em toda sua complexidade, atuando reflexivamente com a flexibilidade e o rigor necessários, isto é, apoiando suas ações em uma fundamentação válida para evitar cair no paradoxo de ensinar a não ensinar [...]”.
Dessa forma, é necessário conhecer e apreender os encaminhamentos a que se refere o ensino de Matemática via resolução de problemas para ser abordado em sala de aula.
2. Resolução de Problemas: encaminhamentos ao
ensino de Matemática
O tema resolução de problemas corresponde a um campo que envolve a resolução de problemas cotidianos e problemas escolares, sendo que as pessoas constroem ao longo de suas vidas organizações mentais mediante o desenvolvimento de processos cognitivos que as auxiliam a resolverem esses problemas (CHI; GLASER, 1992; STERNBERG, 2000; BRITO, 2010). Dessa forma, destaca-se que a resolução de problemas implica em uma habilidade cognitiva complexa que seria o topo da aprendizagem de uma pessoa (GAGNÉ, 1983; CHI; GLASER, 1992).
O desenvolvimento da capacidade para a resolução de problemas pode ser favorecido na escola por meio de um ensino que conduza os alunos a construírem, por exemplo, uma organização mental para compreensão de problemas. Para tal, entendemos que o professor precisa ter conhecimentos, primeiramente, sobre o que é um problema e sobre como ocorre o processo de resolução de problemas. Dessa forma, o passo seguinte é que esse professor tenha conhecimentos sobre como a resolução de problemas deve (deveria) ser abordada em sala de aula, o que implica em saber os encaminhamentos sobre o ensino de Matemática via resolução de problemas.
Echeverría (1998) evidenciou que o significado de problema, na literatura sobre o tema, foi entendido por alguns estudiosos como sendo qualquer atividade matemática e, ao mesmo tempo, como uma situação difícil, por outros. Na visão dessa autora, “para que possamos falar da existência de um problema, a pessoa que está resolvendo essa tarefa precisa encontrar alguma dificuldade que a obrigue a questionar-se sobre qual seria o caminho que precisaria seguir para alcançar a meta.” (ECHEVERRÍA, 1998, p. 48). Portanto, ser um problema:
[...] não é uma propriedade inerente de uma tarefa
matemática. Antes, é uma relação particular entre o indivíduo e a tarefa que
faz da tarefa um problema para ele. A palavra problema é usada aqui nesse sentido relativo, como uma tarefa que é
difícil ao indivíduo que tenta resolvê-la. (SCHOENFELD, 1985, p. 74, grifo do
autor).
Quando a pessoa se depara com uma situação que para ela é um problema, precisará buscar um caminho que a ajude a encontrar uma resposta. A busca desse caminho vai depender de todo um processo de resolução de problemas que envolve etapas/fases do pensamento, organizadas de forma sequencial, porém não linear. Vários pesquisadores apontaram etapas de resolução de problemas (DEWEY, 1910; POLYA, 1994; MAYER, 1992; STERNBERG, 2000; BRITO, 2010), sendo que adotaremos para este artigo as descritas por Proença (2018), baseadas nas quatro etapas seguintes: representação, planejamento, execução, monitoramento.
Proença (2018) apresentou a seguinte caracterização: a) representação – corresponde à compreensão do problema, ou seja, à compreensão que a pessoa realiza do problema com base em seus conhecimentos da língua portuguesa e seus conhecimentos sobre os termos matemáticos que aparecem no enunciado, gerando uma representação mental e simbólica. No entanto, essa compreensão não é absoluta, pois pode ser prejudicada pela má formação de conceitos e procedimentos trazidos pela pessoa no sentido de dificultar seu entendimento de termos matemáticos e até mesmo de perceber informações incompletas e supérfluas; b) planejamento – corresponde ao uso de uma estratégia de resolução, ou seja, um caminho a ser seguido que deriva das preferências da pessoa, podendo optar por meios algébricos ou aritméticos ou geométricos ou outras formas de representação e organização dos dados; c) execução – trata-se de executar a estratégia, ou seja, realizar os cálculos devidos, bem como desenhar as figuras ou outras formas de representação viso-pictórico; monitoramento – corresponde à verificação da resposta, se está de acordo com a pergunta do problema e, assim, se é condizente ao contexto. Também implica em rever o processo seguido, o que permite que a pessoa possa reestruturar ou modificar a estratégia seguida.
Sabendo o significado de problema e que para resolvê-lo a pessoa desenvolve um processo de pensamento que segue etapas, apresentaremos as três abordagens de ensino que foram identificadas por Schroeder e Lester (1989), as quais refletiam e ainda refletem como a resolução de problemas acaba sendo tratada no ensino de Matemática. Essas abordagens estão relacionadas ao momento em que um “problema” é utilizado para abordar determinado conteúdo.
A abordagem ensinar via resolução de problemas implica no uso do problema como
o início do trabalho em sala de aula, ou seja, antes de explicar determinado
conteúdo (defini-lo), o professor deve apresentar aos alunos uma situação que
seja um problema para eles. De acordo com Schroeder e Lester (1989, p. 33), “o
ensino de um tópico matemático começa com uma situação-problema que expressa
aspectos-chave desse tópico e técnicas matemáticas são desenvolvidas como
respostas razoáveis para problemas razoáveis.” Dessa forma, o que se favorece
aos alunos é que se engajem na resolução do problema, desenvolvendo as etapas
anteriormente mencionadas por Proença (2018). A aprendizagem decorrente do
ensino via resolução de problemas é reflexo, portanto, do “[...] movimento do
concreto (um problema do mundo real que serve como exemplo do conceito ou da
técnica matemática) para o abstrato (uma representação simbólica de uma classe
de problemas e técnicas para operar com esses símbolos)” (SCHROEDER; LESTER,
1989, p. 33).
Já na abordagem ensinar para resolução de problemas, o uso do problema é feito após já se ter explicado o conteúdo. Conforme explicaram Schroeder e Lester (1989, p. 34, grifo dos autores), “resolução de problemas é vista como uma atividade em que os alunos somente se engajam depois da introdução de um novo conceito ou para seguir uma habilidade de cálculo ou um algoritmo”. Dessa forma, esses autores destacaram que a preocupação do professor com a aprendizagem da Matemática é que os alunos consigam transferir o que aprenderam para outras situações, ou seja, para resolver “problemas”.
Por último, a abordagem ensinar sobre resolução de problemas é aquela que busca introduzir um problema após ter explicado aos alunos as etapas de resolução de problemas, além de um trabalho com heurísticas e estratégias. “No melhor de suas hipóteses, ensinar sobre resolução de problemas também incluía experiências com, de fato, resolver problemas, mas sempre envolveu muito da discussão explícita de, e ensinar sobre, como problemas são resolvidos” (SCHROEDER; LESTER, 1989, p. 32). Dessa forma, Schroeder e Lester (1989) evidenciaram que a aprendizagem decorre de os alunos terem ciência dessas etapas e que sejam capazes de aplicá-las na resolução de problemas.
Para Schroeder e Lester (1989), a abordagem ensinar via resolução de problemas é a mais coerente e a que deveria ser tratada no ensino de Matemática, pois possibilita estabelecer relações matemáticas entre as ideias dos alunos e os aspectos–chave dos problemas. Já na abordagem ensinar para resolução de problemas, esses autores enfatizaram que apresenta um limite grande no ensino, uma vez que o que se exige dos alunos é a aplicação do que acabaram de aprender em problemas do mundo real, o que não corresponde à resolução de problemas. Por fim, o ensinar sobre resolução de problemas é entendido pelos autores como limitante porque o professor pode considerar a resolução de problemas como um tópico que acaba sendo tratado de forma isolada do conteúdo matemático a ser abordado, bem como das relações matemáticas.
A essência do ensinar via resolução de problemas – ensinar um conteúdo matemático pela introdução de um problema – é uma indicação que já era feita no documento Parâmetros Curriculares Nacionais-PCN (BRASIL, 1998), segundo a qual indicava que o problema é o ponto de partida no ensino de Matemática e não a definição. No documento atual, Base Nacional Comum Curricular-BNCC (BRASIL, 2017), apesar de incentivar o trabalho que favoreça o desenvolvimento de habilidades para resolver problemas, não há indicação pedagógica de como fazê-lo.
Diante disso, há duas propostas pedagógicas que podem ser implementadas na sala de aula e que evidenciam encaminhamentos importantes a serem realizados pelo professor. A primeira é a metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas de Onuchic (1999), a qual Allevato e Onuchic (2014) indicam como sugestão atual a organização em dez etapas: proposição do problema, leitura individual, leitura em conjunto, resolução do problema, observar e incentivar, registro das resoluções na lousa, plenária, busca do consenso, formalização do conteúdo, proposição e resolução de novos problemas. A segunda é o Ensino-aprendizagem de Matemática via resolução de problemas de Proença (2018), a qual envolve uma sequência de cinco ações, a saber: escolha do problema, introdução do problema, auxílio aos alunos durante a resolução, discussão das estratégias dos alunos, articulação das estratégias dos alunos ao conteúdo.
Para este artigo, vamos tomar como referência os encaminhamentos sugeridos por Proença (2018). Dessa forma, a ação de ensino de escolha do problema implica de o professor escolher uma situação de Matemática que os alunos sintam dificuldade e precisem encontrar um caminho de resolução, ou seja, que se torne um problema para eles. Tal escolha precisa valorizar os conhecimentos prévios dos alunos para que estes possam utilizá-los na busca de uma resposta. Essa escolha também implica de o professor ter condições para articular as ideias apresentadas pelos alunos em suas resoluções à estrutura matemática do conteúdo que se quer abordar, ou seja, ter condições, conforme já indicaram Schroeder e Lester (1989), de favorecer a aprendizagem que vai do movimento do problema do mundo real (concreto) às representações simbólicas da matemática (abstrato). Nesse sentido, esta ação de ensino necessita que, para tal, o professor faça uma previsão das possíveis estratégias de resolução.
A ação seguinte é a introdução do problema, a qual consiste em apresentar aos alunos, distribuídos em grupos, a situação de Matemática para que tentem resolvê-la. Neste momento, a situação pode se tornar um problema a eles e, assim, o professor deve sugerir que busquem resolvê-lo da forma como quiserem. No auxílio aos alunos durante a resolução, o professor precisar atuar como observador, incentivador e direcionador da aprendizagem, o que corresponde a verificar as dificuldades dos grupos, incentivar o diálogo e troca de ideias, dar dicas ou direcionamentos a alguma estratégia. Este é um momento em que o professor já pode perceber como os alunos se engajam no processo de resolução de problemas.
A quarta ação de ensino corresponde à discussão das estratégias dos alunos, o que corresponde a um momento em que os grupos devem apresentar, em lousa, como resolveram o problema. Pode-se, assim, socializar suas ideias e suas dificuldades no uso de seus conhecimentos conceituais e procedimentais. Este também é um momento em que o professor tem condições de verificar as dificuldades dos alunos nas etapas de resolução de problemas. Por fim, a articulação das estratégias dos alunos ao conteúdo implica de o professor estabelecer uma articulação entre os aspectos-chave de uma estratégia de algum grupo ou de mais de um grupo e o novo conteúdo a ser abordado. Trata-se de direcionar os alunos a identificarem a relação entre suas ideias e a representação matemática que faz parte desse novo conteúdo. Diante disso, Proença (2018) sugeriu que se não for possível estabelecer essa articulação, então pode-se apresentar aos alunos, diretamente, o novo conteúdo, evidenciando o conceito ou a fórmula matemática que está sendo abordada.
3. Metodologia
A pesquisa realizada é de natureza qualitativa, uma vez que “a abordagem qualitativa parte do fundamento de que há uma relação dinâmica entre o mundo real e o sujeito, uma interdependência viva entre o sujeito e o objeto, um vínculo indissociável entre o mundo objetivo e a subjetividade do sujeito.” (CHIZZOTTI, 2001, p. 79).
Tendo em vista a nossa investigação pelo ensino de Matemática via resolução de problemas – nosso mundo objetivo – buscamos analisar os conhecimentos de professores recém-formados sobre esse ensino – subjetividade do sujeito – de cursos de Licenciatura em Matemática das três universidades de maior destaque do Estado do Paraná. No início de fevereiro de 2019, entramos em contato com os coordenadores dos cursos, solicitando-lhes os e-mails desses estudantes que se formaram no ano de 2018. Dessa forma, recebemos as seguintes quantidades: 14 formados da universidade A (Federal); 19 formados da universidade B (Estadual); 19 formados da universidade C (Estadual).
Para coletar dados sobre os conhecimentos desses professores recém-formados sobre o ensino de Matemática via resolução de problemas, elaboramos um questionário online. Neste questionário, apresentamos o relato de entrevista de um participante que foi investigado na pesquisa de Santana (2016) e que revelou suas ações pedagógicas para tratar da resolução de problemas no ensino de Matemática, as quais se configuraram como um episódio de ensino. Tais ações pedagógicas não estavam de acordo com um ensino que deveria adotar como encaminhamento didático o uso do problema como ponto de partida para abordar um conteúdo. Tratava-se de um ensino tradicional, baseado no ensinar para resolução de problemas (SCHROEDER, LESTER, 1989), e que serviu como base às respostas a cinco itens. O quadro abaixo mostra os itens que fizeram parte do questionário utilizado na coleta de dados.
Quadro 1
Questionário: Relato sobre a resolução de problemas e itens a serem
respondidos.
 Fonte: O autor.
Fonte: O autor.
De acordo com Chaer, Diniz e Ribeiro (2011), a utilização de questionário como instrumento de coleta de dados tem como vantagens: a) evitar gastos com treinamento do pesquisador; b) permitir a participação de um maior número de pessoas, sendo que podem respondê-lo em qualquer lugar geográfico em que estejam; c) permite com que seja respondido no tempo desejado pelas pessoas. No entanto, umas de suas desvantagens é justamente o que ocorreu em nosso estudo que é o risco de parte dos participantes do universo de pesquisa não responder dentro do prazo estabelecido.
Desse modo, o questionário online foi enviado aos e-mails dos 52 professores recém-formados, semanalmente, durante os meses de fevereiro e março de 2019. Tivemos o retorno de apenas uma pequena parcela desse total. Assim, os que responderam ao questionário e que foram os participantes (P) de nosso estudo corresponderam ao seguinte:
-
· Universidade A (Federal): P1 (masculino);
· Universidade B (Estadual): P2, P3 e P4 (masculinos);
· Universidade C (Estadual): P5, P6, P7 (masculinos); P8, P9 e P10 (femininos).
A análise dos dados foi estruturada segundo as técnicas da Análise de Conteúdo de Bardin (2010). Dessa forma, a pré-análise consistiu na elaboração dos itens do questionário e da transcrição das respostas dos estudantes para um arquivo do word. Na exploração do material, fizemos uma leitura flutuante de modo que pudemos organizar os dados segundo três categorias: Conhecimentos sobre como resolver um problema, Conhecimentos a partir do ensino do professor, Formação proporcionada pelo curso de licenciatura em Matemática. Para essas categorias, elaboramos subcategorias para delimitar os dados. Por fim, fizemos a nossa interpretação dos dados com base no quadro teórico.
Para encerrar a análise, apresentamos dados sobre os encaminhamentos ao ensino via resolução de problemas que foram descritos pelos estudantes, revelando seus conhecimentos para abordar um conteúdo matemático na perspectiva das ações do ensino-aprendizagem de Matemática via resolução de problemas.
4. Análise e discussão dos dados
No quadro 2 a seguir, mostra-se os
conhecimentos dos participantes com base em suas respostas sobre o que
corresponde o ato de resolver um problema.
Quadro 2
Respostas sobre o que é resolver um problema.
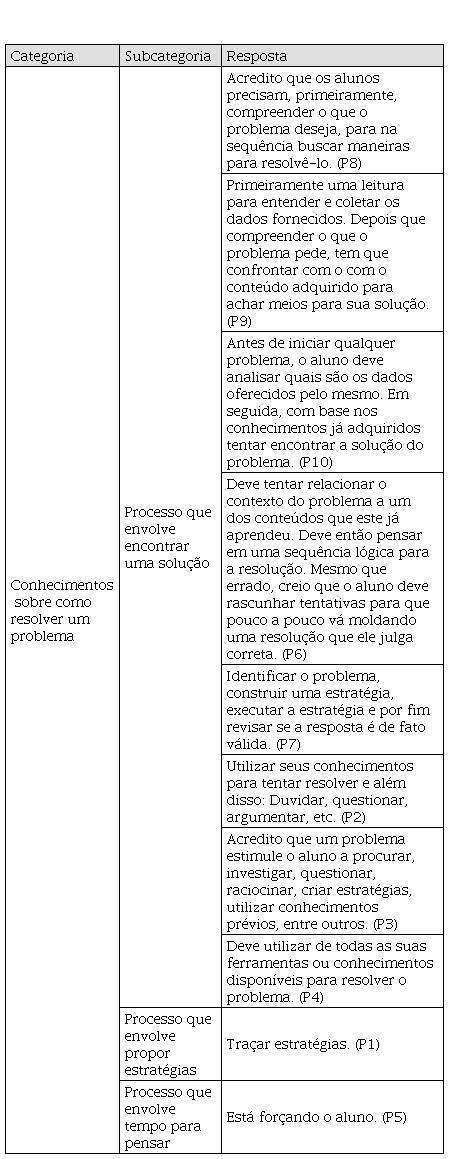 Fonte: O autor.
Fonte: O autor.
|
Categoria
|
Subcategoria
|
Resposta
|
|
Conhecimentos
sobre como resolver um problema
|
Processo
que envolve encontrar uma solução
|
Acredito que os alunos precisam,
primeiramente, compreender o que o problema deseja, para na sequência buscar
maneiras para resolvê-lo. (P8)
|
|
Primeiramente uma leitura para
entender e coletar os dados fornecidos. Depois que compreender o que o
problema pede, tem que confrontar com o com o conteúdo adquirido para achar
meios para sua solução. (P9)
|
|
Antes de iniciar qualquer problema, o
aluno deve analisar quais são os dados oferecidos pelo mesmo. Em seguida, com
base nos conhecimentos já adquiridos tentar encontrar a solução do problema.
(P10)
|
|
Deve tentar relacionar o contexto do
problema a um dos conteúdos que este já aprendeu. Deve então pensar em uma
sequência lógica para a resolução. Mesmo que errado, creio que o aluno deve
rascunhar tentativas para que pouco a pouco vá moldando uma resolução que ele
julga correta. (P6)
|
|
Identificar o problema, construir uma
estratégia, executar a estratégia e por fim revisar se a resposta é de fato
válida. (P7)
|
|
Utilizar seus conhecimentos para
tentar resolver e além disso: Duvidar, questionar, argumentar, etc. (P2)
|
|
Acredito que um problema estimule o
aluno a procurar, investigar, questionar, raciocinar, criar estratégias,
utilizar conhecimentos prévios, entre outros. (P3)
|
|
Deve utilizar de todas as suas
ferramentas ou conhecimentos disponíveis para resolver o problema. (P4)
|
|
Processo
que envolve propor estratégias
|
Traçar estratégias. (P1)
|
|
Processo
que envolve tempo para pensar
|
Está forçando o aluno. (P5)
|
Como se observa no quadro acima, as respostas de oito participantes revelaram que resolver um problema implica em um processo que envolve encontrar uma solução. Tais respostas evidenciaram que esse processo consiste em etapas de resolução como, por exemplo, a de compreensão, relativa à etapa de representação do problema (PROENÇA, 2018). Um dos participantes apenas citou se tratar de uso de estratégias de resolução, relacionado à um processo que envolve propor estratégias. Por fim, como o último participante (P5) apenas deu como resposta que “está forçando o aluno”, entendemos se tratar de menção ao tipo do ensino realizado pelo professor (“Círculo pela sala, verifico, estimulo: “Vamos, faça!” “Rápido”. Seu colega já está montando e elaborando e você ainda não fez!”) e que, para esse participante, revela que resolver um problema implica em processo que envolve tempo para pensar sobre a situação.
Uma vez que Proença (2018) destacou que na resolução de problemas a etapa que envolve compreensão depende dos conhecimentos do solucionador, o qual precisa propor uma estratégia, é necessário que tenha tempo suficiente para organizar uma resolução para encontrar uma resposta. Além disso, quando Proença (2018) discorre sobre a ação de auxílio aos alunos durante a resolução de um problema, é possível perceber que o professor deve dar tempo aos alunos para tentarem resolvê-lo. Isso mostra que o participante P5 revelou uma preocupação importante que é a de não ‘forçar o aluno’ para resolver um problema.
No quadro 3 a seguir, mostra-se os conhecimentos dos participantes sobre o que corresponde um ensino de Matemática via resolução de problemas, derivado do entendimento deles a partir do episódio de ensino do professor.
Quadro 3
Respostas que envolvem conhecimentos sobre o ensino
via resolução de problemas.
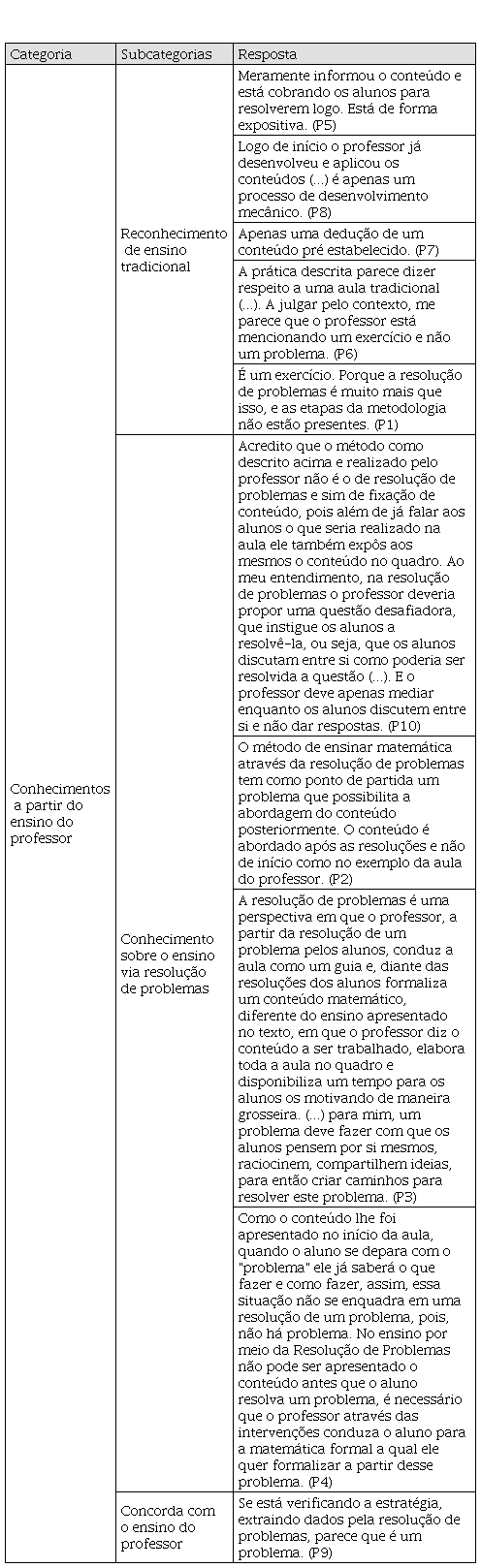 Fonte: O autor.
Fonte: O autor.
|
Categoria
|
Subcategorias
|
Resposta
|
|
Conhecimentos
a partir do ensino do professor
|
Reconhecimento
de ensino tradicional
|
Meramente informou o conteúdo e está
cobrando os alunos para resolverem logo. Está de forma expositiva. (P5)
|
|
Logo de início o professor já
desenvolveu e aplicou os conteúdos (...) é apenas um processo de
desenvolvimento mecânico. (P8)
|
|
Apenas uma dedução de um conteúdo pré
estabelecido. (P7)
|
|
A prática descrita parece dizer
respeito a uma aula tradicional (...). A julgar pelo contexto, me parece que
o professor está mencionando um exercício e não um problema. (P6)
|
|
É um exercício. Porque a resolução de
problemas é muito mais que isso, e as etapas da metodologia não estão
presentes. (P1)
|
|
Conhecimento
sobre o ensino via resolução de
problemas
|
Acredito que o método como descrito
acima e realizado pelo professor não é o de resolução de problemas e sim de
fixação de conteúdo, pois além de já falar aos alunos o que seria realizado
na aula ele também expôs aos mesmos o conteúdo no quadro. Ao meu entendimento,
na resolução de problemas o professor deveria propor uma questão desafiadora,
que instigue os alunos a resolvê-la, ou seja, que os alunos discutam entre si
como poderia ser resolvida a questão (...). E o professor deve apenas mediar
enquanto os alunos discutem entre si e não dar respostas. (P10)
|
|
O método de ensinar matemática
através da resolução de problemas tem como ponto de partida um problema que
possibilita a abordagem do conteúdo posteriormente. O conteúdo é abordado
após as resoluções e não de início como no exemplo da aula do professor. (P2)
|
|
A resolução de problemas é uma
perspectiva em que o professor, a partir da resolução de um problema pelos
alunos, conduz a aula como um guia e, diante das resoluções dos alunos
formaliza um conteúdo matemático, diferente do ensino apresentado no texto,
em que o professor diz o conteúdo a ser trabalhado, elabora toda a aula no
quadro e disponibiliza um tempo para os alunos os motivando de maneira
grosseira. (...) para mim, um problema deve fazer com que os alunos pensem
por si mesmos, raciocinem, compartilhem ideias, para então criar caminhos
para resolver este problema. (P3)
|
|
Como o conteúdo lhe foi apresentado
no início da aula, quando o aluno se depara com o "problema" ele já
saberá o que fazer e como fazer, assim, essa situação não se enquadra em uma
resolução de um problema, pois, não há problema. No ensino por meio da Resolução
de Problemas não pode ser apresentado o conteúdo antes que o aluno resolva um
problema, é necessário que o professor através das intervenções conduza o
aluno para a matemática formal a qual ele quer formalizar a partir desse
problema. (P4)
|
|
Concorda
com o ensino do professor
|
Se está verificando a estratégia,
extraindo dados pela resolução de problemas, parece que é um problema. (P9)
|
Podemos verificar no quadro acima que as respostas de cinco participantes revelaram o reconhecimento de ensino tradicional praticado pelo professor do episódio de ensino. Isso indica que tais participantes entenderam, corretamente, que o episódio não correspondia a um ensino via resolução de problemas, ou seja, que se tratava de um ensino limitante e que é característico do ensinar para resolução de problemas (SCHROEDER; LESTER, 1989).
Já três participantes apresentaram respostas que revelaram, além de que o ensino do professor não foi um ensino via resolução de problemas, terem conhecimento sobre o ensino via resolução de problemas. Esses participantes descreveram, adequadamente, as características que correspondem justamente ao ensinar via resolução de problemas que implica no uso do problema como ponto de partida no ensino de um conteúdo (SCHROEDER; LESTER, 1989; PROENÇA, 2018).
Por fim, um participante permitiu que identificássemos que ele concorda com o ensino do professor, segundo o episódio que leu, ao destacar que o problema adotado no episódio seria um problema porque se está “verificando a estratégia” e “extraindo dados pela resolução de problemas”. Entendemos que talvez esse participante acredite que o simples fato de um aluno extrair dados de uma dada situação e mesmo utilizar uma estratégia que lhe foi dada já se possa apontar que essa situação é um problema e que, assim, estaria trabalhando na perspectiva de um ensino via resolução de problemas. No entanto, conforme destacou Proença (2018), ensinar Matemática via resolução de problemas corresponde a adotar um problema como ponto de partida e não uma definição matemática.
No quadro 4 a seguir, mostra-se como deu a formação proporcionada pelos cursos de licenciatura em Matemática sobre a formação para exercer um ensino de Matemática via resolução de problemas, conforme as respostas dos participantes.
Quadro 4
Respostas sobre a formação ao ensino via da
resolução de problemas.
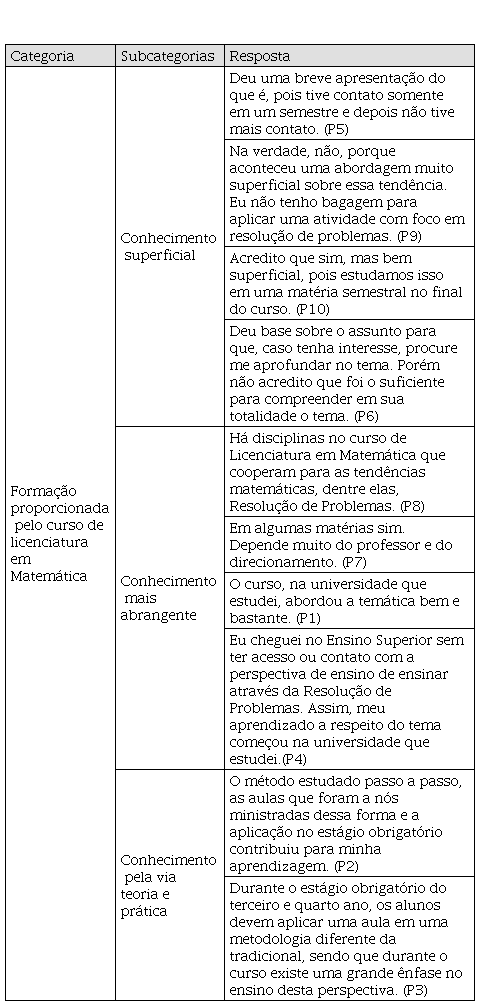 Fonte: O autor.
Fonte: O autor.
|
Categoria
|
Subcategorias
|
Resposta
|
|
Formação
proporcionada pelo curso de licenciatura em Matemática
|
Conhecimento
superficial
|
Deu uma breve apresentação do que é,
pois tive contato somente em um semestre e depois não tive mais contato. (P5)
|
|
Na verdade, não, porque aconteceu uma
abordagem muito superficial sobre essa tendência. Eu não tenho bagagem para
aplicar uma atividade com foco em resolução de problemas. (P9)
|
|
Acredito que sim, mas bem
superficial, pois estudamos isso em uma matéria semestral no final do curso.
(P10)
|
|
Deu base sobre o assunto para que,
caso tenha interesse, procure me aprofundar no tema. Porém não acredito que
foi o suficiente para compreender em sua totalidade o tema. (P6)
|
|
Conhecimento
mais abrangente
|
Há disciplinas no curso de
Licenciatura em Matemática que cooperam para as tendências matemáticas,
dentre elas, Resolução de Problemas. (P8)
|
|
Em algumas matérias sim. Depende
muito do professor e do direcionamento. (P7)
|
|
O curso, na universidade que estudei,
abordou a temática bem e bastante. (P1)
|
|
Eu cheguei no Ensino Superior sem ter
acesso ou contato com a perspectiva de ensino de ensinar através da Resolução
de Problemas. Assim, meu aprendizado a respeito do tema começou na universidade
que estudei.(P4)
|
|
Conhecimento
pela via teoria e prática
|
O método estudado passo a passo, as
aulas que foram a nós ministradas dessa forma e a aplicação no estágio
obrigatório contribuiu para minha aprendizagem. (P2)
|
|
Durante o estágio obrigatório do terceiro e
quarto ano, os alunos devem aplicar uma aula em uma metodologia diferente da
tradicional, sendo que durante o curso existe uma grande ênfase no ensino
desta perspectiva. (P3)
|
De acordo com o quadro acima, podemos observar que as respostas dadas por quatro participantes revelaram uma formação que lhes proporcionou um conhecimento superficial sobre o ensino de Matemática via resolução de problemas. As respostas de outros quatro participantes permitiram-nos identificar que a formação oferecida proporcionou-lhes conhecimento mais abrangente sobre esse ensino. Por fim, dois participantes deram como resposta que a formação que lhes foi dada possibilitou construir conhecimento pela via teoria e prática, ou seja, não apenas pelas disciplinas teóricas, mas ainda por meio de atividades de regência de aula do estágio, implementando o ensino via resolução de problemas.
Percebe-se que, de forma geral, a formação proporcionada ainda precisa ser ampliada. Resultado semelhante ocorreu na pesquisa de Proença (2012), ao buscar favorecer uma formação a quatro licenciandos em Matemática sobre o ensino via resolução de problemas. Esse autor mostrou que na análise dos conhecimentos iniciais desses participantes sobre o tema dois deles revelaram receber uma formação apenas ao nível da importância de ser tratado em sala de aula. Mostrou também que um desses dois participantes e mais outro revelaram uma dicotomia entre teoria e prática nessa formação, ou seja, uma formação apenas teórica sem discussão de uma possível prática e/ou falta de atividades sobre o tema no estágio.
Um estudo atual, o de Rodrigues (2018), ao analisar, entre outros aspectos, como 31 professores tiveram conhecimento sobre a resolução de problemas como metodologia de ensino, mostrou que 13 professores deram como resposta que isso ocorreu na graduação. Esses resultados indicam que na formação inicial ainda é preciso contemplar e favorecer o desenvolvimento de conhecimentos dos licenciandos em Matemática para ensinar via resolução de problemas.
Finalmente, tendo em vista essa análise descrita acima a respeito dos conhecimentos dos participantes sobre o processo de resolução de problemas, sobre o ensino via resolução de problemas e sobre os conhecimentos proporcionados pela formação nos cursos de Licenciatura em Matemática, apresenta-se as ações dos participantes propostas para os encaminhamentos ao ensino via resolução de problemas. A tabela 1 a seguir mostra esses resultados e também mostra que sete participantes fizeram parte desta análise porque tivemos três deles (P3, P5 e P6) que não responderam sobre os encaminhamentos que dariam em sala de aula.
Tabela 1
Encaminhamentos dos participantes com base nas ações de ensino.
 Fonte: O autor.
Fonte: O autor.
|
Ação no ensino
|
Apresentaram
|
Não
apresentaram
|
Total
(n=7)
|
|
Indicação
de conteúdo
|
86%
(6)
|
14%
(1)
|
100%
|
|
Introdução
do problema
|
71%
(5)
|
29%
(2)
|
100%
|
|
Auxílio
aos alunos
|
43%
(3)
|
57%
(4)
|
100%
|
|
Discussão
das estratégias
|
43%
(3)
|
57%
(4)
|
100%
|
|
Articulação
ao conteúdo
|
43%
(3)
|
57%
(4)
|
100%
|
Conforme se verifica na tabela cima,
71% dos participantes propuseram a introdução do problema, ou seja, que o
problema seria utilizado como ponto de partida para abordar o conteúdo. No entanto,
apenas 43% dos participantes apresentaram o uso de ações no ensino de auxílio
aos alunos, de discussão das estratégias dos alunos e de articulação ou
formalização do conteúdo. De forma geral, identificamos que apenas três
participantes (P2, P4 e P8) apresentaram todas as ações para o encaminhamento
do ensino via resolução de problemas, conforme ilustramos na resposta abaixo:
Função. Desenvolveria um problema envolvendo este
conteúdo matemático como ponto de partida. Em seguida, estimularia os alunos
para que buscassem resolvê-lo desenvolvendo estratégias para tal feito,
auxiliando-os sempre que preciso. E, por fim, faria a validação das estratégias
empregadas, relacionando-as ao conteúdo abordado. (Resposta de P8).
Além disso, destacamos que um dos participantes que não apresentou o uso do problema como ponto de partida descreveu um encaminhamento de aulas, segundo o ensino tradicional, a saber: “Não sei. Sistemas de equações. Após uma exposição tradicional, jogaria para o aluno elaborar exercícios para os colegas resolverem.” (P1).
Esses resultados indicam que, possivelmente, a maioria dos participantes de nosso estudo podem ter dificuldades para exercer um ensino de Matemática via resolução de problemas quando estiverem atuando em sala de aula. O estudo de Rodrigues (2018) mostrou justamente que, dos 31 professores que atuam nos anos finais do ensino fundamental e ensino médio, apenas dois professores descreveram realizar aulas que seguem o trabalho didático-pedagógico com a resolução de problemas como metodologia de ensino.
5. Conclusão
Neste nosso estudo, tivemos como objetivo analisar o conhecimento de professores recém-formados de cursos de Licenciatura em Matemática sobre o ensino de Matemática via resolução de problemas. Para tal, aplicamos um questionário online que continha um contexto/episódio de ensino e itens a serem respondidos.
A análise dos dados mostrou que os conhecimentos dos 10 participantes sobre o que é resolver um problema estavam alinhados ao que corresponde adequadamente ao processo de resolução de problemas. Foi possível identificar que os participantes reconhecerem etapas como as aquelas que envolvem a compreensão e a busca de estratégias de resolução.
A partir da análise das respostas sobre o episódio de ensino, verificamos que nove participantes identificaram, de forma adequada, que o trabalho praticado pelo professor não correspondia a um ensino via resolução de problemas. Apenas um participante entendeu, equivocadamente, que o episódio de ensino correspondia a um ensino via resolução de problemas. Possivelmente, este participante entenda que qualquer atividade a ser resolvida seja um problema, ideia diferente daquela em que um problema é uma situação que precisamos encontrar um caminho em busca da solução, segundo visão de Echeverría (1998).
Dentre esses nove participantes que conseguiram fazer essa identificação, verificamos que cinco deles não apresentaram em suas respostas indícios que nos mostrassem que sabiam o que seria um ensino via resolução de problemas, ou seja, aquele em que o problema é utilizado como ponto de partida para abordar um conteúdo. Ao contrário disso, quatro participantes descreveram adequadamente em suas respostas essa característica, revelando não apenas conhecimentos que ajudam a saber o que é, mas ainda o que não é.
Na análise da formação oferecida pelos cursos de licenciatura, verificamos que oito participantes deram indícios de que receberam uma formação não tão consistente sobre conhecimentos para ensinar Matemática via resolução de problemas. Apenas dois participantes evidenciaram em suas respostas aspectos de formação que aliam teoria e prática, ao mencionarem terem vivenciado esse ensino no estágio. Entendemos que tal vivência é uma condição importante da/na formação de professores, pois ajuda a construir e ampliar o uso do ensino via resolução de problemas em sala de aula.
Após evidenciarmos esses conhecimentos dos participantes, buscamos analisar como encaminhariam aulas de Matemática via resolução de problemas. Verificamos que 71% (n=7) deles propuseram a introdução do problema antes de abordar o conteúdo. No entanto, apenas 43% (n=7) dos participantes incluíram as ações de auxílio aos alunos quando estes estão envolvidos na busca de uma solução, de discussão das estratégias dos alunos e de articulação das estratégias dos alunos ao conteúdo. Trata-se de um resultado preocupante, pois além disso, três participantes sequer responderam como fariam esse encaminhamento.
Contudo, de forma geral, apesar de os participantes terem mostrado conhecimentos sobre o que é resolver um problema, sobre o que não corresponde a um ensino via resolução de problemas, ainda há participantes que não apresentaram conhecimentos sobre o que seria um ensino via resolução de problemas. Isso foi possível de ser constatado porque apenas 43% (n=7) deles conseguiram descrever encaminhamentos adequados a serem tratados em sala de aula.
Por fim, no que se refere às implicações de nossa pesquisa, salientamos a dificuldade de contar com os 52 recém-formados (universo do estudo), pois apenas 10 deles responderam ao questionário. Apesar disso, entendemos que o questionário online que utilizamos teve potencial para revelar os conhecimentos dos 10 participantes sobre resolução de problemas e para ensinar via resolução de problemas, pois verificamos, por exemplo, que o fato de dois participantes vivenciarem esse ensino no estágio já revela condições de constituição de conhecimentos teórico-práticos. Diante disso, o que poderia ser investigado de maneira aprofundada seria a formação oferecida nos cursos de licenciatura (grade curricular, análise das aulas dos formadores na graduação, entrevistas com formadores etc.) para revelar como se direciona a construção de conhecimentos pedagógicos relativos ao ensino de Matemática via resolução de problemas.
6. Referências
ALLEVATO, N. S. G.; ONUCHIC, L. R. Ensino-Aprendizagem-Avaliação de Matemática: por que através da Resolução de Problemas? In: ONUCHIC, L. R.; ALLEVATO, N. S. G.; NOGUTI, F. C. H.; JUSTULIN, A. M. (Orgs.). Resolução de Problemas: teoria e prática. Jundiaí: Paco, 2014, p. 35-52.
BARDIN, L. Análise de conteúdo. 4. ed. Trad. Luís Antero Reto e Augusto Pinheiro. Lisboa: Edições 70, 2010.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Educação Infantil e Ensino Fundamental. 3ª ed. Brasília: MEC, 2017.
BRASIL. Secretaria de Ensino Fundamental. Parâmetros curriculares nacionais: 3º e 4º ciclos. Brasília, DF, 1998.
BRASIL. Secretaria de Ensino Fundamental. Parâmetros curriculares nacionais: matemática, 1º e 2º ciclos. Brasília, DF, 1997.
BRITO, M. R. F. Alguns aspectos teóricos e conceituais da solução de problemas matemáticos. In: BRITO, M. R. F. (Org.). 2. ed. Solução de problemas e a matemática escolar. Campinas: Alínea, 2010, p. 13-53.
CAI,
J.; LESTER, F. Por que o ensino com resolução de problemas é importante para a
aprendizagem
do aluno? Boletim GEPEM, n. 60,
jan./jun., 147-162, 2012.
CHAER, G., DINIZ, R. R. P.; RIBEIRO, E. A. A técnica do questionário na pesquisa. Evidência, n. 7, v. 7, p. 251-266, 2011.
CHARLES, R. I. T. The role of problem solving. Arithmetic Teacher, 32, p. 48-50, february, 1985.
CHI, M. T. H.; GLASER, R. A capacidade para a solução de problemas. In: STERNBERG, R. As capacidades intelectuais humanas: uma abordagem em processamento de informações. Trad. Dayse Batista. Porto Alegre: Artes Médicas, 1992, p. 249-275.
CHIZZOTTI, A. Pesquisa em ciências humanas e sociais. 5. ed. São Paulo: Cortez, 2001.
DEWEY, J. How we think. Boston: D.C. Heath & Co, 1910.
ECHEVERRÍA, M. P. P. A solução de problemas em matemática. In: POZO, J. I. (Org.). A solução de problemas: aprender a resolver, resolver para aprender. Porto Alegre: ArtMed, 1998, p. 43-65.
FI, C. D.; DEGNER, K. M. Teaching through problem solving. Mathematics Teacher, v. 105, n. 6, february, p. 455-459, 2012.
GAGNÉ, R. M. Some issues in the Psychology of Mathematics Instruction. Journal for Research in Mathematics Education, Reston, v. 14, n. 1, p. 7-18, 1983.
IMBERNÓN, F. Formação docente e profissional: formar-se para a mudança e a incerteza. 9. ed. (Trad. Silvana Cobucci Leite). São Paulo: Cortez, 2011.
KRULIK, S.; RUDNICK, J. A. Teaching problem solving to preservice teachers. Arithmetic Teacher, v. 29, n. 6, p. 42-45, february, 1982.
MAYER, R. E. Thinking, problem solving, cognition. 2. ed. New York: WH Freeman and Company, 1992.
ONUCHIC, L. R. Ensino-aprendizagem de matemática através da resolução de problemas. In: BICUDO, M. A. V. Pesquisa em Educação Matemática: concepções e perspectivas. São Paulo: UNESP, 1999, 314p., p. 199-218.
POLYA, G. A arte de resolver problemas: um novo enfoque do método matemático. Tradução de Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1994.
POZO, J. I; ANGÓN, Y. M. A solução de problemas como conteúdo procedimental da educação básica. In: POZO, J. I. (Org.). A solução de problemas: aprender a resolver, resolver para aprender. Porto Alegre: ArtMed, 1998, p. 139-165.
PROENÇA, M. C. Resolução de Problemas: encaminhamentos para o ensino e a aprendizagem de Matemática em sala de aula. Maringá: Eduem, 2018.
PROENÇA. M. C. A resolução de problemas na licenciatura em matemática: análise de um processo de formação no contexto do estágio curricular supervisionado. 2012. 208f. Tese (Doutorado em Educação para a Ciência) – Faculdade de Ciências, Universidade Estadual Paulista, Bauru, 2012.
RODRIGUES, E. A. N. Resolução de Problemas como metodologia de ensino: compreensão relatada de professores de Matemática. 2018. 175f. Dissertação (Mestrado em Educação) – Faculdade de Ciências e Tecnologia, Universidade Estadual Paulista, Presidente Prudente, 2018.
SANTANA, G. F. N. Resolução de problemas: ações pedagógicas de professores de matemática dos anos finais do ensino fundamental. 2016. 119 f. Dissertação (Mestrado em Educação para a Ciência e a Matemática) – Centro de Ciências Exatas, Universidade Estadual de Maringá́, Maringá, 2016.
SCHOENFELD, A. H. Problem solving in context(s). In: CHARLES, R. I.; SILVER, E. A. (Eds.). The teaching and assessing of mathematical problem solving. 3 ed. Virginia: Lawrence Erlbaum Associates, 1990, NCTM, 282p., p. 82-92.
SCHOENFELD, A. H. Mathematical problem solving. Orlando: Academic Press, 1985.
SCHROEDER, T. L.; LESTER, F. K., JR. Developing understanding in mathematics via problem solving. In: TRAFTON, P. R.; SHULTE, A. P. (Eds.). New directions for elementary school mathematics. Reston: NCTM, 1989, p. 31-42.
SHULMAN, L. S. Those Who understand: knowledge growth in teaching. Educational Researcher, v. 15, n. 2, fev., p. 04-14, 1986.
STERNBERG, R. Psicologia cognitiva. Trad. Maria Regina Borges Osório. Porto Alegre: ArtMed, 2000.
Autor notes
[1] Doutor
em Educação para a Ciência pela Faculdade de Ciências da Universidade Estadual
Paulista – FC/UNESP, campus de Bauru-SP. Professor do Programa de
Pós-Graduação em Educação para a Ciência e a Matemática da Universidade Estadual
de Maringá – UEM, campus sede em Maringá-PR. Endereço: Avenida Colombo,
5790, Jardim Universitário, 87.020-900, Departamento de Matemática (Bloco F67).
Ligação alternative
https://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/232 (pdf)










