



Artículo de Investigación
Solución al problema del transporte de Aplicación práctica.
Solution to the transportation problem practical application
Ecuadorian Science Journal
GDEON, Ecuador
ISSN-e: 2602-8077
Periodicidad: Semestral
vol. 5, núm. Esp.4, 2021
Recepción: 31 Agosto 2021
Aprobación: 04 Octubre 2021

Como citar: Girón G , M. F., López B , J. R., & Sornoza B, K. J. (2021). Solución al problema del transporte de Aplicación práctica. Ecuadorian Science Journal, 5(4), 61-73. DOI: https://doi.org/10.46480/esj.5.4.170
Resumen: En 1947, T. C. Koopmans presentó su obra “Optimum utilization of the transportation system”, estas dos obras constituyen el pilar fundamental para el desarrollo de los métodos de transporte. Sin embargo, fue William R. Vogel quién comienza a realizar estudios de lo que posteriormente se convirtiera en un modelo de solución y optimización para el problema de transporte. Existen una diversidad de métodos para encontrar una solución óptima al problema del transporte, así podemos mencionar el método de la Esquina Noroeste; método de Aproximación de Vogel y el método del Costo Mínimo. El método de Aproximación de Vogel es un método heurístico y usualmente proporciona una mejor solución de inicio que los demás métodos, es el de mayor aplicación en la solución de temas relacionados con la industria y el comercio en general dado que desde el comienzo toma en consideración los costos unitarios de cada una de las diferentes rutas posibles para minimizar el costo total de la operación. Una de las primeras aplicaciones de las técnicas de programación lineal ha sido la formulación y solución del problema del trans-porte mediante la aplicación de un proceso iterativo hasta determinar lo que se llama “solución básica factible inicial”, la misma que sometida a un proceso de optimización finalmente nos conduce a encontrar las cantidades precisas a ser despachadas, desde cada origen hacia cada destino en función de un costo total operacional mínimo. Para ello, tenemos disponibles los métodos de la esquina nor oeste; método de aproximación de Vogel y método del costo mínimo. Como método de optimización nos apoyamos por lo general en el método MODI.
Palabras clave: Equilibrio, Método, Transporte, Modelos Matemáticos, Multiplicadores.
Abstract: In 1947, T. C. Koopmans presented his work "Optimum utilization of the transportation system", these two works constitute the fundamental pillar for the development of transportation methods. However, it was William R. Vogel who began to carry out studies of what later became a solution and optimization model for the transport problem. There are a variety of methods to find an optimal solution to the transportation problem, so we can mention the Northwest Corner method; Vogel's Approximation method and the Minimum Cost method. The Vogel Approximation method is a heuristic method and usually provides a better starting solution than the other methods, it is the one with the greatest application in solving issues related to industry and commerce in general since from the beginning it takes taking into account the unit costs of each of the different possible routes to minimize the total cost of the operation. One of the first applications of linear programming techniques has been the formulation and solution of the transport problem through the application of an iterative process until determining what is called an "initial feasible basic solution", the same as submitted to an optimization process finally, it leads us to find the precise quantities to be dispatched, from each origin to each destination based on a minimum total operational cost. For this, we have the North West corner methods available; Vogel's approximation method and least cost method. As an optimization method, we generally rely on the MODI method.
Keywords: Balance, Method, Transport, Mathematical Models, Multipliers.
Introducción
El transporte desempeña un papel importante en la economía de las empresas. La disponibilidad de un sistema de transporte seguro y económico es de vital importancia para la supervivencia de las empresas. Una característica de las cadenas de suministros el movimiento del producto desde los varios orígenes hacia un conjunto de diferentes destinos demandantes con el menor costo posible (Hidalgo, 2015). Si de hecho estamos considerando varios orígenes y varios destinos, podemos mencionar que el objetivo básico de solucionar el problema es satisfacer las expectativas de los clientes estableciendo rutas entre las diversas fuentes y destinos a un costo mínimo sin menoscabo de la calidad tanto de los productos como del servicio de distribución. El objetivo es minimizar el costo total de distribuir las unidades fabricadas (Lieberman , 2018).
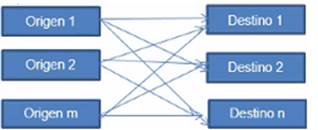
El diagrama mostrado nos permite ver las diferentes rutas para transportar desde cada origen hasta cada destino en función de un costo total mínimo.
Basados en esto, podemos definir el modelo de transporte como una metodología que apunta a determinar un modelo de distribución de productos en general desde los diferentes orígenes hasta los distintos destinos del mercado demandante (González Ariza, 2015).
OBJETIVOS
El método del transporte es una aplicación singular de la programación lineal cuyo objetivo es determinar el esquema de transporte que minimice el costo total de este, conocidos los costos unitarios de transporte desde el origen i hasta el destino j.
MATERIAL Y METODOS
MÉTODOS DE SOLUCIÓN
Método de aproximación de Vogel
Método de la Esquina Nor – Oeste
Método del Costo Mínimo
MÉTODO DE APROXIMACIÓN DE VOGEL
Uno de los objetivos del método de Vogel es reducir al mínimo posible los costos de transportar mercaderías desde los m orígenes (plantas productoras) hasta los n destinos (mercado demandante), con lo cual estamos mejorando los niveles de rentabilidad de la empresa.
Es posible que, en ocasiones en el método de aproximación de Vogel, la solución básica factible inicial encontrada sea la solución óptima, o en su defecto sea necesario un mínimo de iteraciones para llegar a ella. El método de Vogel considera los costos unitarios en forma eficaz puesto que la diferencia representa el mínimo costo adicional en que se incurre por no hacer una asignación en la celda que tiene el menor costo en una determinada fila o columna (Lieberman, 2018). Podríamos decir que esta es la ventaja principal de este método en comparación con otros.
Se considera que es el método mediante el cual se llega rápidamente a la solución óptima.
METODOLOGÍA DE SOLUCIÓN
El proceso se inicia estableciendo la diferencia entre los dos costos más bajos para cada fila y columna. De la totalidad se toma el de mayor valor y esa será la fila o columna a considerar. En función de ello ir asignando volúmenes a transportar comenzando con las celdas de costos más bajos hasta que la oferta o demanda se saturen. De haber valores repetidos, se asigna al azar.
CASO DE ESTUDIO
Producción y despacho de almidón modificado de maíz.
El almidón modificado de maíz es elaborado en 3 plantas ubicadas en 3 ciudades diferentes y requiere ser despachado a 4 clientes localizados en 4 diferentes ciudades dentro del país. Los costos de transporte unitario por tonelada desde cada origen a cada destino y los volúmenes de oferta y de-manda en cientos de toneladas/año son los siguientes:
| Destino # 1 | Destino # 2 | Destino # 3 | Destino # 4 | Total Oferta | |
| Fábrica # 1 | 10 | 0 | 20 | 11 | 15 |
| Fábrica # 2 | 12 | 7 | 9 | 20 | 25 |
| Fábrica # 3 | 0 | 14 | 16 | 18 | 5 |
| Total Demanda | 5 | 15 | 15 | 10 |
Se pide determinar los volúmenes óptimos a despachar desde cada fábrica hacia cada destino teniendo en cuenta que el costo total del transporte sea el mínimo posible.
RESULTADOS
Procedemos a elaborar el primer tablero conocido como “Solución Básica Factible Inicial”. Está formada con los costos unitarios de transporte; las cantidades demandadas por cada destino y las cantidades ofertadas por cada fábrica, se debe verificar que el sistema esté en equilibrio es decir que la ofer-ta sea igual a la demanda. Este método de Vogel nos lleva a aplicar el método de penalizaciones para cada fila y columna. La penalización se obtiene restando en cada fila y columna los dos costos (Ci) más bajos.

PROCEDIMIENTO PARA EL LLENADO DEL TABLERO
En esta primera tabla se observa que la mayor diferencia se encuentra en la fila correspondiente a la fábrica 3 y por tanto trabajaremos en esa fila. (En caso de igualdad entre filas y columnas, rompemos la igualdad de manera arbitraria). Loca-lizamos la celda de menor costo y ahí asignamos la mayor cantidad de carga posible respetando las limitantes de oferta y demanda. La regla indica que la carga a asignar es la menor entre la oferta y la demanda y en este caso corresponde el 5. Las demás celdas de la fila o columna deberán ser clausura-das.
Pasamos ahora a determinar las diferencias 2 y 3 para lo cual seguiremos el mismo procedimiento y tomaremos las mismas precauciones. Los resultados los vemos en el cuadro anterior.
Una vez que se ha llenado el tablero nos corresponde deter-minar el costo total de la solución básica factible encontrada.
El siguiente paso es determinar si la solución es degenerada o no degenerada (Gonzalez Ariza, 2015).
La inecuación nos dice: (# filas + # columnas – 1) es menor o igual al # de celdas asignadas. Es decir: m + n – 1 ≤ #Ca
Veamos ahora si la solución es óptima o no. Para ello utiliza-remos el método de los multiplicadores.
CALCULO DE MULTIPLICADORES
Construimos un nuevo tablero copiando las cifras asignadas en el anterior y agregando el € que nos hace falta. A conti-nuación, en la fila correspondiente a F – 1 asumimos el valor cero y lo tomamos como punto de partida para el cálculo de los demás, pero considerando únicamente las celdas asigna-das (celdas con solución). En este caso, va a primar el con-cepto Ci = ui + vj
Se obtiene entonces siguiente tablero:
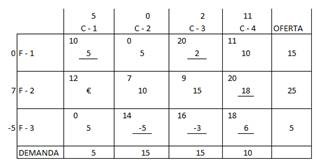
El hecho de que todos los costos marginales son menores que los costos unitarios de transporte nos indica que la solución básica factible inicial corresponde a la solución óptima.
Cálculo de multiplicadores. Optimización
Se procede a la aplicación de u_i= c_ij- v_j para luego calcular los costos marginales correspondientes a cada celda no asignada y finalmente decidir acerca de la reasignación de cifras.
Se comienza por asumir un valor cualquiera para filas (u) o columnas (v). En términos generales se recomienda el valor de 0 para la fila correspondiente a la fábrica 1. Una sugerencia no vinculante es asignar un cero en la fila o columna que tenga la mayor cantidad de celdas asignadas. El proceso sigue mediante sumas y restas hasta completar la totalidad de filas y columnas. Esta operación aplica únicamente a las celdas que el proceso de iteración asignó cantidades a transportar.
Es importante recalcar que la metodología de cálculo supone que el costo de transporte es proporcional a la cantidad transportada en cada ruta considerada (Taha, 2012).
En este caso, la solución básica factible inicial corresponde a la solución óptima y su costo total es de UM315
En tal virtud, la solución óptima al problema planteado queda tal como sigue:
| DESDE | ENVIAR A | CANTIDAD |
| ORIGEN 1 | DEST. 2 | 5 |
| DEST. 4 | 10 | |
| ORIGEN 2 | DEST. 2 | 10 |
| DEST. 3 | 15 | |
| ORIGEN 3 | DEST. 1 | 5 |
MÉTODO DE LA ESQUINA NOR – OESTE
Una gran desventaja de este método es que no considera los costos unitarios de transporte. Esto hace que no se pueda llegar a la solución óptima sino hasta después va varias itera-ciones.
EJERCICIO DE APLICACIÓN
Apliquemos ahora el método de la Esquina N. O. y resolvamos el caso de análisis planteado en el método de Vogel.

Veamos ahora si se trata de una solución óptima:
Primeramente, vamos a utilizar el método de los multiplicado-res:
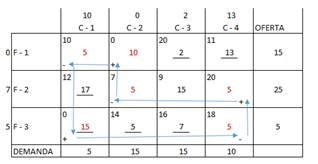
De las celdas marcadas en rojo, seleccionaremos la que tenga el menor costo marginales este caso cero y procedemos a efectuar la redistribución de las cantidades a transportar en función de las celdas que tienen signos positivos y negativos.
Siempre se completará el circuito con los signos alternados.
En el siguiente tablero se muestra la redistribución de cantidades a transportar.
La cantidad a agregar en cada celda con signo positivo es determinada por el menor valor en las celdas con signo negativo.

Ahora veamos si la solución es óptima
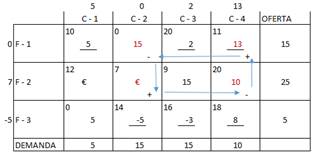
En este nuevo tablero, la única celda que rebasa su Ci es la que tiene por costo marginal 13.
El nuevo tablero es el siguiente:

CT = (5 * 0) + (10 * 11) + (10 * 7) + (15 * 9) + (5 * 0)
CT = 0 + 110 + 70 + 135 + 0 = 315
3 + 4 – 1 ≤ 5
6 ≤ 5
Solución degenerada. Requiere 1€
Veamos ahora si se trata de la solución óptima.
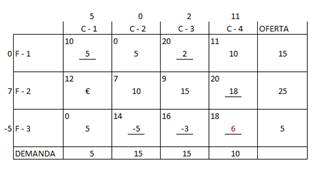
Vemos que ninguno de los costos marginales sobrepasa los valores de Ci en sus correspondientes celdas. Por tanto, hemos llegado a la solución óptima.
La solución final al problema es la siguiente:
| DESDE | ENVIAR A | CANTIDAD |
| ORIGEN 1 | DEST. 2 | 5 |
| DEST. 4 | 10 | |
| ORIGEN 2 | DEST. 2 | 10 |
| DEST. 3 | 15 | |
| ORIGEN 3 | DEST. 1 | 5 |
MÉTODO DEL COSTO MÍNIMO
Algunos autores lo consideran como una versión mejorada del método de la esquina nor oeste. En todo caso nos permite llegar con poco esfuerzo a la solución óptima.
EJERCICIO DE APLICACIÓN
Resolvamos ahora el mismo caso de análisis, pero aplicando el método del costo mínimo.
En este caso siempre trabajaremos en la celda disponible con menor Ci y en este caso cero.

Veamos ahora si la solución es la óptima o no.
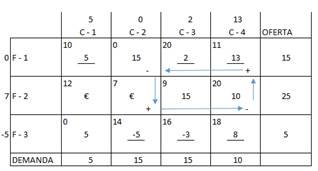
Ahora procedemos a realizar la redistribución de la carga en función del diagrama de flechas presentado y además a verificar si se trata de la solución óptima:
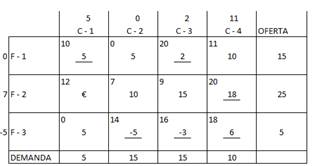
Podemos ver que ninguno de los costos marginales supera el Ci de su celda.
Nuevamente vemos que se cumple que ninguno de los costos marginales supera los costos unitarios de transporte, esto nos dice que hemos llegado a la solución óptima. La solución final será:
| DESDE | ENVIAR A | CANTIDAD |
| ORIGEN 1 | DEST. 2 | 5 |
| DEST. 4 | 10 | |
| ORIGEN 2 | DEST. 2 | 10 |
| DEST. 3 | 15 | |
| ORIGEN 3 | DEST. 1 | 5 |
El costo total de la solución es:
CT = (5 * 0) + (10 * 11) + (10 * 7) + (15 * 9) + (5 * 0)
CT = 315
RESULTADOS
| DESDE | ENVIAR A | CANTIDAD |
| VOGEL | ||
| Origen 1 | Destino 2 | 5 |
| Destino 4 | 10 | |
| Origen 2 | Destino 2 | 10 |
| Destino 3 | 15 | |
| Origen 3 | Destino 1 | 5 |
| NOR OESTE | ||
| Origen 1 | Destino 2 | 5 |
| Destino 4 | 10 | |
| Origen 2 | Destino 2 | 10 |
| Destino 3 | 15 | |
| Origen 3 | Destino 1 | 5 |
| COSTO MIN. | ||
| Origen 1 | Destino 2 | 5 |
| Destino 4 | 10 | |
| Origen 2 | Destino 2 | 10 |
| Destino 3 | 15 | |
| Origen 3 | Destino 1 | 5 |
DISCUSION
En el cuadro se puede apreciar que, en los tres métodos utilizados, los envíos desde cada origen hasta cada destino es la misma. Otro detalle es que las cantidades despachadas desde cada origen se ajustan a las disponibilidades de cada fábrica. Igualmente, las cantidades recibidas en cada destino se ajustan a los volúmenes demandados.
CONCLUSION
Hemos comprobado que cualquiera que sea el método de análisis, el costo total de la solución óptima será el mismo.
La distribución de productos desde cada origen hasta cada destino es la misma.
REFERENCIAS BIBLIOGRÁFICAS
González Ariza, A. (2015). Manual práctico de investigación de operaciones. Barranquilla: Universidad del norte.
Guerrero Salas , H. (2009). Programación Lineal Aplicada. Bogotá: Ecoe Ediciones.
Izar, J. M. (1996). Fundamentos de la Investigación de Operaciones. México.
Lieberman, G. J. (2018). Introducción a la Investigación de Operaciones. México: Mc Graw Hill.
Nápoles Peña, O. (2007). Folleto de Investigación de Operaciones I. La Habana: Universitaria.
Otero, J. M. (2006). Modelos de Optimización Continuos. La Habana : Felix Varela.
Pinzón, F. C. (2012). Investigación Operativa. Ibagué: Universidad de Ibagué.
Rincón, L. A. (2001). Investigación de Operaciones para Ingenierías y Administración de Empresas. Cali: Universidad Nacional.
Salazar, I. M. (2014). Investigación Operativa. Nuevo León - México: Grupo editorial Patria.
Taha, H. A. (2012). Investigación de Operaciones. México: Pearson Prentice Hall.
Taibo, A. (2009). Investigación de operaciones para los no matemáticos. México: Politécnica Nacional - México.
Información adicional
Como citar: Girón G , M. F., López B , J. R., & Sornoza B, K. J. (2021). Solución al problema del transporte de Aplicación práctica. Ecuadorian Science Journal, 5(4), 61-73. DOI: https://doi.org/10.46480/esj.5.4.170

