1. INTRODUÇÃO

Em Portugal, após o final da Segunda Guerra Mundial, as preocupações com o desenvolvimento económico, tecnológico e científico do país que pedia uma maior qualificação da população ativa, assumiram grande importância na evolução do sistema educativo. Esta viragem iniciou com a reforma de Pires de Lima, promulgada pelo Decreto-Lei n.º 36 507, de 17 de Setembro de 1947, seguida da aprovação do Estatuto do Ensino Liceal pelo Decreto-Lei n.º 36 508, do mesmo ano (TEODORO, 2001). Este último repõe o regime do livro único para todas as disciplinas, ou seja, para o ensino de cada disciplina nos diferentes anos de um ciclo era adotado em todos os liceus o mesmo livro. A reforma propunha também a remodelação dos programas liceais, e os novos programas são promulgados em 1948, no Decreto-Lei n.º 37 112, de 22 de Outubro.

Os novos programas do 3.º ciclo liceal reintroduzem o estudo da análise infinitesimal que tinha sido eliminado em 1936 nos programas do ensino secundário. Os programas apresentam essencialmente uma relação de conteúdos a tratar. Assim, temos como grandes temas aglutinadores: a Álgebra, a Trigonometria, a Aritmética Racional e a Geometria. A principal alteração nos novos programas e que está ligada ao estudo da análise é a introdução do estudo de limites, funções, continuidade e derivadas (AIRES & SANTIAGO, 2014; ALMEIDA, 2020). Os conceitos reintroduzidos são abordados no tema Álgebra, que incluía o estudo de funções, limites, polinómios, equações, inequações, análise combinatória, números complexos e derivadas.

No que respeita a livros para o ensino dos temas destes programas, estava previsto no normativo a aprovação de novos livros. O Compêndio de Álgebra para o 3.º ciclo dos liceus, da autoria de António Augusto Lopes, foi o livro aprovado como ‘intérprete’ dos programas de 1948. Este livro único para o ensino da Álgebra foi aprovado em 1950. O trabalho de Almeida (2020) permitiu compreender melhor a polémica em torno da aprovação do Compêndio de Álgebra, livro único aprovado em 1950 para o 3.º ciclo dos liceus e a análise comparativa de duas edições distintas do livro evidenciou uma mudança no conteúdo do livro que implicou um desenvolvimento do conhecimento pedagógico do conteúdo do autor, ilustrando as dificuldades que os autores/professores têm de lidar quando enfrentam uma transição de currículo, especialmente, quando há alterações no conteúdo matemático a ser ensinado.

A criação de Liceus Normais destinados a serem as escolas de preparação prática dos professores do ensino liceal foi determinada pelo modelo de formação de professores instituído em 1930. Neste sistema de formação de professores competia às Faculdades conferir formação científica e conhecimentos pedagógicos (cultura pedagógica). A prática pedagógica era proporcionada pelo trabalho realizado durante um estágio, não remunerado, de dois anos num Liceu Normal - Liceu Pedro Nunes, em Lisboa, e Liceu D. João III, em Coimbra. Nesta experiência profissional, o futuro professor era acompanhado por um professor metodólogo que era responsável pela sua orientação no estágio (ALMEIDA, 2018). A reforma do ensino liceal de 1947 vai centralizar a formação de professores num único liceu, o D. João III, em Coimbra (NÓVOA, 1992; PINTASSILGO, MOGARRO & HENRIQUES, 2010). Atualmente, a renomeada Escola Secundária José Falcão, em Coimbra, conserva na sua Biblioteca, nomeadamente no Arquivo, muitos documentos respeitantes a estágios realizados enquanto sob a designação de Liceu D. João III.

Em momentos de alterações educativas podem ocorrer recomposições relacionadas com o conhecimento do professor, que se manifestam nos conteúdos ou nas metodologias de ensino. Neste texto procuramos entender o modo como ocorreu a reintrodução da análise infinitesimal no ensino liceal e contribuir para aprofundar o conhecimento sobre a formação do conhecimento profissional de professores de matemática do ensino liceal. Para compreender como se processam as recomposições do conhecimento profissional docente, seguiremos as diferenciações no conhecimento profissional dos professores propostas por Shulman (1986, 1987). Esse foi o enquadramento teórico usado em Matos e Monteiro (2011) que destaca a especificidade do conhecimento profissional do professor que inclui, para além do conhecimento pedagógico geral e do conhecimento científico, o conhecimento didático do conteúdo. Shulman sustenta que o conhecimento pedagógico do conteúdo não é uma mera justaposição de conteúdos e didática, trata-se antes da “fusão de conteúdos e pedagogia numa compreensão de como tópicos, problemas e assuntos específicos são organizados, representados e adaptados aos distintos interesses e capacidades dos aprendizes e apresentados para ensino” (SHULMAN, 1987, p. 8). Outro autor Chervel (1990) realça a importância das disciplinas escolares (incluindo o seu currículo) como produtos específicos ou criações próprias da cultura escolar, bem como o carácter relativamente autónomo desta cultura. Julia (2001) aprofunda o trabalho de Chervel, operacionalizando o conceito de cultura escolar. Pela sua condição específica na formação de professores, os Liceus Normais são instituições que adaptam os saberes criando um saber e uma cultura próprios.

As etapas que seguimos inscrevem-se na metodologia da investigação histórica. Para além do normativo legal, as nossas fontes foram revistas pedagógicas e científicas, livro para o ensino e trabalhos produzidos pelos estagiários (documentos manuscritos). O levantamento documental foi realizado no Arquivo Histórico da Secretaria-Geral do Ministério da Educação e no Arquivo da Biblioteca da Escola Secundária José Falcão.

2. OS NOVOS PROGRAMAS DE MATEMÁTICA E O ENSINO DA ANÁLISE: O DEBATE NA IMPRENSA

António Nóvoa (1993) afirma que as informações reveladas pela imprensa têm um carácter único, pois tratam-se, na maioria dos casos, de reflexões bem próximas dos acontecimentos e que assentam “numa lógica de reacção a realidades ou a ideias, normas legais ou a situações políticas” (NÓVOA, 1993, p. XXXII). A Gazeta de Matemática^[1], na secção de pedagogia da revista, vai publicar vários artigos sobre assuntos que interessavam aos professores do ensino secundário. Antes de prosseguir, damos aqui a organização do sistema educativo português, iniciava-se com o ensino primário obrigatório (quatro anos), findo o qual o aluno poderia frequentar o ensino secundário, que englobava dois ramos: liceal (que possibilitava aceder à universidade) e técnico (habilitava para o exercício de uma profissão especializada, viabilizando ainda acesso aos institutos). O ensino nos liceus compreendia três ciclos - 1.º ciclo (10-11 anos), 2.º ciclo (12-14 anos), 3.º ciclo (15-16 anos).

A reforma de Pires de Lima teve os seus novos programas de Matemática para o ensino liceal publicados em outubro de 1948, e, em março de l949, aparecem as primeiras reações a esses programas na Gazeta de Matemática. Num artigo da sua autoria Laureano Barros e Fernando Soares David^[2] fazem uma crítica sobre a qualidade da terminologia matemática usada nesses programas de Matemática, apontando incorreções e imprecisões de linguagem, bem como desconexões no encadeamento dos assuntos versados no programa, e tecem algumas recomendações. Em particular, relativamente aos programas para o 3.º ciclo liceal, Barros e David (1949, pp. 12-l3) dizem

Entre os requisitos fundamentais a que deve obedecer a elaboração dum programa ocupam lugar de destaque a precisão do enunciado dos seus tópicos e um criterioso encadeamento dos vários assuntos. Ora parece-nos que nenhum destes requisitos foi devidamente considerado na elaboração dos novos programas de Matemática. (...) «Limite duma variável» (Álgebra, 6.º ano), expressão sem qualquer sentido; (...) qual o sentido da palavra «elementar» quando dizem «noção elementar de variável o de função« ou «noção elementar de continuidade de uma função»; (...) só no 7.º ano se estuda a noção de derivada e suas aplicações. Parece fora de dúvida que a altura própria para abordar este assunto seria imediatamente a seguir ao estudo dos infinitésimos, tanto mais que é precisamente no 6.º ano que o programa de Física mais necessita dos elementos de cálculo diferencial.

Também Maria Teodora Alves^[3] aborda este tópico num artigo intitulado "O conceito de derivada de uma função na Escola Secundária” na Gazeta de Matemática, n.º 43 de 1950. Maria Teodora Alves (1950, p. 11), apoiando-se em Klein, Borel, Tannery e Laisant, refere que

A derivação de funções, na opinião desses ilustres professores, não deve ser ensinada na escola secundária somente para que os alunos calculem derivadas de funções e resolvam os numerosos exercícios que figuram habitualmente nos cadernos de exercícios. É um instrumento de trabalho que deverá ser usado pelos alunos e cuja utilidade deverá ser por eles reconhecida.

Em todos os programas da escola secundária que conheço e em que foi introduzido o conceito de derivada de uma função (França, Inglaterra, Bélgica, Estados Unidos da América) há consequentemente, como uma das suas aplicações, pelo menos, o estudo da variação de certas funções.

O programa actual dos nossos liceus, introduzindo o conceito de derivada de uma função, mas suprimindo as suas aplicações, apresenta, a meu ver, uma deficiência. O conceito de derivada, assim introduzido no programa equivale, por exemplo, ao estudo das equações do 1.º e 2.º graus sem as aplicar resolução de problemas que possam ser traduzidos por elas. Mais comezinhamente, equivale há aquisição de um microscópio ou de uma máquina fotográfica sem que se saiba utilizar esses instrumentos nem para que servem.

Maria Teodora Alves (1950) considera ser uma falha dos programas não haver algumas aplicações do conceito de derivada de uma função ao estudo de funções. Com efeito, o programa não tem no seu texto qualquer referência a aplicações das derivadas. Barros e David (1949) já haviam comentado os programas relativamente à localização do conceito de derivada com base na sua aplicação à Física e a sua articulação com o estudo dos limites. Teodora Alves (1950, p. 12) tem a mesma opinião que Barros e David (1949), no que respeita à localização do conceito de derivada de uma função, no programa vigente referindo

não me parece que tenha sido muito feliz.

Aquele conceito aparece no 7.º ano entre as seguintes rubricas do programa: «Problemas do 2.º grau, discussão» e «Trigonometria: fórmulas da soma e da diferença de dois ângulos».

Por outro lado, no programa do 6.º ano, seguir às rubricas «Infinitamente grandes; infinitésimos; infinitésimos simultâneos; teoremas relativos ao produto e à soma de infinitésimos. Limite de uma variável; limite de uma função; operações sobre limites. Noção elementar de continuidade de uma função.» aparece esta rubrica «Propriedades dos polinómios inteiros.»

Estava naturalmente indicado, como sequência das primeiras rubricas transcritas, o conceito de derivada de uma função.

Houve ali uma amputação desse conceito para surgir desgarrado no programa de 7.º ano.

Em junho de 1951, o n.º 48 da Gazeta de Matemática publica a primeira parte de um artigo de Maria Teodora Alves, intitulado “O programa de Matemática da actual reforma do ensino liceal”. As segunda e terceira partes serão publicadas no n.º 49 em outubro 1951 e n.º 51 em abril de 1952, respetivamente. Cada artigo é dedicado a um ciclo, sendo o objetivo da crítica de Teodora Alves, em cada ciclo, a didática da Matemática imposta pelo respectivo programa, o encadeamento dos tópicos e a coordenação do programa com o das outras disciplinas. No que respeita ao 3.º ciclo, Teodora Alves reafirma que não sendo possível “introduzir no programa algumas aplicações do conceito de derivada de uma função, é preferível que esse conceito seja suprimido" (ALVES, 1952, p. 7). Propondo um arranjo nas matérias que podem constituir o programa de Matemática do 3.º ciclo, no que respeita o estudo da análise, Maria Teodora Alves (1952, p. 8) recomenda

No 6.º ano seria somente estudada Álgebra e Trigonometria. No 7.° ano seria também somente estudada Álgebra e Aritmética Racional. O actual programa de Álgebra do 6.° ano seria acrescido do conceito de derivada de uma função, colocado a seguir à rubrica do programa actual «Conceito de continuidade de uma função» e tendo como aplicação o estudo da variação das seguintes funções: $y=ax+b;y=a{x}^2+bx+c;y=\frac{ax+b}{a^{\prime }x+b\prime }$

O matemático de grande notoriedade nacional e mentor da reforma da Matemática Moderna em Portugal, Sebastião e Silva^[4] no artigo “A Análise Infinitesimal no Ensino Secundário”, publicado na Gazeta de Matemática, em outubro de 1951, começa por abordar a reintrodução do estudo da análise infinitesimal, nos programas de Matemática do 3.º ciclo liceal promulgados em 1948, e de seguida, desenvolve as suas ideias pedagógicas sobre ensino da análise neste ciclo. O autor manifesta satisfação na reintrodução do estudo da análise no ensino secundário, em primeiro lugar, por estar convicto de que a exclusão completa da análise infinitesimal do programa dos liceus que tinha ocorrido na anterior reforma (1936) trouxera profundas perturbações no ensino global das matérias científicas, nomeadamente ao nível universitário, pois, o aluno ao entrar na universidade sem ter adquirido a mínima familiaridade com o conceito de infinitésimo e de derivada, passava bruscamente a ter de assimilar o método infinitesimal em todas as suas minúcias. Em segundo lugar, porque não perfilha a ideia de que os conceitos como os de infinitésimo e derivada são demasiado complexos para jovens de 15 ou 16 anos. Sebastião e Silva orienta o seu texto suportando-se na ideia de que

a matemática não é só lógica; a matemática é um produto humano, intimamente ligado às necessidades do homem, à sua existência sobre este planeta. Ensinar matemática sem mostrar a origem e a finalidade dos conceitos á como falar de cores a um daltónico: é construir no vazio. Especulações matemáticas que, pelo menos de início, não estejam solidamente ancoradas em intuições, resultam inoperantes, não falam ao espírito, não o iluminam.

O ideal seria conciliar o máximo de intuitividade com o máximo de racionalidade. E por isso mesmo que não há uma fórmula para efectuar esta conciliação é que a pedagogia é mais uma arte da que uma ciência. (SILVA, 1951, p. 2, itálico no original)

Afirmando que a “análise infinitesimal assenta essencialmente sobre os conceitos de função e de limite. E é sobretudo nesta base que reside a delicadeza do problema pedagógico de que nos estamos ocupando.” (SILVA, 1951, p. 2), Sebastião e Silva vai salientar mais adiante que “desde logo se observa, na teoria dos limites, é que a linguagem se torna mais intuitiva, quando se fala de «limite duma variável» em vez de «limite duma sucessão» ou de «limite duma função».” (SILVA, 1951, p. 2 aspas no original). No que concerne ao estudo dos limites de funções, refere

A seguir aos limites de sucessões — os limites de funções (de variável real). E logo aqui surge uma questão delicadíssima. Como se sabe, o conceito de «limite duma função f(x) quando x tende para um número a» pode ser definido pelo menos de duas de limite duma sucessão (orientação do Heine) o directamente, com o conhecido jogo dos δ e dos ε (orientação de Cauchy). A primeira definição é sem dúvida a mais natural. (SILVA, 1951, p. 3, aspas no original)

Sebastião e Silva apresenta em seguida as vantagens da primeira definição (no estilo de Heine), que segundo ele, não se reduzem apenas à naturalidade da definição em si, mas concretizam-se depois nas demonstrações dos teoremas relativos a operações sobre limites. Sendo, portanto, esta definição de limite a que melhor se adapta a esta fase do ensino. Este autor, no que respeita ao estudo das derivadas tem a mesma opinião que Barros, David e Alves, dizendo a este respeito que a “origem do conceito de limite conhece-a já o aluno, através dos exemplos da geometria. Mas a vantagem, a finalidade daquela delicada rede de definições e de teoremas não lhe surgirá tão claramente ao espírito — se logo em seguida não se passar ao estudo das derivadas” (Silva, 1951, p. 4, itálico no original).

3. OS NOVOS PROGRAMAS E O ENSINO DA ANÁLISE: PRODUÇÕES DOS ESTAGIÁRIOS DO LICEU NORMAL DE D. JOÃO III

No regime de formação instaurado em 1930 procura-se salvaguardar as três dimensões que devem estar presentes na formação de um professor do ensino liceal, a saber, preparação académica, preparação profissional teórica e prática profissional, através da articulação de uma licenciatura de base com a frequência do Curso de Ciências Pedagógicas e o estágio num Liceu Normal. Nesses espaços de formação, os professores metodólogos estavam encarregados da preparação pedagógica prática dos futuros professores. Segundo Rodrigues (2003), o Estado Novo manteve a formação de professores e um quadro de metodólogos de reconhecido valor que estava atento às transformações na maneira de ensinar. No que respeita à formação de professores de Matemática, um dos professores metodólogos da disciplina, do Liceu de D. João III, foi José Augusto Cardoso. Este professor foi membro do júri do Exame de Estado e autor de diversos artigos tanto na área da Matemática como na área do Ensino da Matemática (SANTIAGO, 2016).

A pesquisa no Arquivo da Biblioteca da Escola Secundária José Falcão permitiu-nos encontrar trabalhos elaborados pelos professores estagiários durante os dois anos do seu estágio no Liceu Normal de D. João III. Entre os trabalhos produzidos existem Planos de Lição, Relatórios, Palestras Pedagógicas, Ensaios Críticos para o Exame de Estado do Magistério Liceal e Trabalhos Temáticos. Da análise dos trabalhos que encontrámos verificamos que nem todos os estagiários apresentam os mesmos trabalhos.

Este trabalho centra-se em trabalhos desenvolvidos pelos professores que fizeram o estágio no Liceu de D. João III no período compreendido entre 1948 e 1953, um dos períodos em que o professor metodólogo era José Augusto Cardoso e que é um momento de alteração curricular. O grupo que esteve em estágio no intervalo temporal do nosso estudo tem seis elementos: Álvaro João Rocha da Silveira, Maria Vanda Gomes, Tereza Alice de Moura, Maria Tereza de Jesus de Castro Dias Martins Vicente, Alberto Vaz da Cunha Simões da Silva, Ilda Alice Andrade Nogueira Seco. Entre os trabalhos destes estagiários encontramos Relatórios, Conferências Pedagógicas, Ensaios Pedagógicos e Trabalhos Temáticos. Os trabalhos são datilografados.

Entre os trabalhos recolhidos, apenas três se enquadram no nosso estudo. Os trabalhos são dos estagiários Álvaro João Rocha da Silveira, Tereza Alice de Moura e Maria Tereza de Jesus de Castro Dias Martins Vicente. O trabalho de Álvaro da Silveira é um trabalho temático, que inclui a análise infinitesimal, e que foi produzido em 1949, ou seja, um ano após a publicação do programa em vigor, que reintroduzira o estudo da análise infinitesimal no ensino secundário. O trabalho de Tereza Alice de Moura é uma Conferência Pedagógica que consiste numa análise crítica dos programas de matemática. Em 1953, Maria Tereza Vicente produz uma crítica a um dos capítulos do livro único de Álgebra do 6.º ano e desenvolve uma exposição dos assuntos versados no mesmo capítulo

O primeiro trabalho que analisamos foi elaborado por Álvaro da Silveira no ano letivo de 1948/49, no seu segundo ano de estágio. Este trabalho tem como título “Lições de Álgebra”, referindo na respetiva capa, que foram dadas ao 6.º ano, turma B, e está dividido em duas partes, uma parte com 20 páginas e uma outra parte que tem 105 páginas. O trabalho percorre todos os temas do programa do 6.º ano, pela ordem em que aparecem no programa. Na parte com menor número de páginas são abordados: noção elementar de variável e de função; classificação de funções; funções inversas; representação geométrica de algumas funções, e, na outra parte são tratados: infinitamente grandes; infinitésimos; infinitésimos simultâneos; teoremas relativos à soma e ao produto de infinitésimos; limite de uma variável, limite de uma função, operações sobre limites; noção elementar de continuidade de uma função, e propriedades dos polinómios inteiros. O estilo adotado é idêntico ao que poderia ser encontrado num manual escolar. O trabalho não inclui bibliografia, mas há na rubrica relativa às propriedades dos polinómios inteiros Silveira (1949) a referência a que «os n.º 5, 6 e 7 são a cópia integral do trabalho do Exmo. Sr. Dr. José Augusto Cardoso, intitulado “Método de coeficientes indeterminados”» (SILVEIRA, 1949, p. 65). Neste trabalho apresentamos parte da análise relativa à parte mais extensa da proposta apresentada Silveira (1949).

Álvaro da Silveira (1949) não inclui justificação alguma para a definição de limite de uma função que vai usar, todavia ao definir contorno ou vizinhança de um ponto (figura 1), permite-nos conjeturar que irá usar a ‘orientação de Cauchy’.

Figura 1
Definição de contorno ou vizinhança de um ponto.
Silveira (1949, p. 2)

Notamos na exposição dos assuntos uma preocupação de proporcionar conhecimentos que, ainda que não estejam especificamente nos programas (figura 2), permitam ao aluno, uma melhor compreensão de matéria programática que se lecionaria posteriormente, que neste caso, se tratava das operações com infinitésimos.

Figura 2
Teorema
Silveira (1949, p. 11)

A nossa conjetura anterior sobre a definição de limite revela-se acertada. Álvaro da Silveira (1949) vai definir limite finito de uma função como podemos observar na figura 3.

Figura 3
Definição de limite finito de uma função.
Silveira (1949, p. 20)

Uma primeira comparação com o Compêndio de Álgebra, o livro único adotado em 1950, evidencia que na parte menos extensa, o trabalho de Álvaro da Silveira (1949) segue uma apresentação semelhante à do livro único, mas na outra parte isso já não acontece. O número de exercícios que são propostos ao longo da exposição de Álvaro da Silveira é muito escasso.

Tereza Alice de Moura (1950) apresentou, no seu primeiro ano de estágio, uma Conferência Pedagógica com o título “Crítica aos programas de Matemática”. O trabalho tem 23 páginas e abrange todos os ciclos, não tem bibliografia. A estagiária começa por falar sobre as normas a que deve obedecer a elaboração de um programa. Tereza Alice de Moura (1950) formula algumas perguntas relacionadas com os programas e às quais procurará responder ao longo da exposição, fazendo comparações entre composição dos programas em vigor na altura com os que o antecederam desde 1888 e apresentando a sua opinião sobre a mesma. No desenvolvimento da sua análise, no que respeita à organização do programa e aos métodos, justifica as suas posições apoiando-se, por vezes, em autores como, por exemplo, Stanley Hall e Laisant. A estagiária discute também as finalidades do ensino. No que concerne aos programas de Álgebra do 3.º ciclo, Tereza Alice de Moura (1950) considera que, embora com uma ordem diferente, quase todos os programas publicados até 1936 se pareciam bastante com os promulgados em 1948. Salientando que estes últimos teriam grandes vantagens sobre os anteriores afirma que estavam “duma maneira geral, bem organizados e adaptados à mentalidade dos alunos. Parece-me, no entanto que ainda neles se encontram algumas deficiências: umas que dependem da forma por que os assuntos são dados e outras dependem da ordem por que estes assuntos devem ser ensinados.” (MOURA, 1950, p. 17), dando exemplos. Entre outras alterações, esta estagiária propõe que o programa de Geometria Analítica fosse dado nos dois anos do ciclo, para se tornar mais simples para o aluno alguns assuntos tratados na Álgebra, em especial o problema das tangentes. Sobre as finalidades do ensino apresenta as que estão nos programas do 3.º ciclo expressas do seguinte modo

O estudo da Matemática deve constituir para o aluno uma ginástica intelectual que lhe permita raciocinar com clareza e precisão, tanto no campo científico como na vida prática.

Pretende-se que o aluno não só fique na posse de um certo número de princípios e teorias, em que será geralmente exigido o rigor próprio desta disciplina, mas que tenha desenvolvido a iniciativa pessoal e a faculdade de raciocínio, de modo a poder iniciar com confiança os estudos superiores. (Decreto-Lei n.º 37 112, de 22 de Outubro de 1948)

Tereza Alice de Moura (1950) considera que os programas do 3.º ciclo estão organizados de molde a atingirem as finalidades em vista. E, que o tempo para serem ensinados é suficiente.

Maria Tereza Vicente (1953), no seu primeiro ano de estágio, apresentou um trabalho pedagógico composto de duas partes, como o nome indica, “Crítica ao capítulo II do livro único de Álgebra do 6.º ano e Exposição dos assuntos versados no mesmo capítulo”. A matéria versada neste capítulo é: infinitamente grandes; infinitésimos; infinitésimos simultâneos; teoremas relativos à soma e ao produto de infinitésimos; limite de uma variável, limite de uma função, operações sobre limites; noção elementar de continuidade de uma função.

Este trabalho, tem 32 páginas no total distribuídas por uma introdução (2 páginas), pela crítica (3 páginas) e pela exposição (18 páginas), tem uma bibliografia composta de dois livros de Bento Caraça, um livro de Vicente Gonçalves, um livro de A. N. Whitehead e o artigo de Sebastião e Silva sobre o ensino da análise de que já falámos.

Na introdução, Maria Tereza Vicente (1953) afirma que a crítica que apresenta é objetivamente construtiva, procurando ser científica, e explica as opções tomadas na exposição, que sendo um trabalho de didática, tinha que atender à idade dos alunos e focar os pontos que considerava essenciais. A proposta educativa da estagiária para este capítulo segue a orientação de Heine no que respeita ao limite de uma função (figura 4), tal como Sebastião e Silva (1951) tinha recomendado no artigo que foi consultado por Maria Tereza Vicente.

Figura 4
Orientação do ensino.
Vicente (1953, p. 2)

No início da sua crítica Maria Tereza Vicente (1953) apresenta a razão que em seu parecer conduz às imperfeições que o livro único para o ensino da Álgebra revela (figura 5). Salientando que ao falar-se de limites de variáveis deve ser acautelado que essa expressão seja abordada de modo a que não cause confusão no espírito dos alunos. Será a sua percepção das dificuldades de exposição das rubricas daquele capítulo a jovens adolescentes que levará Maria Tereza Vicente a optar pela definição mais intuitiva de limite de uma função.

Figura 5
Origem das imperfeições.
Vicente (1953, p. 3)

Reforçando e focando no autor do Compêndio de Álgebra adotado como livro único, Maria Tereza Vicente aponta a origem das imperfeições (figura 6).

Figura 6
Origem das imperfeiçoes.
Vicente /1953, p. 3)

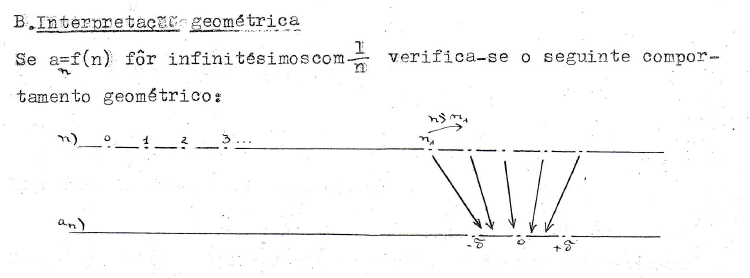
O estilo adotado na exposição de Maria Tereza Vicente (1953) é, tal como no trabalho de Álvaro da Silveira (1949), idêntico ao que poderia ser encontrado num manual escolar. Ao longo da exposição Maria Tereza Vicente introduz algumas interpretações geométricas (figura 7), que não encontramos em Álvaro da Silveira (1949), nem no Compêndio de Álgebra. Este recurso à imagem constitui uma alteração didática relevante, pois está-lhe subjacente a noção de que as imagens são recursos pedagógicos que promovem a apreensão dos conteúdos.

Figura 7
Interpretação geométrica.
Vicente (1953, p. 9)

4. CONSIDERAÇÕES

O estudo da análise foi eliminado entre 1936 e 1948, somente após a Segunda Guerra Mundial foi a análise novamente estudada. A sua introdução espoletou, na imprensa, debates sobre a qualidade da terminologia matemática usada nos programas, bem como sobre as formas como o estudo das derivadas deveria ser articulado com o estudo dos limites.

A interrupção de doze anos que tinha afastado os professores do estudo da análise, iria impor aos professores um refazer da sua cultura matemática e pedagógica, de modo a conseguir a máxima conciliação da intuição com a racionalidade (Silva, 1951). Tentando contribuir para a compreensão de como se processam estas recomposições, seguindo as diferenciações no conhecimento profissional dos professores propostas por Shulman (1986, 1987), analisámos alguns trabalhos elaborados por estagiários durante a formação no Liceu Normal de D. João III.

Os trabalhos realizados no âmbito do estágio pedagógico contribuiriam de modo importante para a construção do conhecimento profissional do futuro professor. A análise de programas permite uma reflexão ligada a métodos de ensino, notando-se uma preocupação de perceber os que melhor se adaptam a cada ciclo de ensino. As propostas educativas apresentam os novos elementos curriculares sob a forma de organização textual dos conteúdos matemáticos, sugerindo a graduação da sua apresentação, mas não sugerem ainda atividades destinadas aos alunos. O trabalho com o metodólogo permitiria ao futuro professor ter experiências que marcassem a sua postura pedagógica e a maneira de trabalhar na sala de aula, percebendo aí que técnicas e métodos “colavam” melhor com a sua maneira de ser e com a idade dos alunos, bem como, a importância de refletir sobre a sua ação, na medida em que a mudança e a inovação pedagógica estão intimamente dependentes deste pensamento reflexivo.

Agradecimentos

Ao Centro Interdisciplinar de Ciências Sociais (CICS.NOVA) - Faculdade de Ciências e Tecnologia da Universidade Nova de Lisboa.

REFERÊNCIAS

AIRES, A. P.; SANTIAGO, A. E. Os programas de Matemática do Ensino Liceal em Portugal. In: ALMEIDA A. J.; MATOS, J. M. (Eds.). A matemática nos programas do ensino não-superior (1835-1974). Caparica: UIED e APM, 2014, p. 71-91.

ALMEIDA, M. C. A formação de professores de Matemática para o ensino liceal (1930-1968). In: MATOS, J. M. (Coord.). A matemática e o seu ensino na formação de professores. Uma abordagem histórica. Caparica: UIED, APM, 2018.

ALMEIDA, M. C. Compêndio de Álgebra para o 3.º ciclo: Reflexões em torna das críticas à sua aprovação. Historia Y Memoria de la educación HMe (História de la Educación Matemática en Iberoamérica), n. 11, p. 191-218, 2020. ISSN: 2444-0043.

CHERVEL, A. História das disciplinas escolares: reflexões sobre um campo de pesquisa. Teoria e Educação, Porto Alegre, v.2, p. 177-229,1990.

JULIA, D. A cultura escolar como objeto histórico. Revista Brasileira de História da Educação, n. 1, p. 9-43, Jan./Jun, 2001.

MATOS, J. M.; MONTEIRO, T. M. Recompondo o conhecimento didático do conteúdo durante o início da matemática moderna em Portugal (1956-69). REMATEC, Revista de Matemática, Ensino e Cultura, v. 6, n. 9, p. 7-25, 2011.

NÓVOA, A. Formação de professores e profissão docente. In: NÓVOA, A. (Coord.). Os professores e a sua formação. Lisboa: Dom Quixote, p. 13-33, 1992.

NÓVOA, António. A Imprensa de Educação e Ensino. Repertório Analítico (séculos XIX–XX). Lisboa: IIE, 1993.

PINTASSILGO, Joaquim; MOGARRO, Maria J.; HENRIQUES, Raquel. A formação de professores em Portugal. Lisboa: Edições Colibri, 2010.

RODRIGUES, A. Liceu José Falcão, Coimbra. In NÓVOA, A.; SANTA-CLARA, A. T. (coord.). Liceus de Portugal. Histórias, Arquivos, Memórias. Porto: Edições Asa, p. 233-242, 2003.

SANTIAGO, A. Os estágios no Liceu D. João III e o papel do metodólogo José Augusto Cardoso. In: Chaquiam, M.; Mendes; I. A; W. Valente (Org.) Anais do III Congresso Ibero-Americano de História da Educação Matemática, p. 219-228. Belém, 2016.

SHULMAN, L. Those who understand: Knowledge growth in teaching. Educational Researcher, v. 15, n. 2, p. 4-14, 1986.

SHULMAN, L. Knowledge and teaching: foundations of the new reform. Harvard Educational Review, Harvard, v. 57, p. 1-22, 1987.

TEODORO, António. A Construção Política da Educação. Estado, Mudança Social e Políticas Educativas no Portugal Contemporâneo. Porto: Edições Afrontamento, 2001.

Notas

Autor notes

Ligação alternative

https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/13008 (pdf)