1 Introdução
Segundo Tall (1995), a linguagem é o meio usado para se formular as propriedades dos objetos, mas na Matemática elementar a descrição é realizada por meio da experiência que se tem com o objeto e não construídas a partir da definição, como é o caso da Matemática avançada. Nos identificamos com Tall (1995), pois entendemos que o raciocínio geométrico se inicia a partir da percepção das formas do mundo em que vivemos, observando, analisando e agindo sobre os objetos e representações geométricas. Percepção, ação e pensamento estão intimamente relacionados a compreensão e construção de conceitos geométricos e para os alunos mais novos é muito importante a experiência com o próprio objeto, para, a partir daí, começarem a descrever propriedades e relações geométricas observadas por meio da linguagem materna.
Com base nesta concepção para o tratamento escolar de conteúdos geométricos, apresentamos episódios extraídos de uma pesquisa que teve como objetivo analisar como um processo de ensino e de aprendizagem, que priorizou tarefas de natureza exploratória-investigativas, contribuiu para desenvolver os saberes dos alunos na construção de mosaicos formados por polígonos regulares. Concretamente, buscamos responder a seguinte questão: Que saberes geométricos são gerados e mobilizados por meio de tarefas exploratório-investigativas nos alunos do 7° ano do Ensino Fundamental, durante a construção de mosaicos?
Realizar estudos na escola com foco no ensino de Geometria pode contribuir para amenizar problemas nesse ensino, suscitar discussões em torno deles e, como consequência, contribuir para a pesquisa em Educação Matemática. Um desses problemas, que fica em relevo na pesquisa de Sena e Dorneles (2013), é a negligência com ensino de Geometria nas escolas. Essas autoras desenvolveram uma pesquisa envolvendo o mapeamento de teses e dissertações produzidas no Brasil no período de 1991 a 2011 e constataram que o estudo da área de Geometria “não é uma das prioridades no ensino da Matemática, apontando para um descaso que parte do processo histórico e se faz presente no cotidiano atual” (SENA e DORNELES, 2013, p.154). Neste cenário, a falta de preparo dos professores é um fator relevante na ausência desse ensino nas escolas.
Especificamente em relação ao uso de mosaicos no ensino de Geometria, Miranda (2014) realizou um estudo bibliográfico sobre as dissertações e teses catalogadas pela revista Zetetiké, o qual teve como intenção a identificação e análise das produções acadêmicas que envolveram a utilização e/ou construção de mosaicos geométricos nos anos finais do Ensino Fundamental, no período de 2000 a 2011.
O aspecto quantitativo do mapeamento desta pesquisadora converge com a conclusão de Sena e Dorneles (2013), ou seja, a pesquisa em Geometria escolar incluindo estudos com mosaicos tem um número muito reduzido de trabalhos. Miranda (2014) observou que num total de 2 513 trabalhos, apenas três dissertações abordaram o tema Mosaicos no Ensino Fundamental, sendo uma no ano de 2003 e duas, de 2009.
Fabricio (2016) ampliou o
mapeamento feito por Miranda (2014), mantendo o mesmo critério de busca até o
ano de 2014 e catalogou mais quatro dissertações oriundas de mestrados
profissionalizantes: dois trabalhos em 2012 e outros dois, em 2014.
O presente estudo vem se juntar aos anteriores naquilo que se refere ao uso de mosaicos no ensino de Geometria mas, ao mesmo tempo, difere deles por colocar em relevo o uso de atividades exploratório-investigativas como estratégia de ensino que pode possibilitar ao estudante o papel de protagonista na busca pelo seu saber.
As tarefas exploratório-investigativas se justificam por contribuírem para
aspectos essenciais da atividade matemática, tais como a formulação e
teste de conjecturas e a procura e demonstração de generalizações. A exploração
de diferentes tipos de investigação geométrica pode também contribuir para
concretizar a relação entre situações da realidade e situações matemáticas,
desenvolver capacidades, tais como a visualização espacial e o uso de
diferentes formas de representação, evidenciar conexões matemáticas e ilustrar
aspectos interessantes da história e da evolução da Matemática. (PONTE,
BROCARDO e OLIVEIRA, 2009, p. 71)
De acordo com Ponte (2005), as atividades exploratório-investigativas fazem parte de uma estratégia de ensino composta por duas outras atividades: a atividade do professor e a atividade do aluno (ou o que se espera que ele faça). Na perspectiva desse autor e de seus colaboradores, a atividade do professor pode ser permeada por um repertório de tarefas a serem oferecidas aos seus alunos: exercícios, problemas, explorações e investigações.
Os exercícios são tarefas sem muita dificuldade e de estrutura fechada. São tarefas que trabalham a memorização de cálculos e procedimentos, importantes para sistematização de técnicas operatórias que facilitem a exploração de tarefas mais complexas.
Já os problemas se enquadram como tarefas de complexidade elevada e estrutura fechada. São tarefas que envolvem questões para serem solucionadas que apresentam certo grau de dificuldade para o aluno.
As explorações tendem a ser mais livres e menos sistemáticas, demandando um tempo relativamente pequeno de trabalho. São frequentemente utilizadas para introduzir um novo tema de estudo ou para problematizar e produzir significados a um conceito matemático.
As investigações, por sua vez, levam mais tempo e demandam, segundo Ponte (2003), quatro momentos principais: exploração e formulação de questões investigativas (ou situações problemáticas), organização de dados e construção de conjecturas, realização de testes, refinamento, sistematização das conjecturas e construção de justificativas, argumentações ou demonstrações, tendo em vista a validação dos resultados.
No entender de Oliveira, Segurado e Ponte (1996), as investigações matemáticas também são importantes do ponto de vista educacional de um modo geral, pois estimulam o envolvimento do aluno necessário para a aprendizagem. Fornecem vários pontos de partida para estudantes em níveis cognitivos diferentes; estimulam um modo mais abrangente de pensamento, relacionando vários aspectos do conhecimento e fornecem uma visão completa da Matemática, já que investigar é algo essencial à atividade matemática.
Em síntese, podemos dizer que as investigações matemáticas diferenciam-se das demais por ser situações-problema desafiadoras e abertas, proporcionando aos alunos alternativas de exploração e investigação. Neste sentido, pode-se trabalhar e investigar sem estabelecer uma distinção clara entre as duas últimas formas de tarefas acima referidas. Por isso, para fazer referência a ambas, utilizamos a expressão tarefas exploratório-investigativas.
A vantagem de trabalhar com tarefas dessa natureza está no fato de colocar o aluno diante do próprio processo de produção matemática. Não exige uma linearidade curricular; possibilita ao aluno trabalhar com verdades provisórias e abre leque para criações matemáticas. O processo de investigação deve possibilitar ao aluno o pensar matemático, ou seja, ver o mundo do ponto de vista matemático e ter os instrumentos para tirar proveito para matematizar com sucesso.
2 Etapas
de uma aula exploratório-investigativa
Uma aula investigativa, segundo orientação de Brocardo (2001), é permeada por três processos básicos: a exploração de possibilidades, a formulação de conjecturas e testes e a busca de argumentos que validem as descobertas realizadas. Esses processos fazem parte das atividades realizadas pelos alunos e mediadas pelo professor durante a exploração-investigação. Entendemos que a autora faz a união da fase de formulação de conjecturas e testes em seus estudos. Isso é possível porque numa tarefa exploratório-investigativa não há uma linearidade, onde o processo ocorra sequencialmente e de forma arbitrária. É possível que as conjecturas surjam antes mesmo da elaboração de dados ou só após a produção de muitos exemplos. Os testes, por sua vez, podem gerar mais questões ou mais conjecturas. Essas classificações não são rigorosas e dependem muito de como o pesquisador vivencia e compreende esse tipo de aula, totalmente dinâmica.
Quanto ao professor, este poderá organizar as aulas investigativas em três etapas principais, assim como caracterizou Ponte, Brocardo e Oliveira (2009): introdução da tarefa, seu desenvolvimento e discussão dos resultados. Essa sequência pode ocorrer em apenas uma aula, caso a tarefa exploratório-investigativa seja simples ou em várias aulas, quando as questões forem mais complexas ou levarem a outras questões interessantes para pesquisa. Isso porque nesse tipo de aula, podemos programar como iniciar as atividades, mas não temos como saber seu término. Isso não significa que seja algo negativo. É preciso que o professor esteja preparado intelectual e emocionalmente para esse tipo de possibilidade, pois como salientam Oliveira, Segurado e Ponte (1996, p. 5), “com ou sem a intervenção sistemática do professor existem sempre alunos que vão mais longe do que se tinha previsto: surgem processos e resultados inesperados”.
Descrevemos “a seguir” as três etapas potencializadoras do contexto das aulas investigativas.
2.1 A
introdução da tarefa
Na etapa de introdução da tarefa temos a fase em que se formulam as questões, que podem ser propostas oralmente ou por escrito. Essas questões podem ser elaboradas pelo professor ou pelos alunos, no entanto, em nossa pesquisa, optamos por planejar as questões previamente e levá-las para a turma, já que os alunos não tinham vivências frequentes com essa modalidade de aula. Trata-se de uma fase muito importante porque poderá motivar ou não o aluno a realizar as atividades e a se envolver com as tarefas propostas. Temos como pressuposto que a ocorrência da aprendizagem é norteada pelo envolvimento dos alunos nas atividades propostas, independente da natureza da tarefa.
Formular boas questões e saber como propor desafios para os estudantes é parte importante do processo de uma aula exploratório-investigativa. O aluno tem que “comprar” a ideia, aceitar o desafio proposto.
Destacamos algumas ações importantes do professor nessa fase da tarefa: primeiramente, a explicitação aos alunos acerca da tarefa, do que precisam explorar e o que se espera que façam. Essa explicação pode ser feita oralmente, escrita ou ambas as formas, principalmente, se os alunos não têm ainda experiência com esse tipo de aula. Ponte, Brocardo e Oliveira (2009) orientaram que mesmo a tarefa sendo fornecida aos alunos por escrito, não dispensa uma explicação oral pelo professor.
É importante que o professor seja cuidadoso ao elaborar os enunciados das questões para que eles não condicionem o aluno a seguir determinado caminho. Ao contrário disso, os enunciados devem possibilitar ao aluno o máximo de autonomia. De acordo com Oliveira, Segurado e Ponte (1996), ao selecionar ou criar uma tarefa, o professor deve definir bem os objetivos a atingir e ter em atenção o nível etário e o desenvolvimento matemático dos alunos. A familiaridade, ou não, dos alunos com este tipo de atividade é um fator muito importante.
Preparar e desenvolver uma tarefa verdadeiramente rica em possibilidades de descobertas que gerem aprendizagens significativas é um verdadeiro desafio para o professor. Quando isso ocorre, segundo, não existe o perigo de que o professor limite a possibilidade de os alunos estabelecerem as suas próprias conjecturas, se der algumas pistas de exploração ou pedir a eles algumas sugestões. Nesse sentido, manter uma postura investigativa durante todo o tempo em que ocorre a tarefa é tão importante quanto preparar uma boa questão, pois esta pode representar apenas “uma pergunta” e não motivar o caráter investigativo dos alunos.
Oliveira, Segurado e Ponte (1996) deixam
claro que o professor é confrontado com decisões difíceis quanto à gestão do
tempo devido ao elevado número de aspectos que necessita de relativizar e
conjugar numa tarefa investigativa. Além desse, outro aspecto importante é o
planejamento de como a tarefa será realizada. O professor deverá decidir
anteriormente se os alunos trabalharão em duplas, em grupos ou individualmente.
Deverá refletir sobre a melhor maneira de trabalho pensando não só na questão
da gestão em sala de aula e gestão de tempo, mas no que será supostamente mais
adequado ao tipo de tarefa. Supostamente porque não é possível prever o que irá
acontecer realmente durante as explorações, mesmo que o planejamento seja
minucioso.
2.2 Desenvolvimento
da tarefa e seus processos
Segue-se a essa primeira etapa a exploração por parte dos alunos que deve ser coordenada pelo professor. Nessa fase, ocorrem alguns processos comuns como a análise dos dados, a elaboração de conjecturas, os testes dessas conjecturas e algumas vezes a produção de mais dados e questões pelos próprios alunos. Também é o momento de elaboração das justificativas e provas das hipóteses levantadas.
Concordamos com Ponte, Brocardo e Oliveira (2009) de que nessa fase cabe ao professor procurar compreender como o trabalho do aluno vai se processando e prestar apoio quando for necessário. Esse apoio dado aos alunos pode ajudá-los a superar bloqueios e tornar mais rica sua exploração/investigação.
Em nossa pesquisa, algumas das atividades desenvolvidas durante a exploração não seguiram as etapas descritas por Ponte, Brocardo e Oliveira (2009) numa sequência linear.
Esse movimento não linear, já discutido
na literatura, é comum, pois algumas vezes a refutação de algumas ideias pode
gerar outros dados para testes. Essa é outra característica das tarefas
investigativas citada por diferentes autores, como Brocardo (2001, p. 99) que dá
um exemplo dessa situação:
(...) quando se
percebe que os testes realizados não confirmam determinada conjectura é
necessário voltar atrás de forma a formular outra conjectura. No entanto, para
isso, é importante perceber-se o que falhou para que a primeira conjectura não
resistisse aos sucessivos testes e procurar ter em conta esse aspecto na
formulação de uma nova conjectura. Deste modo, uma atividade de investigação
não é caracterizada apenas pelos processos matemáticos nela envolvidos, mas,
também, pela interação entre eles, ou seja, pelas relações que se devem
necessariamente estabelecer entre eles.
Ponte, Brocardo e Oliveira (2009) indicam os quatro momentos principais dessa etapa, descritos no Quadro 1. Acrescentamos outros processos (em itálico) observados durante a nossa pesquisa de campo a fim de contribuir com a caracterização de uma aula exploratório-investigativa.
Complementamos esse quadro, pois entendemos que este tipo de atividade do aluno pode ocorrer tanto no início da tarefa, quanto na fase de testes.
Outro fato comum é o aluno refutar uma conjectura no momento em que realiza os testes e já abandoná-la, voltando a fazer outras análises ou reformulando suas conjecturas iniciais.
Esses processos envolvem a formulação de
conjecturas, sua verificação e justificativas por meio de argumentações ou
provas no caso de alunos em nível de escolaridade mais adiantados. Para os
alunos de 6º e 7º anos do Ensino Fundamental, conseguir argumentar
consistentemente e comunicar os resultados obtidos pode ser considerado como
uma habilidade de alto nível. Devido à importância desses processos na aprendizagem
de conceitos matemáticos, buscamos compreender como funcionam e ocorrem dentro
de uma tarefa exploratório-investigativa.
2.3 A
formulação de questões e conjecturas
O processo de elaboração de questões e formulação de conjecturas ocorre quando os alunos começam a explorar os dados da tarefa ou mesmo por analogia com outras tarefas já realizadas. Quando isso ocorre, eles se questionam, questionam uns aos outros e ao professor, e nessa interação surgem algumas ideias que vão ganhando forma até que se tornem afirmações. Essas afirmações muitas vezes são contestadas pelos colegas, o que leva à necessidade de testes e verificações.
Um fato recorrente é os alunos considerarem que suas conjecturas são conclusões. Isso pode ocorrer em virtude da atitude do próprio professor, que segundo Ponte, Brocardo e Oliveira (2009), costuma utilizar a seguinte linguagem quando dialoga com os alunos: Vocês já chegaram a alguma conclusão? ou O que vocês concluíram sobre o que observaram?
O grande problema nesse caso é que muitas vezes os alunos deixam de elaborar justificativas porque acreditam que suas conjecturas são conclusões. Para alunos menores ou em níveis mais elementares de escolaridade é muito difícil aceitar a necessidade de justificar suas conjecturas. No entanto, Ponte, Brocardo e Oliveira (2009) salientam ser importante o professor deixar claro que, por mais que se façam vários testes na tentativa de verificar uma conjectura, esse procedimento não tem estatuto de prova matemática.
Em nossa pesquisa, observamos que um dos aspectos interessantes dessa etapa foi analisar os registros que os alunos fizeram de suas conjecturas e comparar com os registros de áudio e vídeo ou anotações do pesquisador. Percebemos ser comum o aluno não escrever tudo o que fala e possivelmente não dizer tudo aquilo que pensa.
Em termos curriculares vigentes (BRASIL,1998), no trabalho com alunos do 6º e 7º anos do Ensino Fundamental, o processo de justificação ou prova das conjecturas não é muito priorizado, entretanto, é desejável que o processo de argumentação seja bem desenvolvido e refinado com o passar do tempo e das várias experiências vividas com tarefas de natureza investigativa. Não podemos confundir argumentação com uma prova ou demonstração.
De acordo com os Parâmetros Curriculares Nacionais (BRASIL,1998), a argumentação é uma habilidade próxima das práticas discursivas espontâneas e regida pelas leis de coerência da língua materna, enquanto que as demonstrações têm por objetivo provas dentro de um referencial assumido, sendo regidas pelas leis da lógica formal. O processo de argumentação inicia o desenvolvimento de habilidades que permite provar alguns resultados. Com o tempo e a experiência, os alunos vão construindo argumentos mais sólidos e elaborando suas primeiras demonstrações. Uma das grandes dificuldades que tivemos neste aspecto foi fazer sempre boas intervenções, abandonando a postura de professora convencional, acostumada a dar respostas, para uma postura investigativa, na qual formulou outras questões que possibilitaram a busca do próprio aluno por novas descobertas.
3 Percurso metodológico
da pesquisa
Em nossa pesquisa de natureza qualitativa, o papel de pesquisadora e ao mesmo tempo professora, propiciou a seleção, adaptação e elaboração de todas as tarefas e aplicação das mesmas com uma turma do 7º ano do Ensino Fundamental de uma escola pública estadual da cidade de Pilar do Sul, do interior de São Paulo. Para André (2002), quando o pesquisador é o principal responsável pela produção e análise das informações, isso envolve alguma vantagem, que está diretamente relacionada à maior experiência e sensibilidade.
Para a coleta de dados optamos por utilizar várias técnicas, como gravações de áudio e de vídeo, fotografias, registros escritos dos alunos, relatórios sobre as experiências vivenciadas e anotações pessoais da professora em diário de bordo. Algumas falas dos alunos foram gravadas e depois transcritas, compondo material descritivo e rico em detalhes que auxiliaram a análise e a compreensão dos cenários envolvidos durante as tarefas.
Para a coleta de dados optamos por utilizar várias técnicas, como gravações de áudio e de vídeo, fotografias, registros escritos dos alunos, relatórios sobre as experiências vivenciadas e anotações pessoais da professora em diário de bordo. Algumas falas dos alunos foram gravadas e depois transcritas, compondo material descritivo e rico em detalhes que auxiliaram a análise e a compreensão dos cenários envolvidos durante as tarefas.
Para análise da produção de informações, optamos pela técnica de triangulação como recomenda Martins (2006, p. 80): “a convergência de resultados advindos de fontes distintas oferece um excelente grau de confiabilidade à pesquisa, muito além de pesquisas orientadas por outras estratégias”. Das várias triangulações existentes, optamos pela triangulação de fontes de dados, que preconiza o uso de várias fontes de dados de modo a obter uma descrição mais detalhada e completa dos fenômenos, sendo esta a alternativa a mais utilizada pelos investigadores e adotada por nós nesse estudo:
 Figura 1
Triangulação de dados
(Elaboração dos Autores)
Figura 1
Triangulação de dados
(Elaboração dos Autores)
Em um vértice do triângulo analisamos os documentos produzidos durante a realização das tarefas e relatórios sobre as impressões que os alunos tiveram desse tipo de aula. Em outro vértice, contamos com a análise feita acerca das transcrições de áudio e vídeo e no terceiro vértice do “triângulo”, utilizado como esquema, as anotações da observação participante da professora-pesquisadora.
Das tarefas trabalhadas com os alunos do 7º ano do Ensino Fundamental, apresentamos a seguir, aquelas diretamente voltadas à configuração dos mosaicos.
3.1 Tarefa ladrilhando o plano com polígonos
congruentes
Os
alunos desta turma de 7º ano já haviam trabalhado em outras quatro tarefas
exploratório-investigativas geométricas antes da tarefa Ladrilhando o Plano com Polígonos Congruentes. Entre elas,
exploraram algumas propriedades dos ângulos e medidas de ângulos em polígonos
regulares. Tais tarefas foram
fundamentais na preparação dos alunos para a tarefa com polígonos congruentes,
que objetivava à construção de mosaicos geométricos.
O primeiro passo, antes de se iniciar a exploração com os polígonos, foi retomar o conceito de Mosaicos com os alunos por meio de imagens projetadas, fotografias e definições em slides. Em seguida, eles fizeram uma atividade, compondo mosaicos com polígonos irregulares, sem muita preocupação com regras ou definições rígidas. O objetivo nesta etapa foi motivar os alunos e iniciar a percepção da necessidade de que para ser esteticamente agradável, os mosaicos deveriam ter as peças “bem encaixadas”, sem sobrepô-las.
Após esta etapa, os alunos foram organizados em grupos para a realização da tarefa, que foi dividida em três partes: pavimentação com polígonos regulares entre si; estudo do ângulo poliédrico e pavimentações com polígonos regulares não congruentes entre si. Neste texto apresentaremos apenas um recorte desta sequência de tarefas e algumas considerações após as análises da pesquisa.
3.2 Pavimentação com polígonos regulares entre si
No primeiro dia de aplicação desta etapa da tarefa,
haviam 33 dos 36 alunos do 7º ano B. Optou-se por organizá-los em grupos de quatro
ou três alunos para iniciar a exploração, totalizando 9 grupos. Cada aluno
recebeu, em aula anterior, uma coleção de polígonos regulares da
professora-pesquisadora em papel colorido. Eles levaram esse material para
recortar em casa, ganhando-se tempo para a exploração em sala de aula. Os
polígonos regulares escolhidos para o desenvolvimento da exploração foram:
triângulos equiláteros, quadrados, pentágonos, hexágonos, heptágonos,
octógonos, eneágonos e decágonos. Essa escolha se deu pelo fato destes serem os
polígonos sugeridos para o trabalho no material do aluno (SÃO PAULO, 2014) do
qual a maior parte das atividades havia sido
trabalhada anteriormente.
Antes de iniciar a exploração, a professora
conversou novamente com os alunos sobre o objetivo da atividade, enfatizando o
“fazer matemática” por meio da investigação, buscando descobertas e “coisas
escondidas”.
É importante
salientar que o 7º ano B não era uma classe problemática quanto à indisciplina,
no entanto, como qualquer aluno nesta idade, conversava-se bastante. Se não
houvesse uma negociação e estabelecimento de algumas regras antes da realização
das tarefas, o trabalho em grupo poderia não ser exitoso. Foi necessário retomar alguns combinados sobre
como trabalhar em grupo, já que o problema da conversa paralela durante as
explorações dificultou o desenvolvimento das mesmas no tempo planejado. Sobre
essa questão pedagógica, Ponte et al.
(1998) explicam que para que seja possível e proveitosa esta nova maneira de viver na sala de aula é
necessário a negociação e estabelecimento de um conjunto de normas de
relacionamento entre os alunos e o professor, que indiquem, com clareza, o que
se espera de cada um e o que é e não é permitido.
Para essa
exploração foram utilizadas cinco aulas de 50 minutos cada. Duas aulas duplas
para as explorações-investigações e uma aula para discussão e socialização dos
resultados. Foram necessárias a leitura e explicação pormenorizada da tarefa
para a turma já que a questão da leitura e interpretação textual para alguns
desses alunos era bem comprometida. Muitas vezes, os alunos sabiam realizar os
cálculos, compreendiam relações matemáticas, mas não conseguiam resolver
problemas matemáticos. Mesmo tendo clareza de que uma explicação muito
detalhada da tarefa poderia torná-la menos “espontânea” para os alunos, foi
necessária uma intervenção maior, principalmente sobre as regras para a
composição dos mosaicos com polígonos regulares. Os alunos pareciam não
compreender as condições para as construções geométricas. Esse fato foi
observado quando insistiram em pavimentar o plano unindo os polígonos a partir
de seus lados e não de seus vértices. Por esse motivo, após a
entrega dos enunciados na forma escrita procedia-se, sempre, à sua leitura
oral.
 Figura 3
Mosaico com polígonos regulares
congruentes
(Acervo da Pesquisa)
Figura 3
Mosaico com polígonos regulares
congruentes
(Acervo da Pesquisa)
A fase de
introdução (etapa 1) de uma tarefa é um momento muito importante neste tipo de
aula, pois é nesta etapa que se é possível colocar boas questões que mobilizem
os alunos para a busca por soluções. Além disso, um enunciado bem escrito pode
auxiliar no processo de realização da tarefa, principalmente porque o aluno
pode retornar a ele sempre que tiver dúvidas.
3.3 Tarefa da etapa 1
Após a leitura das duas questões de “arranque”, denominadas dessa forma por Ponte, Brocardo e Oliveira (2009) para iniciar a exploração, os alunos começaram a trabalhar. Alguns grupos separaram os polígonos em montes, marcaram o número de lados em cada um para facilitar a visualização e classificação e começaram a construir pavimentações sobre a mesa. Praticamente todos os alunos perderam muito tempo “brincando” com os polígonos ou compondo e decompondo malhas. Eles compunham uma determinada malha, desmontavam e voltavam a compô-la. Era necessário intervir o tempo todo para que se concentrassem nas atividades e após quase uma aula inteira de 50 minutos, não haviam iniciado nenhum registro escrito de qualquer conjectura.
Percebeu-se que os alunos não haviam compreendido que deveriam “encaixar” os polígonos por um vértice comum. Por este motivo a professora-pesquisadora resolveu conversar novamente com toda a turma sobre como deveriam pavimentar o plano e enfatizar o que deveriam investigar:
Professora
Sílvia: Vocês
precisam investigar quais polígonos regulares pavimentam o plano e quais não
pavimentam. Mas tentem explicar porquê isso acontece. É importante explicar
como vocês chegaram a essas ‘conclusões’!
Quase todos os alunos perceberam nas primeiras aulas que apenas o triângulo equilátero, o quadrado e o hexágono regular, dentre os polígonos que possuíam em suas mãos, pavimentavam o plano.
Por meio de estudos mais aprofundados, sabe-se que estes são realmente os únicos polígonos regulares de um mesmo tipo capazes de pavimentar o plano perfeitamente. Tais coberturas são chamadas de mosaicos regulares do plano e são indicadas pelas sugestivas notações (3,3,3,3,3,3), (4,4,4,4) e (6,6,6), conforme notação de Alves e Dalcin (1999).
Nas duas primeiras aulas de 50 minutos os alunos não conseguiram iniciar qualquer tipo de registro escrito sobre suas descobertas. Então, no dia seguinte, optou-se por trabalhar o registro da tarefa com os alunos dispostos em pares, já que em grupos eles não conseguiram manter o foco na atividade devido ao barulho gerado pelas conversas.
Desta vez, construíram com desenhos uma pavimentação em malha pontilhada, com os polígonos regulares que cobrem o plano “perfeitamente”. Essa atividade foi trabalhada com o intuito de retomar a questão investigada no dia anterior e avivar o raciocínio dos alunos, promovendo ainda uma sistematização das ideias geradas até então. Foi explicado a eles que poderiam continuar a exploração-investigação com os polígonos e que deveriam fazer colagens em folhas para registrar suas ideias.
 Figura 4
Polígonos Regulares na Malha Pontilhada
(Acervo
da Pesquisa)
Figura 4
Polígonos Regulares na Malha Pontilhada
(Acervo
da Pesquisa)
Alguns
alunos continuavam colando os polígonos formando faixas, sem unir os vértices.
Por esse motivo, optou-se pelo uso do software GeoGebra para mostrar algumas possibilidades de construções de mosaicos com polígonos regulares. Para
tanto, foram utilizados os exemplos construídos pelos próprios alunos com
triângulos, quadrados e hexágonos. E dando continuidade, a professora iniciou
um diálogo com toda a turma:
Professora
Sílvia: Falem pra
mim um exemplo de polígono que não pavimenta o plano...
Aluno
Thiago: O
pentágono!
Professora
Sílvia: Mas por
quê?
Aluno
Thiago: Porque não
encaixa.
Professora
Sílvia: Então vou
construir aqui. — E construiu os pentágonos em volta de um único vértice — Agora vou clicar na ferramenta ângulo
pra marcar as medidas dos ângulos. Vejam como fica... O que vocês percebem?
Aluno
Yago: Que falta
um pedacinho. Não dá pra colocar outro pentágono.
Professora
Sílvia: Por que
não dá?
Aluno
Yago: Porque o
espaço é pequeno.
Aluno
Thiago: Se não
colocar falta e se colocar outro, passa.
Professora
Sílvia: Vocês
precisam tentar construir as malhas geométricas com os outros polígonos e
registrar as descobertas que forem fazendo.
Houve um pouco de resistência em fazer montagens
com todos os tipos de polígonos por parte da maioria das duplas. Eles
questionavam sempre: Precisa fazer com todos professora? E a resposta era sempre a mesma: Vocês precisam justificar a hipótese de
vocês sobre os polígonos que pavimentam o plano. Precisam fazer testes. Como
vão dizer que não é possível se não tentarem? Se não justificarem? A não ser
que vocês consigam justificar de alguma outra forma.
A
partir daí demoraram demais com as colagens, precisando que fossem lembrados
constantemente de registrar o que estavam pensando. Muitos resistiam em marcar
as medidas dos ângulos internos nos polígonos e alguns usaram o transferidor
para medir, esquecendo-se de usar os conhecimentos trabalhados em aulas anteriores
sobre as medidas dos ângulos internos em polígonos regulares.
3.4 Comunicando e socializando
Na quinta
aula os alunos retomaram suas colagens e melhoraram seus registros escritos.
Então, passou-se para a fase de discussão dos resultados. Nesta etapa a professora
perguntou para os alunos quais os polígonos que realmente pavimentam o plano e
o porquê isso acontece. Como ocorreu em praticamente todas as aulas com tarefas
exploratório-investigativas com essa turma, os mesmos alunos tomaram a palavra
e explicaram o que pensavam:
Professora
Sílvia: Por que a
pavimentação dá certo com o triângulo e não dá certo com o pentágono?
Aluno
Thiago: Eu acho
que sei. Os triângulos têm ... seis triângulos. Cada um tem um ângulo de 60 e
como são seis, 6 x 60 dá 360. E dá certo. Nos pentágonos se colocar mais um
passa de 360º.
Professora
Sílvia: Mas por
que isso acontece?
Aluno
Thiago: Porque os
ângulos têm que dar 360 e com o pentágono não dá.
Aluno
Yago: É porque o
ângulo interno precisa ser divisor de 360º pra dar certo!
Professora
Sílvia: E 108 é
divisor de 360?
Aluno
Yago: Não.
Professora
Sílvia: Então
mostre isso.
É perceptível nesse diálogo a mobilização do
pensamento argumentativo dos alunos. Para se construir argumentações
plausíveis, utilizamos o raciocínio
argumentativo e para elaborar tais conjecturas basta observarmos um determinado
número de casos, passando do particular para o geral (FERNANDES e FONSECA,
2003), como parece ter feito o aluno Yago quando afirmou que o ângulo interno
precisava ser divisor de 360°. Podemos perceber, na fala do aluno, o início do
rigor em seu raciocínio argumentativo – o rigor dos argumentos deve estar
sempre presente no raciocínio dos alunos, sem que tal se relacione
necessariamente com formalismo (FERNANDES e FONSECA, 2003).
No caso dos polígonos regulares, sabemos que o argumento do aluno Yago é válido, mas ele não explicou como chegou à esta hipótese, nem verificou se os demais ângulos internos dos outros polígonos eram ou não divisores de 360. Seria necessário um diálogo mais direto com estes alunos para fazê-los evoluir em seus raciocínios, o que demandaria mais tempo e exigiria que houvesse menos alunos na turma.
Os alunos perceberam que o polígono deveria ter um ângulo interno divisor de 360, mas não justificaram formalmente o motivo dos demais não pavimentarem o plano. Se listassem todos os divisores de 360, talvez conseguissem elaborar argumentos mais consistentes.
Algumas duplas chegaram à mesma hipótese do aluno Yago, outras perceberam a relação de divisibilidade após o colega falar e alguns alunos não conseguiram entender muito bem o que ele estava explicando. Uma dupla de meninos pensava que para dar certo a pavimentação, o “número de lados” do polígono é que devia ser divisor de 360. A professora, então, fez a seguinte pergunta à dupla: “Vocês disseram que o pentágono não pavimenta. Inclusive desenharam e fizeram colagens com pentágonos para mostrar esse resultado. Mas 5 é divisor de 360? Verifiquem.”
Esses alunos concluíram rapidamente que 5 é divisor
de 360, mas como o pentágono não pavimentava o plano, então não era sobre isso
que o colega Yago estava falando. Após algum tempo, um aluno dessa dupla
procurou a professora e disse: “Ah
professora, eu descobri. O ângulo é que tem que ser divisor de 360. Não é?”
3.5 Desenhando e escrevendo nas aulas de Matemática
Os alunos dos nove grupos fizeram alguns registros ao fim desta fase da tarefa. Alguns destes registros foram mais detalhados, outros mais concisos. Neste item, segue nossa análise sobre algumas produções dos alunos.
A escolha da passagem do material manipulável, nas primeiras aulas, para a representação nas malhas pontilhadas se justificou pelo fato de que os objetos geométricos são percebidos primeiramente no espaço para depois serem reelaborados mentalmente, num movimento do raciocínio que envolve a visualização como habilidade para perceber, representar, transformar e criar.
Sobre essa ideia, Santos (2009) salienta que “depois de percebidos no espaço, os objetos são observados e analisados, identificadas e descritas suas propriedades, classificados, conceituados e por fim representados visualmente e mentalmente”. Nesse processo, a visualização ganha importância fundamental.
Para alguns
alunos, a construção dos polígonos em malha pontilhada foi mais difícil do que
imaginávamos que seria. Alguns deles não conseguiram construir triângulos ou
hexágonos regulares e pediram ajuda. Essa transição do concreto manipulável
para o “concreto desenhado” exigiu um tipo de manipulação mental da imagem,
para a qual alguns alunos encontraram dificuldades em operar. Outros faziam as
representações imediatamente, sem nenhuma dificuldade, como foi o caso do aluno
Yago após a construção em malha pontilhada:
 Figura 5
Construindo polígonos regulares em malhas
pontilhadas
(Acervo da Pesquisa)
Figura 5
Construindo polígonos regulares em malhas
pontilhadas
(Acervo da Pesquisa)
Para este
aluno, a tarefa foi muito mais exploratória que investigativa, visto que
percebeu facilmente a condição necessária para que os polígonos regulares
ladrilhassem o plano. Mesmo assim, a tarefa ofereceu-lhe a oportunidade de
perceber por meio da experiência o porquê disto. Suas conjecturas e
questionamentos auxiliaram os demais colegas de grupo ou dupla a organizar
melhor suas próprias ideias. Além disso, durante a realização da tarefa, o
aluno Yago pôde mobilizar os
conhecimentos geométricos que já possuía, ampliando-os enquanto confrontava
suas hipóteses com as de seus colegas. Em sua fala, percebemos que algumas
vezes ele formulava a questão, que não era respondida por ninguém, mas que, de
alguma forma, fazia com que ele próprio pensasse no assunto e elaborasse alguma
conjectura que muitas vezes não era dita. Isso fica mais evidente quando
confrontamos sua fala com o texto que elaborou, ilustrado na Figura 4:
Aluno
Yago: Não pode
por um em cima do outro também, né? Ninguém respondeu.
Aluno
Giovane: Agora vou
ver o de sete lados.
Aluno
Yago: Não! Mas
tipo assim, você pode por esses e então você encaixa o triângulo aqui.
Aluno
Igor: Mas não
pode. É só com um.
Aluno Yago: Não pode por um em cima do outro também, né? Ninguém respondeu. Aluno Giovane: Agora vou ver o de sete lados. Aluno Yago: Não! Mas tipo assim, você pode por esses e então você encaixa o triângulo aqui. Aluno Igor: Mas não pode. É só com um. Importar tabla
Nesta última fala, o aluno Yago queria, a todo custo, encaixar um triângulo no espaço que ficava entre os pentágonos. Muitos alunos tentaram fazer a mesma coisa que ele durante a exploração. No entanto, seu colega Igor foi incisivo, explicando que só poderia ser usado um tipo de polígono.
Já em seus registros, Yago usou termos geométricos adequados e foi bastante claro em suas afirmações: A medida do ângulo interno de uma figura deve ser divisor de 360, do contrário, não podemos fazer a pavimentação. Exemplificou utilizando os polígonos para justificar sua afirmação. Isso mostra uma evolução entre o momento do trabalho em grupo, as discussões e a elaboração do registro escrito.
Já o aluno Thiago não se desligou do trabalho feito com os colegas e redigiu seu relatório recorrendo às percepções que fez com o grupo:
Nós descobrimos que para saber se um polígono
pavimenta o plano tem que ver o ângulo do polígono. Ex.: O quadrado tem cada
ângulo de 90º, se juntarmos 4, temos 360º certos. Já o pentágono tem 108º, se
juntarmos 4 irá passar, se colocar só 3 vai sobrar 36º, que é de um triângulo,
ou seja, ele não tem pavimentação. Nós conseguimos pavimentar com o quadrado,
triângulo e hexágono.
Podemos ver que o aluno Thiago utilizou a
nomenclatura correta para os polígonos e também mediu corretamente os ângulos
das figuras utilizadas (quadrado e pentágono). No entanto, apenas descreveu o
que observou em sua exploração, não chegando a elaborar uma generalização.
3.6 Quando a figura sai do plano
Quando os alunos
insistiram em inserir um pequeno triângulo entre os pentágonos pensamos em
propor uma situação nova para eles. Lançamos a seguinte questão para que
explorassem em grupos de quatro alunos cada:
O enunciado foi acompanhado de uma figura feita com
pentágonos regulares, construída pela professora-investigadora com software GeoGebra. O intuito dessa
figura era relembrar aos alunos
o que haviam verificado na tarefa
anterior. Cada dupla recebeu uma folha com o enunciado da questão e utilizou
polígonos recortados em papel colorido para explorar a situação e registrar
suas conjecturas. Haviam 35 alunos na classe neste dia.
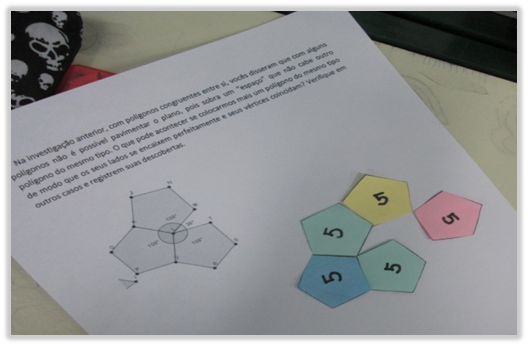 Figura 5
Ângulo poliédrico
(Acervo da Pesquisa)
Figura 5
Ângulo poliédrico
(Acervo da Pesquisa)
Professora
Sílvia: Vocês
lembram-se desta imagem? Alguns de vocês disseram, vamos colocar aqui o caso
do pentágono (a professora usava a imagem em projetor data
show), que não dá pra colocar mais um
pentágono porque se eu colocar mais um passa de...?
Alunos: 360º.
Professora
Sílvia: Passa de
360º... E se eu não colocar, fica faltando. Foi isso que disseram?
Professora
Sílvia: A pergunta
que eu tenho pra vocês agora é a seguinte: E se eu colocar mais um pentágono
aí?
Aluno
Thiago: Não cabe.
Professora
Sílvia: Mas e se
eu forçar? Se eu prender os lados desse pentágono nos lados dos outros,
encostando o vértice no vértice comum aos pentágonos colados no plano? Vamos
tentar fazer?
Passados aproximadamente 20 minutos de
investigação por parte dos alunos.
Professora
Sílvia: O que
aconteceu quando vocês colaram o outro pentágono nesse espacinho aí, que era
de 36º? E vocês colaram um outro pentágono... que tem o ângulo interno de
quanto mesmo?
Alunos: 108º!
Professora
Sílvia: Vocês
tentaram fazer 108 caber dentro de 36 não foi isso?
Aluna
Fernanda: A figura
ficou tridimensional.
Aluno
Yago: Na
verdade, o nosso só não ficou mais uma planificação, ficou com um tipo de uma
“lombadinha” assim... — E mostrou
no papel sua construção para a classe. (...)
Aluno
Giovane: Saiu do
plano professora?
Professora
Sílvia: Saiu do
plano?
A professora
repetiu a pergunta para não respondê-la ao aluno Giovane, tentando fazer com
que eles mesmos refletissem sobre o que estava sendo comentado. O aluno Yago balançava a cabeça afirmativamente.
 Figura 6
Ângulo poliédrico
(Acervo da Pesquisa)
Figura 6
Ângulo poliédrico
(Acervo da Pesquisa)
Professora
Sílvia: Quanto vai
ficar valendo esse ângulo agora?
Aluno
Igor: 432º.
Professora
Sílvia: Bem, o
Igor falou que dá 432º. Vocês têm que verificar se ele fez essa conta
direito. Se o ângulo passou de 360º... ó ... vocês disseram que se têm 360º a
figura fica no plano... Como o ângulo ficou maior, sendo 432º, a figura tá
saindo do plano, não é isso? Será que isso acontece no caso dos outros
polígonos que não pavimentaram o plano, como o heptágono, o octógono?
Após muita conversa e interação com os grupos, eles foram conseguindo fazer as colagens. Embora tenha sido complicada a realização desta etapa da tarefa para os alunos, fazer essa operação apenas mentalmente seria bem mais difícil para a maioria deles. Por isso, optou-se pelo uso do material manipulável. Os registros das alunas Amanda e Ellen podem ser observados na Figura 7.
Entre os 35 alunos que participaram desta exploração-investigação, 28 escreveram que os ângulos obtidos, ao se encaixar mais um polígono congruente na tentativa de pavimentar o plano, tinham a soma superior a 360º. Neste caso, a figura deixava de ser bidimensional, tornando-se tridimensional.
Quanto aos testes realizados, dois alunos os fizeram com 4 tipos de polígonos, seis alunos com 3 tipos, dez alunos fizeram 2 testes e onze alunos fizeram apenas 1 teste. Percebemos nesses resultados a pouca disposição para testar suas conjecturas. Os alunos se cansavam muito rápido em fazer qualquer tipo de atividade e a motivação que aparecia inicialmente, geralmente durava pouco tempo. Foi preciso intervenção contínua durante a aula por parte da professora-pesquisadora e mesmo assim alguns alunos resistiram à necessidade de verificar as afirmações que faziam. No caso desta tarefa, sabemos que poucos testes seriam suficientes para que generalizassem a situação, mas alguns cálculos ou figuras eram importantes para guiar o raciocínio da maioria dos estudantes.
 Figura 7
Ângulo Poliédrico
(Acervo da Pesquisa)
Figura 7
Ângulo Poliédrico
(Acervo da Pesquisa)
3.7 Ladrilhando o plano com polígonos regulares
Na semana seguinte, continuamos a exploração. Desta vez haviam 35 dos 36 alunos da classe e foram utilizadas duas aulas de 50 minutos cada para a exploração e discussão dos resultados. O objetivo desta tarefa era ampliar os conceitos figurais mobilizados nas tarefas anteriores por meio da construção de mosaicos com polígonos regulares não congruentes entre si. Em sua fala, a professora enfatizou que desta vez os polígonos regulares deviam ser diferentes e que as construções seriam feitas em malhas pontilhadas também.
Os grupos foram organizados com 3 ou 4 alunos. Mas para o registro, eles foram agrupados em duplas.

|
Vocês já investigaram as possíveis pavimentações
com polígonos regulares de
um só tipo. Mas, o que acontece se combinarmos polígonos regulares não
congruentes entre si?
|
Após distribuir as folhas em branco e malhas
pontilhadas aos grupos, a professora ficou andando pela sala, conversando com
os alunos e intervindo quando era necessário. Observando que os alunos
apresentavam dificuldades em compreender o enunciado e construir os mosaicos,
fez uma intervenção mais geral, conversando com toda a turma:
Professora
Sílvia: Pessoal,
prestem atenção em uma coisa: Quanto dá a soma dos ângulos internos em volta
de um vértice?
Alunos: 360º.
Professora
Sílvia: Então,
vocês precisam verificar que na hora que vocês conseguem pavimentar, essa
soma também está dando 360º. Pra isso é mais fácil se vocês souberem qual é a
medida do ângulo interno de cada polígono estudado.
Aluno
Yago: O nosso
deu certinho professora: 60, 120 e 180.
Professora
Sílvia: Professora
Sílvia: Aqui você conseguiu formar com triângulos equiláteros e quadrados? Aí
você pode chamar esse aqui de 3, 3, 3... 4, 4? Ficaria igual em todos os
vértices essa sequência 3,3,3,4,4 ?
Reconhecendo a dificuldade da maior
parte dos alunos em compreender a tarefa, a professora pediu para que
interrompessem a exploração, orientando-os como poderiam fazer para nomear as diferentes composições de forma mais
prática, utilizando exemplos dos próprios alunos na lousa:
 Figura 8
Composição 3,3,3,4,4
(Acervo da Pesquisa)
Figura 8
Composição 3,3,3,4,4
(Acervo da Pesquisa)
Interessante é que embora essa primeira configuração tenha sido apontada pela maioria dos alunos, nenhum deles conseguiu estendê-la na malha pontilhada corretamente. Outro fato que se repetiu durante a exploração foi a resistência por parte de alguns alunos em compor os mosaicos nas malhas pontilhadas. Muitos se recusaram em repetir o padrão para verificar se o “molde” encontrado pavimentava realmente o plano. Quando conseguiam dispor os polígonos formando 360º em torno de um vértice, já se davam por satisfeitos. Para eles, era uma complicação desnecessária e um trabalho “chato” ficar construindo e colorindo malhas geométricas.
O que os alunos não perceberam na exploração é que não precisariam ficar tentando construir os “moldes” concretamente, com figuras recortadas ou nas malhas. Bastava que verificassem os conjuntos de ângulos internos de polígonos regulares que resultassem em 360º e a partir daí testassem se essa configuração se estendia no plano.
Os erros cometidos pelos alunos em suas construções geométricas nos levaram a propor uma pesquisa individual em livros, revistas e internet, a fim de explorar as possíveis composições com polígonos regulares de tipos diferentes que poderiam cobrir o plano. Como primeiro passo da pesquisa, a professora-pesquisadora orientou-os para que construíssem uma tabela contendo os valores para os ângulos internos e externos dos 20 primeiros polígonos regulares.
A partir daí propôs a seguinte questão de
investigação:

|
Observando os valores da tabela que você construiu, explique o que é
necessário para que um polígono regular pavimente o plano, formando mosaicos
geométricos.
|
Algumas respostas dos alunos após a pesquisa e
socialização:
Aluno
Giovane: Para ser
um polígono ladrilhante, ele precisa conter os ângulos internos divisores de
360°. Também podemos ladrilhar com polígonos diferentes, mas tem um porém, a
soma de um ângulo com o ângulo do outro polígono tem que dar 360°.
Aluno
David: É
necessário que os ângulos internos se encaixem perfeitamente formando 360°
como: hexágono (três deles formam 360° por causa de seu ângulo interno 120°).
Para facilitar de sabermos se todos os polígonos congruentes pavimentam
certinho é só simplesmente o ângulo interno ser divisível por 360°, mas
quando são diferentes (como decágono, hexágono e quadrado, que juntos formam
os necessários 360°), é preciso somar os ângulos internos de cada um e que dê
360°.
De todos os alunos que realizaram a tarefa exploratório-investigativa
sobre polígonos e a pesquisa extraclasse, apenas três alunos comentaram a
existência de composições diferentes das trabalhadas em sala de aula com os
polígonos regulares não congruentes: a aluna Ellen, o aluno David e a aluna Thais. Mesmo assim, eles não verificaram se essas composições
(moldes) formavam mosaicos.
A aluna Ellen mostrou os moldes para construções dos tipos: 3,3,3,3,3,3; 4,4,4,4; 6,6,6; 3,6,3,6; 3,3,6,6; 3,4,4,6; 3,3,3,4,4; 3,3,4,3,4; 3,3,3,3,6; 4,8,8 e 3,4,6,4. Das combinações que ela descreveu, apenas a 3,4,4,6 não forma um mosaico. Sendo assim, excluindo-se as três composições com polígonos congruentes entre si, Ellen conseguiu mais sete formas de compor mosaicos geométricos.
O aluno David também indicou mais sete combinações que supostamente gerariam mosaicos. Foram as combinações: 4,8,8; 4,4,3,3,3; 6,3,6,3; 20,5,4; 3,4,3,12; 12,12,3 e 12,4,6. Dentre essas combinações, as sequências 20,5,4 e 3,4,3,12 não formam mosaicos geométricos, pois não se estendem no plano.
Após a análise dos dados, percebeu-se que os alunos apresentaram mais dificuldades nesta última tarefa do que nas anteriores. Principalmente na realização dos testes.
Segurado e Ponte (1998) explicam que a realização e trabalho investigativo na sala de aula tem grandes potencialidades, mas também envolve os seus problemas. Por isso, é importante conhecer a origem das dificuldades conceituais que os alunos podem ter sobre as tarefas e das estratégias que podem utilizar durante sua execução.
4 Considerações
O primeiro aspecto a ser considerado é que as aulas de natureza exploratório-investigativas podem ser grandes aliadas no ensino de conceitos geométricos, visto que a Geometria oferece muitas possibilidades para explorações que desenvolvem os raciocínios indutivo e dedutivo do aluno. Por meio das explorações e investigações geométricas os alunos formulam conjecturas baseados, muitas vezes, em suas observações e percepções sensoriais. Essas percepções são a base para o processo de visualização das imagens mentais.
Alguns resultados das análises e reflexões realizadas mostraram alguns apontamentos importantes que ocorreram em praticamente todas das tarefas com a maior parte da turma.
Muitos alunos tinham dificuldades em compreender a tarefa como um todo e interpretar os enunciados. Por esse motivo, todas as tarefas foram acompanhadas de uma explicação pormenorizada por parte da professora-pesquisadora, que leu cada enunciado para a turma antes que iniciassem as explorações-investigações. Essa dependência e dificuldade na interpretação textual, provavelmente, está relacionada ao fato de que os alunos estão mais acostumados a terem respostas do que perguntas, ou mesmo a buscarem respostas para questões abertas. Eles não têm o hábito de pesquisar, de investigar e alguns apresentam dificuldades de interpretação referentes ao vocabulário da própria língua.
A maior parte dos alunos apresentou a tendência de considerar um ou dois testes suficientes para justificar uma conjectura, que logo classificavam como “conclusão”. No início das primeiras tarefas, mesmo os alunos mais aplicados consideravam as justificações de suas conjecturas como algo desnecessário e complicado, evitando ao máximo escrever como encontraram determinados resultados. Eles não tinham o hábito de escrever nas aulas de Matemática. Escrever era “coisa de língua portuguesa”. Outros alunos, pensando que o que importava era a quantidade e não a qualidade de suas conjecturas e argumentos, registravam qualquer observação que faziam, mesmo que trivial, sem dar importância às justificativas.
Com o passar do tempo e desenvolvimento das experiências, os alunos foram evoluindo em seus registros escritos, melhorando a qualidade da linguagem matemática utilizada, elaborando representações figurais, cálculos, expressões, termos matemáticos e geométricos mais adequados e redigindo pequenos textos que explicavam como estavam pensando. A maior parte dos alunos também mostrou maior interesse nas aulas que envolveram explorações em grupo. Diziam que em grupo aprendiam melhor com os colegas.
Concluiu-se ainda que, mesmo que as tarefas tenham sido mais exploratórias do que investigativas, toda a dinâmica que permeou as atividades, proporcionou um ambiente rico para a geração e mobilização de saberes pelos alunos. Eles retomaram procedimentos e conceitos que já possuíam, reconstruíram alguns destes conceitos, ampliando e/ou aprofundando conhecimentos matemáticos por meio do raciocínio e da comunicação. De alguma forma, os alunos mobilizaram vários conceitos geométricos enquanto realizavam as atividades das tarefas propostas. Também se preocuparam em utilizar termos matemáticos específicos, fizeram a construção de várias representações dos polígonos em malhas pontilhadas e no papel em branco, trabalhando a visualização e operando mentalmente as imagens. Esses processos possibilitaram o desenvolvimento dos conceitos figurais envolvidos na exploração-investigação, como os conceitos de ângulos, polígonos, polígonos regulares, vértice e plano.
Ser professor não é tarefa fácil. Ser professor da escola pública no Brasil é tarefa ainda mais árdua. O professor lida com vários dilemas, contrariedades e condições que não favorecem os processos de ensino e de aprendizagem, como turmas numerosas, falta de interesse dos alunos pelos estudos e outros fatores externos que limitam a riqueza de uma boa aula.
Além dos fatores externos, a prática em sala de aula depende tanto do aluno, quanto do professor. Aulas do tipo exploratório-investigativas exigem mais do professor do que aulas expositivas e rotineiras, desde o planejamento até sua realização, em todas as suas etapas. O professor precisa estar atento a tudo o que ocorre nas interações entre os alunos para intervir no momento certo. Deve gerenciar várias situações diferentes, ter flexibilidade e, de certa forma, controlar a própria ansiedade em dar respostas prontas aos alunos.
O professor tem de ser capaz de apreender intuitivamente as situações, articulando pensamento e ação e gerindo dinamicamente relações sociais; tem de ter autoconfiança e capacidade de improvisação perante situações novas (PONTE, 1998). Esse tipo de competência se constrói por meio da experiência e de formação profissional sólida. Não é algo simples, nem tampouco, fácil.
Mesmo diante de todas essas e outras limitações, utilizar aulas de natureza exploratório-investigativa em sala de aula como estratégia de ensino, pode ser uma poderosa ferramenta para o professor que se preocupa em trabalhar com objetivos educacionais que estimulem a compreensão e o raciocínio dos alunos.



















