Resumen: En esta investigación se aplicó una estrategia didáctica centrada en la realización de actividades para el desarrollo de competencias formativas en el aula clase, mediante el vínculo de la teoría con la práctica, a estudiantes que ya habían cursado la asignatura del Cálculo de varias variables que se imparte en la Facultad de Ciencias Físico Matemáticas de la Universidad Autónoma de Nuevo León. Para ello se utilizó el software Cabri Plus 11 como medio para la comprensión de los temas de la asignatura, tomando en cuenta las potencialidades del proceso didáctico, así como las potencialidades del Cálculo de varias variables. Se muestran los resultados parciales de la aplicación de la estrategia.
Palabras clave: Estrategia Didáctica, Competencias, Software Cabri Plus 11.
Abstract: In this research a teaching strategy that focuses on the implementation of activities for the development of skills training in the classroom class through the link theory with practice, students who had already taken the course of calculus of several variables that apply at the Faculty of Physical and Mathematical Sciences at the Autonomous University of Nuevo Leon. For this a Cabri Plus 11 software was used as a mean of understanding the topics of the course, taking into account the potential of the learning process as well as the potential of the calculation of several variables. Partial results of the implementation of the strategy are shown.
Keywords: Didactics Strategy, Competences, Software Cabri Plus 11.
Artigos
EJEMPLIFICACIÓN DE UNA ESTRATEGIA METODOLÓGICA PARA CONTRIBUIR AL DESARROLLO DE COMPETENCIAS EN LA ASIGNATURA DEL CÁLCULO DE VARIAS VARIABLES.
EXEMPLIFICATION OF A METHODOLOGICAL STRATEGY TO HELP DEVELOP POWERS IN THE COURSE OF THE CALCULATION OF SEVERAL VARIABLES.
URL: http://portal.amelica.org/ameli/jatsRepo/437/4372128005/index.html
DOI: https://doi.org/10.26571/2318-6674.a2015.v3.n1.p52-70.i5306

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
En la actualidad se observa una tendencia a cambiar el modelo tradicional de enseñanza por un enfoque basado en competencias, que permita al alumno desarrollar ciertas habilidades necesarias para un eficiente desarrollo al ingresar a la vida laboral.
El interés en el desarrollo de competencias en los programas educativos concuerda con un enfoque de la educación centrado primordialmente en el estudiante y en su capacidad de aprender, que exige más protagonismo y cotas más altas de compromiso puesto que es el estudiante quien debe desarrollar la capacidad de manejar información original, buscarla y evaluarla en una forma más variada (biblioteca, profesores, Internet, etc), (Tuning, 2003).
De acuerdo con (Tobón, 2006) las competencias se proyectan como un enfoque pedagógico y didáctico para mejorar la calidad de la educación, los procesos de capacitación para el trabajo y la formación de investigadores en las diversas instituciones educativas. A través de ellas, se busca trascender el énfasis de la educación tradicional en la memorización de conocimientos descontextualizados de las demandas del entorno, en tanto se basan en el análisis y resolución de problemas con sentido para las personas, con flexibilidad, autonomía y creatividad.
Se impartió el curso del Cálculo de varias variables por uno de los autores durante un semestre escolar 2014 2015 a estudiantes que ya habían tomado esta asignatura (estudiantes reprobados en primera oportunidad de la materia) de la Facultad de Ciencias Físico Matemáticas de la Universidad Autónoma de Nuevo León.
Para el desarrollo de la investigación se les aplicó una encuesta inicial para interpretar los diferentes aspectos de las competencias relacionadas con un tema particular del cálculo de varias variables “Coordenadas polares”, así como el uso de softwares y el trabajo en equipo.
Percepción de los alumnos del proceso de enseñanza-aprendizaje del tema coordenadas polares

Figura 1

Figura 2
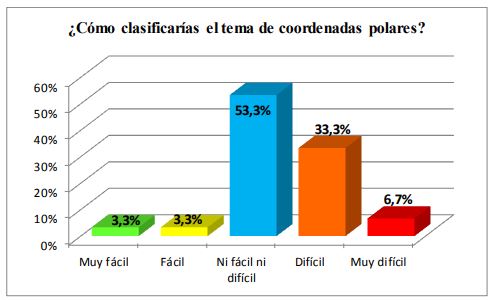
Figura 3

Figura 4
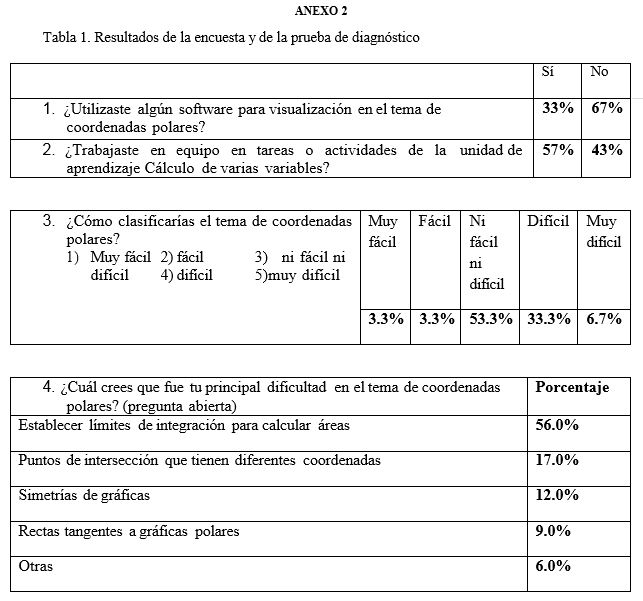
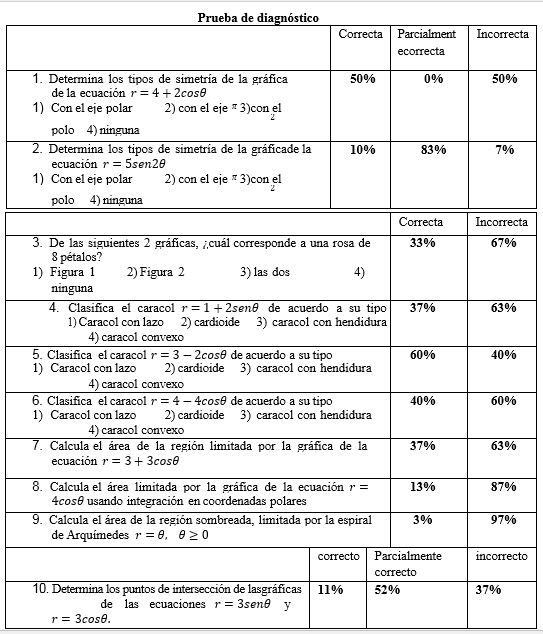
De los resultados obtenidos en la encuesta de diagnóstico, (tabla 1), Anexo 2, observamos lo siguiente:
· Poca participación de los estudiantes en el uso de las TICs como medios para una mejor comprensión de los conceptos de la asignatura del Cálculo de varias variables.
· Escasa participación en las competencias colaborativas.
· Dificultades en los aspectos de coordenadas polares: simetría; identificación de gráficas; determinación de límites de integración para calcular áreas; puntos de intersección de dos curvas con diferentes coordenadas polares.
Tomando en cuenta lo expresado, resulta interesante reflexionar cómo en los momentos actuales y a partir de la incorporación de las nuevas tecnologías de la información para la enseñanza, aún prevalece el uso de los medios tradicionales para el aprendizaje, que, a su vez, no contribuyen a despertar el interés por los contenidos que se imparten en la asignatura del cálculo de varias variables que a su vez poco desarrollo en las competencias formativas en esta asignatura.
Se plantea una estrategia didáctica y su aplicación parcial en un tema de coordenadas polares que permita incidir en un cambio conceptual por el científicamente aceptado. A continuación, se enuncian algunos presupuestos teóricos que fundamentan la estrategia propuesta.
En el plano didáctico, en muchas ocasiones la solución de problemas se mecaniza de tal forma, que un estudiante puede resolver un problema correctamente desde lo cuantitativo, pero no sabe interpretar ese resultado en el contexto del problema presentado.
La Flexibilidad, según (Álvarez, N. 2001) es considerada como lo contrario de rigidez, de intolerancia.
a) Plantearnos varias alternativas para solucionar un problema.
b) Aceptar que los demás solucionen un mismo problema diferente a nosotros, que no piensen igual que nosotros.
c) Aceptar los fracasos, las frustraciones, las situaciones difíciles, sacando la mayor experiencia positiva de los mismos.
d) Adaptarnos a nuevas situaciones, o situaciones totalmente contrarias a nuestro punto de vista.
e) Evitar el tradicionalismo en la solución de los problemas que conlleva a un estancamiento en diferentes esferas de la actividad que realizamos.
Si no se logra esta flexibilidad, entonces los estudiantes no pueden despojarse de las preconcepciones que poseen.
De acuerdo a la experiencia de los autores como profesores durante muchos años en la Facultad de Ciencias Físico Matemáticas de la Universidad Autónoma de Nuevo León, entre los objetivos fundamentales relacionados con la formación integral de los estudiantes están:
1) Complementar las demostraciones formales o abstractas con actividades de visualización, aprovechando las TIC´s, que lleven al alumno al entusiasmo por “descubrir” un resultado y posteriormente probarlo.
2) Propiciar en los alumnos espacios para un sistema de pensamiento y métodos de trabajo capaces de enseñarlos, motivarlos y llevarlos a la necesidad de formular preguntas, así como encauzarlos a dar respuestas ordenadas y lógicas.
3) Que los estudiantes sean capaces de integrar conocimientos de la literatura científica mediante la búsqueda de diferentes fuentes (Internet, artículos, etc.).
4) Capacidad para comunicar su conocimiento y argumentar sus fundamentos con un espíritu crítico y científico.
5) Capacidad para la búsqueda autónoma de información sobre argumentos expuestos en los temas de cualquier asignatura.
6) Fomentar el pensamiento dialógico, que obligue al alumno a obtener paralelos, a proceder por analogía, a crear exclusiones.
7) Capacidad para la búsqueda autónoma de información sobre los argumentos expuestos en cada tema del programa en la bibliografía específica.
De lo planteado se comprende que el Cálculo de varias variables constituye una fuente para la adquisición de la cultura y esto permite al estudiante y avanzando en asignaturas matemáticas de niveles superiores.
Para la formación y desarrollo de las competencias, cuando en el Proceso de Enseñanza–Aprendizaje (PEA) del Cálculo de varias variables se parte de las preconcepciones del alumno, aunque sean conceptos erróneos, lo nuevo que se estudia y que provoca una contradicción, puede comenzar a encontrarle un sentido a lo nuevo que aprende, se motiva.
Sólo se adquiere sentido cuando además del significado existe una interacción “significativa” en la práctica, en la realidad. Por esta razón, la motivación tiene que ser un componente intrínseco del proceso, si no hay motivación no hay interés y por tanto para el estudiante por el Cálculo no posee ni significado ni sentido.
Es necesaria la interacción de la asignatura con la situación docente planteada, la identificación con la misma al ver su utilidad, la necesidad de resolverla. La flexibilidad didáctica tiene que manifestarse en la posibilidad de que el estudiante tenga libertad en determinado momento, proponga sus alternativas, de esta manera armonizan estudiantes y profesores y el profesor deja de ser el protagonista absoluto.
Las tareas deben ser desarrolladas por los educandos preferentemente de forma grupal, siguiendo la dinámica del aprendizaje: de la reflexión individual, a la grupal y de ésta, a la individual enriquecida, asumiendo el tratamiento individual acorde con el desarrollo personal de los educandos. Para ello se parte del diagnóstico del desarrollo potencial de los educandos por medio del planteamiento y resolución de problemas.
Se debe propiciar que la solución de las tareas orientadas por el profesor sea resuelta por los estudiantes por medio de informes orales o escritos, según la actividad prevista, para darlas a conocer en el grupo, con lo que se podrá valorar la evolución en el significado atribuido y el dominio del lenguaje del Cálculo por parte de ellos.
Para lograrlo, las actividades de aprendizaje y las tareas orientadas deben cumplir con los siguientes requisitos:
1) Partir del hecho de que los estudiantes tienen criterios y concepciones sobre los conceptos que se analizarán.
2) Tener en cuenta el nivel lingüístico y de razonamiento de los educandos y que promuevan el desarrollo de los mismos.
3) Propiciar, a partir del conocimiento por parte del profesor de la forma en que el educando percibe los conceptos y razona sobre ellos, pasar a un razonamiento cada vez más abstracto sobre los mismos, de modo que pueda expresarlos y describirlos.
4) Hacer explícitas las concepciones y razonamientos de los educandos y promover los cambios deseados, para lo que es necesario propiciar su expresión verbal, tanto en forma oral como escrita, siendo el diálogo un elemento de vital importancia en este proceso, por lo que el método de discusión es uno de los que juega un papel fundamental en la propuesta.
5) Facilitar el trabajo consciente e intelectual de los educandos en función de los objetivos propuestos con la ayuda de medios materiales (prácticas, demostraciones, literatura docente, programas de computación, etc.) que él mismo manipulará y le dará la posibilidad de corregir sus hipótesis y concepciones previas.
En un ambiente colaborativo, las oportunidades de aprendizaje de un estudiante no dependen sólo de sus propias capacidades, sino también de los otros miembros del grupo y lo que ellos le pueden aportar. Tomando en cuenta este factor es posible mejorar las propuestas de aprendizaje hechas al estudiante basándonos no solamente en el nivel de conocimiento actual de cada uno de ellos.
La conformación de grupos es uno de los elementos clave para mejorar las oportunidades de colaboración en una comunidad de aprendizaje. Está vinculado a la concientización social, lo cual consiste en que los estudiantes estén atentos en todo momento de los intereses y capacidades de los otros miembros de la comunidad.
OBJETIVO GENERAL: La formación por competencias sobre la base del vínculo teoríapráctica a través del PEA (Proceso de Enseñanza -Aprendizaje) de la asignatura del Cálculo de varias variables. (Ruiz, 2005).
Rasgos distintivos:
a) Es integral: porque toma en cuenta las características de la asignatura del Cálculo de varias variables, donde se pretende desarrollar un pensamiento analítico y aplicable a las diversas situaciones de la vida lo que optimiza la asimilación de lo estudiado. Asimismo se apoya en las potencialidades que ofrece la Didáctica para que los estudiantes no sean “repetidores de conceptos”, sino productores de conocimientos a los que les otorguen un significado en todas las esferas de actuación.
b) Es dinámica y flexible: porque permite tomar en consideración las condiciones existentes en el contexto donde se vaya a instrumentar, ya que sus sustentos son aplicables a cualquier medio a partir de las regularidades que se han revelado en el epígrafe anterior.
c) Es desarrolladora: por permitir no solo el desarrollo del pensamiento lógico del alumno, sino también el desarrollo de otras cualidades y valores mediante la interacción y colaboración entre ellos y la creación de espacios para la construcción no sólo de significados, sino también de sentidos.
Requisitos para su aplicación.
1.- Atención a la diversidad.
2.- Enfoque problematizador del contenido para lograr un adecuado desarrollo del pensamiento complejo.
3.- Clima adecuado que favorezca la formación de los alumnos.
4.- Vinculación del contenido con el contexto y la situación actual como vía para lograr la unidad de lo cognitivo y lo afectivo.
Diagnóstico:
Objetivo: Identificar las causas que influyen en las insuficiencias para la formación de competencias del estudiante mediante el proceso de enseñanza aprendizaje del Cálculo de varias variables.
Entre las acciones fundamentales se encuentran:
1.- Determinación de los principales problemas.
2.-Caracterización del grupo y de la enseñanza-aprendizaje del Cálculo de varias variables.
3.- Determinación de las principales causas que influyen en las deficiencias en la formación de los estudiantes y las bajas calificaciones en la materia.
Este momento es esencial por cuanto permite conocer cuestiones de vital importancia para el desarrollo del proceso de enseñanza-aprendizaje, en particular lo relacionado con el objetivo de la estrategia. Uno de los elementos que se requiere explorar son las preconcepciones que posee el estudiante. Otras cuestiones importantes son: la motivación de los estudiantes por la asignatura del Cálculo, conocimientos y habilidades previas. También cómo influyen las condiciones en que se desarrolla la actividad docente, la forma de organizarla, el uso de los medios, las actitudes y cualidades de los estudiantes.
Objetivo:
Diseñar el proceso de enseñanza-aprendizaje en correspondencia con la concepción didáctica del modelo por competencias, de manera tal que se favorezca la formación integral del estudiante. Acciones fundamentales:
1.-Definir las tareas que pueden propiciar la formación en competencias y en correspondencia con ello determinar los objetivos y contenidos específicos de cada tema y clase desde el propio contenido de la asignatura, así como desde las metodologías que se utilicen, si se hace de forma espontánea no se logra un proceso formativo trascendente.
2.- Determinar la organización de los pequeños grupos de manera tal que se combinen las características de los alumnos, su rendimiento académico y pueda realizarse un intercambio en cuanto lo conceptual metodológico y también lo cultural.
Objetivo:
Desarrollar el proceso de enseñanza-aprendizaje de modo tal que se logren las competencias formativas en los estudiantes a partir del tema objeto de estudio.
Acciones fundamentales:
1.- Integración de las tareas docentes que permitan el desarrollo de las competencias formativas.
La dinámica del proceso se debe caracterizar por el fortalecimiento del protagonismo del estudiante. Se les estimula a que se planteen problemas entre ellos y se cuestionen lo que observan, la determinación de las causas, que encuentren ellos mismos sus preconcepciones y la forma de eliminarlas.
2.- Enriquecimiento del aspecto cultural del estudiante.
También es importante que conjuntamente con el contenido del Cálculo se destaquen aquellas personalidades que jugaron un papel en el desarrollo de esta disciplina científica para enriquecer el bagaje cultural de los estudiantes, cómo ha sido el desarrollo histórico de cada parte del Cálculo, lo que unido al uso de medios, formas y métodos que promuevan el interés de los estudiantes hace que se eleve la efectividad del proceso formativo.
Objetivo: Determinar si se ha favorecido la formación en Competencias del estudiante al estudiar el Cálculo de varias variables.
Acciones fundamentales:
1.- Autoevaluación, coevaluación y hetereoevaluacíón: Las actividades en pequeños grupos en los que se trabaja con el software y el equipo permite que los estudiantes se evalúen y ayuden mutuamente. Igualmente, en las tareas investigativas se debe fomentar la coevaluación y autoevaluación tanto en la solución de las tareas docentes como en la conducta.
2.-Corrección de los errores y dificultades. Se sugiere utilizar la observación sistemática y la corrección de las dificultades tanto en el plano instructivo como en el formativo.
A partir de las posibles vías expuestas se presenta a continuación, la ejemplificación en la práctica. La cual se aplicó al grupo de 20 estudiantes encuestados. Se formaron 5 subgrupos de 4 estudiantes de tal manera que cada subgrupo contara con el software de geometría analítica Cabri Plus 11 ya instalado en las computadoras.
Se les informa a los estudiantes que con el software se puede modelar las coordenadas polares vista en la clase. Por razones de espacio solamente se muestra en la aplicación de la estrategia un ejemplo de este tema.
El interés principal de los autores es que con este recurso adicional los alumnos exploren, describan, analicen, justifiquen, interpreten, “descubran” resultados de manera visual (y eso los motive a demostrar analíticamente las regularidades que observan).
La formación de los grupos se dio de la manera que por lo menos un estudiante tuviera las competencias en TICS. Se espera que la realización de estas actividades ayude al estudiante en el desarrollo de las siguientes competencias:
1) Relacionar las ecuaciones polares con sus gráficas
2) Describir las simetrías de las gráficas de ecuaciones polares
3) Visualizar la dirección de algunas gráficas polares
4) Comparar el planteamiento de problemas de áreas en situaciones donde la curvao una parte de la curvase recorre una sola vez y donde se recorre varias veces cuando el ángulo toma valores en ciertos intervalos
5) Clasificar la forma y tipo de caracol de acuerdo a la razón de las constantes a y b que aparecen en las ecuaciones polares
6) Identificar el número y la forma de pétalos de una rosa o si n es par o impar
7) relacionar la longitud de los pétalos de una rosa con el valor de la constante a en la ecuación o
8) Interpretar el área limitada por la gráfica de una ecuación polar como una integral en la que los límites de integración no son necesariamente todos los valores del ángulo sobre los que se construyó la gráfica.
Para el desarrollo de las actividades se proporcionaron a los alumnos archivos realizados en Cabri Plus II por los autores de este trabajo; éstos corresponden a gráficas de las rosas y los caracoles
Situación problémica.
· Varíe los valores de las constantes a, b y n que aparecen en las ecuaciones.
· A través de la observación describee interpreta las figuras que se forman con este software.
A cada grupo se les sugirió diferentes ecuaciones aquí se presenta un ejemplo.
Actividad # 1. La gráfica de la ecuación
Usando los archivos proporcionados, considera la ecuación y contesta las preguntas (1-4) siguientes: (n es un número entero positivo)
1. Con un valor fijo de n, por ejemplo n=2, varía el valor de a en la ecuación y observa la gráfica resultante.Describe los cambios en la gráfica en relación con el valor de a.
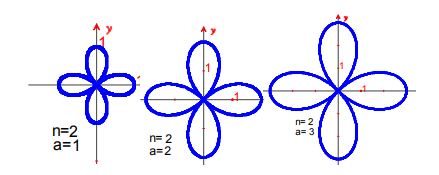
Grafico
Gráficas obtenidas por los alumnos para distintos valores de a
El desarrollo de esta actividad propició la discusión entre los integrantes de los distintos equipos; los alumnos mencionaron la relación entre el valor de la constante a y el valor máximo de r
2. Para un valor de a fijo, varía el valor de n usando números impares.
3. Para un valor de a fijo, varía el valor de n usando números pares.
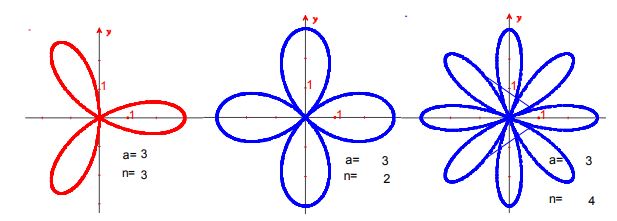
4. De acuerdo a lo observado en las gráficas, interpreta:
a) El número de pétalos para cada rosa, si n impar.
b) El número de pétalos para cada rosa, si n es par
c) Los ángulos para los cuales el valor de r es máximo
d) Los tipos de simetría de cada una de las gráficas
Los alumnos mostraron motivación por la construcción de las gráficas, determinaron el número de pétalos de acuerdo a si n es par o impar, así como la distribución de los pétalos en la gráfica, mencionaron que los pétalos no se empalman, en palabras de ellos, que cada uno tiene su “propio espacio”, las simetrías con el eje polar, con el eje y con el polo según el caso y pudieron observar y discutir sobre la distribución de los pétalos, para cuáles valores de se obtiene la r máxima, y se mostraron con una mayor disposición a obtener analíticamente los valores de para los cuales r es máximo o mínimo.
Por razones de espacio ya no se presentan ejemplos con la aplicación de la estrategia didáctica, que demuestran un mejor resultado a la prueba de diagnóstico aplicada a los estudiantes.
En la observación realizada durante las actividades docentes y en los resultados de la encuesta aplicada a los estudiantes se pudo corroborar que el hecho de utilizar las nuevas tecnologías de la información para el proceso de enseñanza-aprendizaje de los estudiantes, ha favorecido el proceso de construcción de significados y sentidos al propiciarse la interactividad del alumno con el conocimiento, la comprensión de procesos, leyes, propiedades y teorías.
Los fundamentos teórico-metodológicos de la estrategia para el proceso de enseñanza-aprendizaje de la asignatura del Cálculo de varias variables expresan las necesidades actuales de involucrar al estudiante de manera activa en su proceso formativo, en particular mediante el modelo por competencias.



https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/5306 (pdf)

Figura 1

Figura 2

Figura 3

Figura 4

Grafico








