

MODELAGEM MATEMÁTICA ENVOLVENDO ATIVIDADES DE CÁLCULO INTEGRAL
REAMEC – Rede Amazônica de Educação em Ciências e Matemática, vol.. 6, núm. 3, 2018
Universidade Federal de Mato Grosso


Edição Especial
URL: http://portal.amelica.org/ameli/jatsRepo/437/4372089008/index.html
DOI: https://doi.org/10.26571/REAMEC.a2019.v6.n3.p92-104.i7722

Resumo: A Modelagem Matemática desenvolvida na Educação Matemática tem sua origem na Matemática Aplicada e tem se apresentado em pesquisas brasileiras com diferentes concepções. Neste artigo tem-se o objetivo de compreender a contribuição de se utilizar a Modelagem Matemática em atividades de Cálculo Integral aplicada a um grupo de alunos da turma de Cálculo II do curso de Bacharelado em Engenharia Elétrica no Instituto Federal do Maranhão – Campus Imperatriz. A pesquisa teve uma abordagem qualitativa, na medida em que foi analisado o material produzido pelo grupo de alunos em gravações de áudio durante o desenvolvimento das atividades e da observação participante do professor pesquisador. Os resultados encontrados evidenciam que a utilização da Modelagem Matemática na terceira concepção apresentada no trabalho de Klüber (2009) contribui para a aprendizagem dos conceitos de cálculo integral, já que essa vivência torna possível visualizar aplicações cotidianas.
Palavras-chave: Modelagem, Matemática, Educação.
1. INTRODUÇÃO
A Modelagem Matemática tem sua origem em atividades da Matemática Aplicada, onde os pesquisadores buscavam resolver situações problemas com a formulação de modelos ainda não evidenciados. Essa tendência na educação valoriza aplicações em situações problemas de forma contextualizada afim de que motive os alunos na busca por soluções. No Brasil os precursores dessa prática foram Aristides Camargo Barreto, Rodney Carlos Bassanezi e Ubiratan D’Ambrósio (BIEMBENGUT, 2003).
A partir destes pioneiros, surgiram outros pesquisadores nesta área que apresentaram diferentes concepções para o seu desenvolvimento. Em um estudo realizado por Klüber (2009) evidenciou-se três concepções: 1) a Modelagem Matemática entendida como um ambiente de aprendizagem; 2) a Modelagem Matemática como metodologia que visa à construção de Modelos Matemáticos; e 3) a Modelagem Matemática como Metodologia ou estratégia de ensino, focada mais no processo de ensino e de aprendizagem do que no Modelo Matemático.
Diante do exposto, buscou-se desenvolver no primeiro semestre de 2018 atividades de Modelagem Matemática na disciplina de Cálculo II em uma turma de Bacharelado em Engenharia Elétrica do IFMA – Campus Imperatriz. O propósito desta pesquisa foi compreender a contribuição para a aprendizagem de Cálculo Integral quando os alunos são envolvidos em atividades de Modelagem Matemática no ambiente da sala da aula.
Neste sentido, pensar na modelagem matemática como mediadora nas relações de ensino e aprendizagem pode atribuir sentido e construir significados na vida dos estudantes na compreensão de significados que favoreça aproximação da matemática escolar com os problemas extraescolares presente no cotidiano do estudante e na vivência escolar.
2. REFERENCIAIS TEÓRICOS
Fiorentini e Lorenzato (2006) destacam a Modelagem Matemática como uma das linhas de pesquisas em Educação Matemática que começou a ser utilizada na Educação brasileira desde a década de 1970. Os pioneiros foram os professores Aristides Camargo Barreto, Rodney Carlos Bassanezi e Ubiratan D’Ambrósio que iniciaram trabalhando com os alunos do Ensino Superior, da Pós-graduação e professores em formação continuada. Atualmente há diversos pesquisadores abordando a temática e surgiram várias concepções acerca da abordagem de Modelagem Matemática na sala de aula.
Em estudo desenvolvido por Klüber (2009) ao pesquisar as concepções presentes nas 42 comunicações científicas na V Conferência Nacional sobre Modelagem em Educação Matemática – CNMEM observou-se que emergiram três principais concepções: 1) a Modelagem Matemática entendida como um ambiente de aprendizagem; 2) a Modelagem Matemática como metodologia que visa à construção de Modelos Matemáticos e 3) Modelagem Matemática como Metodologia ou estratégia de ensino, focada mais no processo de ensino e de aprendizagem do que no Modelo Matemático.
A concepção que apresenta a Modelagem Matemática como ambiente de apredizagem está representada nos trabalhos de Jonei Cerqueira Barbosa e acolhida nos trabalhos de vários outros pesquisadores sobre Modelagem Matemática. Para Jonei Cerqueira Barbosa a
Modelagem pode ser entendida em termos mais específicos. Do nosso ponto de vista, trata-se de uma oportunidade para os alunos indagarem situações por meio da matemática sem procedimentos fixados previamente e com possibilidades diversas de encaminhamento. Os conceitos e idéias matemáticas exploradas dependem do encaminhamento que só se sabe à medida que os alunos desenvolvem a atividade. (...) Modelagem é um ambiente de aprendizagem no qual os alunos são convidados a indagar e/ou investigar, por meio da matemática, situações oriundas de outras áreas da realidade. (BARBOSA, 2001, p.6, grifo nosso).
A perspectiva atribuída a Modelagem como metodologia que visa à construção de modelos está presente em trabalhos fundamentados principalmente por Bassanezi e Biembengut & Hein. Segundo Klüber (2009) a prática de modelagem neste âmbito segue ritos específicos que não podem ser reproduzidos integralmente no ambiente escolar. Neste caso há sim uma valorização do produto final, apesar de muitos trabalhos reconhecerem a importância do sujeito agente na construção do conhecimento.
Biembengut & Hein (2013, p.12) destacam que “Modelagem matemática é o processo que envolve a obtenção de um modelo.” Esta é uma forte influência da Matemática Aplicada, onde o principal objetivo é a formação do modelo matemática capaz de representar situações reais.
Nesta perspectiva, o professor e pesquisador Rodney Carlos Bassanezi apresenta importantes contribuições para o desenvolvimento de atividades com Modelagem Matemática no país, principalmente nos cursos de graduação e pós-graduação. Bassanezi ao escrever sobre Modelagem como estratégia de ensino e aprendizagem destacou que um fator muito importante no desenvolvimento das atividades é a formação do modelo matemático:
A tônica dos cursos de graduação é desenvolver disciplinas matemáticas “aplicáveis”, em especial aquelas básicas que já serviram como auxiliares na modelagem de fenômenos de alguma realidade como Equações Diferenciais Ordinárias e Parciais, Teoria do Controle Ótimo, Programação Linear e não Linear, [...]. Nos cursos de Mestrado e Doutorado, além de um aprofundamento das disciplinas matemáticas, o objetivo principal é desenvolver a criatividade matemática do aluno no sentido de torná-lo um modelador matemático quando se dedica ao estudo de alguma situação fenomenológica. (BASSANEZI, 2011, p. 35, grifo nosso).
Para Bassanezi e Biembengut & Hein a criação do modelo matemático é fundamental no desenvolvimento de atividades com Modelagem Matemática, como se observa nas citações anteriores, e segundo Klüber (2007, p.102) “Biembengut e Bassanezi não apresentam concepção de ensino ou de aprendizagem explícita” e não há citações de teóricos que tratem dessas concepções em seus trabalhos. O desenvolvimento destas atividades está fortemente ligado a uma epistemologia presente na Matemática Aplicada ou nas Ciências Naturais.
A terceira perspectiva de Modelagem Matemática no Ensino, de acordo com Klüber (2009), está mais associada a uma metodologia ou estratégia de ensino focada no processo de ensino e de aprendizagem do que no modelo matemático propriamente dito. O principal representante desta perspectiva é o professor Dionísio Burak que enuncia:
A Modelagem Matemática constitui-se em um conjunto de procedimentos cujo objetivo é construir um paralelo para tentar explicar, matematicamente, os fenômenos presentes no cotidiano do ser humano, ajudando-o a fazer predições e a tomar decisões. (BURAK, 1992, p. 62).
Nos trabalhos de Burak há uma aproximação com as teorias de ensino e de aprendizagem enfatizando a construção do conhecimento matemático por parte dos alunos. A utilização de concepções que procuram explicar os processos cognitivos durante a aplicação da Modelagem Matemática tem influência das Ciências Humanas e Sociais. Klüber concluiu, ao analisar os trabalhos do professor Burak, que houve
[...] um avanço teórico no âmbito epistemológico da concepção desse autor, que se direciona dos moldes usuais para um ensino por construção e, por conseguinte, persegue mais de perto um ensino contextualizado, fruto de influências recebidas das ciências humanas. (KLÜBER; BURAK, 2008, p. 22)
Sendo assim, ocorreu um distanciamento da epistemologia da Matemática Aplicada visto que, acrescentou-se dois princípios básicos para o desenvolvimento da Modelagem que são: 1) o interesse do grupo; e 2) a obtenção de informações e dados do ambiente, onde se encontra o interesse do grupo.
Para o desenvolvimento das atividades de Modelagem Matemática, Almeida, Silva e Vertuan (2013) apresentam as fases relativas à sua realização que são: inteiração, matematização, resolução, interpretação de resultados e validação. Na inteiração os alunos têm o primeiro contato com a situação-problema e inicia-se um processo de levantamento de dados para se familiarizarem com a questão em estudo. Na matematização os alunos buscarão o conteúdo matemático mais adequado para resolver a situação-problema apresentada e, após esta identificação, realizar a transição da linguagem natural para a linguagem matemática. Em seguida, a fase da resolução onde os alunos pesquisarão um modelo matemático para representar a situação em estudo. Na fase de interpretação de resultados e validação os alunos realizarão uma análise onde verificarão se realmente o modelo desenvolvido representa uma solução para a questão em diferentes contextos de aplicações.
A aplicação da Modelagem Matemática pode trazer contribuições para o ensino de Cálculo Diferencial e Integral, já que esta é uma disciplina fundamental para os cursos das Ciências Exatas e, segundo algumas pesquisas os alunos encontram muita dificuldade de aprendizagem. Pagani e Allevato destacam que:
O ensino e a aprendizagem de conteúdos de Cálculo Diferencial e Integral, há alguns anos, têm sido objeto de estudo e debate. As dificuldades observadas nos cursos iniciais de Cálculo Diferencial e Integral se traduzem nos altos índices de reprovação dessas disciplinas. (PAGANI; ALLEVATO, 2014, p. 62)
Desta forma, reforça-se a importância em realizar pesquisas para buscar compreensões a cerca do desenvolvimento dos alunos na disciplina de Cálculo Diferencial e Integral face às atividades estruturadas na Modelagem Matemática.
3. METODOLOGIA
Este estudo tem uma abordagem qualitativa, pois pretende compreender que contribuições na aprendizagem podem ser identificadas quando um grupo de alunos se envolve em atividades de Modelagem Matemática. Para John W. Creswell (2014) a coleta de dados é realizada em um contexto natural sensível aos lugares e às pessoas com quem se realizam os estudos, sendo que no corpo do trabalho se apresentam as vozes dos participantes, reflexão do pesquisador com sua interpretação e contribuição com a pesquisa.
Para cumprir com o objetivo da pesquisa, o procedimento de produção dos dados foi a observação participante e a gravação da participação de um grupo de cinco alunos ao desenvolverem atividades de Modelagem Matemática envolvendo o Cálculo Integral. As atividades foram desenvolvidas em uma turma do segundo período de Engenharia Elétrica no primeiro semestre de 2018 no Instituto Federal do Maranhão – Campus Imperatriz. Os alunos foram divididos em grupos e deveriam escolher ou propor um problema que pudessem aplicar os conhecimentos de Cálculo Integral que tinham estudado do decorrer do período letivo.
As observações e discussões utilizadas neste trabalho foram colhidas através de gravações de um dos grupos que realizou uma aplicação do Cálculo Integral na Física. A observação para Sampieri (2013) é diferente de apenas ver, tem que estar atento aos acontecimentos, aos detalhes, aos eventos e interações que estão ocorrendo durante o desenvolvimento das atividades.
Foram realizadas as transcrições das gravações feitas durante todo o processo de construção e resolução da questão pelos alunos. O grupo apresentou o trabalho a todos os colegas da turma, como uma maneira de socializar os conhecimentos adquiridos e compartilhar como pensaram em resolver a questão, desde a sua escolha até os processos que se utilizaram para sua resolução.
A análise dos dados se baseou na busca pela identificação das fases da Modelagem Matemática apresentados por Almeida, Silva e Vertuan (2013) e a procura, nas falas dos alunos, de contribuições para a aprendizagem durante a realização destas atividades que envolveram a utilização da Modelagem Matemática.
4. RESULTADOS E DISCUSSÃO
Neste artigo foi adotada a terceira concepção evidenciada por Klüber (2009) que destaca a utilização da Modelagem Matemática como Metodologia ou estratégia de ensino, focada mais no processo de ensino e de aprendizagem do que no Modelo Matemático.
Os alunos ao utilizarem a Modelagem Matemática podem não chegar a estruturação de modelo matemático em si, mas o processo de discussão e pesquisa pelo grupo de alunos resulta em aprendizagem dos conteúdos estudados e devem ser valorizados. É de fundamental importância incentivar os alunos a terem autonomia na pesquisa e na busca de soluções de problemas que estão a sua volta utilizando a matemática para colaborar na elucidação destas questões.
Na primeira etapa para o desenvolvimento do trabalho, buscou-se compreender as concepções de Modelagem Matemática que são evidenciados nos trabalhos sobre o tema. Para isto, foram realizadas leituras de livros que falam sobre o assunto como os de Bassanezi (2011), Biembengut & Hein (2013), Almeida, Silva e Vertuan (2013), além de artigos que discutiam as concepções evidenciadas nos trabalhos sobre Modelagem. O conhecimento a priori tornou possível a compreensão das concepções, a escolha daquela que mais se identificado com a finalidade do trabalho e seu desenvolvimento em uma turma de Engenharia Elétrica no Instituto Federal do Maranhão – Campus Imperatriz.
No início do primeiro semestre de 2018, os alunos do segundo período de Engenharia Elétrica iniciaram a disciplina de Cálculo Diferencial e Integral II no Instituto Federal do Maranhão – Campus Imperatriz. E como os alunos, segundo algumas pesquisas, apresentam dificuldades na aprendizagem da disciplina (PAGANI; ALLEVATO, 2014), foi desenvolvido nesta turma atividades envolvendo Modelagem Matemática com o objetivo de buscar compreensões em relação à aprendizagem dos alunos.
Os alunos receberam as orientações sobre a disciplina e em seguida foram divididos em grupos para, no decorrer da disciplina, já iniciassem a pensar em situações problemas que desejassem resolver a partir de contextos inerentes a seu cotidiano ou de alguma outra disciplina que lhe chamassem a atenção. Todos os grupos deveriam aplicar o Cálculo Integral para auxiliar na resolução dos problemas que escolheram para resolver.
Foram formados sete grupos de alunos, sendo que para a análise deste trabalho foi escolhido apenas um dos grupos. O motivo da escolha deste grupo está na contextualização da aplicação do conteúdo de Cálculo Integral na disciplina de física ao resolver um problema que foi idealizado pelos próprios alunos. A interdisciplinaridade também está presente na medida em que os conhecimentos de outros campos do saber são utilizados para resolver a situaçãoproblema. Fazenda (2011, p. 73) “Considera a interdisciplinaridade como a união dos saberes, contrapondo-se ao isolamento do conhecimento, o qual remete a uma especialização excessiva”. Este grupo de alunos pensou na aplicação de Cálculo Integral na disciplina de Física para resolver um problema que pode surgir no cotidiano de um Engenheiro.
O grupo formado por cinco alunos realizou os encontros na própria Instituição, no IFMA, com o objetivo de definir, discutir e resolver a situação-problema. As reuniões ocorreram em horários vagos, já que eles permanecem na Instituição pela manhã e tarde, sendo que existem horários que estão livres. O professor-pesquisador orientou os alunos na medida em que o procuravam no decorrer da construção da questão e sua resolução.
Os alunos serão identificados pelas letras maiúsculas A, B, C, D e E, no decorrer do trabalho ao serem citadas suas falas ou no momento em que for feito algum comentário individual. Este grupo escolheu trabalhar na construção e resolução de uma questão que envolvesse o volume de sólidos com a utilização do Cálculo Integral e de conhecimentos físicos.
No primeiro encontro que realizaram, começaram a discutir que tipos de situaçãoproblema poderiam relacionar utilizando o Cálculo Integral e a Física. A ideia de relacionar os dois conhecimentos foi do aluno A que logo foi aceita pelo grupo, sendo que o aluno B em seguida fez o seguinte comentário:
Não pow, seria legal, porque ia misturar duas matérias importantes no nosso curso, e dos nossos estudos no curso de engenharia elétrica, e são duas matérias importantes que vamos usar até o fim do nosso curso. (Gravação em áudio do 1º encontro, 01/06/2018)
A partir deste primeiro encontro ficou decidido que buscariam uma situaçãoproblema que envolvesse as duas disciplinas. Observa-se a importância de incentivar os alunos a decidirem a problemática que desejam resolver, isto gera uma motivação para que todos iniciem e se empenhem na resolução da questão proposta. Neste momento, pode-se identificar a fase de Inteiração na fase da Modelagem Matemática em que o grupo procura discutir o problema que irá resolver e os dados que terão que procurar para solucionar a questão (ALMEIDA; SILVA; VERTUAM, 2013).
Um dos motivos da escolha do assunto para pesquisarem, segundo os alunos, é a importância da física para o curso de engenharia. Observa-se que os alunos se empenham com mais dedicação a partir do momento que participam diretamente da escolha e do problema a ser desenvolvido. Neste caso, o professor-pesquisador solicitou a todos os grupos que utilizassem o Cálculo Integral em suas questões, mas que poderiam pesquisar qualquer situação-problema que desejassem solucionar.
O aluno B comenta da importância de se utilizar a Física para contextualizar o Cálculo e que deveriam encontrar uma situação em que iriam precisar usar o Cálculo Integral para calcular volumes de sólidos de revolução. Nesta mesma discussão o aluno C afirma que “A física meche mais com o real, a matemática meche mais com teoria, é estudado mais coisas teóricas” (Gravação em áudio do 2º encontro, 06/06/2018). Nestes encontros é evidenciada a preocupação dos alunos de justificarem o motivo pelo qual estão utilizando a Física para aplicarem os conhecimentos matemáticos, isto fortalece o grupo na busca da situação-problema a ser estudada e sua solução.
Com o objetivo de definirem a situação-problema para iniciarem a busca por sua resolução o aluno A apresenta ao grupo a seguinte situação:
Ai eu estava pensando da gente fazer uma questão assim, da gente ir lá em casa e fizesse tipo uma questão de tensão, essas coisas, por exemplo, alguma coisa pra descobrir o máximo que ele precisa levantar, o volume de algo e ele tem que levantar um cone de base circular. Ai a pinça dele, o tanto que a pinça dele pode conseguir encaixar no volume, o máximo de volume que ela pode pegar, ai tipo ela vai fazer assim, e vai saber o máximo que ela pode levantar. (Gravação em áudio do 3º encontro, 11/06/2018)
Neste momento, os alunos estão combinando a formulação de uma questão de Física e o Cálculo necessário para calcular o volume máximo de um objeto que a pinça possa ser capaz de pegar. Com estas considerações o aluno C questiona aos colegas “Aí onde é que entraria a integral aí, pra saber a área, ou o que?” (Gravação em áudio do 3º encontro, 11/06/2018). O aluno A responde que será o volume máximo que a pinça poderá levantar e que se calcular a função que define um lado do guindaste seria então capaz de aplicar no cálculo de integral para encontrar o volume máximo que o guindaste suportaria. Nesse diálogo, os alunos estão simultaneamente nas fases de inteiração e de matematização, pois ainda estão debatendo as características da situação-problema e já comentam que irão necessitar dos conhecimentos de função para determinar a expressão que representa o braço do guindaste, e em seguida aplicar o cálculo integral de volumes.
Os alunos então iniciaram o estudo da expressão que poderia representar o braço da pinça, depois da identificação da expressão foi possível calcular o volume máximo que poderia suportar utilizando o Cálculo Integral de volumes de revolução. Observe no desenho a seguir a representação da Garra Fechada que os alunos colocaram no trabalho:
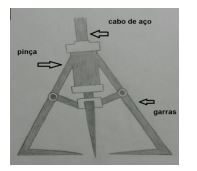
Os alunos estudaram as possíveis representações que a garra poderia ser desenhada em um plano cartesiano, em seguida modelaram a função do primeiro grau que representava a garra para esta atividade. Observe a figura a seguir que os alunos construíram da garra no plano cartesiano:
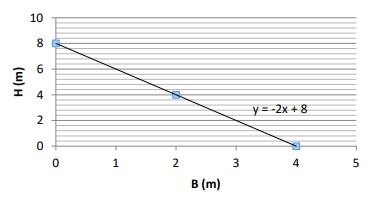
Após a modelação da expressão da função os alunos calcularam o máximo volume que a garra poderia suportar utilizando o Cálculo Integral para volumes de sólidos por discos, rotacionando em torno do eixo y em um intervalo de [0,4] em metros.
Em seguida, os alunos começaram a pensar em utilizar a informação do volume encontrado para calcular a tensão que o guincho pode suportar em seus cabos. Neste momento o aluno C interrompe a discussão e diz “Tensão!!!!? Mas aí já passou de Integral.” (Gravação em áudio do 5º encontro, 18/06/2018). Então o aluno A argumenta:
Não!! Pois é, mas ai a gente pode pensar de integral pra usar. Aí tipo, o volume, a gente descobre o volume, aí tem a constante, a constante do material, e depois tem... Vai ser o peso dele, descobrir o peso. A tensão vai ser igual ao peso!!! (Gravação em áudio do 5º encontro, 18/06/2018)
Os alunos começam a se envolverem também na fase da Resolução da situaçãoproblema e através de algumas modelações encontram o volume máximo que a garra do Guindaste poderia suportar. Para o aluno C a questão já estava concluída, mas em seguida o aluno A comenta em realizar a verificação da tensão que o cabo de aço que sustenta a pinça poderia suportar com aquele volume máximo. Nesta situação, os conhecimentos físicos de Força, Peso, Densidade e a relação entre eles serão de importância para sua resolução.
Os alunos então iniciaram uma pesquisa para encontrarem informações sobre a tração máxima que os cabos poderiam suportar, pois sabiam que a tração do cabo que sustenta a pinça tinha que suportar o peso da pinça juntamente com o peso da peça que iria levantar. Pesquisaram o peso de uma pinça específica e a densidade de um material que a pinça iria pegar. Pelos conhecimentos físicos, a massa é o produto da densidade pelo volume, sendo que a densidade foi dada e o volume foi encontrado pelo cálculo integral. Desta forma, os alunos conseguiram calcular a tração máxima suportada pelo cabo que sustenta a pinça.
Nesta fase foi possível verificar a fase de Interpretação de resultados e validação da questão proposta pelo grupo, pois os alunos se empenharam em fazer todas as verificações antes de entregarem o trabalho escrito e apresentarem os resultados de sua pesquisa aos demais colegas da sala.
Os cálculos matemáticos não foram apresentados neste artigo, pois o objetivo principal foi compreender a importância de se trabalhar com os alunos a Modelagem Matemática para incentivar os alunos a terem uma maior autonomia na pesquisa e nos estudos da matemática. A partir do momento que o aluno se sente motivado a buscar o problema para solucionar e ser capaz de relacionar os conhecimentos matemáticos para resolver as questões, eles se sentem desafiados a realizarem todas as pesquisas necessárias para encontrarem uma solução. Almeida, Silva e Vertuan declaram que:
A questão motivacional e as relações entre matemática e realidade mediadas pela Modelagem Matemática parecem então estar interligadas de modo que, por um lado, atribuir sentido e construir significados em Matemática demandam situações de ensino e aprendizagem que induzam relações entre a Matemática e a vida dos alunos fora da escola; por outro lado, as atividades de Modelagem Matemática podem favorecer a aproximação da matemática escolar com problemas extraescolares vivenciados pelos alunos. (ALMEIDA; SILVA; VERTUAN, 2013, p. 31).
O grupo de alunos apresentou seu trabalho aos demais colegas no dia 26 e junho de 2018 e pode-se constatar que todos os componentes do grupo participaram e realmente se envolveram nas discussões dos problemas, desde sua criação até concretização da solução da questão contextualizada.
5. CONCLUSÃO
Neste artigo, buscou-se compreender a contribuição na aprendizagem dos alunos ao se utilizar a Modelagem Matemática em atividades de Cálculo Integral. A pesquisa foi desenvolvida no primeiro semestre de 2018 em uma turma de Engenharia Elétrica no Instituto Federal do Maranhão – Campus Imperatriz. Analisou-se o desenvolvimento das atividades com um dos grupos formados na turma em estudo e foi possível constatar a motivação gerada nos alunos durante a realização das atividades.
Este trabalho apresentou relatos dos alunos que se dispuseram a construir uma questão que estavam interessados em resolver dentro da disciplina de Física, pois revelaram que tanto o Cálculo Integral quanto a Física eram de grande importância para seus estudos. Constatou-se que em todos os momentos estavam motivados a continuarem a serem criativos na construção da questão e na sua resolução envolvendo os aspectos pensados inicialmente. Foram capazes de realizarem as modelações necessárias na construção das questões e em sua resolução.
Enquanto muitos alunos não se sentem estimulados a participarem de atividades envolvendo o Cálculo Integral, a utilização da Modelagem Matemática, neste caso, ajudou os discentes a interagirem entre si. Até mesmo aqueles alunos que no decorrer das aulas tiveram certa dificuldade nos estudos de Cálculo Integral, durante as atividades participaram de forma mais intensa, pois houve significativa colaboração entre os membros do grupo.
Desta forma, é importante compreender que Modelagem Matemática tem sido alvo de estudos e de pesquisas desde a década de 1970 em nosso país e muitos teóricos tem deixado valiosas contribuições para a educação brasileira. Em trabalhos recentes tem-se evidenciados diferentes concepções de trabalhos em Modelagem Matemática, mas neste artigo se dedicou naquela em que é entendida como Metodologia ou estratégia de ensino, focada mais no processo de ensino e de aprendizagem do que no Modelo Matemático. Houve a valorização do caminho percorrido pelos alunos no processo de aprendizagem. Incentiva-se então a utilização da Modelagem Matemática nas atividades de Cálculo Integral, pois se verificou nesta pesquisa pontos positivos em sua utilização.
REFERÊNCIAS
ALMEIDA, Lourdes Werle de; SILVA, Karina Pessôa da; VERTUAN, Rodolfo Eduardo. Modelagem Matemática na Educação Básica. 1ª Ed. – São Paulo: Contexto, 2013.
BASSANEZI, Rodney Carlos. Ensino-aprendizagem com modelagem matemática: uma nova estratégia. 3. Ed., São Paulo: Contexto, 2011.
BARBOSA, J. C. Modelagem na Educação Matemática: contribuições para o debate teórico. In: REUNIÃO ANUALDA ANPED, 24., 2001, Caxambu. Anais... Rio Janeiro: ANPED, 2001. Disponível em: http://www.ufrgs.br/espmat/disciplinas/funcoes_modelagem/modulo_I/modelagem_barbosa. Acesso em 19 fev. 2018.
BIEMBENGUT, Maria Sallet; HEIN, Nelson. Modelagem Matemática no Ensino. 5. Ed., 3ª reimpressão – São Paulo: Contexto, 2013.
BIEMBENGUT, Maria Salett. Modelagem Matemática: Mapeamento das Ações Pedagógicas dos Educadores de Matemática. Tese de Pós - Doutorado, USP, São Paulo - SP, 2003.
BURAK, D. Modelagem matemática: ações e interações no processo de ensino aprendizagem. Tese de Doutorado. Campinas, Unicamp, 1992.
CRESWELL, J. W. Investigação qualitativa e projeto de pesquisa: escolhendo entre cinco abordagens. 3 ed. Tradução: Sandra Mallmann da Rosa. Porto Alegre: Penso, 2014.
FAZENDA, I. C. A. Integração e interdisciplinaridade no ensino brasileiro: efetividade ou ideologia. 6 ed. São Paulo: Edições Loyola, 2011.
FIORENTINI, Dario; LORENZATO, Sergio. Investigação em Educação Matemática: percursos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006.
KLÜBER; T. E.; BURAK, D. Concepções de Modelagem Matemática: Contribuições Teóricas. Educ. Mat. Pesqui., São Paulo, v. 10, n. 1, p. 17-34, jan.-jun., 2008.
KLÜBER, T. E.. Um olhar sobre a Modelagem Matemática no Brasil sob algumas categorias fleckianas. In: ALEXANDRIA Revista de Educação em Ciência e Tecnologia, Florianópolis. v. 2, n.2, p.219-240, jul. 2009. Disponível em: https://periodicos.ufsc.br/index.php/alexandria/article/view/37963 Acesso em: 19/05/2018.
PAGANI, E. M. L; ALLEVATO, N. S. G. Ensino e aprendizagem de Cálculo Diferencial e Integral: um mapeamento de algumas teses e dissertações produzidas no Brasil. VIDYA, v. 34, n. 2, p. 61-74, jul./dez., 2014 - Santa Maria, 2014.
SAMPIERI, Roberto Hernández; COLLADO, Carlos Fernández; LUCIO, Pilar Baptista. Metodología da pesquisa. Tradução: Daisy Vaz de Moraes; revisão técnica: Ana Gracinda Queluz Garcia, Dirceu da Silva, Marcos Júlio. – 5 ed. – Porto Alegre: Penso, 2013.
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/7722 (pdf)

