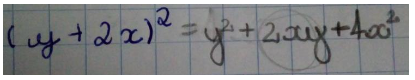Introdução
Segundo dados de 2010 do Instituto Brasileiro de Geografia e Estatística (IBGE), metade da população brasileira é considerada sem instrução ou com o Ensino Fundamental incompleto. Na tentativa de modificar este quadro, foram estabelecidas metas através do Plano Nacional de Educação (PNE) (BRASIL, 2011) para melhorar a qualidade de ensino e o desempenho dos estudantes. Entre as metas estão: elevar a frequência escolar e a qualidade da educação, com a universalização do atendimento dos 4 aos 17 anos; universalizar o ensino para estudantes com deficiência, transtornos globais do desenvolvimento e altas habilidades ou superdotação na rede regular de ensino, em razão da crescente demanda de matrículas deste grupo da população e as diferentes necessidades destes estudantes, para que tenham uma educação de qualidade.
Esta última, citada no PNE como meta 4, justifica-se pelo fato de que no último censo demográfico realizado em 2010 pelo IBGE (IBGE, 2012), constatou-se que, a população que possui ao menos uma das deficiências investigadas na pesquisa (visual, auditiva, motora e mental) chega a 45,6 milhões, o que representa uma parcela de 23,9% da população brasileira. Dentre estes, 18,8% a declaram possuir deficiência visual o que equivale a pouco mais de 35,7 milhões, sendo 6,5 milhões com deficiência visual severa, 0,3% cega e 3,2% com grande dificuldade em enxergar.
Conforme os Parâmetros Curriculares Nacionais: Adaptações Curriculares (PCN-AC) a deficiência visual é definida como:
A redução ou perda total da capacidade de ver com o melhor olho e após a melhor correção ótica. Manifesta-se como: Cegueira: perda da visão, em ambos os olhos, de menos de 0,1 no melhor olho após correção, ou um campo visual não excedente a 20 graus, no maior meridiano do melhor olho, mesmo com o uso de lentes de correção. Sob o enfoque educacional, a cegueira representa a perda total ou o resíduo mínimo da visão que leva o indivíduo a necessitar do método Braille como meio de leitura e escrita, além de outros recursos didáticos e equipamentos especiais para a sua educação; Visão reduzida: acuidade visual dentre 6/20 e 6/60, no melhor olho, após correção máxima. Sob o enfoque educacional, trata-se de resíduo visual que permite ao educando ler impressos a tinta, desde que se empreguem recursos didáticos e equipamentos especiais. (BRASIL, 1998, p.26).
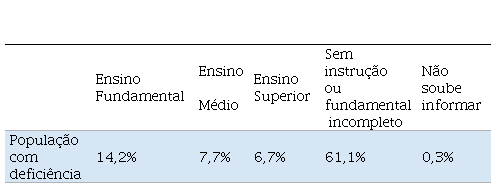
O censo pesquisou também o nível de instrução da população com mais de 15 anos que declarou possuir alguma deficiência (Tabela 1).
Tabela 1
Nível de instrução da população que declarou possuir ao menos uma
deficiência pesquisada
IBGE,
2012
|
Ensino
Fundamental
|
Ensino
Médio
|
Ensino
Superior
|
Sem
instrução ou fundamental incompleto
|
Não
soube informar
|
|
População
com deficiência
|
14,2%
|
7,7%
|
6,7%
|
61,1%
|
0,3%
|
O nível de instrução é fator determinante para a inserção no mercado de trabalho, sendo a renda dos trabalhadores influenciada pelo seu nível de escolarização. O não cumprimento das leis que garantem o ensino para a população com deficiência, acarreta no não cumprimento do direito ao trabalho de qualquer cidadão, impactando na renda da família e dificultando o acesso a uma vida digna e de qualidade.
No que se refere ao processo de aprendizagem da matemática, o baixo desempenho escolar não é exclusividade de estudantes com alguma deficiência. Os dados obtidos entre 1995 e 2011 pelo Sistema de Avaliação de Educação Básica (SAEB/Prova Brasil) que tem como objetivo avaliar o desempenho escolar nas grandes áreas, português e matemática, de alunos do 5º ao 9º ano do ensino fundamental e 3º ano do médio, revela que houve decréscimo nas notas de matemática atingidas pelos estudantes do último ano do ensino médio,
Tabela 2
Média de
desempenho dos alunos em matemática (3a.série do ensino médio)
SAEB/INEP
|
Ano
|
1995
|
1997
|
1999
|
2001
|
2011
|
|
Nota
|
281,9
|
288,7
|
280,3
|
276,7
|
273,9
|
Portanto, não se deve pensar apenas em como incluir os estudantes que possuem necessidades educativas especiais (NEE), mas como o fazer zelando pela qualidade de ensino de todos, independentemente de suas qualidades ou características físicas e sociais. Conversas informais com professores, nos dão indícios de que o planejamento da aula voltada para o estudante com deficiência visual, atinge com qualidade também o restante da turma. Deste modo, é tomado como hipótese que ao se desenvolver uma metodologia de ensino adequada, onde o professor escolhe melhor os recursos didáticos e suas palavras, eliminando dúvidas ou duplas interpretações, utilizando os termos e conceitos corretos, sem priorizar a característica visual da matemática, o ensino da mesma se torna mais inteligível a todos os estudantes.
Considerando estes dados e condições de ensino e que a manipulação de polinômios é frequente na matemática, esta pesquisa teve como objetivo: reconhecer potencialidades e limitações do uso de um material concreto acessível para o ensino de operações com polinômios em uma turma regular com estudantes cegos inseridos.
Para atingir tal objetivo, foram necessárias leituras sobre aspectos específicos como a legislação sobre inclusão, a linguagem dos deficientes visuais, o papel do professor em relação ao ensino destes estudantes, materiais manipuláveis para o ensino de cegos, ensino de álgebra entre outros. Os estudos sobre estes aspectos foram considerados como ações metodológicas no desenvolvimento desta pesquisa realizada no segundo semestre de 2016, para fundamentar a organização e análise de uma situação de ensino desenvolvida em sala de aula regular com estudantes deficientes visuais incluídos, abordando o conteúdo de polinômios utilizando material manipulável. A síntese destas leituras, a descrição do material e a análise realizada será apresentada nos próximos itens.
Sobre a legislação e inclusão de pessoas
com deficiência
No Brasil, é com a Constituição Federal que a Educação Inclusiva ganha destaque, incorporando em seu artigo 208, o dever do estado ao atendimento educacional especializado aos portadores de deficiência, preferencialmente na rede regular de ensino (BRASIL, 1988).
Porém, o papel da escola vai muito além de simplesmente colocar um aluno em sala de aula. Para Mantoan[1] “Não adianta, contudo, admitir o acesso de todos às escolas, sem garantir o prosseguimento da escolaridade até o nível que cada aluno for capaz de atingir. Ao contrário do que alguns ainda pensam, não há inclusão, quando a inserção de um aluno é condicionada à matrícula em uma escola ou classe especial”. (MANTOAN, 2003 apud REIS, 2010, p.50).
A partir da década de 90, percebeu-se grande empenho em inserir os estudantes com deficiência na rede regular de ensino. Entende-se que não é o estudante com deficiência que deve se adequar ao sistema de ensino, mas sim, o sistema de ensino é que deve se adequar às necessidades dos estudantes, surgindo assim, a concepção de inclusão onde não basta apenas inserir a criança no meio escolar, mas também integrá-la, aceitando e valorizando suas diferenças (REIS, 2010).
Em 1998 foi redigido o documento Parâmetros Curriculares Nacionais: Adaptações Curriculares (PCN-AC), onde são propostas adequações curriculares como: alterações nos objetivos, no tratamento e desenvolvimento de conteúdos, no processo avaliativo e no tempo e organização dispensada aos conteúdos, cuja finalidade é subsidiar a prática docente e auxiliar na aprendizagem dos estudantes. O documento ressalta ainda que “O acesso à escola extrapola o ato da matrícula e implica apropriação do saber e das oportunidades educacionais oferecidas à totalidade dos alunos com vistas a atingir as finalidades da educação, a despeito da diversidade na população escolar” (BRASIL, 1998, p.15).
As adaptações propostas no documento levam em consideração as qualidades, capacidades e potenciais da criança, e não se baseiam mais, como até então ocorria, em suas limitações e deficiências. Além disso se caracterizam como medidas pedagógicas a serem adotadas na sala de aula e não só para um aluno individualmente (BRASIL, 1998).
Para Vygotsky os indivíduos cegos possuem desenvolvimento cognitivo normal, e a falta de experiências visuais pode ser suprida com o uso de representações concretas. Vygotsky (1997) ressalta ainda que, não se pode tratar a cegueira apenas como uma deficiência, mas, em certo ponto, como uma Fonte de manifestação de suas capacidades. Sendo assim, faz-se tarefa do professor, buscar estímulos e instrumentos adequados, a fim de que os estudantes possam ter acesso ao conhecimento a partir de intervenções e interações.
Entende-se que a escola inclusiva é aquela em que todos estão em sala de aula regular, recebendo oportunidades e apoio necessários, e deve-se levar em consideração a diversidade no sentido de que também uma criança sem qualquer deficiência se difere das demais. Deste modo, a escola inclusiva vê cada educando como um ser único, dando meios para que o mesmo desenvolva suas potencialidades individuais. Não há em nossa sociedade um estudante padrão (REIS, 2010), logo, não pode existir um professor padrão, uma sala de aula padrão, um sistema de ensino padrão, assim, as aulas deverão ser únicas, para educandos únicos.
Sobre o uso de materiais manipuláveis para
o ensino de matemática
Uma das possibilidades de aproximar o estudante vidente e cego do conhecimento matemático se dá pela utilização de materiais manipuláveis. Lorenzato (2006) refere-se a estes materiais como sendo aqueles em que o estudante pode: tocar, sentir e manejar, classificando-os em dinâmicos e estáticos. Os dinâmicos são aqueles em que há transformação, como por exemplo, a utilização de palitos de churrasco interligados com garrotes, que permitem a construção de várias formas geométricas, ou ainda, o Multiplano, que possibilita ao estudante realizar várias construções e transformações a partir de pinos e elásticos, já os materiais estáticos são aqueles cuja estrutura não pode ser modificada pelo estudante, sendo, por exemplo, jogos, sólidos geométricos, escala cuisenaire e blocos lógicos.
Apesar de existirem no mercado, muitos materiais manipuláveis comercializáveis para a utilização em aula, nem sempre estes estão em formato acessível a alunos cegos, sendo necessário que o professor realize uma adaptação do material. Batista, Miranda e Mocrosky (2016) reforçam a necessidade de utilização destes materiais ao afirmar que,
Na
escola, a vida acadêmica passa pela organização disciplinar dos conteúdos a
serem estudados e as disciplinas apresentadas em sala de aula utilizam muito a
visualização de números, gráficos, letras, símbolos e imagens. Assim, alunos
com cegueira ou baixa visão necessitam de reorganização na estrutura escolar,
com recursos didáticos, tecnológicos e com o auxílio de materiais voltados para
ajudar na compreensão do conteúdo, além de contar com educadores que saibam
utilizar tais recursos e que entendam as dificuldades enfrentadas pelos
deficientes visuais. (BATISTA, MIRANDA, MOCROSKY, 2016, p.116).
O processo de adaptação de materiais para o ensino de matemática a deficientes visuais pode ser realizado de maneira simples, sem a necessidade de grandes ideias que dispensem alto valor financeiro. É necessário utilizar materiais que possam ser tocados, sentidos ou ouvidos, a fim de aguçar os outros sentidos (BATISTA, MIRANDA E MOCROSKY, 2016), como reforçam Sá, Campos e Silva (2007)
[...]
algumas atividades predominantemente visuais devem ser adaptadas com
antecedência e outras durante sua execução por meio de descrição, informação
tátil, auditiva, olfativa e qualquer outra referência que favoreça a
compreensão do ambiente [...] os esquemas, símbolos e diagramas presentes devem
ser descritos oralmente. Os desenhos, gráficos e ilustrações devem ser adaptados
e representados em relevo. (SÁ; CAMPOS; SILVA, p. 25, 2007).
Nesse sentido, a criatividade do professor é fundamental no sentido de usar os recursos disponíveis adaptando-os conforme o objetivo da aula. É importante que os materiais criados tenham tamanhos e texturas diferenciados para facilitar a percepção tátil do estudante
O
relevo deve ser facilmente percebido pelo tato e, sempre que possível,
constituir-se de diferentes texturas para melhor destacar as partes componentes
do todo. Contrastes do tipo liso/áspero, fino/espesso, permitem distinções
adequadas. O material não deve provocar rejeição ao manuseio e ser resistente
que não se estrague com facilidade e resida à exploração tátil e ao manuseio
constante. (SÁ; CAMPOS; SILVA, p. 27, 2007).
Para Sá, Campos e Silva (2007), o ato de se utilizar recursos metodológicos que contemplem a deficiência visual, implica em melhor rendimento do estudante, que demonstra maior compreensão dos conceitos a partir da sensação tátil. Quando o professor cria recursos que auxiliem no aprendizado de estudantes com necessidades educacionais especiais, acaba também por beneficiar o ensino dos demais, facilitando a compreensão de todos (SÁ, CAMPOS, SILVA, 2007).
É importante ressaltar que o professor pode incentivar a participação dos estudantes na confecção de materiais, usando este momento para também ensinar conceitos matemáticos. Além disso, os materiais manipuláveis não podem ser restritos aos estudantes cegos, pois auxiliam também no ensino aos demais, e ao compartilharem a mesma metodologia e material de ensino, toda a classe é beneficiada e cria-se um ambiente mais inclusivo.
Uma possibilidade para o ensino de
polinômios
De acordo com as Diretrizes Curriculares da Educação Básica do Estado do Paraná (DCE) (PARANÁ, 2008), a matemática não se restringe apenas à contagem e aplicação prática, mas se desenvolve através do pensamento abstrato, avançando em relação ao controle de quantidades e superando a operacionalização aritmética, de modo a surgir um novo ramo dentro da ciência matemática, denominado por álgebra: “A álgebra é um campo do conhecimento matemático que se formou sob contribuições de diversas culturas. Pode-se mencionar a álgebra egípcia, babilônica, grega, chinesa, hindu, arábica e da cultura europeia renascentista. Cada uma evidenciou elementos característicos que expressam o pensamento algébrico de cada cultura” (PARANÁ, 2008, p.51).
Educadores matemáticos e psicólogos, afirmam que o desenvolvimento do pensamento e da linguagem algébrica contribui na formação das funções psicológicas mais desenvolvidas do ser humano (SOUSA, PANOSSIAN, CEDRO, 2014). Mas afinal, o que é a álgebra? Este é um questionamento para o qual existem várias respostas, podendo ser uma ferramenta, uma linguagem, um modo de pensar, entre outras.
Sendo um tema que divide opiniões, Usiskin (1995) destaca quatro concepções sobre a álgebra de acordo com o significado que se dá às variáveis, são elas:
-
· Álgebra como aritmética generalizada, onde as letras são vistas como generalizações de padrões e modelos;
· Álgebra como estudo dos métodos para resolver certos problemas concretos (por exemplo, equações), onde as letras são consideradas como incógnitas a serem determinadas;
· Álgebra como estudo de relações entre grandezas (por exemplo, funções), onde as letras são vistas como variáveis dependentes e independentes;
· Álgebra como estrutura, onde as letras, vistas como símbolos abstratos, representam entes pertencentes às estruturas algébricas, por exemplo, corpos, anéis, grupos, etc.
Apesar das diferentes classificações e concepções em torno da álgebra, adota-se nesta pesquisa a concepção da educação algébrica, denominada, segundo Lins e Gimenez (1997) como concepção letrista facilitadora, na qual a utilização de material manipulativo e situações concretas têm como função auxiliar na formalização de estruturas.
O motivo desta escolha se deve ao fato de que se trata de um trabalho com estudantes deficientes visuais e, portanto, têm o tato (entre outros sentidos), como porta de entrada para novos aprendizados, além de considerar que os materiais concretos auxiliam, não apenas o aprendizado de estudantes com deficiência visual, como também o de videntes (LORENZATO, 2006).
A confecção do material utilizado na situação de ensino proposta foi pautada sob a perspectiva do Desenho Universal, que considera que o material deve ser pensado e construído de modo a contemplar todos os tipos de pessoas, com algum tipo de deficiência ou não, sem que haja a necessidade de adaptações.
A expressão Universal Design
(Desenho Universal) foi usada pela primeira vez nos Estados Unidos, em 1985,
pelo arquiteto Ron Mace, que influenciou a mudança de paradigma no
desenvolvimento de projetos urbanos, de arquitetura e design, inclusive de
produtos. [...] o Desenho Universal aplicado a um projeto consiste na criação
de ambientes e produtos que possam ser usados por todas as pessoas, na sua
máxima extensão possíveis. (SÃO PAULO, 2010, p.14).
A proposta de ensino usada nesta pesquisa foi baseada na monografia intitulada “Estudo Básico de Polinômios na Educação de Cegos” (DIAS, SOUZA, 2007), porém com diversas adaptações, tanto na confecção do material quanto no desenvolvimento metodológico.
Aspectos da confecção de um material para o
ensino de polinômios que atenda a todos
Para a confecção do material necessário ao desenvolvimento da situação de ensino analisada, foram utilizados materiais de baixo custo, resistente à manipulação, para que pudessem ser reutilizados em outros momentos e por turmas diferentes.
Foram utilizadas placas de cortiça com 0,5 cm de espessura, e folhas de Etil Vinil Acetato (EVA) com 0,2 cm de espessura, na coloração vermelha. Ao colar uma placa sobre a outra (de cortiça e EVA), obtêm-se um material resistente e de fácil manipulação. A placa de cortiça escolhida já possuía cola em uma de suas faces, para facilitar o trabalho de construção e deixar o acabamento esteticamente melhor.
A cor vermelha da folha de EVA, foi escolhida para representar o monômio negativo, e a cortiça não foi pintada e representava o monômio positivo. A cor da cortiça e da placa de EVA pode facilmente ser modificada de acordo com a preferência do professor.
A partir das placas de cortiça e EVA, foram recortados três tipos de quadriláteros: quadrados grandes de dimensões 9 x 9 cm; retângulos de dimensões 9 x 1,5 cm; e quadrados pequenos de dimensões 1,5 x 1,5 cm. Em seguida, colados em pares, os quadriláteros de mesma medida de materiais diferentes, ao final totalizaram 96 quadrados grandes, 240 retângulos e 576 quadrados pequenos, todos contendo uma face de cortiça e a outra face de EVA.
As peças confeccionadas foram divididas em kits (figura 1), contendo 6 quadrados grandes (9 x 9 cm), 15 retângulos (9 x 1,5 cm) e 36 quadrados pequenos (1,5 x 1,5), totalizando 16 kits, número necessário para atender uma turma que contenha aproximadamente 30 estudantes dispostos preferencialmente em duplas.
Figura 1
Peças que compõe o kit entregue aos estudantes[2]
A autora (2017)
O material foi apresentado aos estudantes levando em conta os três formatos (quadrado grande e pequeno e retângulo) e texturas (macia do EVA e áspera da cortiça). Para efeito de melhor compreensão, segue o quadro a seguir:
Quadro 1
Representação de monômios com a utilização do material desenvolvido
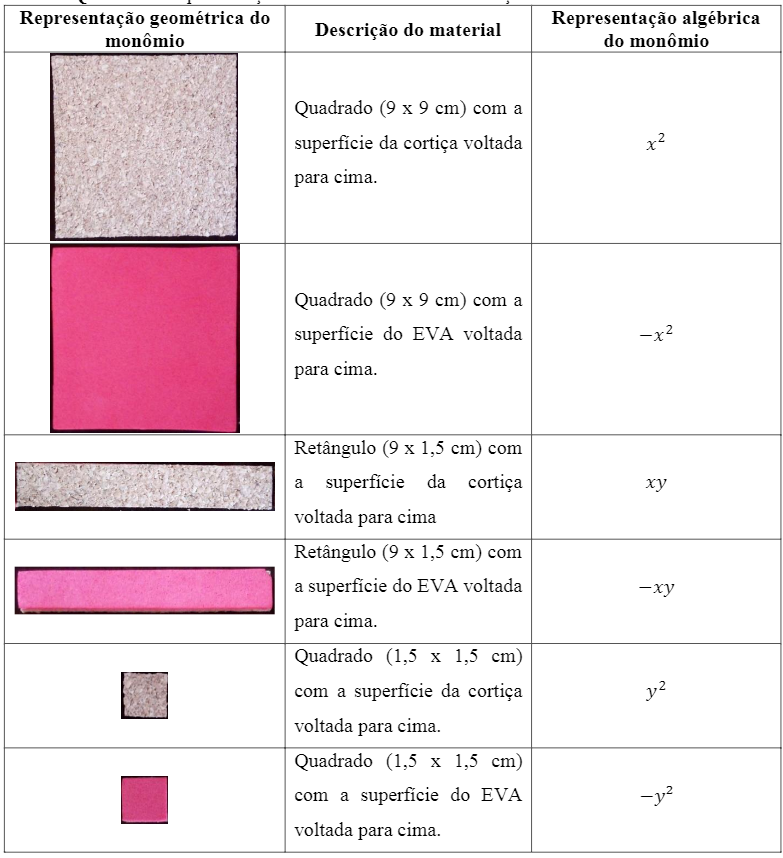A autora (2017)
Para a representação algébrica indicada acima, considera-se as seguintes
medidas (algébricas) de cada quadrilátero:
Quadro 1
Medidas (algébricas) dos quadriláteros
confeccionados
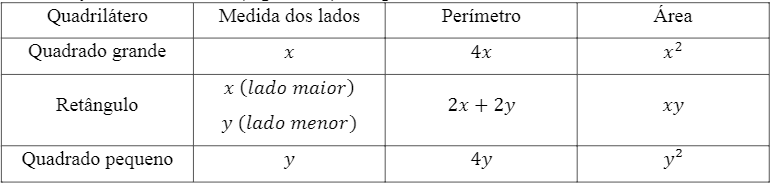A autora (2017)
Sendo assim, para representar um polinômio, basta unir os respectivos
monômios que o representa. Por exemplo:
Figura 2
Representação do
polinômio x2 + 3xy + y2
A autora (2017)
Figura 3
Representação do polinômio -4xy+6y²
A autora (2017)
Conhecendo a representação algébrica dos monômios e a representação com o material, os estudantes têm condições de iniciar o processo com operações entre monômios e polinômios.
Para realizar a adição, deve-se unir os monômios iguais (mesmo formato, tamanho e textura), enquanto que os monômios opostos (mesmo formato e tamanho, porém de diferente textura) anulam-se. Por exemplo:
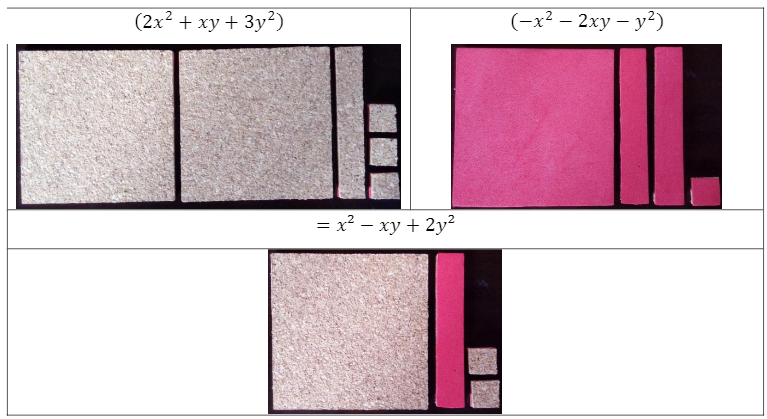Quadro 2
Representação
do polinômio (2x2 +xy +3y2) + (-x2 - 2xy - y2)
A autora (2017)
Para efetuar a subtração de dois polinômios, viram-se
todas as peças do polinômio que sucede o sinal negativo (sinal de subtração), a
fim de trocar todas as texturas, ou seja, o monômio que era positivo passa a
ser negativo e, o monômio que era negativo passa a ser positivo. Em seguida,
basta operar de modo análogo à adição.
Quadro 3
Representação do polinômio (3x2-2xy+y2) - (-x2+5xy-9y2)
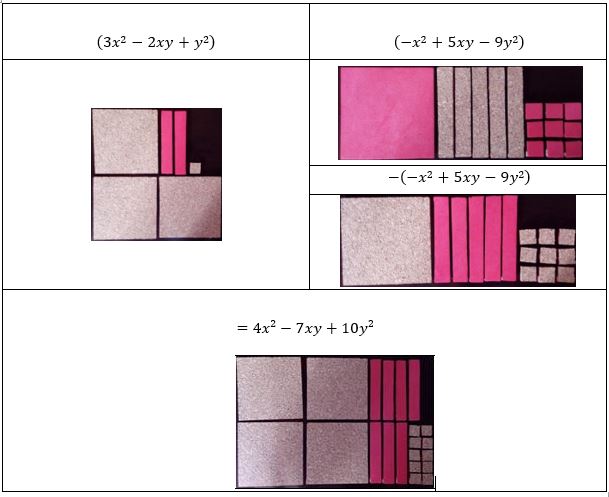A autora (2017)
Para se efetuar a multiplicação entre dois polinômios, dispõe-se um em linha e outro em coluna, de modo que cada um represente um lado de um retângulo, em seguida completa-se este retângulo com as peças que são mais convenientes, assemelhando-se a uma espécie de quebra-cabeça.
É importante ressaltar que no primeiro momento da multiplicação, deve-se considerar a medida lateral das peças, a fim de construir os lados do retângulo, porém, para que se encontre a resposta do produto, considera se a área total das figuras que constituem o retângulo construído. Por exemplo, para efetuar a multiplicação (x+3y). (2x+y) definem-se os seguintes passos:
1º passo: dispomos os dois polinômios de
modo a representarem os lados de um retângulo, com um lado de medida (x+3y) e o outro de medida (2x+y) .
Figura 4
Representação do 1º passo
A autora (2017)
2º passo: completar o retângulo com outras
peças, de modo a fechar a sua área.
Figura 5
Representação do 2o. passo
A autora
(2017)
3º passo: para obtermos o produto, temos
de considerar a soma das áreas que constituem o retângulo formado.
2
quadrados grandes (x2) + 7 retângulos (xy) + 3 quadrados pequenos (y2) .
(x+3y) . (2x+y) = 2x2 +7xy + 3y2
O processo de divisão utilizando o material concreto é semelhante ao processo de multiplicação, porém, na multiplicação os dois polinômios a multiplicar representam os lados de um retângulo, e o retângulo formado representa o produto.
No caso da divisão entre dois polinômios, o dividendo representa as peças que constituem a área do retângulo formado, o divisor representa um dos lados deste retângulo, logo, o estudante, sabendo da quantidade de peças de que dispõe e um dos lados do retângulo a ser montado, deve construir o retângulo a fim de encontrar a medida do outro lado do mesmo, sendo esta medida o quociente da divisão. Por exemplo:
(x2 + 4xy + 3y2) : (x + y)
1ºpasso: separam-se as peças que
representam o dividendo (x2 + 4xy + 3y2) (um quadrado grande, quatro retângulos e
três quadrados pequenos).
Figura 6
Representação do 1º passo
A autora (2017)
2ºpasso: constrói-se um retângulo com as
peças separadas, de tal maneira que uma das dimensões da figura formada seja
representada pelo divisor. (x + y)
Figura 7
Representação do 2º passo
A autora (2017)
3º passo: o outro lado do retângulo
formado nos dá o quociente desejado: x+3y Concluímos, pela
reversibilidade:
(x2 + 4xy + 3y2) : (x + y) = x + 3y
Para o caso onde há sobra de peças que representam o dividendo, de modo a não ser possível formar um retângulo, considerando que um dos lados deve ter a medida do divisor, estas sobras representam o resto da divisão.
Metodologia, desenvolvimento e análise
A intervenção de ensino foi realizada para 22 estudantes do 8º ano de uma escola estadual, na região central de Curitiba/PR em 8 aulas de 50 minutos cada, distribuídas em quatro encontros (duas aulas por encontro) realizados uma vez por semana.
O conteúdo de polinômios já havia sido desenvolvido com aquela turma, entretanto, na visão da professora, os estudantes ainda apresentavam dificuldades. Não haviam estudantes com deficiência visual incluídos nessa turma específica, sendo necessário convidar dois estudantes cegos para participação nas aulas. Um deles estava no 9º ano, e participou apenas no primeiro dia. O outro estava no 7º ano, e participou apenas do terceiro encontro. No segundo e no quarto encontro não houve a participação de estudantes com deficiência visual.
No primeiro encontro foram apresentadas duas situações-problema que deveriam ser expressas através de um polinômio. Neste mesmo encontro o material elaborado com cortiça e EVA foi apresentado para representar monômios e polinômios.
A compreensão de monômios e polinômios positivos e negativos através do material pelos estudantes deu-se a partir de três perspectivas diferentes: Por meio dos sinais de positivo e negativo (+ e -) (Figura 8); das cores (vermelho para negativo e branco para positivo) (Figura 9); do material utilizado (cortiça para positivo e EVA para negativo) (Figura 10). Estas três diferentes formas de representação revelaram a importância de se apresentar diferentes características dos objetos que contemplem os sentidos dos estudantes. Enquanto para alguns o que ficou registrado foi a oralidade (positivo e negativo), para outros foi a percepção tátil (cortiça e EVA) e para outros ainda, o visual (branco/bege e vermelho).
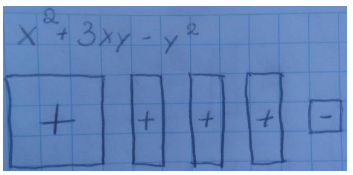Figura 8
Representação de monômios positivos e negativos utilizando sinais
Registro dos estudantes
Figura
9
Representação de monômios
positivos e negativos usando cores
Registro dos estudantes
Figura
10
Representação de monômios
positivos e negativos por meio do material utilizando
Registro dos estudantes
A estudante cega compreendeu a representação dos polinômios com o uso do material, construindo e identificando os polinômios apresentados, de forma consideravelmente rápida em comparação aos métodos comumente utilizados (através do Braille ou do computador), e realizando as devidas correções, quando cometia algum erro.
No segundo encontro foram trabalhadas as operações de soma e subtração de polinômios. Após a explicação, uma estudante relatou ter enfim, compreendido o significado da fala da professora quando dizia que “dois polinômios opostos se cancelam”. A manipulação do material torna alguns conceitos mais concretos para o estudante, facilitando assim a compreensão dos mesmos.
No terceiro encontro foram trabalhadas as noções de multiplicação e divisão de polinômios. Já familiarizados com o material os estudantes se mantiveram concentrados a maior parte do tempo trabalhando em grupos, sendo que o estudante que sabia mais, ajudava os colegas, deste modo, trabalha-se com a inclusão não só do estudante com necessidade educacional especial, mas de todos os demais, contemplando a inclusão em seu significado mais geral.
O material funcionou de maneira satisfatória com o estudante cego, que compreendeu de forma rápida a ideia proposta, bastando que alguém lhe ditasse os polinômios que estavam no quadro, para apresentar o resultado. Este estudante resolveu todos os exercícios em tempo menor que os colegas videntes, o que é surpreendente, se levarmos em consideração que o mesmo cursava um ano anterior (7º ano) ao da turma.
Os demais estudantes enfrentaram algumas dificuldades iniciais associadas ao conceito de áreas e perímetro de figuras planas. Porém, o uso do material se mostrou eficaz para facilitar a compreensão de que o resultado da multiplicação de polinômios do tipo (x+y)(x+y) formava um quadrado, o que surpreendeu os estudantes. Esclarecidos de que isto era o produto notável ou “quadrado perfeito”, esboçavam uma reação engraçada de espanto e contentamento evidenciando que haviam compreendido algo que até então não fazia sentido para eles.
A divisão, operação inversa da multiplicação, gerou maiores dificuldades nos estudantes em relação à compreensão e concretização do raciocínio.
No quarto e último encontro, trabalhou-se ainda com o auxílio do material em EVA e cortiça, para reforçar o conteúdo de produtos notáveis.
Em todos os encontros, havia um momento em que os estudantes apenas manipulavam o material e outro momento em que se solicitava o registro escrito.
De forma geral, o material concreto que foi desenvolvido para esta situação de ensino teve boa aceitação por parte dos estudantes, e possibilitou melhor compreensão das noções de monômios e polinômios, antes vistos de forma abstrata. Ainda neste sentido, as operações de soma, subtração, multiplicação e divisão de polinômios, passaram a ter significado, sendo que os estudantes puderam compreender de forma visual e/ou tátil.
O material possibilitou aos estudantes cegos, agilidade ao efetuar as operações com polinômios, considerando que ao utilizar-se do Braille ou do computador, para registrar estas operações, o tempo dispensado é relativamente maior, e há dificuldades em corrigir os erros.
As aulas, como um todo, passaram a ser mais dinâmicas, pois em um primeiro momento, não se fez necessário à utilização da notação matemática, ou seja, cada estudante dedicou-se primeiramente, a compreender a operação, para só então, preocupar-se com o formalismo necessário do registro. Deste modo, o raciocínio não é interrompido, a compreensão se dá em um curto espaço de tempo, tornando o ensino menos cansativo para o estudante.
O modo de ensino utilizado pelo professor é único, ensinando a todos, sem discriminações e sem práticas especializadas de ensino (MANTOAN, 2003). A abordagem empregada é suficiente tanto para o estudante com deficiência visual quanto para os demais, atendendo ao conceito do Desenho Universal e contemplando assim, o que Mantoan (2003) considera ser uma escola de qualidade.
Escolas assim concebidas não
excluem nenhum aluno de suas classes, de seus programas, de suas aulas, das
atividades e do convívio escolar mais amplo. São contextos educacionais em que
todos os alunos têm possibilidade de aprender, frequentando uma mesma e única
turma. Essas escolas são realmente abertas às diferenças e capazes de ensinar a
turma toda. (MANTOAN, 2003, p.35).
Apesar de ser necessário mais tempo para a explicação do material e uso na situação de ensino quando comparado a uma aula expositiva tradicional, o recurso material gera a motivação e participação dos estudantes. Assim, a atenção dos mesmos em relação às explicações e atividades propostas aumenta, enquanto que as conversas paralelas e casos de indisciplinas diminuem.
Entretanto, na perspectiva do professor, o material apresenta algumas incoerências matemáticas, por exemplo: as medidas dos lados do quadrado e retângulo são identificadas por x e y, e consideradas como uma grandeza variável, o que se faz necessário para o desenvolvimento da situação proposta, porém, o material é apresentado com medidas fixas, não sendo possível ao estudante alterar suas dimensões, sendo assim, matematicamente não se trata de grandezas variáveis, uma vez que não variam no material. Esta questão deve ser trabalhada com os estudantes, de modo a ficar bem entendido que apesar de ser possível medir os lados dos polígonos estes, serão tratados como grandezas sem medida específica e passíveis de variação.
Acredita-se ainda que, para que se efetive o aprendizado, a situação como um todo, deve ser apresentada de forma mais lenta do que foi planejado, pois, com mais aulas o estudante pode relacionar o material concreto com a formalização algébrica de maneira detalhada, de modo que os conceitos presentes possam ser observados pelo próprio estudante, sem a necessidade de intervenção direta do professor.
Os exercícios e explicações também devem ser mais bem elaborados, a fim de abranger todo tipo de polinômio. Por exemplo, não foi possível tratar de multiplicação e divisão de polinômios compostos por monômios negativos, uma vez que não faz sentido considerar uma área negativa. Apesar serem reconhecidos monômios negativos na soma e subtração, este conceito (de negativo e positivo) passa a ter maior complexidade ao se trabalhar com a ideia proposta para multiplicação e divisão.
Outra questão a ser levantada, é a questão da dimensão do material. Geometricamente o material é confeccionado com 3 dimensões (comprimento, largura, altura), uma vez que para haver apenas duas dimensões, seria necessário trabalhar apenas com desenho, ou relevo, em uma folha de papel por exemplo, porém, durante toda a situação didática são consideradas apenas duas dimensões, desprezando-se totalmente a espessura do material. Analisando algebricamente, há ainda outra incoerência, pois, no trabalho com um polinômio, por exemplo, do tipo x2 + x + 1, tem-se o monômio x2 que deve ser representado geometricamente por algo em duas dimensões (por exemplo, um quadrado), o monômio x, deve ser representado geometricamente por algo que possua uma única dimensão (por exemplo, um segmento de reta), por fim, a unidade 1 não deve possuir dimensão, sendo representada, por exemplo, por apenas um ponto. Apesar de estas incoerências terem sido levadas em consideração desde o início da confecção do material, não foi possível chegar à outra representação se não a que foi apresentada, considerando que o material deve ser acessível a estudantes cegos.
Uma alternativa que parece mais aceitável, de acordo com os conceitos algébricos e geométricos de polinômios, é a utilização do Multiplano, pois a partir deste se consegue chegar o mais próximo possível da representação geométrica de um polinômio, como pode ser observado a seguir (Figura 11).
Figura
11
Representação
geométrica do polinômio x2 + x + 1 utilizando o multiplano
A autora (2017)
Com o Multiplano, é possível minimizar o problema referente às dimensões já discutidas anteriormente, além da possibilidade de variação das medidas, tornando o significado de grandezas variáveis de x e y mais fidedigno a tal conceito. Entretanto, o motivo pelo qual não foi utilizado o Multiplano durante a situação de ensino, se deve ao fato de que atualmente poucas escolas possuem este material em seu acervo, as que o possuem, apresentam pouca quantidade do mesmo, não sendo possível a utilização por todos os estudantes.
Dentre os principais erros cometidos está a má compreensão da regra de sinais, na subtração de polinômios, e/ou confusão no momento da representação solicitada. Na figura 12 pode-se perceber que uma dupla, ao efetuar uma operação de subtração de polinômios, sequer representou corretamente o segundo polinômio.
Figura
12
Incompreensão na representação
do polinômio
Registro dos estudantes
Apesar do trabalho com o material facilitar no momento de subtração, uma vez que, bastava ao estudante modificar a textura do material (virando as peças) que representava o polinômio que sucedia o sinal da subtração, para então anular as peças semelhantes com texturas diferentes, acredita-se que alguns estudantes não compreenderam completamente a explicação dada inicialmente, e ainda, que se houvesse mais tempo para o desenvolvimento desta atividade, após breve correção em sala, destes exercícios, estes erros não voltariam a ocorrer ou ainda apresentariam uma diminuição significativa.
Em relação aos produtos notáveis, muitos dos erros cometidos devem-se unicamente ao conceito de potenciação (figura 13).
Figura
13
Erros cometidos em relação ao
cálculo de potências
Registro dos estudantes
Alguns estudantes não atentaram para detalhes do desenvolvimento de
produto notável, por exemplo, para obter o segundo termo do polinômio,
multiplicava-se apenas o primeiro pelo segundo termo do produto notável,
esquecendo-se de multiplicar o resultado obtido por dois (figura 14),
demonstrando possível desatenção no momento da explicação inicial, entretanto,
este erro pode facilmente ser sanado após uma breve correção do exercício,
chamando a atenção para o passo que estava sendo pulado.
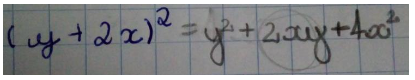Figura
14
Incompreensão
de detalhes do processo de desenvolvimento do produto notável
Registro dos estudantes
De modo geral, considerando que estas foram utilizadas 8 horas/aula para
o trabalho com a representação de polinômio e as operações (soma, subtração,
multiplicação, divisão de polinômios e produto notável), os resultados obtidos
são extremamente relevantes e satisfatórios, pois, certamente se desenvolvida
essa situação, com o tempo normalmente utilizado pelos professores, para o
ensino de tais conceitos, os resultados obtidos seriam muito superiores aos
aqui apresentados.
Considerações finais
O objetivo desta pesquisa foi o de reconhecer potencialidades e limitações do uso de um material concreto acessível para o ensino de operações com polinômios em uma turma regular com estudantes cegos inseridos.
Como potencialidade foi possível reconhecer que o uso do material possibilitou a inclusão dos deficientes visuais potencializando o aprendizado de todos os estudantes da turma na medida em que encontraram significado nas ações executadas. Pode-se afirmar que a situação de ensino proposta motivou os estudantes que se mostraram atentos e participativos. O desenvolvimento de uma situação que permitiu ensinar de um mesmo modo, utilizando os mesmos materiais e a mesma metodologia, gerando interesse para todos os estudantes de uma turma, pode ser considerado um ponto positivo e uma potencialidade deste trabalho com o material.
Assim a utilização do material didático apresentado foi um fator relevante para o sucesso da situação de ensino desenvolvida, pois, através dele atingiu-se o objetivo de possibilitar o trabalho tanto com estudantes cegos quanto com videntes, utilizando a mesma linguagem, além de servir como um facilitador na compreensão de conceitos algébricos relacionados a polinômios. Além disso, o material possibilitou diferentes formas de representação dos estudantes, por meio de sinais, por meio de cores, e do próprio material (cortiça e EVA).
Como limitações foi possível reconhecer que a quantidade de kits a serem montados por um único professor para classes numerosas pode dificultar o trabalho, considerando que em geral os professores não possuem tempo suficiente para os planejamentos e preparação dos materiais. Além disso, os materiais nem sempre são encontrados nas escolas, sendo que o professor precisaria adquiri-los de alguma forma. Matematicamente, como foi explicado, o material apresenta um erro conceitual em sua representação, que pode ser superado com as explicações do professor.
A presente pesquisa contou ainda com o apoio dos profissionais atuantes na sala multifuncional da escola onde foi desenvolvida. Destaca-se o aprendizado dos autores também com estes profissionais e estudantes atendidos, sendo possível reconhecer potencialidades e limitações na atuação do professor para poder atender com qualidade e dedicação a todos os estudantes, contribuindo para o desenvolvimento humano e digno de crianças e adolescentes.
