



Artigos Científicos
Valoración de una experiencia de enseñanza de la desviación estándar a través de la idoneidad didáctica
Assessment of a standard deviation teaching experience through didactic suitability
Avaliação de uma experiência de ensino sobre desvio padrão por meio da idoneidade didática
Revista de Educação Matemática
Sociedade Brasileira de Educação Matemática, Brasil
ISSN: 2526-9062
ISSN-e: 1676-8868
Periodicidad: Cuatrimestral
vol. 17, núm. 1, 2020
Recepción: 07 Septiembre 2020
Aprobación: 09 Octubre 2020
Publicación: 08 Noviembre 2020

Resumen: El objetivo del presente trabajo es valorar el proceso de instrucción de la desviación estándar, para ello utilizamos como marco teórico el Enfoque Ontosemiótico, específicamente algunas de las facetas de la idoneidad didáctica, propuesta por Juan Godino y colaboradores. Los participantes fueron 30 estudiantes chilenos de Enseñanza Media (16 a 17 años), para los cuales se diseñó una situación problema que promovía el surgimiento del objeto desviación estándar. Se trata de una investigación cualitativa, en la que se realiza un análisis de contenido de las producciones realizadas por los estudiantes para responder a la situación planteada. Las respuestas mostraron un limitado conocimiento de conceptos estadísticos, lo que dificulta una argumentación junto con una correcta resolución de la tarea. Las producciones ponen de manifiesto la complejidad que conlleva la apropiación del concepto desviación estándar. Concluimos que la idoneidad didáctica es un instrumento potente que permite analizar de manera profunda las prácticas del profesor de matemática en el aula.
Palabras clave: Medidas de dispersión, Desviación estándar, Enseñanza secundaria, Idoneidad didáctica.
Resumo: O objetivo deste trabalho é avaliar o processo de instrução do desvio padrão, para o qual utilizamos como referencial teórico o Enfoque Ontosemiótico, especificamente algumas das facetas da idoneidade didática, propostas por Juan Godino e colaboradores. Os participantes foram 30 estudantes chilenos do Ensino Médio (16 a 17 anos), para os quais foi proposta uma situação-problema que promoveu o surgimento do objeto desvio padrão. Trata-se de uma pesquisa qualitativa, na qual é realizada uma análise de conteúdo das produções dos estudantes para responder ao objetivo proposto. As respostas mostraram um conhecimento limitado dos conceitos estatísticos, o que torna difícil a argumentação aliada à uma resolução correta da tarefa. As produções revelam a complexidade envolvida na apropriação do conceito de desvio padrão. Conclui-se que a idoneidade didática é um poderoso instrumento que permite uma análise profunda das práticas do professor de matemática em sala de aula.
Palavras-chave: Medidas de dispersão, Desvio padrão, Ensino Médio, Idoneidade didática.
Abstract: The aim of this work is to evaluate the process of instruction of the standard deviation, we use as a theoretical framework the Ontosemiotic Approach, specifically some of the facets of didactic suitability, proposed by Juan Godino and collaborators. The participants were 30 Chilean secondary school students (16-17 years old). A problem situation was designed that promoted the emergence of the standard deviation of the object. This is a qualitative research, in which we analyzed of the content of the students' responses to the task is carried out. The answers showed a limited knowledge of statistical concepts, which makes it difficult to argue along with a correct resolution of the task. The answers show the complexity involved in appropriating the concept of standard deviation. We conclude that didactic suitability is a powerful instrument that allows an in-depth analysis of the practices of the mathematics teacher in the classroom.
Keywords: Dispersion measures, Standard deviation, High school.
1. Introducción
La enseñanza de la Estadística es relevante para la sociedad, por la gran cantidad de información con la que los ciudadanos deben convivir en lo cotidiano, además en su desempeño profesional o laboral. Frente a esta sociedad con acceso a una gran cantidad de datos (CASTELLS, 2000), a través de las diferentes agencias estadísticas, es necesario una formación que provea de conocimientos para analizar e interpretar la información, y con ello conseguir una mejor toma de decisiones (GAL, 2002; 2019).
Al respecto, Batanero et al. (2013) proponen un modelo para el desarrollo de un razonamiento estadístico, basado en diferentes autores, el que persigue explicar y establecer las causas de la variación en el que se destaca la idea de la variabilidad aleatoria como un concepto importante en la Estadística. Entre las investigaciones que apuntan a la importancia del rol de la variación en la estadística, Wild y Pfannkuch (1999) sostienen que la variación se constituye en un aspecto primordial, pues esta idea se conecta con diferentes conceptos estadísticos en el ámbito del análisis exploratorio de datos, como la dispersión, centralización y distribución. Cobb y Moore (1997), advierten la importancia de tener presente que, en el estudio de la variabilidad, el cálculo de las medidas de dispersión, no son sólo números, sino que obedecen a un contexto, el que requiere de una adecuada interpretación de los valores obtenidos.
En esta línea, la dispersión y sus medidas resultan esenciales en el análisis de la distribución de datos, pues complementan a las medidas de posición central, de allí la importancia de su comprensión para el estudio de la estadística (MAKAR; CONFREY, 2005). Por lo tanto, es fundamental enseñar la dispersión para desarrollar el pensamiento estadístico y para que los estudiantes desarrollen una adecuada visión de la variabilidad y la incertidumbre (MOORE, 1990). Por otra parte, también se requiere que los profesores sean conscientes de la importancia de la dispersión en el estudio estadístico (BATANERO et al., 2015a).
Recogiendo esta necesidad, diferentes países han incorporado en sus bases curriculares el estudio de la dispersión, es el caso de los estándares propuestos por el National Council of Teachers of Mathematics (NCTM, 2014) para la enseñanza de la matemática. En el bloque de Datos y Azar aparecen objetivos que abordan la utilización e interpretación de las diferentes medidas de centralización y dispersión para el análisis de datos, tales como Chile, Brasil y España. Siguiendo estas recomendaciones, el currículo chileno no es la excepción, ya que, en el eje de Estadística y Probabilidad, se incorporan tópicos asociados a la dispersión, así como habilidades relacionadas, donde los estudiantes deben “tomar decisiones en situaciones de incerteza que involucren el análisis de datos estadísticos con medidas de dispersión y probabilidades condicionales” (MINEDUC, 2019, p. 29).
En esta perspectiva, la presente investigación tiene por objetivo valorar el proceso de instrucción de la desviación estándar, utilizando elementos de la idoneidad didáctica para establecer el grado de eficacia tanto del diseño de la propuesta como su implementación en el aula. Para eso, se realizó un estudio con un grupo de 30 estudiantes chilenos del tercer año de secundaria (16 a 17 años), cuyo análisis se describe en el presente trabajo.
2. Antecedentes
La enseñanza ha tratado las medidas de dispersión, tradicionalmente, como la aplicación de procedimientos de cálculo (LEHRER; ENGLISH, 2018). Una explicación a ese hecho podría ser que frecuentemente en los curriculum el estudio de la dispersión se centra en las medidas (ESTEPA; PINO, 2013) las que, si bien son importantes en el análisis de los datos, requieren ser complementadas con otros aspectos, por ejemplo, el concepto de dispersión, las técnicas matemáticas para medirla y su explicación dentro de un determinado contexto.
El estudio de la dispersión junto a sus medidas ha sido una temática escasamente abordada en la investigación (BATANERO et al., 2015b) y menos aún en los niveles de secundaria. Esto a pesar de que diferentes estudios han alertado de las dificultades para su enseñanza, debido a que las medidas de centralización y dispersión se han limitado a la aplicación de fórmulas por parte de los estudiantes. Ortega y Estepa (2006), Sánchez (2013) y Batanero et al. (2015b) confirman estas observaciones, agregando que, aunque los estudiantes son capaces de calcular diferentes medidas de dispersión, presentan dificultades en comprender los procesos y los conceptos involucrados, lo que posteriormente se agudiza con el estudio de la inferencia.
En el estudio desarrollado por Orta y Sánchez (2013) con alumnos de secundaria (14 años), detectan lo complejo que resulta interpretar la dispersión, porque los estudiantes realizan comparaciones con valores particulares, evidenciando que el tema carece de simpleza, especialmente cuando se trata de interpretar la dispersión para la toma de decisiones en contextos de riesgo. En esta línea, una enseñanza basada en contexto puede promover un acercamiento a la noción de una distribución y con ello conseguir un mejor análisis y explicación de la dispersión (BAKKER; GRAVEMEIJER, 2004), en lugar de tratar con un mero conjunto de datos aislados que carezcan de contexto.
Por otra parte, a pesar de que las medidas de dispersión son complementarias de las medidas de tendencia central (SHAUGHNESSY, 2006), autores como Garfield y Ben-Zvi (2008) y Estepa y del Pino (2013) detectan en la enseñanza una desvinculación de las medidas de dispersión respecto a las de centralización, pese a la importancia de ambas para el análisis exploratorio de los datos. Pues, como señala Batanero (2001) en el estudio de distribuciones no es suficiente el análisis de las medias, porque puede ocurrir que compartan medidas de tendencia central, es decir igual media y/o mediana y tener diferente variabilidad. En este sentido, un típico error consiste en ignorar la dispersión en la comparación de muestras.
Las medidas de dispersión, como la desviación estándar, permiten establecer la intensidad con que los datos se desvían respecto a la media. En la investigación desarrollada por Loosen, Lioen y Lacante (1985) con estudiantes de psicología, se identificó que las respuestas se basaban en un concepto intuitivo de la variabilidad en que se comparan cuánto varían los valores respecto a otros, en lugar de compararlos con un valor fijo. Tales autores, concluyen que la enseñanza de este tipo de medidas de dispersión, como la desviación estándar, no es un tema sencillo, lo que ya había sido alertado por Hart (1983) señalando que el concepto de desviación estándar resultaba dificultoso para el alumno cuando se inicia en el estudio de la estadística. Una manera que propone Hart (1984) para promover una mejor comprensión de la desviación estándar es tratar esta medida como una continuación de la desviación media, enfatizando el concepto y no solo su cálculo algorítmico.
3. Marco teórico
Para el diseño de la propuesta y su análisis, nos basamos en elementos del enfoque ontosemiótico de la cognición matemática (GODINO; BATANERO; FONT, 2007;2019), teoría que ha abordado la dificultad de la significación y la representación. Específicamente, trabajaremos algunas componentes de la idoneidad didáctica, la que se conforma en una herramienta de utilidad para el profesor, dado que permite valorar el proceso de enseñanza y aprendizaje en la medida en que se acoplen los significados personales mostrados por los estudiantes (aprendizaje) y el significado institucional pretendidos o implementados (aprendizaje), incorporando el contexto y los recursos (entorno).
Los autores Godino, Contreras y Font (2006) y Godino (2013) proponen las siguientes facetas para analizar los procesos de instrucción matemática:
* Idoneidad epistémica: Se trata de la representatividad de los significados implementados o pretendidos en el proceso de enseñanza, respecto a un objeto matemático que se está estudiando. En nuestro caso, corresponde al conocimiento matemático de la desviación estándar (problemas, lenguaje, conceptos, propiedades, argumentos y procedimientos) y procesos asociados.
* Idoneidad cognitiva: Corresponde al grado en que son adheridos los significados personales logrados por los estudiantes con los significados pretendidos y/o implementados por los docentes. Para valorarla se debe conocer el razonamiento, aprendizaje y dificultades que presenten los estudiantes. En el caso de la desviación estándar, con el análisis de las respuestas entregadas por los estudiantes a la situación problema planteada, podremos profundizar y valorar los significados mostrados por estos.
* Idoneidad interaccional: Identifica el grado en que el diseño de enseñanza aprendizaje permite adelantar posibles conflictos semióticos, la manera de resolverlos cuando surgen en el proceso de instrucción y cuanto favorecen la autonomía en el aprendizaje.
* Idoneidad mediacional: Se corresponde con el conocimiento del uso de herramientas tecnológicas, recursos manipulativos necesarios para la enseñanza y aprendizaje, atendiendo al tiempo, tema en estudio y nivel escolar al que es dirigido.
* Idoneidad afectiva: Es el grado en que los estudiantes se involucran en el proceso de enseñanza. En este tipo de idoneidad, se consideran factores institucionales, el estudiante y su historia escolar.
* Idoneidad ecológica: Se refiere al grado en que el proceso de enseñanza aprendizaje se ajusta a un marco local (proyecto educativo del centro) y general (sociedad).
4. Materiales y métodos
La presente investigación tiene un enfoque cualitativo (HERNÁNDEZ; FERNÁNDEZ; BAPTISTA, 2014) pues nos permite obtener un conocimiento profundo que apunta a valorar el proceso de instrucción realizado en la enseñanza del objeto matemático la desviación estándar.
4.1. Muestra
El estudio se desarrolló con 30 estudiantes que cursaban su tercer año de enseñanza media (16-17 años) de un colegio particular subvencionado, ubicado en el norte de Chile. Los participantes cursaban su primer semestre, y pertenecían a una asignatura de matemáticas diferenciadas. Estos estudiantes fueron seleccionados por la accesibilidad a sus profesores, además de su buena disposición de ser parte de la investigación, debido a su gusto por las matemáticas. Para llevar a cabo el estudio, se contó con la debida autorización escrita del director del establecimiento, además de profesores y los alumnos.
4.2. Recogida de datos
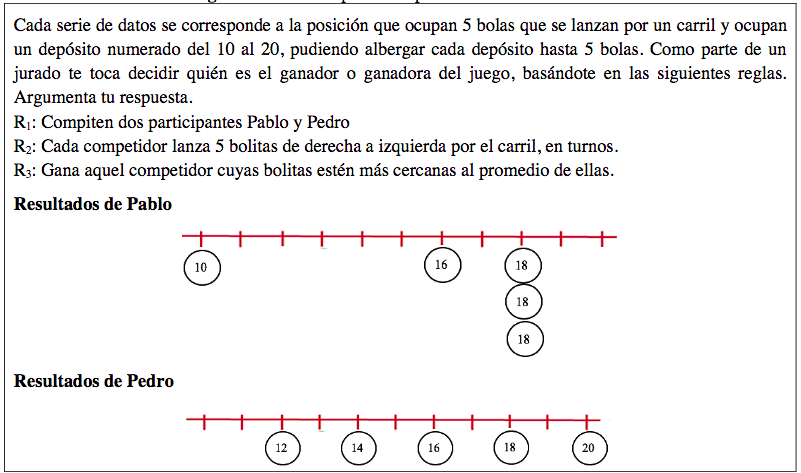
Los participantes resolvieron una tarea con papel y lápiz. La situación problema utilizada (Figura 1), es una adaptación a la empleada por Loosen, Lioen y Lacante (1985). Aunque en este estudio las distribuciones se presentaban a través de bloques, la tarea se sustenta en la idea de que una distribución de frecuencias no puede limitarse al estudio de sus promedios, debido a que distribuciones con medias iguales pueden tener diferentes grados de variabilidad. Cabe señalar, que la situación diseñada es una continuación de un estudio realizado previamente para la enseñanza de la desviación media (PALLAUTA; BONILLA; OLIVARES, 2019). En ese caso se propuso al estudiante un contexto en que las distribuciones propuestas tenían igual media aritmética y rango, y se perseguía que, de manera argumentada, al igual que en este caso, el estudiante pudiera buscar diferentes estrategias que le permitan tomar una decisión. En esta tarea, se añade, además, que ambas distribuciones comparten igual desviación media.
La recogida de los datos contempló notas de campo, además del registro fotográfico de todas las producciones realizadas en el papel y en el pizarrón de la sala de clases.
4.3. La lección
Los participantes se distribuyeron en 5 grupos (G1, G2, G3, G4 y G5) de 6 integrantes. Los conocimientos previos de los estudiantes en torno a la Estadística abarcan las medidas de tendencia central, rango y la desviación media, tratada en el mismo curso.
La realización de la actividad fue desarrollada en una clase de 90 minutos de la asignatura de matemática diferenciada. Los alumnos se dividieron en grupos por afinidad, con el propósito de fortalecer la idoneidad afectiva, en el sentido de compartir en un ambiente de confianza sus ideas y conocimientos.
Luego de motivar la importancia de la toma de decisiones de forma justificada, recordando además las medidas de centralización y algunas de dispersión (rango y desviación media) la profesora que implementa la lección, entrega a cada uno de los estudiantes la situación problema que debían resolver (Figura 1).
5. Análisis
Se analizaron las producciones realizadas por los participantes, para ello se empleó el análisis de contenido, siguiendo etapas (YAREMKO; HARARI; HARRISON; LYNN, 2013) y de modo sistemático, puesto que el objetivo es inferir y describir la inferencia de conocimientos relativos a las condiciones de producción por medio de indicadores, los que pueden ser cuantitativos o no (BARDIN, 1996). Para ello, la revisión bibliográfica, y el marco teórico permitieron definir las categorías de análisis y comprobar su validez (GHIGLIONE; MATALÓN, 1989). Durante el análisis se registra, de manera paralela, los objetos matemáticos utilizados en la elaboración del argumento, finalizando con tablas que permiten resumir los resultados y obtener algunas conclusiones.
A continuación, se describen las categorías de análisis organizadas con lo que se espera de las respuestas de los grupos de estudiantes. También se presentan los objetos matemáticos empleados por los estudiantes, y posteriormente, se analizan algunas facetas consideradas de la idoneidad didáctica, de acuerdo con Godino, Contreras y Font (2006) y Godino (2013) del proceso de instrucción.
5.1 Análisis de la situación problema
Al analizar las producciones, se establecieron en total cuatro posibles estrategias, las que podían ser válidas o insuficientes. Tres de ellas, surgen de la literatura investigativa (ORTA; SANCHEZ, 2013; PALLAUTA; BONILLA; OLIVARES, 2019), mientras que otra (C3) emergió desde las producciones de los estudiantes. En el Cuadro 1 se presentan las categorías de análisis de las producciones realizadas por los participantes.
| Categoría | Descripción | Estrategia de resolución |
| : Los estudiantes utilizan medidas de tendencia central, rango o deviación media. | Los estudiantes emplean medidas como la media, moda, mediana, máximos, mínimos, desviación media o rango. | Estrategia 1: Calculan media aritmética, rango o desviación media, verifican que son iguales para ambos conjuntos de datos, con lo que podría establecer que se genera un empate. O bien, comparan valores particulares del conjunto de datos con alguna medida de tendencia central. |
| : Los estudiantes utilizan gráficos para representar los datos. | Los estudiantes representan gráficamente los datos para evidenciar alguna tendencia. | Estrategia 2: Representan gráficamente los resultados de los lanzamientos de ambos jugadores, y los comparan con la media aritmética. |
| : Los estudiantes de manera intuitiva calculan la desviación estándar. | Los estudiantes basados en el cálculo de distancias empleado en , se acerca al concepto de desviación estándar. | Estrategia 3: Realizan un procedimiento análogo al cálculo de distancias en . Con lo que determinan, la raíz cuadrada, de la suma de los cuadrados de cada lanzamiento respecto a la media. |
| : Los estudiantes utilizan el concepto de desviación estándar o varianza. | Los estudiantes calculan la desviación estándar o varianza de cada serie de datos. | Estrategia 4: Calculan la desviación estándar y/o varianza de ambas series, las comparan decidiendo por la que presenta menor valor. |
5.2 Resultados
A continuación, se presenta el análisis en cuanto al proceso de instrucción el que persigue identificar posibles mejoras del proceso de instrucción realizado. Para ello utilizamos algunos elementos de las facetas para la valoración de la idoneidad didáctica (GODINO; CONTRERAS; FONT, 2006).
En primer lugar, estudiamos los objetos matemáticos, que nos permiten valorar la idoneidad epistémica, pues la resolución de una situación problema requiere de conocimientos básicos tanto en la solución, como en la interpretación de los resultados obtenidos. Para resolver la situación-problema planteada (Figura 1) se requiere realizar prácticas matemáticas, en dichas prácticas intervienen diferentes objetos primarios como el lenguaje (e.g., tabular, gráfico); los conceptos, dados por su definición o descripción (e.g., distancia, media, desviación media, desviación estándar); las proposiciones o propiedades (e.g., la desviación estándar será siempre un valor positivo o cero, en el caso de que los datos sean iguales); los procedimientos (e.g., calcular la desviación estándar de una serie de datos); y los argumentos o razonamientos empleados en la justificación de las proposiciones y procedimientos (deductivo, inductivo, etc.).
Los objetos antes mencionados, están relacionados entre sí formando la configuración (FONT; GODINO; GALLARDO, 2013) expuesta en la Figura 2. Esta herramienta fue empleada para diferenciar los objetos matemáticos que fueron puestos en juego por los estudiantes en la resolución de la situación problema y son detallados en el Cuadro 2.
| Lenguaje | Verbal, Numérico, Gráfico y tabular y Algebraico. |
| Conceptos-definición | Distancia, media aritmética, mediana, varianza, desviación respecto a la media, desviación media, desviación estándar y varianza, gráficos. |
| Proposiciones | I1: Para determinar el ganador ocuparemos la mediana, para ello determinamos la media de cada lanzamiento a la mediana. I2: Como ambas desviaciones son iguales estableceremos una relación entre este valor y la distancia a la media, sumaremos los resultados de cada serie y lo dividiremos por cinco (total de datos de cada serie). I3: Observaremos la tendencia de los datos en un gráfico, y optaremos por la serie que más se acerque a la media aritmética. I4: Se aplica la fórmula de la desviación estándar, puesto que la media aritmética y desviación media son iguales en ambas series de datos. |
| Procedimientos | P1: Determinan la media de la distancia de cada serie respecto a la mediana, comparan ambos valores optan por la menor. P2: Grafican ambas series en un gráfico de líneas y los comparan con el valor de la media aritmética. P3: Calculan las distancias de manera análoga a como se realiza en de cada serie de datos respecto a la media aritmética. P4: Determinan la media de la diferencia de la desviación media con la desviación de cada dato de la serie con la media aritmética de la serie (16). P5: Calculan la desviación estándar y/o varianza de ambas series, comparan los valores obtenidos. |
| Argumentos | A1: Como la suma de las distancias respecto a la mediana fue menor en la primera serie, el ganador de la competencia es Pablo. A2: La raíz cuadrada, de la suma de los cuadrados de cada lanzamiento respecto al promedio, es menor en la primera serie, lo que convierte a Pablo en el ganador. A3: Los datos de la primera serie se ven más cercanos del promedio en el gráfico. A4: La media de la diferencia de la deviación media y la deviación respecto a la media de cada dato de la serie, es menor en Pedro, por lo que él gana. A5: La varianza y desviación estándar de la primera serie de datos es menor, lo que implica que el jugador vencedor es Pedro. |
Las respuestas entregadas para resolver la situación problema, por los cinco grupos con seis estudiantes, organizados como G1, G2, G3, G4 y G5, fueron clasificadas en cuatro categorías anteriormente expuestas (ver Cuadro 1). Cabe mencionar, que este proceso se realizó a partir de estrategias dadas por grupos de estudiantes, posterior a las devoluciones realizadas entre profesor y participantes.
La situación problema fue resuelta de manera exitosa solo por dos grupos (G1 y G3), uno de ellos lo consigue de forma intuitiva (G1), mientras que el otro (G3), uno de sus integrantes conocía la fórmula de la desviación estándar. Los grupos restantes (G2, G4 y G5) apoyaron sus argumentos comparando alguna medida de tendencia central con un dato particular de ambas series, evidenciando una debilidad en la realización de comparaciones de conjuntos de datos. El resumen de los conceptos empleados por los estudiantes para responder a la situación problema son resumidos en la Tabla 1, los que son complementados con algunos ejemplos para una mayor comprensión.
| Categoría | Grupo | Total de estudiantes |
| : Los estudiantes utilizan medidas de tendencia central, rango y deviación media. | G2 y G3 | 12 |
| : Los estudiantes utilizan gráficos para representar los datos. | G4 | 6 |
| : Los estudiantes de manera intuitiva calcula la desviación estándar. | G1, G4 y G5 | 12 |
| : Los estudiantes utilizan el concepto de desviación estándar o varianza. | G3 | 6 |
Las respuestas entregadas por los estudiantes, también nos permiten valorar la idoneidad cognitiva. En ellas, detectamos que la mayoría de los grupos se aferran a las estrategias asociadas a comparar sólo valores particulares de las series de datos con medidas de tendencia central (media, mediana, máximos y mínimos), por lo que deciden basados sólo en esa comparación lo que en ocasiones carece de sentido como se puede observar en el Cuadro 3. Ese hecho podría ocurrir por falta de conocimientos sobre las medidas de dispersión, lo que dificulta que detecten la necesidad de medir la dispersión, pues no es algo evidente, dado que algunos consideran las medidas de tendencia central como absolutas y más sencillas de calcular (SHAUGHNESSY, 2006) y eso podría generar que el estudiante se aferre a estrategias de este tipo.
Por ejemplo, en el Cuadro 3, el grupo G2 considera a Pablo ganador porque la media de las desviaciones de sus lanzamientos respecto a la mediana fue menor, sin tomar en cuenta la regla R3 (ver Figura 1). Esto muestra una dificultad en realizar comparaciones de grupos de datos considerando cada grupo como una unidad o distribución.

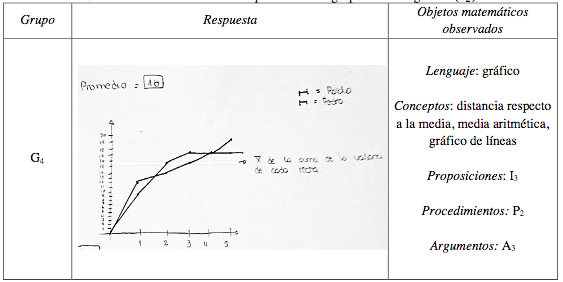
Las estrategias empleadas por los estudiantes muestran una variedad de tipos de lenguaje (numérico, gráfico, algebraico). Sin embargo, apreciamos carencias en el lenguaje algebraico, a pesar del nivel educativo avanzado de los participantes, pues como señala Godino (2002), los símbolos que se emplean en el lenguaje algebraico ocupan un lugar importante en la articulación de los diferentes componentes que intervienen en la resolución de una situación problema. Por lo tanto, se esperaría que este apareciera con mayor fuerza a medida que se progrese de nivel educativo. Otras respuestas, como la entregada por G4 (ver Cuadro 4), muestra debilidades en la construcción de gráficos, lo que repercute en que este tipo de representación sea insuficiente para ofrecer una solución.
Por otra parte, la totalidad de estudiantes fue capaz de establecer que media, rango y desviación media eran iguales (ver Cuadros 3 y 5), poniendo en juego una variedad de estrategias para poder justificar la elección del jugador vencedor. Algunos grupos utilizaron procedimientos centrados en el cálculo de distancias respecto a la media de manera análoga a como esta se determina en R2, lo que les permitió acercarse de manera intuitiva al concepto de desviación estándar como se puede observar en el Cuadro 5.

En el Cuadro 6, podemos observar que un grupo (G3) entregó una respuesta basada en el cálculo de la desviación estándar, esto debido a que un integrante del equipo contaba con este conocimiento, motivado por inquietudes personales, tras conocer el concepto de desviación media. El utilizar el concepto de varianza y desviación estándar, les permitió decidir que el jugador vencedor sería aquel cuyos lanzamientos presentaran un menor valor de estas medidas de dispersión.

Otras facetas de la idoneidad didáctica (GODINO; CONTRERAS; FONT, 2006; GODINO, 2013), que pudimos valorar, en cierta medida, con la información del episodio de la clase, fue la idoneidad interaccional basados en Font, Planas y Godino (2010). Apreciamos que el profesor presentó de manera adecuada la situación problema, activando conocimientos previos tratados con anterioridad con los estudiantes, como las medidas de tendencia central y la desviación media, lo que permitió adentrarse en la situación problema. Así también, la profesora fue un mediador cuando los grupos no llegaban a concesos respecto a la estrategia que utilizarían en la resolución de la tarea. En ningún caso la docente les señalo que eran incorrectas, solo se les proponía conversarla en el equipo buscando que la respuesta convenciera a todos los integrantes.
Por ejemplo, el grupo G4, en primera instancia, construyó un gráfico con los valores de ambas series de datos (ver Cuadro 4). Esa representación presentaba debilidades y era insuficiente para resolver la situación problema a lo que se les planteó buscar otra estrategia para responder. Esto desembocó en que los estudiantes calcularan las distancias de manera análoga a como se realiza en de cada serie de datos respecto a la media aritmética, acércandose de manera intuitiva al concepto de desviación estándar.
Para finalizar la experiencia, un representante de cada grupo debía compartir con el resto de la clase la solución entregada por su equipo, respondiendo a las interrogantes que podían surgir de parte de sus compañeros, los que evaluaban si les parecía correcta la justificación o entregaban sugerencias en el caso que fuese necesario. Terminada esta fase, se les pidió a los alumnos que observaran cada una de las estrategias presentadas por sus compañeros y señalaran cuál de ellas fue la que mejor representaba al conjunto de todas las soluciones mostradas, lo que desembocó en la institucionalización de la desviación estándar.
Tomando en cuenta las diferentes respuestas entregadas por los equipos, la profesora, en conjunto con los estudiantes coinciden de que el jugador ganador es Pedro, para luego institucionalizar el objeto matemático desviación estándar como sigue:
La desviación típica o estándar, corresponde a una medida de dispersión que, para un conjunto de datos, se designa por S y se calcula como sigue:
i) Se obtiene el conjunto de las desviaciones desde la media (D).
ii) Se eleva al cuadrado cada desviación .
iii) Se halla la suma de los cuadrados y se divide por n. , a esta expresión se le denomina varianza y se designa como .
iv) Finalmente se extrae la raíz cuadrada:
Por lo tanto, el conjunto de la clase estableció que la desviación típica o estándar es una medida de dispersión que indica qué tan dispersos están los datos con respecto a la media. Así, una desviación estándar baja indica que la mayor parte de los datos tienden a estar más agrupados a diferencia a cuando toma un valor alto, que indica que los datos se extienden sobre un rango de valores más amplio.
6. Conclusiones
Se considera que la noción idoneidad didáctica utilizada en el análisis del proceso de instrucción presentado, proporciona herramientas para la realización de un análisis sistemático. Este tipo de análisis cuenta con distintas facetas, lo que lo convierte en una herramienta útil para que el profesor de matemáticas pueda estimar qué tan eficiente fue la instrucción realizada, dado que se incorporan diferentes aspectos y que en su conjunto permiten establecer la idoneidad del proceso de enseñanza.
Una parte de la valoración cognitiva nos permitió obtener información referente a los significados personales y algunas dificultades presentadas por los estudiantes. Tales resultados coinciden con otros estudios (GARFIELD; BEN-ZVI, 2008; ORTA; SÁNCHEZ, 2013), donde los estudiantes emplean estrategias en que priorizan la comparación de un valor particular de la serie de datos con alguna medida de tendencia central o la desviación media. Valoramos de manera positiva que los estudiantes buscaran diferentes estrategias para resolver la situación problema planteada, aunque se ha detectado un limitado conocimiento de conceptos estadísticos que les permitieran resolver, argumentar y comunicar de mejor manera la problemática propuesta.
El proceso de instrucción y su análisis permitió observar que la enseñanza y el aprendizaje de la desviación estándar carece de ser una tarea sencilla. Una vez que requiere la comprensión profunda de diferentes conceptos, que quedaron de manifiesto en el análisis de los objetos matemáticos que intervienen en la resolución de la situación problema, se entiende que en el estudio de la desviación estándar se debe abordar no sólo desde la perspectiva algorítmica, sino que aplicado e interpretado su valor en determinados contextos.
En este trabajo, destacamos la herramienta idoneidad didáctica, porque nos permitió generar un puente entre la teoría y la realidad de la clase de matemáticas, en la que participan una variedad de factores que son considerados por este modelo, y permiten al profesor reflexionar sobre su práctica de manera sistemática. Finalmente, nuestra propuesta permite ser replicada en diferentes aulas, y de este modo dotar al profesor de propuestas que puedan promover en los estudiantes la comprensión e interpretación de la desviación estándar, objeto que en la mayoría de los casos es abordado principalmente desde la perspectiva algorítmica.
7. Referencias
BAKKER, A.; GRAVEMEIJER, K. Learning to reason about distribution. In: BEN-ZVI, D.; GARFIELD, J. (eds.). The challenge of developing statistical literacy, reasoning and thinking. Países Bajos: Springer, 2004, p. 147–168.
BARDIN, L. Análisis de contenido. Madrid: Akal Ediciones, 1996.
BATANERO, C. Didáctica de la Estadística. Granada: Universidad de Granada, 2001.
BATANERO, C.; GONZALEZ-RUIZ, I.; LOPEZ-MARTIN, M. M.; CONTRERAS, J. M. La dispersión como elemento estructurador del currículo de estadística y probabilidad. Epsilon: Revista de la Sociedad Andaluza de Educación Matemática "Thales". V. 32, n. 2, p. 7–20. 2015a.
BATANERO, C.; LÓPEZ-MARTÍN, M.; GONZÁLEZ-RUIZ, I.; DÍAZ-LEVICOY, D. Las medidas de dispersión en el estudio de la inferencia estadística. In: XIX Jornadas Nacionales de Educación Matemática, 19, 2015b, Villarrica. Anais […]. Villarrica: Sociedad Chilena de Educación Matemática, 2015b, p. 312-316.
BATANERO, C.; DÍAZ, C.; CONTRERAS, J. M.; ROA, R. El sentido estadístico y su desarrollo. Números: Revista de didáctica de las Matemáticas, v. 83, p. 7-18, 2013.
CASTELLS, Manuel. A Sociedade em rede. São Paulo: Paz e Terra, 2000.
COBB, G. W; MOORE, D. S. Mathematics, statistics, and teaching. The American Mathematical Monthly, v. 104, n. 9, p. 801-823, 1997.
ESTEPA, A.; PINO, J. D. Elementos de interés en la investigación didáctica y enseñanza de la dispersión estadística. Números: Revista de Didáctica de las Matemáticas, n. 83, p. 43-63, 2013.
FONT, V.; GODINO, J. D. La noción de configuración epistémica como herramienta de análisis de textos matemáticos: su uso en la formación de profesores. Educação Matemática Pesquisa, v. 8, n. 1, p. 67-98, 2006.
FONT, V.; PLANAS, N.; GODINO, J. D. Modelo para el análisis didáctico en educación matemática. Infancia y aprendizaje, v. 33, n. 1, p. 89-105, 2010.
FONT, V.; GODINO, J. D.; GALLARDO, J. The emergence of objects from mathematical practices. Educational Studies in Mathematics, v. 82, n. 1, p. 97-124, 2013.
GAL, I. Adults' statistical literacy: Meanings, components, responsibilities. International statistical review, v. 70, n. 1, p. 1-25, 2002.
GAL, I. Understanding statistical literacy: About knowledge of contexts and models. In: Tercer Congreso Internacional Virtual de Educación Estadística, 3, Granada, Anais […]. Granada, 2019. Disponible en: www.ugr.es/local/fqm126/civeest.html.
GARFIELD, J.; BEN-ZVI, D. Developing students’ statistical reasoning: Connecting research and teaching practice. New York: Springer, 2008.
GHIGLIONE, R.; MATALÓN, B. Las encuestas sociológicas. México: Trillas, 1989.
GODINO, J. D. Un enfoque ontológico y semiótico de la cognición matemática. Recherches en Didactiques des Mathematiques, v. 22, n. 2-3, p. 237-284, 2002.
GODINO, J. D. Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, v. 8, n. 11, p. 111-132, 2013.
GODINO, J. D.; BATANERO, C.; FONT, V. The onto-semiotic approach to research in mathematics education. ZDM: The International Journal on Mathematics Education, v. 39, n. 1-2, p. 127-135, 2007.
GODINO, J. D.; BATANERO, C.; FONT, V. The onto-semiotic approach: Implications for the prescriptive character of didactics. For the Learning of Mathematics, v. 39, n. 1, p. 38-43, 2019.
GODINO, J. D.; CONTRERAS, A.; FONT, V. Análisis de procesos de instrucción basado en el enfoque ontológicosemiótico de la cognición matemática. Recherches en Didactiques des Mathematiques, v. 26, n. 1, p. 39-88, 2006.
HART, A. E. The non-standard deviation. Teaching Statistics, v. 5, n. 1, p. 16-20, 1983.
HART, A. E. How should we teach the standard deviation? Teaching Statistics, v. 6, n. 1, p. 24-27, 1984.
HERNÁNDEZ, R.; FERNÁNDEZ, C.; BAPTISTA, P. Metodología de la investigación (6ª ed.). México: Mcgraw-Hill, 2014.
LEHRER, R.; ENGLISH, L. Introducing children to modeling variability. In: BEN-ZVI, D.; MAKAR, K.; GARFIELD, J. (eds.). International handbook of research in statistics education. Cham: Springer, 2018, p. 229-260.
LOOSEN, F.; LIOEN, M.; LACANTE, M. The standard deviation: some drawbacks of an intuitive approach. Teaching Statistics, v. 7, n. 1, p. 2-5, 1985.
MAKAR, K.; CONFREY, J. Variation talk: Articulating meaning in statistics. Statistics Education Research Journal, v. 4, n. 1, p. 27-54, 2005.
MINEDUC. Bases curriculares 3º y 4° medio. Santiago: Ministerio de Educación, 2019.
MOORE, D. S. Uncertainty. In: STEEN, L. A. (ed.). On the shoulders of giants: New approaches to numeracy, 1990, p. 95–137.
NCTM. Principles to actions: Ensuring mathematical success for all. Reston, Virginia: National Council of Teachers of Mathematics, 2014.
ORTA, J.A.; SÁNCHEZ, E. Interpretación de la dispersión de datos en contexto de riesgo por estudiantes de secundaria. In: BERCIANO, A.; GUTIÉRREZ, G.; ESTEPA, A.; CLIMENT, N. (eds.). Investigación en Educación Matemática, XVII Simposio SEIEM. Anais [...]. Bilbao: Sociedad Española de Investigación en Educación Matemática, 2013, p. 421-430. Disponible en: http://funes.uniandes.edu.co/12058/1/Orta2014Interpretacion.pdf.
ORTEGA, J. M.; ESTEPA, A. C. Meaning of the dispersion and its measures in secondary education. In: The International Conference on Teaching Statistics – ICOTS 7. Anais […]. Salvador, 2006. Disponible en: http://iase-web.org/documents/papers/icots7/2B2_ORTE.pdf?1402524964.
PALLAUTA, J.D.; BONILLA, D.; OLIVARES, D. La desviación media: estrategias empleadas por estudiantes de secundaria en una situación didáctica. Épsilon, n. 102, p. 7-23, 2019.
SÁNCHEZ, E. S. Elementos de estadística y su didáctica a nivel bachillerato. México: Secretaría de Educación Pública, Subsecretaría de Educación Media Superior, 2013.
SHAUGHNESSY, J. M. Research on students’ understanding of some big concepts in statistics. In: BURRIL. G. (ed.). Thinking and reasoning with data and chance. Reston, VA: National Council of Teachers of Mathematics, 2006, p. 77–98.
YAREMKO, R. M.; HARARI, H.; HARRISON, R. C.; LYNN, E. Handbook of research and quantitative methods in psychology: For students and professionals. Hilldale, NJ: Erlbaum, 2013.
WILD, C.; PFANNKUCH, M. Statistical thinking in empirical enquiry. International Statistical Review, v. 67, n. 3, p. 223-248, 1999.
Enlace alternativo
https://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/449 (pdf)

