Resumen: El presente trabajo trata sobre la determinación experimental de la distribución de la presión lateral activa, de un suelo granular contra un muro de contención rígido que sufre traslación horizontal y rotación respecto al tope. La medida de la presión fue llevada a cabo utilizando celdas de carga como sensores, siendo las variables la densidad relativa del relleno y la rugosidad del paramento. La colocación del relleno en estado denso y suelto fue obtenida por el uso de los métodos de pluviación y extracción de la malla respectivamente. El movimiento del muro se controló mediante un sistema mecánico simple. Los resultados experimentales obtenidos condujeron a la conclusión general de que los suelos sueltos muestran una distribución lineal, y los suelos densos una distribución no lineal. Particularmente, la distribución de la presión lateral de un relleno denso contra un muro que se traslada horizontalmente y rota alrededor del tope, exhibe dos picos. Este hecho es explicado por la mecánica granular, como la yuxtaposición de las dos distribuciones de presión correspondientes a la traslación horizontalmente y rotación respecto al tope.
Palabras clave: cinemática del muro de contención, presión lateral activa, suelo granular.
Abstract: This paper is about the experimental determination of the active lateral pressure distribution of a granular soil on a rigid retaining wall undergoing a horizontal translation and a rotation about the top. The pressure measurement was made using load cells as sensors, being the variables the relative density of the backfill and the rugosity of the wall backside. The placement of backfill in loose and dense state was obtained by using the pluviation and the mesh extraction methods, respectively. The wall movement was controlled by a simple mechanical system. The experimental results obtained lead to the general conclusion that loose soils show a linear distribution, and dense soils, a non-linear distribution. Particularly, the distribution of the lateral pressure of a dense backfill against wall that moves horizontally and rotates about the top, shows two peaks. This fact is explained by the Granular Mechanics as the juxtaposition of two pressure distributions related to horizontal translation and rotation about the top.
Keywords: kinematics of the retaining wall, active lateral pressure, granular soil.
Artículos de Investigación
Determinación experimental del empuje activo contra muros de contención que sufren traslación y rotación respecto al tope
EXPERIMENTAL DETERMINATION OF THE ACTIVE LATERAL PRESSURE AGAINST RETAINING WALLS UNDERGOING TRANSLATION AND ROTATION ABOUT THE TOP
Recepción: 18/02/2019
Aprobación: 13/05/2019
Un problema clásico de mecánica de suelos es determinar la distribución de presión lateral que el suelo ejerce sobre un muro de contención, con el fin de que su diseño sea satisfactorio. Usualmente se asume que esta distribución es lineal, pero según los ensayos realizados por varios autores [1] [2] [3] [4] [5] [6], conducen a la conclusión de que la forma de la distribución depende principalmente de la cinemática del muro; habiéndose reconocido tres mecanismos elementales: a) rotación respecto a la base (RB), que muestra una distribución lineal; b) traslación horizontal (T), que refleja una distribución no lineal con el valor máximo cerca de la base; y c) rotación respecto al tope (RT), que genera una distribución no lineal con el valor máximo cerca del tope (ver Figura 1).
Además, la cinemática del muro puede complicarse debido a la combinación de dos o más movimientos elementales; siendo éste un problema no resuelto satisfactoriamente hasta la fecha. En adición a la cinemática, la naturaleza granular del suelo le confiere una complicación adicional a la distribución de presión lateral, pues los suelos en determinadas situaciones se arquean. Para estudiar experimentalmente la distribución de la presión lateral de los suelos granulares, se construyó un equipo con el fin de hacer ensayos a escala reducida con rellenos horizontales de arena con diferentes compacidades, y muros verticales con diferentes rugosidades del trasdós, a fin de determinar experimental la distribución de la presión lateral activa, de un suelo granular contra un muro de contención rígido que sufre traslación horizontal y rotación respecto al tope.
Se han propuesto varias teorías para explicar la distribución no lineal de la presión lateral de suelos contra muros de contención. La más conocida es aquella que atribuye una redistribución del esfuerzo en la masa de suelo debido al fenómeno denominado efecto de arco en suelos por Terzaghi [1]. Pero la introducción de líneas de falla singulares verticales en el suelo fue propuesta por Janssen [8] para establecer la ecuación diferencial de equilibrio en un elemento plano de ancho constante e igual al diámetro del silo de granos, asumiendo que la relación entre el esfuerzo vertical y horizontal es constante. La solución obtenida por Janssen tiene forma exponencial y es muy conocida. Desde entonces se han planteado diversas teorías para calcular la presión lateral del suelo sobre los muros de contención, basadas en diversas hipótesis, siendo la principal aquella que se refiere a la condición inclinada de la línea de falla según la Teoría de Rankine. La ecuación obtenida por Handy [9] es exponencial y es la más antigua y simple.
La ecuación obtenida por Paik y Salgado [10] también es exponencial, se refiere a los muros que se trasladan horizontalmente hacia afuera, y toma en cuenta la trayectoria de los esfuerzos principales. Koshravi et al. [11] han derivado una ecuación exponencial a partir de las ecuaciones diferenciales de equilibrio en dos dimensiones y de las condiciones de contorno, que se ajusta bien a los datos experimentales. La ecuación es la siguiente:
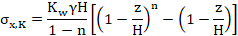 (1)
(1)Donde z es la profundad, γ es el peso volumétrico del suelo, H la altura del muro, Kw, μw y n constantes que dependen del ángulo de rozamiento interno del suelo, ϕ, y del ángulo de fricción suelo-muro, δ, y son dadas por las siguientes expresiones:
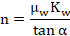 (2)
(2)
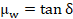 (3)
(3)
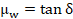 (4)
(4)
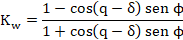 (5)
(5)
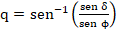 (6)
(6)Otra teoría propuesta para explicar la distribución no lineal, es aquella que se basa en dos hipótesis de trabajo [12] [13]: los materiales granulares pueden ser modelados como un ensamblaje de esferas uniformes y ordenadas [14], los esfuerzos en la masa se transmiten como cadenas conjugadas de fuerzas de contacto [15]. Además, cuando se considera que la línea de falla es lineal, la distribución de la presión lateral adquiere una forma muy sencilla. Esta teoría incluye la inclinación del relleno, paramento y la del muro, el ángulo de rozamiento interno y la fricción suelo-muro. Otro aspecto relevante de esta teoría es que toma en cuenta el tipo de movimiento del muro y su impacto en la cinemática de los granos. Si el muro rota alrededor de la base hacia afuera, la cuña se deforma horizontalmente entre el paramento y la línea de falla, originando que el grano superior del ensamble rómbico se introduzca verticalmente entre los dos granos inferiores hasta alcanzar el estado de falla, este análisis conduce a la conclusión de que la distribución de la presión es lineal.
Si el muro se traslada horizontalmente hacia afuera, la cuña se moviliza paralelamente entre el paramento del muro y la línea de falla, en forma rígida. Esto significa que el ensamble rómbico de granos permanece inalterado y las cadenas de fuerzas tienen la inclinación correspondiente al estado de reposo. Esta diferencia de inclinaciones de las cadenas de fuerzas y de la línea de falla, muestra una distribución bilineal de presiones laterales. Si el muro rota alrededor del tope, la cuña se deforma de abajo hacia arriba a lo largo de la línea de falla.
Por ello, el ensamble rómbico de granos se distorsiona de tal modo que el grano inferior tiende a moverse, originando una cadena de fuerzas pasiva en la dirección del muro. Esto genera una distribución bilineal con el pico hacia el tope. Para el caso particular de un relleno horizontal y un muro vertical, y la distribución de la presión lateral queda dada por la expresión (7) (ver Figura 2) [12]:
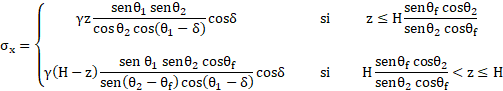 (7)
(7)
Donde θ1 y θ2 son los ángulos de las cadenas de fuerzas con respecto a la vertical, que adoptan diferentes valores dependiendo del movimiento que sufra el muro de contención y compacidad que se encuentra el relleno (ver Tabla 1).
El ángulo θo corresponde al estado de reposo, θf al estado plástico activo, y θfp, al estado plástico pasivo, que se obtienen de las siguientes expresiones:
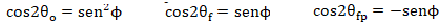 (10)
(10)Depósito de prueba es el lugar donde se coloca el relleno, consta de dos paredes laterales gruesas de vidrio transparente que permiten observar el desarrollo de las deformaciones del suelo. Estas dos paredes y una tercera llamada pantalla movible se apoyan y ajustan en un marco reticular rígido formado por perfiles de acero. La cuarta pared está constituida por el muro de contención rígido que se puede mover como un todo con la ayuda de un sistema de control durante la ejecución del ensayo (ver Figura 3). La longitud del relleno puede variar a intervalos de 6,7 cm hasta un máximo de 88,0 cm trasladando la pantalla movible observado en la Figura 3, su ancho a intervalos de 2,5 cm desde 22,0 a 77,0 cm si se mueven las paredes laterales (ver Figura 4). Su alto si se usa un muro de diferente elevación hasta un máximo de 95,0 cm. Para esta investigación se utilizó 35,0 cm de longitud, 47,0 cm de ancho y dos alturas: 35,0 y 40,0 cm.
La elección de dichas dimensiones fue tomando en cuenta los experimentos realizados por otros autores [5] [6]. El depósito de ensayo se colocó en una mesa que contenía una compuerta inferior para la evacuación rápida de la muestra ensayada (ver Figura 5a).
El movimiento del muro se controló con una estructura de acero, que principalmente consistía de dos barras de sección circular conectadas por medio de una cadena que genera rotación diferencial de una con respecto a la otra, de modo que el muro se traslada horizontalmente y rota respecto al tope (Figura 5b y 5c). La magnitud del movimiento se midió mediante comparadores de desplazamiento. El conjunto de todos estos accesorios constituye el sistema de control.
El marco rígido está conformado por ángulos estructurales de acero de 1½” x 1½” x 1/8” de diferentes longitudes, y planchas cuadradas de acero de 12,0 x 12,0 cm con un espesor de 1/8”. En las uniones de cada esquina se usaron 3 planchas, 18 pernos hexagonales de 5/16” x ¾” con sus tuercas y volandas de 5/16”; para las paredes laterales se empleó planchas de vidrio de 8,0 mm de espesor. En el caso del muro de contención, la pantalla movible y la compuerta de la mesa son tableros de MDF, con un espesor de 5,0 cm para el muro de contención y de 1,8 cm para los demás.
Una de las propiedades del suelo granular es el cambio de volumen de la muestra sujeta a la acción de los esfuerzos de corte, relacionado a una respuesta mecánica diferente. Este es un fenómeno estudiado primero por Reynolds [14] y luego por Casagrande [16]. De aquí se deduce que la forma de colocación de la muestra de arena en el depósito es una de las tareas más importantes en el ensayo, además que el relleno tiene que ser homogéneo y reproducible [17]. En este trabajo, el estado suelto del suelo se consiguió mediante el método de la extracción de la malla y el estado denso, mediante el método de la pluviación.
El método de la extracción de la malla consiste en utilizar un molde con una malla instalada en la base (ver Figura 6a), en el cual se vierte el suelo granular. Luego, es halada hacia arriba hasta que pase toda la muestra.
Se construyeron tres moldes con una malla de 4,7 mm de abertura, dicha dimensión se seleccionó para que los granos de suelo no se atasquen en la malla. El molde 01 sirvió para determinar el peso específico mínimo, se construyó a partir de un tubo de PVC de 4”, cuyo diámetro externo se redujo para ser introducido holgadamente en un depósito de 10,15 cm de diámetro. La malla se fijó en el extremo del molde con silicona (ver Figura 7a). El molde 02 se usó para evaluar el peso volumétrico alcanzado en depósitos más grandes, se construyó usando planchas de MDF de 1,8 cm de espesor, cuyas dimensiones fueron escogidas de modo que pueda ingresar holgadamente en un depósito de 26,8 cm de largo por 25,0 cm de ancho (ver Figura 7b). El molde 03 sirvió para colocar la arena en el depósito de prueba elaborado con el mismo material del molde 02 (ver Figura 7c).

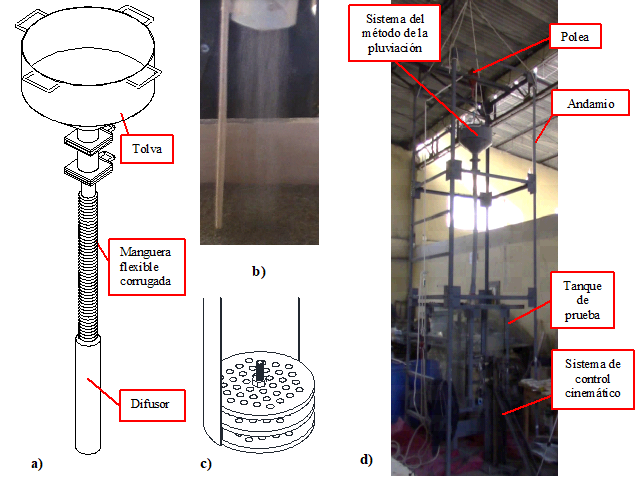
La obtención de la muestra en estado denso se realizó mediante el método de la pluviación, consiste en hacer caer el suelo por gravedad desde una altura de caída de 3,0 m mediante una manguera flexible corrugada el cual termina en un difusor que genera lluvia de arena, la parte inferior interna del difusor consiste de 3 placas circulares con un patrón y diámetro de agujeros determinados (ver Figura 8). La altura de caída se define como la distancia desde el extremo inferior de la tolva hasta el fondo del depósito a formar. Todas las medidas utilizadas fueron basadas en el trabajo de Srinivasan et. al. [17], los cuales después de realizar varias pruebas concluyeron que éstas dimensiones son las más optimas respecto a la máxima compacidad alcanzada (Dr =100%) y al tiempo empleado en la colocación de la muestra en el depósito de prueba. Además, se construyó un andamio de 4,0 m de altura, constituido de perfiles de acero y dotado de un sistema de poleas que permitían levantar el molde 03, así como la tolva cargada.
Los sensores usados en esta investigación fueron celdas de cargas, la presión resultante se logró dividiendo la fuerza desplegada por el sensor entre el área del disco de contacto, (ver Figura 9a). Dichos sensores se instalaron en el eje central de los muros y nivelados con el paramento del muro (ver Figura 9b).
Los sensores se calibraron de dos formas: la primera consistió en la colocación de pesas patrón sobre cada uno de los sensores ensamblados en el muro de contención en posición horizontal (ver Figura 10a). La segunda se colocó el muro en posición vertical, simulando la condición del experimento y usando agua para generar la presión lateral (ver Figura 10b). Con tal propósito, se construyó un prisma rectangular constituido de planchas de acrílico transparente de 4,0 mm de espesor pegadas utilizando cloroformo.

Para evitar la fuga de agua entre las uniones se usó silicona líquida transparente, y se perforaron orificios a la altura de cada sensor, cubiertos por una membrana elástica de modo que no se mojaran durante el llenado con el agua. Los ensayos mostraron que las presiones hidrostáticas calculadas coincidían con las presiones obtenidas con los sensores (Figura 11).
El diámetro de los discos de contacto de los sensores es de 2,3 cm con el fin de cumplir con las recomendaciones establecidas en ensayos anteriores [18]: la relación entre el diámetro del disco de contacto, D, y el diámetro medio de las partículas, D50, debe ser mayor a 10; la relación entre el diámetro del disco de contacto D y su deflexión deben ser mayor a 2000, como mínimo. En el presente caso, las relaciones consideradas fueron: 31.1, para la primera recomendación y 2300, para la segunda, cumpliendo con los valores especificados.
El trasdós liso del muro de contención se modeló usando una plancha de acrílico, y el trasdós rugoso, mediante un tapiz de papel lija, adecuados para dejar libres los discos de contacto. Considerando que en el espacio formado por las horadaciones del trasdós del muro y los bordes de los discos de contacto podían ingresar algunos granos pequeños distorsionando la respuesta del sensor mostrada en la Figura 9b, se cubrieron los bordes con una membrana elástica delgada (ver Figura 12).
La arena usada en el ensayo fue preparada tamizando el suelo seleccionado entre las mallas de 0,5 mm y 1,1 mm de abertura; obteniéndose una arena mal graduada (SP) según el Sistema Unificado de Clasificación de Suelos. Se seleccionó como suelo de prueba arena casi uniforme, considerando la experiencia de otros autores que han demostrado que el uso de arenas bien graduadas colocadas mediante el método de la pluviación, puede llevar a la obtención de una muestra no homogénea debido a la diferencia de velocidades de caída de las partículas de distinto tamaño, y a la diferencia de energía de impacto [17].
Se utilizó un molde de Próctor Estándar para determinar el peso volumétrico mínimo mediante dos procedimientos diferentes: el vertido lento de la arena en el molde hasta llenarlo, eliminado el exceso por enrasado; extracción vertical de la malla empleando el molde 01, habiéndose obtenido 11,8 kN/m3 y 11,3 kN/m3, respectivamente. Según esto, el peso volumétrico mínimo de la muestra fue tomado como 11,3 kN/m3. Luego se determinó el peso volumétrico con el método de la extracción de la malla con el molde 02, y depósitos de 26,8 cm de largo, 25,1 cm de ancho y con alturas de 8,1 16,1 y 25,0 cm (ver Figura 13).

Se utilizaron estos 3 depósitos de diferentes capacidades volumétricas para verificar si esta variable influye en los pesos volumétricos alcanzados, la cual no se hallaron valores diferentes. El peso volumétrico obtenido fue de 12,3 kN/m3, correspondiendo a una densidad relativa del 39,8 % ((14,2/12,3) x ((12,3-11,3)/ (14,2-11,3)) x 100 % = 39,8 %.
Se determinó con la utilización del método de la pluviación, ya que con este se obtienen mayores pesos unitarios que el método de la ASTM D4253-06 [19] [17] [20]. Al igual que el punto anterior se utilizaron los mismos depósitos de diferentes capacidades volumétricas, obteniendo el mismo peso volumétrico de 14,2 kN/m3, definiéndolo como peso volumétrico máximo y correspondiéndole una densidad relativa del 100% ((14,2/14,2) x ((14.2-11,3)/(14,2-11,3)) x 100 % = 100 %).
Se obtuvieron dos ángulos de rozamiento interno determinados en una máquina de corte directo convencional, uno correspondiente a una muestra de peso volumétrico 14,2 kN/m3 (Dr = 100%), y otra con un peso volumétrico de 12,3 kN/m3 (Dr = 39.8%), en ambos casos se midió también la deformación vertical para verificar el comportamiento dilatante y contractivo, en la Figura 14 se observa la gráfica de los datos obtenidos. En la figura 14a se presentan las curvas esfuerzo deformación del suelo denso sometido a diferentes esfuerzos verticales. En esta figura se observa que, cuando se incrementa la deformación, el esfuerzo crece rápidamente hasta alcanzar un pico, a partir del cual el esfuerzo de corte disminuye en forma cóncava hacia arriba y asintóticamente a la horizontal.
En la figura 14b se observa que las curvas esfuerzo deformación para un suelo suelto crecen en forma cóncava hacia abajo y asintóticamente a la horizontal cuando la deformación crece. En la figura 14c se presenta la relación entre la deformación vertical y la deformación horizontal, en ella se observa que el suelo denso es por naturaleza dilatante, mientras que el suelo suelto es contractivo. Como se sabe, este comportamiento distinto según la densidad relativa de los suelos granulares fue observado originalmente por Casagrande [16].
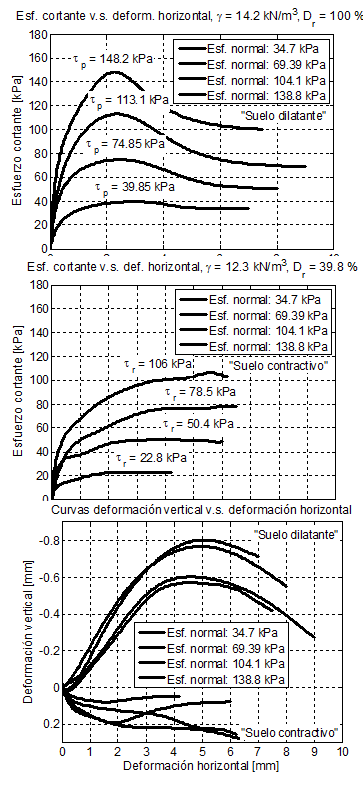
Para la muestra densa (γ=14,2 kN/m3) se obtuvo un ángulo de fricción interna, ϕ = 45,0°, y para la muestra suelta (γ=12,3 kN/m3) se obtuvo un ϕ = 34,3° (Figura 15).
Como trasdós del muro, se utilizaron dos materiales: acrílico y papel lija. El ángulo de rozamiento externo entre éstos y el suelo granular se obtuvo con la máquina de corte directo adecuada para este fin. Los valores hallados fueron: 26,8° para el acrílico, y 35,9°, para el papel lija (ver Figura 16).
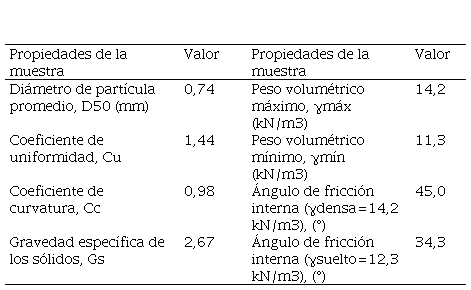
En la tabla 2 se muestra las propiedades del suelo granular utilizado.
Los ensayos consistieron en medir el volumen del relleno, colocar la muestra ya sea por el método de la pluviación o de la malla, tomando nota de la cantidad introducida, y finalmente, mover el muro hasta que los datos sensados no varíen. Tanto antes como después de la realización de cada ensayo, se midió la presión hidrostática para verificar constantemente el buen funcionamiento de los sensores. En los siguientes párrafos y figuras, se muestran los datos de los ensayos en los cuales se evidencia principalmente la diferencia de la distribución de presión lateral entre un relleno suelto y denso bajo una misma cinemática del muro de contención.
En la Figura 17 se presentan los resultados experimentales correspondientes a la presión lateral de la arena en estado suelto γsuelto = 12,3 kN/m3, Dr = 39.8 %, ϕ = 34,3°. La Figura 17a presenta los datos de un muro vertical de 40,0 cm de altura con un trasdós de acrílico, en este caso, la presión lateral dada por las Teorías de Rankine, de Coulomb y de la Mecánica Granular, es la misma considerando un δ = 0°.
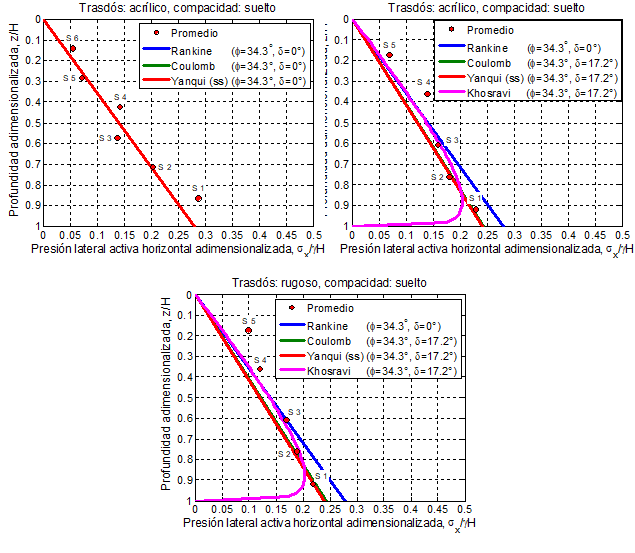
En las Figuras 17b y 17c los datos corresponden a un muro de 35,0 cm de altura, en la primera se usó un trasdós de acrílico, y la segunda de papel lija, se observa que la ecuación de Rankine se ajusta mejor. Sin embargo, si se consideran sólo los datos de los sensores S3, S2 y S1, el ajuste coincide con Coulomb y la Mecánica Granular, para un δ = 0,5 ϕ. Se puede observar que el uso de diferentes rugosidades de trasdós influye muy poco en los datos experimentales obtenidos.
Los diagramas de mayor importancia se presentan en la Figura 18, pues se refiere a los suelos densos, cuya respuesta es no lineal. En este caso, se observan dos picos en la distribución de la presión lateral del suelo, lo cual sugiere que ésta es la consecuencia de la yuxtaposición de las presiones laterales causadas por la traslación horizontal del muro y la rotación alrededor del tope. En este caso, los datos experimentales solamente pueden ser comparados con las ecuaciones proveídas por la Mecánica Granular, para ϕ = 45,0° y δ = 0,5 ϕ. Se han escogido algunas distribuciones de presiones laterales medidas directamente en los ensayos para ilustrar el comportamiento del relleno, mostrado en la Figura 18a a la 18d.
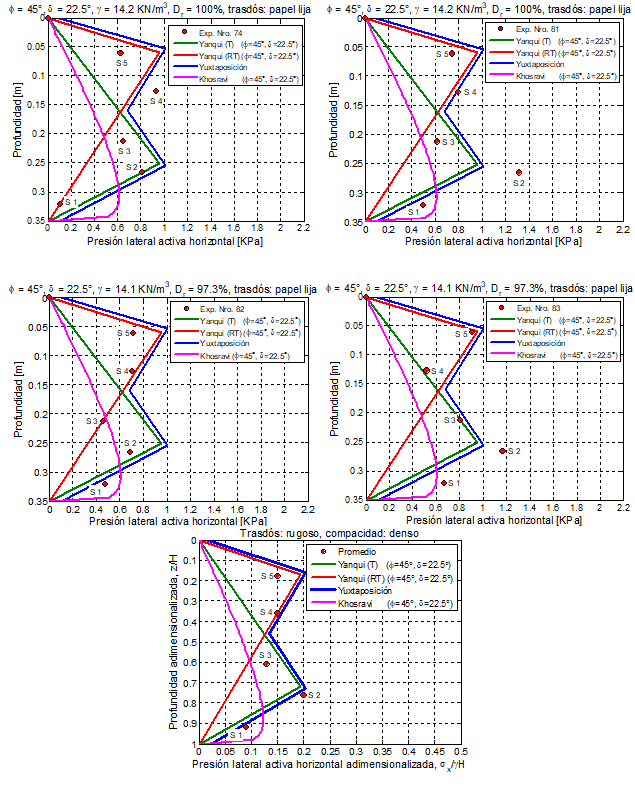
En ellas se observa el doble pico que la mecánica granular explica como una yuxtaposición de presiones laterales. La síntesis de los resultados experimentales en la arena densa se presenta en la figura 18e. Con este propósito, los datos fueron adimensionalizados y corregidos usando procedimientos estadísticos. Es preciso advertir que todos estos datos corresponden para un muro de 35,0 cm de altura, y un trasdós de papel lija.
Es importante notar que no se han utilizado los ángulos de fricción externa suelo – trasdós del muro de contención, obtenidos mediante la máquina de corte directo observado en la Figura 16, debido a que el mejor ajuste entre los datos experimentales y las curvas teóricas se logró utilizando el valor δ=0,5 ϕ siendo el menor al valor experimental obtenido. Esto se debe a que las cargas a las cuales estuvieron sometidos tanto el acrílico como el papel lija contra el suelo en la máquina de corte directo, fueron mucho mayores a las cargas sometidas en los experimentos, lo que ocasiona que los granos se incrusten ya sea en el acrílico o en el papel lija, por lo tanto se obtengan un ángulo de fricción mayor al que se obtendría si se sometieran a condiciones de cargas mucho menores. En investigaciones posteriores se recomienda determinar el ángulo de fricción externa suelo–trasdós en una máquina de corte directo equipada con sensores más precisos.
La distribución de la presión lateral, según los datos experimentales, es lineal si el suelo se halla en estado suelto o contractivo, independiente de la cinemática del muro, ajustándose a las Teorías de Rankine y Coulomb, así como a la Mecánica Granular de los suelos sueltos. La distribución de la presión lateral, según los datos experimentales, es no lineal cuando el suelo se halla en estado denso o dilatante, y depende de la cinemática del muro de contención. Cuando éste sufre una traslación horizontal y una rotación alrededor del tope exhibe dos picos, uno en la parte inferior y otro en la parte superior, estos datos experimentales se ajustan bien a los resultados teóricos de la Mecánica Granular.
A la Universidad Nacional de San Agustín de Arequipa por el financiamiento brindado para la ejecución del presente trabajo de investigación mediante el contrato N° 137 – 2016 – UNSA.
[Artículo corregido , vol. 20, 14] https://revistas.ucla.edu.ve/index.php/gt/article/view/2222
A la Universidad Nacional de San Agustín de Arequipa por el financiamiento brindado para la ejecución del presente trabajo de investigación mediante el contrato N° 137 – 2016 – UNSA.









