1. PRELIMINARES

1.1. Descomposición del factorial

A continuación en la Tabla 1 se descompone n! en factores primos, con n tomando valores de 1 a 53, aunque la factorización puede continuar infinitamente para todo valor de :

Con la descomposición de n! en sus factores primos, se puede notar ciertas características en los cambios de los exponentes de cada factor primo, una de ellas es que en la descomposición del factorial aparece un nuevo número primo cada vez que los exponentes de los números primos ya encontrados como factores, coinciden en no cambiar. Esta característica se puede expresar de la siguiente manera:

considérese a

1.2. Cambio de los exponentes de los factores primos del factorial

Si se analizan los exponentes de los factores primos, también se observará otra característica importante, y es el hecho de que en los cambios o aumentos de los valores de los exponentes se presentan diferentes distancias.

Teorema 1.2.1. Cada exponente del número primo P se repite cada P veces al ir aumentando el valor de n en n!.

Ahora para simplificar los cálculos y eliminar estas repeticiones, al enésimo exponente n de P que se desea hallar se le suma un valor T=T =0, 1, 2,3,……, (P-1) para que dé como resultado el múltiplo de P siguiente,

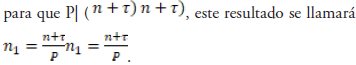
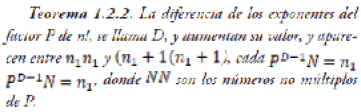
“Para x real, el símbolo [x] denota el máximo entero menor o igual a x”. (Niven & Zukcerman 1969, 75).

El siguiente Teorema es similar a: “supóngase que P denota un número primo. Entonces el mayor expo-

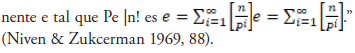
Teorema 1.2.4. El enésimo exponente n del número primo P en la factorizacion de n! es:

A continuación, se multiplican los resultados VD con sus distancias correspondientes, y se suman los resultados entre sí, y esto da el valor del enésimo exponente buscado.

Esto se expresa con la siguiente formula:

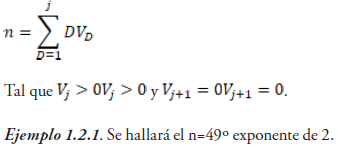
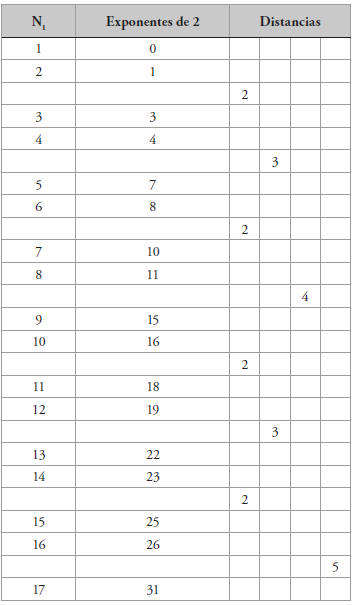
Observando los exponentes en la tabla, en estos se van presentando diferentes distancias: 2, 3, 4,5,…

Para no tener en cuenta la repetición de cada exponente, entonces: n1= (49º+1)/2=25º

Conociendo que el enésimo exponente buscado es el 25º sin repetición, se utiliza la fórmula (1):

V1=12 V2=6 V3=3 V4=2 V5=1 V6=:0

Como V6=0=0, solo se usaran las distancias 1, 2, 3, 4 y 5.

Ahora los anteriores resultados se multiplican con sus distancias correspondientes, y los resultados se suman entre sí:

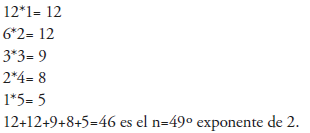
2. SISTEMAS DE DISTRIBUCIÓN

Considérese la siguiente tabla:

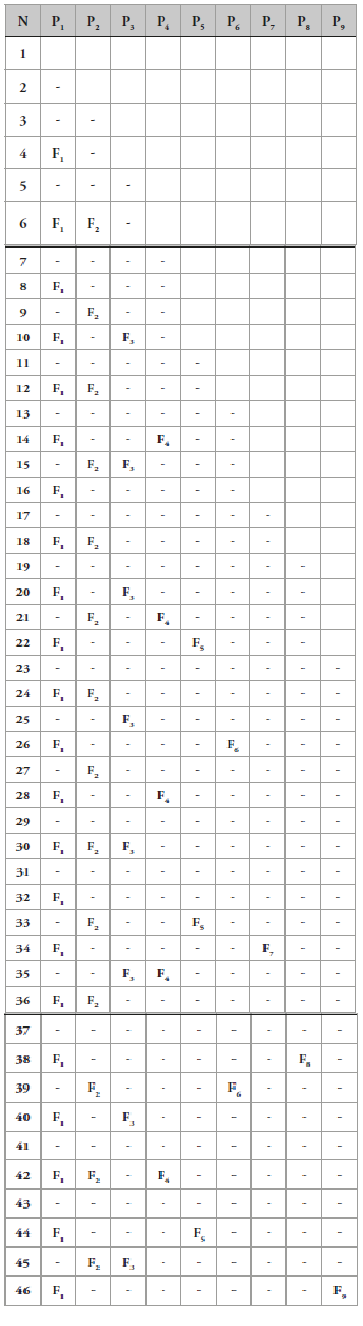
La anterior tabla puede continuar indefinidamente horizontal y verticalmente, y los números primos aparecen en las filas coloreadas en azul.

Demostración 2.1. Se llamará frecuencia de distribución Fn de cada primo , a los múltiplos de cada primo, es decir que las frecuencias son distintas para cada primo, así por ejemplo, la frecuencia F1 de 2 aparece cada 2 números desde 2, la frecuencia F2 de 3 aparece cada 3 números a partir de 3, y así sucesivamente. A medida que se van determinando números primos, se van estableciendo nuevas frecuencias, y la aparición de cada frecuencia determinara los sistemas de distribución.

Demostración 2.2. Se llamará sistemas de distribución Sn de cada número primo n, a las distancias Dk secuenciales que determinaran la aparición de los números primos, construidos por las frecuencias de los números primos ya encontrados.

Demostración 2.3. Sea Dk las distancias de distribución de un sistema Sn, cuyos valores son determinados por las diferencias de los números en los que no hay presencia de frecuencias, es decir, los números primos determinados por Sn, de manera que las distancias son las que determinan números primos en Sn..

Anteriormente se observó que en la descomposición del factorial aparecía un nuevo número primo cuando en ningún primo de la descomposición cambiaban sus exponente. Ahora este fenómeno aplica de forma similar en la anterior tabla, en donde aparece un nuevo número primo cuando no aparece ninguna frecuencia en las filas.

A continuación, se construirá la tabla de frecuencias de distribución por partes con el primer número primo, así:

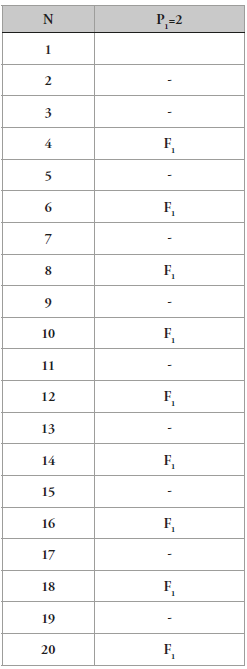
El primer número primo es P1=2, cuya frecuencia es F1=2 a partir de 2. Así con el 2 y su frecuencia se construye el primer sistema de distribución S1.

Ahora imagínese que este sistema es el único, de manera que a partir de 2, los siguientes números primos serán aquellos números que no estén en la frecuencia, los cuales son: 3,5,7,9,11,…., es decir, los números impares, así se construye el primer sistema de distribución, que empieza a funcionar desde el siguiente número primo de 2, es decir, 3, que es el primer número que está antes de su primer frecuencia o su primer múltiplo 4, y así 3 es el siguiente número primo, esto quiere decir que con S1=2-2-2-2-2-2-…. Los siguientes primos aparecerán cada dos números a par-tir de 3. Así, a partir de tres, los números primos serán: 3+2=5+2=7+2=9+2=11+2=13+2=……… (es evidente que 9 no es un número primo, este error será explicado con la Demostración del defecto de secuencia).

Ahora constrúyase la tabla de frecuencias de distribución con los números primos 2 y 3:

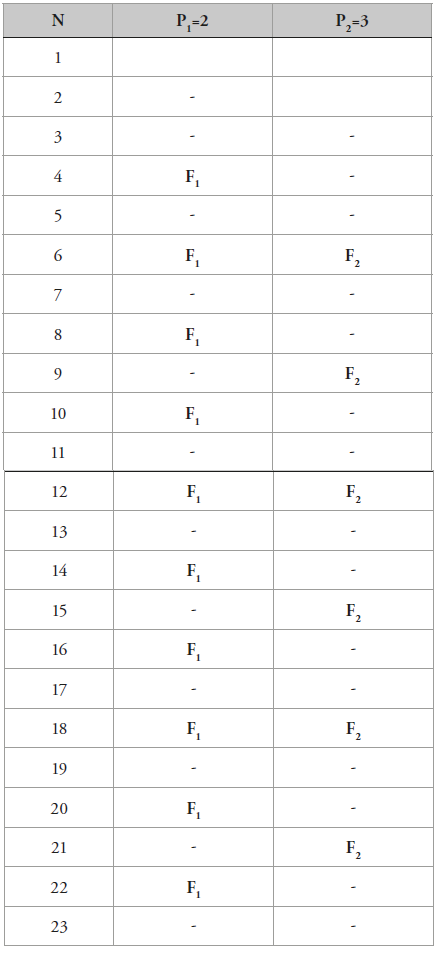
Aquí aparecen dos frecuencias, F1=2 y F2=3, imagínese que solo existen estas dos frecuencias, y con ellas se construye el segundo sistema de distribución S2=2-4-2-4-2-4-2-4-… esto quiere decir que con S2, que empieza a funcionar a partir del siguiente número primo del primo hasta donde se construyó el sistema, es decir el siguiente de 3 que es 5, los siguientes números primos aparecerán con las siguientes distancias:2-4-2-4-2-4-2-4-…, así por ejemplo a partir de 5 los números primos siguientes serán: 5+2=7+4=11+2=1 3+4=17+2=19+4=23+2=25+4=29+2=…

Hay que aclarar que los sistemas cambian con cada primo que se encuentra.

Así, como se vio anteriormente, se pueden construir los sistemas S3, S4. S5, S6,…Sn.

Ahora encontrando las distancias presentes en cada sistema, se puede construir un cuadro como el siguiente (el cuadro puede continuar indefinidamente):

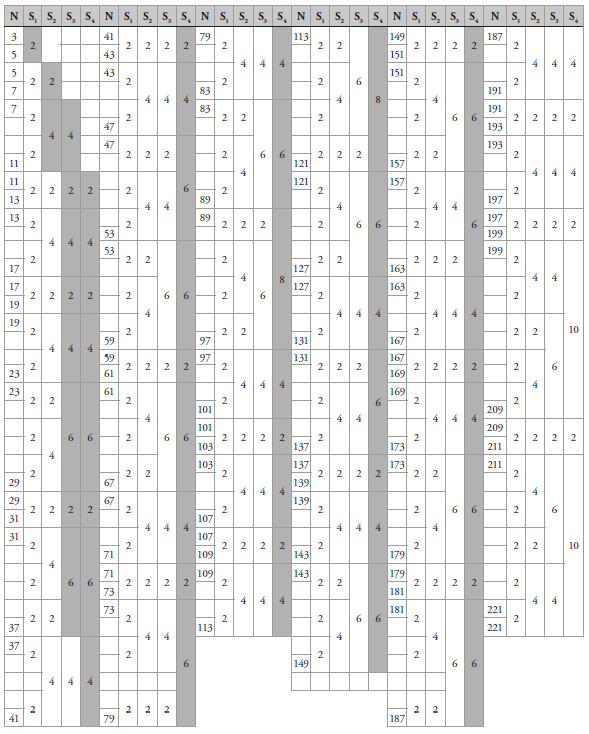
El cuadro anterior solo se hizo hasta S4 donde P4=7, y como S4 funciona bien hasta el cuadrado de P5=11, es decir que desde 121 empiezan a aparecer también números compuestos como 121, 143, 169, 187, 209, 221,…, pero si el cuadro de las distancias de los sistemas de distribución se completa hasta Sn, se perfecciona.

Demostración 2.4. Se llamará secuencia de distribución Cn (coloreado en azul para la columna de cada sistema Sn de la Tabla 2.4) al patrón de distancias de Sn que se repite, así por ejemplo, las secuencias:

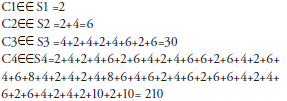
Y así sucesivamente.

La razón de que en los sistemas hayan secuencias que se repiten, es porque en la determinación de las distancias de tal sistema, llegará el momento en que la primera frecuencia en las distancias del sistema coincidirá de nuevo en ubicación, como al inicio, con respecto a las frecuencias de las distancias de los sistemas anteriores, así por ejemplo, en la Tabla 2.1, en P3=5, la primera frecuencia que aparece está ubicada en el número 10 (por ser el primer factor de 5), que coincide en ubicación horizontal con una frecuencia de S1 también en 10 (por ser un factor de 2) y justo en la fila de arriba, en el número 9, aparece una frecuencia de S2 (por ser 9 un factor de 3) y estas frecuencias están entre los primos 7 y 11, cuya distancia es 4, que es la primera distancia en C3, como se muestra en la Tabla 2.5:

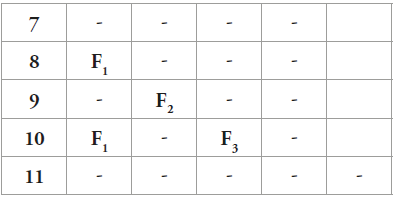
Así:

S1, P1=2, F1 está en 10 S2, P2=3, F2 está en 9 S3, P3=5, F3 está en 10

Ahora el lugar siguiente donde se vuelve a repetir

esta misma ubicación de las frecuencias es:

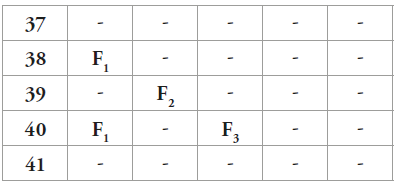
Así:

S1, P1=2, F1 está en 40 S2, P2=3, F2 está en 39 S3, P3=5, F3 está en 40

Y estos valores están entre los números primos 37 y 41, cuya diferencia es 4 que es el primer valor de la segunda aparición de la secuencia C3.

Teorema 2.1. Las distancias Dk EE Cn del sistema Sn construido hasta Pn, se empiezan a sumar desde Pn+1.

Demostración 2.5. Ya se sabe que en Sn el patrón de Cn se vuelve a repetir, y las distancias DkEE Cn del sistema Sn se empiezan a sumar desde Pn+1, y no desde Pn, porque la distancia D0= Pn+1 - Pn pertenece al sistema Sn-1 ya que en adelante en Sn no se presenta-ran múltiplos de Pn como primos, así cuando se repita Cn, el primer primo que inicie esta repetición que será igual a Pk =x(Cn)+ Pn+1, donde x va tomando valores tal que x EE N, no tendrá antes un múltiplo de Pn a una distancia D0.

Teorema 2.2. El valor de la suma de las distancias de las secuencias de cada sistema coincide con el valor del producto de los primos con los que se construyó el sistema, es decir:

Así por ejemplo, el sistema S3 se construyó con los números primos 2, 3 y 5, ahora el producto (primorial: ) 2*3*5 es =30, que coincide con el valor de la suma de las distancias de la secuencia C3, así 4+2+4+2+4+6+2+6=30.

Demostración. La razón por la cual la suma de las distancias de la secuencia de un sistema coincide con el producto de los primos con los que se construyó el sistema, es porque tal producto determina en qué lugar, o cada cuanto, se volverá a repetir la ubicación inicial del sistema con respecto a los sistemas anteriores, es decir, cuando la ubicación de las frecuencias del sistema del último primo encontrado se alinean en la misma ubicación inicial con las frecuencias de los sistemas anteriores hasta S1, y esto se logra con el m.c.m=Pn#Pn#, y como son primos, el m.c.m= , por ejemplo el m.c.m de 2,3 y 5 es 2*3*5=30 en S3, y se representa lo anterior en la siguiente Tabla:

Nótese que en la anterior tabla las frecuencias de 2,3 y 5 coinciden en alineación en cero y en 30.

Así en la secuencia de S2=24, sus distancias suman 2+4=6, que coincide en el producto de P1*P2 =2*3=6.

De esta manera se puede predecir que la suma de las distancias de la secuencia C4 de S4 es igual al producto P1*P2*P3*P4=2*3*5*7=210.

Teorema 2.3. Pk - D0 es necesariamente un múltiplo de Pn.

Demostración. Pk =x (Cn)+ Pn+1, por el Teorema 2.2. se sabe que , y Pn+1 = Pn + D0, de manera que:

Teorema 2.5. El número 1 no es un número primo.

Demostración. En el estudio anterior se definieron los sistemas de distribución desde S1, ahora considérese la existencia de S0.

Recuérdese que los sistemas de distribución se construyen a partir de las frecuencias y distancias de distribución, considérese el sistema S1 construido por el numero primo P1=2, en este sistema la frecuencia F1 son los múltiplos de P1, es de decir, la multiplicación de 2 por todos los números naturales N>1, ya que si se multiplica por 1, el resultado sería que el mismo P1 sería una frecuencia, lo que implicaría que P1 no es primo ya que F≠P, lo que lleva a una contradicción, ya que P1 E P.

Ahora suponer la existencia de un sistema S0, supone la existencia de un numero primo anterior a 2, y el único número natural diferente de cero anterior a 2 es 1, así P0=1. Ahora para construir el S0 se determinan sus frecuencias que serán los múltiplos de P0=1, es decir el producto de P0=1 con todos los números naturales mayores a 1, pero se sabe que todo número multiplicado por 1 da él mismo, lo que significa que las frecuencias F0 son todos los números naturales mayores a 1, y como F0≠P, esto quiere decir que, según S0, no existirán más números primos a excepción de P0=1, lo cual no es cierto, por ello el S0 es inexistente, y P0 no existe, de ahí se concluye que 1 no es primo.

Teorema 2.6. Para Sn, x(Pn#) + 1 será un numero primo, y será el penúltimo número primo determinado por Cn.

Demostración. Como en la Demostración del Teorema 2.1., llámese:

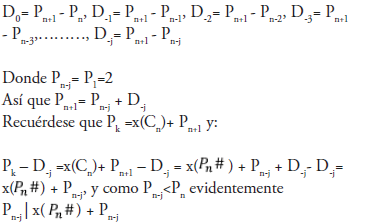
Así que Pk – D-j no es un numero primo, así que el único número anterior a Pn-j= P1=2 es 1, es decir que se debe retrocedes una unidad ya que 2-1=1, pero por el Teorema 2.5., 1 no es un numero primo, de manera que x(Pn#) + Pn-j -1= x(Pn# ) + 2 -1= x(Pn# ) + 1 no es un múltiplo de ningún numero primo, al menos hasta Pn, de manera que para Sn, x( ) + 1 será un numero primo, y será el penúltimo número primo determinado por Cn.

Teorema 2.7. La ultima distancia Dk Cn es igual a Pn+1 -1.

Demostración. Ahora como el último número primo en cualquier repetición de Cn tiene la forma x(Pn#)+ Pn+1 según el Teorema 2.4., y el penúltimo número primo determinado por Cn tiene la forma x(Pn#) + 1 según el Teorema 2.6., la diferencia del ultimo primo y el penúltimo primo en Cn es:

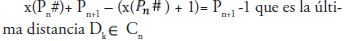
Teorema 2.8. Cada sistema Sn funcionará perfectamente en la determinación de números primos hasta llegar al cuadrado del primo Pn+1, siguiente al primo Pn hasta donde se construyó el sistema.

Demostración: El cuadrado del primo siguiente al primo hasta donde se construyó el sistema, es el primer número que no es múltiplo de los primos con los que se construyó el sistema, por ello no se puede considerar como frecuencia. Esto se explica Así:

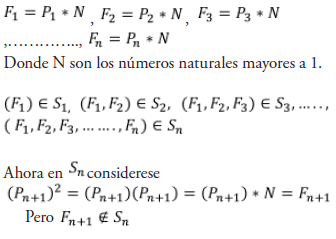
De manera que la aparición de (Pn+1)2=Fn+1 en Sn hace que Sn sea correcta en la determinación de números primos hasta llegar a (Pn+1)2 , de ahí en adelante el sistema determinará tanto números primos como números primos falsos que serán todo tipo de combinación de productos de números primos diferentes a los números primos de las frecuencias pertenecientes a Sn así por ejemplo, el S1 se construyó con el primo 2, y el siguiente número primo de 2 es 3, y el cuadrado de 3 es 9, así S1 ^funcionara bien hasta llegar a 9, ya que 9 no es primo, y a partir de ahí el S1 predecirá tanto números primos como números impares compuestos; ahora S2 se construyó con los primos 2 y 3, y el siguiente primo de 3 es 5, y el cuadrado de 5 es 25, es decir, que S2 funcionara perfectamente hasta llegar a 25, ya que 25 no es primo.

Demostración 2.5. Llámese defecto de secuencia al hecho de que en un sistema Sn se supere el valor de P2n+1 antes de terminar la primera secuencia, de manera que Pn+1+Cn=Pn+1+Pn#>P2n+1 .

Demostración 2.6. Llámese producto de fusión, a aquel producto que en la construcción de un sistema hace que se fusionen o unan dos distancias. Los productos de fusión en Sn son los productos de Pn con los primos determinados con las distancias de la secuencia Cn-1, es decir, con los números que son diferentes a los primos anteriores a Pn o a sus múltiplos, esto para que en Sn los múltiplos de Pn ya no sean considerados como primos Así por ejemplo en la TABLA 2.8, se observa que en S2 hay una distancia 4, resultado de la fusión de las dos distancias 2 y 2 de S1, presentes entre los números primos 7 y 11. Así mismo se llamara distancias de fusión a las distancias resultado de fusionar dos distancias del sistema anterior por un producto de fusión.

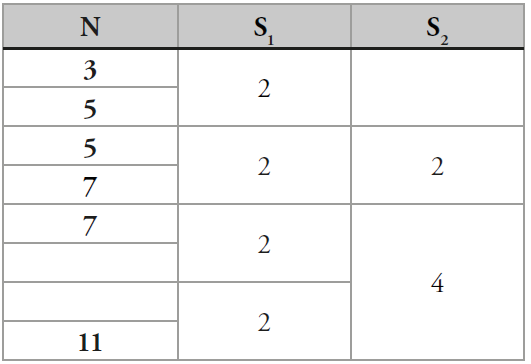
Así un producto de fusión en Sn elimina un falso número primo construido por Sn-1, y lo define como múltiplo de Pn..

Demostración 2.7. Llámese bloque de secuencia bk a la suma de las distancias de una secuencia de un sistema desde D1 o desde la distancia siguiente a la distancia en que termina el bloque anterior, hasta aquella distancia siguiente que es una fusión de dos distancias del sistema inmediatamente anterior, así por ejemplo, en el cuadro de las distancias de los sistemas de distribución, los dos bloques del sistema S3 en su secuencia son:

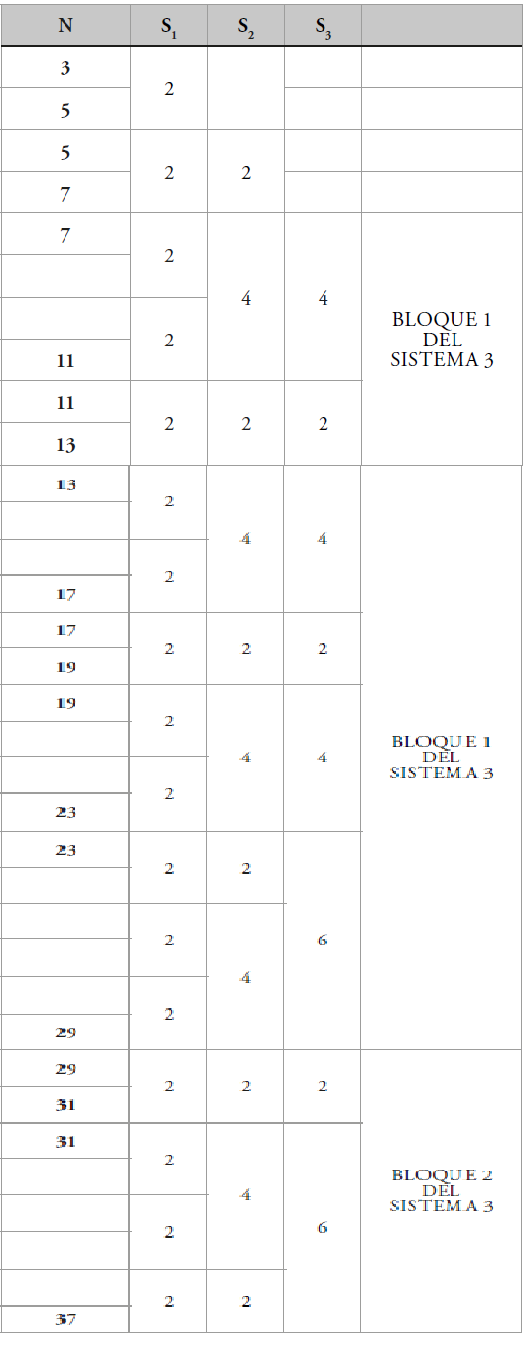
Demostración 2.8. Llámese productos de fusión de defecto de secuencia de Sn a los productos de fusión de todos los sistemas Sn+k, con k>=1 , esto es, todo tipo infinitos de combinación y repetición de productos de primos de la forma Pn+k, con k>=1, estos productos no son primos, pero para Sn si lo son, por eso están en el defecto de secuencia.

Teorema 2.9. Sea Rn la cantidad de productos de fusión que unen distancias en un sistema Sn, y sea Qn-1 la cantidad de distancias existentes en un Cn-1, de manera que Rn=Qn-1.

Demostración. La cantidad de productos de fusión Rn presentes en un Sn es igual a los productos de Pn con los primos determinados con las distancias de la secuencia Cn-1, esto para que en Sn los múltiplos de Pn ya no sean considerados como primos, sin incluir a Pn-1, ni a los primos anteriores, ya que los múltiplos de estos mismos ya se excluyeron de ser números primos en los sistemas anteriores. Sea Qn-1 la cantidad de distancias existentes en un Cn-1, que es igual a la cantidad de primos determinados con las distancias de la secuencia Cn-1, de manera que Rn=Qn-1.

Teorema 2.10. El primer producto de fusión en Cn es P2n y el segundo producto de fusión es PnPn+1

Demostración. Como se explicó en la Demostración del Teorema 2.9., los productos de fusión en Cn es igual a los productos de Pn con los primos determinados con las distancias de la secuencia Cn-1, esto para que en Sn los múltiplos de Pn ya no sean considerados como primos, sin incluir a Pn-1, ni a los primos anteriores, pero si a Pn y a los primos posteriores determinados con las distancias de la secuencia Cn-1, ya que los múltiplos de Pn-1, y de los primos anteriores ya se excluyeron de ser números primos en los sistemas anteriores, pero los múltiplo de Pn y de los primos posteriores aún no se han excluido. Los múltiplos de Pn son de la forma Pn*N, pero para que Pn*N sea un producto de fusión en Cn, N >= Pn, ya que si N < Pn, N tomara valores de primos anteriores a Pn o números anteriores a Pn compuestos por primos anteriores a Pn. así que Pn*N con N =Pn, es un producto de fusión en Cn.

Considérese los dos casos diferentes:

• El primer producto de fusión en Cn es Pn * Pn-k, Pn-k< Pn, así que Pn-k es anterior a Pn, lo que quiere decir que ya habrá creado antes de Sn un sistema Sn-k en el que se habrán excluido los múltiplos de Pn-k, y Pn *Pn-k sería un múltiplo de Pn-k, de manera que en Sn no hay necesidad de eliminar el numero primo falso Pn * Pn-k, porque ya ha sido eliminado por el sistema Sn-k , por ello el primer producto de fusión en Cn no es Pn * Pn-k.

• El primer producto de fusión en Cn es Pn * Pn+k, donde Pn+k fue determinado en Cn-1 ,Pn+k> Pn, así que Pn+k será posterior a Pn, así que Pn * Pn+k si es un producto de fusión en Cn pero no será el primero, ya que Pn * Pn también es un producto de fusión en Cn, y Pn * Pn < Pn * Pn+k, por eso el primer producto de fusión en Cn no es Pn * Pn+k.

Así queda demostrado que el primer producto de fusión en Cn es Pn * Pn=P2n

Bien, PnPn+k>PnPn+1 para k>1 , de manera que ninguno de los productos de fusión de la forma para k es el segundo producto de fusión.

Solo resta demostrar que P3n>PnPn+1, ahora Considérese el importante postulado de Bertrand: “para todo entero positivo n existe un primo P tal que n<P<= 2n” (Niven y Zukcerman 1969, 181).

Sea n=Pn, así se tiene que Pn < Pn+1 < 2P2n, supóngase que Pn+1 = 2Pn, de manera que PnPn+1=Pn2Pn=2P2n, y 2P2n<P3n, para Pn >2, pero con comprobación numérica se ve que el segundo producto de fusión es PnPn+1 para Pn >=2.

Teorema 2.11. El último producto de fusión en Cn es igual a Pn por el penúltimo número primo determinado por Cn-1, y es de la forma X(Pn#)+Pn

Demostración. Por la Demostración del Teorema 2.6., se sabe que el penúltimo número primo determinado por Cn-1 es de la forma x(Pn-1#)+1, y por la Demostración del Teorema 2.3., se sabe que x(Pn#)+ Pn es el producto de fusión que hace que la última distancia Dk Cn sea una fusión, ahora haciendo la división: (x(Pn#)+Pn)/Pn=x(Pn-1#)+1 que es el penúltimo numero primo determinado por Cn-1.

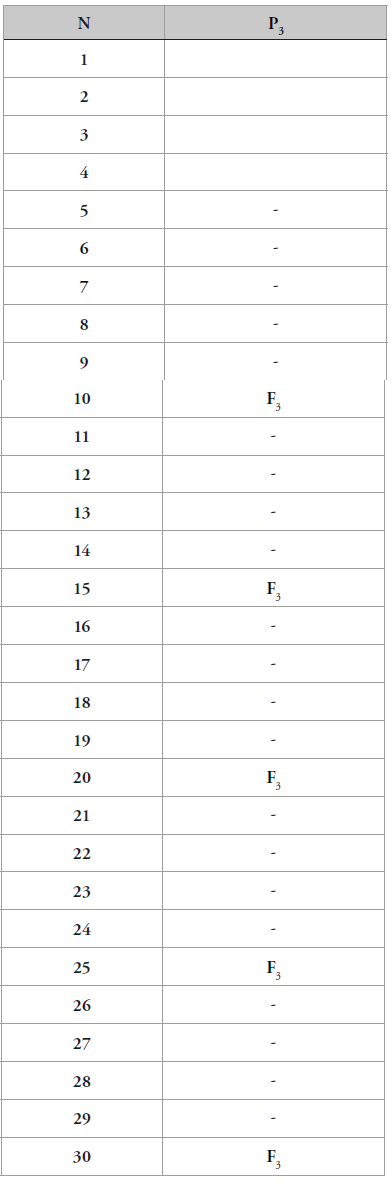
En esta tabla se observa que 7 es simétrico con 23, 11 es simétrico con 19 y 13 es simétrico con 17, también se ve que 29 no es simétrico con 1 porque 1 no es primo. Igualmente se observa que 1sim3 llega hasta Pn #=P3#=30

CONCLUSIÓN

La distribución de los números primos parece aleatoria por la aparición aparentemente caótica de sus distancias, pero en realidad su distribución es sistemática, como se observó en la construcción de los sistemas de distribución y sus secuencias, pero a medida que se va determinando un nuevo número primo, este afecta la distribución y se crea un nuevo sistema con una nueva secuencia que cambia la manera de predecir números primos, y así los sistemas se van volviendo más complejos, con secuencias más extensas y distancias más variadas, así que los números primos presentan, como se puede llamar, una distribución compleja.

Referencias

Apostol, TM (1980), Introducción a la teoría analítica de números,

Caro, VE (1937), Los números, Editorial Minerva S.A., Bogotá.

Grossman, S (1996), Algebra lineal. Quinta edición, McGraw-

Jiménez, LR, Gordillo, JE & Rubiano, GN (2004), Teoría de números [para principiantes], segunda edición, Universidad Nacional de Colombia, Bogotá.

Mora, W (2014), Introducción a la teoría de números. Ejemplos y algoritmos, primera edición, Revista digital matemática, educación e internet, Recuperado de: https://repositoriotec.tec.ac.cr/bitstream/handle/2238/6299/introducci%C3%B3n-teor%C3%ADa-n%C3%BAmeros.pdf?sequence=1&isAllowed=y

Niven, I, Zuckerman, HS (1969). Introducción a la teoría de números, Limusa-Wiley, México.

Ross, KA., Wright, CR (1990), Matemáticas discretas, segunda edición, Prentice-Hall Hispanoamericana S.A., México.

Vinogradov, I (1977), Fundamentos de la teoría de los números, segunda edición, Editorial MIR, Moscú.

Vorobiov, NN (1974). Números de Fibonacci, Editorial MIR, Moscú.