



Essentially non-oscillatory schemes applied to Buckley-Leverett equation with diffusive term
Latin-American Journal of Computing
Escuela Politécnica Nacional, Ecuador
ISSN: 1390-9266
ISSN-e: 1390-9134
Periodicity: Semestral
vol. 11, no. 1, 2024
Received: 15 February 2023
Accepted: 12 May 2023

Abstract: The purpose of this work was to investigate the flow of two-phase fluids via the Buckley-Leverett equation, corresponding to three types of scenarios applied in oil extraction, including a diffusive term. For this, a weighted essentially non-oscillatory scheme, a Runge-Kutta method and a central finite difference were computationally implemented. In addition, a numerical study related to the precision order and stability was performed. The use of these methods made it possible to obtain numerical solutions without oscillations and without excessive numerical dissipation, sufficient to assist in the understanding of the mixing profiles of saturated water and petroleum fluids, inside pipelines filled with porous material, in addition to allowing the investigation of the impact of adding the diffusive term in the original equation.
Keywords: Numerical methods, Immiscible two-phase fluid, Petroleum flow.
Resumen: El propósito de este trabajo fue investigar el flujo de fluidos bifásicos a través de la ecuación de Buckley-Leverett, correspondiente a tres tipos de escenarios aplicados en la extracción de petróleo, incluyendo un término difusivo. Para ello, se implementaron computacionalmente: un esquema esencialmente no oscilatorio ponderado, un método de Runge-Kutta y un esquema de diferencias finitas centrado. Además, se realizó un estudio numérico relacionado con el orden de precisión y estabilidad. El uso de estos métodos permitió obtener soluciones numéricas sin oscilaciones y sin disipación numérica excesiva, suficientes para auxiliar en la comprensión de los perfiles de mezcla de agua saturada y fluidos derivados del petróleo, en el interior de tuberías llenas de material poroso, además de permitir la investigación del impacto de sumar el término difusivo en la ecuación original.
Palabras clave: Métodos numéricos, Fluido bifásico inmiscible, Flujo de petróleo.
I. INTRODUCTION
The technological advances achieved after the Industrial Revolution, followed by the development of equipment dependent on energy sources from petroleum, made the oil industry reach a crucial role in the world economy. As it is an exhaustible natural source and a potential pollutant, if disposed of in an erroneous way, the efficiency in the extraction process and the detailed understanding of the phenomena involved become indispensable for the challenges of delivering a product inserted within a clean economy.
A central problem in this sector is the displacement of petroleum through pipes filled with a porous medium, characterized by the injection of another fluid (saturated water) to help maintain the flow inside the tube. In this sense, a mathematical model used to describe the flow of two-phase incompressible fluids is the classical Buckley-Leverett equation [1]. In this work, the authors obtained solutions considered unrealistic due to the appearance of discontinuities, indicating the need for studies on the propagation of singularities.
Since then, different researchers started to investigate numerical solutions to the original Buckley-Leverett flow equation. The characteristic of non-linearity of the partial differential equation enables the use of numerical methods and computational techniques, in an attempt to find approximate solutions without spurious oscillations or excessive numerical dissipation.
Fayers and Sheldon [2] used a finite difference scheme for the partial differential equation for flow two-phase incompressible fluids. In [3], numerical methods dependent on Riemann solvers were applied to follow the discontinuities evolution (shock waves). However, this procedure requires the calculation of propagation velocities at each point of the established grid.
Currently, experiments in laboratory of two-phase flow in porous medium reveal complex profiles that include fluid infiltrations modelled by diffusive and dispersive terms, which suggest modifications to the classical Buckley-Leverett equation [4].
Central schemes of finite volume were used by [5] and a fully space-time mixed hybrid finite element/volume discretization was developed by [6], both to solve the modified Buckley-Leverett equation.
In preliminary studies, Garcia and Silveira [7] investigated a fifth-order weighted essentially non-oscillatory scheme applied in the classical Buckley-Leverett equation. Continuing the research, in this work the authors began to evaluate the addition of a diffusive term.
In this way, the objective of this paper was to apply a weighted essentially non-oscillatory scheme, coupled to a three-stage Runge-Kutta method and a central finite difference scheme in the discretization of the Buckley-Leverett equation with diffusive term and obtain numerical solutions capable of representing the temporal evolution starting from three initial scenarios, represented by discontinuous functions such as Heavise step, barrier and well rectangular. In addition to carrying out a study on the impact of the diffusive term on the numerical solution of the classical Buckley-Leverett equation. The modeling of the phenomenon under study will be explained in Section 2, the numerical methods used are in Section 3 and, finally, in Section 4, the results achieved regarding the evolution of the mixture between saturated water and oil are shown. The computational implementation was carried out in Octave, with our own codes.
II. MATHEMATICAL MODELING
Currently, a problem of global interest is the extraction of petroleum underground through a tube filled with a porous medium. After drilling the soil to the underground oil reservoir, a certain amount is drained due to the high pressure that the oil is found, but as the extraction progresses, there is a decrease in pressure with consequent interruption of the flow, still leaving a lot of petroleum in the subsoil. A standard method subsequent to the initial extraction is to pump water into rest oil reservoir to force the continuation of extraction. In this case, the fluid is two-phase, oil and water, and the flow is restarted in the porous medium consisting of rock or sand.
The mathematical modeling consists of representing the oil one-dimensional flow through the tube filled with porous material, by water pumping [8]. Such a model was initially proposed by Buckley and Leverett, 1942 [1], in studies on the flow of two-phase incompressible fluids in porous media.
Let 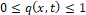 be the fraction of saturated water and
be the fraction of saturated water and 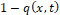 the fraction of oil contained in a pipe filled with a porous material. Such fluids are essentially incompressible, which ensures that the total flow between the pipe ends is equal to any smaller portion of the pipe.
the fraction of oil contained in a pipe filled with a porous material. Such fluids are essentially incompressible, which ensures that the total flow between the pipe ends is equal to any smaller portion of the pipe.
In this way, in regions of the tube where (pure oil) or q=1 (pure water), the velocities are constant and distinct, but when , the difference between the surface tensions of fluids causes them to move and mix. Buckley and Leverett proposed a model in which the rate of change of over time ( ) is described by the following conservation law:
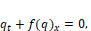 (1)
(1) in which is the water flux, represents the porosity of the medium and is  the oil flux,with
the oil flux,with 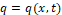 . Equation (1) models a flow from left to right, in which the tube thickness does not influence the dynamics in question.
. Equation (1) models a flow from left to right, in which the tube thickness does not influence the dynamics in question.
The reestablishment of the oil flow, from left to right, can be done by filling part of the pipe on the left with saturated water, allowing the resumption of oil extraction. An initial condition for modeling that procedure is the following conservation law:
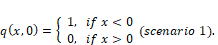 (2)
(2)Another situation that can occur is, after an injection of water, the flow is restarted and a second oil portion enters the pipeline, soon after the interruption in the supply of saturated water. This is the desired circumstance, when only an amount of water injected is enough for the continuity of the extraction. The condition to represent that scenario is the conservation law:
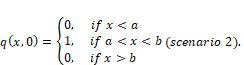 (3)
(3)The third situation considered arises when following the injection of water, a small amount of oil is extracted and then there is a new interruption of flow, making it necessary to inject more saturated water after a small amount of oil is extracted. So,
 (4)
(4)The three situations represented mathematically by the initial conditions, in (2)-(4), have the flow described by (1).
Considering the spatial domain  , the boundary condition on the left was of the Dirichlet type and on the right of the radiation type, that is, when the dynamics reach the boundary, the flow simply goes through the boundary, is not being affected by the edge.
, the boundary condition on the left was of the Dirichlet type and on the right of the radiation type, that is, when the dynamics reach the boundary, the flow simply goes through the boundary, is not being affected by the edge.
Adding the effects of infiltration in porous media, van Duijin, Peletier, and Pop [9] proposed the following modification to (1):
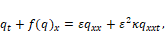 (5)
(5) in which ɛ is a diffusibility coefficient and κ is a dispersive coefficient. As one of the objectives of this work is to observe the effect of diffusion in the Buckley-Leverett equation (1), it was considered that  , so the dispersive term was neglected.
, so the dispersive term was neglected.
The choice of numerical methods to solve (1) and (5) is essential, as a numerical scheme that has a high degree of numerical dissipation can stand out and mask the real effect of the diffusive term of (5), impairing the interpretation of the results.
III.Numerical Methods
Choosing a numerical method requires care that depends on the differential equation and the initial conditions imposed by the model under study. The discontinuities of the functions defined by (2), (3) and (4) can evolve to excessive dispersion (oscillation) and/or numerical dissipation, harming the quality of the numerical solution. Thus, for this work, a weighted essentially non-oscillatory scheme (WENO-5 method) was adopted for spatial discretization and the third-order Runge-Kutta TVD method (Total Variation Diminishing) was assumed for temporal discretization.
A. Non-oscillatory schemes and WENO-5
The essentially non-oscillatory (ENO) schemes proposed by [10] and [11] proved to be efficient in terms of decreasing numerical dissipation, in addition to avoiding oscillations in the discontinuity regions of the solutions. One important properties of these methods is to determine the smoothest stencil among the options, in order to preserve high order of accurate.
In general, to approximate the flow a rth-order ENO scheme selects the smoothest stencil among r possibilities [12]. On the other hand, the weighted essentially non-oscillatory (WENO) schemes make a convex combination of all stencils, for the numerical flow approximation. A weight is designated to each stencil, describing its contribution portion to the process.
The weights are defined by optimal weights in smooth regions, while maintaining the high order of accuracy. In non-smooth regions, weights close to zero are assigned for stencils that contain discontinuities [13].
The WENO method technique is based on the flow definition of the ENO schemes, considering a one-dimensional conservation law  . The spatial operator that approximates
. The spatial operator that approximates 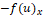 in
in 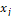 is
is
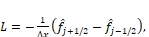 (6)
(6) in which is the spatial discretization size and 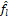 is the numerical flux [13].
is the numerical flux [13].
The r stencils are denoted by 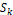 ,
, 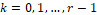 , of the form conservation law:
, of the form conservation law:
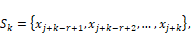
in which defines the amount of points of ,
that will be applied to calculate the value of  . Therefore, a 3rd-order ENO scheme
(
. Therefore, a 3rd-order ENO scheme
(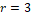 ) is
going to have: ,
) is
going to have: , 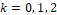 , described by
, described by  , which results in
, which results in 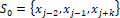 for k=0,
for k=0, 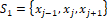 , for k=1, and
, for k=1, and 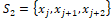 for k=2.
for k=2.
ENO
schemes approximate 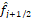 through a polynomial interpolation at the
points of each stencil [13] and [14]. This approximation
is given by
through a polynomial interpolation at the
points of each stencil [13] and [14]. This approximation
is given by
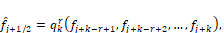 (7)
(7)in which
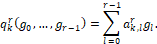
Let 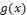 be
a smooth function. The average approximation of
be
a smooth function. The average approximation of 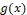 in cell
in cell 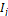 is defined by:
is defined by:
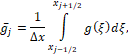
where 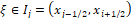 .
.
To obtain the constants 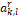 in (7), consider the primitive function of
in (7), consider the primitive function of 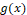 defined by
defined by 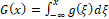 .
The value of
.
The value of 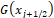 is:
is:
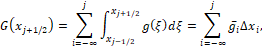
It means that, once the average approximations of the cells 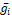 are known, then
are known, then  at the boundary of cell
at the boundary of cell 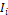 are also known. Thus, the constants
are also known. Thus, the constants 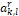 are determined by interpolating
are determined by interpolating  by a
by a  degree polynomial
degree polynomial  , at most. Therefore, approximation is given by:
, at most. Therefore, approximation is given by:
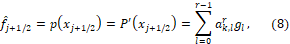 (8)
(8) in which  are obtained from the Lagrange interpolating polynomial [14], with the data in Table I.
are obtained from the Lagrange interpolating polynomial [14], with the data in Table I.
| 3 | 0 | 1/3 | -7/6 | 11/6 |
| 1 | -1/6 | 5/6 | 1/3 | |
| 2 | 1/3 | 5/6 | -1/6 |
A rth-order ENO scheme leads to a (2r-1)th-order WENO scheme, so a 3rd-order ENO results to a 5th-order WENO. As mentioned, in the WENO method, for each possible stencil , 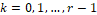 , a weight
, a weight  is assigned and these are used to calculate the numerical flux:
is assigned and these are used to calculate the numerical flux:
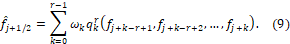 (9)
(9) The weight 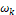 for the stencil
for the stencil 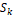 is defined by given
is defined by given
and 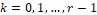
Taking p=r, the coefficients 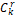 are optimal values to determine
are optimal values to determine 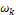 [14]. The term
[14]. The term  is an indicator of smoothness and for
is an indicator of smoothness and for 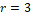 we have:
we have:
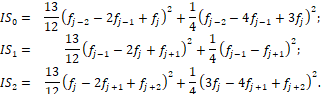
This
measure was introduced by [13], with the aim of achieving high accurate for the
case where 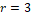 .
Note that as
.
Note that as 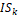 increases, the smoothness decreases and,
consequently,
increases, the smoothness decreases and,
consequently, 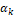 becomes close to zero as does
becomes close to zero as does  ,
meaning that a weight close to zero will be assigned to
non-smooth solutions.
,
meaning that a weight close to zero will be assigned to
non-smooth solutions.
B. Third-order Runge-Kutta TVD
Once the spatial discretization is concluded, a method for temporal discretization that maintains the non-oscillatory characteristics achieved is necessary.
Numerical methods belonging to the TVD class (Total Variation Diminishing) have the property of avoiding oscillations that are not typical of the phenomenon under study [8]. A good alternative is the high-order Runge-Kutta TVD methods, which were developed by [12] in research related to efficient implementations for ENO's schemes.
A Total Variation Diminishing (TVD) technique has the following definition: if, for any data set 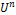 , the values
, the values 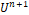 computed satisfy
computed satisfy 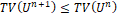 , where
, where
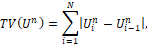
is the total variation. In this work, a third-order Runge-Kutta TVD (RK3-TVD) method was chosen, whose expressions are given by
 (10)
(10) in which 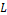 is the spatial operator of differential equation.
is the spatial operator of differential equation.
The WENO and RK3-TVD methods numerically solve the classical Buckley-Leverett equation. To discretize the diffusive term of the modified Buckley-Leverett equation, we use a central finite difference scheme.
C. Fourth-order central finite difference scheme
Once there are at least two ways to numerically add the term in the conservation law: one is to discretize the diffusive term in the flux context [15], given by:
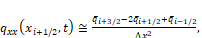 (11)
(11)and the other in the finite difference context [5], which
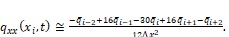 (12)
(12)In this work, both discretizations were performed, as for the interpretation of the results there were no significant differences between them, we selected (12) to keep in our codes, is that, the fourth-order central finite difference scheme (CFDS-4). We use a central finite difference scheme.
D. Numerical study of the methods
The numerical study of the WENO-5 method makes it possible to verify its convergence order (which is the number of significant algharisms that are correct when the solution is obtained), that is, it allows the computational verification of the consistency of the method. For numerical simulations, consider the function, 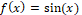 , for
, for 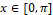 and the values for the spacing
and the values for the spacing 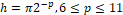 .
.
Asymptotically, the error made by the approximation has a behavior of the form , where 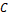 is a positive constant independent of
is a positive constant independent of 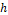 and
and 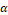 is the order of convergence. Thus, in the dilog graph,
is the order of convergence. Thus, in the dilog graph, 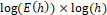 , the error has an approximately linear behavior and the slope of the line provides the order
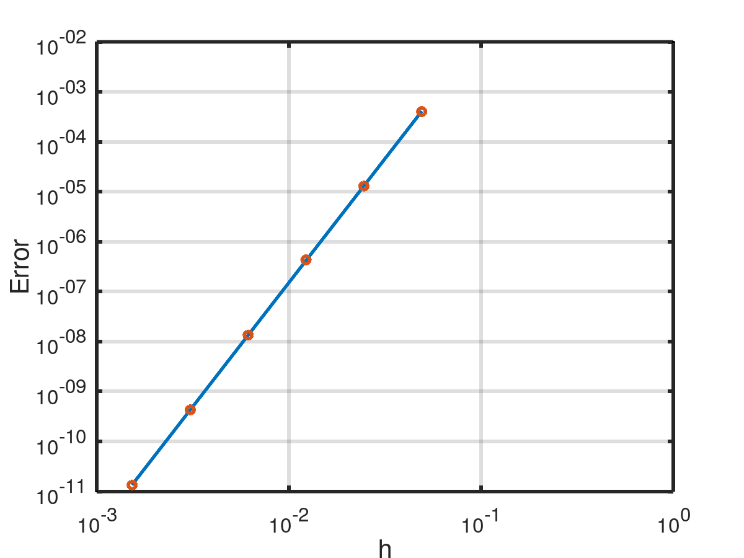
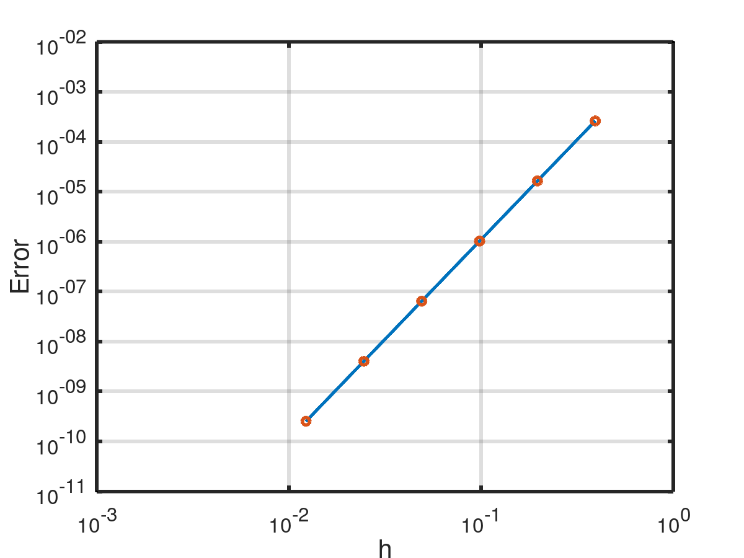
, the error has an approximately linear behavior and the slope of the line provides the order 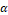 of the method. Fig. 1 shows the scatter plot for the fit of the model, for calculating the order of convergence of the WENO-5 method, whose value obtained was
of the method. Fig. 1 shows the scatter plot for the fit of the model, for calculating the order of convergence of the WENO-5 method, whose value obtained was 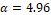 , that is, a 5th-order.
, that is, a 5th-order.
The numerical study of the RK3-TVD method was carried out with the aim of verifying the order of convergence, that is, computing the consistency of the method. For numerical simulations, we consider the initial value problem 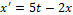 , with
, with 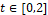 , and with the spacings
, and with the spacings 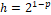 ,
,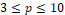 . The analytical solution is
. The analytical solution is 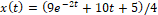 .
.
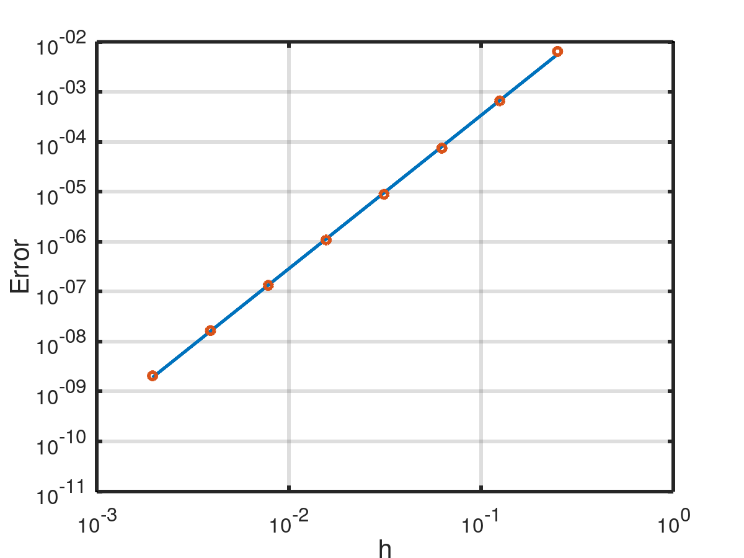
The error for the approximation is obtained following the same procedures for the numerical study of the WENO-5. Thus, Fig. 2 shows the scatter plot for the fit of the model, for calculating the order of convergence of the RK3-TVD method, whose order obtained was α=3.07 (3rd-order).
The numerical study of the CFDS-4 allows to obtain consistency of the method, Fig. 3. For numerical simulations, consider the function 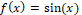 , for
, for  and the values for the spacing
and the values for the spacing 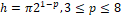 .
.
Estimating the second derivative  of
of  via CFDS-4, determining the maximum absolute error for each
via CFDS-4, determining the maximum absolute error for each 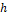 , and finding the slope on the dilog graph, we get
, and finding the slope on the dilog graph, we get 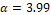 (4th-order).
(4th-order).
E. Analysis of stability
To find a relationship between the spacings and , which keep stable a numerical method obtained by spatial and temporal discretizations via WENO-5 and RK3-TVD, respectively, the linear stability analysis is applied.
The importance of this relationship is to guarantee the convergence of the approximate solution using Lax Equivalence Theorem [16], which states: for any consistent method to generate a sequence of convergent approximate solutions, it is necessary and sufficient that the method be stable, that is, a consistent method is convergent if and only if it is stable.
In this case, the semi-discretization of the solution is represented by the discrete Fourier series in space [16], so by the superposition principle, it is possible to work with only one term of the series and in this way, the numerical solution can be represented by:
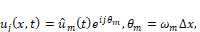 (13)
(13)with 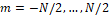
We consider that the operator L , defined by a conservation law, is written in the form 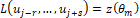 . Temporal semi-discretization is performed using the RK3-TVD method. As it is an explicit scheme, the solution in
. Temporal semi-discretization is performed using the RK3-TVD method. As it is an explicit scheme, the solution in 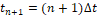 is represented by
is represented by  ,
, 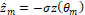 ,
,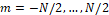 ,
, 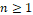 , where
, where 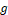 is the amplification factor that depends on
is the amplification factor that depends on 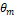 and
and  .
.
Thus, a spatial discretization coupled with a time discretization will be stable, if the amplification factor satisfies the following discrete von Neumann criterion, 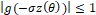 ,
,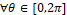 . Such a stability condition establishes an upper bound on
. Such a stability condition establishes an upper bound on  , which keeps the method linearly stable. Therefore, if the domain of the spatial variable was discretized by a regular spacing , the stability condition allows finding a value for the temporal spacing
, which keeps the method linearly stable. Therefore, if the domain of the spatial variable was discretized by a regular spacing , the stability condition allows finding a value for the temporal spacing 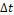 , which keeps the method stable.
, which keeps the method stable.
WENO-5 linearization and stability analysis
Let be a spatial operator of a conservation law described by 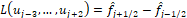 . We linearize [17], considering a solution represented by the Fourier series and we substitute it in the conservaation law, we have the amplification factor given by:
. We linearize [17], considering a solution represented by the Fourier series and we substitute it in the conservaation law, we have the amplification factor given by:
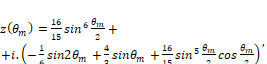
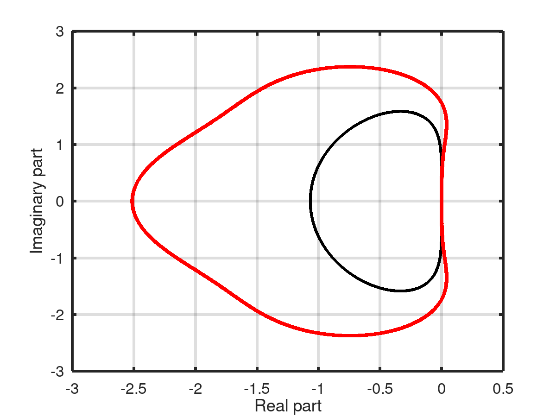
in which 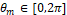 . Equation (14) is represented in the complex plane Fig. 4, varying
. Equation (14) is represented in the complex plane Fig. 4, varying 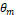 from 0 to
from 0 to 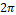 , black line.
, black line.
RK3-TVD stability
For stability analysis of the RK3-TVD method, the polynomial that characterizes the method is considered,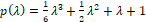 , as the
, as the 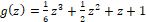 amplification factor , the boundary of the stability region is
amplification factor , the boundary of the stability region is 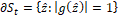 , where
, where 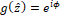 , with
, with 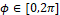 . Hence, for each value of
. Hence, for each value of  , a third degree polynomial equation is defined. Solving the equations for each
, a third degree polynomial equation is defined. Solving the equations for each  in the Octave and selecting the roots with the highest magnitude for each
in the Octave and selecting the roots with the highest magnitude for each  , we obtain the region of stability represented by the red color in Fig. 4.
, we obtain the region of stability represented by the red color in Fig. 4.
So, the computational implementation of the WENO-5 numerical method with RK3-TVD consists of applying the temporal discretization of the classical Buckley-Leverett equation by (10), with the spatial operator defined by (6) and (7).
CFDS-4 stability
With
regard to the stability analysis for this method, the value found in the
literature for second-order central finite difference schemes applied in the
heat equation was used as a reference, that is, 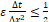 [8].
[8].
IV. Simulations
In this section, the simulations for the classical Buckley-Leverett equation (Section IV.A), the modified Buckley-Leverett equation (Section IV.B) and an analysis of diffusive term (Section IV.C) are shown.
A. Classical Buckley-Leverett equation
The simulations were performed for three scenarios, according to the initial conditions defined in Section 2. For all scenarios, we have 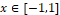 with 128 subintervals,
with 128 subintervals, 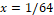 , and
, and 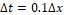 , satisfying the stability condition for all methods, according to Fig. 4. Furthermore,
, satisfying the stability condition for all methods, according to Fig. 4. Furthermore, 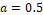 was assigned to the constant that characterizes the porous medium, in (1).
was assigned to the constant that characterizes the porous medium, in (1).
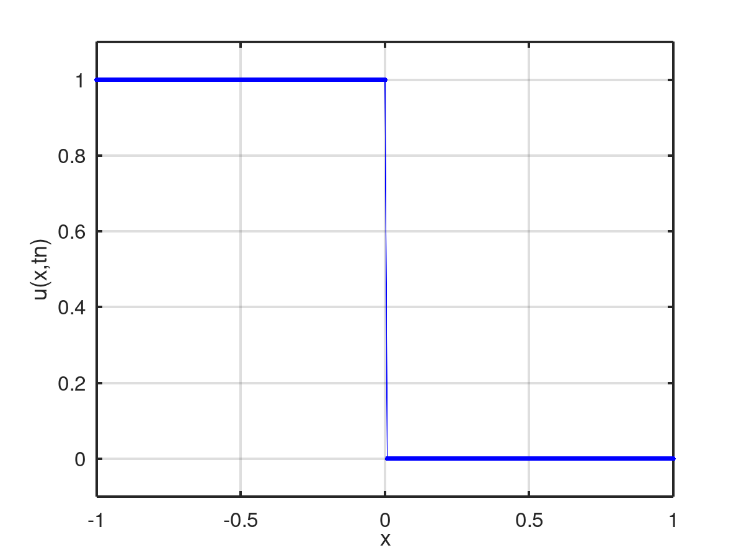
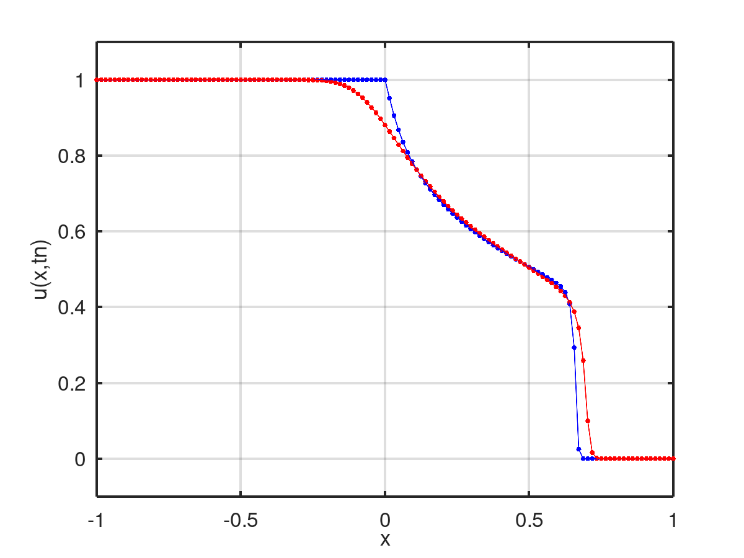
The first scenario is represented by the initial condition whose shape is a step, Fig. 5. The numerical solution obtained after 256 iterations is in Fig. 6. The comparison of the graphs reveals the emergence of a region where the fluids mix, between the values of (pure water) and (pure petroleum), while the fluid dynamics develops to on the right.
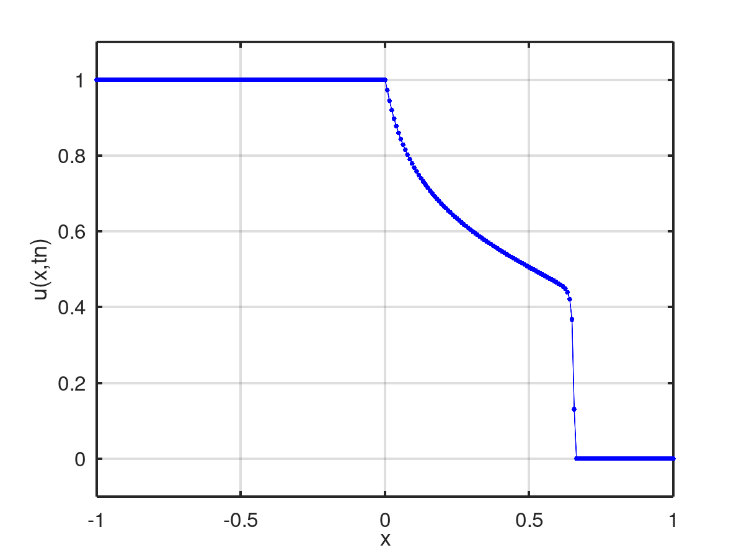
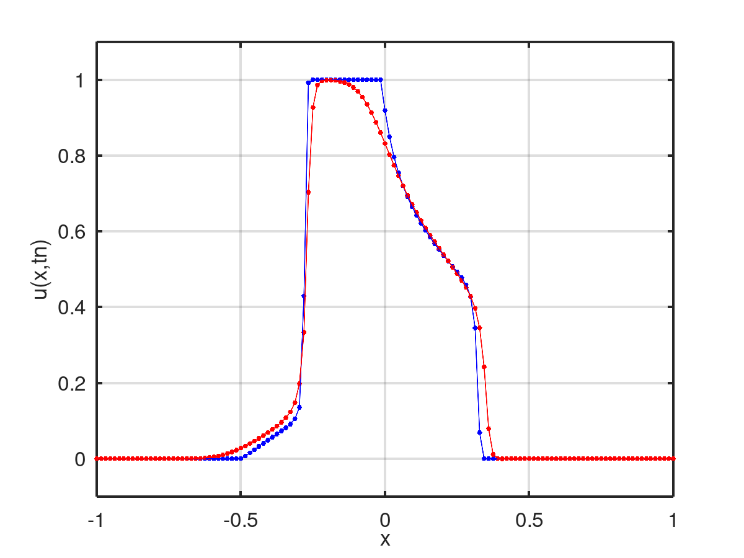
The second scenario has the barrier function as an initial condition, Fig. 7. In the numerical solution obtained after 128 iterations, Fig. 8, it is possible to verify two different profiles of mixture between saturated water and petroleum, a linear profile and a non-linear profile similar to the first scenario.
Linear mixing is faster than second mixing and Fig. 9 displays the moment when the linear mixture reaches the non-linear profile. In Fig. 10, the interference of the linear mixture can be noted, that is, there is a decrease in the peak of the graph, with no region containing only water.
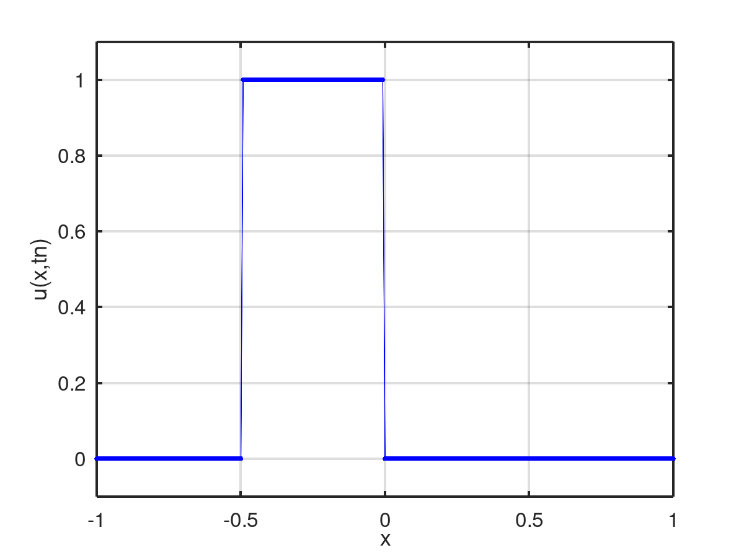
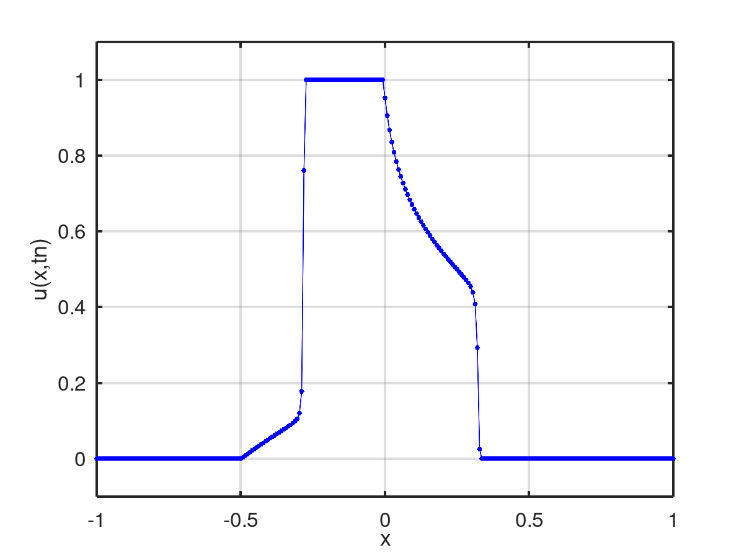
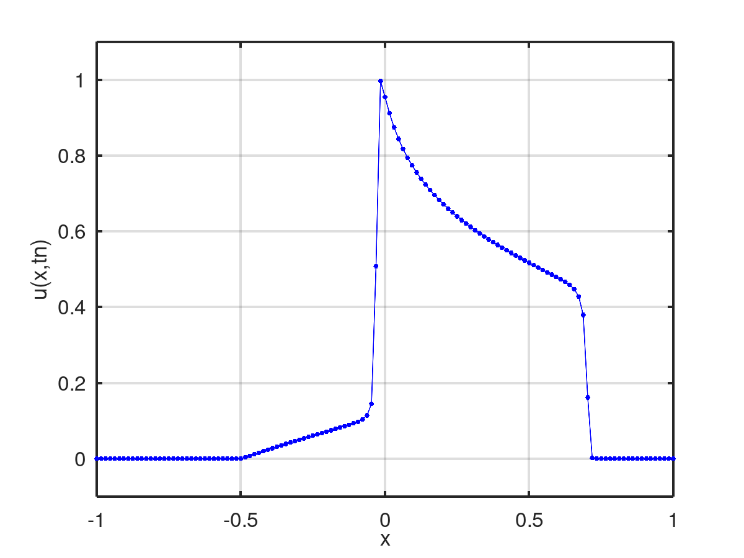
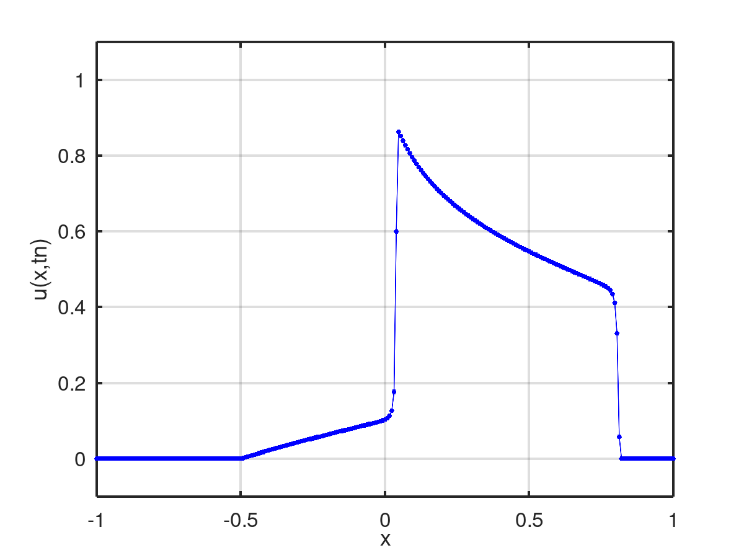
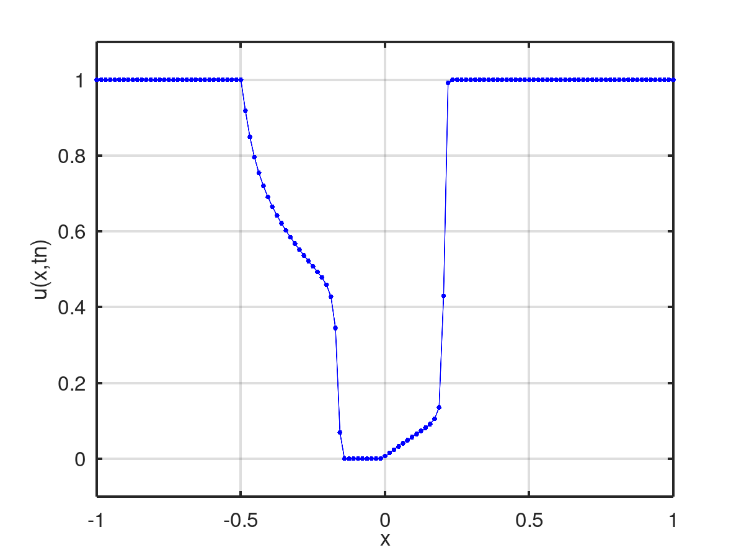
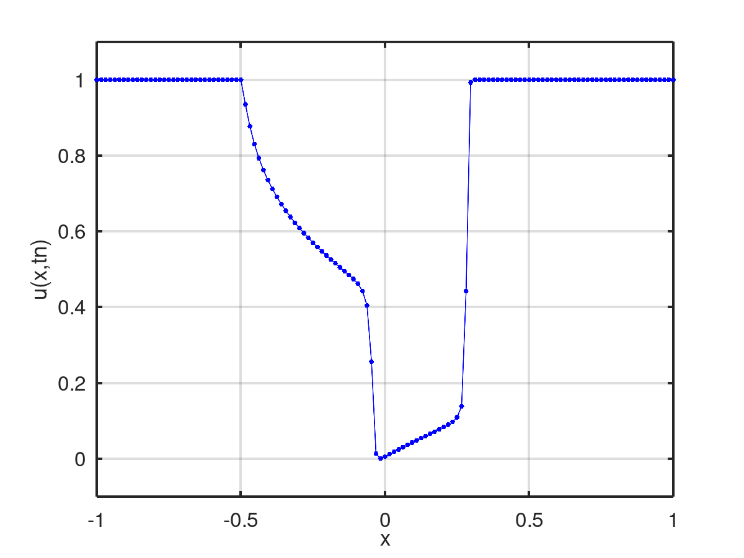
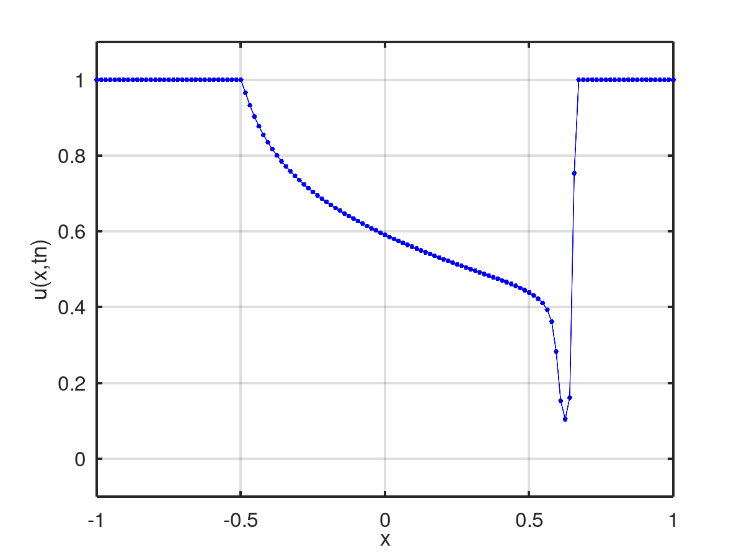
The third scenario presents an initial condition in the well format, Fig. 11. In the numerical solution found after 128 iterations, two mixing profiles similar to the second scenario is obtained, Fig. 12. However, linear mixing is slower than non-linear mixing, which in turn is reached by the other profile after 175 iterations, Fig. 13. After 398 iterations, there is the moment when the nonlinear profile is close to the fluid region with only water, Fig. 14.
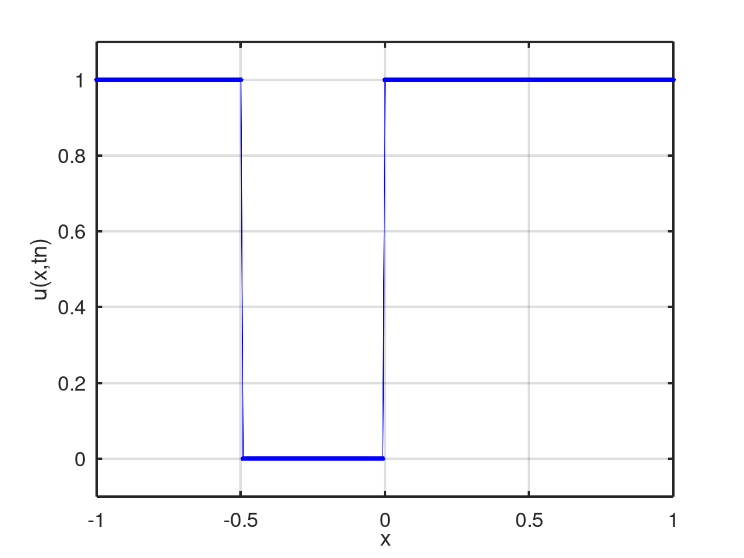
After observing the solution profiles of the classical Buckley-Leverett equation for each scenario, the next step is to consider the addition of the diffusive term and perform comparisons between the solutions.
B. Modified Buckley-Leverett equation
In order
to investigate the diffusive term, we considered (5) with 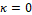 ,
that is, to (1):
,
that is, to (1):
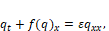 (15)
(15)in which  . In
the rest, the same scenarios of the Section (IV.A) were adopted, with the same
profile of space and time discretizations. For all simulations in this section,
blue color represents numerical solution obtanied by classical Buckley-Leverett
equation and red color represents solutions of the modified Buckley-Leverett
equation.
. In
the rest, the same scenarios of the Section (IV.A) were adopted, with the same
profile of space and time discretizations. For all simulations in this section,
blue color represents numerical solution obtanied by classical Buckley-Leverett
equation and red color represents solutions of the modified Buckley-Leverett
equation.
The first scenario with diffusive term (Fig. 15) reveals that there is more water scattered in the oil than in the scenario without diffusion. This is noticeable by the fact that the transitions between pure water, mixture and pure petroleum profiles became smoother.
In terms of execution time, when adding CFDS-4 in the code, the CPU time went from 73.93s to 77.34s, that is, an increase of 4.6%.
The second and third scenarios have similar behavior to the first scenario. The transitions are smoothed by the diffusion, increasing the mixing region between water and oil. See Figs. 16 and 17 for second scenario, and Figs. 18, 19 and 20 for third scenario, where the blue graph represents the numerical solution of the classical Buckley-Leverett equation and the red graph is the solution obtained from the same equation, adding diffusive term.
In Fig. 16, there is an intense smoothing close to and such smoothing is maintained as time evolves, Fig. 17. This effect is characteristic of the added diffusion in the classical Buckley-Leverett equation.
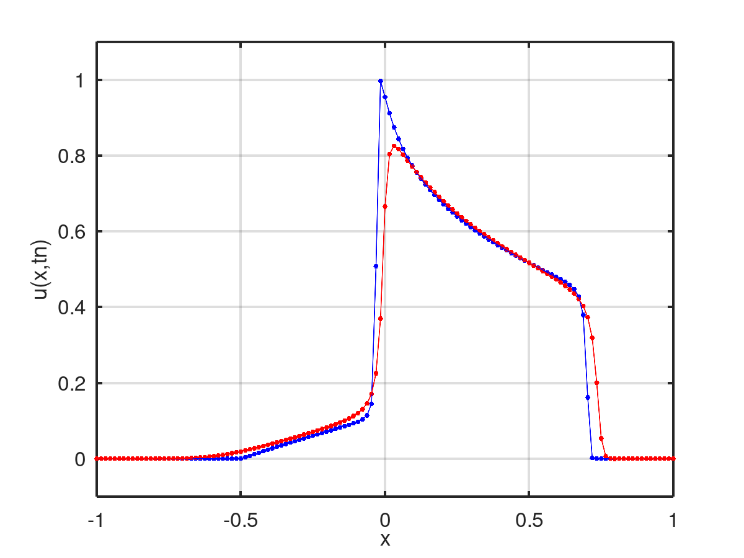
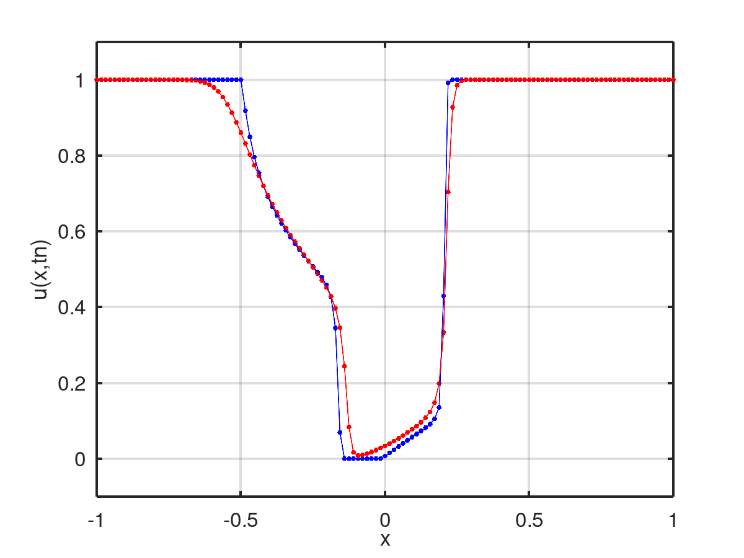
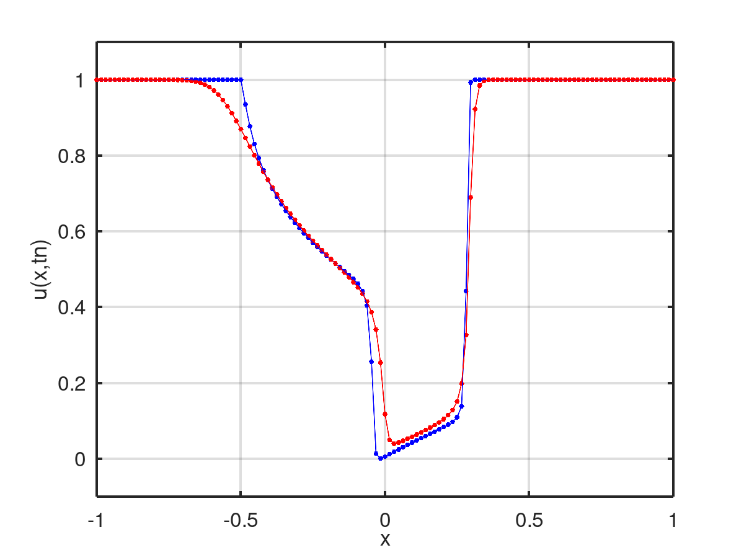

In the graphs of Figs. 18 and 19, one can see the evolution of two more intense smoothings, one close to 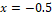 and the other close to
and the other close to 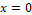 . In Fig. 20, the smoothings are close to x= -0.5 and x=0.6 .
. In Fig. 20, the smoothings are close to x= -0.5 and x=0.6 .
Thus, we were able to follow the temporal evolution of the mixture between water and oil in two situations, one where there is only influence of the non-linear advective term (1), and another where there is also a diffusive term (5).
C. Diffusion effect
The focus of the simulations in this section is to verify the impact of the diffusivity coefficient on the solutions of the Buckley-Leverett equation. For this, in the three scenarios presented in Sections (IV.A) and (IV.B), five different values for were used, keeping the final time fixed in each scenario.
For all scenarios, the following colors and values were defined: 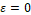 (blue color);
(blue color); 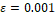 (green color);
(green color);  (red color);
(red color); 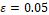 (black color) and
(black color) and 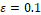 (magenta color).
(magenta color).
For the first three values of  , the relationship between the spacings was
, the relationship between the spacings was 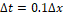 and for the last two values, it was necessary to define
and for the last two values, it was necessary to define 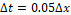 to keep the numerical methods stable.
to keep the numerical methods stable.
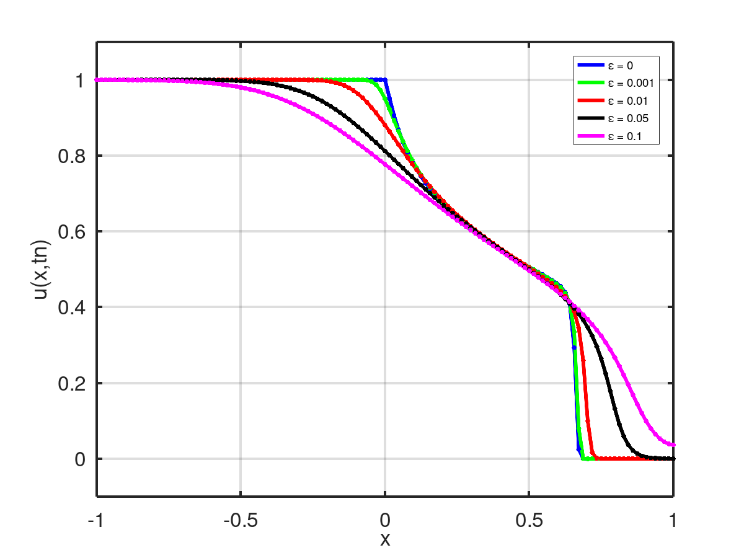
With the final time of 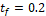 for scenario 1, Fig. 21 shows the numerical solution for the five values of
for scenario 1, Fig. 21 shows the numerical solution for the five values of  . It is noticed that the closer the
. It is noticed that the closer the  value is to zero, the more the solution profile resembles the classic Buckley-Leverett solution, and as the
value is to zero, the more the solution profile resembles the classic Buckley-Leverett solution, and as the  value increases, the more the solution is influenced by diffusion, spreading each time plus the mixture of water and oil in the pipeline, represented by the interval
value increases, the more the solution is influenced by diffusion, spreading each time plus the mixture of water and oil in the pipeline, represented by the interval 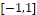 .
.
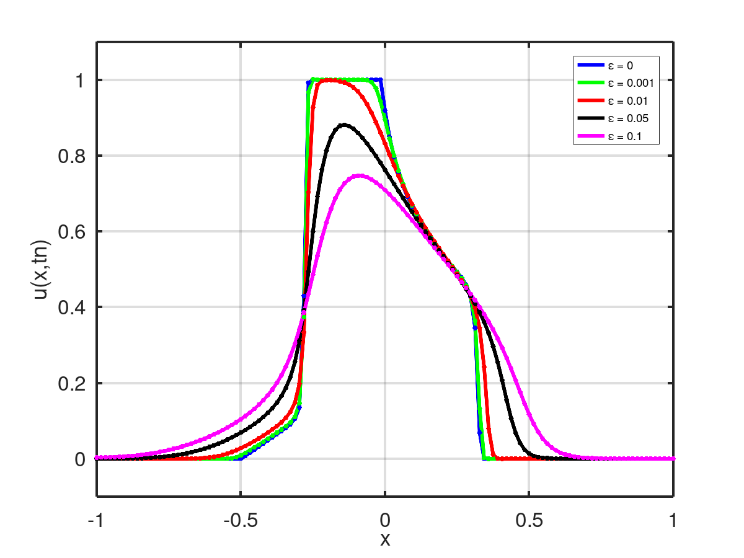
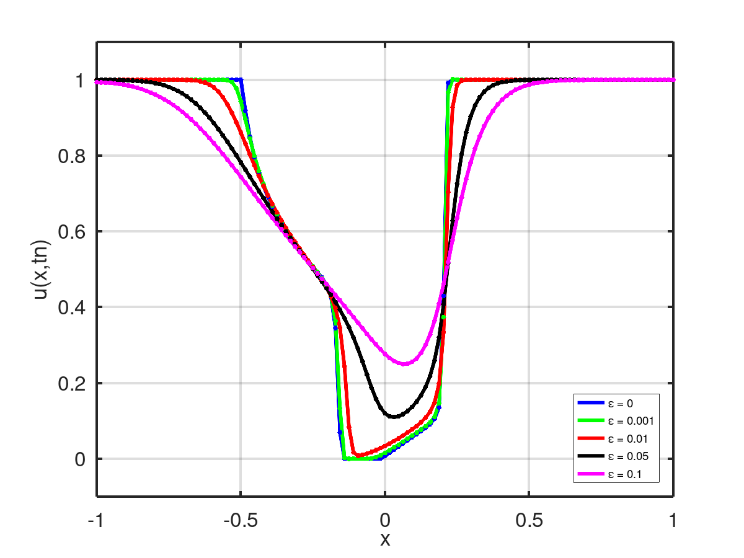
On the scenario 2, Fig. 22, and scenario 3, Fig. 23, follow the same behavior of the increase in the mixture spreading, as we increase  the value, observed in scenario 1 (Fig. 21). In both scenarios, the final time was
the value, observed in scenario 1 (Fig. 21). In both scenarios, the final time was 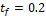 .
.
With essentially non-oscillatory methods, which have low numerical dissipation, it was possible to vary the diffusibility coefficient and analyze its impact on the solution of the Buckley-Leverett equation, Figs. 21, 22 and 23.
V. CONCLUSION
In this study, the WENO-5 and RK3-TVD methods were approached, together with a numerical study on the order of convergence of each method, as well as a stability analysis. The methods were applied to the classical Buckley-Leverett equation in order to investigate the temporal evolution of three real scenarios, which may occur during petroleum extraction by injection of saturated water.
The simulations showed mixtures with linear and non-linear profiles due to discontinuities in the initial conditions of each scenario. It is important to note that during the transitions between the profiles there were no oscillations of the numerical solutions or excessive dissipation, indicating that the combination of the WENO-5 and RK3-TVD methods, within the stability condition, provides solutions sufficiently close to the analytical solution.
By adding the diffusive term in the Buckley-Leverett equation, we use the finite difference scheme to discretize it and evaluate the impact of diffusion on the solutions of the three flow scenarios studied. With the methods applied, we were able to vary the parameter and observe that the lower its value, the numerical solution approaches the classical Buckley-Leverett solution, and the higher the value of  , the more the mixture between water and oil is spread through the pipeline, smoothing the transitions between regions containing water, mixture and petroleum.
, the more the mixture between water and oil is spread through the pipeline, smoothing the transitions between regions containing water, mixture and petroleum.
References
[1] S. E. Buckley, and M. C. Leverett, “Mechanism of fluid displacement in sands,” Trans. AIME, vol. 146, pp. 187–196, 1942.
[2] F. L. Fayers, and J. W. Sheldon, “The effect of capillary pressure and gravity on two-phase fluid flow in porous medium,” Trans. AIME, vol. 216, pp. 147-155, 1959.
[3] W. Proskurowski, “A note on solving the Buckley-Leverett equation in the presence of gravity,” J. Comput. Phys., vol. 41, pp. 136-141, 1981.
[4] D. A. DiCarlo, “Experimental measurements of saturation overshoot on infiltration,” Water Resour. Res., vol. 40, pp. 4215-1-4215.9, 2004.
[5] Y. Wang, and C-Y. Kao, “Central schemes for the modified Buckley–Leverett equation,” J. Comput. Sci., vol. 4, pp. 12-23, 2013.
[6] E. Abreu, and J. Vieira, “Computational numerical solutions of the pseudo-parabolic Buckley-Leverett equation with dynamic capillary pressure,” Math. Comput. Simulation, vol. 137, issue C, pp. 29-48, 2017.
[7] R. O. Garcia, and G. P. Silveira, “Essentially non-oscillatory schemes applied to Buckley-Leverett equation,” in XXV ENMC - Encontro Nacional de Modelagem Computacional, XIII ECTM - Encontro de Ciência e Tecnologia de Materiais, 9º MCSul - Conferência Sul em Modelagem Computacional, and IX SEMENGO - Seminário e Workshop em Engenharia Oceânica, 2022 [Online]. Available: https://www.even3.com.br/anais/enmcmcsulsemengo2022/534872-essentially-non-oscillatory-schemes-applied-to-buckley-leverett-equation/ [Acessed: Feb. 2, 2023].
[8] R. J. Leveque, Finite Volume Methods for Hyperbolic Problems. New York: Cambridge University Press, 2002.
[9] C. J. van Duijin, L. A. Peletier, and I. S. Pop, “A new class of entropy solutions of the Buckley-Leverett equation,” , SIAM J. Math. Anal., vol. 39, no. 2, pp. 507-536, 2007.
[10] A. Harten, and S. Osher, “Uniformly high-order accurate non-oscillatory schemes I,” SIAM J. Numer. Anal., vol. 24, pp. 279-309, 1987.
[11] A. Harten, S. Osher, B. Engquist, and S. Chakravarthy, “Uniformly high-order accurate non-oscillatory schemes III,” J. Comput. Phys., vol. 71, pp. 231-303, 1987.
[12] C-W. Shu, and S. Osher, “Efficient implementation of essentially non-oscillatory shock capturing schemes,” J. Comput. Phys., vol. 77, pp: 439-471, 1988.
[13] G-S. Jiang, and C-W Shu, “Efficient Implementation of Weighted ENO Schemes,” J. Comput. Phys., vol. 126, pp: 202-228, 1996.
[14] G. A. Gerolymos, D. Sénéchal, and I. Vallet, “Very-high-order WENO schemes,” J. Comput. Phys., vol. 228, pp. 8481-8524, 2009.
[15] G. P. Silveira, and L. C. Barros, “Numerical methods integrated with fuzzy logic and stochastic method for solving PDEs: An application to dengue,” Fuzzy Sets Syst., vol. 225, pp. 39-57, 2013.
[16] J. W. Thomas, Numerical Partial Differential Equations: Finite Difference Methods. New York: Springer, 1995.
[17] M. Motamed, C. B. Macdonald, and S. J. Ruuth, “On the linear stability of the fifth-order WENO discretization,” J. Sci. Comput., vol. 47, pp. 127-149, 2011.

