



Deflection Analysis of Beams from Vehicle Velocity
Latin-American Journal of Computing
Escuela Politécnica Nacional, Ecuador
ISSN: 1390-9266
ISSN-e: 1390-9134
Periodicity: Semestral
vol. 10, no. 2, 2023
Received: 13 March 2023
Accepted: 17 May 2023
Abstract: In this work, the modeling and calculations referring to the deflection of special artworks are presented. The type train is modeled as two degrees of freedom and mobile base, with the bridge deck being considered the mobile base. The base is treated as an elastic beam, according to the Euler-Bernoulli theory. The fundamental assumption made is that the relative displacements between the vehicle and the bridges are synchronous. This allows the calculation of natural frequencies, eigenvalues and normal modes of vibration of the beam. The temporal response of the beam deflection is obtained, assuming that the vehicle employs, at each instant of time, an impulse load on the beam. Numerical simulations are performed to improve the understanding of the dynamic behavior of the structure.
Keywords: Vehicle-bridge interaction (VBI), Bridge dynamics, Bridge deflection.
I. Introduction
Due to their great importance, large structures known as Special artworks, such as bridges and viaducts, must have their performance monitored periodically. This is because large structures have a small margin for safety estimates. When it comes to bridges and viaducts, factors such as structural access make it impossible to diagnose the conditions of use, therefore, when a bridge requires interdiction for maintenance or recovery, the impacts on society are considerable, from the creation of large traffic jams, deviations of long journeys or even structural collapse.
Stimuli caused by heavy vehicles cause vibrations that can significantly affect structural integrity. One way to understand the behavior of structures subject to vibrations is to describe a correct modeling based on the boundary conditions defined in the project. In this context, studies aimed at obtaining a structural response have gained strength in recent years. Research involving numerical models for vehicle-bridge interaction analysis can be seen in Zou et al. [1]; Yang and Lin [2] and Zhu and Law [3]. Eigenvalues and eigenfunctions problems for bridges idealized as Euler-Bernoulli beams were studied in Hayashikawa and Watanabe [4]. In Matsuoka and Tanaka´s [5] work, a new method for estimating bridge deflection based on track irregularities, measured by a moving train, was studied. efficient according to the authors. In Corbally and Malekjafariam [6], a new approach is proposed that introduces the concept of operational deflection shape ratios from the measured responses in two axes of a bridge segment. Other results related to the dynamic analysis of structures can be detailed in Kwon et al. [7]; Yang et al. [8]; Meyer et al. [9].
In this approach, the main physical variable to be measured is displacement. For this measurement, the displacement field is seen as a response to excitation suffered by the structure. In the case of special artworks, the main excitations are the dynamic loads generated by the flow of vehicles, in this context the objective of the work is to present a model of dynamic analysis of structures, idealized as beams traveled by a train-type with constant speed.
II. Methodology
Special artworks are modeled as beams. The equations of motion that describe the behavior of the structure as well as its initial and boundary conditions can be derived from Hamilton's generalized variational principle. To obtain the energy functional, the Euler-Bernoulli theory is employed. According to this theory the main hypothesis is that the effects of rotation of the cross section, constant, is disregarded when compared with the translational displacement. Furthermore, the shear strain is disregarded when compared with the bending strain. It should also be noted that the present methodology is applied when the thickness of the beam is small, around ten times, when compared to its length. It is also considered that the deformations due to bending are small when compared to the length of the structure. So, in this context, evaluating that the vertical displacement of the beam is , the displacement field is:
The deformation components, referring to the displacements defined in (1) are:
The strain energy for , denoted by U, can be expressed as:
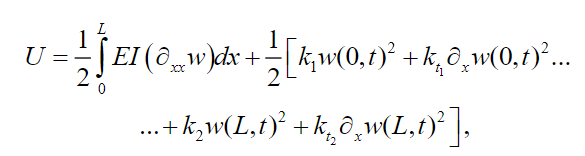 (4)
(4)where the second term on the right side of (4) represents the deformation, translational and rotational energy of the spring I and denotes the moment of inertia of the cross section of the beam about axis y,
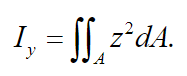 (5)
(5) The kinetics energy is given by:
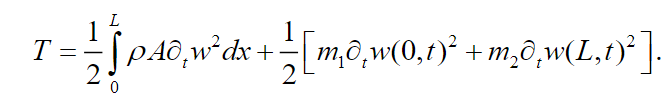 (6)
(6) In (6) the first term on the right side represents the kinetic energy of the beam, and the second term indicates the kinetic energy of masses coupled to the beam contours. The work done by the transverse distributed loading is given by:
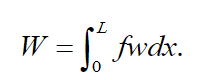 (7)
(7) By Hamilton's generalized variational principle, we obtain the differential equation of transverse motion of the beam
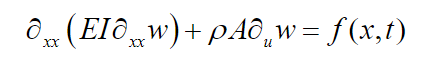 (8)
(8)with the following board conditions:
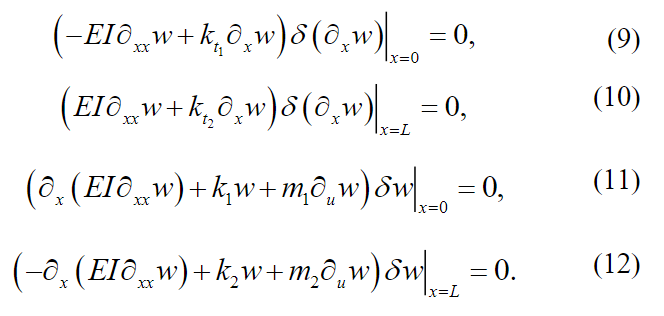 9) (10) (11) (12)
9) (10) (11) (12)The equations in (9) imply the following board conditions. In
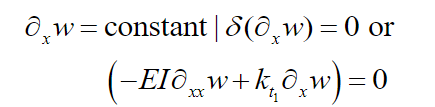 (13)
(13)and
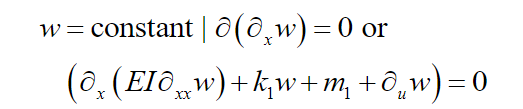 (14)
(14) In ,
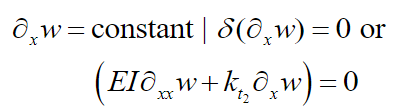 (15)
(15)e
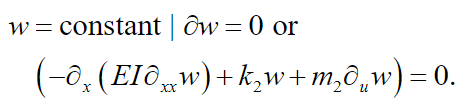 (16)
(16) For free vibrations, it is assumed that the external excitation is zero:
therefore, the equation of motion, (8), reduces to:
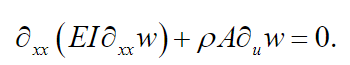 (18)
(18)For beams made of uniform, constant material and constant cross-sectional area, (2) can be expressed as:
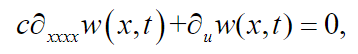 (19)
(19) where
The methodology for solving the free frequencies is based on solving the eigenvalues and eigenfunctions of the problem (19) that can be found using the method of separation of variables as:
replacing (21) in (19) we have:
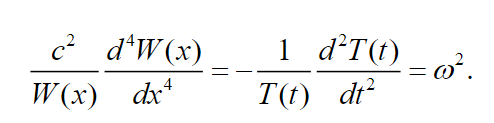 (22)
(22) Equation (22) can be decomposed into the set of two equations:
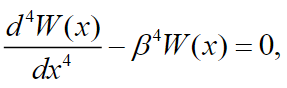 (23)
(23)
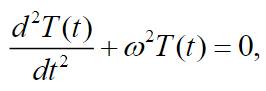 (24)
(24) where
 (25)
(25) The solution of (25) is given by:
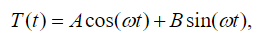 (26)
(26) where A and B are constants found from the initial conditions of the problem. The solution of (23) is provided by means of an exponential form:
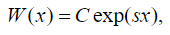 (27)
(27)where and are constants. Replacing (27) into (23) we get the auxiliary equation:
whose square are given by:
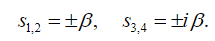 (29)
(29)So, the solution of (23) can be expressed as:
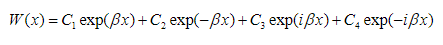 (30)
(30) where are constants. It follows from (25) that the natural frequencies of the beam can be determined as:
The function W(x) is known as the normal mode of vibration of the structure, characteristic function or even eigenfunction associated with the problem (23). For any type of beam, there will be an infinite number of eigenfunctions of (23) with an associated frequency, or eigenvalue. The constants in (30) and the value of in (31) can be determined from the boundary conditions of the problem. In particular, if we denote by the -ésimo eigenvalue corresponding to the eigenfunction the total response to free vibration of the beam can be obtained by the principle of superposition of normal modes as:
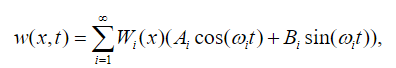 (32)
(32) where the constants and , calculated from the initial conditions of the beam.
III. Modeling of Structures
The deflections presented in bridges subject to mobile loads can be correctly expressed taking into account the pre-established boundary conditions, used to determine the normal modes of vibration. Following the ideas presented by Kwon et al. [7]; the vertical displacements of bridges crossed by heavy vehicles are modeled as a mass-spring model on a mobile elastic base. It is understood by base the beam that is considered of the Euler-Bernoulli type and therefore the modeling of the foundation must consider the elastic behavior of the structure. Figure 1 presents the analysis scheme where e e e they are the spring constant, mass and damping for the vehicle body and wheel, respectively.

A. Equations of Motion
In this section, the modeling of the bridge will be done along with the standard train. For this, the structure will be represented by a beam, simulating a mobile base. On the other hand, the standard train will be described as the coupling of two bodies, as shown in Figure 1, whose masses will be denoted respectively by m1 e m2. Together with the masses we will also consider the elastic constants representing the elastic and dissipative forces of the system, for more details see Rao [10]. Following Kwon et al. [7], the following hypotheses will be assumed:
The structure is idealized as an Euler-Bernoulli beam;
Only the vertical displacements generated by the vehicle are considered;
The vehicle moves at a constant speed.
According on image 1 represent, respectively, the displacement of the body and structure of the vehicle, while denoting the displacement of the bridge. The modeling is done considering the bridge as a mobile base but with elastic behavior. Using the free-body diagram for the mass and , see Figures 1 and 2.


According to the equations of motion, the following is valid:
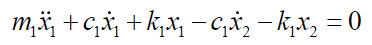 (33)
(33)
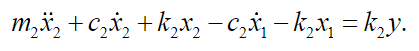 (34)
(34)Because it is an elastic body and taking into account the Euler-Bernoulli theory, it satisfies the following equation:
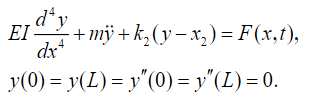 (35)
(35)where F(x,t) denotes the charge concentration due to vehicle displacement being given by:
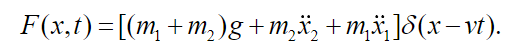 (36)
(36) As it is usual in vibration analysis, we will consider the solutions as being harmonic functions, that is, the three displacements, , , and they present movement synchrony:
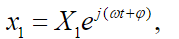 (37)
(37)
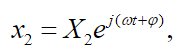 (38)
(38)Calculating 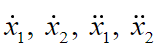 and substituting in equations (33) and (34) we get:
and substituting in equations (33) and (34) we get:
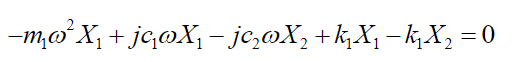 (39)
(39)
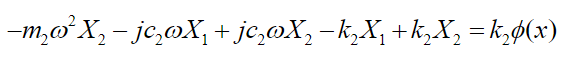 (40)
(40) The set of equations (39)-(40) can be written in matrix form:
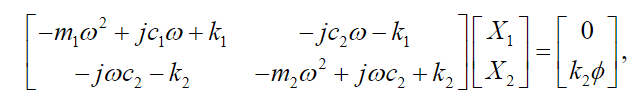
whose solution, by Cramer's rule, is given by:
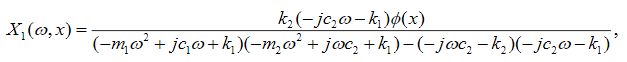 (41)
(41)
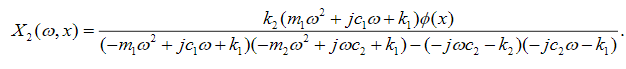 (42)
(42)In what follows, we will make use of the following notation:
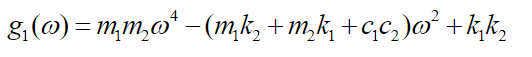 (43)
(43)
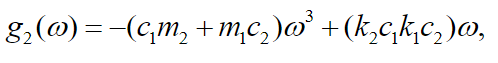 (44)
(44)
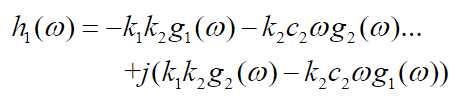 (45)
(45)
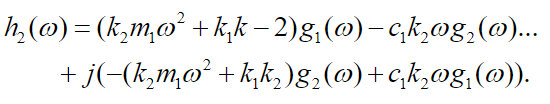 (46)
(46)Using equations (43), (44), (45) and (46) and simplifying equations (41) and (42) we get:
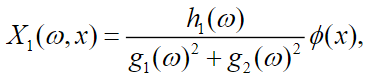 (47)
(47)
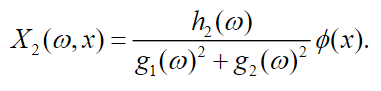 (48)
(48)In equations (47) and (48), it can be seen that the oscillation amplitude of the vehicle depends both on the frequency and the position of the particle.
For the calculation of the displacement of the base, the following equation must be satisfied for:
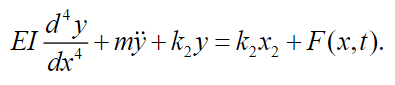 (49)
(49)Note that if we consider the operator
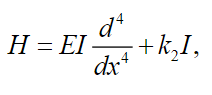 (50)
(50)acting on space , see in Meirovitch [11], with board conditions given in (35), then equation (50) can be written as:
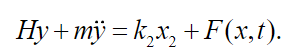 (51)
(51)According to Meirovitch [11], the first step to solve equation (51) is to calculate the natural frequency of the system of equation (51), which naturally leads to the system of eigenvalues for the operator H,
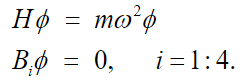 (52)
(52)The eigenvalues problem in equation (52) leads to the frequency equation given by:
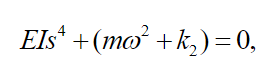 (53)
(53)Doing it 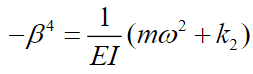 we get:
we get:
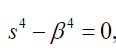 (54)
(54) which implies that the solutions to the problem must be of the form:
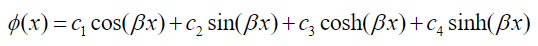 (55)
(55)It follows from the boundary conditions of the problem and imposing the condition of existence of non-trivial solutions, that the following condition is satisfied:
where the matrix is defined by:
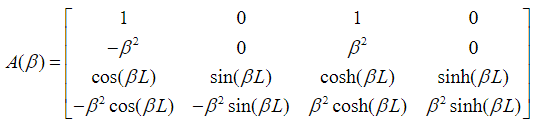
To get values from note that:
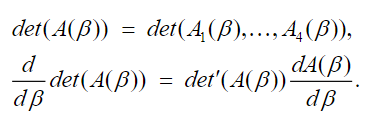 (57)
(57)The expression on the right in the second equation in (57) is defined by:
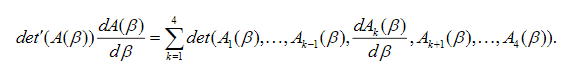 (58)
(58)Using the expression in (58) together with Newton's method, approximate solutions in (56) can be computed by generating the sequence of eigenvalues .
The system of equations (33) and (34) together with the boundary condition (35) is solved taking into account the eigenvalues problem in (52). Using the fact that the solution is decomposed into normal vibration modes we have:
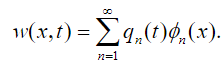 (59)
(59)From (51) we get that the following equation is valid:
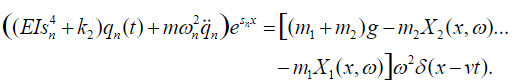 (60
(60Multiplying both sides of (60) by and integrating from 0 to L we get:
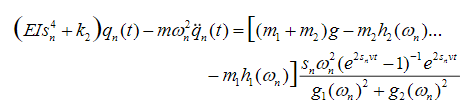 (61)
(61)Equation (61) is the bridge oscillation amplitude response. Note that (61) shows the explicit dependence of the system output on the oscillation frequency and vehicle speed.
The image 2 presents the solutions of (61) for values of , and image 4 is the sum of all displacements

IV. Numerical Results and Conclusions
The analyzed project is a reinforced concrete viaduct with 34.50m in length and 13.20m in width, executed on a state highway in the municipality of Goiás. The superstructure is designed in a straight line, consisting of three spans: a central one measuring 14.00m and two adjacent to the central span measuring 7.00m. The spans are constituted by an independent structure simply supported. The structure is formed by the set of 9 beams in the central span as shown in image 3. The work was designed for class 45, using a type 45tf vehicle as prescribed by NBR 7188/82 (brazilian rule), moving at a constant speed of approximately 80km/h. For this class of structures images 2 and 4, respectively represent the displacements of several normal modes of vibration and the displacement involving the sum of ten modes of vibrations. It can be seen from image 4 a damping factor of the structure, even though the equation is a free frequency model. The justification for this fact is that one must take into account the fact that concrete is a composite material, and steel is the main damping factor.

| Module of Elasticity | Density of Material | Section Area | Moment of Inertia |
| 35000 (Mpa) | 300 (kgf/cm²) | 4,81 (m²) | 49,33x10-4 (m4) |


References
[1] Q. Zou, L. Deng, T. Guo, and X. Yin, “Comparative Study of Different Numerical Models for Vehicle–Bridge Interaction Analysis”. World Scientific Publishing Company, vol. 16, no. 28, 2016.
[2] Y. B. Yang, B. H. Lin, “Vehicle–bridge interaction analysis by dynamic condensation method”. Journal Struct. Eng., ASCE, vol.121, pp. 1636-1643, 1995.
[3] X. Q. Zhu, S. S. Law, “Structural Health Monitoring Based on Vehicle-Bridge Interaction: Accomplishments and Challenges”. Advances in Structural Engineering, vol. 18, pp.1999-2015, 2015.
[4] T. Hayashikawa, N. Watanabe, “Dynamic behavior of continuous beams with moving loads”.Journal of Engineering Mechanics Division, ASCE, vol. 107, pp. 229-246, 1981.
[5] K. Matsuoka, H. Tanaka, “Drive-by deflection estimation method for simple support bridgesbased on track irregularities measured on a traveling train”. Mechanical Systems and Signal Processing, vol. 182, pp. 109-149, 2023.
[6] R. Corbally, A. Malekjafarian, “Bridge damage detection using operating deflection shape ratiosobtained from a passing vehicle”. Journal of Sound and Vibration, vol. 27, pp.117-125, 2022.
[7] H. C. Kwon, M. C. Kim, I. W. Lee, “Vibration Control of Bridges Under Moving Loads”. Computer e Structures, vol. 66, pp. 473-480, 1998.
[8] Y. B. Yang, C. W. Lin, J. D. Yau, “Extracting bridge frequencies from the dynamic response of a passing vehicle”. Journal of Sound and Vibration, vol. 272, pp. 471-493, 2004.
[9] M. V. Meyer, D. Cantero, R. Lenner, “Dynamics of long multi-trailer heavy vehicles crossingshort to medium span length bridges”. Engineering Structures, vol. 247, pp. 113-149, 2021.
[10] S. S. Rao, Mechanical vibrations”, 5º ed., Pearson, Miami. 2010.
[11] L. Meirovitch, Computational methods in structural dynamics, Springer Science & BusinessMedia 1980.

