



A Fractional SIRC Model For The Spread Of Diseases In Two Interacting Populations
Latin-American Journal of Computing
Escuela Politécnica Nacional, Ecuador
ISSN: 1390-9266
ISSN-e: 1390-9134
Periodicity: Semestral
vol. 10, no. 2, 2023
Received: 20 January 2023
Accepted: 12 May 2023
Abstract: In this contribution we address the following question: what is the behavior of a disease spreading between two distinct populations that interact, under the premise that both populations have only partial immunity to circulating stains of the disease? Our approach consists of proposing and analyzing a multi-fractional Susceptible (S), Infected (I), Recovered (R) and Cross-immune (C) compartmental model, assuming that the dynamics between the compartments of the same population is governed by a fractional derivative, while the interaction between distinct populations is characterized by the proportion of interaction between susceptible and infected individuals of both populations. We prove the well-posedness of the proposed dynamics, which is complemented with simulated scenarios showing the effects of fractional order derivatives (memory) on the dynamics
I. INTRODUCTION
The astonishing spread of infection diseases in recent years (e.g., influenza and the COVID-19 pandemic) is among the main concerns of human civilization because they represent one of the main causes of population mortality, e.g., [13]. The track of the recent pandemics shows that one important mechanism for their global spread is the interaction between distinct populations. Furthermore, many infection diseases are capable of gene recombination with those of currently circulating strains, giving rise to new viral sub-types capable of escaping (partially) the immune system defenses of previously infected or vaccinated hosts, conferring only a partial immunity (cross-immunity) of the population, See, [1,10] and references therein.
Many mathematical models have been proposed to describe the dynamics of diseases and their mutations in the population (see [4] for a review). A typical approach uses multiple SIR, connected via some cross-immunity parameters, to model the interactions between individuals that are (or have been) infected by different viral strains, e.g., [2]. The analysis of these models has shown that multiple strains of certain diseases can persist in the human population and that their prevalence can exhibit self-sustained oscillations through time. In [12] the author suggested a model with immunity loss to incorporate re-infection by distinct strains. In [9] the proposed model incorporates a ‘temporary partial immunity’ for the R compartment to handle the virus mutation. In [3], a new compartment (C), for cross-immune individuals (individuals that are not fully susceptible (S) or recovered (R)) is introduced. Individuals in this new compartment have their immune responses boosted by exposition to mutated strains. This model is called SIRC. In [7,8], a fractional and multi-fractional dynamics for the SIRC model (called (F)-SIRC and (MF)-SIRC models, respectively) are proposed and analyzed. The authors show that the (MF)-SIRC model is capable of describing with better agreement data from the H1N1 influenza diseases. Moreover, the fractional dynamics allows for accounting for memory in the immune system (immunological memory).
In the approaches above cited, the interaction between populations is not considered. The main contributions of this manuscript are the proposal and the analysis of a multi-fractional SIRC model with two populations that interact ((MP)-FSIRC model). This method allows determining the effects of immunological memory in one sub-population (for example, acquired through vaccination) on disease propagation into a second sub-population, as well as the effects on disease dissemination and cross-immunity.
Outline: In Section II, we present the (MP)-FSIRC model with two populations that interact. We show the well-posedness of the proposed dynamic in Section III. In Section IV, we analyze numerically some simulated scenarios for the proposed model. In Section V, we formulate some conclusions and future directions.
II. MATHEMATICAL MODELING
We assume two distinct sub-populations exist, with the total number of individuals in each sub-population Nj(t) = Sj(t) + Ij(t) + Rj(t) + Cj(t) distributed in the compartments of Susceptible Sj, Infected or Infectious ( Jj), Recovered or Removed (Rj) and Cross-immune (Cj), for j=1,2. Furthermore, there is an interaction between the individuals of the distinct populations. Such interactions allow susceptible individuals from sub-population i to become infected through contact with infected individuals from sub-population j for i,j=1,2 and i j . The probability of the aforementioned fact happening is proportional to the contact between the distinct sub-populations and is given by , for i,j=1,2 and i j. We also consider that each sub-population has some immunological memory and that such immunological memory is described by the fractional dynamics given by the Caputo fractional derivative operator (.) of order (see [5] for the definition of the Caputo derivative and its memory-enhancing effect).
In other words, the disease dynamics follows the multi-fractional coupled system (MP)-FSIRC, given by:

and initial conditions

(2)
for i,j=1,2 and i j. All the parameters in the model (MP)-FSIRC (1) are assumed to be constant. The parameters and are the average inverses of the time spent by individuals in the three compartments Ij , Rj and Cj , respectively. The birth and mortality rates is given by . The average reinfection probability of an individual in Cjis . For i,j=1,2, respectively, represents the infection rate between individuals in the same population if i=j , whereas represents the infection rate between distinct populations in case of i j.

III. WELL-POSEDNESS FOR THE (MP)-FSIRC MODEL
In this section, we show the existence of a unique continuous solution

or of the (MP)-FSIRC model (1) with initial conditions (2). We also show that such a solution is continuously dependent on the initial conditions, system parameters, and the fractional-order of the Caputo derivatives , for . We begin showing some preliminary results concerning the (MP)-FSIRC model (1).
Lemma 1: Let , where is the total of individuals of sub-population . Then is constant for any .
Proof: It follows from the linearity of the fractional derivative (see [5]) that
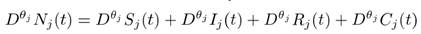
for j=1,2. Summing up the right hand side of (MP)-FSIRC model (1), we have that , for any j=1,2. Hence Nj(t) is constant, for j=1,2 (see e.g., [5]) and the assertion follows.
Lemma 2: If a solution X(t) of (MP)-FSIRC (1) model with initial conditions (2) exists, then it is uniformly bounded by N(0). In particular all the coordinates of X(t) are uniformly bounded.
Proof: Let ||.||1 be the 1-norm in. It follows that ||X(t)||1 ||N(t)||1, for any t 0. Since N(t) is constant (see Lemma 1), the assertion follows.
Let the map F: [0, ) x given by

, where and , are the right hand side , for i,j=1,2, with i j , respectively. Proposition 1: Let the map defined above F(t,X(t)) defined above. Then:
i. F(t, X(t)) is continuous for t 0.
ii. There exist constants and such that .
iii. F(t, X(t)) is Lipschitz continuous w.r.t. the second coordinate.
Proof: Item i) is derived from the fact that each coordinate of F(t,X(t)) is made up of the sum and product of continuous functions. Using Lemma 2, we can conclude that the first coordinate of F(t,X(t)) is such that

where and .
With analogous arguments presented above for each coordinate of , the assertion on item~ii follows. Applying the Mean Value Theorem, we get the existence of a such that, for any ,

,(3)
where is the Jacobian of the map , given by

Here denotes the 4 x 8 null matrix. Since JF1(t,X(t))=A1 + A2 where A1 and A2 are given by

and

, respectively for

On the other hand, JF2(t, X(t)) is given by

, where

Hence, it follows from Lemma 2 that each coordinate of JF(t, X(t)) is uniformly bounded. As a results, there exists L 0 such that ||JF(T,X(t))||L. Therefore, from (3) and the Cauchy-Schwarz inequality, the assertion iii) follows.
The theorem that follows is the main theoretical result of this contribution.
Theorem 1: Let the (MP)-FSIRC (1) and the corresponding initial conditions (2). Then:
[Existence and uniqueness] There is a unique continuous solution X(t) for the (MP)-FSIRC model (1), for .
[Continuous dependence] The (MP)-FSIRC model (1) solution X(t) is continuously dependent on the model parameters and fractional derivatives , for any j=1,2.
Proof: Integrating the (MP)-FSIRC model (1) with order for j=1,2 results in the model being equivalent to Volterra's system of equations

(4)
where and represents the k-coordinate of F(t,X(t))
with , if k=1,...,4 and if k=5,...,8.
Let . Then (4) can be rewritten as

for k=1,2,...,8, where,

Let  be the expression of the vector map F(t,X(t)) with
coordinates corresponding to
be the expression of the vector map F(t,X(t)) with
coordinates corresponding to  , for k=1,...,8. . We know from Proposition 1 itens-i)-iii)
that F(t,X(t)) is continuous with respect to Importar imagen and
Lipschitz is continuous with respect to X(t). A direct calculation reveals that
, for k=1,...,8. . We know from Proposition 1 itens-i)-iii)
that F(t,X(t)) is continuous with respect to Importar imagen and
Lipschitz is continuous with respect to X(t). A direct calculation reveals that  also meets these requirements. Therefore, the Fixed Point Theorem (as used in
the Picard theorem - see also Theorem 8.3 in [5]) can be applied to guarantee
the existence of a unique continuous solution X(t) for the (MP)-FSIRC (1) with
initial conditions (2), in the interval [0,T*] for some T* > 0. Moreover, Proposition 1,
ii) implies F is linearly
increased. Therefore, the assumptions of Theorem 3.1 in [11] are satisfied. It
implies that the solution X(t)can be continuously extended to the positive real
line. It concludes the assertion i). Furthermore, Proposition 1 implies that
the assumptions of Theorem~6.20 - 6.22 in [5] hold true. Hence, item ii)
follows.
also meets these requirements. Therefore, the Fixed Point Theorem (as used in
the Picard theorem - see also Theorem 8.3 in [5]) can be applied to guarantee
the existence of a unique continuous solution X(t) for the (MP)-FSIRC (1) with
initial conditions (2), in the interval [0,T*] for some T* > 0. Moreover, Proposition 1,
ii) implies F is linearly
increased. Therefore, the assumptions of Theorem 3.1 in [11] are satisfied. It
implies that the solution X(t)can be continuously extended to the positive real
line. It concludes the assertion i). Furthermore, Proposition 1 implies that
the assumptions of Theorem~6.20 - 6.22 in [5] hold true. Hence, item ii)
follows.
IV. SIMULATED SCENARIOS
In this section, we present some simulated scenarios for the (MP)-FSIRC (1). The numerical solution for the (MP)-FSIRC (1) calculated using a trapezoidal type method with a mesh size of of (5), proposed in [6]. Since the mesh-size corresponds to the time scale, we re-scale all the parameters accordingly. The simulations are run for a time corresponding to 120 days and for choices of the fractional derivatives of order.
A. Scenario with Symmetric Sub-populations
In this section, we present distinct scenarios of the proposed dynamics for a symmetric population. It means that .The remaining parameters are given by

The initial conditions are such that , implying that only the sub-population 1 is infected at Importar imagen , whereas the population 2 is infection-free.


Figures 1 and 2 show the dynamics of infection and cross-immunity for both sub-populations. Looking only at the simulated scenarios (the simulated scenarios in “black---”, “cyan---” and “red---” are almost coincident, as well as the ones in “blue---” and “green---”) for the sub-population 1, we conclude that the best strategy is the one in which the sub-population 1 has more immunological memory (). The scenario with and (plotted “yellow---”) has a minor peck of infection as well as a minor cross-immunity percentage, whereas (no immunological memory in the sub-population 1) has a higher peck of infection as well as a higher percentage of cross-immunity.
The simulated scenarios for sup-population 2, presented in Figures 3 and 4 lead to a similar conclusion as described above (the simulated scenarios in “blue---” and “red---” as well as the ones in “yellow---”, “cyan---” and “green---” are nearly identical), where it can be seen that the relation corresponds to cases where the diseases have fewer infected persons at the epidemiological peck and a lower percentage of cross-immunity.




B. Scenario with Non-symmetric Sub-populations
In the following, we analyze some simulated scenarios of the proposed dynamics where the populations are non-symmetric. In the simulations, we use N1=10 and N2=1.
The remaining parameters used are , , , ,, for two scenarios of initial infections.
First scenario: The disease starting in sub-population 1: We first simulate the scenario where the sub-population has infected individuals, while sub-population 2 is free of infection at Importar imagen . It is equivalent to the initial condition X(0)= (9.99,0.01,0,0,1,0,0,0,0,0)T
Figures 7 to 10 show the dynamics of infection and cross-immunity for both sub-populations in this scenario (the simulated scenarios in “red---”, “cyan---” and “yellow---” are almost coincident, as well as those in “blue---” and “green---”.). Analyzing the results for the sub-population 1 in Figure 7 and 8, we conclude that the favorable scenario is the one with . The most favorable scenario is depicted in “black---”, in which sub-population 2 has more immunological memory . However, we cannot conclude that is the best strategy because the ones with and (shown in “green---”) are just as bad as the ones with no memory (shown in “blue---”).






The analysis of the dynamics of the total population depicted in Figures 11 and 12 shows that the scenarios are favorable if both populations have some memory with . Otherwise, if (no memory for the sub-population 1), then even if the sub-population 2 has some memory, it is not enough to diminish the effects of the disease (depicted in “green---”). This scenario shows that the strategy is to guarantee immunological memory for both sub-populations, giving more importance to the smallest sub-population. Hence, the simulated scenarios sugget that any vaccination campaing any vaccination campaign should start, if possible, as in the symmetric case, in the sub-population that is disease-free.
Second scenario: The disease starting in sub-population 2: We assume that sub-population 2 has infected individuals while sub-population 1 is free of infection at t=0. This scenario corresponds to the initial condition .
Figures 13 to 16 show the dynamics of infection and cross-immunity for both sub-populations in this scenario (the simulated scenarios in “red---”, “cyan---” and “yellow---” are almost coincident, as well as those in “blue---” and “green---”.). The results for the sub-population 1 in Figure16 show a favorable scenario if ( ) while for the sub-population 2 is the one with () depicted in “yellow---”.






On the other hand, the simulated scenarios for the total population depicted in Figure 17 and 18 show that the scenarios are favorable for lower values of , with . This scenario shows that the strategy is to guarantee immunological memory for the sub-populations jointly, giving more importance to the biggest sub-population. This means that, in such a scenario, any vaccination campaign should start for the sub-population that is disease-free, as before.
V. CONCLUSIONS
We propose a multi-fractional derivative dynamics for the SIRC model for disease dissemination as an alternative to describe the existence of immunological memory in a setting with two populations that interact, called (MP)-FSIRC. We prove the well-posedness of the proposed (MP)-FSIRC-model and also present distinct simulated scenarios for the fractional derivative as well as for the sub-population sizes and disease prevalence at t=0. The numerical results show that the existence of immunological memory in both sub-populations (described by the fractional dynamics), in general, presents a favorable epidemiological situation, with smaller infection pecks and less cross-immunity. The most favorable epidemiological scenarios are those in which the disease-free sub-population at t=0 has greater immunological memory, as discussed in Section IV. It turns out that any vaccination campaign should start, if possible, with the sub-population that is disease-free.
The theoretical questions of existence and stability for stationary points as well as simulated scenarios with other choices for the model parameters and fractional order derivatives will be addressed by the authors in future contributions.
References
[1] B. Adams and A. Sasaki, “Antigenic distance and cross-immunity, invariability and coexistence of pathogen strains in an epidemiological model with discrete antigenic space”. Theoretical population biology, 76, 157-167, 2009.
[2] V. Andreasen, J. Lin, and S. Levin, “The dynamics of co-circulating influenza strains conferring partial cross-immunity”. Journal of mathematical biology, 35, 825-842, 1997.
[3] R. Casagrandi, et al., “The SIRC model and influenza A”. Mathematical biosciences, 200, 152-169, 2006.
[4] O. Diekmann, J. A. J. Metz, and J. A. P Heesterbeek, “The legacy of Kermack and McKendrick,'', in Epidemic Models: Their Structure and Relation to Data, Mollison, D. E. (ed.), Cambridge University Press, Cambridge, 1995.
[5] K. Diethelm, “The analysis of fractional differential equations: An application-oriented exposition using differential operators of Caputo type'', Springer Science \& Business Media, Braunschweig, 2010.
[6] R. Garrappa, “Trapezoidal methods for fractional differential equations: Theoretical and computational aspects”. Mathematics and Computers in Simulation, 110, 96-112, 2015.
[7] A. C. F. N. Gomes, and A. De Cezaro, “Um estudo sobre a memória epidemiológica: modelo SIRC fracionário”. C.Q.D. – Revista Eletrônica Paulista de Matemática, 10, 194-210, 2017.
[8] A. C. F. N. Gomes, and A. De Cezaro, “On a multi-order fractional SIRC model for Influenza”. C.Q.D. – Revista Eletrônica Paulista de Matemática, 22, 1-15, 2022.
[9] M. G. M. Gomes, L.J. White, and G. F. Medley, “Infection, reinfection, and vaccination under suboptimal immune protection: epidemiological perspectives”. Journal of theoretical biology, 228, 539- 549, 2004.
[10] K. Kuszewski, and L. Brydak,, “The epidemiology and history of influenza”. Biomedicine and pharmacotherapy, 54, 188- 195, 2000.
[11] W. Lin, “Global existence theory and chaos control of fractional differential equations”. J.Math. Anal. Appl, 1, 332, 709-726, 2007.
[12] C. M. Pease, “An evolutionary epidemiological mechanism, with applications to type A influenza”. Theoretical population biology, 31, 422- 452, 1987.
[13] J. Piret, and G. Boivin, “Pandemics Throughout History”. Frontiers in Microbiology, 11, 1-16, 2021.

