Abstract: In the present work we studied the β-decay of various isotopes in the heavy region using the empirical formula of Fiset and Nix. It is found from the half-life that as the neutron number increases the possibility of β-decay increases. From the dependence of beta decay half-life on neutron number of parent and Q- value, we modified empirical formula of Fiset and Nix for beta decay half-life. We also developed an empirical formula for the Z-value of most stable isobar against β-decay. From the study of mass parabola for different isobars with mass number ranging from 200-223 it was found that the lowest point in the parabola, which is the Z-value of most stable isobar against β-decay, matches well with our formula predictions.
Keywords: Beta decay, Mass parabola, Nuclides.
Articles
Beta Decay Studies of Nuclides in the Heavy Region
Received: 04 September 2020
Revised: 23 September 2020
Accepted: 30 September 2020
Published: 09 November 2020
Corresponding author: preethinambiarmk@gmail.com

This work is licensed under Creative Commons Attribution 4.0 International.
Many of the nuclei produced in the lab are radioactive. The degree of instability grows as the distance of a given nuclide increases from the stable nuclide with the same mass number. An unstable nuclide attains stability through different decay mechanisms such as alpha decay, beta decay, gamma decay, cluster radioactivity etc. Alpha decay is a radioactive decay process in which heavy nuclei emit alpha particles to reduce their mass and move towards stability. For many of the unstable nuclei alpha decay cannot be possible and such nuclei undergo beta decay in order to become stable. In contrast with alpha decay, progress in understanding beta decay has been achieved at an extremely slow pace. The probability of a nuclide decaying due to beta and other forms of decay is determined by its binding energy. The binding energies of all existing nuclides form what is called the nuclear valley of stability [1]. Often the experimental results have created new puzzles that challenged existing theories.
The most basic beta decay process is the conversion of a proton to a neutron or a neutron to a proton inside the nucleus maintaining a constant mass number. It is a nuclear decay process mediated by weak nuclear interaction. Beta decay provides a convenient way for an unstable nucleus to slide down the mass parabola of constant A and to approach the stable isobar. Through the process of beta decay an unstable atom obtains a more stable ratio of protons and neutrons. The stability of this ratio forms the nuclear valley of stability [1].
The three processes grouped under beta decay are β--decay, β+-decay and orbital electron capture. Neutron rich isotopes usually undergo β- decay in which a neutron is converted into a proton with the emission of an electron and an antineutrino. 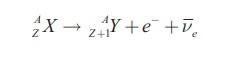
The effect of this process is to increase the atomic number by one, but leave the mass number unchanged. The emitted electron can be observed and its energy is measured. The associated antineutrino has very small interaction probability and so is expected to escape unobserved. The Q-value of the process is given by the mass difference of parent and daughter atoms. Since the reaction will proceed only when the Q-value is positive, β−-decay can occur when the mass of parent atom is greater than the mass of daughter atom [2].
Isotopes having a surplus of protons can decay through either by β+-decay or orbital electron capture. In positive beta decay a proton in the nucleus is converted to neutron with the emission of a positron and a neutrino. 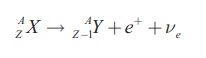
In electron capture [3-6] the nucleus capture one of the orbital electrons and a neutrino is emitted. 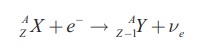
These two processes result in the same change to the nucleus, the atomic number reduces by one without changing mass number. They compete each other to reduce the atomic number of proton rich nuclei and which one will dominate depends on the Q-value. The reaction will proceed only when the Q-value is positive. So β+-decay can occur when the mass of parent atom exceeds that of daughter by at least twice the mass of the electron. Since the binding energy of the electron is much less than the mass of the electron, nuclei that can undergo β+-decay can always also undergo electron capture, but the reverse is not true [2].
In β-decay, the transition starts from ground state of the parent nuclei to different exited states of daughter nuclei according to the selection rule. All these transitions are possible within the energy window defined by Q-value. Quantum mechanically, the interaction leading to beta decay can be considered as a weak perturbation and thus Fermi’s Golden Rule can be applied to find an expression for the kinetic energy spectrum of emitted beta particles. The maximum kinetic energy corresponds to that expected from the exact rest mass energies of the parent and daughter atoms or nuclei.
Many theoretical works related to β-decay are available in the literature [7-10]. Ren et al. [11] used shell model calculation for their study on β- decays. Sorlin et al. [12] have done an experimental study on the β-decay of several neutron rich nuclei at GANIL and compared the half-lives of certain isotopes with those obtained from QRPA calculation. Nishimura et al. [13] measured the β-decay half-lives of 38 very neutron rich nuclei at RIKEN.
In our previous works [14] we have developed a semi empirical formula for both phase space factor and Nuclear Matrix Element for computing the neutrinoless double beta decay half-lives. Recently we have also developed an empirical formula [15] for phase space factor and nuclear matrix element to study two neutrino double beta decay half-lives. The present work is an attempt to study the possibility of β--decay from various isotopes in the heavy region with Z ranging from 80-99 using the empirical formula of Fiset and Nix [16]. We have developed a formula for finding the most stable isobar for a given mass number against beta decay. We also studied the mass parabolas for different mass numbers.
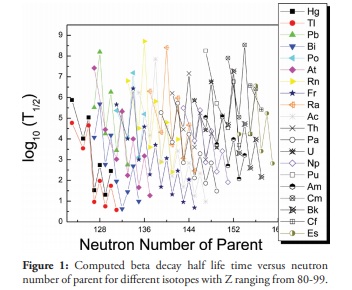
Figure 1
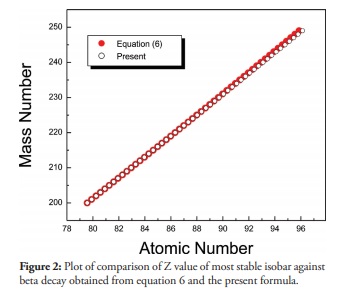
Figure 2
Plot of comparison of Z value of most stable isobar against beta decay obtained from equation 6 and the present formula.
The half-life for beta decay depends strongly upon the energy released in the process and weakly upon the variations in the intrinsic structure of the original and final nuclei involved [16]. The beta decay half-lives are obtained from the decay energies by means of approximations similar to those used by Seeger et al. [17]. These approximations completely neglect variations in the nuclear matrix elements and the degree of forbiddenness of transitions. In the present work we use Fiset and Nix formula for half life which is
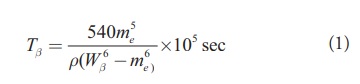 [Eq1]
[Eq1]where me is the rest mass of electron in MeV, ρ is the density of nuclear states and is given by ρ = e(-A/290) x number of states within 1MeV ground state and is obtained from the results of Seeger et al. [17]. W is the total maximum energy of the emitted beta particle, i.e.
The energy released in a beta decay process is its Q-value and is given as,
Here Z and N are the proton and neutron number of the parent nucleus respectively. The Q-value must be positive for any decay process to occur.
In the present work we have computed the β--decay half- lives from various isotopes in the heavy region with Z ranging from 80-99 using the empirical formula of Fiset et al. [16]. The Q-values are computed using the experimental binding energies of Audi et al. [18].
Figure 1. represents the computed beta decay half-life time versus neutron number of parent nuclei in the heavy region with Z ranging from 80-99. It is clear from the plot that beta decay half-lives decreases with increase in neutron number. That is, beta decay occurs in isotopes which are neutron rich. When the number of neutrons in the nucleus increases, the Coulomb force becomes weak due to the hindrance to the repulsive force among the protons. In such cases, the width of the two turning points is very large and the barrier height is small. Thus, the probability of alpha decay in this region is minimum and these types of nuclei are stable against alpha or cluster radioactivity. In such isotopes beta emission is the possible decay mode. Atoms which undergo beta decay are located below the line of stable elements on the chart of the nuclides, and are typically produced in nuclear reactors. The Q-value for a reaction is the amount of energy released by that reaction. The value relates to the enthalpy of a chemical reaction or the energy of radioactive decay products. Q-values affect reaction rates.
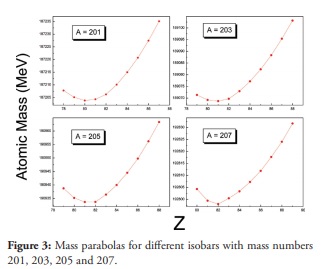
Figure 3
Mass parabolas for different isobars with mass numbers 201, 203, 205 and 207.
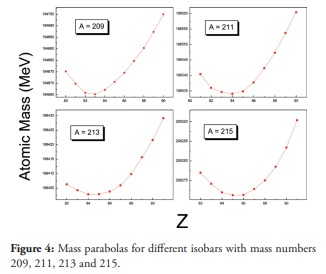
Figure 4
Mass parabolas for different isobars with mass numbers 209, 211, 213 and 215.
It is obvious that neutron number of the parent and the decay energy have a good role in the beta decay half-lives. Comparative half-life of beta decay is inversely proportional to the square of nuclear matrix element. From the available values of comparative half-lives we have extracted the nuclear matrix element values and studied their dependence on (NQ3/2)1/2. It is found that as (NQ3/2)1/2 increases, the value of nuclear matrix element decreases. Hence we have considered this parameter in the empirical formula of Fiset and Nix and is given as
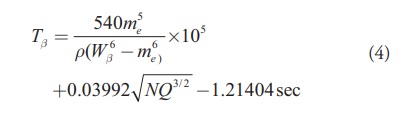 [Eq.4]
[Eq.4]We have also computed the standard deviation using the formula given below
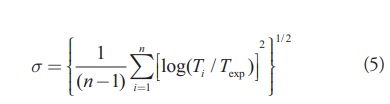 [Eq.5]
[Eq.5]From experimental beta decay half-life values of 101 nuclei, the estimated standard deviation for the present formula prediction and the formula predictions of Fiset and Nix are 1.991417 and 2.333264 respectively. It is clear that the present formula prediction is better than the formula prediction of Fiset and Nix. Tables 1-4 represent the computed Q-values and β- half-life times for the formula predictions of Fiset et al. [16], the modified formula prediction and the experimental values for the different isotopes in the heavy region with Z ranging from 80-99. It is obvious that the modified formula predictions are in close agreement with the experimental [19] values as compared with the formula predictions of Fiset and Nix.
One of the main applications of Bethe-Weizsacker semi empirical mass formula is the prediction of the most stable isobar of a given A against beta decay. The Z-value of such isobar is given by minimizing the atomic mass including the mass of electron from the semi empirical mass formula. This gives
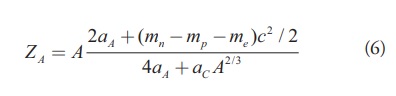 [Eq. 6]
[Eq. 6]Where aA = 23 MeV and aC = 0.72MeV are the coefficient of asymmetry term and Coulomb term in the semi empirical mass formula and mn, mp, me are mass of neutron, proton and electron respectively.
Volume & Issue: Vol 8, Issue-1; August 2020
Copyright: © 2020 M.K. Preethi Rajan, R.K. Biju and K.P. Santhosh. This is an Open Access article published in Journal of Nuclear Physics, Material Sciences, Radiation and Applications (J. Nucl. Phy. Mat. Sci. Rad. A.) by Chitkara University Publications.
It is published with a Creative Commons Attribution- CC-BY 4.0 International License. This license
permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are
credited.
PP: 43-53
https://jnp.chitkara.edu.in/index.php/jnp/article/view/231 (pdf)
https://jnp.chitkara.edu.in/index.php/jnp/article/view/187 (pdf)
https://jnp.chitkara.edu.in/index.php/jnp/article/view/97 (pdf)
https://jnp.chitkara.edu.in/index.php/jnp/article/view/95 (pdf)
https://jnp.chitkara.edu.in/index.php/jnp/article/view/169 (pdf)
[Corrected article , vol. 3, 165-177] https://jnp.chitkara.edu.in/index.php/jnp/article/view/131
preethinambiarmk@gmail.com

Figure 1

Figure 2
Plot of comparison of Z value of most stable isobar against beta decay obtained from equation 6 and the present formula.

Figure 3
Mass parabolas for different isobars with mass numbers 201, 203, 205 and 207.

Figure 4
Mass parabolas for different isobars with mass numbers 209, 211, 213 and 215.


