



Articles
Homogenization Effects of VVER-1000 Fuel Assembly on Criticality Calculations
Journal of Nuclear Physics, Material Sciences, Radiation and Applications
Chitkara University, India
ISSN: 2321-8649
ISSN-e: 2321-9289
Periodicity: Bianual
vol. 8, no. 1, 2020
Received: January 26, 2020
Revised: February 20, 2020
Accepted: May 12, 2020
Published: 10 August 2020

Abstract: Due to cost effective and simplicity homogeneous reactors have been widely used for experimental and research purposes. Parameters which are difficult to get from a heterogeneous reactor system can be easily obtained from a homogeneous reactor system and can be applied in the heterogeneous reactor system if the major parametric differences are known. In this study, homogenization effects of VVER (Water Water Energetic Reactor)-1000 fuel assembly on neutronic parameters have been analyzed with the universal probabilistic code MCNP (Monte Carlo N-Particle). The infinite multiplication factor (k∞) has been calculated for the reconfigured heterogeneous and homogenous fuel assembly models with 2 w/o U-235 enriched fuel at room temperature. Effect of mixing soluble boron into the moderator/ coolant (H2O) has been investigated for both models. Direct and fission detected thermal to higher energy neutron ratio also has been investigated. Relative power distributions of both models have been calculated at critical and supercritical states. Burnup calculations for both the reconfigured cores have been carried out up to 5 years of operation. Effective delayed neutron fraction (βeff) and prompt neutron lifetime (ℓ) also have been evaluated. All the results show significant differences between the two systems except the average relative power.
Keywords: Homogenization effect, Criticality calculation, Thermal neutron, Point kinetic parameter, VVER-1000.
1. Introduction
is important to know the critical boron concentration of the systems at the beginning of cycle (BOC), before continuing any further calculations as a critical system would be the best state for the calculations to investigate. Critical boron concentration for the MCNP HET and HOM models are estimated carefully through graphically using the linear interpolation method. Thermal and high
Bangladesh is going to run two units VVER-1200 reactors at Rooppur, Pabna (RNPP) within a few years. This VVER-1200 version which is under construction is the modified version of the VVER-1000 with increased power output and additional passive safety features. Concerning the facts, we have started research on the VVER-1000 reactor with the assistance of IAEA TECDOC-847 [3]. In the earlier study, we have benchmarked VVER-1000 fresh fuel assembly [4]. Now we are mainly concerned about the fuel burnup calculation as it will take a long time to complete fuel burnup calculation of a power reactor (VVER-1000) due to having a huge number of fuel cells and other components. Alternatively, it would be thought to perform fuel burnup calculation with the HOM assembly model. The main advantage of using a HOM assembly model is that it treats like a single cell. It could be made by uniformly mixing with the same amount of fuel material and the same amount of moderator material that an assembly contains. In order to make it, it is, therefore, necessary to know the parametric differences of several neutronics calculations between single HOM and HET fuel assembly model. In this study, a HOM and a HET VVER-1000 fuel assembly models have been developed to investigate the homogenization effects on the criticality calculations.
It is important to know the critical boron concentration of the systems at the beginning of cycle (BOC), before continuing any further calculations as a critical system would be the best state for the calculations to investigate. Critical boron concentration for the MCNP HET and HOM models are estimated carefully through graphically using the linear interpolation method. Thermal and higher energy neutron generation and their contribution in fission are important for neutron physics calculation of nuclear reactor. In this study, their ratios are calculated and compared graphically. The design of the initial core loading pattern (power distribution) has a great important role in nuclear power plant operation. In this study, radial power distribution has been investigated for both systems. The power peaking factor ensures the link between the nuclear and thermal-hydraulics analysis of the reactor core as they define maximum power released locally in the core. In this study, the radial power peaking factor is calculated for both the systems. The kinetic parameters such as effective delayed neutron fraction (βeff) and prompt neutron lifetime (ℓ) play an important role in the reactivity transient analysis, safety, and control of nuclear reactors. Hence, evaluation of them is of great importance in the reactor physics calculations. In the light water reactor 0.65% of the neutrons emitted in the fission process is delayed by up to several tens of seconds [5]. They are called delayed neutrons which result from the radioactive decay of certain fission products. The remaining 99.35% are called prompt neutrons which are emitted immediately during fission. Prompt neutron lifetime is the average time from the emission of a prompt neutron in fission to the removal of the neutron by some physical process such as escape, capture, or fission. Both of these parameters have been calculated for MCNP VVER-1000 fuel assembly models at the BOC.
2. Calculation Tools and Techniques
Monte Carlo method based computer code MCNP has been used in the whole study. It is a world-recognized universal code because; it is more beneficial than other deterministic codes. It can provide a very accurate probabilistic transport solution [6]. Moreover, it simulates individual particle tracks of continuous energy through a given system of exact geometrical description. In this study, Monte Carlo simulations have been performed with MCNP5 [6] to ascertain the accuracy for the criticality calculation fuel assembly of the VVER-1000 type reactor prepared with the assistance of IAEA-TECDOC -847 [3].
In order to investigate all the calculations, two MCNP fuel assembly models have been reconfigured: a heterogeneous (HET) model and a homogenous (HOM) model with the assistance of the earlier developed MCNP fuel assembly model [4]. The general description of the MCNP fuel assembly model and material compositions are presented in Tables 1 and 2 respectively. In the MCNP HET model, 312 cylinders of UO2 pellets (2 w/o enriched U-235) were loaded into the fuel rod position. There was one central thimble and 18 control rod positions filled with water (Figure 1a). On the other hand, UO2 fuel with 2 w/o enriched U-235 was mixed with H2O in the MCNP HOM model (Figure 1b). In both systems materials of instrumentation tube, guide tube, fuel cladding, and spacer grid have been neglected for simplicity.
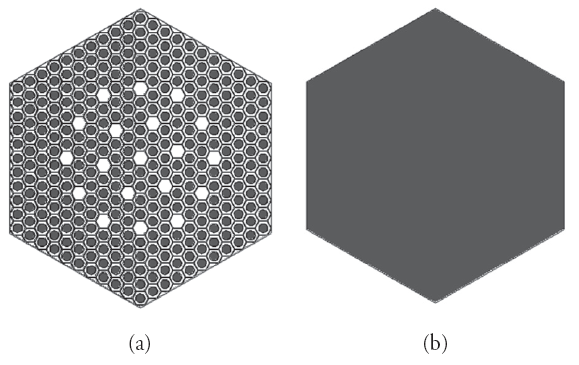
Fuel material UO2 Fuel cell lattice pitch 1.275 cm Fuel assembly lattice pitch 23.600 cm Height of fuel pin/cell 353.000 cm Radius of fuel pin 0.386 cm Mass of fuel per pin/cell 1560 gm
| Fuel material | UO2 |
| Fuel cell lattice pitch | 1.275 cm |
| Fuel assembly lattice pitch | 23.600 cm |
| Height of fuel pin/cell | 353.000 cm |
| Radius of fuel pin | 0.386 cm |
| Mass of fuel per pin/cell | 1560 gm |
| Model | Material | Component | Atom Density (atoms/barn-cm) |
| HET | UO2 (2 w/o U-235) | U-235 | 0.000469778 |
| U-238 | 0.022728356 | ||
| O-16 | 0.046396267 | ||
| H2O | H-1 | 0.666666667 | |
| O-16 | 0.333333333 | ||
| HOM UH2O3 (2 w/o U-235) | U-235 | 0.000161187 | |
| U-238 | 0.007798415 | ||
| H-1 | 0.023878807 | ||
| O-16 | 0.015919205 | ||
3. Results and Discussions
3.1. Critical Boron Calculation
A reactor is supercritical (keff>1) at the BOC, and the reactivity could be found to be significantly higher than a core in equilibrium (keff=1). To compensate for the excess reactivity, it is necessary to add burnable poison or a burnable neutron absorber having a large neutron absorption cross-section into the reactor core or is directly mixed in moderator at the starting of life. Finally, this neutron absorber is converted into a nuclide with a low absorption cross-section as the result of neutron absorption. Thus, the increase in reactivity accompanying the burnup of the poison compensates to some amount for the decrease in the reactivity due to fuel burnup. The major advantage of using a burnable poison is that it can usually be distributed more uniformly than control rods. Hence, this poison is less disturbing to the core’s power distribution. In the MCNP VVER-1000 fuel assembly models soluble boron was used as burnable poison to analysis the critical boron concentration.
At first, k∞ was calculated for both the MCNP HET and HOM fuel assembly models without mixing boron into the moderator/coolant. It was observed that initially both the systems were found to be supercritical i.e. reactivity of both the systems was significantly higher than a model in equilibrium. In the MCNP HET model, the fuel (UO2) was surrounded by moderator material (H2O). At first, fission took place within the fuel and the neutrons are partially moderated by means of inelastic scattering until they escape from the fuel and finally initiated the final process of moderation through elastic scattering with the moderator nuclei. The number of elastic scattering collisions between two fuel rods depends on the separation distances of the rods (pitch). Neutrons emitted within the fuel rod (higher energy neutron) and travel through a fuel region caused fast fission with U-238 before escaping the fuel rod. Thus the fast fission factor (ε) of the HET system was larger than unity. The thermal utilization factor (f) decreased in the HET system because of the fuel self-shielding for the absorption of thermal neutrons. The resonance escape probability (p) increased significantly in HET systems as a result of two effects: pitch and fuel self-shielding. In the MCNP HOM model, the fission neutrons were in immediate contact with the moderator atoms. The neutrons were moderated by means of elastic scattering before they are absorbed by the fuel nuclei. As a result, the neutron had not had enough energy to cause fast fission through inelastic scattering in U-238. The fast fission factor of the HOM system was nearly equal to unity, ε =1. Thus the fast fission factor (ε) and the resonance escape probability (p) increased the k∞ value in the HET model compared to that of the HOM model at supercritical state.
Addition of soluble boron into the moderator/coolant is necessary at the beginning of life, to compensate for the excess reactivity. Boron at 1000, 2000, 3000, 4000 and 5000 ppm was added into the moderator/coolant of the HET model. On the other hand, the same amount of boron was mixed with H2O and UO2 in the HOM model. Reactivity reductions of the models due to the mixing of soluble boron into the systems are depicted in Figure 2. It is seen that the HET model provides a slight curve like shape while the HOM model a straight line. In the MCNP HOM model ratio of neutron production and absorption were remained the same in each mixing step of boron which resulted in a straight line. However, in the MCNP HET model nuclear properties changed from one zone to another due to the separation of the fuel and moderator material. Neutron flux fluctuated drastically over a very short distance. The basic reason for the spatial variation of neutron flux in the HET model was because adjacent material regions could have different absorption crosssections or some zones could have materials with strong resonance peaks. This is why the HET model did not show a straight line. The critical boron concentration of the models was estimated from the graph using the linear interpolation method, at k∞=1. Criticality achievements were observed at 3000 and 4600 ppm boron for the HET and HOM model, respectively [Table 3]. In the MCNP HET model production of total neutrons in the core is higher compared to that of the MCNP HOM model. However, in the MCNP HET model production of thermal neutrons in the liquid region may be lower compared to that of the MCNP HOM model. As a consequence, it has been taken more amount of boron to make the system critical.
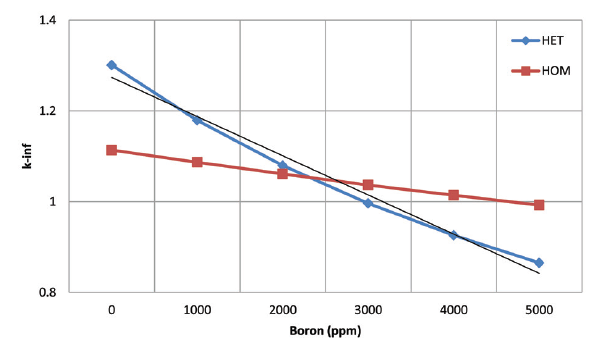
| Model | k∞±Δ* | Critical Boron (ppm) |
| HET | 1.00099±0.00018 | 3000 |
| HOM | 1.00107±0.00019 | 4600 |
Figure 3 shows thermal to higher energy neutrons ratios for the MCNP HET and HOM models with mixing of different ppm soluble boron into the moderator/coolant. It is seen that both the MCNP HET and HOM model produced a greater number of higher energy neutrons than thermal neutrons at each step of boron ejection in the moderator/coolant. The MCNP HET model produced around 3.54414% larger number of higher energy neutrons than thermal neutrons without boron ejection in the system while the MCNP HOM model produced approximately 0.03259% greater number of higher energy neutrons than thermal neutrons. In the boron free system, the MCNP HET model produced approximately 17% more fission detected thermal neutrons than the HOM model. At each step of boron ejection, thermal neutrons of both systems absorbed by the boron molecule and flux dropped gradually.
3.2. Power Distribution Calculation
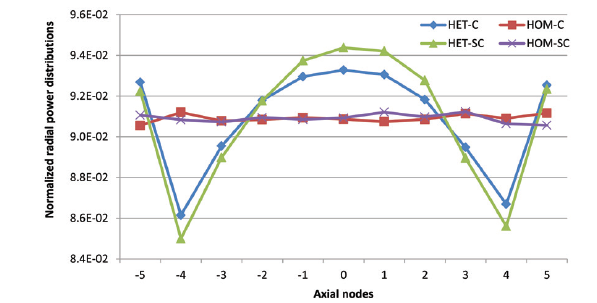
Figure 4 shows normalized assembly power in the radial direction at critical and supercritical state for both MCNP HET and HOM model. The calculations have been done with 2 w/o U-235 fuel cell at the BOC that is at zero burnup condition. The calculations were done at room temperature without any neutron absorber mechanism. It is seen from the figure that the power of the HET model is concentrated in the core center due to the presence of more neutrons flux in that region compared to that of the periphery. On the other hand, the power of the HOM model is flat everywhere due to the presence of almost the same neutrons fluxes overall the core. The average relative assembly power of the MCNP HET and HOM models is the same (0.0909) at critical state. The radial power peaking factor of the MCNP HET and HOM models are 1.026092547 and 1.00299688 respectively at critical state (Table 4). It can be concluded that the spatial flux, as well as power distributions in HET cores, are inherently more sensitive to changes in composition, loading pattern, etc., as compared to HOM cores.
3.3. Core Burnup Calculation
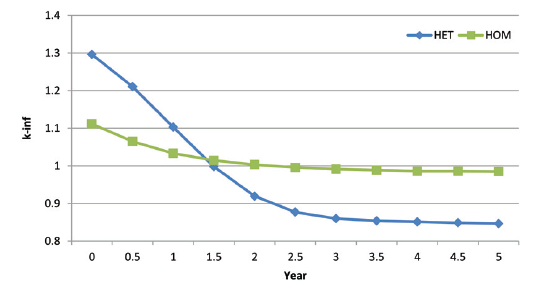
Figure 5 depicts the results of core burnup calculations of the assembly models using 2 w/o U-235. Core temperature and pressure were remained constant in each simulation. The burnup step employed for assembly core burnup calculation is 6 months, in which core power and burnup distribution were assumed constant during that period. The result shows that the MCNP HOM core remains critical up to 2.5 years of operation while the MCNP HET core remains critical up to 1.5 years of operation. It can be concluded that a HOM core having the same amount of fuel and moderator material can sustain criticality for a long time than a HET core at the same power.
3.4. Kinetic Parameters Calculation
The beta coefficient provides the number of delayed neutrons that are obtained in the system. The following equation was used to calculate the delayed neutron fractions:
where, kp and kT are the multiplication factor obtained by only the prompt neutrons and the multiplication factor using both prompt and delayed neutrons, respectively.
| Model | HET-C | HOM-C | HET-SC | HOM-SC |
| k∞±∆* | 1.0004±0.00018 | 1.00018±0.00019 | 1.30107±0.00014 | 1.11398±0.00019 |
| PPF | 1.026092547 | 1.00299688 | 1.0349087 | 1.00326514 |
| Kinetic Parameters | HET | HOM | ||
| MCNP (prompt) | MCNP (adjoint) | MCNP (prompt) | MCNP (adjoint) | |
| βeff±Δ* | 0.006711 ± 0.000205 | 0.00746 ± 0.00052 | 0.006933 ± 0.000269 | 0.00669 ± 0.00034 |
| ℓ ±Δ* (sec) | 3.4800E-05 ± 1.0425E-08 | 2.1042E-05 ± 9.7718E-09 | ||
The value of the effective delayed neutron fraction, βeff for the MCNP HET and HOM model at room temperature through the prompt method i.e. by using equation (i) are 0.006711±0.000205 and 0.006933±0.000269 respectively (Table 5). The value of the HOM model is closer to the literature value (0.0074) compare to the HET model. βeff for the MCNP HOM model is 6.31% smaller compared to the literature value and the result is in good agreement. In addition, it also has been found with the enhanced feature of MCNP5 for adjoint weighted calculation. In this method, the obtained values are 0.00746±0.00052 and 0.00669±0.00034 for the HET and HOM model respectively. In this case, βeff for the MCNP HET model is very closer (0.81% larger) to the literature value compare to the HOM model. The prompt neutron lifetime (ℓ) of the MCNP HET and HOM model at room temperature are 3.4800E-05±1.0425E-08 and 2.1042E-05±9.7718E-09 second respectively. This indicates that the prompt neutron produced from fission in the HET core can get more time for contributing further fission than the HOM core.
Conclusions
The effects of homogenization on neutronic parameters of VVER-1000 fuel assembly geometry are systematically estimated through comparisons between reconfigured HET and HOM models. In order to find out all the neutronic parameters, the universal computer code MCNP has been used. At first, critical boron concentration for both the systems was estimated and found that the HOM reactor system required 1600 ppm more boron than the HET system to achieve criticality at BOC. During boron ejection in the systems, the criticality dropped gradually following a straight line by the HOM reactor system while the HET system followed a slight curve. The radial power distribution was flat over the HOM core at critical and supercritical state. In the HET system, radial power distribution concentrated at the center and dropped gradually from the core center to the periphery. The HOM reactor system provided the best power peaking factor, 1.00299688 at critical state. It was investigated that the HOM reactor system sustained criticality for a single year more than the HET system during five years of operation. Point kinetic parameter, the effective delayed neutron fraction (βeff) was found better for the HOM reactor system calculated by the prompt method while it was found better for the HET system calculated by the adjoint method. The prompt neutron of the HOM system provided a larger lifetime (ℓ) compared to that of the HOM reactor system. The neutronic parameters that make differences in technical and economic performance characteristics between HOM and HET systems are small, each system has advantages as well as disadvantages, and there is no prevailing reason to favor one over the other.
References
[1] A. Hebert and P. Benoist, Nucl. Sci. Eng. 109, 360 (1991). https://doi.org/10.13182/NSE109-360
[2] J. Mondot, Proc. Specialists’ Mtg. Homogenization Methods in Reactor Physics, Lugano, Switzerland, November 13–15, 1978, IAEA-TECDOC-231, p.389, International Atomic Energy Agency (1980).
[3] International Atomic Energy Agency (IAEA), IAEATECDOC-847, Vienna, 1995.
[4] S. M. Shauddin, M. S. Mahmood and M. J. H. Khan, International Journal of Nuclear Energy Science and Technology 11, 175 (2017). https://doi.org/10.1504/IJNEST.2017.085775
[5] Bernard, J. A., “Nuclear Power Plant Dynamics and Control”, Class Notes, Massachusetts Institute of Technology, Massachusetts, 22, 921 (2012).
[6] X-5 Monte Carlo Team, “MCNP – A General Monte Carlo N-Particle Transport Code”, Version 5, LA-UR03-1987(revised October 3rd, 2005).
[7] X-5 Monte Carlo Team, “MCNP – A General Monte Carlo N-Particle Transport Code”, Version 5, LACP-03-0245, April 24, 2003 (revised October 3rd, 2005; February 1st, 2008).
[8] R. K. Meulekamp, S. C. van der Marck, Nuclear Science and Engineering 152, 142 (2006). https://doi.org/10.13182/NSE03-107
[9] B. C. Kiedrowski et al., MCNP5-1.60 Feature Enhancement & Manual Clarifications, Los Alamos National Laboratory, LA-UR-10-06217 (2010).
[10] M. B. Chadwick et al., Nuclear Data Sheets 107, 2931 (2006). https://doi.org/10.1016/j.nds.2006.11.001
Additional information
Journal: J. Nucl. Phys. Mat. Sci. Rad. A.
Volume & Issue: 8 & 1
Year: 2020
Page: 1-6
Journal homepage: https://jnp.chitkara.edu.in/
Publisher: Chitkara University Publications
Alternative link
https://jnp.chitkara.edu.in/index.php/jnp/article/view/198/190 (pdf)

