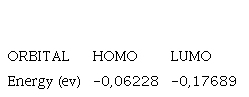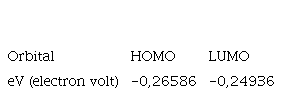INTRODUCTION
The term graphene was first introduced by Hanns-Peter Boehm (1962). He was the one who intended to use this term to describe a single layer carbon foil. Many scientists thought that carbon plate, at this small thickness which is equal to the diameter of a carbon atom, could not be stable, and for many years thereafter, the researches were not continued on this subject. (Konstantin Novoselov and Andre Geim, 2004), for the first time, successfully used adhesive tape to separate the graphene plates. The continuous tape was repeatedly used to separate graphite into thinner pieces. Then the strip of separated pieces of graphite was dissolved in acetone and, after a few processes, single layer of grapheme was deposited on a silicon disc. It should be mentioned that an optical microscope was used to control these steps. This method is known as the Scotch tape and was a surprise for the physics community, and for this reason, Jim and (Geim et al. 2010) from the University of Manchester won the Nobel Prize in Physics. The graphene produced by this method was very expensive since the production process was difficult. Hence, today, with the passage of time and the development of new methods, the process of graphene sheet exfoliation is performed by much less expensive ways. Graphene was previously studied by Wallace (1947). He studied the physics of solid graphene and predicted its electronic structure.
Today, graphene can be produced in large quantities through thermal and chemical reduction, and thermal dissolution of graphene oxide. These multi-purpose methods are measurable and suitable for a wide variety of applications. Potential applications are emerging to exploit the graphene properties. One example is optical electrodes and plasma devices which are based on optical and electronic properties. Both optical and electrical properties are the most important new developments of photocatalyst (Adán-Más, 2013). At present, after the production of grapheme, the most attractive aspect is to create a regulatory band gap within the initial graphene sheets (Zou, 2018).
Due to its unique physical properties, graphene has widespread applications in the electronic field. Among these properties, the mobility of charged particles inside the grapheme which is shown by the letter μ, is very important. The mobility of graphene is 100,000 cm2 / v.s, and the saturation velocity has been reported to be about 5 × 107 m / s. All of these properties made graphene a potent conductor for electronic applications including transistors (Huang, 2018). Graphene layers in multi-layer graphene are joined together with van der Waals forces. The existence of these van der waals forces can change the static and dynamic behavior, as well as the mechanical and electrical properties of multi-layered graphene. In studying the static and dynamic behavior of multilayer graphene, various methods such as molecular dynamics simulation, molecular mechanics and continuous media mechanics (continuum mechanics) are used. Due to the hardware constraints and spending a lot of time to simulate on a relatively large scale, the use of analytical methods is of greater interest to researchers. In analytical methods, each graphene layer is modeled based on Euler-Bernoulli or Tymoshenko beam theory and classical and Mindlin plate theory, the classical theories of modulated plates, and the forces resulting from interlayer van der waals bonding, in the form of a pressure term that is proportional to the relative displacement between the adjacent layers. According to this definition, only the compressive and tensile effects of van der waalse force can be modeled. While the experiments showed that graphene plates have the potential to slip on each other and van der Waals forces show shear strength. Therefore, in these types of analyses, the interlayer shear effect of multi-layered graphene is ignored (Bonaccorso, 2015). The mechanical exfoliation d is capable of producing single-layer and multi-layer graphite, but the graphite thickness obtained by this method is 10 nm which is approximately equal to 30 layers of single-layer graphene. In fact, by this method, graphene layers that by the van der Waals interaction are interconnected in a graphite structure can be separated from the graphite surface. Finally, by compressing cellophane strips on the final substrate, the graphene layer can be transferred to another surface. This method requires a very high accuracy otherwise the thick layers of graphite will be producing (Zavabeti et al. 2017). None of the mention synthesis methods, such as chemical synthesis, lithography, and cutting graphene sheets into narrow strips cannot producing these tapes in large-scale. On the other hand, the CVD method is only able to creating metal- grapheme strips. While to use graphene nano-strips to produce the electronic devices such as field-effect transistors or sensors, a method that allows producing graphen strips in large scale and in the form of semiconductors was needed. Untwisting and cutting carbon nanotubes in the longitudinal direction not only can produce high-quality graphene nano-strips on a large scale, by patterning the process of cutting nanotubes, it can also create nano-strips with different electronic properties (Agel, 2012). In order to utilizing the high conductivity of this material along with its potential to provide a thin film, usually chemical reduction of graphite oxide used. (Kumar, 2017).
In most cases, ultrasonic vibration is used to remove the gap between the plates and produce a fully distributed single-layer graphene oxide which crushes the plates. The resulting plates are so small (from hundreds of nm to several microns) that are not suitable to be used in electrical devices. To reduce this problem, other methods such as magnetic stirring can be used to separate the plates from each other (Muthoosamy, 2017).
In analytical methods, according to Euler-Bernoulli or Tymoshenko beam theory and classical and Mindlin plate theory, and the forces generated by interlayer van der waals bonds, each graphene layer is usually modeled as compression term proportional to the relative displacement of adjacent layers. The definition of this model can only model the compressive and tensile effects of van der waals bonds. While the experiments showed that the graphene plates have the ability to slid on each other and the van der Waals forces exhibit a resistive effect to interlayer slip which is shown as shear strength. Therefore, in this type of analysis, the interlayer shear effect of multi-layered graphene resulted from the interlayer van der waals forces is ignored. Studies have shown that in multi-layer grapheme, the interlayer shear modulus is about 0.25 GPa. Although the interlayer shear modulus is lower than in-plane elastic modulus, the same shear modulus can influence the static and dynamic behavior of multi-layer graphene. Interlayer interaction and relative displacement of multilayered graphene have not yet been thoroughly investigated (Chen, 2017).
A particular type of layered graphite compounds have been used as the precursor in the production of colloidal suspensions from single-layer graphene sheets. Ideally, the use of graphite, layered graphite compounds and expandable graphite create the possibility of producing a suspension of high quality graphene sheets (almost pure graphene). Colloidal suspensions from graphene sheets in organic solvents such as NMP were obtained using ultrasonic radiation of graphite powder. Although the concentration of suspension (1-12%) is not high, the use of this method leads to the production of high quality graphene. Using a model that contains graphene surface energy and coherence energy of the solvent, good solvents are classified to form a homogeneous colloidal suspension (Kim, 2018).
Sa’d Abadi (2018) investigated the production and characterization of reduced graphene oxide nanocomposite- zinc oxide nanocomposite and its medical applications. The results showed that the existence of zinc in the RGO-ZnO nanocomposite was confirmed by Zn peaks in EDS data. Finally, the toxic effect of graphene oxide (anti-cancer) and three samples with different percentages of nano-composite on the vitality of the N2A cells were investigated. Furthermore, the higher concentration has more toxic effect on these cells. However, in the case of RGO-ZnO nanocomposite with GO / Zn (Ac) = 0/72, this effect was observed at lower concentrations.
Rezaei (2018) studied the synthesis, detection and performance of drug release in graphene oxide- protein nano-composites. In this project, the drug delivery system based on graphene oxide and human serum albumin was designed to increase the time of Oxaliplatin delivery. Protein synthesis was accomplished by dissolution method and graphene oxide using Hummer’s method. Furthermore, the results of the study showed that for both structures, the drug release mechanism is of penetration type. Using cyclic voltammetric test, release mechanism was evaluated and the results were in agreement with the results of absorption spectroscopy.
Zhang et al. (2017) investigated the direct exfoliation of graphite in graphene aqueous solution using a new surfactant derived from motor oil. The results showed that, graphene dispersion with high constancy had higher concentration (0.477 mg / mL) from other surfactants with an optimum SUEO dose of 0.5 g / L at 4-hour extraction time. The SUEO function can be attributed to its specific molecular structure, which its hydrophobic components consists cycloalkanes / aromatics with different molecular weights and / or the side-chain R with different lengths. This study presents a new classification of dispersion factors for graphene, which helps the process of exfoliating in water with high-concentration and stabilization of graphene plates against the re-accumulation.
Monajjemi (2017) in a research investigated the liquid phase exfoliating (LPE) of graphite for graphene. In this study, they showed that sulfone groups in surfactants are most effective for any dispersion in the LPE process. In addition, ionic surfactants in compare with non-ionic surfactants or zevitune shapes have excellent efficiency. Generally, these sequences are shown for each dispersion in the LPE process: cation> anion> zwitterion> nonionic. In this research, with the choice of graphite Nano layer with suitable length and dimensions able to interact with anionic surfactant molecules which according to the results of the DFT calculations performed in the previous chapter, had positive and proper results. The results of Gaussian calculations and energy levels and bonding intervals indicate the success of flakiness in the graphite layers by anionic surfactants, which in this chapter, is illustrated the results of interaction between graphite layers together and with the intended anionic surfactant by quantum mechanical calculations of DFT and proposing suggestions in this matter.
MATERIALS AND METHODS
Gaussian Software
Gaussian software is able to predict the properties of many molecules and reactions. Theory is achieved with basis sets. The program is able to predict various properties of molecules and reactions, such as drawing optimum structure of molecules, binding energies and reaction, reaction mechanism, energy of basis state structures and transition states, studying the visible spectra-ultraviolet, Raman, IR and NMR, molecular orbitals, computations of atomic charges and multipolar momentum, electron affinity and ionization potential, polarization capability, coating constants, magnetic permeability, electrostatic potentials and electron density, vibration frequency and thermochemistry properties. By using the Gaussian software (Gaussian09w software) along with empirical results or without it, can simulate the state of molecule its reactions and mechanism. Gaussian Software input file is a simple text file. The simplicity of this file means that the file should be free from any written format such as font type and size, paragraph, color etc. Due to this reason for providing input files, a simple text editor software such as Vi or Gedit must be used in the Unix environment or Notepad environment in Windows. The Gaussian software does not have a graphical interface, so the input file must be made with other software such as Gaussview or HyperChem. For doing computations, the computation method and set basis must be specified.
Molecular Dynamic
In order to do the molecular dynamics, (least) force that each atom enters into other atoms is calculated. This is the total gradient of the system’s energy according to the coordinates of the atom. A Bayesian method was used for dynamic modeling, which on average used dynamic parameters instead of estimating them. Inspired by the fact that the nonlinear regression averaging resulted in a Gaussian process (GP) model, shown that integration on the parameters can also be done in the closed form of nonlinear dynamic systems. The Gaussian Process of Dynamic Model (GPDM), was completely defined by the set of data’s compact representation and learned by both , the observed dynamic and the mapping from GP regression ) (Figure 1 as a natural consequence of the general regression, GPDM eliminates the need to select several parameters associated with the approximators function, while it retains nonlinear dynamic control and observation.
 Figure 1 Time series graphic models (a) Non-linear hidden variable model for time series. (Hyperparameters) alpha and beta are not shown (b) GPDM model. Since the mapping parameters of A and B are marginalized, all the latent ordinates X = [x1, x2, ... xn] are jointly correlated, as all of them are dependent to Y = [y1, y2, ... yn].
Figure 1 Time series graphic models (a) Non-linear hidden variable model for time series. (Hyperparameters) alpha and beta are not shown (b) GPDM model. Since the mapping parameters of A and B are marginalized, all the latent ordinates X = [x1, x2, ... xn] are jointly correlated, as all of them are dependent to Y = [y1, y2, ... yn].
Two main issues are the use of switching linear models and nonlinear transition functions such as Radial Basis Functions. Both of these approaches needed enough educational data that could include parameters of the switching system or basis functions. It was difficult to determine the proper number of basic functions. In Kernel or dynamic modeling, linear dynamics was used to model the nonlinear systems but a density function was not generated on the data.
RESULT
The computational DFT method was one of the most comprehensive computational methods, according to the information it provided. Due to these capabilities, the DFT computational method was selected for evaluation. Therefore, all the desired structures were optimized by using DFT density theory method at the Cam-B3LYP / Lanl2dz level, which a brief description of its implementation steps is presented in below.
Simulation Steps
Initially, the chemical structure of the graphite plates and set of graphite layers were designed in the absence and presence of surfactants in Gaussian VIO software, which in Figure. 2 schema of this step presented.
 Figure 2. is the schema of designing graphene and surfactant structure in the Gaussian software on the right side figure and designed structure of graphene plate by the same software on the left side figure.
Figure 2. is the schema of designing graphene and surfactant structure in the Gaussian software on the right side figure and designed structure of graphene plate by the same software on the left side figure.
In the next step, in the computing section they were converted into Gaussian software input files (glf postfix) which in the Figure 4 schema of this simulation step were presented.
First, the graphite layer and some graphite layers were plotted ,and the related calculations were performed ,and then the surfactant was entered into the system of two and more layers, and energy calculations and repetitive layered distances and the results of the pre and post input of the surfactant were calculated. To conduct the NBO command in Gaussian software, # B3LY / 6-311 ++ G * POP = NBO command was used and then the program was run. The energy which forms the Graphene structure designed was computed by Gaussian and the data available in table 1 were obtained.
Table 1. Energy which forms Graphene structure designed by Gaussian.

| Graphene | Energy Form (HF12) | Dipole | Symmetric |
| C24H12 | -916.804.377 (Hartree Fock) | -0,0000044 | C01 |
Spectrum IR structure of Graphene designed by Gaussian in the Figure 3 has been presented.
 Figure 3. Spectrum InfraRed of Graphene sheet
Figure 3. Spectrum InfraRed of Graphene sheet
The mass of electrons cloud of Van der Waals bond of Graphene sheet considered in figure 4.
 Figure 4. Electronic structure of Van der Waals bond of Graphene sheet considered.
Figure 4. Electronic structure of Van der Waals bond of Graphene sheet considered.
In Table 2. orbital energy level HOMO, LUMO, Graphene sheet has been given according to volt electron.
Table 2 Orbital energy HOMO, LUMO, Graphene sheet

| MOLECULER ORBITAL | HOMO | LUMO |
| Energy (ev) | -0,20740 | -0,0530 |
The shape of the HOMO orbital of two Graphene layers has been shown in Figure. 5, because of the Pi Bond resonance in the natural molecular orbital Graphene structure, this molecule is very vast and contiguous.
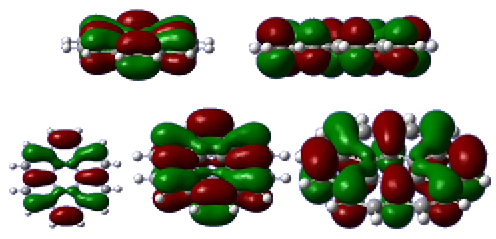 Figure 5. Orbitals HOMO , Graphite one layer
Figure 5. Orbitals HOMO , Graphite one layer
In Figure 6, orbital LUMO, single Graphene sheet has been given. Due to the continuous structure and resonance existent, the large unbounded molecular orbital is observed in this structure.
 Figure 6. Orbitals LUMO, single Graphite layer
Figure 6. Orbitals LUMO, single Graphite layer
In table 3, energy which forms dipole, Graphite, symmetrical groups obtained from Gaussian DFT computations has been shown.
Table 3. Energy which forms Graphite 2 layers based on Hartree Fock

| Structure | Energy Form (HF) | Dipole | Symmetric |
| C48H24 | -1833,425826 (Hartree Fock) | -0,0003502 | C01 |
NBO Reviews
Table 4. Rate of energy of orbitals HUMO and LUMO, Graphite 2 layers
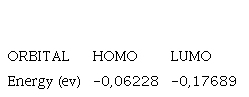
| ORBITAL | HOMO | LUMO |
| Energy (ev) | -0,06228 | -0,17689 |
Review of bonding intervals of Graphite 2 layers
Table 5. Review of bonding and interlayer arrangements of Graphite 2 layers

| Type of Bond | Bond Arrangement (Angstrom) | Descriptions |
| C-H | 1,10076 | |
| Belonging to One Loop | 1,36896 | C-C First Type |
| 1,40867 | C-C Second Type |
| 1,42912 | C-C Third Type |
| in the Absence of Surfactant | 3,36978 | Arrangement of 2 layers |
In figure 7, the mechanism of arrangement using anionic surfactants has been given. (Trainer et al., 2017).
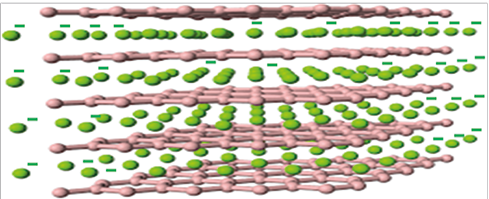 Figure 7. Graphite sheets and their ductility by anionic surfactant molecules through electron repulsion.
Figure 7. Graphite sheets and their ductility by anionic surfactant molecules through electron repulsion.
LUMO Orbital review:
The empty orbital of this compound is also important because they are able to interact with the electron mass. Therefore, the HOMO and LUMO energy levels of the surfactant molecule play a very important role in generating the interaction between this molecule and the graphite layers (Figure 8). This interaction helps to emplace this compound between the layers and will cause the formation energy and stability of the system to be less negative (Figure 8).
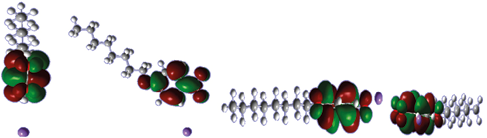 Figure 8. orbital LUMO Surfactant Sodium -4-Aktylvksy Benzoate from different angles.
Figure 8. orbital LUMO Surfactant Sodium -4-Aktylvksy Benzoate from different angles.
After designing the structure and its implementation as the Gaussian input file, the structure and input of the optimization command, the structure of output of the Gaussian software, the structure of optimization of Graphene sheets in presence of the desired surfactant were presented. That by measuring the arrangements of the sheets and the bonds, it can be found out that the repulsion between Serbenzoate and Carboxylic group with Graphite sheets is more than the linear sequence (Alkene) of this surfactant that way in the part which arrangement sequence of two graphite sheets is present less than the part which Benzoate is present. The optimal structure of output of the software has been shown in the following figure.
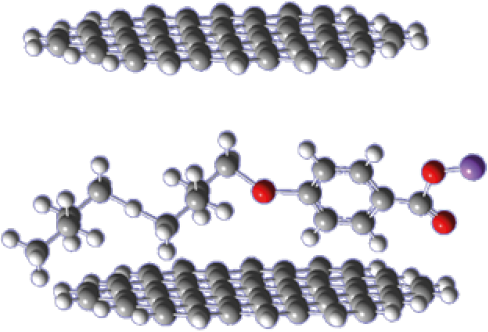 Figure 9. Arrangement of anionic surfactant between two Graphene layers
Figure 9. Arrangement of anionic surfactant between two Graphene layers
Due to the arrangement of anionic surfactant between two Graphite layers Figure 9, input of the surfactant through the interaction of the pi electronic cloud and the massive bonds network existed in the graphite sheets occur. Also, the interaction between the load of the carboxylic acid surfactant group and the graphite pi orbitals occurs, and following this interaction, the alkene sequence also enters the gap between the two layers of Graphene and makes sheets in the structure separated and distributed monotonously. Also, the C-O-C Ether group available in the structure of this surfactant prevents the Graphite sheets are re-bonded after initial separation. If surfactant sequence is longer, the desire and ability for separating the sheets will be increased by surfactant.
The energy which forms surfactant and two layers of Graphite
The formation energy of three-layer graphite in the presence of sodium 4- oxylox benzoate is presented in the following table.
Table 6. The formation of three layers of graphite in the presence of sodium 4- Aktylvksy Benzoate based on the Harti Fouc unit

| Structure | Energy Form (HF) | Dipole | Symmetric Group |
| Two Layers and Surfactant | -2492,0096 (Hartree Fock) | -0,4729374 | C01 |
In Figure 10, the arrangement of sodium 4-anethoxyacetiloxy benzoate anionic surfactant in graphite layers is presented. The gap between the layers in the presence of surfactant has increased significantly, indicating the success of the anionic surfactants in the delamination of the graphite sheets. The electrostatic repulsion between the negative charge of the anionic surfactants and the electron mass of the stacked graphite sheet is a useful and effective factor in the delamination of graphite sheets and the distance between the sheets.
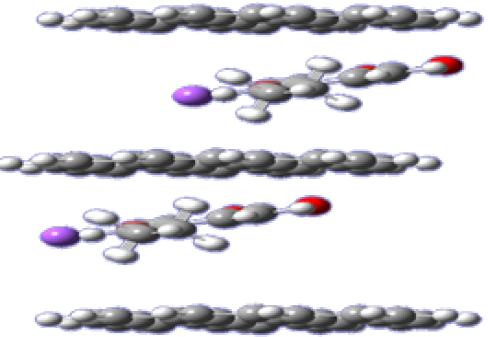 Figure 10. The arrangement of anionic surfactant between the graphite layers
Figure 10. The arrangement of anionic surfactant between the graphite layers
Molecular gap
Interlayer gaps and bond lengths related to the interaction between surfactants and graphene layers are shown in table 7. The gap between graphite layers have significantly increased in the presence of this supractane. Of course, intramolecular bonds have grown insignificantly.
Table 7. Interlayer gaps and bond lengths related to the interaction between surfactants and graphene layers
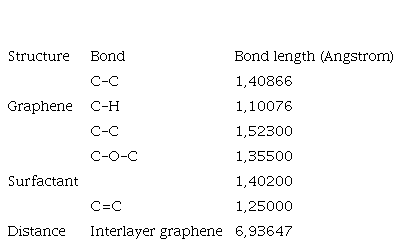
| Structure | Bond | Bond length (Angstrom) |
| Graphene | C-C | 1,40866 |
| C-H | 1,10076 |
| C-C | 1,52300 |
| Surfactant | C-O-C | 1,35500 |
| 1,40200 |
| C=C | 1,25000 |
| Distance | Interlayer graphene | 6,93647 |
Electrostatic and van der waals interaction
The electrostatic and van der waals interaction between graphite sheets, sodium 4-oxyloxybenzoate surfactant and van der waals electron cloud is shown in figure 11. In the red areas which are related to the repellent regions, the gap between the two layers are far more than the white areas (the area of the alken surfactant sequence).
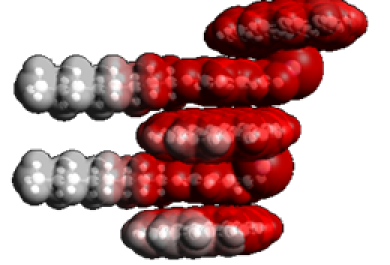 Figure 11. Electrostatic interaction of graphite sheets and sodium surfactant 4- actyloxybenzoate
Figure 11. Electrostatic interaction of graphite sheets and sodium surfactant 4- actyloxybenzoate
Graphite layers and Sodium Laurate Surfactant
In this research, the arrangement of sodium laurate between graphite layers, interlayer gap, NBO orbitals, structural energy and geometric structure is investigated.
Studying NBO
At the beginning of the study, the single layer graphene was evaluated and the energy changes and the amount of interaction, repulsion and HOMO and LUMO orbitals were evaluated, which will be described in the following sections, respectively Table 8.
Table 8. HOMO and LUMO energy levels of three layers of graphite in the presence of laurate anion
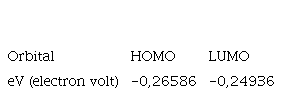
| Orbital | HOMO | LUMO |
| eV (electron volt) | -0,26586 | -0,24936 |
HOMO orbital
The shape of a double layer graphite HOMO orbital in the presence of sodium laurate surfactant is presented in figure 12.
 Figure 12. Double layer graphite HOMO orbital in the presence of sodium laurate surfactant
Figure 12. Double layer graphite HOMO orbital in the presence of sodium laurate surfactant
LUMO orbital
The shape of a double layer graphite LUMO orbital in the presence of sodium laurate surfactant is presented in figure 13.
 Figure 13. Double layer graphite LUMO orbital in the presence of sodium laurate surfactant
Figure 13. Double layer graphite LUMO orbital in the presence of sodium laurate surfactant
Electrostatic interaction
In Figure 14, the electrostatic interaction of graphite plates and sodium laurates surfactant is presented. In red areas, negative charge accumulation is more than white and blue areas and on the other hand, the negative charge accumulation of graphene sheet and anionic surfactant causes electrostatic repulsion and, consequently, increases the gap between graphite layers.
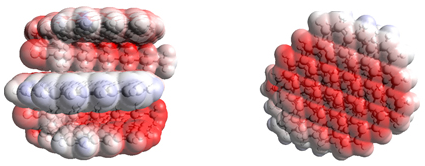 Figure 14. Electrostatic interaction of graphite plates and parallel sodium laurate surfactant (left) and perpendicular to graphite plates (right)
Figure 14. Electrostatic interaction of graphite plates and parallel sodium laurate surfactant (left) and perpendicular to graphite plates (right)
Investigating Graphite layers and Laurate Sodium Surfactant
The emplacement of sodium Laurate content between graphite layers and interlayer distance and NBO orbitals and structural energy and geometric structure was investigated which is presented as follows.
NBO reviews
At the beginning of the investigation, the graphite single layer was evaluated and the energy changes and the amount of interaction and repulsion and HOMO and LUMO orbitals were evaluated, which will be described respectively (Table 9).
Table 9. Investigating the flakiness of graphene sheets in n the presence of surfactants

| Orbital | HOMO | LUMO |
| amount of energy (electron-volt) ev | -0.28896 | -0.28896 |
The interaction of the three layers is similar to the two electrical layers and due to the spaces between the graphite layers, the interaction of the layers with each other will be significantly reduced and eventually, we will achieve the purpose of the distribution and separation of the layers in the desired solvent.
Link distances related to the graphene molecule before and after interactions with surfactant is presented in table 10. Intramolecular link distances have been increased slightly due to the new interactions between surfactant and graphite but the distance between two layers has considerably increased which indicates the success of this surfactant in the separation of graphite layers.
Table 10. Link distances related to the graphene molecule before and after interactions with sodium laurates surfactant.

| Link | Molecular distance (Ångström) |
| Graphite without surfactant | Graphite without surfactant |
| C-C | 1,40867 | 1,42913 |
| C-C | 1,42913 | 1,4317 |
| C-C | 1,42912 | 1,4315 |
| H-C | 1,10076 | 1,11074 |
| H-C | 1,10078 | 1,11069 |
| Distance of two layers | 2,37570 | 5,8456 |
Sodium surfactant has better ability to create a distance between graphite plates and sodium laurate, which one is due to the presence of benzene ring, either groups and carboxylic simultaneously in this molecule. These groups are rich in electron and negative charge and contribute to the creation of electrostatic repulsion and increasing the distance between the graphite plates. Sequence length also helps to keep the distance in other areas where there is less negative charge. The length of the Alkene sequence helps to maintain distance and like a space obstacle prevent from joining to graphite layers.
DISCUSSION
Regading to the structure and energies obtained from DFT calculations by Gaussian software the following results were obtained for two surfactant structures with graphite plates. The optimal structure showed that the presence of benzene, ether and carboxylic groups lead to facilitate the entry of surfactants into the plates and is a factor for starting the separation of grapheme sheets. The longer the surfactant sequence is the desire and ability to separate the plates by surfactant increase. The presence of an aromatic group in surfactant causes pi-pi interaction among the surfactants, and makes the placement of the plates in parallel with the plate of the benzene ring and also creates distance in flat graphene sheets. In fact, the benzene end acts as a contributing factor to the success of sodium surfactant 4-(acetyloxy) benzoate to enhance the ability of this surfactant for separating grapheme sheets. Sodium surfactant has a better ability to create a distance between graphite plates than sodium laurate, due to the presence of benzene ring and the ether and carboxylic group simultaneously in this molecule. These groups are rich in electrons and negative charge and contribute to the creation of an electrostatic repulsion and increasing the distance between the graphite layers. The sequence length also helps to keep this distance in other areas where there is less negative charge. The length of the Alkene sequence helps to maintain the distance and in fact, like a space obstacle prevent from joining of graphite layers. The linear and elongated structure of surfactant leads to maintain the distance among various areas of the two graphene sheets. Extensive physical volume of surfactant creates distance and maintains the distance between two graphene layers. Therefore, the important parameter in the selection of the surfactant is its chemical structure and it is attempted to use extensive structures with elongated Alkene sequences. In addition to the chemical structure, surfactant is also effective. Structures containing the functional groups with negative charge including acids, esters and ketones can improve the properties of surfactant for flakiness of graphite. Choosing the appropriate base set is very effective in Gaussian calculations and the proper and correct selection of it will result in accurate results consistent with the experimental results. In this study, the base set B3LYP / 6-311 ++ G (D.P.) and the model were selected, and the results from the base set have shown a better match with the experimental results. By comparing the results of this study regarding to surfactant, it can be found out that the distance created between graphene sheets is different for two surfactants; also the difference of surfactants of polarity leads to create final polarity of surfactant system and grapheme; thus, the polarity rate of the solvent will be different.
SUGGESTIONS
According to the results of this study, the following points are suggested:
1. It is suggested to investigate the interaction of graphite with cationic surfactants.
2. It is suggested to investigate the interaction of graphite with non-ionic surfactants.
3. It is suggested to evaluate the investigation of the interaction of graphite with short cyclo-linear polymers.
4. It is suggested to evaluate the investigation of interaction of graphite with surfactants by Gaussian with 2 or 3 different methods and compare them with each other.
5. It is suggested to investigate the interaction of boron nitride plates with anionic surfactants and compare them with the results of graphite plates.
It is suggested to investigate the interaction of silicate plates with anionic surfactants.
References
Saadabadi, M., Khorsand Zak, A., Doroodi, M., Hamidi Yadegar, M., 2018. Production and characterization of reduced graphene oxide nanocomposite, zinc oxide and considering its capability for medical applications, Research of many-particle system.
Aqel, A., El-Nour, K. M. A., Ammar, R. A., & Al-Warthan, A. 2012. Carbon nanotubes, science and technology part (I) structure, synthesis and characterisation. Arabian Journal of Chemistry, 5(1), 1-23.
Rezaei, F., Saeedifar, M., Javaheri, M., 2018. Synthesis, identification and performance of drug release in graphene-protein oxide nanocomposites, Master’s thesis, Nanoscience Research Institute, Materials and Energy Research Center.
Adán-Más, A., Wei, D., 2013. “Photoelectrochemical Properties of Graphene and Its Derivatives”, Nanomaterials, Review, 3: 325-356,
Bonaccorso, F., Colombo, L., Yu, G., Stoller, M., Tozzini, V., Ferrari, A. C., ... & Pellegrini, V. 2015. Graphene, related two-dimensional crystals, and hybrid systems for energy conversion and storage. Science, 347(6217), 1246501.
Chang, H. S., Agrawal, A., Ganesh, A., Desai, A., Mathur, V., Hough, A., & McCallum, A. 2018. Efficient Graph-based Word Sense Induction by Distributional Inclusion Vector Embeddings. arXiv preprint arXiv:1804.03257.Chen, P., Li, N., Chen, X., Ong, W. J., & Zhao, X. 2017. The rising star of 2D black phosphorus beyond graphene: Synthesis, properties and electronic applications. 2D Materials, 5(1), 014002.
Kim, D. W., Heo, U. S., Kim, K. S., & Park, D. W. 2018. One-step synthesis of TiC/multilayer graphene composite by thermal plasma. Current Applied Physics, 18(5), 551-558.
Kumar, M., Swamy, B. K., Asif, M. M., & Viswanath, C. C. 2017. Preparation of alanine and tyrosine functionalized graphene oxide nanoflakes and their modified carbon paste electrodes for the determination of dopamine. Applied Surface Science, 399, 411-419.
Muthoosamy, K., & Manickam, S. 2017. State of the art and recent advances in the ultrasound-assisted synthesis, exfoliation and functionalization of graphene derivatives. Ultrasonics sonochemistry, 39, 478-493.Zavabeti, A., Ou, J. Z., Carey, B. J., Syed, N., Orrell-
Trigg, R., Mayes, E. L., ... & Kalantar-zadeh, K. 2017. A liquid metal reaction environment for the room-temperature synthesis of atomically thin metal oxides. Science, 358(6361), 332-335.
Zhan, Y., Zhang, J., Wan, X., Long, Z., He, S., & He, Y. 2017. Epoxy composites coating with Fe3O4 decorated graphene oxide: Modified bio-inspired surface chemistry, synergistic effect and improved anti-corrosion performance. Applied Surface Science, 436, 756-767.
Zou, L., Wang, L., Wu, Y., Ma, C., Yu, S., & Liu, X. 2018. Trends Analysis of Graphene Research and Development. Journal of Data and Information Science, 3(1), 82-100.
Trainer, D. J., Putilov, A. V., Wang, B., Lane, C., Saari, T., Chang, T. R., ... & Bansil, A. 2017. Moiré superlattices and 2D electronic properties of graphite/MoS2 heterostructures. Journal of Physics and Chemistry of Solids.
Monajjemi, M. (2017). Liquid-phase exfoliation (LPE) of graphite towards graphene: An ab initio study. Journal of Molecular Liquids, 230, 461-472.
Zhang, K., Zhang, X., Li, H., Xing, X., Jin, L. E., Cao, Q., & Li, P. (2018). Direct exfoliation of graphite into graphene in aqueous solution using a novel surfactant obtained from used engine oil. Journal of materials science, 53(4), 2484-2496.
Sa’ad Abadi,M., Khorsand Zak,A., Doroodi,M., Hamidi Yadgar,M. (2017). Construction and characterization of reduced-graphene oxide nanocomposite-zinc oxide and its ability to examine for medical applications. Magnetic Resonance Systems Research.
Chen, P., Li, N., Chen, X., Ong, W. J., & Zhao, X. (2017). The rising star of 2D black phosphorus beyond graphene: Synthesis, properties and electronic applications. 2D Materials, 5(1), 014002.
Zavabeti, Ali, Jian Zhen Ou, Benjamin J. Carey, Nitu Syed, Rebecca Orrell-Trigg, Edwin LH Mayes, Chenglong Xu et al. “A liquid metal reaction environment for the room-temperature synthesis of atomically thin metal oxides.” Science 358, no. 6361 (2017): 332-335.
Huang, M., Cheng, Y., Cheng, Z., Chen, H., Mao, X., & Gong, R. (2018). Based on graphene tunable dual-band terahertz metamaterial absorber with wide-angle. Optics Communications, 415, 194-201.
Wallace, P. R. 1947. The band theory of graphite. Physical Review, 71(9), 622.
Geim, A. K., & Novoselov, K. S. 2010. The rise of graphene. In Nanoscience and Technology: A Collection of Reviews from Nature Journals (pp. 11-19).
Novoselov, K. S., Geim, A. K., Morozov, S. V., Dubonos, S. V., Zhang, Y., & Jiang, D. 2004. Room-temperature electric field effect and carrier-type inversion in graphene films. arXiv preprint cond-mat/0410631.
Boehm, H. P., Clauss, A., Fischer, G. O., & Hofmann, U. 1962. Dünnste kohlenstoff-folien. Zeitschrift Für Naturforschung B, 17(3), 150-153.